A&A 429, 569-580 (2005)
DOI: 10.1051/0004-6361:20041668
Nonlinear particle acceleration at reverse shocks in supernova remnants
D. C. Ellison 1 -
A. Decourchelle2 -
J. Ballet2
1 - Department of Physics, North Carolina State
University, Box 8202, Raleigh NC 27695, USA
2 -
Service d'Astrophysique, DSM/DAPNIA, CEA Saclay,
91191 Gif-sur-Yvette, France
Received 15 July 2004 / Accepted 7 September 2004
Abstract
Without amplification, magnetic fields in expanding ejecta
of young supernova remnants (SNRs) will be orders of magnitude below
those required to shock accelerate thermal electrons, or ions, to
relativistic energies or to produce radio synchrotron emission at the reverse
shock. The reported observations of such emission give support to the
idea that diffusive shock acceleration (DSA) can amplify magnetic
fields by large factors. Furthermore, the uncertain character of the
amplification process leaves open the possibility that ejecta fields,
while large enough to support radio emission and DSA, may be much
lower than typical interstellar medium values. We show that DSA in
such low reverse shock fields is extremely nonlinear and efficient in
the production of cosmic-ray (CR) ions, although CRs greatly in excess
of mc2 are not produced.
These nonlinear effects, which occur at the forward shock as well, are
manifested most importantly in shock compression ratios  4 and
cause the interaction region between the forward and reverse shocks to
become narrower, denser, and cooler than would be the case if
efficient cosmic-ray production did not occur.
The changes in the SNR structure and
evolution should be clearly observable, if present, and they convey
important information on the nature of DSA and magnetic field
amplification with broad astrophysical implications.
4 and
cause the interaction region between the forward and reverse shocks to
become narrower, denser, and cooler than would be the case if
efficient cosmic-ray production did not occur.
The changes in the SNR structure and
evolution should be clearly observable, if present, and they convey
important information on the nature of DSA and magnetic field
amplification with broad astrophysical implications.
Key words: ISM: cosmic rays - acceleration of particles - shock waves
- ISM: supernova remnants - X-rays: ISM
It is clear in many supernova remnants (SNRs) that the forward, blast
wave shock, interacting with the interstellar medium (ISM) magnetic
field, produces radio (and sometimes X-ray) synchrotron emission.
Presumably this is accomplished when the forward shock accelerates
thermal and pre-existing cosmic-ray (CR) electrons by diffusive shock
acceleration (DSA) (also called the first-order Fermi mechanism). The
reverse shock, however, will not produce relativistic electrons from
thermal ones if the only magnetic field that is present is the ambient
field from the progenitor star. Any progenitor field will be vastly
diluted by expansion and flux freezing and, for expected white dwarf
or massive star magnetic field values, after <100 yr, will fall
below levels necessary to support particle acceleration to radio
emitting energies.
For example, if the surface field of a white dwarf of radius
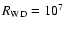 m is
m is
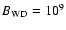 G, the diluted magnetic field after
G, the diluted magnetic field after  100 yr at the reverse shock, which is typically at a radius
100 yr at the reverse shock, which is typically at a radius
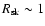 pc from the explosion site, is
pc from the explosion site, is
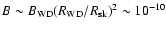 G. For 10-10 G, the diffusive acceleration time to
10 GeV is
G. For 10-10 G, the diffusive acceleration time to
10 GeV is 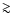 100 yr and the upstream diffusion length at a
104 km s-1 shock of a 10 GeV electron is >1 pc, making the
production of radio emitting electrons unlikely. Similar results are
expected for massive progenitors. Furthermore, with such low fields,
even if relativistic electrons are present in large numbers from compressed
pre-existing cosmic rays or whatever, the radio emissivity may be too
low to be observable.
100 yr and the upstream diffusion length at a
104 km s-1 shock of a 10 GeV electron is >1 pc, making the
production of radio emitting electrons unlikely. Similar results are
expected for massive progenitors. Furthermore, with such low fields,
even if relativistic electrons are present in large numbers from compressed
pre-existing cosmic rays or whatever, the radio emissivity may be too
low to be observable.
The expanded ejecta bubble may be one of the lowest magnetic field
regions in existence and if reverse shocks in some SNRs are
accelerating electrons by DSA to radio emitting energies or higher
(as has been suggested by recent radio and X-ray observations,
e.g., Rho et al. 2002; DeLaney et al. 2002; Gotthelf et al. 2001), there
are important consequences for:
- magnetic field generation and amplification in strong
shocks;
- the intrinsic efficiency of DSA and cosmic-ray
production, including heavy elements; and
- the structure and evolution of the X-ray emitting
interaction region between the forward (FS) and reverse shocks (RS).
At the forward shock in some SNRs (see, in particular, Cas A; Vink & Laming 2003), there is convincing evidence for magnetic fields far
greater than normal ISM values. It has been suggested that the
diffusive shock acceleration process can amplify ambient fields
(e.g., Lucek & Bell 2000; Bell & Lucek 2001) to the observed
levels, and evidence for this is mounting in specific SNRs,
(e.g., Berezhko et al. 2003a,b; Berezhko & Völk 2004). If such
amplification occurs generally, SNRs will be capable of accelerating
cosmic rays to above 1017 eV (e.g., Ptuskin & Zirakashvili 2003; Drury et al. 2003),
possibly solving the decades old problem of smoothly generating CRs to
the spectral knee near 1015 eV and beyond. Since DSA is expected
to occur in diverse environments on all astrophysical scales, the
confirmation and characterization of magnetic field amplification is
of extreme importance.
In this paper, we first discuss in Sect. 2 the general effects of a low
magnetic field on the efficiency of DSA. We show that nonlinear
effects, most noticeable in producing compression ratios 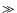 4, can
be extremely large for a range of magnetic field below that of the
average ISM (i.e., for
4, can
be extremely large for a range of magnetic field below that of the
average ISM (i.e., for
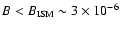 G). We then discuss
in Sect. 3 the relevance of low fields and strong nonlinear effects in
DSA at reverse shocks in SNRs. To our knowledge, this is the first
attempt to consider such effects in an evolutionary model of SNRs. A
number of aspects concerning the acceleration process, the nature of
the magnetic field, and the physical conditions in the unshocked
ejecta material (e.g., temperature, ionization fraction, etc.) are not
well-known. Because of these uncertainties, we show a number of
examples where important parameters are varied over fairly wide
ranges. We emphasize, however, that the effects of efficient DSA on
the structure and evolution of SNRs may be large and current
instruments should be sensitive enough to importantly constrain many
of these poorly known parameters.
G). We then discuss
in Sect. 3 the relevance of low fields and strong nonlinear effects in
DSA at reverse shocks in SNRs. To our knowledge, this is the first
attempt to consider such effects in an evolutionary model of SNRs. A
number of aspects concerning the acceleration process, the nature of
the magnetic field, and the physical conditions in the unshocked
ejecta material (e.g., temperature, ionization fraction, etc.) are not
well-known. Because of these uncertainties, we show a number of
examples where important parameters are varied over fairly wide
ranges. We emphasize, however, that the effects of efficient DSA on
the structure and evolution of SNRs may be large and current
instruments should be sensitive enough to importantly constrain many
of these poorly known parameters.
Nonlinear DSA is a complex process that is difficult to describe
completely. In order to allow the coupling of the particle
acceleration to a hydrodynamic model of SNR evolution, we use an
approximate, algebraic model of DSA developed by Berezhko & Ellison (1999) and
Ellison et al. (2000).
While more complete models exist (e.g., Berezhko et al. 1996), they tend to be
more computationally intensive and not as easy to include in a
hydrodynamical simulation. Despite the simplifications made in our
acceleration model, we believe it adequately describes the essential
physics when the maximum momentum of accelerated particles
 .
It is less accurate when
.
It is less accurate when
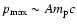 as we
describe more fully below. Here, A is the mass number,
as we
describe more fully below. Here, A is the mass number, 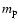 is the
proton mass, and c is the speed of light.
is the
proton mass, and c is the speed of light.
In a complicated, nonlinear fashion, the acceleration efficiency (i.e.,
the fraction of total ram kinetic energy going into superthermal
particles)![[*]](/icons/foot_motif.gif) depends on the sonic and Alfvén Mach numbers
(
depends on the sonic and Alfvén Mach numbers
(
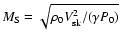 and
and
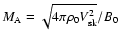 respectively), on the particle injection and on the
maximum particle momentum achieved
respectively), on the particle injection and on the
maximum particle momentum achieved
 .
Here,
.
Here, 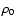 is the unshocked mass density,
P0 is the unshocked pressure, B0 is the unshocked magnetic
field,
is the unshocked mass density,
P0 is the unshocked pressure, B0 is the unshocked magnetic
field,
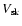 is the shock speed, and
is the shock speed, and 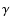 is the ratio of
specific heats.
The particle injection is modeled by two parameters: the
injection efficiency
is the ratio of
specific heats.
The particle injection is modeled by two parameters: the
injection efficiency
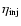 ,
i.e., the fraction of total particles
which end up with superthermal energies, and
,
i.e., the fraction of total particles
which end up with superthermal energies, and
 ,
which determines the value of the injection momentum (
,
which determines the value of the injection momentum (
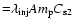 ,
where
,
where
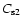 is the sound speed in the downstream region). The parameter
is the sound speed in the downstream region). The parameter
 ,
by definition >1, is arbitrarily taken to
be 4 in our calculations (see Berezhko & Ellison 1999, for a full discussion).
,
by definition >1, is arbitrarily taken to
be 4 in our calculations (see Berezhko & Ellison 1999, for a full discussion).
For simplicity, in all our examples we assume a single ion species,
generally protons, but in Sect. 4.4, oxygen, with the electron temperature
equal to the ion temperature = 104 K. We ignore any wave damping
from neutral material
(see Sect. 5.2.5 below for a discussion).
The maximum momentum protons achieve is
determined by setting the acceleration time equal to the SNR age
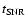 ,
or by setting the diffusion length of the highest energy
particles equal to some fraction,
,
or by setting the diffusion length of the highest energy
particles equal to some fraction,
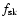 ,
of the shock radius
,
of the shock radius
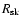 ,
whichever gives the lowest
,
whichever gives the lowest
 (see, for
example, Baring et al. 1999).
(see, for
example, Baring et al. 1999).
We assume strong turbulence (i.e., Bohm diffusion) so that the
scattering mean free path is on the order of the gyroradius, i.e.,
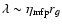 ,
with
,
with
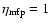 .
The magnetic field
strength is thus an important factor in determining
.
The magnetic field
strength is thus an important factor in determining
 .
If the
turbulence is, in fact, weaker than Bohm diffusion (
.
If the
turbulence is, in fact, weaker than Bohm diffusion (
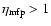 ),
),
 will be smaller for a given background B and the shock
compression ratio
will be smaller for a given background B and the shock
compression ratio
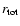 will be
less.
Consistent with assuming strong turbulence (
will be
less.
Consistent with assuming strong turbulence (
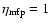 ), we set,
following Völk et al. (2002), the downstream magnetic field
), we set,
following Völk et al. (2002), the downstream magnetic field
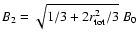 .
.![[*]](/icons/foot_motif.gif)
In the acceleration model of Berezhko & Ellison (1999), the magnetic field also
enters in a calculation of the transfer of energy from energetic
particles to the background gas via Alfvén waves, i.e.,
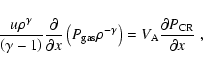 |
(1) |
where
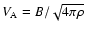 is the Alfvén velocity, u is the
flow speed,
is the Alfvén velocity, u is the
flow speed,
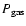 is the pressure in the background gas, and
is the pressure in the background gas, and
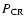 is the pressure in the relativistic particles, i.e., cosmic rays. It is
implicitly assumed that the turbulence saturates when
is the pressure in the relativistic particles, i.e., cosmic rays. It is
implicitly assumed that the turbulence saturates when
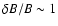 and the wave energy is then rapidly damped to heat. Thus, magnetic
field amplification is not included in this description.
and the wave energy is then rapidly damped to heat. Thus, magnetic
field amplification is not included in this description.
It is via this energy transfer from energetic particles
that the magnetic field has its largest effect on the acceleration process
and even small amounts of background heating from the damping of Alfvén
waves can significantly reduce the acceleration efficiency compared to
the case where only adiabatic heating is included.
As explained in detail in Berezhko & Ellison (1999), compression ratios >4 occur
in DSA for two reasons. First, as relativistic particles are produced
and contribute significantly to the total pressure, their softer
equation of state makes the shocked plasma more compressible (as
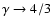 ,
,
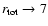 ).
Second, as the highest energy particles escape from the shock, they
drain away energy flux which must be compensated for by ramping up the
overall compression ratio to conserve the fluxes. Just as in
radiative shocks, this is equivalent to
).
Second, as the highest energy particles escape from the shock, they
drain away energy flux which must be compensated for by ramping up the
overall compression ratio to conserve the fluxes. Just as in
radiative shocks, this is equivalent to
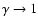 and
and
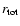 can become arbitrarily large. Compression ratios as large as
we show here occur in independent steady-state calculations of
nonlinear DSA which account for particle loss
(e.g., Jones & Ellison 1991; Eichler 1984; Malkov 1998; Blasi 2002). We note that as the
overall compression ratio increases (
can become arbitrarily large. Compression ratios as large as
we show here occur in independent steady-state calculations of
nonlinear DSA which account for particle loss
(e.g., Jones & Ellison 1991; Eichler 1984; Malkov 1998; Blasi 2002). We note that as the
overall compression ratio increases (
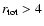 ), the subshock
compression ratio,
), the subshock
compression ratio,
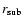 ,
which is responsible for heating the gas,
becomes less than the test-particle value (
,
which is responsible for heating the gas,
becomes less than the test-particle value (
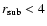 ), causing the
temperature of the shocked gas to drop below test-particle values.
), causing the
temperature of the shocked gas to drop below test-particle values.
Two important qualifications must be made concerning particle escape
and the production of compression ratios greater than 7. First, the
explicit assumption in the model of Berezhko and Ellison (and the
others mentioned above) is that steady-state conditions apply and
particle acceleration is terminated as particles diffuse away from the
shock. If, instead, the acceleration time becomes comparable to the
shock age while the diffusion length is still a small fraction of the
shock radius, the acceleration process may terminate without particle
escape (e.g., Drury 1983).
It is less clear what happens in this case, although the work of
Berezhko and co-workers (e.g., Berezhko 1996; Berezhko et al. 1996) suggests
that for the forward shock in SNRs, geometrical factors
determine
 over most of the lifetime. These geometrical
factors, i.e., the diffusion of particles upstream from the shock, the
increase in the shock size and upstream volume, the slowing of the
shock speed, and the adiabatic cooling of the energetic particles,
produce effects similar to those from escaping particles even though
particles, in fact, remain in the SNR system (see a comparison
of the modeling of SN1006 using the simple, steady-state model used
here with the time-dependent model of Berezhko and co-workers
in Ellison et al. 2000).
over most of the lifetime. These geometrical
factors, i.e., the diffusion of particles upstream from the shock, the
increase in the shock size and upstream volume, the slowing of the
shock speed, and the adiabatic cooling of the energetic particles,
produce effects similar to those from escaping particles even though
particles, in fact, remain in the SNR system (see a comparison
of the modeling of SN1006 using the simple, steady-state model used
here with the time-dependent model of Berezhko and co-workers
in Ellison et al. 2000).
The situation is more uncertain for the inward facing, reverse shock
since the upstream region has a finite volume and particles streaming
far upstream can conceivably reach the shock on the opposite side of
the explosion site without being lost. In this case, particles may
still be lost from spatial effects if they diffuse far enough
downstream to reach the contact discontinuity. However, large magnetic
fields are expected at the contact discontinuity due to compression
and stretching of the field lines by Rayleigh-Taylor instabilities,
and might act as a magnetic wall confining the particles in the ejecta
material.
In any case, for either the forward or reverse shock, a precise
determination of the compression ratio in a time-dependent situation
requires a detailed knowledge of the wave-particle interactions in the
self-generated magnetic turbulence responsible for particle diffusion.
This knowledge does not yet exist so approximations remain necessary.
We simply assume that particles at either the forward or reverse shock
leave the system when their acceleration time
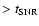 or their
upstream diffusion length
or their
upstream diffusion length
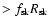 .
In all of the SNR models we
show in this paper, we arbitrarily take
.
In all of the SNR models we
show in this paper, we arbitrarily take
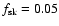 and note that
and note that
 and
and
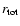 would increase with increasing
would increase with increasing
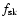 .
.
The second qualification is that the approximations in the Berezhko
and Ellison model assume that
 and thus, that a
sizable fraction of the total pressure is in relativistic particles. Despite
this limitation, we show cases where
and thus, that a
sizable fraction of the total pressure is in relativistic particles. Despite
this limitation, we show cases where
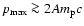 and
warn that our lower
and
warn that our lower
 results have a greater intrinsic error
than those with
results have a greater intrinsic error
than those with
 .
In fact, from comparisons with
Monte Carlo results (not shown here), we find that the Berezhko and
Ellison model underestimates
.
In fact, from comparisons with
Monte Carlo results (not shown here), we find that the Berezhko and
Ellison model underestimates
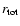 when
when
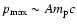 .
.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig1.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg68.gif) |
Figure 1:
Compression ratio versus unshocked magnetic field for a
constant shock speed
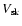 and different values of the injection
efficiency
and different values of the injection
efficiency
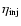 ( top panel), and for a constant injection
efficiency and different values of the shock velocity ( bottom
panel). For each set of parameters, the upper curve corresponds to
adiabatic heating in the precursor and the lower one to Alfvén-wave
heating in the precursor. In the latter case,
( top panel), and for a constant injection
efficiency and different values of the shock velocity ( bottom
panel). For each set of parameters, the upper curve corresponds to
adiabatic heating in the precursor and the lower one to Alfvén-wave
heating in the precursor. In the latter case,
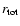 is
dramatically reduced as B0 increases.
is
dramatically reduced as B0 increases. |
| Open with DEXTER |
In this section, we investigate how the acceleration efficiency
depends on the upstream magnetic field B0 for a fixed set of
parameters;
 ,
,
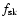 ,
,
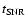 ,
and proton number density
,
and proton number density
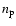 .
We chose a value of
.
We chose a value of
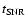 large enough to ensure that
large enough to ensure that
 is determined by diffusive escape. In this case, since we set
is determined by diffusive escape. In this case, since we set
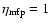 and
and
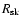 and
and
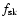 are fixed,
are fixed,
 depends
only on B0 and
depends
only on B0 and
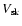 :
:
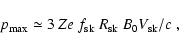 |
(2) |
where Z is the charge number or ionization state and e is the
electronic charge.
Figure 1 shows the variation of the overall shock
compression ratio
 versus magnetic field (top panel) for
different values of the injection parameter
versus magnetic field (top panel) for
different values of the injection parameter
 with
with
 set
to 5000 km s-1 and (bottom panel) for different values of the shock
velocity with
set
to 5000 km s-1 and (bottom panel) for different values of the shock
velocity with
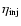 set to 10-3. In both panels,
set to 10-3. In both panels,
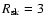 pc,
pc,
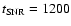 yr,
yr,
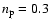 cm-3, and the plasma is composed
of protons and electrons only.
cm-3, and the plasma is composed
of protons and electrons only.
Each value of
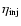 has two curves, one with only adiabatic
heating in the precursor and one with Alfvén-wave heating in the
precursor. The transfer of energy from the energetic particles to the
background gas via Alfvén waves reduces
has two curves, one with only adiabatic
heating in the precursor and one with Alfvén-wave heating in the
precursor. The transfer of energy from the energetic particles to the
background gas via Alfvén waves reduces
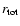 dramatically as B0increases. With Alfvén-wave heating, very large compression ratios are
obtained only for values of the magnetic field much lower than that
typical of the interstellar medium (i.e., for
dramatically as B0increases. With Alfvén-wave heating, very large compression ratios are
obtained only for values of the magnetic field much lower than that
typical of the interstellar medium (i.e., for
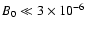 G). This compression ratio increases with decreasing
magnetic field up to a maximum, whose position and intensity depend on
the injection parameter, and then decreases to the test-particle value of 4.
G). This compression ratio increases with decreasing
magnetic field up to a maximum, whose position and intensity depend on
the injection parameter, and then decreases to the test-particle value of 4.
In the top panel, the sonic Mach number is fixed and the only relevant
varying parameters are
 and the Alfvén Mach number,
and the Alfvén Mach number, 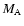 .
As
B0 decreases,
.
As
B0 decreases,
 decreases and
decreases and 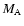 increases. For
increases. For
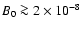 G, the magnetic field is strong enough to allow a
significant transfer of energetic particle energy through Alfvén waves
to heat, lowering the acceleration efficiency. The greater B0, the
smaller
G, the magnetic field is strong enough to allow a
significant transfer of energetic particle energy through Alfvén waves
to heat, lowering the acceleration efficiency. The greater B0, the
smaller 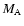 and the more important this effect becomes, causing
and the more important this effect becomes, causing
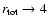 .
For
.
For
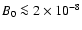 G,
G, 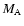 is large
enough that it is no longer important, but now
is large
enough that it is no longer important, but now
 becomes small
enough that the fraction of pressure in relativistic particles drops below
that required to maintain a strongly modified shock. As B0decreases, the transition from a strongly modified shock with
becomes small
enough that the fraction of pressure in relativistic particles drops below
that required to maintain a strongly modified shock. As B0decreases, the transition from a strongly modified shock with
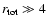 to an unmodified one with
to an unmodified one with
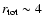 occurs and can be
extremely abrupt. As explained in Berezhko & Ellison (1999), the larger
occurs and can be
extremely abrupt. As explained in Berezhko & Ellison (1999), the larger
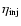 is, the more difficult it is to have a high-Mach number, unmodified
solution. This is the reason that the maximum value of the compression
ratio increases, and that the position of the maximum shifts towards
lower B0, as
is, the more difficult it is to have a high-Mach number, unmodified
solution. This is the reason that the maximum value of the compression
ratio increases, and that the position of the maximum shifts towards
lower B0, as
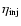 increases.
increases.
In the bottom panel, both 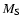 and
and 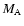 vary.
With Alfvén-wave heating, as B0 decreases, the curves for
vary.
With Alfvén-wave heating, as B0 decreases, the curves for
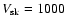 and 2000 km s-1 end before the compression ratio drops to 4:
in these cases,
and 2000 km s-1 end before the compression ratio drops to 4:
in these cases,
 becomes low enough (
becomes low enough (
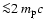 )
to
invalidate the approximations of the Berezhko and Ellison model.
)
to
invalidate the approximations of the Berezhko and Ellison model.
As B0 increases and 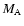 drops, the damping effects of the
magnetic field increase and cause
drops, the damping effects of the
magnetic field increase and cause
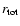 to drop toward 4, regardless
of the sonic Mach number. For values of magnetic field near
10-8 G in the Alfvén-wave heating curves, the compression ratio
peaks strongly as the shock velocity and, therefore,
to drop toward 4, regardless
of the sonic Mach number. For values of magnetic field near
10-8 G in the Alfvén-wave heating curves, the compression ratio
peaks strongly as the shock velocity and, therefore, 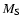 increase.
As B0 decreases below
increase.
As B0 decreases below
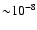 G, the lowering of
G, the lowering of
 ,
and subsequent reduction of pressure in relativistic particles, causes the
transition to unmodified solutions regardless of
,
and subsequent reduction of pressure in relativistic particles, causes the
transition to unmodified solutions regardless of 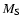 .
The magnetic
field where
.
The magnetic
field where
 is a maximum shifts slightly toward lower B0 as
is a maximum shifts slightly toward lower B0 as
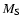 increases. Using the Berezhko and Ellison model, an approximate
expression for the magnetic field strength, B*, at the transition
point between unmodified and strongly modified solutions can be
derived in two regimes (for
increases. Using the Berezhko and Ellison model, an approximate
expression for the magnetic field strength, B*, at the transition
point between unmodified and strongly modified solutions can be
derived in two regimes (for
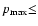 or
or
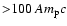 ):
):
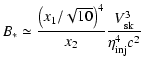 |
|
|
(3) |
if
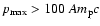 ,
,
or
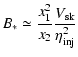 |
|
|
(4) |
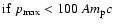 ,
,
where
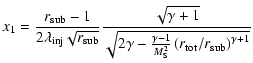 |
|
|
(5) |
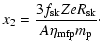 |
|
|
(6) |
At the transition,
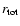 can be estimated as
can be estimated as
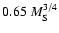 and
and
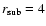 (Berezhko & Ellison 1999). The break at
(Berezhko & Ellison 1999). The break at
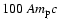 mirrors the
break in the Berezhko and Ellison model between a three-component
power law when
mirrors the
break in the Berezhko and Ellison model between a three-component
power law when
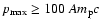 and a two-component power law
when
and a two-component power law
when
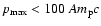 .
.
Figure 1 illustrates that even if extremely high
compression ratios are theoretically possible, normal ISM magnetic
field values, i.e.,
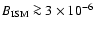 G, with Alfvén-wave
heating, are sufficiently high to limit compression ratios to
G, with Alfvén-wave
heating, are sufficiently high to limit compression ratios to
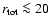 ,
regardless of how efficient the injection is or how high
the sonic Mach number is. The energy converted to magnetic turbulence
and heat lowers the subshock Mach number and the overall acceleration
efficiency. Also, when
,
regardless of how efficient the injection is or how high
the sonic Mach number is. The energy converted to magnetic turbulence
and heat lowers the subshock Mach number and the overall acceleration
efficiency. Also, when 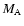 is low, the speed of the magnetic
scattering centers in the fluid (assumed to be Alfvén waves) can become
comparable to the shock speed, lowering the effective difference (for
acceleration) between the downstream and upstream flow
speeds
is low, the speed of the magnetic
scattering centers in the fluid (assumed to be Alfvén waves) can become
comparable to the shock speed, lowering the effective difference (for
acceleration) between the downstream and upstream flow
speeds![[*]](/icons/foot_motif.gif) .
The low magnetic fields in expanding supernova ejecta offer a unique
possibility of seeing non-radiative shocks with
.
The low magnetic fields in expanding supernova ejecta offer a unique
possibility of seeing non-radiative shocks with
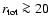 .
.
We model the effects of cosmic-ray acceleration on the evolution
of a SNR using a one-dimensional, cosmic-ray hydrodynamic (CR-hydro)
simulation as described in Ellison et al. (2004).
We initialize the CR-hydro simulation at some time t0 after the
explosion with a power-law ejecta density distribution,
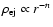 (of index n = 7), combined with a constant density
plateau region at small radii. The plateau is required to keep the
total ejecta mass finite. Beyond the ejecta, we assume a uniform ISM
mass density
(of index n = 7), combined with a constant density
plateau region at small radii. The plateau is required to keep the
total ejecta mass finite. Beyond the ejecta, we assume a uniform ISM
mass density
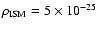 g cm-3 corresponding to a proton
number density of 0.3 cm-3.
A constant density ISM is more appropriate for a type Ia
supernova, whereas a type II supernova is likely to explode in a
pre-SN stellar wind with a
g cm-3 corresponding to a proton
number density of 0.3 cm-3.
A constant density ISM is more appropriate for a type Ia
supernova, whereas a type II supernova is likely to explode in a
pre-SN stellar wind with a
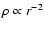 density structure.
The presence of a stellar wind will affect the density
and temperature structure of the shocked ejecta and this, in turn,
will change the
quantitative aspects of particle acceleration at the reverse
shock. Qualitatively, however, the effects we describe for a uniform
ISM will be present in type II supernovae as well.
density structure.
The presence of a stellar wind will affect the density
and temperature structure of the shocked ejecta and this, in turn,
will change the
quantitative aspects of particle acceleration at the reverse
shock. Qualitatively, however, the effects we describe for a uniform
ISM will be present in type II supernovae as well.
The hydrodynamical simulation only
recognizes the matter density, but the acceleration model depends on
the ion species and is limited to a single species, as we discuss
below. We assume that the ejecta speed varies linearly with radius
from zero to some maximum speed
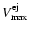 .
In the simulation, the
initial maximum radius of the ejecta is set by the maximum ejecta
speed and t0. Thus, the early stages of the simulation will
depend on
.
In the simulation, the
initial maximum radius of the ejecta is set by the maximum ejecta
speed and t0. Thus, the early stages of the simulation will
depend on
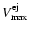 and t0. As long as the total kinetic energy
and ejecta mass stay the same, however, the later evolution of the
SNR is independent of both
and t0. As long as the total kinetic energy
and ejecta mass stay the same, however, the later evolution of the
SNR is independent of both
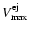 and t0.
and t0.
In Fig. 2 we show how the early evolution depends on
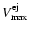 for a particular set of SNR parameters. For all of our other
examples, except those indicated in Fig. 2, we take
for a particular set of SNR parameters. For all of our other
examples, except those indicated in Fig. 2, we take
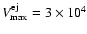 km s-1
km s-1
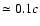 .
As long as t0 is
earlier than the time when
.
As long as t0 is
earlier than the time when
 becomes greater than
becomes greater than
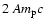 ,
as is the case in Fig. 2, our results are independent of
t0.
,
as is the case in Fig. 2, our results are independent of
t0.
For comparison, we also show in Fig. 2 (dot-dashed curve)
the results obtained analytically for the same set of parameters using
modified Chevalier solutions (Decourchelle et al. 2000). Good agreement is
reached after a few tens of years and, in fact, all of our simulation
results, after a few decades, are independent of our starting
conditions and consistent with analytic solutions, as long as the
self-similar conditions required for the analytic solutions are valid.
Given the general behavior of DSA in low magnetic fields, we begin our
study of SNRs by assuming a constant ejecta magnetic field upstream
from the reverse shock.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1668fig2.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg107.gif) |
Figure 2:
All curves are for the reverse shock and use the same set
of parameters with a constant magnetic field
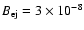 G.
The only variable is the maximum speed of the ejecta G.
The only variable is the maximum speed of the ejecta
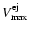 which
is
which
is
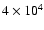 km s-1 for the solid curves, km s-1 for the solid curves,
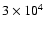 km s-1 for the
dotted curves, and km s-1 for the
dotted curves, and
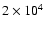 km s-1 for the dashed curves. For
comparison, we show the results obtained analytically, where km s-1 for the dashed curves. For
comparison, we show the results obtained analytically, where
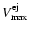 is not limited, for the same set of parameters using
modified Chevalier solutions. While all curves converge after
several decades, the early evolution depends on the different
hydrodynamic initial conditions. The simulation curves are
truncated when
is not limited, for the same set of parameters using
modified Chevalier solutions. While all curves converge after
several decades, the early evolution depends on the different
hydrodynamic initial conditions. The simulation curves are
truncated when
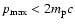 . . |
| Open with DEXTER |
For the CR-hydro model, we use the following parameters: supernova
explosion kinetic energy
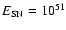 erg, ejecta mass
erg, ejecta mass
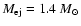 ,
and
,
and
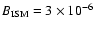 G for the upstream ISM field
(this is B0 for the forward shock). For the acceleration
calculation, we take
G for the upstream ISM field
(this is B0 for the forward shock). For the acceleration
calculation, we take
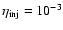 here and in all following
models for both the forward and reverse shocks
here and in all following
models for both the forward and reverse shocks![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig3.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg111.gif) |
Figure 3:
In each panel, RS results are shown for
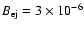 G
(solid curves), G
(solid curves),
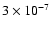 G (dot-dashed curves), G (dot-dashed curves),
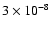 G (dashed
curves), and G (dashed
curves), and
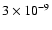 G (dotted curves). The long-dashed curves
in the top and middle panels are analytic results with G (dotted curves). The long-dashed curves
in the top and middle panels are analytic results with
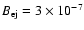 G. In the bottom panel, G. In the bottom panel,
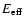 is the RS
acceleration efficiency and
is the RS
acceleration efficiency and
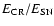 is the fraction of SN
explosion energy going into CRs. The curve labeled "FS'' is
is the fraction of SN
explosion energy going into CRs. The curve labeled "FS'' is
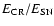 for the FS (FS results are insensitive to
for the FS (FS results are insensitive to
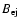 ). In
all cases, ). In
all cases,
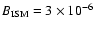 G and curves are truncated when G and curves are truncated when
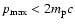 . . |
| Open with DEXTER |
The top panel of Fig. 3 shows the variation of the
compression ratio with SNR age for different values of the constant
upstream ejecta magnetic field
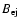 (B0 for the reverse
shock). For
(B0 for the reverse
shock). For
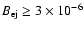 G, the compression ratio is smaller
than 20 for a SNR age larger than 100 yr. For
G, the compression ratio is smaller
than 20 for a SNR age larger than 100 yr. For
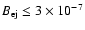 G,
however, the reverse shock compression can be extremely high:
G,
however, the reverse shock compression can be extremely high:
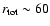 at
at
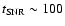 yr for
yr for
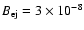 G (dashed
curve). The analytical results for
G (dashed
curve). The analytical results for
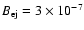 G are shown as
long-dashed curves in the top two panels. As explained for
Fig. 2, the early evolution depends on
G are shown as
long-dashed curves in the top two panels. As explained for
Fig. 2, the early evolution depends on
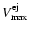 but good
agreement is obtained for higher
but good
agreement is obtained for higher
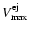 or, in any case, after
or, in any case, after 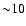 yr. The change in the slope in the simulation curves at
yr. The change in the slope in the simulation curves at
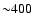 yr corresponds to the passage of the reverse shock from the power-law
envelope into the plateau. Such a transition is not included in the
analytic result which is only valid while the reverse shock remains in
the power-law profile.
yr corresponds to the passage of the reverse shock from the power-law
envelope into the plateau. Such a transition is not included in the
analytic result which is only valid while the reverse shock remains in
the power-law profile.
Lowering
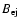 causes the particle gyroradius and acceleration time
to increase so in a shock of a given size and age,
causes the particle gyroradius and acceleration time
to increase so in a shock of a given size and age,
 decreases,
as seen in the middle panel of Fig. 3. Below some
minimum value,
decreases,
as seen in the middle panel of Fig. 3. Below some
minimum value,
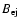 will be too weak to allow the acceleration of
particles to radio emitting energies. This opens up the possibility
that a range of
will be too weak to allow the acceleration of
particles to radio emitting energies. This opens up the possibility
that a range of
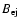 may exist greater than the minimum value needed
to produce observable radio emission but less than
may exist greater than the minimum value needed
to produce observable radio emission but less than
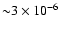 G
so that the full nonlinear effects of efficient Fermi acceleration of
ions occurs
G
so that the full nonlinear effects of efficient Fermi acceleration of
ions occurs![[*]](/icons/foot_motif.gif) .
.
The efficiency of the DSA process can be extremely high. In the bottom
panel of Fig. 3 we show the instantaneous acceleration
efficiency
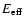 ,
defined as the fraction of incoming energy flux
(in the shock rest frame) put into relativistic particles. After a few
decades, all of the models show
,
defined as the fraction of incoming energy flux
(in the shock rest frame) put into relativistic particles. After a few
decades, all of the models show
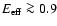 .
The curves in the
bottom panel on the right show the fraction of the supernova explosion
energy
.
The curves in the
bottom panel on the right show the fraction of the supernova explosion
energy
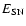 put into relativistic particles, i.e.,
put into relativistic particles, i.e.,
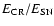 .
The
reverse shocks are able to put
.
The
reverse shocks are able to put 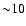 % of
% of
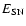 into CRs after
1000 yr. The forward shocks put
into CRs after
1000 yr. The forward shocks put 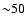 % of
% of
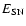 into CRs, as
shown by the heavy-weight solid curve labeled "FS''
into CRs, as
shown by the heavy-weight solid curve labeled "FS''![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1668fig4.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg124.gif) |
Figure 4:
The top panel shows the plasma density vs. radius and the
bottom panel shows the temperature vs. radius. In both panels, the
solid curves include the effects of efficient DSA with a constant
ejecta magnetic field
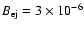 G, the dashed curves assume G, the dashed curves assume
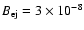 G, and the dotted curves are results with no
acceleration (i.e., test-particle). In all cases the results are
calculated at G, and the dotted curves are results with no
acceleration (i.e., test-particle). In all cases the results are
calculated at
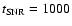 yr with yr with
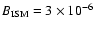 G. G. |
| Open with DEXTER |
In the strong nonlinear regime, radical changes in the structure of
the interaction region between the forward and reverse shocks occur.
In Fig. 4 we compare nonlinear density and temperature
profiles with
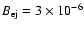 G (solid curves) and
G (solid curves) and
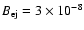 G
(dashed curves) against profiles obtained with no acceleration (dotted
curves). All of the profiles are plotted at
G
(dashed curves) against profiles obtained with no acceleration (dotted
curves). All of the profiles are plotted at
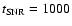 yr. In the
cases with efficient particle acceleration, the increased compression
ratios make the interaction region narrower, denser, and cooler than with
no acceleration. This is particularly true for the width of the shocked
ejecta region which, compared to the case with no acceleration, shrinks
by a factor of
yr. In the
cases with efficient particle acceleration, the increased compression
ratios make the interaction region narrower, denser, and cooler than with
no acceleration. This is particularly true for the width of the shocked
ejecta region which, compared to the case with no acceleration, shrinks
by a factor of 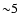 when
when
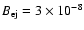 G and where the temperature
drops from greater than 108 K to
G and where the temperature
drops from greater than 108 K to
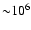 K.
K.
Note that the density and temperature profiles drop abruptly with
no apparent precursors (the small precursors seen in
Figs. 4 and 6 below, are numerical
from a finite grid). This is because our current CR-hydro model does
not explicitly include the cosmic-ray precursor in the
hydrodynamics. The precursor effects essential for the nonlinear
acceleration (i.e., shock smoothing and pre-heating) are included in
the particle acceleration model. For the solid curves in
Fig. 4, the upstream density precursor at the
reverse shock would be
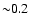 pc in extent to be consistent with
our assumption that
pc in extent to be consistent with
our assumption that
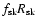 sets the upstream diffusion length of
particles of momentum
sets the upstream diffusion length of
particles of momentum
 .
We further note that regardless
of the density precursor, a precursor in thermal X-rays is not expected
because the temperature in the precursor is too low.
The nonthermal X-ray precursor will be much narrower
than the density precursor if the electron spectrum is limited by
cooling, as suggested by the narrow width of the filaments.
.
We further note that regardless
of the density precursor, a precursor in thermal X-rays is not expected
because the temperature in the precursor is too low.
The nonthermal X-ray precursor will be much narrower
than the density precursor if the electron spectrum is limited by
cooling, as suggested by the narrow width of the filaments.
The changes in structure and evolution of the SNR brought about by
efficient DSA are so large that, even considering the difficulties
projection effects present and other uncertainties, they should be
observable with current techniques. On the other hand, if radio
emission is unambiguously observed at reverse shocks without such
dramatic structural changes, this would be evidence for either
magnetic field amplification beyond several 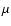 G, or that DSA doesn't
produce large compression ratios as the theory with particle escape
predicts, or that the injection rate is considerably lower than the
value
G, or that DSA doesn't
produce large compression ratios as the theory with particle escape
predicts, or that the injection rate is considerably lower than the
value
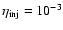 we have assumed.
we have assumed.
The structure of the magnetic field in SNR ejecta is clearly more
complex than assumed in the previous section. As the ejecta expands,
the conservation of magnetic flux will cause the field strength to
decrease rapidly and after only a few years,
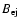 may fall below the
may fall below the
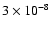 G value used in Fig. 3. The highest possible
initial values of the magnetic field are expected for white dwarf (WD)
progenitors of type Ia supernovae and range between 105 and
109 G (e.g., Liebert 1995). Further enhancement of the WD
magnetic field by convection effects could occur prior to explosion
during the phase of quasi-static burning of carbon and could possibly
lead to equipartition between the kinetic energy density and magnetic
field density. If this occurs, fields as high as
1010-1011 G
might result (e.g., Ruiz-Lapuente & Spruit 1998), providing the upper limit on the
initial magnetic field intensity we consider in the following.
G value used in Fig. 3. The highest possible
initial values of the magnetic field are expected for white dwarf (WD)
progenitors of type Ia supernovae and range between 105 and
109 G (e.g., Liebert 1995). Further enhancement of the WD
magnetic field by convection effects could occur prior to explosion
during the phase of quasi-static burning of carbon and could possibly
lead to equipartition between the kinetic energy density and magnetic
field density. If this occurs, fields as high as
1010-1011 G
might result (e.g., Ruiz-Lapuente & Spruit 1998), providing the upper limit on the
initial magnetic field intensity we consider in the following.
After the explosion of the progenitor, the rapid expansion of the
ejecta will dilute the magnetic field. We obtain expressions for the
magnetic field at time, t, in the core (i.e., the plateau region) of
the ejecta
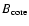 ,
and in the outer, power-law part of the ejecta
,
and in the outer, power-law part of the ejecta
 ,
as a function of fluid speed V, by assuming that the
magnetic field is initially uniform in a constant density progenitor
and then carried passively over during the explosion with the magnetic
flux being conserved during the expansion. Therefore,
,
as a function of fluid speed V, by assuming that the
magnetic field is initially uniform in a constant density progenitor
and then carried passively over during the explosion with the magnetic
flux being conserved during the expansion. Therefore,
Here,
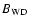 is the magnetic field in the white dwarf before the
explosion,
is the magnetic field in the white dwarf before the
explosion,
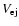 is the constant fluid velocity at the core-power-law
transition point, Ra is the radius within the white dwarf
enclosing the mass of what will become the core of the ejecta, and n
is the ejecta density power-law index. Given
is the constant fluid velocity at the core-power-law
transition point, Ra is the radius within the white dwarf
enclosing the mass of what will become the core of the ejecta, and n
is the ejecta density power-law index. Given
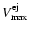 ,
,
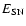 and
t0,
and
t0,
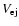 is obtained numerically in the hydro simulation and
is obtained numerically in the hydro simulation and
![\begin{displaymath}R_a= R_{\rm WD}\left [ \frac{n-3}{n - 3 (V_{{\rm max}}^{{\rm ej}}/V_{\rm ej})^{3-n}} \right ]^{1/3},
\end{displaymath}](/articles/aa/full/2005/02/aa1668/img137.gif) |
(9) |
where
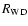 is the white dwarf radius before the explosion.
is the white dwarf radius before the explosion.
Despite specifying white dwarf parameters in the above equations,
similar behavior is expected for the ejecta in type II supernovae but
starting with a lower magnetic field at a larger radius.
Basically, any pre-SN field will be diluted by the
expanding ejecta such that
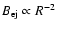 .
.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig5.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg141.gif) |
Figure 5:
Results from two models with diluted magnetic fields are
shown. In all panels, the solid curves are RS values with
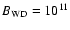 G, the dashed curves are RS values with G, the dashed curves are RS values with
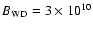 G, and the dot-dashed curves are FS values, which are
insensitive to G, and the dot-dashed curves are FS values, which are
insensitive to
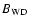 .
For both models, .
For both models,
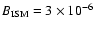 G and
only values where G and
only values where
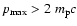 are plotted.
are plotted. |
| Open with DEXTER |
In Fig. 5, we show the variations of
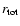 ,
,
 ,
and
,
and
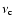 versus
versus
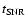 for a diluted field B0, as defined by
Eqs. (7) and (8). The frequency
for a diluted field B0, as defined by
Eqs. (7) and (8). The frequency
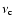 is the critical frequency (e.g., Rybicki & Lightman 1979) where
synchrotron emission from an electron of
is the critical frequency (e.g., Rybicki & Lightman 1979) where
synchrotron emission from an electron of
 peaks, i.e.,
peaks, i.e.,
![\begin{displaymath}\nu_{\rm c} = 3 p_{\rm max}^2 e B / \left[4 \pi (m_{\rm e}c)^3\right]
.
\end{displaymath}](/articles/aa/full/2005/02/aa1668/img143.gif) |
(10) |
Here 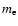 is the electron mass and we have taken the sine of the
pitch angle =1 for convenience.
is the electron mass and we have taken the sine of the
pitch angle =1 for convenience.
The solid curves in Fig. 5 show the extreme case with
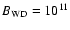 G. In this case, the ability of the reverse shock to
produce
G. In this case, the ability of the reverse shock to
produce 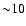 GeV particles lasts until
GeV particles lasts until
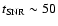 yr, after
which B0 drops below
yr, after
which B0 drops below
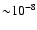 G. The dashed curves show
results for
G. The dashed curves show
results for
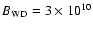 G. Despite
G. Despite
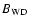 being as high as
being as high as
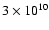 G, few GeV particles are produced at the RS. This is
contrasted by the FS (dot-dashed curves) where
G, few GeV particles are produced at the RS. This is
contrasted by the FS (dot-dashed curves) where
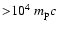 particles are produced after
particles are produced after
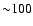 yr.
yr.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1668fig6.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg149.gif) |
Figure 6:
This figure shows the density and temperature profiles
with diluted ejecta fields. The dotted curves are results with no
shock acceleration, the solid curves are results with
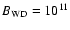 G, and the dashed curves are results with G, and the dashed curves are results with
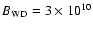 G. G. |
| Open with DEXTER |
Even though the maximum momenta produced in these diluted magnetic
field examples are low, large structural changes occur early in the
evolution, as shown in Fig. 6, where the density and
temperature profiles are plotted at
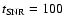 yr. The differences
between the test-particle case (dotted curves) and the efficient
acceleration cases (solid and dashed curves) are greater for the
forward shocks, but are substantial at the reverse shocks. The
structure changes at the reverse shocks lessen as
yr. The differences
between the test-particle case (dotted curves) and the efficient
acceleration cases (solid and dashed curves) are greater for the
forward shocks, but are substantial at the reverse shocks. The
structure changes at the reverse shocks lessen as
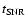 becomes
greater than 100 yr.
becomes
greater than 100 yr.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig7.eps}\end{figure}](/articles/aa/full/2005/02/aa1668/Timg151.gif) |
Figure 7:
Integrated synchrotron emission for constant and diluted
ejecta magnetic fields at
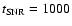 yr. The upper three curves
are calculated assuming a constant field yr. The upper three curves
are calculated assuming a constant field
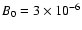 G upstream
of the forward shock and constant G upstream
of the forward shock and constant
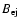 as labeled. The solid and
dashed curves are the emission from the reverse shock assuming a
diluted white dwarf field of
as labeled. The solid and
dashed curves are the emission from the reverse shock assuming a
diluted white dwarf field of
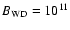 G and G and
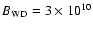 G,
respectively. All curves are calculated for a distance of 2 kpc. G,
respectively. All curves are calculated for a distance of 2 kpc. |
| Open with DEXTER |
In Fig. 7 we show the reverse shock synchrotron emission
predicted for the
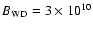 and 1011 G examples shown in
Fig. 5, along with emission from the forward and reverse
shocks where
and 1011 G examples shown in
Fig. 5, along with emission from the forward and reverse
shocks where
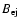 is held constant at
is held constant at
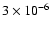 G and
G and
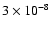 G
as labeled. For calculating synchrotron emission here and elsewhere, we
assume the electron to proton density ratio at relativistic energies to be
0.01, similar to that observed for galactic cosmic rays
(see Ellison et al. 2000; Baring et al. 1999, for discussions of how electrons are treated and synchrotron emission calculated in this model).
These curves are calculated at
G
as labeled. For calculating synchrotron emission here and elsewhere, we
assume the electron to proton density ratio at relativistic energies to be
0.01, similar to that observed for galactic cosmic rays
(see Ellison et al. 2000; Baring et al. 1999, for discussions of how electrons are treated and synchrotron emission calculated in this model).
These curves are calculated at
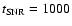 yr at a distance of 2 kpc,
typical of SN1006. At 1 GHz radio frequencies, the reverse shock
emission from even the most extreme white dwarf case with dilution
falls more than 5 orders of magnitude below that of the forward
shock
yr at a distance of 2 kpc,
typical of SN1006. At 1 GHz radio frequencies, the reverse shock
emission from even the most extreme white dwarf case with dilution
falls more than 5 orders of magnitude below that of the forward
shock![[*]](/icons/foot_motif.gif) .
For the constant
.
For the constant
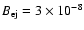 G case, the reverse shock emission is
about a factor of 100 below the reverse shock emission with
G case, the reverse shock emission is
about a factor of 100 below the reverse shock emission with
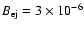 G at 1 GHz. Note that the
G at 1 GHz. Note that the
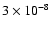 G field is too
weak to produce X-ray synchrotron emission as reported for SNR RCW 86
(Rho et al. 2002).
G field is too
weak to produce X-ray synchrotron emission as reported for SNR RCW 86
(Rho et al. 2002).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1668fig8.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg153.gif) |
Figure 8:
Integrated synchrotron emission for a diluted ejecta
magnetic field of
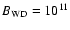 G calculated at different ages:
30 yr (solid curves), 100 yr (dashed curves), 300 yr (dot-dashed
curves) and 103 yr (dotted curves). The upper set of curves is
from the forward shock and the lower set is from the reverse
shock. Note that the dotted and dot-dashed curves for the FS almost
overlay each other. The shock and SNR parameters are the same as in
Fig. 7. G calculated at different ages:
30 yr (solid curves), 100 yr (dashed curves), 300 yr (dot-dashed
curves) and 103 yr (dotted curves). The upper set of curves is
from the forward shock and the lower set is from the reverse
shock. Note that the dotted and dot-dashed curves for the FS almost
overlay each other. The shock and SNR parameters are the same as in
Fig. 7. |
| Open with DEXTER |
The evolution of the synchrotron emission is shown in
Fig. 8 for our extreme diluted ejecta magnetic
field
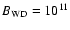 G. The difference in radio emission at 1 GHz
between the forward and reverse shocks is about a factor of 20 at 30
years and drops to more than five orders of magnitude at 1000 years,
as shown in Fig. 7.
G. The difference in radio emission at 1 GHz
between the forward and reverse shocks is about a factor of 20 at 30
years and drops to more than five orders of magnitude at 1000 years,
as shown in Fig. 7.
In the examples we have shown so far we considered only acceleration
in fully ionized hydrogen. However, ejecta material is expected to be
composed mainly of heavy elements and, in particular, type Ia
supernovae are essentially devoid of hydrogen. There are two reasons
for the acceleration process to be modified in the case of heavy
elements.
First, the acceleration time and diffusion length depend on
charge. For relativistic particles, the time required to accelerate an ion
with charge q= Ze to momentum p is proportional to 1/Z.
Likewise, the diffusion length of an ion with momentum p is
proportional to 1/Z (e.g., Baring et al. 1999). Therefore, for
given shock parameters,
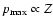 regardless of whether
regardless of whether
 is determined by a finite shock age or size. A higher
is determined by a finite shock age or size. A higher
 tends to increase the acceleration efficiency if heavy ions are
dominant compared to protons being dominant.
tends to increase the acceleration efficiency if heavy ions are
dominant compared to protons being dominant.
Second, a species with mass number A must have momentum
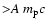 to be relativistic. Since
to be relativistic. Since
 only increases as Z, this tends
to result in a lower fraction of relativistic particles, and a
only increases as Z, this tends
to result in a lower fraction of relativistic particles, and a 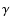 closer to 5/3, than in the case where protons are dominant. This
tends to decrease the acceleration efficiency. In a mixed plasma
containing light and heavy ions, the modified shock structure
resulting from efficient DSA produces an additional effect whereby
ions with the largest mass to charge ratio are accelerated from
thermal energies most efficiently. This is described in detail in
Ellison et al. (1997) but is not considered here where we treat only single
component plasmas.
closer to 5/3, than in the case where protons are dominant. This
tends to decrease the acceleration efficiency. In a mixed plasma
containing light and heavy ions, the modified shock structure
resulting from efficient DSA produces an additional effect whereby
ions with the largest mass to charge ratio are accelerated from
thermal energies most efficiently. This is described in detail in
Ellison et al. (1997) but is not considered here where we treat only single
component plasmas.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1668fig9.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg157.gif) |
Figure 9:
Reverse shock
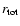 's and 's and
 's for material
containing only protons or fully ionized oxygen, as labeled. The
ejecta magnetic field is taken to be constant at 's for material
containing only protons or fully ionized oxygen, as labeled. The
ejecta magnetic field is taken to be constant at
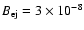 G in the solid and dashed curves, while a diluted field
with G in the solid and dashed curves, while a diluted field
with
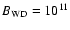 G is used for the dot-dashed and dotted
curves. Only results where G is used for the dot-dashed and dotted
curves. Only results where
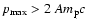 are shown.
are shown. |
| Open with DEXTER |
In Fig. 9, using a constant
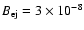 G (solid and
dashed curves) and our extreme white dwarf diluted field
G (solid and
dashed curves) and our extreme white dwarf diluted field
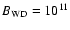 G (dot-dashed and dotted curves), we compare
G (dot-dashed and dotted curves), we compare
 and
and
 for a hydrogen plasma and for a fully ionized oxygen
plasma. All other parameters are the same as those used for the
examples shown in Fig. 3. For the constant
for a hydrogen plasma and for a fully ionized oxygen
plasma. All other parameters are the same as those used for the
examples shown in Fig. 3. For the constant
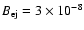 G case, the difference in
G case, the difference in
 between protons and
fully ionized oxygen becomes minor after
between protons and
fully ionized oxygen becomes minor after  yr. For the
diluted magnetic field case, however, there are large differences in
yr. For the
diluted magnetic field case, however, there are large differences in
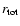 between the two species. The oxygen plasma shows a lower
maximum
between the two species. The oxygen plasma shows a lower
maximum
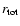 peaking at an earlier age than the proton
plasma. Based on this alone, whatever structural and temperature
changes which occur in the interaction region are expected to be
greater in hydrogen dominated type II supernovae envelopes than in
heavy ion dominated type Ia supernovae.
peaking at an earlier age than the proton
plasma. Based on this alone, whatever structural and temperature
changes which occur in the interaction region are expected to be
greater in hydrogen dominated type II supernovae envelopes than in
heavy ion dominated type Ia supernovae.
Projection effects and other problems make it difficult to reliably
associate radio or X-ray nonthermal emission with reverse shocks in
SNRs. Nevertheless, there have been recent claims for both.
Gotthelf et al. (2001) have identified the forward and reverse
shocks in Cassiopeia A and showed that radio and Si emissivity radial
profiles both show a sharp rise at what they characterize as the
reverse shock. The sharp rise and fairly sharp falloff in radio
emissivity as one moves outward from the center of the Cas A SNR is a
good indication of the local acceleration of relativistic electrons,
but, as noted, projection effects make the precise determination of
the reverse shock difficult. Furthermore, Gotthelf et al. (2001) chose
to ignore a secondary Si peak near 80 arcsec inside the main Si
peak. The main Si peak seems clearly associated with radio emission,
but the inner secondary peak is not and could alternately mark the
reverse shock.
Using new VLA observations of Kepler's SNR,
DeLaney et al. (2002) suggest that two distinct radio structures
are present. These flat- and steep-spectrum components are partially
decoupled in some areas and the steep-spectrum component tracks the
X-ray emission seen by ROSAT, which is mainly line emission from
shocked ejecta. They conclude that the flat- and steep-spectrum radio
emission come from the forward and reverse shocks, respectively.
However the steep regions could also mark the interface rather than
the reverse shock. For example, Vink & Laming (2003) interpreted the (steep)
radio emission from Cas A as arising at the interface.
Rho et al. (2002) claim that the detailed morphology of soft and
hard X-rays in SNR RCW 86 strongly supports the case for different
origins for these components. They conclude that the hard X-rays are
most likely a combination of a synchrotron continuum plus Fe K emission from shocked ejecta material. This implies, in their
estimation, that the reverse shock may be accelerating electrons to
energies of the order of 50 TeV!
emission from shocked ejecta material. This implies, in their
estimation, that the reverse shock may be accelerating electrons to
energies of the order of 50 TeV!
While other interpretations are certainly possible, e.g., relativistic
electrons produced at the forward shock might travel to the reverse
shock and brighten in radio in the compressed magnetic field, the
above observations provide some evidence that reverse shocks in SNRs
can directly produce relativistic electrons; GeV in the case of radio and TeV
in the case of nonthermal X-rays. If this is so, there are a number of
important consequences both for interpreting a wide range of
astrophysical sources where DSA is believed to generate relativistic
electrons, and for our understanding of the basic functioning of DSA.
If relativistic electrons are accelerated at the reverse shock, the
production of observable radio emission requires that the magnetic
field upstream of the reverse shock be amplified by many orders of
magnitude over values expected in the expanding unshocked ejecta. If
such field amplification is taking place, it is likely that it is
directly associated with DSA (i.e., Bell & Lucek 2001).
We speculate that early in the SNR evolution (i.e.,
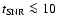 yr)
the unamplified ejecta field may be strong enough to
start the DSA process even with dilution. Once energetic particles are
produced, the magnetic field may be amplified by them and maintained
against dilution at a level where DSA continues.
yr)
the unamplified ejecta field may be strong enough to
start the DSA process even with dilution. Once energetic particles are
produced, the magnetic field may be amplified by them and maintained
against dilution at a level where DSA continues.
Shocks are widespread in astrophysics with parameters not widely
different from those in SNRs. If DSA can amplify magnetic fields in
SNR shocks, the process should work in other environments as well.
Since the maximum energy individual particles obtain in DSA scales as
B, widespread B-field amplification will lead to a systematic
increase in the expected maximum proton energy produced by
astrophysical shocks.
The theory of nonlinear diffusive shock acceleration predicts
compression ratios far in excess of the test-particle value of
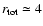 (e.g., Eichler 1984; Malkov 1998; Berezhko & Ellison 1999; Ellison & Eichler 1984; Blasi 2002; Bell 1987).
For high sonic Mach numbers,
(e.g., Eichler 1984; Malkov 1998; Berezhko & Ellison 1999; Ellison & Eichler 1984; Blasi 2002; Bell 1987).
For high sonic Mach numbers,
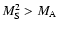 ,
and strongly modified
steady-state conditions, the compression ratio can be approximated by
,
and strongly modified
steady-state conditions, the compression ratio can be approximated by
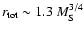 or by
or by
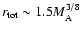 when
when
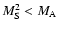 (Berezhko & Ellison 1999; Kazanas & Ellison 1986).
(Berezhko & Ellison 1999; Kazanas & Ellison 1986).
We have shown that if
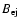 falls in a range
falls in a range
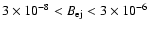 G with typical SNR parameters,
G with typical SNR parameters,
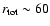 may occur
(see Fig. 3); a value considerably larger than is likely
to occur in any other non-radiative astrophysical environment.
Compression ratios this large should produce unmistakable changes in
the SNR structure (see Figs. 4 and
6) and X-ray emission, thermal and nonthermal.
Confirmation of this prediction would support the premise that DSA is
intrinsically extremely efficient.
may occur
(see Fig. 3); a value considerably larger than is likely
to occur in any other non-radiative astrophysical environment.
Compression ratios this large should produce unmistakable changes in
the SNR structure (see Figs. 4 and
6) and X-ray emission, thermal and nonthermal.
Confirmation of this prediction would support the premise that DSA is
intrinsically extremely efficient.
Unfortunately, shock compression ratios are not directly observable
for remote systems such as SNRs with large Mach numbers (see
Sects. 2.2.3.1 and 2.4 in Drury et al. 2001; Raymond 2001, respectively).
Shocks in the heliosphere are directly observable but have low Mach
numbers and even here, the direct measurement of compression ratios
requires multiple spacecraft simultaneously sampling the upstream and
downstream plasmas. Until the launch of CLUSTER this was not possible
and the prediction of
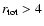 has not been clearly demonstrated in
astrophysical shocks, although indirect support does exist for the
Earth bow shock (Ellison et al. 1990).
has not been clearly demonstrated in
astrophysical shocks, although indirect support does exist for the
Earth bow shock (Ellison et al. 1990).
The large structural changes brought about in SNRs if
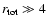 offer a unique opportunity to see the effects of extremely efficient
diffusive shock acceleration. In the extreme cases we show here, i.e.,
Fig. 3, more than 90% of the bulk flow energy flux (in
the shock rest frame) is placed in relativistic ions. Even in cases when
offer a unique opportunity to see the effects of extremely efficient
diffusive shock acceleration. In the extreme cases we show here, i.e.,
Fig. 3, more than 90% of the bulk flow energy flux (in
the shock rest frame) is placed in relativistic ions. Even in cases when
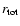 is not as extreme, acceleration efficiencies near 50% are
predicted for both the forward and reverse shocks. Over the lifetime
of a SNR,
is not as extreme, acceleration efficiencies near 50% are
predicted for both the forward and reverse shocks. Over the lifetime
of a SNR, 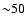 % of
% of
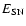 is predicted to be put into cosmic
rays depending on the average injection rate over the surface of the
SNR (e.g., Berezhko et al. 1996; Ellison et al. 2004; Dorfi 1990; Berezhko et al. 2002). The energy which
goes into relativistic ions comes out of the bulk thermal plasma and produces
a drastic reduction in the shock temperature.
is predicted to be put into cosmic
rays depending on the average injection rate over the surface of the
SNR (e.g., Berezhko et al. 1996; Ellison et al. 2004; Dorfi 1990; Berezhko et al. 2002). The energy which
goes into relativistic ions comes out of the bulk thermal plasma and produces
a drastic reduction in the shock temperature.
Direct observations of shocks in the heliosphere and most theories of
DSA show that collisionless shocks put far more energy into ions than
electrons. Thus, even though the presence of relativistic electrons suggested
our description of strong nonlinear effects, the signature of
nonlinear DSA in the structure and evolution of the radio and X-ray
emitting interaction region between the forward and reverse shocks,
will be evidence for the efficient production of cosmic-ray ions, not
necessarily electrons (see Berezhko et al. 2003a, for a discussion of SN 1006 in this
regard). Detection of pion-decay 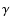 -rays would be a
more direct confirmation that relativistic ions are produced in SNRs, however
this has not yet been unambiguously done. It is also clear from
-rays would be a
more direct confirmation that relativistic ions are produced in SNRs, however
this has not yet been unambiguously done. It is also clear from
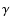 -ray models of young SNRs, that parameters can be chosen where
efficient DSA occurs, but either the
-ray models of young SNRs, that parameters can be chosen where
efficient DSA occurs, but either the 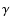 -ray flux is below detectable
levels, or detectable TeV
-ray flux is below detectable
levels, or detectable TeV 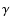 -rays are dominated by inverse-Compton emission
from electrons rather than protons (e.g., Ellison et al. 2001).
-rays are dominated by inverse-Compton emission
from electrons rather than protons (e.g., Ellison et al. 2001).
Modeling the SNR structure offers two advantages. First, if
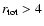 is inferred from observations, it is evidence for the efficient
production of CR ions whether or not a pion-decay feature is observed
since the observability of pion-decay
is inferred from observations, it is evidence for the efficient
production of CR ions whether or not a pion-decay feature is observed
since the observability of pion-decay 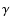 -ray's depends on other
factors besides acceleration efficiency (e.g., ambient density).
Second, if the structure is inconsistent with efficient DSA and
-ray's depends on other
factors besides acceleration efficiency (e.g., ambient density).
Second, if the structure is inconsistent with efficient DSA and
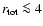 ,
this is clear evidence that the efficient shock
acceleration of ions is not occurring. Due to the freedom of
,
this is clear evidence that the efficient shock
acceleration of ions is not occurring. Due to the freedom of
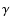 -ray models, the lack of a
-ray models, the lack of a 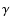 -ray detection is unlikely ever
to be able to eliminate the possibility that efficient DSA is
occurring.
-ray detection is unlikely ever
to be able to eliminate the possibility that efficient DSA is
occurring.
For efficient particle acceleration, the postshock densities are
larger and the postshock temperatures smaller than in the test-particle case
(see Figs. 4 and 6). As a consequence,
the heating of electrons in the downstream region by Coulomb
interaction with the population of protons (
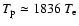 without further heating at the shock) will be more efficient than in
the test-particle case. In the shocked ejecta, the electron temperature can be
almost equal to that of the protons for an injection of
without further heating at the shock) will be more efficient than in
the test-particle case. In the shocked ejecta, the electron temperature can be
almost equal to that of the protons for an injection of
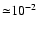 ,
while in the shocked ambient medium the electrons may reach
up to 30 % of the proton temperature (Decourchelle & Ellison 2001).
,
while in the shocked ambient medium the electrons may reach
up to 30 % of the proton temperature (Decourchelle & Ellison 2001).
Another constraint on the efficiency of particle acceleration comes
from the observation of a strong Fe K-alpha line in the shocked ejecta
of young SNRs (like Cas A, Kepler and Tycho). In Kepler, for efficient
particle acceleration at the reverse shock, it was shown that the
shocked ejecta temperature gets too low to produce the Fe K-line
(Decourchelle et al. 2000). Line excitation by the nonthermal population can be
invoked, however the ionization state of iron is expected to be very
low even when taking into account the ionization from a nonthermal
power-law population (Porquet et al. 2001). Thus, the prediction from
efficient DSA that postshock temperatures are low in the RS presents a
problem in SNRs where a strong Fe K-alpha line is observed.
For DSA acceleration to occur at all, the unshocked ejecta material
must be fully ionized or, at least, have a sizable ionization
fraction. Otherwise the magnetic turbulence necessary to scatter
particles will be damped (e.g., Drury et al. 1996). The expanding ejecta
will cool rapidly and would be largely neutral unless ionized by some
source. This could possibly be X-ray emission from shock heated gas or
the cosmic rays may contribute to the ionization themselves. If the
ionization fraction is initially large enough for some cosmic-ray
production to occur, these CRs may further ionize the precursor
material, making acceleration more efficient, etc.
The Balmer-dominated spectra of nonradiative shocks in a number of SNRs
(e.g., Ghavamian et al. 2001) has been interpreted as charge exchange
between protons and neutrals. If synchrotron radio and/or X-ray
emission is observed at these shocks as well, which is possibly the
case in the northeastern rim of Tycho, this would indicate that DSA is
at work even in a partially neutral medium. The reported presence of
reverse shock radio emission suggests that the ejecta material is
ionized, at least in the region upstream of the shock, where DSA is
taking place.
It has long been believed that forward shocks in SNRs sweep up and
accelerate ISM ions to produce galactic cosmic rays and to accelerate
electrons to produce in situ radio emission. The mechanism most
likely responsible for this is DSA, which is predicted to be extremely
efficient, i.e., >50% of the ram kinetic energy may go into
relativistic ions. At reverse shocks in young SNRs, however,
straightforward estimates of the diluted ejecta magnetic field from
the pre-SN white dwarf or massive star show it to be many orders of
magnitude below that required to either accelerate relativistic electrons
from the thermal background, or to produce observable radio
intensities from background cosmic-ray electrons.
Nevertheless, some recent observations provide evidence for radio
emission associated with reverse shocks in two SNRs: Kepler and Cas A,
and X-ray synchrotron continuum emission in RCW 86. If the reverse shocks in
these remnants are accelerating electrons to GeV or even TeV energies
via DSA, it immediately suggests that the magnetic field at the
reverse shock is orders of magnitude higher than expected to produce
radio and higher still to produce X-ray synchrotron. If true, the most likely
explanation is that the acceleration process is amplifying the
magnetic field, perhaps as Bell & Lucek (2001) have suggested. The
importance of shock acceleration in a wide variety of astrophysical
objects, and the strong dependence of DSA on the magnetic field, make
it critically important to first, verify the difficult reverse shock
observations and second, to explore the ramifications of efficient DSA
at reverse shocks in young SNRs.
While radio observations imply magnetic field amplification to values
far larger than the diluted progenitor field, there is, as yet, no way
to precisely determine the value. This opens the possibility that the
ejecta field
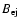 is large enough to produce observable radio
emission, but still far lower than normal ISM values. We have shown
here that, for typical SNR parameters, having
is large enough to produce observable radio
emission, but still far lower than normal ISM values. We have shown
here that, for typical SNR parameters, having
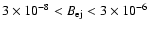 G results in extremely large nonlinear effects in DSA, i.e.,
compression ratios
G results in extremely large nonlinear effects in DSA, i.e.,
compression ratios  4 and shocked temperatures
4 and shocked temperatures 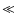 than
test-particle temperatures. If these nonlinear effects occur, they
will produce large changes in the structure and evolution of SNRs
which should be observable with existing instruments. We have
detailed these effects in the remnant hydrodynamics and estimated
synchrotron emission for a limited range of parameters.
than
test-particle temperatures. If these nonlinear effects occur, they
will produce large changes in the structure and evolution of SNRs
which should be observable with existing instruments. We have
detailed these effects in the remnant hydrodynamics and estimated
synchrotron emission for a limited range of parameters.
Supernova remnants may offer the best known laboratory for studying
both magnetic-field amplification and DSA. Current and future ground
and space-based observatories offer high spatial and energy resolution
of several remnants and provide information that is available nowhere
else. Shocks in the Heliosphere are accessible to spacecraft and a
great deal has been learned of their properties. However, the
point-like nature of heliospheric observations, the low Mach number
and small size of heliospheric shocks which limits particle
acceleration, and the unique geometry of the intensely studied Earth
bow shock, limit what can be learned and transferred to other
astrophysical systems. The difficult plasma physics has also limited
the success of analytic investigations, and direct PIC computer
simulations are decades away from being able to simulate the injection
and acceleration of a electron-proton plasma to relativistic energies.
Acknowledgements
The authors wish to thank J. Blondin for providing his hydrodynamic
simulation code VH-1 and for other help with this project. We
are also grateful to the International Space Science Institute (ISSI)
in Bern, Switzerland, where some of this work was done. This work was
supported, in part, by a NSF-CNRS grant (NSF INT-0128883, CNRS-12974)
and by an NASA ATP grant (ATP02-0042-0006).
- Baring, M.
G., Ellison, D. C., Reynolds, S. P., Grenier, I. A., & Goret,
P. 1999, ApJ, 513, 311 [CrossRef] (In the text)
- Bell, A. R. 1987,
MNRAS, 225, 615
- Bell, A. R., &
Lucek, S. G. 2001, MNRAS, 321, 433 [CrossRef]
- Berezhko, E. G.
1996, Astropart. Phys., 5, 367 [CrossRef]
- Berezhko, E. G., &
Ellison, D. C. 1999, ApJ, 526, 385 [CrossRef] (In the text)
- Berezhko, E. G., Elshin,
V. K., & Ksenofontov, L. T. 1996, JETP, 82, 1 (In the text)
- Berezhko, E. G.,
Ksenofontov, L. T., & Völk, H. J. 2002, A&A, 395,
943 [EDP Sciences] [CrossRef]
- Berezhko, E. G.,
Ksenofontov, L. T., & Völk, H. J. 2003, A&A, 412,
L11 [EDP Sciences] [CrossRef] (In the text)
- Berezhko, E. G.,
Pühlhofer, G., & Völk, H. J. 2003, A&A, 400,
971 [EDP Sciences] [CrossRef]
- Berezhko,
E. G., & Völk, H. J. 2004, A&A, 419,
L27 [EDP Sciences] [CrossRef] (In the text)
- Blasi, P. 2002,
Astropart. Phys., 16, 429 [CrossRef]
-
Decourchelle, A., & Ellison, D. C. 2001, Space Sci. Rev., 99,
219 [CrossRef] (In the text)
- Decourchelle, A.,
Ellison, D. C., & Ballet, J. 2000, ApJ, 543, L57 [CrossRef] (In the text)
- DeLaney, T.,
Koralesky, B., & Rudnick, L. 2002, ApJ, 580, 914 [CrossRef]
- Dorfi, E. A. 1990,
A&A, 234, 419
- Drury, L. O'C. 1983,
Rep. Prog. Phys., 46, 973 [CrossRef] (In the text)
- Drury, O. C., Duffy, P.,
& Kirk, J. G. 1996, A&A, 309, 1002 (In the text)
- Drury, L. O'C.,
Ellison, D. C., Aharonian, F. A., et al. 2001, Space Sci.
Rev., 99, 329 [CrossRef]
- Drury, L. O'C.,
van der Swaluw, E., & Carroll, O. 2003
[arXiv:astro-ph/0309820]
- Eichler, D. 1984,
ApJ, 277, 429 [CrossRef]
- Ellison, D. C.,
Berezhko, E. G., & Baring, M. G. 2000, ApJ, 540, 292 [CrossRef] (In the text)
- Ellison, D. C.,
Decourchelle, A., & Ballet, J. 2004, A&A, 413, 189 [EDP Sciences] [CrossRef] (In the text)
- Ellison, D. E., Drury, L.
O'C., & Meyer, J.-P. 1997, ApJ, 487, 197 [CrossRef] (In the text)
- Ellison, D. C., &
Eichler, D. 1984, ApJ, 286, 691 [CrossRef]
- Ellison, D. C.,
Möbius, E., & Paschmann, G. 1990, ApJ, 352, 376 [CrossRef] (In the text)
- Ellison, D. C.,
Slane, P., & Gaensler, B. M. 2001, ApJ, 563, 191 [CrossRef] (In the text)
-
Ghavamian, P., Raymond, J., Smith, R. C., & Hartigan, P. 2001,
ApJ, 547, 995 [CrossRef] (In the text)
- Gotthelf, E.
V., Koralesky, B., Rudnick, L., et al. 2001, ApJ, 552,
L39 [CrossRef]
- Jones, F. C., &
Ellison, D. C. 1991, Space Sci. Rev., 58, 259
- Kazanas, D., & Ellison,
D. C. 1986, ApJ, 304, 178 [CrossRef]
- Liebert, J. 1995,
in Cape Workshop on Magnetic Cataclysmic Variables, ed. D. A. H.
Buckley, & B. Warner (San Francisco: ASP), ASP Conf., 85,
59
(In the text)
- Lucek, S. G., &
Bell, A. R. 2000, MNRAS, 314, 65 [CrossRef]
- Malkov, M. A. 1998,
Phys. Rev. E, 58, 4911 [CrossRef]
- Porquet, D.,
Arnaud, M., & Decourchelle, A. 2001, A&A, 373, 1110 [EDP Sciences] [CrossRef] (In the text)
- Ptuskin, V. S.,
& Zirakashvili, V. N. 2003, A&A, 403, 1 [EDP Sciences] [CrossRef]
- Raymond, J.
2001, Space Sci. Rev., 99, 209 [CrossRef]
- Rho, J., Dyer, K. K.,
Borkowski, K., & Reynolds, S. P. 2002, ApJ, 581, 1116 [CrossRef]
- Ruiz-Lapuente, P.,
& Spruit, H. C. 1998, ApJ, 500, 360 [CrossRef] (In the text)
- Rybicki, G. B., &
Lightman, A. P. 1979, Radiative Processes in Astrophysics (John
Wiley & Sons), 171
(In the text)
- Vink, J., &
Laming, J. M. 2003, ApJ, 584, 758 [CrossRef] (In the text)
- Völk, H. J.,
Berezhko, E. G., Ksenofontov, L. T., & Rowell, G. P. 2002,
A&A, 396, 649 [EDP Sciences] [CrossRef] (In the text)
Copyright ESO 2004
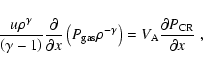
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig1.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg68.gif)
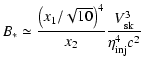
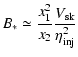
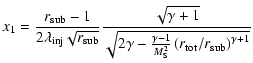
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1668fig2.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig3.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg111.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1668fig4.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg124.gif)
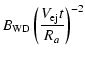
![$\displaystyle B_{\rm core}\left(\frac{V}{V_{\rm ej}}\right)^{-2}
\left[1+ \frac...
...ft(1-\left(\frac{V}{V_{\rm ej}}\right)^{3-n}
\right)\right]^{\frac{2}{3}}
\cdot$](/articles/aa/full/2005/02/aa1668/img135.gif)
![\begin{displaymath}R_a= R_{\rm WD}\left [ \frac{n-3}{n - 3 (V_{{\rm max}}^{{\rm ej}}/V_{\rm ej})^{3-n}} \right ]^{1/3},
\end{displaymath}](/articles/aa/full/2005/02/aa1668/img137.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig5.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg141.gif)
![\begin{displaymath}\nu_{\rm c} = 3 p_{\rm max}^2 e B / \left[4 \pi (m_{\rm e}c)^3\right]
.
\end{displaymath}](/articles/aa/full/2005/02/aa1668/img143.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1668fig6.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg149.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1668fig7.eps}\end{figure}](/articles/aa/full/2005/02/aa1668/Timg151.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1668fig8.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg153.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1668fig9.eps} \end{figure}](/articles/aa/full/2005/02/aa1668/Timg157.gif)