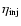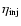Note the difference between injection efficiency $\eta _{\rm inj}$ and acceleration efficiency. The acceleration efficiency can and does vary with shock parameters even for a constant $\eta _{\rm inj}$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

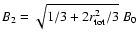... $B_2= \sqrt{1/3 + 2 r_{\rm tot}^2/3}~B_0$ .

Everywhere, the subscript 0 (2) implies unshocked (shocked) quantities.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... speeds

Note that even though we consider cases where the speed of the scattering centers is high, we neglect second-order Fermi acceleration.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... shocks

In an actual SNR, of course, the injection efficiency might vary with time, vary over the shock surface, or be different at the forward and reverse shocks (as in our model of Kepler's SNR; Decourchelle et al. 2000). If the actual 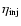$\eta _{\rm inj}$ is less than 10^-3, the nonlinear effects we show will be less dramatic.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... occurs

Note that we do not show solutions in Fig. 3 for 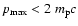$p_{\rm max}< 2~m_{\rm p}c$ , i.e., below the limit of validity of the Berezhko and Ellison model.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... "FS''

As noted by Berezhko et al. (2002), injection may vary over the surface of the SNR and be significantly less where the magnetic field is highly oblique. They estimate that to supply the galactic CR population the overall efficiency need only be 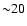${\sim} 20$ % of the maximum values obtained by DSA.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... shock

The properties of the forward shock are quite insensitive to the ejecta magnetic field so each of these four models have similar forward shock synchrotron emission.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.