A&A 429, 747-753 (2005)
DOI: 10.1051/0004-6361:20040270
Sensitivity of a "dispersed-speckles'' piston sensor
for multi-aperture interferometers and hypertelescopes
V. Borkowski 1,2 - A. Labeyrie 1
- F. Martinache 1
- D. Peterson 3
1 - Collège de France & Laboratoire d'Interférométrie Stellaire et Exo-planétaire LISE-Observatoire de Haute-Provence - CNRS, 04870 Saint-Michel
l'Observatoire, France
2 -
Alcatel Space Industries, 100 bd du Midi, BP 99, 06156 Cannes la Bocca Cedex, France
3 -
Department of Physics and Astronomy, Stony Brook University, Stony Brook, NY
11794-3800, USA
Received 13 February 2004 / Accepted 2 September 2004
Abstract
In multi-aperture interferometers and hypertelescopes,
the piston errors can be determined from multi-spectral images of
the speckle pattern using a 3-dimensional Fourier transform. We
study the limiting magnitude of the method in the case of
non-redundant apertures using analytical derivations and numerical
simulations. We show specifically for the case of sub-r0apertures that a few photons per aperture within the full spectral
bandwidth will suffice to measure piston errors. The method's
sensitivity is thus comparable to that of the Shack-Hartmann and
other methods used with monolithic apertures.
Key words: turbulence - techniques: interferometric - atmospheric effects
1 Introduction
The image enhancement achieved by adaptive optics in large
telescopes requires mapping the wavefront bumpiness, i.e.
measuring piston errors at many points across the aperture. The
established methods for achieving such wavefront sensing, mainly
the Shack-Hartmann and Curvature methods, rely upon the
continuity of the wavefront. However, there is no such continuity
in dilute multi-aperture interferometers. Their direct-imaging
forms, called Fizeau interferometers, and "hypertelescopes'' if there
is a densified exit-pupil (Labeyrie 1996), therefore require
different methods of piston sensing. A method for solving this
more general problem was proposed by Labeyrie (Labeyrie 2002).
It extends to more than two apertures the group-delay or
"dispersed fringes'' measurement method used since Michelson and Pease (1921), Koechlin et al. (1996), and which now provides pairwise
piston measurements for up to six apertures at the NPOI. Here, we
calculate the limiting magnitude of this "dispersed speckles''
method and verify with numerical simulations. In Sect. 2 we recall
the principle of the algorithm. We briefly discuss the effect of
redundancy, which requires refined procedures to discriminate the
piston values. In Sect. 3, we discuss the sensitivity performance
of the method, using numerical simulations with photon noise and
analytical derivations. In Sect. 4, we discuss the comparison with
other algorithms which have been proposed. In Sect. 5, we discuss
the future prospects for this method. A separate article
(Borkowski et al., in preparation) describes a prototype piston
sensor instrument and its laboratory performance.
2 Principle of the "dispersed speckles'' algorithm
As briefly described earlier (Labeyrie 2002; Borkowski et al. 2002) we
consider the image of an unresolved guide star, formed with
multiple apertures in the presence of piston errors. The image
typically shows speckles, each having a spectrum which is itself
speckled. The method extracts the information on piston errors
which is contained in the spatio-spectral speckles.
The aperture may be diluted, and possibly highly diluted
like in a long-baseline multi-element Fizeau interferometer, in
which case it can be re-arrranged to provide a densified exit
pupil as in a hypertelescope. The aperture can also be compact and
highly redundant like in the Keck telescopes. Although this
article deals mostly with non-redundant examples, much of it is
applicable to redundant apertures, as discussed in more detail by
(Martinache 2004). We ignore here the wavefront errors within each
sub-aperture, i.e. tip-tilt, defocus and higher-order aberrations,
since they can be analyzed efficiently with established sensing
methods, and be corrected adaptively at each aperture separately.
The issue is to remove the remaining piston offsets.
![\begin{figure}
\par\rotatebox{360}
{\resizebox{14cm}{9cm}{\includegraphics[clip]{0270fig1.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg5.gif) |
Figure 1:
Description of the algorithm. The example uses a triple aperture for a simplified ("honeycomb-like'') 3-dimensional structure of dispersed speckles. Clockwise from top-left: A- aperture ; B- its Fourier transform, in intensity form, which is the recorded star image, in blue light. C- layering of a blue and red image, before re-scaling; D- input cube with all wavelength layers, re-scaled. With 3 apertures, it is a honeycomb pattern, tilted in response to the piston values. With more apertures, it has 3-dimensional speckles. E- output cube, calculated as a 3-dimensional Fourier transform of D. Its active columns contain "signal dots'' at heights proportional to the piston value in the corresponding baseline. The six dots here obtained with 3 apertures are in a plane tilted like the piston value map. |
| Open with DEXTER |
The speckled image is detected and recorded at a series of
wavelengths simultaneously, using a spectro-imaging instrument. As
described in Borkowski et al. (in preparation), a small
spectrograph with a mosaic of optical wedges near its grating can
do it by "exploding'' the spectrum into a series of parallel
spectra, each formed by one resel (resolution element) of the
image. Unlike the usual spectrographs, the slit is replaced by a
highly de-magnified pupil, and the image is highly magnified in
the grating plane. Thus, there is typically one image speckle
received onto each wedge and providing a distinct spectrum. In the
computer the spectra are rearranged as a 3-dimensional
"dispersed speckles'' image, interpolated to be linear in inverse
wavelength. The monochromatic patterns are then layered into a
"data cube'' representing the dispersed speckle pattern (Fig. 1).
Its 3-dimensional Fourier transform is then
calculated to obtain an "output cube''.
For each pair of apertures, defining a baseline, the output cube has an "active'' column containing a "signal dot''. Its position along the column is a measure of the piston
difference among the two apertures. There are several dots in columns corresponding to redundant baselines.
The positions of the "active'' columns in the output cube match those of the peaks in the pupil's autocorrelation and the 3-dimensional Fourier transformation can be accelerated by calculating only
these columns.
Martinache (2004) has shown that the data cube is the 3-dimensional
energy spectrum of the unknown piston map, i.e.
the square modulus of its 3-dimensional Fourier transform, if this map
is defined as a binary function of both aperture coordinates and the
piston value, with zeros and ones defining locally the presence of an
aperture at all positions and possible piston values. He thus concludes
that the output cube is a 3-dimensional autocorrelation function of the piston map. Both have real and positive values. These results show that the general
problem of reconstructing the piston map is a problem of inverting
the 3-dimensional autocorrelation. It has an exact, easily
obtained at high illumination levels, if the aperture
is non-redundant. There is however in all cases a spurious solution, related to the true solution through a 3-dimensional centro-symmetry. The true solution can be discriminated if the known
aperture shape has no center of symmetry, like in the examples below, where an odd number of apertures are arrayed along a ring, with sometimes also one aperture at the center.
The centro-symmetry of a redundant array can easily be destroyed
by removing or adding one aperture. A redundant array with an odd
number of apertures can be centro-symmetrical only if it has a
sub-aperture in the center. Solving for piston values in the
redundant case proved possible when the aperture is not perfectly
symmetrical using a 3-dimensional Fienup routine and more direct
methods may prove feasible (Martinache 2004).
At low illumination levels providing few photon events, the
high-illumination-level speckled data cube becomes a 3-dimensional
cloud of Dirac dots, assuming a photon counting detector. As in
ordinary speckled images recorded with such detectors at low
levels, the random Poisson sampling of the speckles results in a
"compounded Poissone'' statistical distribution, classically known
as the Bose-Einstein distribution (Dainty 1974).
In the output cube, now calculated as the 3-dimensional Fourier
transform of the Dirac cloud, the high-illumination-level pattern
of N(N-1) discrete "signal dots'' (N is the number of
apertures), real, positive, and having a dark background (the
background is fully dark in the 3-dimensional autocorrelation of
the wavefront map, but the finite size of the data cube
intermediate here causes sidelobes to appear when calculating its
Fourier transform), is now contaminated with a speckled
background.
The contributing complex amplitudes being randomly phased,
the average modulus of this background is 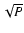 ,
if P is the number of photons in the Dirac cloud. The modulus of the
central speckle, corresponding to the central dot of the high
level pattern (i.e. with an infinite number of photons), which is
the 3-dimensional auto-correlation of the piston map, is Psince it receives phased contributions. The modulus of the "signal
dots'', being N times fainter at high illumination levels,
is therefore P/N. Their signal/background modulus contrast
is therefore
,
if P is the number of photons in the Dirac cloud. The modulus of the
central speckle, corresponding to the central dot of the high
level pattern (i.e. with an infinite number of photons), which is
the 3-dimensional auto-correlation of the piston map, is Psince it receives phased contributions. The modulus of the "signal
dots'', being N times fainter at high illumination levels,
is therefore P/N. Their signal/background modulus contrast
is therefore
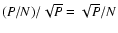 ,
and the
intensity contrast is
,
and the
intensity contrast is
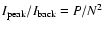 .
The
detection of a given signal dot with appreciable confidence
requires that this contrast be significantly higher than 1, a
condition which may be written P>N2.
.
The
detection of a given signal dot with appreciable confidence
requires that this contrast be significantly higher than 1, a
condition which may be written P>N2.
Since however N-1 output columns contain a signal dot
pertaining to a given piston value, fewer photons will be needed
in practice if the information from these output columns can be
combined, and the condition then becomes P>N. At least,
one photon event must be recorded from each sub-aperture, within
the full bandwidth.
One way of achieving such a combination involves multiple
correlations, as illustrated in Fig. 2. The
computational burden grows faster than the (N-1)th power of the
number of piston steps. We have not yet attempted to include this
correlation analysis in our simulations, and the results presented
here are therefore likely to be pessimistic in terms of the
limiting sensitivity and magnitude.
An alternate method, the 3-dimensional Fienup algorithm used by Martinache (2004),
does provide a global solution where the minimal number of photons
is approximately
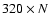 .
It may be that other, more
sensitive, methods will be found and will better approach the N photon limit mentioned above.
.
It may be that other, more
sensitive, methods will be found and will better approach the N photon limit mentioned above.
Since a star of given magnitude provides a number of photons P proportional to N, the limiting magnitude in this regime
would not depend on N. The condition P>N, is similar
to the limitation of a conventional Shack-Hartmann sensor using a
lens array of N elements, if the interferometer's
sub-apertures are assumed to match r0. Thus, with "dispersed-speckles'' piston sensing, an N-aperture diluted
interferometric array or hypertelescope can be phased with
adaptive optics and be expected to reach the same limiting
magnitude for the guide star as a monolithic adaptive telescope
having the same collecting area and N actuators.
![\begin{figure}
\par\rotatebox{360}
{\resizebox{7cm}{6cm}{\includegraphics[clip]{0270fig2.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg10.gif) |
Figure 2:
Statistical reconstruction of piston values from the output cube,
here shown in the case of a 5-aperture circle. N subsets
from the set of output columns (only 3 of 5 are shown here), each
related to a given "starting'' aperture, are extracted from the
cube and repositioned so that identical "target'' apertures
(indicated by arrows in the sketches at right) are aligned
vertically in separate layers. The set of signal dots in each
layer is, in principle, globally translated vertically according
to the piston value of the "starting'' aperture. This error can be
determined by intercorrelating the layers, using a multiple
correlation of order (N-1) applied to the vertical translations
along the columns. |
| Open with DEXTER |
Applications such as coronagraphy require a phasing accuracy
much better than 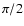 .
This takes more photons than calculated
above. Indeed, the background speckles in the output columns not
only affect the detection of the signal dots, when their level is
comparable, but also affect slightly the position of their
photocenter along the column, even when the signal dot is much
more intense than the neighbouring speckles.
.
This takes more photons than calculated
above. Indeed, the background speckles in the output columns not
only affect the detection of the signal dots, when their level is
comparable, but also affect slightly the position of their
photocenter along the column, even when the signal dot is much
more intense than the neighbouring speckles.
This effect of "dot pushing'' along a column of the output
cube can be crudely modelled locally by adding complex amplitude
distributions typical of a signal dot and of a fainter speckle
peak located close to it, within less than a speckle diameter.
Near both peaks, their moduli profiles along the column can be
approximated by a quadratic function of the
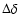 position relative to the true position of the signal dot. These can be expressed respectively as
position relative to the true position of the signal dot. These can be expressed respectively as
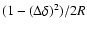 and
and
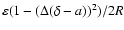 ,
a similar
approximation of the closest speckle, shifted by a along the
column and with relative modulus
,
a similar
approximation of the closest speckle, shifted by a along the
column and with relative modulus
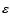 .
R is the
curvature radius of the peaks, of the order of the speckle size.
Depending on the phase difference, the complex addition tends to
displace the signal dot towards the contaminating speckle or away
from it. It has a neutral effect in the case of quadrature phase.
.
R is the
curvature radius of the peaks, of the order of the speckle size.
Depending on the phase difference, the complex addition tends to
displace the signal dot towards the contaminating speckle or away
from it. It has a neutral effect in the case of quadrature phase.
The displacement in the column direction is of the order of
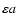 Pending refined calculations, a may be
taken as typically equal to the speckle size, thus indicating that
the signal dot's position error along the column is, in units of
the speckle size, of the order of
Pending refined calculations, a may be
taken as typically equal to the speckle size, thus indicating that
the signal dot's position error along the column is, in units of
the speckle size, of the order of
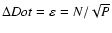 .
Since the speckle unit corresponds to the
high-illumination-level vertical resolution of piston
measurements, which is
.
Since the speckle unit corresponds to the
high-illumination-level vertical resolution of piston
measurements, which is
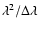 ,
the
piston measurement accuracy in length units is
,
the
piston measurement accuracy in length units is
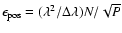 .
.
If measurements from the N signal dots carrying information
on a given piston are combined, for example as shown in Fig. 2 the error drops as 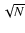 ,
thus becoming
,
thus becoming
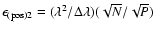 .
If the array is expanded by adding apertures, the star magnitude being fixed, then P = k N and
.
If the array is expanded by adding apertures, the star magnitude being fixed, then P = k N and
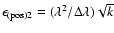 remains constant. If instead the sub-aperture sizes are changed along with their number to keep a constant collecting area, then P is
constant on a given star and
remains constant. If instead the sub-aperture sizes are changed along with their number to keep a constant collecting area, then P is
constant on a given star and
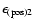 varies as
varies as
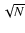 .
Figure 4 shows that these
expressions are consistent with the simulation results in the
region where the
.
Figure 4 shows that these
expressions are consistent with the simulation results in the
region where the
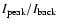 contrast is moderate,
less than 100, which is the region of practical interest. At the
higher contrast values, the analytical expression overestimates
markedly the contrast. A good reason for this discrepancy is that
the analytical derivation ignores the presence of side-lobes
associated with each signal dot even at high photon levels, a
consequence of the data cube's finite size. The contamination can
be attenuated, if needed when dealing with many apertures, by
apodizing the data cube. Its two image dimensions are naturally
apodized if the image envelope is smaller than the pixel array.
contrast is moderate,
less than 100, which is the region of practical interest. At the
higher contrast values, the analytical expression overestimates
markedly the contrast. A good reason for this discrepancy is that
the analytical derivation ignores the presence of side-lobes
associated with each signal dot even at high photon levels, a
consequence of the data cube's finite size. The contamination can
be attenuated, if needed when dealing with many apertures, by
apodizing the data cube. Its two image dimensions are naturally
apodized if the image envelope is smaller than the pixel array.
The relations found between the accuracy of piston measurements,
the number of apertures and the number of photons collected do not
depend on the range of piston values. A larger range obviously
requires a denser sampling of the input cube, along the wavenumber
axis, so as to resolve highly tilted fringes. More spectral
channels are therefore needed in the instrument, within a given
spectral range, but our equations indicate that the accuracy of
piston measurements remains constant if the total number of
photons detected within this range is kept constant.
We have simulated the formation of the spectro-images or
data cube by calculating a series of 2-dimensional Fourier
transforms from the complex amplitude pattern in the aperture,
where a single point is assigned to each sub-aperture. Incremental
wavenumbers 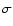 are used for each Fourier transform. Instead
of doing the chromatic re-scaling post-detection, as will be done
when using the real instrument, the simulation does it directly
when calculating the image, by modifying the classical phase
expression 2
are used for each Fourier transform. Instead
of doing the chromatic re-scaling post-detection, as will be done
when using the real instrument, the simulation does it directly
when calculating the image, by modifying the classical phase
expression 2
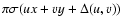 in the formulation
of the Fourier transform. Instead, the chromatically re-scaled
series of Fourier transforms are here expressed as:
in the formulation
of the Fourier transform. Instead, the chromatically re-scaled
series of Fourier transforms are here expressed as:
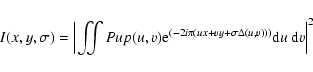 |
(1) |
where I is the image intensity, Pup(u, v) describes the
interferometer entrance pupil configuration,
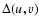 is the
optical path difference resulting from static piston values and
the atmospheric turbulence, x and y are the spatial
frequencies in the Fourier domain,
is the
optical path difference resulting from static piston values and
the atmospheric turbulence, x and y are the spatial
frequencies in the Fourier domain,
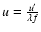 ,
,
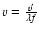 ,
,
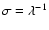 and f (the
focal length) is included in
and f (the
focal length) is included in 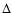 .
The monochromatic images,
thus re-scaled and calculated at incremental values of
.
The monochromatic images,
thus re-scaled and calculated at incremental values of 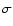 ,
are numerically stacked and Poisson sampled to generate the
simulated "input cube'' having limited photon count. Its
3-dimensional Fourier transform is then calculated to generate the
output cube where signal dots may be searched in those columns
which are located at the auto-correlation points of the aperture.
,
are numerically stacked and Poisson sampled to generate the
simulated "input cube'' having limited photon count. Its
3-dimensional Fourier transform is then calculated to generate the
output cube where signal dots may be searched in those columns
which are located at the auto-correlation points of the aperture.
The 3-dimensional Fourier transform producing the output cube may
then be expressed as:
output(u, v, z) = 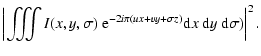 |
(2) |
The "output cube'' is simply the 3 dimensional Fourier transform of
the dispersed image cube (Fig. 1).
3 Minimal photon count found from numerical simulations
As discussed in Sect. 2.2, a photon-starved data cube generates a degraded output cube where a speckled background affects the visibility of the signal dots. Measuring the position of a signal dot along its column to derive the corresponding piston value first requires that the dot be correctly identified among the speckles. The confidence level improves with the peak/background contrast. If the dot is correctly identified, the
accuracy of the piston measurement remains affected by the dot's deformation, induced by the neighbouring speckles.
Our simulation code calculates the peak/background contrast of signal dots and then finds, from a series of exposures made with a single frozen piston map, the dispersion of the piston measurements, indicative of the accuracy reachable. At this stage however, no attempt was made to exploit the piston information redundancy mentioned in Sect. 2.2, and the sensitivity estimates given here are therefore pessimistic. Trial and error indicated the photon count needed to achieve piston measurements accurate enough for: 1) diffraction-limited imaging, according to Rayleigh's 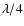 classical tolerance (i.e. 0.1 to 0.2
classical tolerance (i.e. 0.1 to 0.2 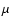 m at visible wavelengths); and 2) coronagraphic imaging with
m at visible wavelengths); and 2) coronagraphic imaging with
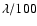 tolerance (i.e. 4 to 8 nm at visible wavelengths).
tolerance (i.e. 4 to 8 nm at visible wavelengths).
We present here results for ring arrays having 3 to 10 apertures. In cases with an even number N of apertures we locate N-1 apertures on a ring and one at the center to make the configuration non-redundant. All the simulations are made with 64 wavelengths. As expected, the number of spectral channels, adjacent within the 400-800 nm visible bandwidth utilized, influences the maximal piston value but not the minimal photon
count. The photon counts are specified per data cube.
We have looked at the column profiles in order to determine the minimal photon count needed to detect the signal dot. Typical column profiles are shown for ring pupils with six apertures (Fig. 3). As expected, the column background, normalized to the
intensity of the signal peak, is dark at high photon level and speckled at lower levels.
Figure 4 indicates the evolution of the peak's contrast
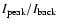 averaged on all the N(N-1) active columns versus the number of apertures, at constant total photon count. With 6 apertures, 320 photons per cube or 54 photons per aperture are needed to recover piston values as can be seen on top of Fig. 3. The average (S/N) is approximately 8. In Fig. 4, a signal/noise ratio S/N higher than 4 in each column, provides a sufficient confidence level for distinguishing signal from noise. The ratio
averaged on all the N(N-1) active columns versus the number of apertures, at constant total photon count. With 6 apertures, 320 photons per cube or 54 photons per aperture are needed to recover piston values as can be seen on top of Fig. 3. The average (S/N) is approximately 8. In Fig. 4, a signal/noise ratio S/N higher than 4 in each column, provides a sufficient confidence level for distinguishing signal from noise. The ratio
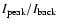 varies from column to column but its average on all the columns has to be larger than 5. With 10 apertures, a total of 960 photons, thus 96 photons per aperture (at the bottom
of Fig. 3), are needed. The ratio
varies from column to column but its average on all the columns has to be larger than 5. With 10 apertures, a total of 960 photons, thus 96 photons per aperture (at the bottom
of Fig. 3), are needed. The ratio
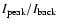 ,
which is approximately equal to 8, is averaged on all the active columns within the data cube, thus, for some of them, less than 960 photons will suffice to determine the piston values. The minimal number of photons providing detectable signal dots in the output columns, and therefore measurable piston values, in each aperture configuration, are summarized in Fig. 5 (curve labelled minimum) and in Table 1.
,
which is approximately equal to 8, is averaged on all the active columns within the data cube, thus, for some of them, less than 960 photons will suffice to determine the piston values. The minimal number of photons providing detectable signal dots in the output columns, and therefore measurable piston values, in each aperture configuration, are summarized in Fig. 5 (curve labelled minimum) and in Table 1.
![\begin{figure}
\par\resizebox{7cm}{6cm}{\includegraphics[clip]{0270fig3.ps}}\par\resizebox{7cm}{6cm}{\includegraphics[clip]{0270fig3_bis.ps}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg35.gif) |
Figure 3:
Intensity along one active column with no noise (solid lines) and with one realization of photon noise (dotted lines) Top: with 320 photons per cube for six apertures arranged as shown. Bottom: with 1600 photons per cube for ten apertures
arranged as shown. |
| Open with DEXTER |
![\begin{figure}
\par\rotatebox{270}{\resizebox{6cm}{8.8cm}{\includegraphics[clip]{0270fig4.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg36.gif) |
Figure 4:
Contrast of the signal dots with 3 to 10 apertures. Curves with line points show simulations with, from top to bottom, 6400 photons, 3200 photons, 1600 photons, 960 photons and 640 photons per cube. From top right to bottom, curves without line
points are based on theory, showing cases with 6400 photons, 3200 photons, 1600 photons and 960 photons per cube. |
| Open with DEXTER |
![\begin{figure}
\par\rotatebox{270}{\resizebox{6cm}{8.8cm}{\includegraphics[clip]{0270fig5.ps}} }\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg37.gif) |
Figure 5:
From top to bottom: evolution of the number of photon needed in order to do coronagraphy, imaging and recover signal from noise with 3 to 10 apertures. |
| Open with DEXTER |
Our estimates for the accuracy of the piston measurements are summarized in Fig. 5 and in Table 1. With 6 apertures, precisions better than
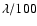 are achieved with
are achieved with
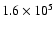 photons per data cube or
photons per data cube or
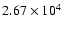 per aperture. With 10 aperture, precisions better than
per aperture. With 10 aperture, precisions better than
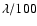 are reached with
are reached with
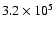 photons per data cube or
photons per data cube or
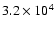 per aperture. With 6 apertures, precisions better than
per aperture. With 6 apertures, precisions better than 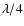 are achieved with
are achieved with
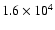 photons per data cube or 2667 per aperture. In the case of an interferometer with 10 apertures
photons per data cube or 2667 per aperture. In the case of an interferometer with 10 apertures
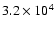 photons per data cube or 3200 per aperture are needed so
as to reach
photons per data cube or 3200 per aperture are needed so
as to reach 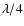 accuracy.
accuracy.
Table 1:
Evolution of the number of photons, limiting magnitudes and Strehl ratio in function of the number of apertures and in function of the considered mode. Imaging and
coronagraphic modes require respectively precision of 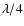 and
and
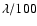 .
From left to right: 1- number of apertures; 2- minimum, imaging or coronagraphic modes; 3- number of photons needed to achieve the required precision; 4- limiting stellar
magnitude for an optical bandwidth of
.
From left to right: 1- number of apertures; 2- minimum, imaging or coronagraphic modes; 3- number of photons needed to achieve the required precision; 4- limiting stellar
magnitude for an optical bandwidth of
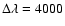 Åand for a constant aperture diameter of 8 m; 5- limiting stellar magnitude for a collecting surface of 150 m2 (
Åand for a constant aperture diameter of 8 m; 5- limiting stellar magnitude for a collecting surface of 150 m2 (
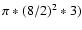 ;
6- Strehl ratio.
;
6- Strehl ratio.
We used the numbers of photons indicated by the simulations to calculate
the stellar magnitudes reachable. The limiting stellar magnitude mv for guide stars, again in the same
pessimistic case, is calculated with Muller & Buffington's expression (Muller & Buffington 1974).
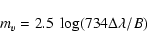 |
(3) |
where
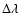 is the total optical bandwidth in Ä and
B is the photon flux per cm2.
is the total optical bandwidth in Ä and
B is the photon flux per cm2.
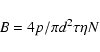 |
(4) |
where p is the number of photons, d is the diameter of sub-apertures in cm, 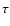 is the seeing lifetime,
is the seeing lifetime, 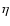 is the overall quantum efficiency.
For the numerical calculations we use
is the overall quantum efficiency.
For the numerical calculations we use
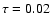 s and
s and
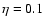 .
We have chosen the third dimension of our input cube as:
.
We have chosen the third dimension of our input cube as:
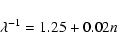 |
(5) |
with n = 0 to 63 for 64 wavelengths, thus
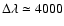 Å.
Å.
The results are summarized in Table 1 and in Fig. 6, for a constant sub-aperture size of 8 m or for a constant collecting interferometer area. The varying sub-aperture size in the latter case, in the presence of adaptive optics within
the sub-apertures, changes the optimal exposure duration. The simulation curves however use fixed exposures. Basically, more apertures require more photons. Figure 6 shows, for a given number of apertures, a gap of 2 mag (particularly for 10 apertures) between imaging and coronagraphy curves. Indeed, if the diameter of sub-apertures d is constant, with 10 apertures,
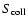 (the collecting interferometer area) increases significantly (
(the collecting interferometer area) increases significantly (
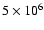 cm2) compared to the case where d
varies in order to keep
cm2) compared to the case where d
varies in order to keep
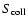 constant.
constant.
![\begin{figure}
\par\rotatebox{270}
{\resizebox{6cm}{8.8cm}{\includegraphics[clip]{0270fig6.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg55.gif) |
Figure 6:
From top to bottom: evolution of the limiting stellar magnitudes for coronagraphy, for imaging and for minimal signal detection, with 3 to 10 apertures. Solid curves correspond to interferometers with a constant collecting area of 150 m2 and
dotted lines to a constant 8 m-aperture size. Exposures last 0.02 s and the global quantum efficiency is 10%. |
| Open with DEXTER |
In order to have an idea of the performance attainable, we have calculated the
signal attenuation obtained with the accuracy
levels found above for the coronagraphic, imaging and minimum modes (see Table 1). Considering four 8 m telescopes, organized as the 4 UTs (Unit Telescope) of the Very Large Telescope Interferometer (VLT), the signal attenuation is approximately equal to 98%, 95% and 52% respectively for
coronagraphy, imaging and recover signal from noise, the number of photons per cube being respectively
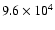 ,
,
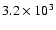 and 100, and the stellar magnitude 12.72, 16.42 and 19.91.
and 100, and the stellar magnitude 12.72, 16.42 and 19.91.
Pending more complete simulations of our method, it can be remarked that the signal attenuation is not much degraded when the number of apertures increases if the total number of photons remains higher than
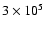 photons per data cube. With 10 apertures and
photons per data cube. With 10 apertures and
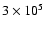 per cube, the signal attenuation is above 70%.
per cube, the signal attenuation is above 70%.
4 Discussion and future prospects
The method allows phasing apertures efficiently with a wave sensor instrument which can also serve as the science camera. The case of redundant apertures, discussed elsewhere, is of possible interest for compact mosaic mirrors such as those of the Keck and Grantecan telescopes, as well as their Extremely Large Telescope successors. These have required edge sensors to position the mirror segments, but they may become unnecessary with the
dispersed-speckles method if guide stars are available.
The VIDA (VLTI Imaging with a Densified Array) mode of hypertelescope observing proposed for the VLT interferometer (Lardière et al. 2002) may also benefit from the global piston measurement achieved with the dispersed-speckles method, in spite of the small
number of apertures. It consists of coupling the VLT telescopes using a densified pupil mode. When the global reduction algorithm, exploiting the redundant information in output columns, will be fully optimized and coded for simulations, it will be of interest
to compare with other multi-aperture piston sensing methods, such as those of (Pedretti 1999), where beams are combined triplet-wise hierachically (hereafter called method 1), pair-wise (method 2) or with 2-dimensional Fourier transforms (method 3) for non redundant configurations. The signal attenuations were about 52%, 99% and
98% respectively for the 3 methods and for
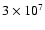 photons, 8 wavelengths and 27 apertures. For
photons, 8 wavelengths and 27 apertures. For
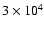 photons, these signal attenuations remain unchanged
photons, these signal attenuations remain unchanged
On Earth the method may be applied for active or adaptive piston sensing. Output cubes, calculated from short exposures, can be co-added to gain sensitivity. The signal dot in each column moves in response to the phase shifts of seeing and the shadow pattern.
The time-integrated dot is therefore widened but gives the average piston value, usable for active optics. If detectable, the short-exposure dot can also be exploited to activate fast actuators for adaptive piston correction.
For coronagraphs the correction is perhaps best with wave sensing achieved coarsely before the coronagraph and finely with an additional wave sensor probing the residual speckles after the coronagraph. The "dispersed speckles'' method is applicable in both
stages. One or preferably two stages of actuators provide the correction, preferably before and after the coronagraph (Codona & Angel 2004, submitted; Labeyrie 2004, in preparation). These results are encouraging and justify laboratory testing.
5 Conclusion
Unlike the established wavefront sensing methods, such as the Shack-Hartmann, requiring
continuous optical surfaces, the dispersed-speckles method is applicable to multi-aperture
imaging interferometers of arbitrary dilution and particularly to those providing
hypertelescope images, with a densified pupil. Theory and the preliminary simulations
reported here are consistent and indicate that a high sensitivity, approaching that of
Shack-Hartmann sensing, can be expected. Limiting magnitudes of the order of 23.7
appear attainable for the guide star in the case of the VIDA hypertelescope imager
proposed for the VLTI if each sub-aperture is already corrected with
conventional adaptive optics. This is also consistent with the simulation
results of (Martinache 2004), using a different mathematical algorithm
for data reduction. Both indicate that largenumbers of
sub-apertures can be used, and the method therefore seems applicable to the mosaic mirrors of Keck and various proposed successors, for which edge sensors may become unnecessary in the presence of adequate guide stars. The method is also of interest for the demanding needs of coronagraphy, with instruments such as the Exo-Earth Discoverer, a proposed space hypertelescope designed for detecting Exo-Earths (Labeyrie 2002). A simple prototype of an instrument to test these principles has been built by some of us (AL, VB). The results will be reported on separately (Borkowski et al., in preparation).
Acknowledgements
The authors are grateful to Ettore Pedretti for helpful discussions. This paper is part of the Ph.D. Thesis of V. Borkowski.
- Borkowski, V.,
Martinache, F., Peterson, D., & Labeyrie, A. 2002, Proc. ESLAB
36 Symposium, Earth-Like Planets and Moons, ESTEC, Noodwijk, 514,
273
- Codona, J. L., &
Angel, R. 2004, ApJ, submitted
- Dainty J. C. 1974,
MNRAS, 169, 631 (In the text)
- Hartmann J. 1900, Z.
Instrumenkd, 20, 47
- Koechlin L.,
Lawson, P. R., Mourard, D., et al. 1996, Appl. Opt., 35,
3002 (In the text)
- Labeyrie, A. 1996,
A&AS, 118, 517 (In the text)
- Labeyrie, A., Borkowski,
V., Martinache, F., et al. 2002, Proc. ESO Venice Conf.,
Beyond Conventional Adaptive Optics, 58, 109
(In the text)
- Labeyrie, A.
2002, Proc. ESLAB 36th Symp., Earth-Like Planets and Moons, ESTEC,
245
- Lardière, O.,
Dejonghe, J., Riaud, P., et al. 2002, ASP Conf. Ser., 266,
608
- Lardière, O.,
Labeyrie, A., Mourard, D., et al. 2002, Poc. SPIE, 4838,
1018 (In the text)
- Martinache, F. 2004, J.
Opt. A: Pure Appl. Opt., 6, 216 [CrossRef] (In the text)
- Michelson, A. A., &
Pease, F. G. 1921, AJ, 53, 249 [CrossRef] (In the text)
- Muller, R. A., &
Buffington, A. 1974, J. Opt. Soc. Am., 64, 9 (In the text)
- Pedretti, E., &
Labeyrie, A. 1999, A&AS, 137, 543
- Pedretti, E. 1999, ASP
Conf. Ser., 194, 271 (In the text)
- Roddier, F. 1988, Appl. Opt,
27, 1223
- Shook P. V., &
Platt, B. C. 1971, J. Opt. Soc. Am., 61, 656
Copyright ESO 2004
![\begin{figure}
\par\rotatebox{360}
{\resizebox{14cm}{9cm}{\includegraphics[clip]{0270fig1.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg5.gif)
![\begin{figure}
\par\rotatebox{360}
{\resizebox{7cm}{6cm}{\includegraphics[clip]{0270fig2.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg10.gif)
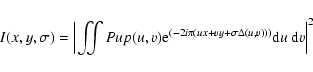
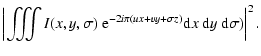
![\begin{figure}
\par\resizebox{7cm}{6cm}{\includegraphics[clip]{0270fig3.ps}}\par\resizebox{7cm}{6cm}{\includegraphics[clip]{0270fig3_bis.ps}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg35.gif)
![\begin{figure}
\par\rotatebox{270}{\resizebox{6cm}{8.8cm}{\includegraphics[clip]{0270fig4.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg36.gif)
![\begin{figure}
\par\rotatebox{270}{\resizebox{6cm}{8.8cm}{\includegraphics[clip]{0270fig5.ps}} }\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg37.gif)
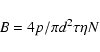
![\begin{figure}
\par\rotatebox{270}
{\resizebox{6cm}{8.8cm}{\includegraphics[clip]{0270fig6.ps}}}\end{figure}](/articles/aa/full/2005/02/aa0270-04/Timg55.gif)