A&A 429, 161-172 (2005)
DOI: 10.1051/0004-6361:20041023
A family of models of partially relaxed stellar systems
I. Dynamical properties
M. Trenti1 -
G. Bertin2
1 - Scuola Normale Superiore, Piazza dei Cavalieri 7,
56126 Pisa, Italy
2 -
Dipartimento di Fisica, Università di Milano, via
Celoria 16, 20133 Milano, Italy
Received 5 April 2004 / Accepted 27 August 2004
Abstract
Recently we have found that a family of models of
partially relaxed, anisotropic stellar systems, inspired earlier by
studies of incomplete violent relaxation, exhibits some interesting
thermodynamic properties. Here we present a systematic investigation
of its dynamical characteristics, in order to establish the basis for
a detailed comparison with simulations of collisionless collapse,
planned for a separate paper. For a full comparison with the
observations of elliptical galaxies, the models should be extended to
allow for the presence a sizable dark halo and of significant
rotation. In the spherical limit, the family is characterized by two
dimensionless parameters, i.e.  ,
measuring the depth of the
galaxy potential, and
,
measuring the depth of the
galaxy potential, and  ,
defining the form of a third global
quantity Q, which is argued to be approximately conserved during
collisionless collapse (in addition to the total energy and the total
number of stars).
,
defining the form of a third global
quantity Q, which is argued to be approximately conserved during
collisionless collapse (in addition to the total energy and the total
number of stars).
The family of models is found to have the following properties.
The intrinsic density profile beyond the half-mass radius rM is
basically universal and independent of  .
The projected
density profiles are well fitted by the R1/n law, with nranging from 2.5 to 8.5, dependent on
.
The projected
density profiles are well fitted by the R1/n law, with nranging from 2.5 to 8.5, dependent on  ,
with n close
to 4 for concentrated models. All models exhibit radial anisotropy
in the pressure tensor, especially in their outer parts, already
significant at
,
with n close
to 4 for concentrated models. All models exhibit radial anisotropy
in the pressure tensor, especially in their outer parts, already
significant at
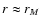 .
At fixed values of
.
At fixed values of  ,
models
with lower
,
models
with lower  are more anisotropic; at fixed values of
are more anisotropic; at fixed values of  ,
models with lower
,
models with lower  are more concentrated and more
anisotropic. When the global amount of anisotropy, measured by
are more concentrated and more
anisotropic. When the global amount of anisotropy, measured by
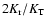 ,
is large, the models are unstable with respect to the
radial-orbit instability; still, a wide region of parameter space
(i.e., sufficiently high values of
,
is large, the models are unstable with respect to the
radial-orbit instability; still, a wide region of parameter space
(i.e., sufficiently high values of  ,
for
,
for 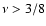 )
is
covered by models that are dynamically stable; for these, the line
profiles (line-of-sight velocity distribution) are Gaussian at the
)
is
covered by models that are dynamically stable; for these, the line
profiles (line-of-sight velocity distribution) are Gaussian at the
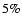 level, with a general trend of positive values of h4 at
radii larger than the effective radius
level, with a general trend of positive values of h4 at
radii larger than the effective radius 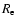 .
.
Key words: stellar dynamics - galaxies: evolution - galaxies:
formation - galaxies: kinematics and dynamics - galaxies:
structure
A simple picture for the incomplete violent relaxation of stellar
systems considers the collapse of a dynamically cold cloud of
stars or star-clumps initially far from equilibrium. The study of
this ideal and relatively simple process, pioneered by important
analysis in the 60s (starting with Lynden-Bell 1967) and simulations
in the 80s (see van Albada 1982), is still incomplete. A proper
understanding of such process is a prerequisite to more ambitious
attempts at constructing physically justified models of elliptical
galaxies in which the problem of galaxy formation is set in the
generally accepted cosmological context of hierarchical
clustering.
Before the development of such cosmological scenarios, a first
step (in the direction of incorporating in a simple analytical and
physically justified framework the clues gathered from simulations
of collisionless collapse) had been taken in terms of the
so-called
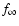 models (Bertin & Stiavelli 1984). These
models are constructed from a distribution function which, in the
spherical limit, reduces to
models (Bertin & Stiavelli 1984). These
models are constructed from a distribution function which, in the
spherical limit, reduces to
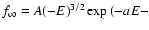 cJ2/2), for negative values of E, and vanishes for positive
values of E; here A, a, and c are positive constants and
E and J denote the specific star energy and angular momentum.
cJ2/2), for negative values of E, and vanishes for positive
values of E; here A, a, and c are positive constants and
E and J denote the specific star energy and angular momentum.
From those earlier investigations, it immediately became clear
that the physical clues gathered from the picture of collisionless
collapse (i.e., that incomplete violent relaxation leads to
systems that are well relaxed in their inner regions, 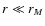 ,
and characterized by radially anisotropic envelopes for
,
and characterized by radially anisotropic envelopes for 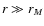 )
do not lead uniquely to the
)
do not lead uniquely to the
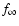 models, but instead
identify a wide class of attractive distribution functions of
which
models, but instead
identify a wide class of attractive distribution functions of
which
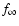 represents just one simple and interesting
case. At that time, the primary goal of a series of investigations
(described, e.g., by Bertin & Stiavelli 1993) was to test whether
the models inspired by studies of collisionless collapse were
realistic and thus could serve as a useful tool to interpret the
observations. Indeed, the
represents just one simple and interesting
case. At that time, the primary goal of a series of investigations
(described, e.g., by Bertin & Stiavelli 1993) was to test whether
the models inspired by studies of collisionless collapse were
realistic and thus could serve as a useful tool to interpret the
observations. Indeed, the
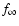 models turned out to
"explain'' the R1/4 luminosity law (de Vaucouleurs 1948) and,
extended to the two-component case, were used successfully to
probe the presence and size of dark halos in elliptical galaxies.
models turned out to
"explain'' the R1/4 luminosity law (de Vaucouleurs 1948) and,
extended to the two-component case, were used successfully to
probe the presence and size of dark halos in elliptical galaxies.
Because of the focus on such astronomical applications, the
problem of a detailed comparison between the
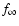 or other
models and the products of collisionless collapse from N-body
simulations was given lower priority and basically left aside.
Yet, it was pointed out that, with respect to the products of
numerical simulations of collisionless collapse, the
or other
models and the products of collisionless collapse from N-body
simulations was given lower priority and basically left aside.
Yet, it was pointed out that, with respect to the products of
numerical simulations of collisionless collapse, the
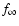 models had the undesired feature of being too isotropic. Some
authors (Merritt et al. 1989) thus suggested that the
models had the undesired feature of being too isotropic. Some
authors (Merritt et al. 1989) thus suggested that the
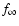 models
should be extended to and used in the parameter domain where a <
0; however, this attempt failed, not only because a proper
physical justification was lacking, but especially because such
"negative-temperature'' models suffer from the opposite
difficulty, i.e. they were shown to be so anisotropic that they
are violently unstable and bound to evolve on a time scale even
smaller than the typical crossing time.
models
should be extended to and used in the parameter domain where a <
0; however, this attempt failed, not only because a proper
physical justification was lacking, but especially because such
"negative-temperature'' models suffer from the opposite
difficulty, i.e. they were shown to be so anisotropic that they
are violently unstable and bound to evolve on a time scale even
smaller than the typical crossing time.
In a recent paper (Bertin & Trenti 2003) we have revisited the problem of
the structure and dynamics of partially relaxed stellar systems
starting from a thermodynamic description. In view of the paradigm
of the gravothermal catastrophe (see Antonov 1962; Lynden-Bell & Wood
1968; Katz 1978,1979,1980), we found it appropriate
to approach the problem in terms of the so-called  models (for a definition, see following Sect. 2); with respect to
the
models (for a definition, see following Sect. 2); with respect to
the
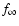 models, the
models, the  models follow from a
statistical mechanical derivation (Stiavelli & Bertin 1987) that is formally
straightforward, while they are also known to have generally
similar and reasonably realistic structural properties. It should
be noted that the dynamical properties of the
models follow from a
statistical mechanical derivation (Stiavelli & Bertin 1987) that is formally
straightforward, while they are also known to have generally
similar and reasonably realistic structural properties. It should
be noted that the dynamical properties of the  models
had not been studied earlier in detail. Such recent investigation,
focusing on the issue of the gravothermal catastrophe, convinced
us that the
models
had not been studied earlier in detail. Such recent investigation,
focusing on the issue of the gravothermal catastrophe, convinced
us that the  models do have many attractive features;
in particular, these models turn out to have a higher degree of
radial pressure anisotropy with respect to the
models do have many attractive features;
in particular, these models turn out to have a higher degree of
radial pressure anisotropy with respect to the
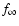 models, making them more suitable to describe the results of
simulations of collisionless collapse. Such encouraging
preliminary inspection was the basis for a thorough study that we
have thus performed and that we present here.
models, making them more suitable to describe the results of
simulations of collisionless collapse. Such encouraging
preliminary inspection was the basis for a thorough study that we
have thus performed and that we present here.
In this paper we provide a systematic description of the dynamical
properties of the  models. In the spherical limit,
these models define a two-parameter family, characterized by
the dimensionless parameter
models. In the spherical limit,
these models define a two-parameter family, characterized by
the dimensionless parameter  ,
measuring the depth of the
galaxy potential, and the dimensionless parameter
,
measuring the depth of the
galaxy potential, and the dimensionless parameter  ,
defining
the form of a third global quantity Q (which is argued to be
approximately conserved during collisionless collapse, in addition
to the total energy and the total number of stars; see Sect. 2 for
the relevant definitions). In Sect. 3 we present intrinsic and
projected density profiles and fit the latter structural
characteristics in terms of the R1/n law (Sersic 1968). We
then proceed to illustrate in detail their phase space properties,
in particular by calculating the relevant pressure tensor
profiles, the pressure anisotropy content, the projected velocity
dispersion profiles, the line profiles (line-of-sight velocity
distribution), and the relevant phase space densities N(E, J2)and N(E) (Sect. 4). In Sect. 5 we examine the stability of the
models with respect to the radial orbit instability, not only by
inspection of well-known global anisotropy indicators, but also
with the aid of a number of N-body simulations. In
Sect. 6 we perform a first test of the viability of
these models by applying them to the observed properties of
NGC 3379, a galaxy that is characterized by lack of significant
rotation and is likely to possess only small amounts of dark
matter. The conclusions are drawn in Sect. 7.
,
defining
the form of a third global quantity Q (which is argued to be
approximately conserved during collisionless collapse, in addition
to the total energy and the total number of stars; see Sect. 2 for
the relevant definitions). In Sect. 3 we present intrinsic and
projected density profiles and fit the latter structural
characteristics in terms of the R1/n law (Sersic 1968). We
then proceed to illustrate in detail their phase space properties,
in particular by calculating the relevant pressure tensor
profiles, the pressure anisotropy content, the projected velocity
dispersion profiles, the line profiles (line-of-sight velocity
distribution), and the relevant phase space densities N(E, J2)and N(E) (Sect. 4). In Sect. 5 we examine the stability of the
models with respect to the radial orbit instability, not only by
inspection of well-known global anisotropy indicators, but also
with the aid of a number of N-body simulations. In
Sect. 6 we perform a first test of the viability of
these models by applying them to the observed properties of
NGC 3379, a galaxy that is characterized by lack of significant
rotation and is likely to possess only small amounts of dark
matter. The conclusions are drawn in Sect. 7.
This paper also sets the basis for a detailed comparison between
the  family of models and the products of collisionless
collapse resulting from N-body simulations, to be presented in a
follow-up paper. For a full comparison with the observations of
elliptical galaxies, the models should be extended to allow for
the presence of a sizable dark halo and of significant rotation.
family of models and the products of collisionless
collapse resulting from N-body simulations, to be presented in a
follow-up paper. For a full comparison with the observations of
elliptical galaxies, the models should be extended to allow for
the presence of a sizable dark halo and of significant rotation.
The need for anisotropic models to describe elliptical
galaxies can be traced back to the strong empirical arguments
that come from the observations of non-spherical geometry in the
absence of significant rotation (e.g., see the discussion provided
by Bertin & Stiavelli 1993, and references therein); to be sure, direct
evidence for pressure anisotropy in round systems is not easy to
obtain, because so far the observed line profiles show only modest
deviations from a Gaussian (e.g., see Gerhard et al. 2001).
The main goal of this paper is to study the properties of a given
specific dynamical context able to provide physical justification for
the existence of anisotropic equilibria, that is the dynamical
framework of collisionless collapse. The process of collisionless
collapse, together with its accompanying mechanism of incomplete
violent relaxation, is one (but not the only) element that is expected
to play an important role in the formation of stellar systems. In
spite of the many papers that have addressed issues related to such
dynamical context (in addition to the papers cited earlier in the
Introduction, e.g. see Shu 1978, 1987; Voglis 1994; Hjorth & Madsen 1995), it is not yet clear whether an analytically tractable
distribution function, or family of distribution functions, can be
assigned to the products of such collisionless collapse. This paper
tries to provide a contribution to this problem. At the same time, we
still need to establish how far the properties of such products, often
studied in a simplified one-component picture, would be from those of
observed stellar systems, and in which way.
An enormous amount of work has focused and is currently focusing on
the demands (on galactic structure) from the cosmological context. In
particular, this has led astronomers to look for the presence, in
observed objects, of cuspy density distributions of dark matter,
following a universal profile suggested by cosmological simulations
(see Navarro et al. 1997; Moore et al. 1998; Ghigna et al. 2000). Other studies have addressed the issue of the establishment
of the galaxy scaling laws (such as the Fundamental Plane for
elliptical galaxies; e.g., see Ghigna et al. 2000; Lanzoni et al. 2004)
in the accepted cosmological scenario. These demands are beyond the
scope of the present paper, but should eventually be faced, as a point
of contact between dynamical investigations of individual galaxies and
studies of the evolving universe from which they were formed.
In this respect, a point to be noted, to avoid unnecessary confusion
about the aims of purely dynamical studies, is the following. A
priori, studies of collisionless collapse within the line of research
adopted in this paper have nothing to say about some important issues
such as the establishment of the Fundamental Plane (but see
Gonzalez-Garcia & van Albada 2003; Nipoti et al. 2003), because the
relevant scaling laws depend on physics that goes beyond pure
dynamics, which is inherently scale-free. In turn, pure dynamical
studies can try to explain why galaxies prefer the R1/4 law,
which is a structural property, instead of just accepting it as an
empirical fact (as often done in a number of otherwise important
astrophysical studies).
Thus we would like to emphasize that this paper represents only one
step in the direction of a comparison with the observations. To deal
fruitfully with the presence of dark matter and other important
ingredients (such as significant rotation and the possible presence of
an additional disk component), one first has to master the properties
of one-component models, which, as shown in this paper, turn out to
exhibit a variety of interesting dynamical properties. In fact, it is
rewarding and a priori unexpected to find that, as a result of a
simple conjecture about the way to characterize incomplete violent
relaxation (the addition of Q to the natural constraints under which
Boltzmann entropy is extremized; see Sect. 2), one-component spherical
models are identified able to fit products of N-body simulations over
nine orders of magnitude in density (see Bertin & Trenti 2004) and,
at the same time, the observed photometric profile (over about ten
magnitudes) and the inner kinematic profile (inside 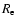 )
of the best
studied elliptical galaxy (see Sect. 6). Therefore, in spite of its
incompleteness, the stage reached so far is definitely interesting
from the physical point of view. Discrepancies with respect to the
observations play the welcome role of providing concrete indications
about the role of the ingredients that are a priori ignored by
the purely dynamical and highly simplified picture considered in this
paper.
)
of the best
studied elliptical galaxy (see Sect. 6). Therefore, in spite of its
incompleteness, the stage reached so far is definitely interesting
from the physical point of view. Discrepancies with respect to the
observations play the welcome role of providing concrete indications
about the role of the ingredients that are a priori ignored by
the purely dynamical and highly simplified picture considered in this
paper.
2 Model construction and the relevant parameter
space
In the spherically symmetric limit, in order to allow for the
possibility that a stellar system is only partially relaxed, one
may extremize the Boltzmann entropy
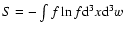 under the constraint that the total energy
under the constraint that the total energy
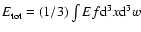 ,
the total mass
,
the total mass
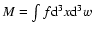 ,
and the additional quantity
,
and the additional quantity
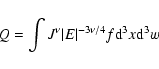 |
(1) |
are constant (Stiavelli & Bertin 1987). Here
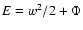 and
and
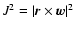 represent the specific energy and the
specific angular momentum square of a single star subject to a
spherically symmetric mean potential
represent the specific energy and the
specific angular momentum square of a single star subject to a
spherically symmetric mean potential 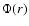 .
(We have decided to
use the symbol w, instead of v, for the velocity variable so as to
avoid confusion with the symbol
.
(We have decided to
use the symbol w, instead of v, for the velocity variable so as to
avoid confusion with the symbol  .) If only
.) If only
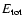 and M were
kept fixed, the extremization process would lead to a Maxwellian, that
is to an isothermal and isotropic distribution function, appropriate
for a fully relaxed system. Some arguments have been provided as to
why a quantity such as Q should be, at least approximately,
conserved (Stiavelli & Bertin 1987) and those will not be repeated here. In any
case, the conservation of Q should be taken as a conjecture. In a
follow-up paper (Trenti et al. in preparation) we will
discuss this problem further by examining a set of collapse
simulations, for which the conservation of Q will be tested.
and M were
kept fixed, the extremization process would lead to a Maxwellian, that
is to an isothermal and isotropic distribution function, appropriate
for a fully relaxed system. Some arguments have been provided as to
why a quantity such as Q should be, at least approximately,
conserved (Stiavelli & Bertin 1987) and those will not be repeated here. In any
case, the conservation of Q should be taken as a conjecture. In a
follow-up paper (Trenti et al. in preparation) we will
discuss this problem further by examining a set of collapse
simulations, for which the conservation of Q will be tested.
Such extremization leads to the following expression for the  distribution function:
distribution function:
![\begin{displaymath}
f^{(\nu)} = A \exp {\left[- a E - d \left(
\frac{J^2}{\vert E\vert^{3/2}}\right)^{\nu/2}\right]},
\end{displaymath}](/articles/aa/full/2005/01/aa1023/img57.gif) |
(2) |
where  ,
a, A, and d are positive real
constants. This set of constants provides two dimensional scales
(for example a mass scale
,
a, A, and d are positive real
constants. This set of constants provides two dimensional scales
(for example a mass scale
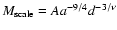 and
a reference radius
and
a reference radius
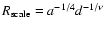 )
and two
dimensionless parameters. For the latter two quantities, we may
refer to
)
and two
dimensionless parameters. For the latter two quantities, we may
refer to  and
and
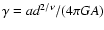 .
The
distribution function is taken to vanish for unbound orbits, that
is for E > 0.
.
The
distribution function is taken to vanish for unbound orbits, that
is for E > 0.
The two-parameter family of models is then constructed by solving
the Poisson equation:
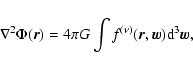 |
(3) |
for the potential 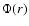 .
As briefly described by
Bertin & Trenti (2003), the solution is obtained numerically
after the equation has been cast in dimensionless form:
.
As briefly described by
Bertin & Trenti (2003), the solution is obtained numerically
after the equation has been cast in dimensionless form:
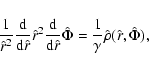 |
(4) |
with
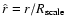 and
and
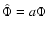 (for the adopted scaling, see the Appendix). The Poisson equation
is integrated with "initial'' conditions
(for the adopted scaling, see the Appendix). The Poisson equation
is integrated with "initial'' conditions
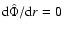 and
and
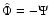 at r = 0 and the parameter
at r = 0 and the parameter 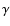 is
determined as an eigenvalue,
is
determined as an eigenvalue,
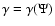 ,
in order to
satisfy the condition of Keplerian decay (
,
in order to
satisfy the condition of Keplerian decay (
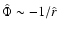 )
at large radii. The general behavior of the function
)
at large radii. The general behavior of the function
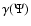 is similar to that of the corresponding function
for the
is similar to that of the corresponding function
for the
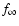 models; after some oscillations,
models; after some oscillations, 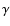 tends to a "plateau'' at large values of
tends to a "plateau'' at large values of  (as indicated by
Fig. 1).
(as indicated by
Fig. 1).
We have explored the parameter space
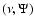 by means of an
equally spaced grid from
by means of an
equally spaced grid from 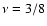 to
to 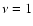 at steps of 1/8,
and from
at steps of 1/8,
and from 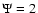 to
to 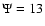 at steps of 0.2. A given model
will be denoted by the values of the two parameters
at steps of 0.2. A given model
will be denoted by the values of the two parameters
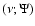 in parentheses.
in parentheses.
For given
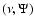 ,
once the solution for the potential
,
once the solution for the potential
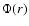 is obtained, it can be inserted in the expression of
is obtained, it can be inserted in the expression of
 ,
from which all the intrinsic and observable profiles and
properties of the model can be calculated. In particular the
density
,
from which all the intrinsic and observable profiles and
properties of the model can be calculated. In particular the
density 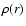 and the anisotropy profile
and the anisotropy profile 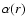 ,
defined
as
,
defined
as
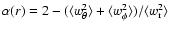 ,
require the evaluation
of a double integral over the velocity space (see also Bertin & Trenti 2003).
,
require the evaluation
of a double integral over the velocity space (see also Bertin & Trenti 2003).
The problem of constructing the line profiles F(w,R) for a given
distribution function of the form f(E,J2) is often discussed in the
literature (see Gerhard 1991, 1993; Carollo et al. 1995). The calculation requires
the evaluation of a triple integral (two integrations over the
velocity space orthogonal to the line of sight and one over the radial
coordinate along the line of sight), which we have performed
numerically with the same adaptive algorithm used to compute the
density (Berntsen et al. 1991). In practice, we have followed the procedure
described by Gerhard (1991). The calculation of the quantities
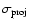 and h4 is then performed as described at the end of
Sect. 4.3, where they are introduced and defined.
and h4 is then performed as described at the end of
Sect. 4.3, where they are introduced and defined.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig1.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg75.gif) |
Figure 1:
Relation
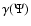 for the
for the  family of models,
for selected values of
family of models,
for selected values of  .
To fit the adopted frame, the .
To fit the adopted frame, the
 values corresponding to
values corresponding to 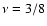 have been multiplied
by a factor 1/6 and the ones corresponding to
have been multiplied
by a factor 1/6 and the ones corresponding to 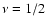 by a
factor 2/3.
by a
factor 2/3. |
| Open with DEXTER |
In the following we will often refer to the parameter  as
the concentration parameter. Strictly speaking, such term is
justified only at relatively large values of
as
the concentration parameter. Strictly speaking, such term is
justified only at relatively large values of  (
(
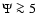 ).
).
A more intuitive measure of the central concentration of a model
is given by the ratio
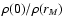 of the central density
to the value of the density attained at the half-mass radius
rM. As illustrated in Fig. 2, this ratio
is a monotonic increasing function of
of the central density
to the value of the density attained at the half-mass radius
rM. As illustrated in Fig. 2, this ratio
is a monotonic increasing function of  only beyond a minimum
at
only beyond a minimum
at
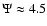 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig2.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg79.gif) |
Figure 2:
Density contrast between the center and the half-mass
radius along the equilibrium sequence for different values of
 .
The solid line refers to .
The solid line refers to 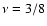 ;
at fixed ;
at fixed  ,
models
with higher values of ,
models
with higher values of  are less concentrated.
are less concentrated. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig3.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg83.gif) |
Figure 3:
Density profile of some representative  models, with
models, with 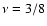 ,
1/2, and 1, and ,
1/2, and 1, and 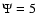 and 10. The most concentrated model corresponds to (3/8;10) and the least concentrated to (1;5). If the scales are fixed
so that
and 10. The most concentrated model corresponds to (3/8;10) and the least concentrated to (1;5). If the scales are fixed
so that
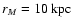 and
and
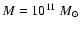 ,
the units
for the density are ,
the units
for the density are
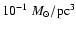 .
The density profiles overlap in the
outer parts, beyond a radius that becomes smaller and smaller as .
The density profiles overlap in the
outer parts, beyond a radius that becomes smaller and smaller as
 increases. In the plot we also record the
increases. In the plot we also record the 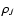 profile,
shown here on an arbitrary scale for a convenient comparison.
profile,
shown here on an arbitrary scale for a convenient comparison. |
| Open with DEXTER |
3 Density profiles
In this section we start with the discussion of the properties of
the density distribution.
In the outer parts, i.e. at radii such that 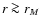 ,
the
density profile (Fig. 3) is basically the
same for all models of the
,
the
density profile (Fig. 3) is basically the
same for all models of the  family. In fact, the dimensionless
density associated with the
family. In fact, the dimensionless
density associated with the  distribution function can be
expressed, at large values of r, as:
distribution function can be
expressed, at large values of r, as:
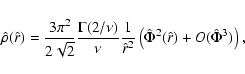 |
(5) |
where 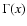 is the standard Gamma function Abramowitz & Stegun
(1965). Curiously, the 1/r4 behavior is found to
start from well inside the main body of the system, not too far
beyond rM, while the density distribution of the inner half of
the system is similar to that of an isothermal sphere. A power-law
of the form r-3.2 fits reasonably well the profiles in the
transition region from rM to 3rM.
is the standard Gamma function Abramowitz & Stegun
(1965). Curiously, the 1/r4 behavior is found to
start from well inside the main body of the system, not too far
beyond rM, while the density distribution of the inner half of
the system is similar to that of an isothermal sphere. A power-law
of the form r-3.2 fits reasonably well the profiles in the
transition region from rM to 3rM.
As the concentration parameter  increases, the point where
the density profiles merge into a profile common to all the models
sets in at smaller and smaller radii, so that for increasing
values of
increases, the point where
the density profiles merge into a profile common to all the models
sets in at smaller and smaller radii, so that for increasing
values of  the models appear to converge toward a common
(singular) model with a central cusp. In these respects, the
general behavior of the intrinsic density profiles is similar to
that of the
the models appear to converge toward a common
(singular) model with a central cusp. In these respects, the
general behavior of the intrinsic density profiles is similar to
that of the
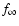 models. Therefore, the behavior of
concentrated models is well captured by the following simple
formula (Jaffe 1983):
models. Therefore, the behavior of
concentrated models is well captured by the following simple
formula (Jaffe 1983):
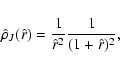 |
(6) |
as shown in Fig. 3. Here, and in the
remaining part of this subsection, a hat symbol denotes that a
quantity is expressed in a suitable dimensionless form, obviously with
no reference to the scaling procedure described after
Eq. (2).
In turn, low- models are characterized by a prominent core. In
fact, some models have density profiles close to that of the isochrone
model (Hénon 1959) or of the so-called perfect sphere (
models are characterized by a prominent core. In
fact, some models have density profiles close to that of the isochrone
model (Hénon 1959) or of the so-called perfect sphere (
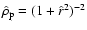 ). The core may be even represented by the
density profile of a Plummer sphere (Plummer 1915),
). The core may be even represented by the
density profile of a Plummer sphere (Plummer 1915),
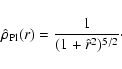 |
(7) |
These density profiles are mentioned to better illustrate the
properties of the mass distribution of the  models in terms of
well-known profiles. For a discussion of the merits and limitations of
physically based models (such as the
models in terms of
well-known profiles. For a discussion of the merits and limitations of
physically based models (such as the  models) with respect to
other models constructed on the basis of analytical convenience (e.g.,
see Merritt 1985; Hernquist 1990), the reader is referred to the review
article by Bertin & Stiavelli (1993). On the other hand, in relation
to phase-space properties, we should emphasize the following point. As
will be clear from Sect. 4, in the approach adopted in this paper (in
which the distribution function is constructed from physical
arguments) the final velocity dispersion and pressure anisotropy
profiles cannot be set independently, but follow from the
self-consistent solution. In other words, all the "observable"
profiles can be seen as consequences of the physical framework
considered. This is in sharp contrast with other modeling procedures
that are descriptive, rather than predictive (e.g., see Merritt 1985).
models) with respect to
other models constructed on the basis of analytical convenience (e.g.,
see Merritt 1985; Hernquist 1990), the reader is referred to the review
article by Bertin & Stiavelli (1993). On the other hand, in relation
to phase-space properties, we should emphasize the following point. As
will be clear from Sect. 4, in the approach adopted in this paper (in
which the distribution function is constructed from physical
arguments) the final velocity dispersion and pressure anisotropy
profiles cannot be set independently, but follow from the
self-consistent solution. In other words, all the "observable"
profiles can be seen as consequences of the physical framework
considered. This is in sharp contrast with other modeling procedures
that are descriptive, rather than predictive (e.g., see Merritt 1985).
3.2 The projected density profile
We have then proceeded to compute a library of projected density
profiles (which may be compared to observed luminosity profiles,
under the assumption of a constant M/L ratio). A first way to
characterize these profiles is to fit them with the R1/n law
(Sersic 1968). Such fit has been performed over a very wide radial
range, from
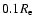 to
to
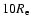 .
It shows that the
.
It shows that the  family is well represented by the R1/n law, with the index
n ranging from 2.5 to 8.5 (see Fig. 4; the
slightly bumpy behavior of the
family is well represented by the R1/n law, with the index
n ranging from 2.5 to 8.5 (see Fig. 4; the
slightly bumpy behavior of the 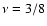 curve just reminds us
of the uncertainties associated with the best-fit determination of
n). The n = 4 behavior, characteristic of the de Vaucouleurs
law (de Vaucouleurs 1948), is mostly associated with concentrated
high-
curve just reminds us
of the uncertainties associated with the best-fit determination of
n). The n = 4 behavior, characteristic of the de Vaucouleurs
law (de Vaucouleurs 1948), is mostly associated with concentrated
high- models, but we note that many intermediate-
models, but we note that many intermediate- models also have the same structural property. The residuals from
the R1/n best fit (see Fig. 5) are typically
within 0.05 mag for concentrated models, while at low values of
models also have the same structural property. The residuals from
the R1/n best fit (see Fig. 5) are typically
within 0.05 mag for concentrated models, while at low values of
 they are within 0.2 mag; the general behavior can be
compared with that of the
they are within 0.2 mag; the general behavior can be
compared with that of the
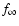 models (see Fig. A.1 in Bertin et al.
2002).
models (see Fig. A.1 in Bertin et al.
2002).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig4.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg92.gif) |
Figure 4:
Best fit value of the index n (of the R1/n law)
associated with the projected density profile of the  models, for selected values of
models, for selected values of  . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig5.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg93.gif) |
Figure 5:
Residuals
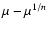 ,
in magnitudes, obtained
by fitting the R1/n law to the projected density profiles of the ,
in magnitudes, obtained
by fitting the R1/n law to the projected density profiles of the
 models for
models for 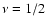 and selected values of
and selected values of  .
The quality of the fit is excellent for concentrated models ( .
The quality of the fit is excellent for concentrated models (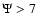 ). ). |
| Open with DEXTER |
Here we describe the properties of the  models related to the
velocity space.
models related to the
velocity space.
The pressure anisotropy of the models can be described by means of
the anisotropy profile 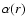 ,
defined as
,
defined as
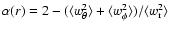 .
This function, illustrated in
Fig. 6, shows that the cores are approximately
isotropic and that in the outer parts the pressure is mostly in
the radial direction, in line with the qualitative expectations of
the violent relaxation scenario (Lynden-Bell 1967). Higher values of
.
This function, illustrated in
Fig. 6, shows that the cores are approximately
isotropic and that in the outer parts the pressure is mostly in
the radial direction, in line with the qualitative expectations of
the violent relaxation scenario (Lynden-Bell 1967). Higher values of
 are associated with a sharper transition from central
isotropy to radial anisotropy.
are associated with a sharper transition from central
isotropy to radial anisotropy.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig6.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg94.gif) |
Figure 6:
Anisotropy profiles 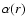 of
of 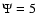 models for
different values of
models for
different values of  . . |
| Open with DEXTER |
The degree of anisotropy globally present in our models can be
characterized in terms of the ratio
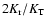 ,
where
,
where 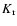 is
the total kinetic energy associated with the radial degree of
freedom, and
is
the total kinetic energy associated with the radial degree of
freedom, and 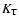 the corresponding quantity related to the two
tangential directions. All models present an excess of kinetic
energy in the radial direction, as illustrated in
Fig. 7. The ratio
the corresponding quantity related to the two
tangential directions. All models present an excess of kinetic
energy in the radial direction, as illustrated in
Fig. 7. The ratio
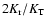 is greater than
is greater than
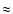 1.3 over the whole sequence and becomes larger than 2 in
the low-
1.3 over the whole sequence and becomes larger than 2 in
the low- region. As a general trend, at fixed
region. As a general trend, at fixed  ,
,
 models with higher values of
models with higher values of  are more isotropic.
are more isotropic.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig7.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg98.gif) |
Figure 7:
Global anisotropy of the  models shown in terms
of the parameter
models shown in terms
of the parameter
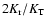 (group of curves starting from the top
left) and of the ratio
(group of curves starting from the top
left) and of the ratio
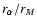 (anisotropy radius to
half-mass radius; group of curves starting from the bottom left) as
a function of
(anisotropy radius to
half-mass radius; group of curves starting from the bottom left) as
a function of  .
For low values of .
For low values of  the global anisotropy
the global anisotropy
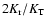 is basically independent of
is basically independent of  .
At fixed value of .
At fixed value of
 the global anisotropy decreases with
the global anisotropy decreases with  . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig8.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg101.gif) |
Figure 8:
Intrinsic "pressure" profiles (
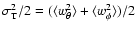 and
and
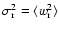 )
for selected )
for selected  models with
models with 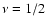 . .
|
| Open with DEXTER |
In addition to
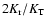 ,
as a global anisotropy indicator we
can also refer to the parameter
,
as a global anisotropy indicator we
can also refer to the parameter
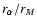 (see Fig. 7);
here the radius
(see Fig. 7);
here the radius
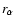 denotes the
anisotropy radius, defined from the relation
denotes the
anisotropy radius, defined from the relation
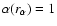 .
In contrast with the
.
In contrast with the
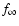 models,
for which
models,
for which
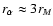 for relatively large values
of
for relatively large values
of  ,
here we find that concentrated models are characterized
by
,
here we find that concentrated models are characterized
by
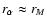 .
.
As we have seen, the models can be characterized by significant
"pressure" anisotropy. This can be illustrated directly by the
intrinsic velocity dispersion profiles, for which one may find
significant differences between the tangential
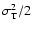 and the
radial dispersion
and the
radial dispersion
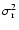 as far in as
as far in as
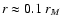 (see
Fig. 8). These velocity space properties, in
combination with the density distribution, give rise to the projected
velocity dispersion profiles (calculated from the line profiles, as
described in the next subsection), which may eventually be compared
with the observed kinematical profiles; some projected velocity
dispersion profiles are shown in Fig. 9.
(see
Fig. 8). These velocity space properties, in
combination with the density distribution, give rise to the projected
velocity dispersion profiles (calculated from the line profiles, as
described in the next subsection), which may eventually be compared
with the observed kinematical profiles; some projected velocity
dispersion profiles are shown in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig9.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg110.gif) |
Figure 9:
Projected velocity dispersion profile for selected
 models. If the scales are fixed so that
models. If the scales are fixed so that
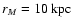 and
and
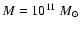 ,
the velocity
dispersion ,
the velocity
dispersion
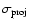 is given in units of
is given in units of
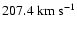 . . |
| Open with DEXTER |
4.3 Line profiles
Pressure anisotropy can affect the shape of the velocity
distribution integrated along a given direction, which can be
tested observationally by studying the profiles of the lines used
to determine the observed velocity dispersion. In this context,
since observational limitations prevent us from obtaining accurate
measurements of line profiles, comparisons between data and models
are often carried out in terms of certain shape parameters, which
measure the deviations from a Gaussian profile (e.g., see Gerhard
1991; de Zeeuw et al. 2002). In view of this approach, we have first
computed the line profiles for a number of models, following the
procedure described in Sect. 2 and then we have
extracted from them the related value of the h4 parameter
(being non rotating and spherically symmetric, the  models are
associated with line profiles characterized by vanishing h3).
models are
associated with line profiles characterized by vanishing h3).
To extract the velocity dispersion
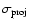 and the value h4 we
fit the line profile F(w,R), at fixed R, with a Gaussian corrected by
a fourth order Gauss-Hermite polynomial Abramowitz & Stegun (1965):
and the value h4 we
fit the line profile F(w,R), at fixed R, with a Gaussian corrected by
a fourth order Gauss-Hermite polynomial Abramowitz & Stegun (1965):
| F(w,R) |
= |
![$\displaystyle F_0 \exp{ \left[-(w/\sigma_{\rm proj})^2/2\right]}$](/articles/aa/full/2005/01/aa1023/img111.gif) |
(8) |
| |
|
![$\displaystyle \times \left\{ 1+ h_4 \left[
12-48\right(\frac{w}{\sigma_{\rm proj}}\left)^2+ 16
\right(\frac{w}{\sigma_{\rm proj}}\left)^4 \right] \right\},$](/articles/aa/full/2005/01/aa1023/img112.gif) |
|
where F0,
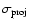 ,
and h4 are free parameters. The fit
has been performed with a Simulated Annealing method
(Press et al. 1992).
,
and h4 are free parameters. The fit
has been performed with a Simulated Annealing method
(Press et al. 1992).
In general, the deviations from a Gaussian are modest, 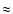
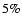 ,
and reduce to within
,
and reduce to within 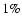 for
for
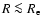 .
The h4parameter takes on slightly negative values at the center of the
system and then becomes positive in the outer parts (see
Fig. 10), in line with the results found by Gerhard
(1991).
.
The h4parameter takes on slightly negative values at the center of the
system and then becomes positive in the outer parts (see
Fig. 10), in line with the results found by Gerhard
(1991).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fi10.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg115.gif) |
Figure 10:
Profiles of the h4 parameter for selected  models
with
models
with 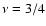 and different values of
and different values of  (the
(the 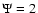 model is denoted by squares,
model is denoted by squares,
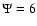 by triangles, and
by triangles, and 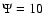 by stars).
by stars). |
| Open with DEXTER |
In view of a comparison with N-body simulations, a physically
interesting way to characterize the phase space properties of the
 models is in terms of the N(E,J2) and N(E) densities,
defined in such a way that
models is in terms of the N(E,J2) and N(E) densities,
defined in such a way that
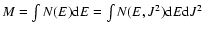 .
Therefore, the relation between
.
Therefore, the relation between
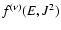 and the phase
space density N(E,J2) is given by the Jacobian of the
transformation from
and the phase
space density N(E,J2) is given by the Jacobian of the
transformation from
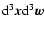 to
to
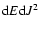 :
:
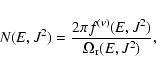 |
(9) |
where
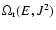 is the radial frequency of
stellar orbits in the given potential
is the radial frequency of
stellar orbits in the given potential 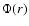 .
At variance with
the
.
At variance with
the
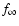 models, the
models, the  models exhibit a singular
behavior of N(E,J2) near the origin in the
models exhibit a singular
behavior of N(E,J2) near the origin in the
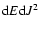 phase space
(see Fig. 11).
phase space
(see Fig. 11).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1023fi11.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg122.gif) |
Figure 11:
The phase space density N(E,J2) for the (1/2;6.2)  model. The graph has been obtained by a Monte Carlo sampling of
the distribution function with
model. The graph has been obtained by a Monte Carlo sampling of
the distribution function with
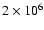 points.
points. |
| Open with DEXTER |
5 Stability
The study of the stability of the  models could be approached
either through a linear modal analysis (see Bertin et al. 1994) or
by means of N-body simulations. Here we prefer the latter
approach, starting from initial conditions obtained by sampling
the relevant distribution functions with Monte Carlo techniques.
models could be approached
either through a linear modal analysis (see Bertin et al. 1994) or
by means of N-body simulations. Here we prefer the latter
approach, starting from initial conditions obtained by sampling
the relevant distribution functions with Monte Carlo techniques.
A simple criterion for the onset of the radial orbit instability
states that instability occurs for systems with
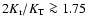 (Polyachenko & Shukhman 1981; see also Fridman & Polyachenko 1984). We
thus note that models with
(Polyachenko & Shukhman 1981; see also Fridman & Polyachenko 1984). We
thus note that models with
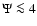 should be unstable, in a
way that is basically independent of
should be unstable, in a
way that is basically independent of  (cf.
Fig. 7).
(cf.
Fig. 7).
We have simulated the evolution of different  models by means
of an improved version (see Trenti 2004) of a code written
originally by van Albada & van Gorkom (1977; see also van Albada
1982). The evolution of the system is collisionless
because the simulation particles interact with one another via a
mean field computed with Fourier techniques; the mean density
associated with the particle distribution is expanded in spherical
harmonics with contributions up to l=4 (the code can handle
contributions up to l=6). This choice of code is well suited for
our problem, since its performance has been tested to be high for
quasi-equilibrium conditions and for smooth spherically symmetric
spatial distributions. To further check our results, we have run a
comparison simulation with the tree code of Londrillo (see Londrillo et al.
2003) for the (1;3.2) model and found no
significant differences.
models by means
of an improved version (see Trenti 2004) of a code written
originally by van Albada & van Gorkom (1977; see also van Albada
1982). The evolution of the system is collisionless
because the simulation particles interact with one another via a
mean field computed with Fourier techniques; the mean density
associated with the particle distribution is expanded in spherical
harmonics with contributions up to l=4 (the code can handle
contributions up to l=6). This choice of code is well suited for
our problem, since its performance has been tested to be high for
quasi-equilibrium conditions and for smooth spherically symmetric
spatial distributions. To further check our results, we have run a
comparison simulation with the tree code of Londrillo (see Londrillo et al.
2003) for the (1;3.2) model and found no
significant differences.
In order to sample points from the  distribution function and thus
to create the initial conditions needed to study the stability of the
distribution function and thus
to create the initial conditions needed to study the stability of the
 models, we have used an exact inversion of the cumulative mass
profile and a two-dimensional hit/miss method in the
models, we have used an exact inversion of the cumulative mass
profile and a two-dimensional hit/miss method in the
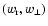 velocity space. The angles needed to complete the
assignment of the position and velocity vectors of the simulation
particles are generated randomly. In principle, the models extend out
to infinity. In practice, we set a cut-off radius
velocity space. The angles needed to complete the
assignment of the position and velocity vectors of the simulation
particles are generated randomly. In principle, the models extend out
to infinity. In practice, we set a cut-off radius
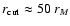 ,
and we rescale the mass profile in such a way that
,
and we rescale the mass profile in such a way that
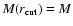 .
The introduced mass "loss'' is generally less than
.
The introduced mass "loss'' is generally less than
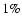 .
.
Most simulations have been run with
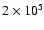 particles. If we
refer to a system with total mass
particles. If we
refer to a system with total mass
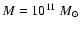 and
half-mass radius
and
half-mass radius
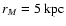 ,
the evolution is followed from t = 0up to
,
the evolution is followed from t = 0up to
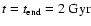 .
This corresponds to more than
.
This corresponds to more than
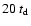 ,
with the natural dynamical time defined as
,
with the natural dynamical time defined as
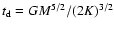 (here
(here
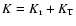 is the total kinetic energy); in fact, for the
range of
is the total kinetic energy); in fact, for the
range of
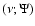 considered and the above scales for M and
rM, we have
considered and the above scales for M and
rM, we have
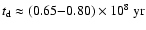 .
At
.
At
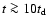 the system, even when it has initially evolved because of
initial unstable conditions, settles down into an approximate
equilibrium state.
the system, even when it has initially evolved because of
initial unstable conditions, settles down into an approximate
equilibrium state.
The total energy is typically conserved within 10-5 over one
dynamical time. The models are non-rotating; the total angular
momentum remains within 10-4 around the small value generated
in the initialization process.
To quantify the effects of the radial orbit instability, we have
especially focused on the evolution of the central density
concentration, of the shape of the inertia ellipsoid, computed on
the basis of the distribution of the simulation particles within a
sphere of radius 3 rM, and of the global anisotropy
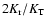 ratio.
The end-products of unstable initial conditions are
characterized by a final prolate state (with axial ratios
ratio.
The end-products of unstable initial conditions are
characterized by a final prolate state (with axial ratios
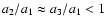 ), with maximum projected ellipticity
consistent with that of an E3 galaxy. For initially unstable
models, the central density concentration drops during evolution,
but the radial scale of the system remains approximately constant.
For example, for the (1/2;3) model, the central concentration at
the end of the simulation is more than 10 times smaller than
that of the initial conditions, but the radius of the sphere that
contains
), with maximum projected ellipticity
consistent with that of an E3 galaxy. For initially unstable
models, the central density concentration drops during evolution,
but the radial scale of the system remains approximately constant.
For example, for the (1/2;3) model, the central concentration at
the end of the simulation is more than 10 times smaller than
that of the initial conditions, but the radius of the sphere that
contains 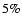 of the total mass increases only by
of the total mass increases only by 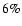 ,
while
the half-mass radius remains basically unchanged.
,
while
the half-mass radius remains basically unchanged.
We have studied the evolution of the unstable models in terms of
exponential growth curves of the form
![\begin{displaymath}g(t) = g_0 + g_1 [\exp{(kt)}-1],
\end{displaymath}](/articles/aa/full/2005/01/aa1023/img138.gif) |
(10) |
where g0, g1, and the growth rate k are free
parameters and g represents a global quantity such as the global
anisotropy ratio. To capture the initial, approximately linear
phase of the evolution, we have decided to make the fit in terms
of the exponential growth over a reduced time interval, from t =
0 to
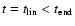 ,
defined implicitly by the relation:
,
defined implicitly by the relation:
![\begin{displaymath}\left(\frac{2K_{\rm r}}{K_{\rm T}}\right)(t_{\rm lin})=\frac{...
...rm end})
+\left(\frac{2K_{\rm r}}{K_{\rm T}}\right)(0)\right]. \end{displaymath}](/articles/aa/full/2005/01/aa1023/img140.gif) |
(11) |
Obviously, this choice of
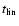 is arbitrary and
should be considered only as a convenient reference time-scale.
is arbitrary and
should be considered only as a convenient reference time-scale.
The results of the simulations are reported in Table 1. The
threshold for instability is found to be at
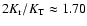 ,
consistent with the criterion of Polyachenko & Shukhman
(1981). Close to conditions of marginal stability, quantities such
as
,
consistent with the criterion of Polyachenko & Shukhman
(1981). Close to conditions of marginal stability, quantities such
as
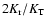 vary slowly and by very small amounts, so that the
fit in terms of exponential growth curves is not well determined.
vary slowly and by very small amounts, so that the
fit in terms of exponential growth curves is not well determined.
An interesting result is the following. We checked whether the final
state reached as a result of the instability could be represented by a
model of the  family to which the initial unstable model
belonged. To do this, we fitted the spherically averaged density and
anisotropy profiles of the end-states of the simulations by means of
the same family of
family to which the initial unstable model
belonged. To do this, we fitted the spherically averaged density and
anisotropy profiles of the end-states of the simulations by means of
the same family of  models. The best fit model thus identified
(note the quality of the fit in relation to both kinematics and
density distribution) turns out to be the marginally stable model of
the sequence with the same value of
models. The best fit model thus identified
(note the quality of the fit in relation to both kinematics and
density distribution) turns out to be the marginally stable model of
the sequence with the same value of  (see also the interesting
arguments and results by Palmer et al. 1990). In the case of
(see also the interesting
arguments and results by Palmer et al. 1990). In the case of 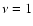 ,
which we studied in greatest detail, the profiles of the end-states
obtained starting from initially unstable models with
,
which we studied in greatest detail, the profiles of the end-states
obtained starting from initially unstable models with  in the
range from 3 to 4 are well fitted by the
in the
range from 3 to 4 are well fitted by the 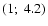 model (see
Fig. 12). For the violently unstable initial
model (see
Fig. 12). For the violently unstable initial 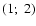 model, the final state is best reproduced by the (7/8; 4) model,
which is still moderately unstable.
model, the final state is best reproduced by the (7/8; 4) model,
which is still moderately unstable.
We have also run a number of simulations of models expected to be
stable and checked that indeed the models preserve their state for
many dynamical time scales. The most concentrated model that we
have been able to simulate properly is the
(1/2; 9.4) model, for
which we recall that the central concentration is
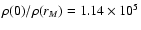 .
This also quantifies the
kind of gradients and ranges of densities that our code is able to
handle (see Fig. 13).
.
This also quantifies the
kind of gradients and ranges of densities that our code is able to
handle (see Fig. 13).
Table 1:
Growth rate k, with an estimate of the related
uncertainty 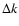 ,
for the radial orbit instability from the
simulation of a set of
,
for the radial orbit instability from the
simulation of a set of  models. Here
models. Here
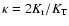 is
the global anisotropy parameter and
is
the global anisotropy parameter and
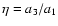 is the axis
ratio of the inertia ellipsoid referred to the sphere of radius
3 rM. For
is the axis
ratio of the inertia ellipsoid referred to the sphere of radius
3 rM. For
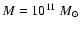 and
and
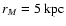 ,
k is
given in units of
,
k is
given in units of
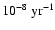 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1023fi12.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg151.gif) |
Figure 12:
On the
left frames, density and anisotropy profiles of the end-products of
a simulation starting from the unstable (1;3.2) model (error bars)
fitted by the marginally stable (1;4.2) model of the  family
(solid line); units for
family
(solid line); units for 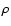 are the units adopted in the
simulation. The right frames show the residuals
are the units adopted in the
simulation. The right frames show the residuals
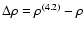 and
and
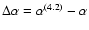 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1023fi13.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg154.gif) |
Figure 13:
Evolution of the fractional mass radii (of the sphere containing,
from the bottom
to the top,
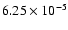 , ,
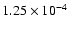 ,
0.01,
0.05, 0.5, 0.7, 0.95, 0.99 M, respectively) for a simulation
with ,
0.01,
0.05, 0.5, 0.7, 0.95, 0.99 M, respectively) for a simulation
with
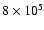 particles of the
concentrated
particles of the
concentrated  model (1/2;9.4). The model is stable over
the time interval considered (about 10 dynamical times). The
radius r and the
time t are given in units of
model (1/2;9.4). The model is stable over
the time interval considered (about 10 dynamical times). The
radius r and the
time t are given in units of
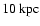 and
and
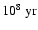 . . |
| Open with DEXTER |
6 A first comparison with the observations
The results in terms of the R1/n law described in
Sect. 3.2 already show that the  models possess
realistic density profiles. This encouraged us to consider a
direct comparison with an observed galaxy. For the purpose, we
picked the round elliptical galaxy NGC 3379, which apparently does
not possess significant amounts of dark matter (Saglia et al. 1992; Romanowsky et al.
2003; note that the models discussed in the present paper
are one-component models and thus are not applicable to systems
with prominent dark halos). This galaxy has an R1/4luminosity profile (de Vaucouleurs & Capaccioli 1979; Capaccioli et al. 1990). For the
kinematics, we considered the data of Statler & Smecker-Hane
(1999) and recently published data-points based on planetary
nebulae that extend well beyond
models possess
realistic density profiles. This encouraged us to consider a
direct comparison with an observed galaxy. For the purpose, we
picked the round elliptical galaxy NGC 3379, which apparently does
not possess significant amounts of dark matter (Saglia et al. 1992; Romanowsky et al.
2003; note that the models discussed in the present paper
are one-component models and thus are not applicable to systems
with prominent dark halos). This galaxy has an R1/4luminosity profile (de Vaucouleurs & Capaccioli 1979; Capaccioli et al. 1990). For the
kinematics, we considered the data of Statler & Smecker-Hane
(1999) and recently published data-points based on planetary
nebulae that extend well beyond 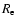 (Romanowsky et al. 2003).
(Romanowsky et al. 2003).
The  model that best describes the data is shown in
Figs. 14-15. From such model, by
adopting a distance of
model that best describes the data is shown in
Figs. 14-15. From such model, by
adopting a distance of
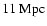 for the galaxy and an absolute
magnitude in B band MB=-20.0, we obtain a mass-to-light ratio
M/LB = 4.7 in solar units. Population synthesis models for NGC 3379
predict a mass-to-light ratio between 4 and 9 (Gerhard et al. 2001). In
comparison, Romanowsky et al. (2003) report a mass-to-light ratio
for the galaxy and an absolute
magnitude in B band MB=-20.0, we obtain a mass-to-light ratio
M/LB = 4.7 in solar units. Population synthesis models for NGC 3379
predict a mass-to-light ratio between 4 and 9 (Gerhard et al. 2001). In
comparison, Romanowsky et al. (2003) report a mass-to-light ratio
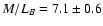 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fi14.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg157.gif) |
Figure 14:
Comparison between the photometric profile of NGC
3379 and the (1/2; 9.4) model of the  family. The photometric
profile in B is taken from de Vaucouleurs & Capaccioli
(1979). Other members of the family (e.g. the (1; 9.2) model) could
better reproduce the observed data especially at large radii, but
they would perform less well on the velocity dispersion profile.
family. The photometric
profile in B is taken from de Vaucouleurs & Capaccioli
(1979). Other members of the family (e.g. the (1; 9.2) model) could
better reproduce the observed data especially at large radii, but
they would perform less well on the velocity dispersion profile. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fi15.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg158.gif) |
Figure 15:
Kinematic data for NGC 3379 described in terms of
the (1/2; 9.4) model of the  family. The inner data (plain error
bars) are taken from the stellar spectroscopy of Statler &
Smecker-Hane (1999), while the outer data (crosses with error bars)
refer to the binned velocity dispersion determined from the study of
planetary nebulae (Romanowsky et al. 2003).
family. The inner data (plain error
bars) are taken from the stellar spectroscopy of Statler &
Smecker-Hane (1999), while the outer data (crosses with error bars)
refer to the binned velocity dispersion determined from the study of
planetary nebulae (Romanowsky et al. 2003).
|
| Open with DEXTER |
In this paper we have studied the structural and dynamical
properties of a two-parameter family of models of partially
relaxed stellar systems. These models had been proposed earlier
(Stiavelli & Bertin 1987) as physically relevant to the galaxy
formation scenario based on collisionless collapse and incomplete
violent relaxation. They had been noted to possess some realistic
properties (for  in the range 1/2-1 and for relatively
large values of
in the range 1/2-1 and for relatively
large values of  ). However, they had been left basically
aside and not studied further in systematic detail. Additional
physical interest was noted recently (Bertin & Trenti 2003), in
an investigation focused on their thermodynamic properties, in
relation to the paradigm of the gravothermal catastrophe. Because
of such physical interest, we have decided to undertake a thorough
comparison between the models and the products of collisionless
collapse, as generated in N-body simulations. Such a comparison
will be the subject of a follow-up paper, of which the present
article forms the necessary basis. In that paper we will consider
a relatively large set of simulations of collisionless collapse,
starting from a variety of initial conditions. We will address the
issue of the conservation of Q and identify the range of
). However, they had been left basically
aside and not studied further in systematic detail. Additional
physical interest was noted recently (Bertin & Trenti 2003), in
an investigation focused on their thermodynamic properties, in
relation to the paradigm of the gravothermal catastrophe. Because
of such physical interest, we have decided to undertake a thorough
comparison between the models and the products of collisionless
collapse, as generated in N-body simulations. Such a comparison
will be the subject of a follow-up paper, of which the present
article forms the necessary basis. In that paper we will consider
a relatively large set of simulations of collisionless collapse,
starting from a variety of initial conditions. We will address the
issue of the conservation of Q and identify the range of  for which the global quantity is best conserved. Furthermore, we
will show that in many cases the
for which the global quantity is best conserved. Furthermore, we
will show that in many cases the  models can provide a
surprisingly good fit to both the density and the pressure
profiles, over nine orders of magnitude of the density
distribution (see Bertin & Trenti 2004). The best-fit models will
turn out to be close to marginal stability with respect to the
radial orbit instability.
models can provide a
surprisingly good fit to both the density and the pressure
profiles, over nine orders of magnitude of the density
distribution (see Bertin & Trenti 2004). The best-fit models will
turn out to be close to marginal stability with respect to the
radial orbit instability.
Here we have shown that the family of  models exhibits a
variety of structural properties, within a common general
behavior. The model characteristics can be summarized by referring
to three separate regimes: low-
models exhibits a
variety of structural properties, within a common general
behavior. The model characteristics can be summarized by referring
to three separate regimes: low- models (typically,
models (typically, 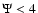 ), intermediate-
), intermediate- models (typically,
models (typically,
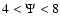 ), and
high-
), and
high- models (typically,
models (typically, 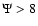 ). In practice, the
values of
). In practice, the
values of  that mark the transition between different
regimes do not depend significantly on the value of
that mark the transition between different
regimes do not depend significantly on the value of  ,
at
least in the range explored in this paper (i.e., from
,
at
least in the range explored in this paper (i.e., from 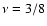 to
to 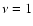 ).
).
In the intermediate- and the high-
and the high- regimes the
concentration ratio
regimes the
concentration ratio
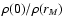 increases monotonically
with
increases monotonically
with  ;
models with lower values of
;
models with lower values of  have larger values
of
have larger values
of
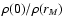 (by up to one order of magnitude at given
(by up to one order of magnitude at given
 ,
in the explored range of
,
in the explored range of  ). In the same regimes, as
). In the same regimes, as
 increases, the density distribution converges onto a common
profile characterized by an approximate r-4 behavior at r >
rM and by an approximate r-2 behavior at r < rM, with an
inner core that becomes smaller and smaller. In contrast, models
in the low-
increases, the density distribution converges onto a common
profile characterized by an approximate r-4 behavior at r >
rM and by an approximate r-2 behavior at r < rM, with an
inner core that becomes smaller and smaller. In contrast, models
in the low- regime have a substantial core, comparable in
structure to that of a Plummer or of an isochrone model. In
general, the projected density distribution of the models is well
fitted by the R1/n law, with n ranging from 2.5 to 8.5.
Typically, high-
regime have a substantial core, comparable in
structure to that of a Plummer or of an isochrone model. In
general, the projected density distribution of the models is well
fitted by the R1/n law, with n ranging from 2.5 to 8.5.
Typically, high- models are accurately described in terms of
the R1/4 law.
models are accurately described in terms of
the R1/4 law.
The models are all characterized by significant radially-biased
pressure anisotropy. In terms of the global anisotropy ratio
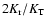 ,
at given
,
at given  models in the low-
models in the low- regime have
similar amounts of pressure anisotropy, which increases rapidly as
regime have
similar amounts of pressure anisotropy, which increases rapidly as
 decreases. In practice, all low-
decreases. In practice, all low- models should all be
unstable with respect to the radial-orbit instability.
Intermediate-
models should all be
unstable with respect to the radial-orbit instability.
Intermediate- and high-
and high- models appear to be safely stable,
but they may be only marginally so for the lowest value of
models appear to be safely stable,
but they may be only marginally so for the lowest value of  that
we considered. This latter remark also explains why we have decided
not to move below
that
we considered. This latter remark also explains why we have decided
not to move below 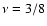 ,
given the fact that radial pressure
anisotropy is larger for lower-
,
given the fact that radial pressure
anisotropy is larger for lower- models. In terms of velocity
dispersion profiles, to some extent pressure anisotropy is already
significant at
models. In terms of velocity
dispersion profiles, to some extent pressure anisotropy is already
significant at
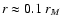 ,
even for stable models. However,
out to
,
even for stable models. However,
out to
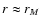 the line profiles of stable models deviate very
little from a Gaussian, with h4 within the
the line profiles of stable models deviate very
little from a Gaussian, with h4 within the 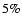 level.
level.
By means of an improved version of a code introduced earlier by
van Albada, we have checked the properties of the models with
respect to the radial-orbit instability, confirming the general
expectations based on the global anisotropy parameter
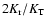 .
Curiously, we find that unstable models tend to evolve by staying
close to the equilibrium sequence, while moving up in
.
Curiously, we find that unstable models tend to evolve by staying
close to the equilibrium sequence, while moving up in  so as
to reach marginal stability. Furthermore, we have been able to
show that the N-body code is able to handle highly concentrated
models (up to
so as
to reach marginal stability. Furthermore, we have been able to
show that the N-body code is able to handle highly concentrated
models (up to
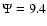 ,
with
,
with
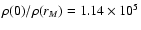 ), of which it has demonstrated the long-term stability.
), of which it has demonstrated the long-term stability.
Finally, a comparison with the observed surface brightness and
kinematical profiles for the galaxy NGC 3379 has shown some merits and
some limitations of the one-component family of  models when applied to
observed objects. In particular, it is interesting to see that, within
the extremely idealized framework at the basis of the construction of
these models (see also the general comments made in Sect. 1.1), the
observed luminosity profile is very well reproduced over about ten
magnitudes; at the same time the models can well reproduce the inner part
of the relevant kinematical profile, inside
models when applied to
observed objects. In particular, it is interesting to see that, within
the extremely idealized framework at the basis of the construction of
these models (see also the general comments made in Sect. 1.1), the
observed luminosity profile is very well reproduced over about ten
magnitudes; at the same time the models can well reproduce the inner part
of the relevant kinematical profile, inside 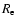 .
This comparison
supports the view that the models studied in this paper may be helpful to
describe the luminous component of elliptical galaxies. The obvious
limitations of the one-component models that we are considering are
clearly brought out by their inadequacy to capture the change in the
observed kinematical profile occurring around
.
This comparison
supports the view that the models studied in this paper may be helpful to
describe the luminous component of elliptical galaxies. The obvious
limitations of the one-component models that we are considering are
clearly brought out by their inadequacy to capture the change in the
observed kinematical profile occurring around 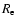 and thus their
failure to reproduce such profile in the outer parts. This is interpreted
as a signature of the presence of an additional component that our
models, in the form developed so far, a priori ignore.
and thus their
failure to reproduce such profile in the outer parts. This is interpreted
as a signature of the presence of an additional component that our
models, in the form developed so far, a priori ignore.
Acknowledgements
We would like to thank T. S. van Albada and P. Londrillo, for their
collaboration and for a number of useful comments and suggestions,
and N. Douglas and A. Romanowsky, for providing us with the data
for NGC 3379. The interested reader is welcome to contact M.
Trenti, who will be glad to provide the relevant numerical
routines to initialize N-body simulations and to compute intrinsic
and projected profiles for the  family of models.
family of models.
From the definition of the  distribution function (see
Eq. (2)), the constants (A,a,d) have the following
dimensions:
distribution function (see
Eq. (2)), the constants (A,a,d) have the following
dimensions:
| |
|
A = [ML-6T3], |
(A.1) |
| |
|
a = [L-2T2], |
(A.2) |
| |
|
![$\displaystyle d = [L^{-\nu /2}T^{-\nu /2}].$](/articles/aa/full/2005/01/aa1023/img163.gif) |
(A.3) |
Therefore, as scales for mass and radius we may refer
to:
| |
|
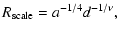 |
(A.4) |
| |
|
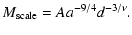 |
(A.5) |
Then we introduce the dimensionless quantities
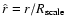 (and thus
(and thus
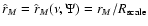 ),
),
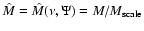 ,
where
,
where
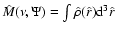 ,
,
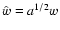 ,
and
,
and
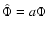 for radius, mass, velocity,
and potential, respectively.
for radius, mass, velocity,
and potential, respectively.
Recalling the expression for 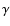 (see Sect. 2, after
Eq. (2)), for given
(see Sect. 2, after
Eq. (2)), for given  we can express (A,a,d) in
terms of
we can express (A,a,d) in
terms of
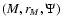 :
:
- Abramowitz, M., &
Stegun, I. 1965, Handbook of Mathematical Functions (New York:
Dover)
(In the text)
- Antonov, V. A. 1962,
Vestnik Leningr. Univ., No. 19, 96 (Engl. Transl.: in Structure and
Dynamics of Elliptical Galaxies, ed. T. de Zeeuw (Dordrecht:
Reidel), 1986, 531)
(In the text)
- Berntsen, J. T. E.,
& Genz, A. 1991, ACM Tran. Mat. Soft., 17, 437 [MathSciNet] (In the text)
- Bertin, G., Ciotti, L.,
& Del Principe, M. 2002, A&A, 386, 149 [EDP Sciences] [CrossRef] (In the text)
- Bertin, G., Pegoraro, F.,
Rubini, F., & Vesperini, E. 1994, ApJ, 434, 94 [CrossRef] (In the text)
- Bertin, G., &
Stiavelli, M. 1984, A&A, 137, 26 (In the text)
- Bertin, G., &
Stiavelli, M. 1993, Rep. Progr. Phys., 56, 493 (In the text)
- Bertin, G., & Trenti,
M. 2003, ApJ, 584, 729 [CrossRef] (In the text)
- Bertin, G., &
Trenti, M. 2004, AIP Conf. Proc. 703, ed. G. Bertin, D. Farina, R.
Pozzoli (Melville, New York: American Institute of Physics),
318
(In the text)
- Capaccioli, M., Held, E.
V., Lorenz, H., & Vietri, M. 1990, AJ, 99, 1813 [CrossRef] (In the text)
- Carollo, C. M., de Zeeuw,
P. T., & van der Marel, R. P. 1995, MNRAS, 276, 1131 (In the text)
- de Vaucouleurs, G. 1948,
Annales d'Astrophysique, 11, 247 (In the text)
- de Vaucouleurs, G., &
Capaccioli, M. 1979, ApJS, 40, 699 [CrossRef] (In the text)
- de Zeeuw, P. T.,
Bureau, M., Emsellem, E., et al. 2002, MNRAS, 329, 513 [CrossRef] (In the text)
- Fridman, A. M., &
Polyachenko, V. L. 1984, Physics of Gravitating Systems (Berlin:
Springer-Verlag)
(In the text)
- Gerhard, O. 1991, MNRAS,
250, 812 [MathSciNet] (In the text)
- Gerhard, O. 1993, MNRAS,
265, 213 (In the text)
- Gerhard, O., Kronawitter,
A., Saglia, R. P., & Bender, R. 2001, AJ, 121, 1936 [CrossRef] (In the text)
- Ghigna, S., Moore, B.,
Governato, F., et al. 2000, ApJ, 544, 616 [CrossRef] (In the text)
- Gonzalez-Garcia, C.,
& van Albada, T. S. 2003, MNRAS, 342, 36 [CrossRef] (In the text)
- Hénon, M. 1959,
Annales d'Astrophysique, 22, 126 (In the text)
- Hernquist, L. 1990, ApJ,
356, 359 [CrossRef] (In the text)
- Hjorth, J., & Madsen,
J. 1995, ApJ, 445, 55 [CrossRef] (In the text)
- Jaffe, W. 1983, MNRAS,
202, 995 (In the text)
- Katz, J. 1978, MNRAS,
183, 765 (In the text)
- Katz, J. 1979, MNRAS,
189, 817 (In the text)
- Katz, J. 1980, MNRAS,
190, 497
- Lanzoni, B., Ciotti, L.,
Cappi, A., Tormen, G., & Zamorani, G. 2004, ApJ, 600, 640 [CrossRef] (In the text)
- Londrillo, P., Nipoti,
C., & Ciotti, L. 2003, Mem. Soc. Astron. It. Suppl., 1, 18 (In the text)
- Lynden-Bell, D. 1967,
MNRAS, 131, 101 (In the text)
- Lynden-Bell, D., &
Wood, R. 1968, MNRAS, 138, 495 (In the text)
- Merritt, D. 1985, AJ, 90,
1027 [CrossRef] (In the text)
- Merritt, D., Tremaine,
S., & Johnstone, D. 1989, MNRAS, 236, 829 (In the text)
- Meza, A., Navarro, J. F.,
Steinmetz, M., & Eke, V. R. 2003, ApJ, 590, 619 [CrossRef]
- Moore, B., Governato, F.
Quinn, T., Stadel, J., & Lake, G. 1998, ApJ, 499, 5 [CrossRef] (In the text)
- Navarro, J. F., Frenk, C.
S., & White, S. D. M. 1997, ApJ, 490, 593 (In the text)
- Nipoti, C., Londrillo,
P., & Ciotti, L. 2003, MNRAS, 342, 501 [CrossRef] (In the text)
- Palmer, P. L.,
Papaloizou, J., & Allen, A. J. 1990, MNRAS, 246, 415 (In the text)
- Plummer, H. C. 1915,
MNRAS, 76, 107 (In the text)
- Polyachenko, V., &
Shukhman, I. 1981, SvA, 25, 533 (In the text)
- Press W. H., Teukolsky S.
A., Vetterling W. T., & Flannery B. P. 1992, Numerical Recipes
in C (UK: Cambridge University Press)
(In the text)
- Romanowsky, A. J.,
Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [CrossRef] (In the text)
- Saglia, R. P., Bertin,
G., & Stiavelli, M. 1992, ApJ, 384, 433 [CrossRef] (In the text)
- Sersic, J. L. 1968, Atlas
de galaxias australes, Observatorio Astronomico, Cordoba
(In the text)
- Shu, F. 1978, ApJ, 225,
83 [CrossRef] (In the text)
- Shu, F. 1987, ApJ, 316,
502 [CrossRef] (In the text)
- Statler, T. S., &
Smecker-Hane, T. 1999, AJ, 117, 839 [CrossRef] (In the text)
- Stiavelli, M., &
Bertin, G. 1987, MNRAS, 229, 61 (In the text)
- Trenti, M. 2004, Ph.D.
Thesis, Scuola Normale Superiore, Pisa, in progress
(In the text)
- van Albada, T. S. 1982,
MNRAS, 201, 939 (In the text)
- van Albada, T., S., &
van Gorkom, J. H. 1977, A&A, 54, 121 (In the text)
- Voglis, N. 1994, MNRAS,
267, 379 (In the text)
Copyright ESO 2004
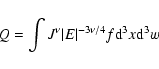
![\begin{displaymath}
f^{(\nu)} = A \exp {\left[- a E - d \left(
\frac{J^2}{\vert E\vert^{3/2}}\right)^{\nu/2}\right]},
\end{displaymath}](/articles/aa/full/2005/01/aa1023/img57.gif)
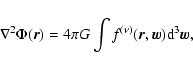
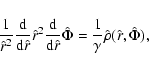
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig1.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig2.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig3.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg83.gif)
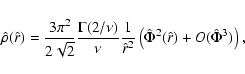
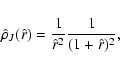
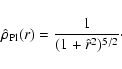
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig4.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg92.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig5.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig6.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig7.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig8.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fig9.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg110.gif)
![$\displaystyle \times \left\{ 1+ h_4 \left[
12-48\right(\frac{w}{\sigma_{\rm proj}}\left)^2+ 16
\right(\frac{w}{\sigma_{\rm proj}}\left)^4 \right] \right\},$](/articles/aa/full/2005/01/aa1023/img112.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fi10.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg115.gif)
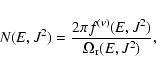
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1023fi11.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg122.gif)
![\begin{displaymath}\left(\frac{2K_{\rm r}}{K_{\rm T}}\right)(t_{\rm lin})=\frac{...
...rm end})
+\left(\frac{2K_{\rm r}}{K_{\rm T}}\right)(0)\right]. \end{displaymath}](/articles/aa/full/2005/01/aa1023/img140.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1023fi12.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg151.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1023fi13.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg154.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fi14.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg157.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1023fi15.eps} \end{figure}](/articles/aa/full/2005/01/aa1023/Timg158.gif)
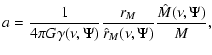
![$\displaystyle d = [4 \pi G \gamma(\nu,\Psi)]^{\nu/4} \left(
\frac{M}{\hat{M}(\nu,\Psi)} \right)^{\nu/4} \left(
\frac{\hat{r}_M(\nu,\Psi)}{r_M}\right)^{5 \nu/4},$](/articles/aa/full/2005/01/aa1023/img172.gif)
![$\displaystyle A = \frac{1}{[4 \pi G \gamma(\nu,\Psi)]^{3/2}}
\left(\frac{\hat{r...
...\nu,\Psi)}{r_M}\right)^{3/2}\left(\frac{\hat{M}(\nu,\Psi)}{M}\right)^{1/2}\cdot$](/articles/aa/full/2005/01/aa1023/img173.gif)