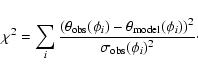A&A 428, 131-137 (2004)
DOI: 10.1051/0004-6361:20041419
Self consistent modelling of the projection factor for interferometric distance determination
N. Nardetto 1 - A. Fokin 1,2,5 - D. Mourard 1 -
Ph. Mathias 1 - P. Kervella 3 - D. Bersier 4
1 - Observatoire de la Côte d'Azur, Dpt. Gemini, UMR
6203, 06130 Grasse, France
2 - Institute of Astronomy of the
Russian Academy of Sciences, 48 Pjatnitskaya Str., Moscow 109017,
Russia
3 - Observatoire de Paris-Meudon, LESIA, UMR 8109, 5 place
Jules Janssen, 92195 Meudon Cedex, France
4 - Space Telescope
Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
5 - Isaak Newton Institute, Moscow Branch
Received 4 June 2004 / Accepted 28 July 2004
Abstract
The distance of galactic Cepheids can be derived through
the interferometric Baade-Wesselink method. The interferometric
measurements lead to angular diameter estimations over the whole
pulsation period, while the stellar radius variations can be
deduced from the integration of the pulsation velocity. The latter
is linked to the observational velocity deduced from line profiles
by the so-called projection factor p. The knowledge of p is
currently an important limiting factor for this method of distance
determination. A self-consistent and time-dependent model of the
star  Cep is computed in order to study the dynamical
structure of its atmosphere together with the induced line
profile. Different kinds of radial and pulsation velocities are
then derived. In particular, we compile a suitable average value
for the projection factor related to different observational
techniques, such as spectrometry, and spectral-line or wide-band
interferometry. We show that the impact on the average projection
factor and consequently on the final distance deduced from this
method is of the order of 6%. We also study the impact of a
constant or variable p-factor on the Cepheid distance
determination. We conclude on this last point that if the average
value of the projection factor is correct, then the influence of
the time dependence is not significant as the error in the final
distance is of the order of 0.2%.
Cep is computed in order to study the dynamical
structure of its atmosphere together with the induced line
profile. Different kinds of radial and pulsation velocities are
then derived. In particular, we compile a suitable average value
for the projection factor related to different observational
techniques, such as spectrometry, and spectral-line or wide-band
interferometry. We show that the impact on the average projection
factor and consequently on the final distance deduced from this
method is of the order of 6%. We also study the impact of a
constant or variable p-factor on the Cepheid distance
determination. We conclude on this last point that if the average
value of the projection factor is correct, then the influence of
the time dependence is not significant as the error in the final
distance is of the order of 0.2%.
Key words: stars: atmospheres - stars: distances - stars:
oscillations - stars: variables: Cepheids
The period-luminosity (P-L) relation of the Cepheids is the
basis of the extragalactic distance scale, but its calibration is
still uncertain at a
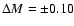 mag level. In order to
calibrate this relation, two procedures have been recently
considered, both based on the Baade-Wesselink method (hereafter
BW), with distances deduced from the ratio of radius to angular
variations.
mag level. In order to
calibrate this relation, two procedures have been recently
considered, both based on the Baade-Wesselink method (hereafter
BW), with distances deduced from the ratio of radius to angular
variations.
The first method is the near-infrared surface brightness method
introduced by Welch (1994), and later by Fouqué &
Gieren (1997). The angular diameter variation is
photometrically inferred from calibrations of the V light and
(V-K) color curves, and compared to the radius variation obtained
spectroscopically. In the second method, called the
interferometric version of the Baade-Wesselink method (hereafter
IBW), the angular diameter variation is directly measured through
the latest generation of long-baseline interferometers in the
visible and in the IR, and then again compared to radius
variations in order to derive distances (Kervella et al.
2004a; Lane et al. 2002) and then calibrate
the P-L relation (Kervella et al. 2004b).
Both methods are in perfect agreement on the angular diameter,
with a discrepancy of less than 1.5% (Kervella et al.
2004c). However, a difficulty remains in the
derivation of the radius variation. The radius displacement is
obtained through the integration of the pulsation velocity curve,
hereafter called
 .
But when one measures radial
velocities from line profiles, hereafter called
.
But when one measures radial
velocities from line profiles, hereafter called
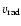 ,
they include the integration in two directions over the surface,
through limb-darkening, and over the radius, through velocity
gradients in line forming regions. Moreover, both the
limb-darkening and velocity gradients depend on the pulsation
phase, as already pointed out by Marengo et al. (2003).
Therefore, the knowledge of the projection factor, defined as
,
they include the integration in two directions over the surface,
through limb-darkening, and over the radius, through velocity
gradients in line forming regions. Moreover, both the
limb-darkening and velocity gradients depend on the pulsation
phase, as already pointed out by Marengo et al. (2003).
Therefore, the knowledge of the projection factor, defined as
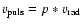 ,
is of crucial importance for
deriving a correct estimate of the radius variation curves from
the integration of the pulsation velocity curve.
,
is of crucial importance for
deriving a correct estimate of the radius variation curves from
the integration of the pulsation velocity curve.
The problem of the projection factor has been first studied by
Eddington (1926), Carroll (1928) and Getting (1935).
These authors consider both effects of limb-darkening and
atmospheric expansion at constant velocity on the line profile.
These studies led to a p-value of
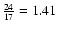 ,
which
was used for several decades in the Baade-Wesselink method.
,
which
was used for several decades in the Baade-Wesselink method.
Later, Van Hoof & Deurinck (1952) showed that when the
natural width of the line is much smaller than the shift induced
by the Doppler effect, the resulting profile must be distorted,
and the p-factor can be measured from the convolution of the
static line profile with this distortion function. Parsons
(1972), using a model atmosphere with uniform expansion,
numerically determined p-values between 1.31 and 1.34 depending
on the width of the line.
Karp (1973, 1975) introduced a velocity gradient within
the line forming regions and computed the emerging flux for both
weak and strong lines. Weak lines, appear asymmetrical similar to
the ones obtained by Van Hoof & Deurinck (1952), while the
distortion for the stronger lines is mainly due to the velocity
gradient within the atmosphere. Albrow & Cottrell (1994)
determine values for p larger by 10% than those obtained by
Parsons (1972), a difference interpreted as due to the use of
a different limb-darkening law. Indeed, the p-factor depends on
many parameters, such as the wavelength (p is larger in the
infrared, Sasselov & Lester 1990), or the effective
temperature of the star (Hindsley & Bell 1986;
Montañés Rodriguez & Jeffery 2001).
From an observational point of view, Burki et al. (1982)
determined p=1.36 from the measure of the centroid of the
correlation profile, a value which has been widely used in
spectroscopy.
Finally, since p is determined both through geometrical effects
and atmospheric dynamics, which change during the pulsation cycle,
it should itself vary with the pulsation phase. In particular,
Sabbey et al. (1995) showed that this effect on p can
increase the BW radius by about 6%.
We apply for  Cep a nonlinear self-consistent
hydrodynamical model (Fokin 1990). In addition, radiative
transfer is considered in the outer layers to produce a realistic
atmosphere model. The derived quantities have been found to be in
good agreement with observations for different classes of
pulsators such as RR Lyrae (Fokin & Gillet 1997),
RV Tauri (Fokin 2001), post-AGB (Jeannin et al.
1997), BL Herculis (Fokin & Gillet 1994) and more
recently
Cep a nonlinear self-consistent
hydrodynamical model (Fokin 1990). In addition, radiative
transfer is considered in the outer layers to produce a realistic
atmosphere model. The derived quantities have been found to be in
good agreement with observations for different classes of
pulsators such as RR Lyrae (Fokin & Gillet 1997),
RV Tauri (Fokin 2001), post-AGB (Jeannin et al.
1997), BL Herculis (Fokin & Gillet 1994) and more
recently 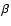 Cephei stars (Fokin et al. 2004). In
particular, this model has already been used in the case of
Cephei stars (Fokin et al. 2004). In
particular, this model has already been used in the case of
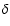 Cep (Fokin et al. 1996). Our model has some
limitations (no convection, no adaptive grid), but is able to
reproduce the main observational characteristics such as the
presence of shocks or the correct shape and amplitude of the
velocity curve. Thus we are confident that our model is valid for
our study, and that the results are consistent.
Cep (Fokin et al. 1996). Our model has some
limitations (no convection, no adaptive grid), but is able to
reproduce the main observational characteristics such as the
presence of shocks or the correct shape and amplitude of the
velocity curve. Thus we are confident that our model is valid for
our study, and that the results are consistent.
The influence of the projection factor on the distance
determination of Cepheids can be safely studied in the context of
the IBW method. The main objectives of this paper are, firstly, to
have an idea of the best value of the p-factor for
interferometric observations, and to compare it with the generally
used value of p=1.36, and secondly, to quantify the impact of a
constant or time-dependent projection factor on the distance
determination of the star.
The paper is organized as follows. In Sect. 2 we
describe our model of the prototype of the Cepheids,
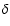 Cep, constrained from observational parameters
referenced in the literature. In Sect. 3, we
define the radial and pulsation velocities considered in the
following. Section 4 deals essentially with the study
of the projection factor and Sect. 5 concerns the
impact of the choice of a time-varying p-factor on the distance
determination. Finally, Sect. 6 presents the
conclusions of this work.
Cep, constrained from observational parameters
referenced in the literature. In Sect. 3, we
define the radial and pulsation velocities considered in the
following. Section 4 deals essentially with the study
of the projection factor and Sect. 5 concerns the
impact of the choice of a time-varying p-factor on the distance
determination. Finally, Sect. 6 presents the
conclusions of this work.
2 The model of 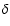 Cep
Cep
The model needs only 4 input parameters: the luminosity (L), the
effective temperature (
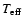 ), the mass (M) and the chemical
composition (X and Y). The model is run until it reaches its limit
cycle (for
), the mass (M) and the chemical
composition (X and Y). The model is run until it reaches its limit
cycle (for 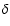 Cep this is the fundamental mode). Radiative
transfer in the line is then solved in the frame of this
hydrodynamical model to provide line profiles (Fokin 1991).
For the present study, which is a first step, we have arbitrarily
considered the metallic line Fe I 6003.012 Å. Therefore,
we can compare the velocity in a given mass zone (
Cep this is the fundamental mode). Radiative
transfer in the line is then solved in the frame of this
hydrodynamical model to provide line profiles (Fokin 1991).
For the present study, which is a first step, we have arbitrarily
considered the metallic line Fe I 6003.012 Å. Therefore,
we can compare the velocity in a given mass zone (
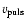 )
with the velocity measured from the synthetic line profile
(
)
with the velocity measured from the synthetic line profile
(
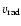 ). The latter was determined by two methods:
measuring the velocity associated with the pixel at the minimum of
the line profile (hereafter called profile minimum), and the
Gaussian method in which we fit the whole profile with a Gaussian
function. Note that theoretical variations follow the usual
convention in which the pulsation phase
). The latter was determined by two methods:
measuring the velocity associated with the pixel at the minimum of
the line profile (hereafter called profile minimum), and the
Gaussian method in which we fit the whole profile with a Gaussian
function. Note that theoretical variations follow the usual
convention in which the pulsation phase 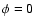 corresponds to
maximum luminosity.
corresponds to
maximum luminosity.
Since the main stellar quantities of 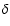 Cep (HD 213306)
are still uncertain, we tried several sets of luminosity L,
effective temperature
Cep (HD 213306)
are still uncertain, we tried several sets of luminosity L,
effective temperature
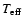 and mass M in order to get suitable
observational quantities such as the pulsation period, the average
radius of the star, bolometric and radial velocity curves, and
line profiles. This leads to the following set for the 106-zone
model:
and mass M in order to get suitable
observational quantities such as the pulsation period, the average
radius of the star, bolometric and radial velocity curves, and
line profiles. This leads to the following set for the 106-zone
model:
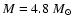 ,
,
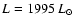 ,
,
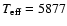 K. This latter is
in agreement with the one measured by Fernley et al.
(1989). Mass and luminosity are related through the M-L
relation of Chiosi et al. (1993):
K. This latter is
in agreement with the one measured by Fernley et al.
(1989). Mass and luminosity are related through the M-L
relation of Chiosi et al. (1993):
where Y=0.28 and Z=0.02 correspond to typical Pop. I
chemical composition. The inner boundary has been fixed at about
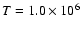 K, corresponding to about 16% of the
photospheric radius, so the model envelope with the atmosphere
contains about 7% of the stellar mass. The atmosphere itself
contains about
K, corresponding to about 16% of the
photospheric radius, so the model envelope with the atmosphere
contains about 7% of the stellar mass. The atmosphere itself
contains about
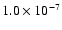 of the total stellar mass. In
the hydrodynamical model we used the OPAL92 opacity table. Note
that in the following line transfer calculation for each chosen
phase we used the snapshots of the pulsating atmosphere given by
the nonlinear model. In addition, we used the relevant
frequency-dependent atomic opacities both in the continuum and in
the line.
of the total stellar mass. In
the hydrodynamical model we used the OPAL92 opacity table. Note
that in the following line transfer calculation for each chosen
phase we used the snapshots of the pulsating atmosphere given by
the nonlinear model. In addition, we used the relevant
frequency-dependent atomic opacities both in the continuum and in
the line.
We started the hydrodynamical calculations with an initial
velocity profile with a value of 25 km s-1 at the surface. At the
limit cycle the pulsation period is 5.419 days, very close (1%)
to the observational value deduced by Szabados et al.
(1980). Bolometric and radial velocity amplitudes are
respectively
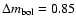 mag and
mag and 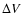 =
35 km s-1. The relative radius amplitude at the surface is
=
35 km s-1. The relative radius amplitude at the surface is
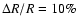 .
The mean photospheric radius is about
.
The mean photospheric radius is about
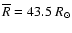 ,
in agreement with interferometric and
parallax measurements obtained by Mourard et al. (1997),
Nordgren et al. (2000) and Benedict et al.
(2002).
,
in agreement with interferometric and
parallax measurements obtained by Mourard et al. (1997),
Nordgren et al. (2000) and Benedict et al.
(2002).
We then generated a series of snapshots of the atmospheric
structure (about 60 per pulsation period) and after the line
profile computation we deduced the radial velocity variations. For
all phases we assume the same microturbulence velocity of 1 km s-1,
and we neglect the rotation (
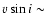 5 km s-1, Breitfellner
& Gillet 1993).
5 km s-1, Breitfellner
& Gillet 1993).
3 Velocities
To study the projection factor, we now define different radial and
pulsational velocities.
3.1 The radial velocity
Theoretical line profiles deduced from the 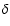 Cep model are
used to determine apparent radial velocities considering either
the minimum of the profile or the Gaussian fit. The maximum
velocity difference between these two methods reaches about
0.7 km s-1 during extrema phases (
Cep model are
used to determine apparent radial velocities considering either
the minimum of the profile or the Gaussian fit. The maximum
velocity difference between these two methods reaches about
0.7 km s-1 during extrema phases (
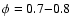 and
and
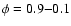 ), see Fig. 1. We will show later that
such a difference is not negligible for the projection factor
determination.
), see Fig. 1. We will show later that
such a difference is not negligible for the projection factor
determination.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1419f1.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg29.gif) |
Figure 1:
Difference between the theoretical radial velocity curves
measured by the profile minimum method (
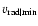 )
and the
Gaussian fitting method ( )
and the
Gaussian fitting method (
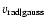 ). The small
difference induces a bias in the determination of the p-factor.
The horizontal line is the zero velocity in the stellar rest
frame. ). The small
difference induces a bias in the determination of the p-factor.
The horizontal line is the zero velocity in the stellar rest
frame. |
| Open with DEXTER |
3.2 The pulsation velocity
The projection factor may have different definitions depending on
the pulsating layer considered. From a spectroscopic point of
view, one considers the gas velocity associated to the optical
barycenter of the line forming region. However, the instruments,
spectrograph and interferometer, do not probe the same layers of
the star. For instance, with the IBW method, the layers that are
seen by the interferometer depend on the spectral resolution.
Indeed, a wide spectral band will rather probe the continuum
(photospheric) region. Conversely, in a specific line, the
visibility function is the Fourier transform of the image of the
star in the considered line. Thus different cases, corresponding
to each type of observation, have to be considered.
Firstly, for spectroscopic observations the gas velocity is that
of the line-forming layers. However this region may represent an
appreciable fraction of the height of the atmosphere. Sabbey et
al. (1995) determined the layer corresponding to the optical
center of gravity of the line from contribution functions. In our
case, we consider the standard definition in which the line core
is formed at an optical depth of 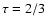 .
Hence, we use the
definition:
.
Hence, we use the
definition:
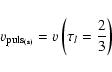 |
(1) |
where 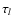 is the optical depth at the center of the line and
"(s)'' means "Spectroscopy''.
is the optical depth at the center of the line and
"(s)'' means "Spectroscopy''.
Secondly, for interferometric observations in one particular line,
it is better to consider the velocity of optical layers
corresponding to an optical depth of
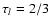 .
It is not the
gas velocity that is considered here but the velocity of the
optical layer deduced from the pulsation model, defined by:
.
It is not the
gas velocity that is considered here but the velocity of the
optical layer deduced from the pulsation model, defined by:
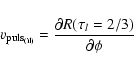 |
(2) |
where "(il)'' is for "Interferometry in one Line''.
Similarly, for interferometric observations in a wide band, the
most appropriate pulsation velocity is the one associated to the
photospheric layer that corresponds, by definition, to 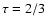 in the continuum:
in the continuum:
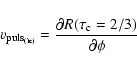 |
(3) |
where "(ic)'' is for "Interferometry in the Continuum''.
Note that we consider here the continuum next to the line.
Figure 2 represents the different pulsation velocities
defined above. These three pulsation velocity curves are different
by a maximum of 5% during the extrema phases, because the
atmosphere is not co-moving. The asymmetry in the profile is
maximum during the phases of extrema of the radial velocity curve,
thus there should be a large velocity gradient between the
different layers.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1419f2.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg35.gif) |
Figure 2:
Pulsation velocities vs. phase. The dashed curve shows
the velocity of the photospheric layer (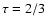 in the
continuum), the dot-dashed curve the velocity of the layer
corresponding to
in the
continuum), the dot-dashed curve the velocity of the layer
corresponding to 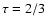 in the spectral center of the line and
the dotted curve the gas velocity corresponding to
in the spectral center of the line and
the dotted curve the gas velocity corresponding to
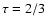 in the line. The horizontal line is the zero velocity
in the stellar rest frame.
in the line. The horizontal line is the zero velocity
in the stellar rest frame. |
| Open with DEXTER |
4 The projection factor
4.1 Combination of radial and pulsation velocities
It is now possible to combine the radial velocities (two cases)
with the pulsation velocities (three cases) to derive the
projection factor. Figures 3a-c shows the three
pulsation velocities together with the radial velocity using the
Gaussian method. Note that the estimators of radial and pulsation
velocities, in (s) and (il) cases, are supposed to probe the same
part of the star, the line forming region. In other words the two
curves should cancel at the same phase respectively in Figs.
3a and 3b, which is actually the case with a
good precision (
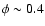 ). This is an indication that our
estimator of the optical barycenter
). This is an indication that our
estimator of the optical barycenter 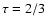 is correct. The
result should have been the same considering the profile minimum
as the velocity curve cancels at the same phase (see
is correct. The
result should have been the same considering the profile minimum
as the velocity curve cancels at the same phase (see 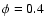 in
Fig. 1). However, we note in Fig. 3c that the
zero point of the photospheric velocity is at a slightly later
phase. This is the result of asynchronous motions in the
atmosphere.
in
Fig. 1). However, we note in Fig. 3c that the
zero point of the photospheric velocity is at a slightly later
phase. This is the result of asynchronous motions in the
atmosphere.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1419f3.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg38.gif) |
Figure 3:
Radial velocity curve deduced from the theoretical line
profiles by the Gaussian method together with a) the gas velocity
corresponding to 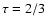 in the line forming region according
to Eq. (1), b) the
in the line forming region according
to Eq. (1), b) the 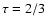 "optical layer''
velocity according to Eq. (2), c) the velocity of the
photospheric layer (
"optical layer''
velocity according to Eq. (2), c) the velocity of the
photospheric layer (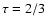 in the continuum, see Eq. (3)).
in the continuum, see Eq. (3)). |
| Open with DEXTER |
All these curves, with their amplitude and shape, will have an
impact on the projection factor and its variation over the
pulsation. In the following section we compute a suitable average
value of the projection factor for each case, considering two
estimators which are not simply the average of the ratio of
pulsation to radial velocities. In Sect. 5, we
consider more specifically the time dependence of the projection
factor.
4.2 Two estimators of p
To determine a constant projection factor, we cannot simply
consider the mean value of the ratio of the pulsation to radial
velocities. Due to the non-comoving character of the atmospheric
motions, this would lead to a ratio of physical quantities close
to zero (
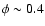 )
but not exactly at the same phase,
whatever the case considered in Fig. 3. Consequently,
two more suitable tests were used to estimate a constant value of
p. The first consists in applying a classical
)
but not exactly at the same phase,
whatever the case considered in Fig. 3. Consequently,
two more suitable tests were used to estimate a constant value of
p. The first consists in applying a classical 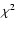 minimization algorithm between the quantity
minimization algorithm between the quantity
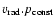 and the considered pulsation velocity (hereafter estimator
1):
and the considered pulsation velocity (hereafter estimator
1):
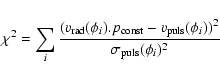 |
(4) |
where
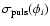 is the statistical error in
the pulsation velocity, arbitrarily fixed to a reasonable value of
1 km s-1, in order to evaluate the corresponding error on p.
The phases
is the statistical error in
the pulsation velocity, arbitrarily fixed to a reasonable value of
1 km s-1, in order to evaluate the corresponding error on p.
The phases 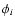 ,
in this case, are sampled following the
snapshots of the model. Here,
,
in this case, are sampled following the
snapshots of the model. Here,
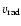 is the radial velocity
deduced from either the profile minimum or the Gaussian fit, and
is the radial velocity
deduced from either the profile minimum or the Gaussian fit, and
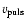 is related to Eqs. (1)-(3).
is related to Eqs. (1)-(3).
The second estimator of the p-factor is directly based on the
radius variation of the star, obtained either by integration of
the radial velocity or directly by the position of the layer as
provided by the radius of the mass zone involved. Hence, the
quantity defined by
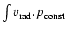 is compared
with the pulsating radius (hereafter estimator 2):
is compared
with the pulsating radius (hereafter estimator 2):
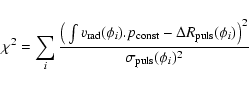 |
(5) |
where
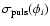 is the statistical error in
the pulsation radius, fixed to 0.1
is the statistical error in
the pulsation radius, fixed to 0.1 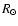 to obtain the same
uncertainty in the p-factor for both estimators. The quantity
to obtain the same
uncertainty in the p-factor for both estimators. The quantity
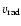 is the same as in estimator 1. The radius variation
is the same as in estimator 1. The radius variation
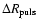 may be either:
may be either:
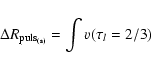 |
(6) |
or
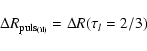 |
(7) |
or
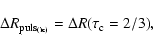 |
(8) |
with each case corresponding theoretically to the integration of
Eqs. (1)-(3). However,
note that for Eqs. (7) and (8) the radius
variations are deduced directly from the model. An integration
algorithm was used to derive Eq. (6). We also define
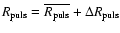 for
each case.
for
each case.
4.3 Results and discussion
Table 1 lists the computation results for the
twelve cases considered, leading to the following conclusions.
Table 1:
Optimal constant values for the p-factor for different
cases of interest.
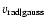 and
and
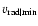 are
the radial velocity deduced from theoretical line profiles using
the Gaussian and minimum method respectively. Estimator (1) and
(2) of the constant projection factor correspond to Eqs. (4) and (5) respectively. In each case the
pulsational velocity
are
the radial velocity deduced from theoretical line profiles using
the Gaussian and minimum method respectively. Estimator (1) and
(2) of the constant projection factor correspond to Eqs. (4) and (5) respectively. In each case the
pulsational velocity
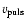 and radius
and radius
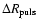 used are indicated.
used are indicated.
Firstly, the p-factors obtained considering the two estimators
differ by 2% in extreme cases. This is expected for two
reasons. On the one hand, the two minimized quantities are
different, so it is expected that the associated p-factor values
will also be different. On the other hand, when the radius is fitted,
the estimator may be less sensitive to velocity variation shapes.
Secondly, these results indicate a systematic shift of 0.02-0.04 (or 3%) in p-values between the radial velocities associated
with the Gaussian and the profile minimum methods. This is
logically linked to the systematic difference in velocity curves,
as shown in Fig. 1. Therefore it is important to choose
the p-factor value that corresponds to the method that was
used to estimate the projected velocity. In addition, it is best
to use the method that is least sensitive to velocity gradients
and marginal effects, in order to obtain a value for the
p-factor that is generally applicable. That is why in the
following discussions, we consider only the radial velocity
deduced from the Gaussian method.
Thirdly, the difference between the pulsation layers considered
should be related to the different observational techniques, as we
pointed out in Sect. 3. For spectroscopic
measurements of the gas velocity within the line, the recommended
value is p=1.35, which is close to the classical value of
p=1.36 (Burki et al. 1982). In this case, one should
preferably consider the first estimator since one has to deal with
the pulsation velocity of the gas to account for the atmosphere
dynamics. Conversely, for interferometric observations in a
"photospheric'' line, the best value is p=1.32, and one should
consider the second estimator (this result will be confirmed in
the next section). For broadband interferometric observations, one
should use a lower value of p=1.27. These results indicate that
an error of 6% can be made if one takes the usual value of
p=1.36 regardless of the observational method used.
Finally, an initial error of 1 km s-1 in the pulsation velocity, or
0.1 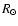 in the pulsation radius, leads to a final statistical
error in the p-factor of about 0.01 for both estimators.
in the pulsation radius, leads to a final statistical
error in the p-factor of about 0.01 for both estimators.
5 The effect of a constant projection factor on distance determination
The IBW method combines interferometric and spectrometric
observations to deduce the distance of the star (see Kervella et
al. 2004a). In the previous section we have obtained
different average values for p, considering different kinds of
velocities and estimators. We now study the influence of the
time-dependence of p on distance determination. Since the
definition of p involves phase-dependent factors, p itself
should be time-dependent. This is illustrated in Fig. 4
which shows the quantity
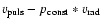 .
As it has already been pointed out in Sect. 4.2,
plotting the p-factor against the phase is misleading as the
ratio of pulsation to radial velocities is not representative when
these quantities are close to zero (
.
As it has already been pointed out in Sect. 4.2,
plotting the p-factor against the phase is misleading as the
ratio of pulsation to radial velocities is not representative when
these quantities are close to zero (
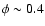 ). Moreover, in
the framework of the IBW method, the quantity of interest is the
pulsation velocity rather than the projection factor itself.
). Moreover, in
the framework of the IBW method, the quantity of interest is the
pulsation velocity rather than the projection factor itself.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1419f4.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg59.gif) |
Figure 4:
The quantity
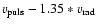 versus the
phase in the case of Fig. 3a:
versus the
phase in the case of Fig. 3a:
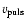 is the
gas velocity corresponding to
is the
gas velocity corresponding to 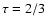 in the line formation
region according to Eq. (1), and
in the line formation
region according to Eq. (1), and
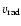 is the
radial velocity curve deduced from the theoretical line profiles
by the Gaussian method. p=1.35 is the optimum value obtained
from the estimator 1, as described in Sect. 4.2
is the
radial velocity curve deduced from the theoretical line profiles
by the Gaussian method. p=1.35 is the optimum value obtained
from the estimator 1, as described in Sect. 4.2 |
| Open with DEXTER |
On the one hand, we simulate angular diameters
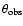 ,
fixing arbitrarily the distance of the star (d=275 pc) and using
the radius variations provided by the pulsation model:
,
fixing arbitrarily the distance of the star (d=275 pc) and using
the radius variations provided by the pulsation model:
![\begin{displaymath}
%
\theta_{\rm obs}(\phi_{i}) = 9.305~\left(\frac{
R_{\rm puls}(\phi_{i})}{275}\right) [{\rm mas}]
\end{displaymath}](/articles/aa/full/2004/46/aa1419/img61.gif) |
(9) |
where
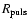 (in
(in 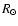 )
is one of the three
quantities:
)
is one of the three
quantities:
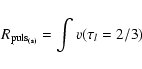 |
(10) |
or
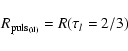 |
(11) |
or
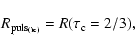 |
(12) |
as provided by the integration of Eqs. (1)-(3). The phases
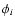 are sampled from the snapshots of the model. Figure 5 shows the simulated angular diameter curve considering
are sampled from the snapshots of the model. Figure 5 shows the simulated angular diameter curve considering
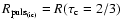 .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1419f5.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg66.gif) |
Figure 5:
Simulated angular diameter points deduced from Eq. (9) with
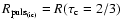 .
Each point is shown with its arbitrary theoretical error bar of
0.01 mas. This curve simulates interferometric observations used
in the IBW method. .
Each point is shown with its arbitrary theoretical error bar of
0.01 mas. This curve simulates interferometric observations used
in the IBW method. |
| Open with DEXTER |
On the other hand, the IBW method is used as follows. Firstly, a
radial velocity curve is derived from the synthetic spectra
considering both the Gaussian fit and the minimum profile methods.
Then, a constant value for the p-factor is chosen corresponding
to one of the twelve cases of Table 1.
Finally, the integration of the pulsation velocity deduced from
the radial velocity and the projection factor leads to an
estimation of the radius variation of the star. This leads to an
angular variation curve:
![\begin{displaymath}
%
\theta_{\rm model}(\phi_{i}) = \overline{\theta} +
9.305~\left(\frac{\Delta R(\phi_{i})}{d}\right) [{\rm mas}],
\end{displaymath}](/articles/aa/full/2004/46/aa1419/img67.gif) |
(13) |
where
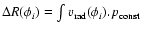 .
Finally, applying a classical
.
Finally, applying a classical
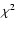 minimization
algorithm, we fit both the average angular diameter
minimization
algorithm, we fit both the average angular diameter
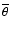 and the distance d to the star. The
minimized quantity is:
and the distance d to the star. The
minimized quantity is:
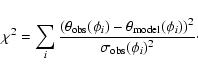 |
(14) |
The values for
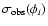 are arbitrarily fixed
to 0.01 mas which is a realistic value considering the
measurement precision achieved recently by long-baseline
interferometers (see Fig. 5).
are arbitrarily fixed
to 0.01 mas which is a realistic value considering the
measurement precision achieved recently by long-baseline
interferometers (see Fig. 5).
Table 2 gives the computed distances using
the p-factors shown in Table 1. The mean
angular diameters obtained correspond to the anticipated values of
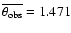 mas for the (ic) case and
mas for the (ic) case and
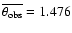 for (s) and (il) cases. The
statistical errors obtained are around 0.001 mas.
for (s) and (il) cases. The
statistical errors obtained are around 0.001 mas.
Table 2:
Distance results corresponding to the mean p-factor
results of Table 1. The different
expressions of the radius refer to Eqs. (10)-(12)
respectively and correspond to the quantity used in the Eq. (9) of
the simulated angular diameters.
Since p is constant, we have
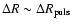 ,
and any departure from the predefined distance (275 pc) is the
result of the time-dependence of the projection factor or the
choice of the estimator: there is no model effect. It appears that
the computed and reference distances are closer for estimator 2.
Thus, estimator 2 provides projection factors less biased than
those provided by estimator 1 in the frame of the IBW method.
,
and any departure from the predefined distance (275 pc) is the
result of the time-dependence of the projection factor or the
choice of the estimator: there is no model effect. It appears that
the computed and reference distances are closer for estimator 2.
Thus, estimator 2 provides projection factors less biased than
those provided by estimator 1 in the frame of the IBW method.
An important conclusion is that for the best p-factor value, the
systematic error in the derived distance does not exceed 0.2%,
independent of the radial and pulsation velocities considered.
This important result indicates that a time-dependent p-factor
is not required at the moment since the final error of 0.2% is
well below our best estimation of recent distance determination.
Finally, note that the initial uncertainty of 0.01 mas in
theoretical angular diameters leads to a final statistical error
in the distance of 7.2 pc.
6 Conclusion
A self-consistent nonlinear model for 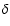 Cephei was
generated reproducing the main observational features of this
star.
Cephei was
generated reproducing the main observational features of this
star.
On the basis of this model we studied the effect of the projection
factor which links radial and pulsation velocity on the IBW method
for distance determination. Two methods were considered for
deriving the radial velocity curve: a Gaussian fit and the
profile-minimum method. Similarly, three pulsation velocities were
defined corresponding to different regions of the stellar
atmosphere: two concern the line forming region, while the third
corresponds to the photosphere. These three pulsation velocities
are linked to different observational techniques such as
spectrometry and wide-band or spectral-line interferometry. An
important result of this study is the very weak influence of the
time-dependence of the p-factor on distance determination. The
choice of a constant p-factor instead of one that is
time-dependent gives a systematic error in the final distance of
the order of 0.2%, which is below the best estimations of
current distance determination. More important, the projection
factor should be chosen depending on the observational techniques
used. For spectroscopic observations, if we use the Gaussian
method to derive the radial velocity, we propose p=1.35. For
wide-band interferometry, the best value is p = 1.27, and for
interferometric observations in a specific (metal) line it is p =
1.32. Note that this latter value has been determined for a given
line: considering lines formed in other atmospheric regions should
lead to different values. An extensive study of this dependence,
outside the scope of the present paper, is currently in progress.
Note also that these values have been determined for 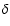 Cep. The generalization of our results to other classical Cepheids
will require the study of a larger sample of stars. The AMBER
instrument (Petrov et al. 2000) will also permit
observations in one particular line with a good resolution
("Interferometry in one Line''). Cepheids are bright sources and
observations in an absorption line of their atmospheres appears
feasible in terms of signal to noise ratio of as long as one can
use large telescopes and adaptive optics. It will be then possible
to compare the same layer of the star with interferometry and
spectrometry.
Cep. The generalization of our results to other classical Cepheids
will require the study of a larger sample of stars. The AMBER
instrument (Petrov et al. 2000) will also permit
observations in one particular line with a good resolution
("Interferometry in one Line''). Cepheids are bright sources and
observations in an absorption line of their atmospheres appears
feasible in terms of signal to noise ratio of as long as one can
use large telescopes and adaptive optics. It will be then possible
to compare the same layer of the star with interferometry and
spectrometry.
Acknowledgements
We thank Ph. Berio for having provided the 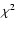 minimization
algorithm and for useful discussions. A. Fokin acknowledges the
Observatoire de la Côte d'Azur for financial support.
minimization
algorithm and for useful discussions. A. Fokin acknowledges the
Observatoire de la Côte d'Azur for financial support.
-
Albrow, M. D., & Cottrell, P. L. 1994, MNRAS, 267, 584
In the text
-
Benedict, G. F., McArthur, B. E., Fredrick, L. W., et al. 2002, AJ, 124, 1695
In the text
-
Breitfellner, M. G., & Gillet, D. 1993, A&A, 277, 524B
In the text
-
Burki, G., Mayor, M., Benz, W. 1982, A&A, 109, 258
In the text
-
Caroll, M. A. 1928, MNRAS, 88, 548
In the text
-
Chiosi, C., Wood, P. R., & Capitanio, N. 1993, ApJS, 86, 541
In the text
-
Eddington, A. S. 1926, The Internal Constitution of the Stars (Cambridge University Press), 185
In the text
-
Fernley, J. A., Skillen, I., & Jameson, R. F. 1989, MNRAS, 237, 947
In the text
-
Fokin, A. B. 1990, Ap&SS, 164, 95
In the text
-
Fokin, A. B. 1991, MNRAS, 250, 258
In the text
-
Fokin, A. B. 2001, in Stellar pulsation - nonlinear studies ASSL
series, ed. M. Takeuti, & D. D. Sasselov, 257, 103
In the text
-
Fokin, A. B., & Gillet, D. 1994, A&A, 290, 875
In the text
-
Fokin, A. B., & Gillet D. 1997, A&A, 325, 1013
In the text
In the text
-
Fokin, A. B., Gillet, D., & Breitfellner, M. G. 1996, A&A, 307, 503
In the text
-
Fokin, A. B., Mathias, Ph., Chapellier, E., Gillet, D., & Nardetto,
N. 2004, A&A, 426, 687
In the text
-
Fouqué, P., & Gieren, W. P. 1997, A&A, 320, 799
-
Getting, I. A. 1935, MNRAS, 95, 141
In the text
-
Hindsley, R., & Bell, R. A. 1986, PASP Conf. Ser., 98, 881
In the text
-
Jeannin L., Fokin A. B., Gillet D., & Baraffe I. 1997, A&A, 326, 203
In the text
-
Karp, A. H. 1973, ApJ, 180, 895
In the text
-
Karp, A. H. 1975, ApJ, 201, 641
In the text
-
Kervella, P., Nardetto, N., Bersier, D., et al. 2004a, A&A, 416,
941
In the text
-
Kervella, P., Bersier, D., Mourard D., Nardetto, N., & Coudé Du Foresto, V. 2004b, A&A, 423, 327
In the text
-
Kervella, P., Fouqué, P., Storm, J., et al. 2004, ApJ, 604, L113
In the text
-
Lane, B. F., Creech-Eakman, M., & Nordgren, T. E. 2002, ApJ, 573, 330
In the text
-
Parsons, S. B. 1972, ApJ, 174, 57
In the text
-
Petrov, R., Malbet, F., Richichi, A., et al. 2000, Proc. SPIE, 4006, 68
In the text
-
Marengo, M., Karovska, M., Sasselov, D. D., et al. 2003, ApJ,
589, 975
In the text
-
Montañés Rodriguez, P., & Jeffery, C. S. 2001, A&A, 375, 411
In the text
-
Mourard, D., Bonneau, D., Koechlin, L., et al. 1997, A&A, 317,789
In the text
-
Nordgren, T. E., Armstrong, J. T., Germain, M. E., et al. 2000, ApJ, 543, 972
In the text
-
Sabbey, C. N., Sasselov, D. D., Fieldus, M. S., et al. 1995, ApJ, 446, 250
In the text
-
Sasselov, D. D., & Lester, J. B. 1990, ApJ, 362, 333
In the text
-
Szabados L. 1980, Comm. Konkoly Obs. Hungary., 76, 1
In the text
-
Van Hoof, A., & Deurinck, R. 1952, ApJ, 115, 166
In the text
-
Welch, D. L. 1994, AJ, 108, 1421
In the text
Copyright ESO 2004
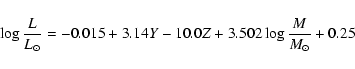
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1419f1.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg29.gif)
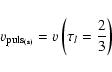
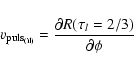
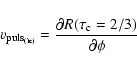
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1419f2.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1419f3.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg38.gif)
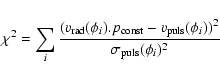
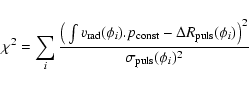
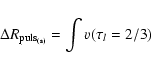
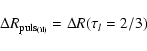
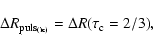
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1419f4.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg59.gif)
![\begin{displaymath}
%
\theta_{\rm obs}(\phi_{i}) = 9.305~\left(\frac{
R_{\rm puls}(\phi_{i})}{275}\right) [{\rm mas}]
\end{displaymath}](/articles/aa/full/2004/46/aa1419/img61.gif)
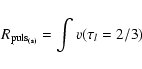
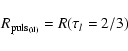
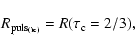
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1419f5.ps}\par\end{figure}](/articles/aa/full/2004/46/aa1419/Timg66.gif)
![\begin{displaymath}
%
\theta_{\rm model}(\phi_{i}) = \overline{\theta} +
9.305~\left(\frac{\Delta R(\phi_{i})}{d}\right) [{\rm mas}],
\end{displaymath}](/articles/aa/full/2004/46/aa1419/img67.gif)