A&A 428, 261-285 (2004)
DOI: 10.1051/0004-6361:20041335
A long-term numerical solution for the insolation quantities of the Earth
J. Laskar1 - P. Robutel1 - F. Joutel 1
- M. Gastineau1 - A. C. M. Correia1,2 - B. Levrard1
1 - Astronomie et Systèmes Dynamiques, IMCCE - CNRS UMR8028,
77 Av. Denfert-Rochereau, 75014 Paris, France
2 -
Departamento de Física da Universidade de Aveiro,
Campus Universitário de Santiago, 3810-193 Aveiro, Portugal
Received 23 May 2004 / Accepted 11 August 2004
Abstract
We present here a new solution for the astronomical computation of the insolation
quantities on Earth spanning from -250 Myr to 250 Myr.
This solution has been improved with respect to La93 (Laskar et al. 1993)
by using a direct integration of the gravitational equations for the orbital motion, and by
improving the dissipative contributions, in particular in the evolution of the Earth-Moon
System. The orbital solution has been used for the calibration of
the Neogene period (Lourens et al. 2004),
and is expected to be used for age calibrations of paleoclimatic data
over 40 to 50 Myr, eventually over the full Palaeogene period (65 Myr) with
caution. Beyond this time span, the chaotic evolution of the orbits prevents
a precise determination of the Earth's motion. However, the
most regular components
of the orbital solution could still be used over a much longer time span, which is why
we provide here the solution over 250 Myr.
Over this time interval, the most striking feature of the obliquity solution,
apart from a secular global increase due to tidal dissipation,
is a strong decrease of about 0.38 degree in the next few millions
of years, due to the crossing
of the
s6+g5-g6 resonance (Laskar et al. 1993).
For the calibration of the Mesozoic time scale (about 65 to 250 Myr), we propose to use
the term of largest amplitude in the eccentricity, related to g2-g5,
with a fixed frequency of 3.200''/yr, corresponding to a period of 405 000 yr.
The uncertainty of this time scale over 100 Myr should be about 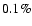 ,
and
,
and 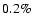 over the full Mesozoic era.
over the full Mesozoic era.
Key words: chaos - celestial mechanics - ephemerides - Earth
Due to gravitational planetary perturbations, the elliptical elements of
the orbit of the Earth are slowly changing in time, as is the orientation of
the planet's spin axis. These changes induce variations of the insolation received
on the Earth's surface.
The first computation of the secular variations of the Earth's orbital
elements were made by Lagrange (1781, 1782), and then Pontécoulant (1834),
but it was the work of Agassiz (1840), showing geological evidence
of past ice ages, that
triggered the search for a correlation between the geological evidence
of large climatic changes, and the variations of the Earth's astronomical parameters.
Shortly after, Adhémar (1842) proposed that these climatic variations
originated from the precession of the Earth's rotation axis.
After the publication of a more precise
solution of the Earth by Le Verrier (1856), that
took into account the secular perturbations of all main planets except
for Neptune, Croll (1890) proposed that the variation of the Earth's
eccentricity was also an important parameter for the understanding of the past
climates of the Earth.
The first computations of the variations of the obliquity (angle between the
equator and orbital plane) due to the secular variations of the orbital plane of the Earth
are due to Pilgrim (1904), and were later used by Milankovitch (1941)
to establish his theory of the Earth's insolation parameters.
Since then, the understanding of the climate response to the orbital forcing
has evolved, but all the necessary ingredients for
the insolation computations were present in Milankovitch's work.
The revival of the Milankovitch theory of paleoclimate can be related to
the landmark work of Hays et al. (1976), that established a correlation
between astronomical forcing and the
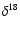 O records over the
past 500 kyr. The Milankovitch theory has since been confirmed overall
with variations in the climate response to the insolation forcing
(see Imbrie & Imbrie 1979; Imbrie 1982, for more historical details; and
Zachos et al. 2001; Grastein et al. 2004, for a recent review on
the astronomical calibration of geological data).
O records over the
past 500 kyr. The Milankovitch theory has since been confirmed overall
with variations in the climate response to the insolation forcing
(see Imbrie & Imbrie 1979; Imbrie 1982, for more historical details; and
Zachos et al. 2001; Grastein et al. 2004, for a recent review on
the astronomical calibration of geological data).
Since the work of Pilgrim (1904) and Milankovitch (1941),
the orbital and precession
quantities of the Earth have undergone several improvements.
Le Verrier's solution (1856) consisted in the linearized equations for the
secular evolution of the planetary orbits. Stockwell (1873), and Harzer (1895)
added the planet Neptune to Le Verrier's computations.
A significant improvement is due to Hill (1897)
who discovered that the proximity of a resonance in Jupiter and Saturn's
motion induces some important complements at the second order
with respect to the masses. The solution of Brouwer & Van Woerkom (1950)
is essentially the solution of Le Verrier and Stockwell, complemented
by the higher order contributions computed by Hill.
This solution was used for insolation computations by Sharav & Boudnikova (1967a,b)
with updated values of the parameters, and later on by Vernekar (1972).
The computations of Vernekar were actually used by Hays et al. (1976).
The next improvement in the computation of the orbital data
is by Bretagnon (1974), who computed the terms of second order and
degree 3 in eccentricity and inclination in the secular equations,
but omitted the terms of degree 5 in the Jupiter-Saturn system from Hill (1897).
This solution was then used by Berger (1978) for the computation of the
precession and insolation quantities of the Earth, following
Sharav & Boudnikova (1967a,b). All these works assumed implicitly that
the motion of the Solar system was regular and that the solutions could be
obtained as quasiperiodic series, using perturbation theory.
When Laskar (1984, 1985, 1986) computed in an extensive way the secular
equations for the Solar system, including all terms up to order 2 in the masses
and 5 in eccentricity and inclination, he realized that the
traditional perturbative methods could not be used for the integration of
the secular equations, due to strong divergences that became apparent in the
system of the inner planets (Laskar 1984). This difficulty was overcome by switching
to a numerical integration of the secular equations, which could be done in a
very effective way, with a very large stepsize of 500 years.
These computations provided a much more accurate solution for the orbital motion of
the Solar system (Laskar 1986, 1988), which also included a full solution for the
precession and obliquity of the Earth for insolation
computations over 10 Myr (million of years).
Extending his integration to 200 Myr, Laskar (1989, 1990) demonstrated
that the orbital motion of the planets, and especially of the terrestrial
planets, is chaotic, with an exponential divergence corresponding to
an increase of the error by a factor of 10 every 10 Myr, thus destroying
the hope to obtain a precise astronomical solution for paleoclimate
studies over more than a few tens of million of years (Laskar 1999).
The first long term direct numerical integration (without averaging)
of a realistic model of the Solar system, together with the
precession and obliquity equations,
was made by Quinn et al. (1991) over 3 Myr.
Over its range, this solution presented very small differences with
the updated secular solution of Laskar et al. (1993) that was computed
over 20 Myr, and has since been extensively used for paleoclimate computations
under the acronym La93. The orbital motion of the full Solar system has
also been computed over 100 Myr by Sussman & Wisdom (1992), using
a symplectic integrator with mixed variables (Wisdom & Holman 1991),
confirming the chaotic behaviour found by Laskar (1989, 1990).
Following the improvement of computer technology, long term integrations
of realistic models of the Solar system become more easy to perform, but are still
challenging when the time interval is the age of the Solar system or
if the accuracy of the model is comparable to the precision of short term
planetary ephemeris. The
longest integration was made over several billions of years by
Ito & Tanikawa (2002) with a Newtonian model that did not contain
general relativity or lunar contributions, while a recent
long term integration of the orbital motion of the
Solar system including general
relativity, and where the Moon is resolved was
made by Varadi et al. (2003) over about 50 Myr.
Here we present the result of the
efforts that we have conducted in the past years in our group in order to obtain
a new solution for Earth paleoclimate studies over the Neogene period (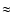 23 Myr)
and beyond. After a detailed analysis of the main limiting factors
for long term integrations (Laskar 1999), and the design of new
symplectic integrators (Laskar & Robutel 2001), we have obtained
a new numerical solution for both orbital and rotational motion of the Earth
that can be used over about 50 Myr for paleoclimate studies, and even
over longer periods of time if only the most stable features of the solution
are used.
Apart from the use of a very complete dynamical model for the orbital motion
of the planets, and of the new symplectic integrator of Laskar & Robutel (2001)
(see next section), a major change
with respect to La93 (Laskar et al. 1993)
is the consideration, in the precession solution,
of a more complete model for the Earth-Moon tidal interactions
(Sect. 4.1).
23 Myr)
and beyond. After a detailed analysis of the main limiting factors
for long term integrations (Laskar 1999), and the design of new
symplectic integrators (Laskar & Robutel 2001), we have obtained
a new numerical solution for both orbital and rotational motion of the Earth
that can be used over about 50 Myr for paleoclimate studies, and even
over longer periods of time if only the most stable features of the solution
are used.
Apart from the use of a very complete dynamical model for the orbital motion
of the planets, and of the new symplectic integrator of Laskar & Robutel (2001)
(see next section), a major change
with respect to La93 (Laskar et al. 1993)
is the consideration, in the precession solution,
of a more complete model for the Earth-Moon tidal interactions
(Sect. 4.1).
Table 1:
Main constants used in La2004. IAU76 refers to the resolutions of the International Astronmical Union
of 1976, IERS1992, and IERS2000, refers to the IERS conventions (McCarthy 1992; McCarthy & Petit 2004).
The present solution (La2004) or some of its
previous variants have already been distributed (Laskar 2001) and used
for calibration of sedimentary records over extended time interval
(Pälike 2002), and in particular
for the construction of a new astronomically calibrated geological time scale
for the Neogene period (Lourens et al. 2004). The full solution is available
on the Web site www.imcce.fr/Equipes/ASD/insola/earth/earth.html,
together with a set of routines for the computation of the
insolation quantities following (Laskar et al. 1993).
In addition to the numerical output of the orbital and rotational
parameter of the Earth that is available on the Web site, we have
made a special effort to provide in Sect. 8
very compact analytical approximations for the orbital and
rotational quantities of the Earth, that can be used in many cases
for a better analytical understanding of the insolation variations.
Finally, in the last sections, the stability of the solution La2004
is discussed, as well as the possible chaotic transitions
of the arguments present in the main secular resonances.
2 Numerical model
The orbital solutions La90-93 (Laskar 1990; Laskar et al. 1993) were obtained
by a numerical integration of the averaged equations of the Solar system,
including the main general relativity and Lunar perturbations. The averaging
process was performed using dedicated computer algebra routines. The
resulting equations were huge, with about 150 000 polynomial terms,
but as the short period terms were no longer present, these equations
could be integrated with a step size of 200 to 500 years, allowing very extensive
long term orbital computations for the Solar system.
Although these averaged equations solutions could be improved by
some new adjustment of the initial conditions and parameters
(Laskar et al. 2004), it appears that
because of the improvements of computer technology,
it becomes now possible to obtain more precise results over a few tens of million of years
using a more direct numerical integration of the gravitational equations, and this is how
the present new solution La2004 is obtained.
A detailed account of the dynamical equations and numerical integrator is not in the scope
of the present paper, but will be made in a forthcoming
publication. Nevertheless, we will
report here on the main issues concerning the numerical integrator,
and will more extensively discuss on the dissipative terms in
the integration (see Sect. 4.1).
The orbital model differs from La93, as it comprises now all 9 planets of the
Solar System, including Pluto. The post-Newtonian
general relativity corrections of order 1/c2 due to the Sun
are included following Saha & Tremaine (1994).
The Moon is treated as a separate object. In order to
obtain a realistic evolution of the Earth-Moon system,
we also take into account the most important coefficient (
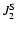 )
in the gravitational potential of the Earth
and of the Moon (Table 1), and the tidal dissipation in the Earth-Moon System
(see Sect. 4.1).
We also integrate at the same time the precession and obliquity equations for the Earth and the evolution
of its rotation period in a comprehensive and coherent way, following
the lines of Néron de Surgy & Laskar (1997), Correia et al. (2003)
(see Sect. 3).
)
in the gravitational potential of the Earth
and of the Moon (Table 1), and the tidal dissipation in the Earth-Moon System
(see Sect. 4.1).
We also integrate at the same time the precession and obliquity equations for the Earth and the evolution
of its rotation period in a comprehensive and coherent way, following
the lines of Néron de Surgy & Laskar (1997), Correia et al. (2003)
(see Sect. 3).
In order to minimize the accumulation of roundoff errors,
the numerical integration was performed with the new
symplectic integrator scheme
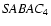 of (Laskar & Robutel 2001),
with a correction step for the integration of the Moon.
This integrator is particularly adapted to perturbed systems where the
Hamiltonian governing the equations of motion can be
written in the form
of (Laskar & Robutel 2001),
with a correction step for the integration of the Moon.
This integrator is particularly adapted to perturbed systems where the
Hamiltonian governing the equations of motion can be
written in the form
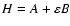 ,
as the sum of an integrable part A
(the Keplerian equations of the planets orbiting the
Sun and of the Moon around the Earth), and a small perturbation potential
,
as the sum of an integrable part A
(the Keplerian equations of the planets orbiting the
Sun and of the Moon around the Earth), and a small perturbation potential
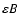 (here the small parameter
(here the small parameter 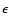 is of the order of the
planetary masses).
Using this integrator with step size
is of the order of the
planetary masses).
Using this integrator with step size 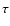 is then equivalent to integrate exactly a close by Hamiltonian
is then equivalent to integrate exactly a close by Hamiltonian
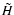 ,
where
the error of method
,
where
the error of method
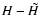 is of the order of
is of the order of
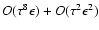 ,
and even
,
and even
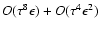 when the correction step
is added, while the same quantity is of the order
when the correction step
is added, while the same quantity is of the order
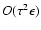 ,
in the widely used symplectic integrator of (Wisdom & Holman 1991).
More precisely, the integration step
,
in the widely used symplectic integrator of (Wisdom & Holman 1991).
More precisely, the integration step 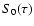 with
with
 is
is
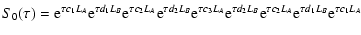 |
|
|
(1) |
where 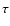 is the integration step, Lf is the differential operator defined by
is the integration step, Lf is the differential operator defined by
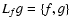 ,
where
,
where 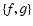 is the usual Poisson bracket, and the coefficients ci and di are
is the usual Poisson bracket, and the coefficients ci and di are
| c1 |
= |
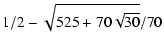 |
|
| c2 |
= |
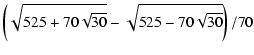 |
|
| c3 |
= |
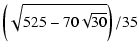 |
(2) |
| d1 |
= |
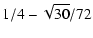 |
|
| d2 |
= |
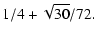 |
|
For the integration of the Earth-Moon system, we have added a correction step (see Laskar & Robutel 2001),
and the full integrator steps 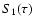 of
of
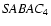 then becomes
then becomes
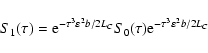 |
(3) |
where
b= 0.00339677504820860133 and
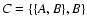 .
The step size used in the integration was
.
The step size used in the integration was
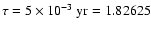 days.
The initial conditions of the integration were least square adjusted
to the JPL ephemeris DE406, in order to compensate for small
differences in the model. In particular, we do not take into account the
effect of the minor planets, and the modelization of the
body interactions in the Earth-Moon system is more complete in DE406 (see Williams et al. 2001). The integration
time for our complete model, with
days.
The initial conditions of the integration were least square adjusted
to the JPL ephemeris DE406, in order to compensate for small
differences in the model. In particular, we do not take into account the
effect of the minor planets, and the modelization of the
body interactions in the Earth-Moon system is more complete in DE406 (see Williams et al. 2001). The integration
time for our complete model, with
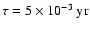 is about one day per 5 Myr
on a Compaq Alpha (ev68, 833 Mhz) workstation.
is about one day per 5 Myr
on a Compaq Alpha (ev68, 833 Mhz) workstation.
In Fig. 1a is plotted the evolution of the
total energy of the system from -250 Myr to +250 Myr. The energy presents a secular trend
that corresponds to the dissipation in the Earth-Moon system.
Indeed, after removing the computed energy change due to the secular evolution of the
Earth-Moon semi-major axis, the secular trend in the energy evolution disappears
and we are left with a residual that is smaller than
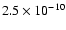 after 250 Myr, and seems to behave as a random walk (Fig. 1b). The normal component
of the angular
momentum is conserved over the same time with a relative error of less than
after 250 Myr, and seems to behave as a random walk (Fig. 1b). The normal component
of the angular
momentum is conserved over the same time with a relative error of less than
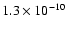 (Fig. 1c).
(Fig. 1c).
![\begin{figure}\par
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig1}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg98.gif) |
Figure 1:
Conservation of integrals. a) Relative variation of the total energy of the system versus time (in Myr)
from -250 Myr to +250 Myr. b) The same after correction of the secular trend due to
the tidal dissipation in the Earth-Moon system. c) Relative variation of the normal component of the
total angular momentum.
|
| Open with DEXTER |
![\begin{figure}
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig2}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg99.gif) |
Figure 2:
Normalized repartition of the energy numerical error for 1000 yr steps, over the whole integration, from -250 Myr to +250 Myr. Practically superposed to this curve is the computed normal distribution
given by Eqs. (4) and (5).
|
| Open with DEXTER |
In order to test the randomness of the numerical error in the integration,
we have plotted the distribution of the difference of total energy
from one 1000 year step to the next. After normalization to 1 of the area
of the distribution curve (Fig. 2), we obtain a curve that is almost
identical to the normalized Gaussian function
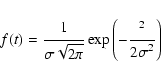 |
(4) |
where
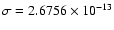 is the computed standard deviation
is the computed standard deviation
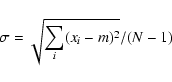 |
(5) |
while the mean
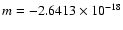 is neglected.
The integration stepsize is
is neglected.
The integration stepsize is
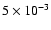 yr, the standard deviation per step
is thus
yr, the standard deviation per step
is thus
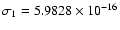 ,
that is about
,
that is about
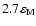 ,
where
,
where
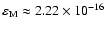 is the machine Epsilon in double precision.
Assuming that the machine error is uniformly distributed in the interval
is the machine Epsilon in double precision.
Assuming that the machine error is uniformly distributed in the interval
![$[-\varepsilon_{\rm M}/2,+\varepsilon_{\rm M}/2]$](/articles/aa/full/2004/46/aa1335/img108.gif) ,
the standard error of an elementary operation is
,
the standard error of an elementary operation is
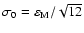 ,
and the error over one step
thus corresponds to
,
and the error over one step
thus corresponds to
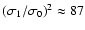 elementary operations.
This value is thus extremely small, and we believe that
we will not be able to improve
elementary operations.
This value is thus extremely small, and we believe that
we will not be able to improve  unless we decrease
unless we decrease 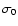 by switching to higher machine precision. For example, in quadruple precision
(128 bits for the representation of a real number),
by switching to higher machine precision. For example, in quadruple precision
(128 bits for the representation of a real number),
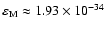 .
Moreover, the Gaussian distribution
of the increments of the energy (Fig. 2) ensures that we do
not have systematic trends in our computations, and that the
numerical errors behave as a random variable with zero mean.
The total energy error reflects mostly the behavior of the outer planets,
but we can assume that the numerical error will behave in roughly the same for all the planets,
although for Mercury, due to its large eccentricity, some
slight increase of the error may occur. This should not be the case for the
error of method,
resulting from the truncation in power of
.
Moreover, the Gaussian distribution
of the increments of the energy (Fig. 2) ensures that we do
not have systematic trends in our computations, and that the
numerical errors behave as a random variable with zero mean.
The total energy error reflects mostly the behavior of the outer planets,
but we can assume that the numerical error will behave in roughly the same for all the planets,
although for Mercury, due to its large eccentricity, some
slight increase of the error may occur. This should not be the case for the
error of method,
resulting from the truncation in power of 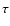 in the integrator,
where the error should decrease as the period of the planet increases.
in the integrator,
where the error should decrease as the period of the planet increases.
3 Precession equations
![\begin{figure}
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig3} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg115.gif) |
Figure 3:
Fundamental planes for the definition of precession and obliquity.
Eqt and Ect are the mean equator and ecliptic at date t.
Ec0 is the fixed ecliptic at Julian date J2000, with equinox 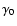 .
The general precession in longitude .
The general precession in longitude 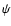 is defined by
is defined by
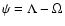 . .  is the longitude of the node, and i the inclination.
The angle
is the longitude of the node, and i the inclination.
The angle
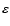 between Eqt and Ect is the obliquity.
between Eqt and Ect is the obliquity.
|
| Open with DEXTER |
We suppose here that the Earth is a homogeneous rigid
body with moments of inertia A < B < C and we assume
that its spin axis is also the principal axis of inertia.
The precession 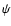 and obliquity
and obliquity
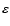 (Fig. 3)
equations for the rigid Earth in the presence of
planetary perturbations are given by
Kinoshita (1977), Laskar (1986), Laskar et al. (1993), Néron de Surgy & Laskar (1997).
(Fig. 3)
equations for the rigid Earth in the presence of
planetary perturbations are given by
Kinoshita (1977), Laskar (1986), Laskar et al. (1993), Néron de Surgy & Laskar (1997).
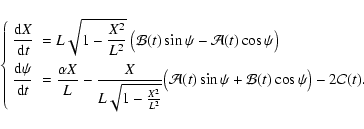 |
(6) |
With
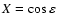 ,
, 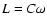 ,
where
,
where 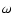 is the spin rate of the Earth, and
is the spin rate of the Earth, and
![\begin{displaymath}\left\{ \begin{array}{lll}
{\cal A}(t) &=\displaystyle
\frac...
...2mm]
{\cal
C}(t) &= q\dot p - p\dot q \\
\end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img120.gif) |
(7) |
where
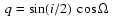 and
and
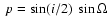 ,
and where
,
and where 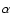 is the
"precession constant'':
is the
"precession constant'':
![$\displaystyle \alpha= {{\displaystyle\strut3G}\over{\displaystyle\strut2\omega}...
...trut3}\over{\displaystyle\strut2}}\sin^2 i_{\rm M}\right) \Bigg] ~ {E_{\rm d}}.$](/articles/aa/full/2004/46/aa1335/img124.gif) |
|
|
(8) |
For a fast rotating planet like the Earth,
the dynamical ellipticity
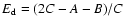 can be considered as proportional to
can be considered as proportional to 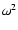 ;
this corresponds to
the hydrostatic equilibrium (see for example Lambeck 1980). In this approximation,
;
this corresponds to
the hydrostatic equilibrium (see for example Lambeck 1980). In this approximation, 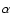 is thus proportional to
is thus proportional to 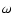 .
The quantities
.
The quantities
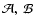 and
and
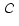 are related to the secular evolution of the orbital plane of the Earth
and are given by the integration of the
planetary motions.
are related to the secular evolution of the orbital plane of the Earth
and are given by the integration of the
planetary motions.
4.1 The body tides
Following (Darwin 1880; Mignard 1979), we assume that
the torque resulting from tidal friction is proportional to the time lag 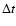 needed for the deformation to reach the equilibrium.
This time lag is supposed to be constant, and
the angle between the direction of the tide-raising body and
the direction of the high tide (which is
carried out of the former by the rotation of the Earth)
is proportional to the speed of rotation.
Such a model is called "viscous'', and corresponds to the case for which 1/Q is proportional to
the tidal frequency.
needed for the deformation to reach the equilibrium.
This time lag is supposed to be constant, and
the angle between the direction of the tide-raising body and
the direction of the high tide (which is
carried out of the former by the rotation of the Earth)
is proportional to the speed of rotation.
Such a model is called "viscous'', and corresponds to the case for which 1/Q is proportional to
the tidal frequency.
After averaging over the mean anomaly of the Moon and Earth (indices M and 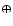 ),
and over the longitude of node and perigee of the Moon,
we have at second order in eccentricity for the contributions of the solar tides
),
and over the longitude of node and perigee of the Moon,
we have at second order in eccentricity for the contributions of the solar tides
![\begin{displaymath}\left\{\begin{array}{ll}
{{\displaystyle\strut{\rm d}{L}}\ove...
...{2}}} {e_\odot}^2\right) n_\odot\bigg] \\
\end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img130.gif) |
(9) |
where 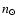 is the mean motion of the Sun (index
is the mean motion of the Sun (index 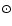 )
around the Earth, while the contribution
of the lunar tides is
)
around the Earth, while the contribution
of the lunar tides is
![\begin{displaymath}\left\{\begin{array}{l}
{{\displaystyle\strut{\rm d}{L}}\over...
...ight) ~ n_{\rm M}~\cos i_{\rm M}\bigg]. \\ \end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img133.gif) |
(10) |
The "cross tides'', are obtained by the perturbation of the tidal
bulge raised by the Sun or the Moon on the other body.
Their importance was noticed by Touma & Wisdom (1994).
These tidal effects tend to drive the equator towards the ecliptic, and have both
the same magnitude
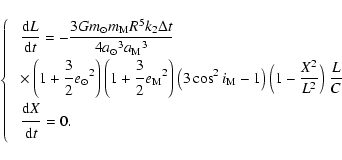 |
(11) |
At second order in eccentricity, we
have for the orbital evolution of the Moon (Mignard 1979, 1980, 1981; Néron de Surgy & Laskar 1997)
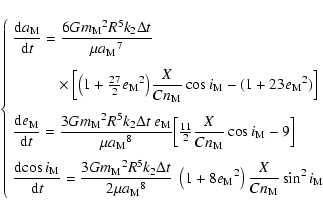 |
(12) |
where
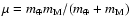 ,
and for the Sun
,
and for the Sun
![\begin{displaymath}\left\{
\begin{array}{ll}
{{\displaystyle\strut{\rm d}{a_\odo...
...2}}} {X \over
{C n_\odot}} - 9 \Big] \\
\end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img137.gif) |
(13) |
where
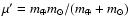 .
However, both last variations are negligible: about 3 meters per Myr for
.
However, both last variations are negligible: about 3 meters per Myr for
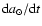 and 10-12 per Myr for
and 10-12 per Myr for
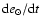 .
.
We have also taken into account the tidal effect raised by the Earth on the Moon,
following Néron de Surgy & Laskar (1997), with the following
simplifying assumptions that the Moon is locked in synchronous spin-orbit resonance
with the Earth (i.e.
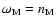 ), and expanding only at first order in the Moon
inclination (6.41
), and expanding only at first order in the Moon
inclination (6.41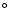 at
at
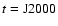 ). We thus obtain the additional contributions
). We thus obtain the additional contributions
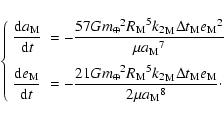 |
(14) |
With the numerical values from Table 1, these contributions
represent 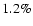 of the total
of the total
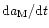 and
and 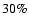 of the total
of the total
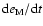 for
present conditions.
Finally, the tides raised on the Moon by the Sun can be neglected because the ratio of the
magnitudes of solar and terrestrial tides on the Moon is
for
present conditions.
Finally, the tides raised on the Moon by the Sun can be neglected because the ratio of the
magnitudes of solar and terrestrial tides on the Moon is
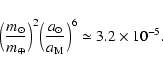 |
(15) |
The core and the mantle have different dynamical
ellipticities, so they tend to have different precession rates. This
trend produces a viscous friction at the core-mantle boundary
(Poincaré 1910; Rochester 1976; Lumb & Aldridge 1991).
We will consider here that an effective viscosity 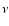 can account for a weak
laminar friction, as well as a strong turbulent one which thickens the boundary layer
(e.g. Correia et al. 2003).
can account for a weak
laminar friction, as well as a strong turbulent one which thickens the boundary layer
(e.g. Correia et al. 2003).
The core-mantle friction
tends to slow down the rotation and to
bring the obliquity down to 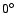 if
if
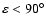 and up to
and up to 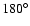 otherwise, which
contrasts with the effect of the tides.
Furthermore, one can see that, despite the strong coupling by pressure forces,
there can be a substantial contribution to the variation of
the spin for high viscosities and moderate speeds of rotation.
otherwise, which
contrasts with the effect of the tides.
Furthermore, one can see that, despite the strong coupling by pressure forces,
there can be a substantial contribution to the variation of
the spin for high viscosities and moderate speeds of rotation.
The Earth's atmosphere also undergoes some torques which can be transmitted to the surface by
friction: a torque caused by the gravitational tides raised by the Moon and the Sun, a magnetic
one generated by interactions between the magnetosphere and the solar wind. Both effects
are negligible; see respectively Chapman & Lindzen (1970) and Volland (1978).
Finally, a torque is produced by the daily solar heating which induces a redistribution of the
air pressure, mainly driven by a semidiurnal wave, hence the so-called thermal atmospheric tides
(Chapman & Lindzen 1970). The axis of symmetry of the resulting bulge of mass is permanently
shifted out of the direction of the Sun by the Earth's rotation. As for the body tides, this
loss of symmetry is responsible for the torque which, in the present conditions, tends to accelerate
the spin (Correia & Laskar 2003).
Volland (1978) showed that this effect is not negligible, reducing
the Earth's despinning by about 7.5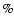 .
But, although the estimate of their long term contributions
deserves careful attention, we have not taken the atmospheric tides into account in the
computations presented in the next sections, assuming that, as the uncertainty on some of the other
factors is still large, the global results obtained here will not differ much when taking this
additional effect into consideration.
.
But, although the estimate of their long term contributions
deserves careful attention, we have not taken the atmospheric tides into account in the
computations presented in the next sections, assuming that, as the uncertainty on some of the other
factors is still large, the global results obtained here will not differ much when taking this
additional effect into consideration.
Several internal geophysical processes are able to affect the moments of
inertia of the Earth and thereby its precession constant value.
Redistribution of mass within the Earth can
occur as a consequence of plate subduction, upwelling plumes, mantle
avalanches or density anomalies driven by mantle convection. Typical
time-scales of these phenomena range from  10 to 100 Myr. However, their impact is still poorly known.
Forte & Mitrovica (1997) computed convection-induced perturbations in
the dynamical ellipticity of the Earth over the last 20 Myr, using
different sets of 3D seismic heterogeneity models and mantle viscosity
profiles. Most of the models indicate that mantle convection led to a
mean relative increase of the precession constant close to
10 to 100 Myr. However, their impact is still poorly known.
Forte & Mitrovica (1997) computed convection-induced perturbations in
the dynamical ellipticity of the Earth over the last 20 Myr, using
different sets of 3D seismic heterogeneity models and mantle viscosity
profiles. Most of the models indicate that mantle convection led to a
mean relative increase of the precession constant close to 
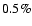 since the beginning of the Neogene period (
since the beginning of the Neogene period ( 23 Myr ago).
Although this value is similar to our estimate of the tidal dissipation
effect (but in the opposite direction, see Sect. 9), we did not take
account of its impact in our computations.
Because of its still large uncertainty, we feel that it is more
appropriate to include its possible contribution as a perturbation of the
tidal dissipation parameter.
23 Myr ago).
Although this value is similar to our estimate of the tidal dissipation
effect (but in the opposite direction, see Sect. 9), we did not take
account of its impact in our computations.
Because of its still large uncertainty, we feel that it is more
appropriate to include its possible contribution as a perturbation of the
tidal dissipation parameter.
![\begin{figure}
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig4} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg158.gif) |
Figure 4:
Differences La2003-DE406 over the full range of DE406 (-5000 yr to +1000 from J2000).
The units for semi-major axis (a) are AU, arcsec for mean longitude (l) and longitude of perihelion
(perihelion). The eccentricity (e) and the inclinations variables (
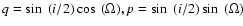 ), where i and ), where i and 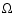 are the inclination and node from the
ecliptic and equinox J2000.
are the inclination and node from the
ecliptic and equinox J2000. |
| Open with DEXTER |
Climate friction is a positive and dissipative feedback between obliquity
variations and climate which may cause a secular drift of the spin axis.
In response to quasi-periodic variations in the obliquity, glacial and
interglacial conditions drive transport of water into and out of the polar
regions, affecting the dynamical ellipticity of the Earth. A significant
fraction of the surface loading is compensated by viscous flow within the
Earth, but delayed responses in both climatic and viscous relaxation
processes may introduce a secular term in the obliquity evolution
(Rubincam 1990, 1995). Because both the ice load history and the
visco-elastic structure of the Earth are not strongly constrained, it is
difficult to produce accurate simulations and predictions of the coupled
response of the entire system. Nevertheless, simplifying assumptions have
been used to estimate the magnitude and the direction of the secular
drift. Several analyses have examined this phenomenon, suggesting that
climate friction could have changed the Earth's obliquity by more that 20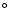 over its whole geological history (Bills 1994; Ito et al. 1995; Williams et al. 1998). A more detailed theoretical and
numerical treatment of climate friction has been developped by Levrard &
Laskar (2003). Using available constraints on the ice volume response to
obliquity forcing based on
over its whole geological history (Bills 1994; Ito et al. 1995; Williams et al. 1998). A more detailed theoretical and
numerical treatment of climate friction has been developped by Levrard &
Laskar (2003). Using available constraints on the ice volume response to
obliquity forcing based on
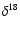 O oxygen-isotope records, they
showed that climate friction impact is likely negligible. Over the last 3 Ma, corresponding to the intensification of the Northern Hemisphere
glaciation, a maximal absolute drift of only
O oxygen-isotope records, they
showed that climate friction impact is likely negligible. Over the last 3 Ma, corresponding to the intensification of the Northern Hemisphere
glaciation, a maximal absolute drift of only 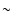
 /Myr has
been estimated for a realistic lower mantle viscosity of 1022 Pa. s.
Before 3 Ma, climate friction impact is expected to be much more
negligible because of the lack of massive ice caps. In this context, this
effect was not taken into account in our long-term computations. Indeed, the
uncertainty on the tidal dissipation is still important and it is expected
that most of the possible effect of climate friction would be absorbed by
a small change of the main tidal dissipation parameters.
/Myr has
been estimated for a realistic lower mantle viscosity of 1022 Pa. s.
Before 3 Ma, climate friction impact is expected to be much more
negligible because of the lack of massive ice caps. In this context, this
effect was not taken into account in our long-term computations. Indeed, the
uncertainty on the tidal dissipation is still important and it is expected
that most of the possible effect of climate friction would be absorbed by
a small change of the main tidal dissipation parameters.
Nevertheless, glaciation-induced perturbations in the dynamical
ellipticity of the Earth change the precession frequency and thereby the
obliquity frequencies leading to a temporal shift between a perturbated
and a nominal solution (see Sect. 9). Estimates of this offset have been
performed by Mitrovica & Forte (1995) and Levrard & Laskar (2003) for
a large set of mantle viscosity profiles. It may reach between 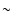 0.7 and 8 kyr after 3 Myr, corresponding respectively to extreme lower mantle
viscosities of
0.7 and 8 kyr after 3 Myr, corresponding respectively to extreme lower mantle
viscosities of
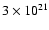 and 1023 Pa. s. In the last case, the Earth
is nearly rigid on orbital timescales and the corresponding offset can be
thus reasonably considered as a maximal value.
and 1023 Pa. s. In the last case, the Earth
is nearly rigid on orbital timescales and the corresponding offset can be
thus reasonably considered as a maximal value.
5 Comparison with DE406
Table 2:
Maximum difference between La2004 and DE406 over the whole time interval of DE406
(-5000 yr to +1000 yr with origin at J2000); Col. 1: -100 to + 100 yr; Col. 2:-1000 to + 1000 yr;
Col. 3: -5000 to +1000 yr. EMB is the Earth-Moon barycenter.
Using a direct numerical integrator, our goal is to provide
a long term solution for the orbital and precessional elements of the Earth
with a precision that is comparable with the usual accuracy of a
short time ephemeris.
We have thus compared our solution with the most advanced present
numerical integration, DE406, that was itself adjusted to
the observations (Standish 1998).
Over
the full range of DE406, that is from -5000 yr to + 1000 yr from the present date,
the maximum difference
in the position of the Earth-Moon barycenter is less than 0.09 arcsec
in longitude, and the difference in eccentricity
less than 10-8. The difference in the longitude of the Moon
are more important, as the dissipative models that are used in the two integrations
are slightly different. They amount to 240 arcsec after 5000 years, and
the eccentricity difference is of the order of
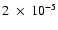 ,
but it should be noted that
only the averaged motion of the Moon will have some significant influence on
the precession and obliquity of the Earth.
Table 2 summarizes the maximum differences between La2004 and DE406
for the main orbital elements, over the
whole interval of DE406, for different time intervals.
,
but it should be noted that
only the averaged motion of the Moon will have some significant influence on
the precession and obliquity of the Earth.
Table 2 summarizes the maximum differences between La2004 and DE406
for the main orbital elements, over the
whole interval of DE406, for different time intervals.
6 Comparison with La93
![\begin{figure}\par
\includegraphics[width=13cm,clip]{figures_pdf/1335fig5} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg166.gif) |
Figure 5:
Eccentricity of the Earth over 25 Myr in negative time
from J2000. The solid line stands for the present solution La2004, while the dotted line
is the eccentricity in the La93 solution (Laskar et al. 1993). The differences
of the two solutions becomes noticeable after 10 Myr, and significantly different after 15-20 Myr. |
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=13cm,clip]{figures_pdf/1335fig6}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg167.gif) |
Figure 6:
Inclination (in degrees) of the Earth with respect to the fixed ecliptic J2000 over 25 Myr in negative time
from J2000. The solid line stands for the present solution La2004, while the dotted line
is the eccentricity in the La93 solution (Laskar et al. 1993). The differences
of the two solutions become noticeable after 15 Myr, and significantly different after 20 Myr.
|
| Open with DEXTER |
Table 3:
Main secular frequencies gi and si of La2004 determined over 20 Ma for the four inner planets, and over 50 Ma for the 5 outer planets (in arcsec yr-1).
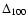 and
and
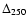 are the observed variations of the frequencies over respectively 100 and 250 Myr. In the last column, the period
of the secular term are given.
are the observed variations of the frequencies over respectively 100 and 250 Myr. In the last column, the period
of the secular term are given.
We have compared in Figs. 5 and 6 the eccentricity and inclination
of the secular solution La93 and the new present solution La2004.
Over 10 Myr, the
two orbital solutions La93 and La2004 are nearly identical, and do not differ significantly
over 20 Myr.
The differences in eccentricity
increase regularly with time, amounting to about 0.02 in the eccentricity
after 20 Myr, about 1/3 of the total amplitude 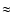 0.063, while the
difference in the orbital inclination reaches 1 degree, to compare to a maximum variation of 4.3 degrees.
These differences result mostly from a small difference in the main
secular frequency g6 from Jupiter and Saturn that is now
g6=28.2450 arcsec/year
(Table 3)
instead of 28.2207 arcsec/year in the previous solution. Beyond 20 million years,
the differences between the two solutions become more noticeable.
The solutions in obliquity and climatic precession are
plotted in Figs. 7 and 8.
The difference in obliquity over 20 Myr amounts to about 2 degrees,
which means that the obliquity cycles of the two solutions become nearly out
of phase after this date.
The differences
La2004-La93 are plotted in (a), while in (b) only the precession model
has been changed and in (c) only the orbital model has been changed.
Comparing 7b and 7c shows that
most of the differences between the La93 and La2004 obliquity solutions
result from the change
in the dissipative model of the Earth-Moon system, while the only change of the
orbital solution would lead to a
much smaller change of only 0.6 degree in obliquity after 20 Myr.
Similar conclusions can be made for the climatic precession
(Figs. 8a-c).
0.063, while the
difference in the orbital inclination reaches 1 degree, to compare to a maximum variation of 4.3 degrees.
These differences result mostly from a small difference in the main
secular frequency g6 from Jupiter and Saturn that is now
g6=28.2450 arcsec/year
(Table 3)
instead of 28.2207 arcsec/year in the previous solution. Beyond 20 million years,
the differences between the two solutions become more noticeable.
The solutions in obliquity and climatic precession are
plotted in Figs. 7 and 8.
The difference in obliquity over 20 Myr amounts to about 2 degrees,
which means that the obliquity cycles of the two solutions become nearly out
of phase after this date.
The differences
La2004-La93 are plotted in (a), while in (b) only the precession model
has been changed and in (c) only the orbital model has been changed.
Comparing 7b and 7c shows that
most of the differences between the La93 and La2004 obliquity solutions
result from the change
in the dissipative model of the Earth-Moon system, while the only change of the
orbital solution would lead to a
much smaller change of only 0.6 degree in obliquity after 20 Myr.
Similar conclusions can be made for the climatic precession
(Figs. 8a-c).
![\begin{figure}\par
\includegraphics[width=7.6cm,clip]{figures_pdf/1335fig7} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg168.gif) |
Figure 7:
Differences in obliquity (in degrees) La2004-La93(1, 1) versus time (in Myr) over 20 Myr
from present a). In La2004 both orbital and
precession models have been changed. In b) only the precession model has been changed,
while in c) only the orbital motion has been changed.
It is thus clear that the main change in La2004 arise from the change of precession model.
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=7.6cm,clip]{figures_pdf/1335fig8} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg170.gif) |
Figure 8:
Differences in climatic precession (
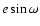 ,
where ,
where
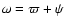 is the
perihelion from the moving equinox) La2004-La93(1, 1) versus time (in Myr) over 20 Myr
from present a). In La2004 both orbital and
precession models have been changed. In b) only the precession model has been changed,
while in c) only the orbital motion has been changed.
It is thus clear that the main change in La2004 arise from the change of precession model.
is the
perihelion from the moving equinox) La2004-La93(1, 1) versus time (in Myr) over 20 Myr
from present a). In La2004 both orbital and
precession models have been changed. In b) only the precession model has been changed,
while in c) only the orbital motion has been changed.
It is thus clear that the main change in La2004 arise from the change of precession model.
|
| Open with DEXTER |
7 Secular frequencies
Over long time scales, the determination of longitude of the planet on its orbit is not
very important, and we are more concerned by the slow evolution of the Earth orbit
under secular planetary perturbations. The semi-major axis of the Earth
has only very small variations (Fig. 11). Indeed, as shown by Laplace (1773) and Lagrange (1776),
there are no secular variations of the semi-major axis of the planets at
first order with respect to the masses, while some terms of higher order
can be present (Haretu 1885). These terms are very small for the inner planets,
but more visible in the solutions of the outer planets where the proximity of
some mean motion resonances
increases their contribution at second order with respect to the masses
(Milani et al. 1987; Bretagnon & Simon 1990).
For the solution of the Earth, they are so small that they will not induce any
noticeable change of the mean Earth-Sun distance, or of the duration of the year
in the geological past, at least over the past 250 millions of years.
It was first shown by Lagrange (1774, 1777) that the inclination and nodes of the planets
suffer long term quasiperiodic variations. Shortly after, Laplace (1776) demonstrated that
this was the same for the eccentricity and longitudes.
Both computations were made using the linearization of the first order averaged equations of
motion. In this approximation, if we use the complex notations
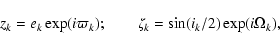 |
(16) |
the equations of motion are given by a linear equation
![\begin{displaymath}{{\displaystyle\strut{\rm d} [x]}\over{\displaystyle\strut{\rm d}t}} = {i}A [x]
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img172.gif) |
(17) |
where [x] is the column vector
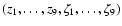 ,
and
,
and
 |
(18) |
where the  matrices (for 9 planets) A1,A2 depend on the planetary masses and
semi-major axis of the planets. The resolution of these equations is now classical,
and is obtained through the diagonalization of the matrix A by the change of coordinates
into proper modes u
matrices (for 9 planets) A1,A2 depend on the planetary masses and
semi-major axis of the planets. The resolution of these equations is now classical,
and is obtained through the diagonalization of the matrix A by the change of coordinates
into proper modes u
The solution in the proper modes
![$[u]=(z_1^\bullet,\dots,z_9^\bullet,\zeta_1^\bullet,\dots,\zeta_9^\bullet)$](/articles/aa/full/2004/46/aa1335/img176.gif) is then given by the diagonal system
is then given by the diagonal system
![\begin{displaymath}{{\displaystyle\strut{\rm d} [u]}\over{\displaystyle\strut{\rm d}t}} = {i}D [u]
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img177.gif) |
(20) |
where
D=S-1A S is a diagonal matrix
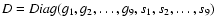 ,
where all the eigenvalues gk,sk are real. The solutions of the proper modes
,
where all the eigenvalues gk,sk are real. The solutions of the proper modes
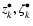 are
are
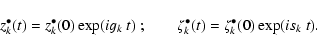 |
(21) |
The solutions in the elliptical variables
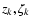 are then given
as linear combinations of the proper modes (19), and
becomes quasiperiodic functions of the time t, that is sums of pure periodic
terms with independent frequencies.
are then given
as linear combinations of the proper modes (19), and
becomes quasiperiodic functions of the time t, that is sums of pure periodic
terms with independent frequencies.
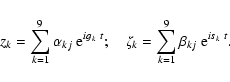 |
(22) |
Lagrange (1781, 1782) actually did this computation for a planetary system including
Mercury, Venus, Earth, Mars, Jupiter and Saturn. Pontécoulant (1834)
extended it to the 7 known planets of the time, but with several errors in the numerical constants.
The first precise solution for the Earth was given by Le Verrier (1856) for 7 planets, and was later on extended
by Stockwell (1873) with the addition of Neptune.
The validity of the linear approximation (17)
was also questioned and subsequent improvements introduced some additional contribution of higher degree
in eccentricity and inclination in Eq. (17), as well as terms of higher order
with respect to the planetary masses in the averaged equations (Hill 1897;
Brouwer & Van Woerkom 1950; Bretagnon 1974; Duriez 1977; Laskar 1985).
With the addition of additional non linear terms
 (of degree
(of degree  in eccentricity and inclination), the secular equations
in eccentricity and inclination), the secular equations
![\begin{displaymath}{{\displaystyle\strut{\rm d} [x]}\over{\displaystyle\strut{\rm d}t}} = {i}A [x] + B(x,\bar x)
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img185.gif) |
(23) |
are no longer integrable. Nevertheless, one can formally perform a Birkhoff normalization of
Eq. (23) and after truncation, obtain some quasiperiodic expressions
where
 ,
,
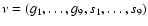 ,
and
,
and
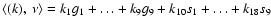 .
The quasiperiodic
expressions
.
The quasiperiodic
expressions
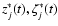 ,
have been computed at various orders
and degrees in eccentricity and inclination of expansion (Hill 1897; Bretagnon 1974; Duriez 1977;
Laskar 1984, 1985), but as forecasted by Poincaré (1893), it was found that when all the main planets are
taken into account, these formal expansions do not converge (Laskar 1984), for initial conditions
close to the initial conditions of the Solar System, even at the lowest orders, and thus
will not provide good approximation of the Solar System motion over very long time.
In other terms, it appears that the actual solution of the Solar System is not
close to a KAM tori (see Arnold et al. 1988) of quasiperiodic solutions.
,
have been computed at various orders
and degrees in eccentricity and inclination of expansion (Hill 1897; Bretagnon 1974; Duriez 1977;
Laskar 1984, 1985), but as forecasted by Poincaré (1893), it was found that when all the main planets are
taken into account, these formal expansions do not converge (Laskar 1984), for initial conditions
close to the initial conditions of the Solar System, even at the lowest orders, and thus
will not provide good approximation of the Solar System motion over very long time.
In other terms, it appears that the actual solution of the Solar System is not
close to a KAM tori (see Arnold et al. 1988) of quasiperiodic solutions.
Over a finite time of a few millions of years, one can still numerically integrate the
equation of motion, and then search through frequency analysis (Laskar 1990, 1999, 2003) for
a quasiperiodic approximation of the solution of the form (23).
The non regular behavior of the solution will induce a drift of the frequencies
in time, related to the chaotic diffusion of the trajectories (Laskar 1990, 1993, 1999).
In Table 3, the fundamental frequencies of the solution La2004
have been computed by frequency analysis
over 20 Myr of the proper modes
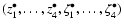 related to the inner planets (Mercury, Venus, Earth, Mars), and over 50 Myr
for the proper modes
related to the inner planets (Mercury, Venus, Earth, Mars), and over 50 Myr
for the proper modes
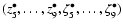 associated to the
outer planets (Jupiter, Saturn, Uranus, Neptune, Pluto) (Table 3).
This difference reflects the fact that the main source of chaotic behavior
comes from overlap of secular resonances in the inner planet system, and that
the outer planets secular systems is more regular than the inner one.
Actually, in Cols. 2 and 3 of Table 3, we give the maximum observed
in the
variation of the secular frequencies over 100 and 250 Myr, in both positive and negative time,
for our nominal solution La2004.
These figures are in very good agreement with the equivalent quantities given in Table X of (Laskar 1990)
for the integration of the secular equations.
The number of digits of the fundamental frequencies in Table 3 is different for each
frequency and reflects the stability of the considered frequency with time.
Additionally, we have given in Figs. 9 and 10 the actual evolution of the
secular frequencies obtained with a sliding window with a step size of 1 Myr
(compare to Laskar 1990, Figs. 8 and 9).
associated to the
outer planets (Jupiter, Saturn, Uranus, Neptune, Pluto) (Table 3).
This difference reflects the fact that the main source of chaotic behavior
comes from overlap of secular resonances in the inner planet system, and that
the outer planets secular systems is more regular than the inner one.
Actually, in Cols. 2 and 3 of Table 3, we give the maximum observed
in the
variation of the secular frequencies over 100 and 250 Myr, in both positive and negative time,
for our nominal solution La2004.
These figures are in very good agreement with the equivalent quantities given in Table X of (Laskar 1990)
for the integration of the secular equations.
The number of digits of the fundamental frequencies in Table 3 is different for each
frequency and reflects the stability of the considered frequency with time.
Additionally, we have given in Figs. 9 and 10 the actual evolution of the
secular frequencies obtained with a sliding window with a step size of 1 Myr
(compare to Laskar 1990, Figs. 8 and 9).
8 Analytical approximations
It is interesting for practical use to have an analytical expression for
the main orbital quantities of the Earth.
From the numerical values of La2004, we have performed a frequency analysis
(Laskar 1990, 1999, 2003) in order to obtain a quasiperiodic approximation of
the solutions over a few Myr.
In order to be consistent with the remaining part of the paper,
we chose a time interval covering 20 Myr.
As we are mostly interested over negative time, we made the analysis
from -15 Myr to +5 Myr, as usually, the precision of the approximation decreases
at the edges of the time interval.
The analysis of the eccentricity variables
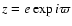 is given in Table 4.
z is obtained as
is given in Table 4.
z is obtained as
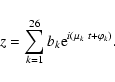 |
(25) |
It should be noted that in the present complex form, the approximation is much more precise than
what would give an equivalent quasiperiodic approximation of the eccentricity.
Even with twice the number of periodic terms, the direct approximation
of the eccentricity is not as good as the approximation obtained in complex variables.
Moreover, here we obtain at the same time the approximation of
the longitude of perihelion of the Earth from the fixed J2000 equinox ( ).
The comparison of this approximation,
limited to only 26 terms, to the actual solution for the eccentricity of the Earth,
is plotted in Fig. 12 (top).
).
The comparison of this approximation,
limited to only 26 terms, to the actual solution for the eccentricity of the Earth,
is plotted in Fig. 12 (top).
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig9} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg198.gif) |
Figure 9:
Variation of the secular frequencies g1-9 from -250 to +250 Myr.
The frequencies are computed over 20 Myr for g1-4 and over 50 Myr for g5-9,
after transformation of elliptical elements to proper modes (Laskar 1990).
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig10} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg199.gif) |
Figure 10:
Variation of the secular frequencies s1-9 from -250 to +250 Myr.
The frequencies are computed over 20 Myr for s1-4 and over 50 Myr for s6-9,
after transformation of elliptical elements to proper modes (Laskar 1990).
|
| Open with DEXTER |
Table 4:
Frequency decomposition of
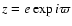 for the Earth on the
time interval [-15,+5] Myr (Eq. (25)).
for the Earth on the
time interval [-15,+5] Myr (Eq. (25)).
Nevertheless, for information, we will give also here the leading terms in the expansion of
the eccentricity as they may be useful in paleoclimate studies (Table 6).
The three leading terms in eccentricity are well known in paleoclimate studies
g2-g5 (405 kyr period), g4-g5 (95 kyr period), and g4-g2 (124 kyr period).
The solution for the inclination variables
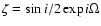 where
where 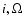 are the Earth
inclination and longitude of node with respect to the fixed ecliptic and equinox J2000, limited to 24 quasiperiodic terms
are the Earth
inclination and longitude of node with respect to the fixed ecliptic and equinox J2000, limited to 24 quasiperiodic terms
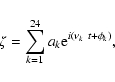 |
(26) |
is given in Table 5. The comparison of this quasiperiodic approximation
with the complete solution is given in Fig. 12 (bottom). It should be noted that in Table 5, the first 22 terms are the terms of largest amplitude in the frequency decomposition
of the inclination variable 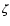 ,
but the two last terms, of frequency
,
but the two last terms, of frequency 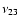 and
and 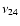 are of much smaller amplitude. They have been kept in the solution,
as they are close to the resonance with the main precession frequency.
are of much smaller amplitude. They have been kept in the solution,
as they are close to the resonance with the main precession frequency.
The solutions for precession and obliquity are obtained through the precession Eq. (6).
In absence of planetary perturbations, the obliquity is constant (
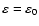 ), and
), and
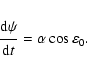 |
(27) |
We have thus
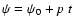 where
where
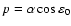 is the precession frequency. This can be considered as
a solution of order zero. If we keep only the terms of degree one in inclination in Eqs. (6), we obtain
the solution of order one
is the precession frequency. This can be considered as
a solution of order zero. If we keep only the terms of degree one in inclination in Eqs. (6), we obtain
the solution of order one
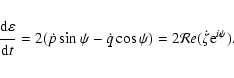 |
(28) |
With the quasiperiodic approximation
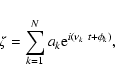 |
(29) |
of Table 5,
the first order solution in obliquity will be a similar quasiperiodic
function
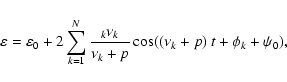 |
(30) |
with a similar form for the solution of precession 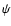 .
This first order approximation will only be valid when we are far from resonance,
that is
.
This first order approximation will only be valid when we are far from resonance,
that is
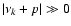 .
This is not the case for the last term
.
This is not the case for the last term
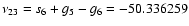 arcsec yr-1 in Table 5, as
arcsec yr-1 in Table 5, as
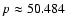 arcsec yr-1. This
resonant term can lead to a significative change in the obliquity variations, and have been studied in detail
in Laskar et al. (1993).
arcsec yr-1. This
resonant term can lead to a significative change in the obliquity variations, and have been studied in detail
in Laskar et al. (1993).
Another difficulty, arising with the obliquity solution, is due to the dissipation in the Earth-Moon system,
which induces a significant variation of the precession frequency with time, as the Earth rotation 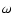 slows down, and the Earth-Moon distance
slows down, and the Earth-Moon distance 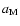 increases.
increases.
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig11} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg218.gif) |
Figure 11:
Variation of the semi-major axis of the Earth-Moon barycenter (in AU) from -250 to +250 Myr.
|
| Open with DEXTER |
Table 5:
Frequency decomposition of
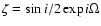 for the Earth on the
time interval [-15,+5] Myr (Eq. (26)).
for the Earth on the
time interval [-15,+5] Myr (Eq. (26)).
![\begin{figure}\par
\includegraphics[width=14cm,clip]{figures_pdf/1335fig12} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg221.gif) |
Figure 12:
( Top) Eccentricity of the Earth from -11 to +1 Myr. The solid curve is the solution La2004.
Almost completely hidden behind the solid
curve is a dashed curve representing
the quasiperiodic approximation of Table 4 with 26 periodic terms.
( Bottom) Inclination of the Earth from -11 to +1 Myr. The solid curve is the solution La2004.
The dashed line (almost identical to the solid curve) is the quasiperiodic approximation of Table 5 with 24 periodic terms.
On both plots, as the two curves are nearly identical, the difference of the two solutions is also plotted
in dotted curve.
|
| Open with DEXTER |
We have plotted in Fig. 14 the evolution of the obliquity of the Earth from -250 to + 250 Myr.
The effect of the tidal dissipation is clearly visible on this timescale, and there is a general increase
of the obliquity from -250 Myr to present time. In positive time, there is an obvious singularity
in the obliquity, with a decrease of about 0.4 degree. This results from the crossing of the resonance
with the term
s6+ g5-g6 that was already described in a different context in Laskar et al. (1993).
After this sudden decrease, the obliquity increases again, with roughly the same trend.
An additional (but smaller singularity is observable around +150 Myr, that corresponds
to the crossing of the resonance
with the term 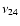 (Table 5). The averaged obliquity can be well approximated in negative time
with the expression
(Table 5). The averaged obliquity can be well approximated in negative time
with the expression
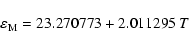 |
(31) |
where
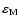 is in degree, and T in billion of years (Gyr).
In the interval
is in degree, and T in billion of years (Gyr).
In the interval
![$[+20 ~{\rm ~Myr},+130 ~{\rm ~Myr}]$](/articles/aa/full/2004/46/aa1335/img224.gif) this approximation becomes
this approximation becomes
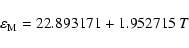 |
(32) |
so the main effect of the crossing of the resonance is a decrease of 0.377602 degree of the obliquity.
This effect can be easily understood with the analytical integration
of a simple model, in terms of Fresnel integrals (see Appendix A).
Table 6:
Frequency decomposition of the eccentricity of the Earth on the
time interval [-15,+5] Myr. For all computations, the data of Table 4
should be preferred. Here,
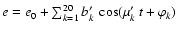 with
e0=0.0275579. For each term, in the first column is the corresponding combination of
frequencies where gi are the fundamental frequencies (Table 3), and
with
e0=0.0275579. For each term, in the first column is the corresponding combination of
frequencies where gi are the fundamental frequencies (Table 3), and 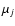 the
frequencies of the terms in z from Table 4.
the
frequencies of the terms in z from Table 4.
8.3 Approximation for the obliquity
As for the solutions of the orbital elements, we have obtained an
approximation formula for the evolution of the obliquity of the Earth
over the period from -15 Myr to +5 Myr. Obtaining this solution presents some
additional difficulties because of the dissipative effects in the Earth-Moon
system that induces a significative change of the precession frequency.
The obliquity is obtained on the form
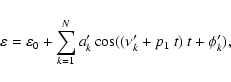 |
(33) |
where
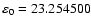 degrees, and the coefficients
degrees, and the coefficients
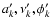 are given in Table 7. The coefficent p1 (Eq. (35))
results from the secular change of the precession frequency (34)
due to tidal dissipation (see next).
are given in Table 7. The coefficent p1 (Eq. (35))
results from the secular change of the precession frequency (34)
due to tidal dissipation (see next).
The comparison with the full solution is given in Fig. 15, over selected periods of time, from -11 Myr to the present. In Table 7, the terms of frequency 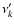 are recognized
as combinations of the form
are recognized
as combinations of the form 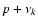 ,
where p is the precession frequency, and
,
where p is the precession frequency, and 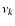 a secular frequency from the secular motion of the orbital plane (from Table 5).
The approximation is made over
the interval
a secular frequency from the secular motion of the orbital plane (from Table 5).
The approximation is made over
the interval
![$[-15 {\rm ~Myr}, +2 {\rm ~Myr}]$](/articles/aa/full/2004/46/aa1335/img240.gif) with
p = p0 +p1 T,
where p0 and p1 are taken from Eq. (35).
with
p = p0 +p1 T,
where p0 and p1 are taken from Eq. (35).
Table 7:
Approximation for the obliquity of the Earth, following Eq. (33). This expression is not
strictly quasiperiodic, because of the presence of
the dissipative term p1 in the evolution of the precesion frequency (33).
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig13} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg249.gif) |
Figure 13:
a) Evolution of length of the day for the Earth, in hours, from -250 to +250 Myr. b) Residuals with the fit of the averaged solution with
the polynomial expression (41).
|
| Open with DEXTER |
The full approximate solution for the precession is more complicated because of the presence of
the secular resonance
s6+g5-g6. In fact, the proximity of this resonance is responsible for the largest periodic term in the expression of the precessionangle (Fig. 16).
The precession angle can thus be approximate by (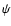 in arcsec, t in years)
in arcsec, t in years)
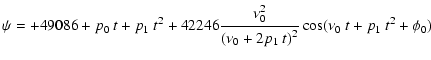 |
|
|
(34) |
where
It should be noted that in this formula, the cosine term is an approximation
for a more complicated expression that arises from a double integration
of the term
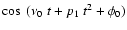 in the expression of
the derivative of the obliquity (6). In order to obtain an expression as simple as possible,
without expressions involving Fresnel integrals (Appendix A), we had to restrain
its interval of validity to [-15,+2] Myr.
in the expression of
the derivative of the obliquity (6). In order to obtain an expression as simple as possible,
without expressions involving Fresnel integrals (Appendix A), we had to restrain
its interval of validity to [-15,+2] Myr.
![\begin{figure}\par\includegraphics[width=8cm,clip]{figures_pdf/1335fig14}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg328.gif) |
Figure 14:
Evolution of the obliquity of the Earth in degrees, from -250 to +250 Myr. The grey zone is the actual obliquity, while the black curve
is the averaged value of the obliquity over 0.5 Myr time intervals. The dotted line is a
straight line fitted to the average obliquity in the past.
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig15} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg259.gif) |
Figure 15:
Comparison of the solution of the obliquity La2004 (solid line)
with its approximation using Table 7 (dotted line) with 26 periodic terms.
The difference of two solutions (+22 degrees) is also plotted.
|
| Open with DEXTER |
For paleoclimate studies, the usual quantity that relates more
directly to insolation is the climatic precession
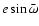 ,
where
,
where
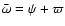 is the longitude of the perihelion from the moving equinox.
We have thus
is the longitude of the perihelion from the moving equinox.
We have thus
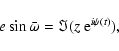 |
(36) |
where the decomposition of
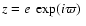 is provided in Table 4,
and the precession angle
is provided in Table 4,
and the precession angle 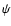 is given by Eq. (34).
The comparison of this approximation with the complete solution from -11 to +1 Myr is given in Fig. 17. The solution
for climatic precession is thus on the form
is given by Eq. (34).
The comparison of this approximation with the complete solution from -11 to +1 Myr is given in Fig. 17. The solution
for climatic precession is thus on the form
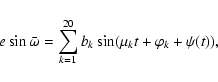 |
(37) |
where
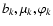 are from Table 4, and
where
are from Table 4, and
where 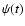 is given by Eq. (34).
The frequencies of the terms of the climatic precession are thus of the form
is given by Eq. (34).
The frequencies of the terms of the climatic precession are thus of the form
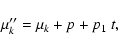 |
(38) |
where p, p1 are given in Eqs. (34) and (35).
In Fig. 18, the evolution of the Earth-Moon semi-major  axis is plotted
over 250 Myr in positive and negative time. The grey area corresponds to the short period variations
of the Earth-Moon distance, obtained in the full integration of the system, while the
black curve is the integration of the averaged equations that is used for the precession computations.
The agreement between the two solutions is very satisfying.
axis is plotted
over 250 Myr in positive and negative time. The grey area corresponds to the short period variations
of the Earth-Moon distance, obtained in the full integration of the system, while the
black curve is the integration of the averaged equations that is used for the precession computations.
The agreement between the two solutions is very satisfying.
We have searched for a polynomial approximation for the secular evolution of 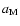 ,
in order to provide
a useful formula for simple analytical computations. In fact, the Earth-Moon
evolution is driven by the tidal dissipation equations (Sect. 4.1),
that involve the obliquity of the planet.
The important singularity of the obliquity in the future (see previous section)
prevents from using a single approximation
over the whole time interval, and we have used a different polynomial in positive and negative time.
,
in order to provide
a useful formula for simple analytical computations. In fact, the Earth-Moon
evolution is driven by the tidal dissipation equations (Sect. 4.1),
that involve the obliquity of the planet.
The important singularity of the obliquity in the future (see previous section)
prevents from using a single approximation
over the whole time interval, and we have used a different polynomial in positive and negative time.
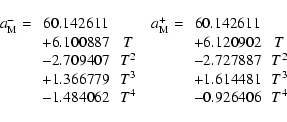 |
(39) |
where T is in billions of years (Gyr), and
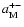 in Earth radius (see Table 1). In the residuals
plot (Fig. 18b), we can check that this polynomial approximation is
very precise for negative time, but in positive time, we have an additional singularity
around 150 Myr, resulting from the secular resonance of the precession frequency with
in Earth radius (see Table 1). In the residuals
plot (Fig. 18b), we can check that this polynomial approximation is
very precise for negative time, but in positive time, we have an additional singularity
around 150 Myr, resulting from the secular resonance of the precession frequency with
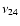 (Table 5).
(Table 5).
In the same way, it is possible to approximate the evolution of the precession frequency of the Earth p
as the Moon goes away and the rotation of the Earth slows down with time. The polynomial approximation
of the precession frequency is then in arcsec yr-1, with T in Gyr
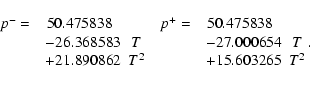 |
(40) |
It should be said that the initial value is kept equal for both positive and negative time to avoid
discontinuities. It is clear from Fig. 19 that for the period between +30 and +130 Myr,
a better approximation could be obtained by adding to the constant part
the offset
+0.135052 arcsec yr-1. It is interesting to note again the dramatic influence
of the resonance 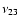 on the evolution of the precession frequency.
The equivalent formulas for the length of the day are (in hours)
on the evolution of the precession frequency.
The equivalent formulas for the length of the day are (in hours)
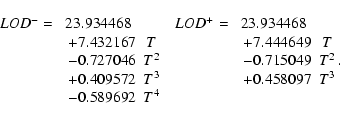 |
(41) |
One should note that Eqs. (39) and (41) correspond at the origin J2000 to a change in the semi major axis of the Moon of about 3.89 cm/yr, and a change
of the LOD of 2.68 ms/century. These values slightly differ from the
current ones of Dickey et al. (1994) (
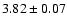 cm/yr for the receding of the Moon).
This is understandable, as the Earth-Moon model in our integration that was adjusted to DE406 is
simplified with respect to the one of DE406.
cm/yr for the receding of the Moon).
This is understandable, as the Earth-Moon model in our integration that was adjusted to DE406 is
simplified with respect to the one of DE406.
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig16}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg274.gif) |
Figure 16:
Comparison of the solution of the precession La2004 with its approximation from -15 to +2 Myr.
The grey curve is obtained after removing uniquely the secular trend
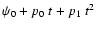 .
The dark curve are the residual (in radians)
after removing the resonant term (Eq. (34)), which is also displayed in solid line. .
The dark curve are the residual (in radians)
after removing the resonant term (Eq. (34)), which is also displayed in solid line.
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig17} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg275.gif) |
Figure 17:
Comparison of the solution of the climatic precession
of La2004 with its approximation from -11 to +1 Myr.
The grey curve is the full climatic precession
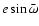 .
The dark curve are the residual
after removing the approximation
given by Eq. (37). .
The dark curve are the residual
after removing the approximation
given by Eq. (37).
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig18} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg276.gif) |
Figure 18:
a) Evolution of the Earth-Moon semi major axis (in Earth radii) from -250 to +250 Myr. The grey zone is the result of the integration of the
full equations, while the black curve is the integration of the averaged equations,
as used in the precession computations; b) residuals with the fit of the averaged solution with
the polynomial expression (39).
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=8.3cm,clip]{figures_pdf/1335fig19} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg277.gif) |
Figure 19:
a) Evolution of the precession frequency of the Earth p (in arcsec/yr)
-250 to +250 Myr; b) residuals with the fit of the averaged solution with
the polynomial expression (40).
|
| Open with DEXTER |
9 Stability of the solution
In such long term numerical computations, the sources of errors are
the error of method due to the limitation of the
numerical integration algorithm, the numerical roundoff error resulting
from the limitation of the representation of the real numbers in the computer,
and the errors of the initial conditions and of the model which are
due to our imperfect knowledge of all the physical parameters in the Solar system,
and to the necessary limitations of the model.
Some of the main sources of uncertainty in the model
for long term integrations were reviewed in (Laskar 1999).
The effect of all these errors is amplified by the chaotic
behaviour of the system, with an exponential increase of
the difference between two solutions with different settings,
until saturation due to the limited range of the
considered variables. A summary
of these limitations, extracted from (Laskar 1999) is given in Table 8,
but it should be noted that these times of validity are probably
pessimistic, as they correspond to analytical estimates based on the "worst case''
situation.
Our requirement for the precision of a long term solution
is also not the same as for precise short term ephemeris.
For the long term solutions, aimed at paleoclimate or qualitative studies,
two solutions can be considered as similar, as long
as the pattern of the two solutions (eccentricity for example), resulting
(at first order) from the combination of various proper modes
remain similar. This will last until some of the main proper modes
get completely out of phase (see Sect. 7). It will be the
same for the solutions in obliquity and precession.
Table 8:
Main sources of uncertainty in the orbital solution (from Laskar 1999).
For each limiting factor, an analytical estimate of the time of validity of the solution 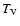 is given (in Myr), taking into account the exponential growth of the error.
is given (in Myr), taking into account the exponential growth of the error.
![\begin{figure}\par
\includegraphics[width=8.2cm,clip]{figures_pdf/1335fig20} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg278.gif) |
Figure 20:
Stability of the solution for eccentricity of the Earth. a) Difference of the nominal solution
La2004 with stepsize
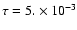 years, and La2004*, obtained with
years, and La2004*, obtained with
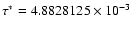 years; b) difference of the nominal solution with the
solution obtained while setting
years; b) difference of the nominal solution with the
solution obtained while setting
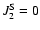 for the Sun (instead of
for the Sun (instead of
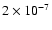 in the nominal solution).
in the nominal solution).
|
| Open with DEXTER |
Practically, we have tested the stability of our solution by comparison
of the eccentricity (Fig. 20) and inclination
(Fig. 21) with different solutions.
In Figs. 20a and 21a,
the nominal solution La2004 (with stepsize
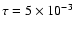 years)
is compared to
an alternate solution, La2004*, with the same dynamical model, and
a very close stepsize
years)
is compared to
an alternate solution, La2004*, with the same dynamical model, and
a very close stepsize
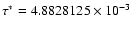 years (Table 9).
This special value was chosen
in order that our output time span h=1000 years corresponds to an integer number (204 800)
of steps, in order to avoid any interpolation problems in the check of the numerical accuracy.
This is thus a test of the time of validity for obtaining a precise numerical solution,
resulting from method and roundoff errors of the integrator.
It is thus limited here to about 60 Myr.
years (Table 9).
This special value was chosen
in order that our output time span h=1000 years corresponds to an integer number (204 800)
of steps, in order to avoid any interpolation problems in the check of the numerical accuracy.
This is thus a test of the time of validity for obtaining a precise numerical solution,
resulting from method and roundoff errors of the integrator.
It is thus limited here to about 60 Myr.
This limitation of 60 Myr is a limitation for the time of validity of
an orbital solution, independently of the precision of the dynamical model.
In order to go beyond this limit, the only way will be to increase the numerical accuracy of
our computations, by improving the numerical algorithm, or with an extended precision
for the number representation in the computer.
A second test is made on the uncertainty of the model. Several sources of
uncertainty were listed in (Laskar 1999), and it was found that
one of the main sources of uncertainty was due to the imprecise knowledge
of the Solar oblateness (
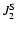 )
(Table 8).
Its most recent determination, obtained with
the SOHO and GONG helioseismic data give
)
(Table 8).
Its most recent determination, obtained with
the SOHO and GONG helioseismic data give
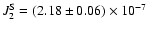 (Pijpers 1998), with a very similar value adopted in DE406 (
(Pijpers 1998), with a very similar value adopted in DE406 (
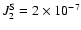 ,
Standish 1998), while in DE200, it was not taken into account (Newhall et al. 1983).
We will thus consider that comparing the nominal solution La2004 (with
,
Standish 1998), while in DE200, it was not taken into account (Newhall et al. 1983).
We will thus consider that comparing the nominal solution La2004 (with
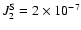 )
with an alternate solution (La20040) with
)
with an alternate solution (La20040) with
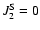 is representative of the uncertainty
of the dynamical model for our long term integrations
is representative of the uncertainty
of the dynamical model for our long term integrations![[*]](/icons/foot_motif.gif) (Table 9).
(Table 9).
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig21} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg282.gif) |
Figure 21:
Stability of the solution for inclination of the Earth. a) Difference of 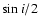 for the nominal solution La2004 with stepsize
for the nominal solution La2004 with stepsize
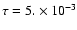 years, and for La2004*, obtained with years, and for La2004*, obtained with
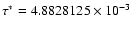 years; b) difference of years; b) difference of 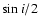 for
the nominal solution with the
solution obtained while setting
for
the nominal solution with the
solution obtained while setting
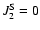 for the Sun
(instead of
for the Sun
(instead of
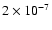 in the nominal solution).
in the nominal solution).
|
| Open with DEXTER |
Table 9:
Variants of the La2004 solutions. The nominal solution La2004
is obtained for a stepsize
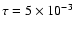 ,
and a
Solar oblateness
,
and a
Solar oblateness
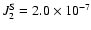 .
The other solutions, with
different setting have been computed to test
the stability of the nominal solution. In the last column
.
The other solutions, with
different setting have been computed to test
the stability of the nominal solution. In the last column 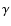 is the
tidal dissipation factor.
is the
tidal dissipation factor.
The results La2004 - La20040 for the Earth's eccentricity and inclination
are displayed in (Figs. 20b and 21b)
over 100 Myr. As for Mars (Laskar et al. 2004),
the effect of
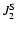 becomes noticeable after about 30 Myr (26 Myr were predicted
with an analytical estimate in (Laskar 1999), and the solution remains very similar over 40 Myr, and totally out of phase after 45 Myr. We will thus consider here that 40 Myr is
about the time of validity of our present orbital solution for the Earth.
Other integrations made with
becomes noticeable after about 30 Myr (26 Myr were predicted
with an analytical estimate in (Laskar 1999), and the solution remains very similar over 40 Myr, and totally out of phase after 45 Myr. We will thus consider here that 40 Myr is
about the time of validity of our present orbital solution for the Earth.
Other integrations made with
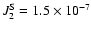 and
and
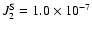 (Table 9) gave
practically the same estimates.
It should be noted that with our present algorithms, we are much more limited by the precision
of the model (Figs. 20b and 21b) than by the numerical accuracy (Figs. 20a and 21a).
(Table 9) gave
practically the same estimates.
It should be noted that with our present algorithms, we are much more limited by the precision
of the model (Figs. 20b and 21b) than by the numerical accuracy (Figs. 20a and 21a).
9.2 Obliquity and precession
For the obliquity and precession, as was already mentioned in
(Laskar et al. 1993), the main source of uncertainty is the evolution of
the tidal dissipation and other related factors (see Sect. 4.1).
Among these factors, one can mention the variations of the
dynamical ellipticity of the Earth resulting from changes of the ice caps,
or mantle convections. The maximal contribution of these
effects can be estimated (see Levrard & Laskar 2003),
but it is very difficult to obtain at
present a precise value of their contributions. Moreover,
the largest dissipative term, resulting from body tides can evolve
substantially as a result of the variation of the distribution of the
continents, as most of the tidal dissipation occurs in shallow seas
(Jeffreys 1920, 1976; Egbert & Ray 2000).
In Fig. 22, we have explicited the result of
a difference of 5% (Figs. 22a and c) and 10% (Figs. 22b and d)
in the tidal dissipation term of the Earth and the Moon (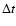 and
and
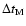 in Table 1).
With 5% error (La2004(0.95)), the solution of
obliquity is valid over about 20 Myr, but with a 10% error (La2004(0.90)),
the solution is out of phase after 20 Myr.
Nevertheless, the uncertainty in the tidal dissipation appears mostly
as a small change of the precession frequency p, which
reveals in the obliquity solution as
a time offset that does not change much the obliquity pattern.
Indeed, in Figs. 22e and f, we have made a readjustment of the
time scale for the solutions La2004(0.95) and La2004(0.90)of respectively
in Table 1).
With 5% error (La2004(0.95)), the solution of
obliquity is valid over about 20 Myr, but with a 10% error (La2004(0.90)),
the solution is out of phase after 20 Myr.
Nevertheless, the uncertainty in the tidal dissipation appears mostly
as a small change of the precession frequency p, which
reveals in the obliquity solution as
a time offset that does not change much the obliquity pattern.
Indeed, in Figs. 22e and f, we have made a readjustment of the
time scale for the solutions La2004(0.95) and La2004(0.90)of respectively
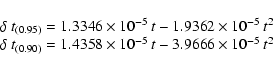 |
(42) |
where t is in Myr. With this new time scales, the different
solutions become very close over 40 Myr, that is over the full
range of validity of the orbital solution (Figs. 22e and f).
An uncertainty of 10% in the tidal dissipation term
thus corresponds mostly to an uncertainty in the timescale of 16 kyr after 20 Myr, and 63 kyr after 40 Myr.
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig22} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg291.gif) |
Figure 22:
Difference in obliquity for different
tidal dissipation factor (Table 9): a)
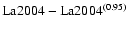 ;
b) ;
b)
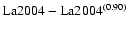 .
In c) and d), the nominal solution
of the obliquity is plotted in solid line, while La2004(0.95) c) and La2004(0.90) d) are in dotted line. After an adjustment of
the time scale, the differences of the solutions are much smaller
over 40 Myr: e) .
In c) and d), the nominal solution
of the obliquity is plotted in solid line, while La2004(0.95) c) and La2004(0.90) d) are in dotted line. After an adjustment of
the time scale, the differences of the solutions are much smaller
over 40 Myr: e)
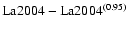 ;
f) ;
f)
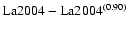 . .
|
| Open with DEXTER |
10 Resonant angles
![\begin{figure}\par
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig23} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg292.gif) |
Figure 23:
Resonant arguments (in radians versus time in Myr)
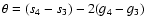 ( top) and
( top) and
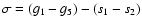 ( bottom) for different solutions:
a) is the secular solution La93 (Laskar 1990; Laskar et al. 1993) while b) is the present nominal solution La2004.
The characteristics of the other variants La20041.5 c), La20040 d),
La2004** e) are listed in Table 9. The arrows indicate
the portions of the solutions when the argument
(s4-s3)-(g4-g3) is in
libration.
( bottom) for different solutions:
a) is the secular solution La93 (Laskar 1990; Laskar et al. 1993) while b) is the present nominal solution La2004.
The characteristics of the other variants La20041.5 c), La20040 d),
La2004** e) are listed in Table 9. The arrows indicate
the portions of the solutions when the argument
(s4-s3)-(g4-g3) is in
libration.
|
| Open with DEXTER |
Using the secular equations, Laskar (1990, 1992), demonstrated that
the chaotic behavior of the Solar system arises from multiple
secular resonances in the inner solar system.
In particular, the critical argument associated to
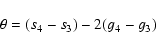 |
(43) |
where g3, g4 are related to the precession of the perihelion of the Earth and Mars,
s3, s4 are related to the precession of the node of the same planets,
is presently in a librational state, but can evolve in a rotational state,
and even move to libration in a new resonance, namely
|
(s4-s3)-(g4-g3) = 0.
|
(44) |
This reveals
that a region of relatively strong instability
results from the overlap (Chirikov 1979) of these two resonances.
This result was questioned by Sussman & Wisdom (1992), as they did not recover such a large
variation for the secular frequencies, but reached only
2(s4-s3)-3(g4-g3) = 0 instead of
Eq. (44).
We have tested these resonant arguments in the nominal solution La2004, and in
the alternate solutions La2004**, La20040, La20041.5 (Table 9).
In all variants of La2004 (Fig. 23 (top)), the
resonant argument corresponding to
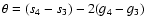 was in libration over
the first 40 Myr, while the transition to
circulation occurred at about 25 Myr in La93. All the solutions La2004, La2004**, La20040,
La20041.5 differ significantly beyond 40 to 50 Myr, but they all enter
the
(s4-s3)-(g4-g3) resonance within 100 Myr, comforting the conclusions
of (Laskar 1990, 1992). In Fig. 23 (top), the portions of the
solutions where the argument of
(s4-s3)-(g4-g3) is in libration
are pointed by arrows. It should be noted that at least over 250 Myr,
the diffusion seems to remain confined
between the resonances
(s4-s3)-2(g4-g3) and
(s4-s3)-(g4-g3).
The other important resonant argument (
(g1-g5) -(s1-s2)) that was identified
by Laskar (1990, 1992) as the origin
of the chaotic behavior of the inner planets presents in all the variations
of the numerical solutions La2004, La2004**, La20040,
La20041.5 a similar behavior as for the secular solution La93 (Fig. 23 (bottom)).
was in libration over
the first 40 Myr, while the transition to
circulation occurred at about 25 Myr in La93. All the solutions La2004, La2004**, La20040,
La20041.5 differ significantly beyond 40 to 50 Myr, but they all enter
the
(s4-s3)-(g4-g3) resonance within 100 Myr, comforting the conclusions
of (Laskar 1990, 1992). In Fig. 23 (top), the portions of the
solutions where the argument of
(s4-s3)-(g4-g3) is in libration
are pointed by arrows. It should be noted that at least over 250 Myr,
the diffusion seems to remain confined
between the resonances
(s4-s3)-2(g4-g3) and
(s4-s3)-(g4-g3).
The other important resonant argument (
(g1-g5) -(s1-s2)) that was identified
by Laskar (1990, 1992) as the origin
of the chaotic behavior of the inner planets presents in all the variations
of the numerical solutions La2004, La2004**, La20040,
La20041.5 a similar behavior as for the secular solution La93 (Fig. 23 (bottom)).
The date of the first transition from libration to circulation
of the resonant argument related to
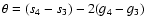 is a macroscopic feature
displaying the chaotic diffusion of the planetary orbits.
It is thus very tempting to search whether this feature could be observed
in the geological data that extend now in continuous records beyond 30 Myr.
is a macroscopic feature
displaying the chaotic diffusion of the planetary orbits.
It is thus very tempting to search whether this feature could be observed
in the geological data that extend now in continuous records beyond 30 Myr.
The direct observation of the individual arguments related to
g3,g4,s3,s4 is certainly out of reach.
But it may be possible to follow the evolution in time of the differences g3-g4 and s3-s4.
Indeed, s3-s4 appears as a beat of about 1.2 million of years in the solution of obliquity,
as the result of the beat between the p+s3 and p+s4 components of the obliquity, where
p is the precession frequency of the axis (see Laskar 2004, Fig. 7). In a similar way,
g3-g4 appears as a beat with period of about 2.4 Myr in the climatic precession.
One understands that because of the occurrence of these beats, the detection of
the resonant state in the geological data can be possible, as one has to search now for
phenomena of large amplitude in the geological signal. Indeed, in the
newly collected data from Ocean Drilling Program Site 926, the modulation of 1.2 Myr
of the obliquity appears clearly in the spectral analysis of the paleoclimate record
(Zachos et al. 2001). Moreover, using the ODP legs 154 and 199, Pälike et al. (2004)
could find some evidence that the critical argument of 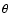 did not show a transition to circulation at 25 Myr, as in La93, but
remained in libration over 40 Myr, as in the present new solution La2004.
This result is very impressive, although
the search for the determination of these resonant angles
in the geological data is just starting. We may expect that a careful analysis, and new data
spanning the most recent 60 to 100 Myr, will allow to determine the possible succession
of resonant states in the past, allowing, for example, to discriminate between the solutions displayed in
Fig. 23. Of particular importance would be the detection of the first
transition from libration to circulation of the
resonant argument
(s4-s3)-2(g4-g3). This program, if completed,
will provide some extreme constraint for the gravitational model of the Solar System.
Indeed, the observation of a characteristic feature of the solution at 40 to 100 Myr
in the past, because of the exponential divergence of the solutions, will provide
a constraint of 10-4 to 10-10 on the dynamical model of the Solar System.
did not show a transition to circulation at 25 Myr, as in La93, but
remained in libration over 40 Myr, as in the present new solution La2004.
This result is very impressive, although
the search for the determination of these resonant angles
in the geological data is just starting. We may expect that a careful analysis, and new data
spanning the most recent 60 to 100 Myr, will allow to determine the possible succession
of resonant states in the past, allowing, for example, to discriminate between the solutions displayed in
Fig. 23. Of particular importance would be the detection of the first
transition from libration to circulation of the
resonant argument
(s4-s3)-2(g4-g3). This program, if completed,
will provide some extreme constraint for the gravitational model of the Solar System.
Indeed, the observation of a characteristic feature of the solution at 40 to 100 Myr
in the past, because of the exponential divergence of the solutions, will provide
a constraint of 10-4 to 10-10 on the dynamical model of the Solar System.
![\begin{figure}\par
\includegraphics[width=8.3cm,clip]{figures_pdf/1335fig24} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg295.gif) |
Figure 24:
Stability of the g5 ( top) and g2-g5 ( bottom) arguments.
The difference (in radians) of the angles related to g5 and g2-g5
from the nominal solution La2004 and an alternate solution La20041.5 a), La20040 b), and
La2004* c) (Table 9).
|
| Open with DEXTER |
11 Mesozoic timescale
An astronomically calibrated time scale for geological data
has been achieved successfully over the Neogene period (0-23.03 Myr) (Lourens et al. 2004),
and the next challenge will be to improve the astronomical precision of the solution, in order to extend this
over the Paleogene (23 to 65 Myr). Beyond this time length, it is hopeless to expect to
obtain a precise solution for the orbital elements of the Earth.
On the other hand, some features of the solution have a longer time of stability,
if they are related to the outer planets secular frequencies (Laskar 1990).
A very important period present in geological records is the 405 kyr period related
to the g2-g5 argument, that is the leading term in the solution of eccentricity
(Table 6). In Fig. 24, we have tested the stability of this argument over
the full period of our integrations, that is over 250 Myr, that extents over the
Mesozoic geological era (about 65 to 250 Myr). First, we have compared the argument related to g5 over 3 variants (La2004*, La20040, La20041.5) of La2004, that reflect
both the numerical errors and the errors of the model. This argument, related to Jupiter
and Saturn is extremely
stable, and does not show variations of more than 0.05 radians over the full 250 Myr period
(Fig. 24 (top)). In Fig. 24 (bottom), we have plotted
the same quantities for g2-g5. The dispersions over 50, 100, and 250 Myr are about 0.3, 1.0, 6.2 radians, that correspond to absolute error in time respectively
of about 20, 70, and 400 kyr over the same periods.
It is thus possible to use this argument, that is visible in many sedimentary records
of the Early Mesozoic (Olsen & Kent 1999, and references therein) as an absolute geological time scale
over the whole Mesozoic period. In order to facilitate the establishment of this timescale,
we have searched for a best fit or the period of this argument
over all the solutions of Table 9.
Within the uncertainty of this procedure, the best value for the
frequency g2-g5 is
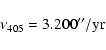 |
(45) |
which corresponds exactly to a period
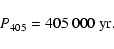 |
(46) |
This value differs by less than 0.001''/yr from the same quantity from
Table 6, where the direct output of the frequency analysis is given.
We propose here that in the establishment of
geological timescales, the value 3.200''/yr should be used. The maximum error
over 50, 100, 200, and 250 Myr should then be less than respectively 30, 150, 350, and 500 kyr.
The 405 kyr term is the largest term of the eccentricity solution. In Fig. 26, the eccentricity of the Earth from La2004, filtered in the interval
![$[2.2 {\rm ''/yr}, 8 {\rm ''/yr}]$](/articles/aa/full/2004/46/aa1335/img36.gif) ,
is plotted, as well as
a solution for the eccentricity, limited to the single 405 Kyr term
,
is plotted, as well as
a solution for the eccentricity, limited to the single 405 Kyr term
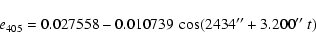 |
(47) |
where t is in yr. As it is apparent in the figure, the agreement
between the two solutions is extremely good over 100 Myr.
Beyond that time, the various possible solutions will become out of phase,
within the uncertainty of Fig. 25. One should note that
the initial phase at the origin (2434 arcsec)
corresponds to an offset of only 760 yr, so in most cases
it can be neglected.
![\begin{figure}\par
\includegraphics[width=8.3cm,clip]{figures_pdf/1335fig25} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg300.gif) |
Figure 25:
405 kyr term in eccentricity.
Maximum difference (in radians) of the argument
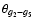 of g2-g5
in all 6 solutions of Table 9
(La2004, La2004*, La2004**, La20040, La20041.0, La20041.5)
with respect to the linear approximation
of g2-g5
in all 6 solutions of Table 9
(La2004, La2004*, La2004**, La20040, La20041.0, La20041.5)
with respect to the linear approximation
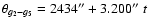 where t is in yr. where t is in yr.
|
| Open with DEXTER |
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig26} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg301.gif) |
Figure 26:
Eccentricity of the Earth. Nominal solution
La2004 filtered in the interval
![$[2.2 {\rm ''/yr}, 8 {\rm ''/yr}]$](/articles/aa/full/2004/46/aa1335/img36.gif) (solid line),
and approximation with a single periodic term (47) (dotted line).
(solid line),
and approximation with a single periodic term (47) (dotted line).
|
| Open with DEXTER |
12 Discussion and future work
The new orbital solution of the Earth that is presented here can be used for paleoclimate
computations over 40 to 50 Myr. Beyond that time interval, the precision of the solution
cannot be guaranteed but we nevertheless provide the solution over 100 Myr on our
Web site www.imcce.fr/Equipes/ASD/insola/earth/earth.html
as reference, and for a possible use, with caution, over the
full Paleogene period (up to 65 Myr).
As in Laskar et al. (1993), the solution for precession and obliquity is not as accurate
as the orbital solution. This is mainly due to the uncertainty that remains in
the tidal dissipation in the Earth-Moon system. We expect the present
solution to be precise over about 20 Myr (see Sect. 9.2),
but additional work is certainly needed
here.
When taking into account the dissipation in the Earth-Moon system, it is remarkable
that in the time interval
![$[-250 {\rm ~Myr}, +250 {\rm ~Myr}]$](/articles/aa/full/2004/46/aa1335/img302.gif) ,
the only major event
in the obliquity of the Earth occurs in the vicinity of the present time (Fig. 14).
We have discarded the possibility of some numerical artefact by integrating different models.
In particular, we find the same slow decrease of about 0.38 degrees
in the obliquity over about 20 Myr either when we integrate
the obliquity and precession equations of Sect. 4
at the same time as the orbital equations, or
when the precession and obliquity are computed afterwards, with a forced
orbital motion.
Moreover, the behavior of the solution is perfectly explained by the crossing of the
s6+g5-g6 resonance, as it is explicited in full details
in the appendix.
,
the only major event
in the obliquity of the Earth occurs in the vicinity of the present time (Fig. 14).
We have discarded the possibility of some numerical artefact by integrating different models.
In particular, we find the same slow decrease of about 0.38 degrees
in the obliquity over about 20 Myr either when we integrate
the obliquity and precession equations of Sect. 4
at the same time as the orbital equations, or
when the precession and obliquity are computed afterwards, with a forced
orbital motion.
Moreover, the behavior of the solution is perfectly explained by the crossing of the
s6+g5-g6 resonance, as it is explicited in full details
in the appendix.
The crossing of this resonance will occur in the next 20 Myr, but
one could wonder whether this crossing could have also occured in the
recent past and thus had a possible impact on the past Earth climate.
In (Laskar et al. 1993), we searched for the
possibility to encounter this resonance in the past
by changing the momentum of inertia of the Earth
as a result of the ice load changes occuring during an ice age,
but it seems that our values for the
change of momentum of inertia during an ice age was
overestimated (Mitrovica & Forte 1995; Levrard & Laskar 2003).
In a similar way, Forte & Mitrovica (1997) have advocated
the mantle convection as a mean to change the values of
the momentum of inertia of the Earth in the past, and thus to
eventually cross the
s6+g5-g6 resonance in the past.
Their results are very sensitive to their models, and
it is not clear that the induce change of momentum of inertia
will be able to counteract the effect of tidal dissipation
that drives the obliquity away from the resonance in the past.
Moreover, the analysis of geological data in the past few Myr
(Lourens et al. 2001; Pälike & Shackleton 2001)
tends to show that the precession frequency has actually increased
in the past and thus, that the system was driven away from the resonance.
Additional studies on this topic are certainly welcome,
and we should still search for the possibility of a crossing of the
s6+g5-g6 resonance in the past, as it may have
impacted the climatic history of the Earth,
but in absence of new evidence, we should consider that
the proximity of this resonance is pure coincidence.
The next step for the improvement of the
solutions will be to obtain an accurate orbital solution over the full Paleogene
period (65 Myr). The numerical accuracy of our integrator already fulfills this
requirement (Fig. 23), although we expect to slightly improve it by switching
to extended computer precision.
The improvement of the model and parameters is much more difficult, and will require
additional work. First, we will have to include in our model
supplementary contributions in order to compare much more closely to DE406.
In particular, in the present work, to save computer time, we had to simplify
the interactions in the Earth-Moon system. In the next integration, we will take
into account additional contributions in the body body interactions of the Earth-Moon system,
and also the libration of the Moon. We will also have to adapt the tidal model
in the Earth-Moon system.
We will need to take into account the effect of the 5 main asteroids that are present
in DE406, and probably derive a small model for the contribution of the 295 additional
asteroids that are considered in DE406.
Indeed, the consideration of the main asteroids appears as the next most
important source of uncertainty for the long term solution (Table 8).
Some of the other factors listed in Table 8 can easily be taken into account,
as the consideration of the main Galilean satellites, or the mass loss of the
Sun.
Finally, it will also be important to reestablish the precision of the
parameter of the model by a direct comparison to the observations. For this part, we expect to
benefit from the effort that is developed at present in our laboratory for the improvement of
short time ephemeris devoted to the reduction of Earth based and space missions observations
(Fienga & Simon 2004).
The fulfilment of this program will allow to improve on the main limiting
factors listed
in Table 8.
It should be stressed again here that the limiting times listed in
Table 8 are somewhat pessimistic. We can thus hope that after
completing this effort, the orbital solution may be valid over 50 to 65 Myr.
Nevertheless, although this program may lead to a solution valid over about 60 Myr, obtaining a precise solution for the precession and obliquity
of the Earth's axis over 65 Myr is much more difficult, as it will require
a modelization of the evolution of the various dissipative contributions
(see Sect. 4.1)
over this period. An alternate way will be to fit the evolution of the
main precession frequency to the geological data over the Paleogene period.
Although some results have been already obtained in this direction over
some shorter time span (Lourens et al. 2001; Pälike & Shackleton 2001),
to extract the variation of the precession frequency from paleoclimate stratigraphic
data is still a challenge, but we hope that the present paper will
provide a good basis for this future work.
Appendix A: Fresnel integrals and resonances
![\begin{figure}
\includegraphics[width=7.7cm,clip]{figures_pdf/1335figA1} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg303.gif) |
Figure A.1:
Fresnel functions C(x) (solid line) and S(x) (dotted line).
|
In this section, we show that Fresnel integrals are very good approximations
for the crossing of the resonance.
Let us define the Fresnel integrals (we have dropped here the usual 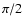 factor)
as
factor)
as
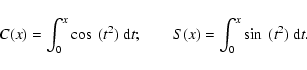 |
(A.1) |
We have the expansions, for 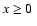 (Abramowitz & Stegun 1965)
(Abramowitz & Stegun 1965)
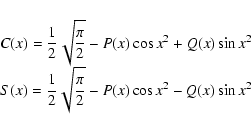 |
(A.2) |
with the asymptotic expansions
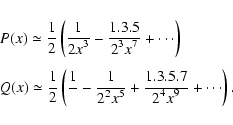 |
(A.3) |
We thus have a jump from the asymptotic value at  to the value at
to the value at  of
of
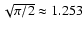 (Fig. A.1).
Due to tidal dissipation, the precession angle evolves in first approximation as Eq. (34)
(Fig. A.1).
Due to tidal dissipation, the precession angle evolves in first approximation as Eq. (34)
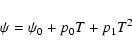 |
(A.4) |
with this evolution, a term of frequency 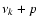 in Eq. (30) may cross the
resonance. In particular, we can compute the contribution of the term
in Eq. (30) may cross the
resonance. In particular, we can compute the contribution of the term 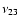 in the quasiperiodic decomposition of
in the quasiperiodic decomposition of 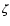 (Table 5).
We will have from Eq. (28),
(Table 5).
We will have from Eq. (28),
 |
(A.5) |
More generally, for a>0, the integral of
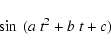 |
(A.6) |
is
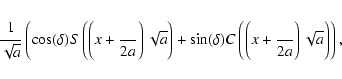 |
(A.7) |
where
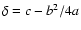 ,
and the asymptotic
offset
,
and the asymptotic
offset
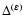 due to the crossing of the resonance of the term (A.6)
is easily obtained as
due to the crossing of the resonance of the term (A.6)
is easily obtained as
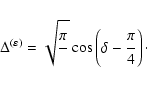 |
(A.8) |
With the data for the resonant term  ,
we have
,
we have
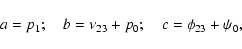 |
(A.9) |
and as the term is of amplitude
 ,
we obtain (Fig. A.2) an offset of amplitude
,
we obtain (Fig. A.2) an offset of amplitude
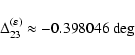 |
(A.10) |
that is very close to the value 0.377602 deg obtained in Sect. 8.3
for the complete integration.
It should be noted that the amplitude of the offset depends critically of the phase
 .
Indeed, a maximum amplitude for the offset will be obtained when
.
Indeed, a maximum amplitude for the offset will be obtained when
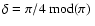 ,
which leads to
,
which leads to
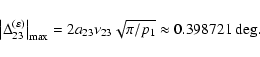 |
(A.11) |
while no offset will occur when
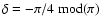 .
In the present case, the actual value of the
offset is thus close to its maximum possible value.
One should also note that apart from the drift that occurs at the resonance, which ranges from about -0.4to +0.4 degree, the maximum oscillation of the
obliquity is of about 0.1 degree (Fig. A.2).
.
In the present case, the actual value of the
offset is thus close to its maximum possible value.
One should also note that apart from the drift that occurs at the resonance, which ranges from about -0.4to +0.4 degree, the maximum oscillation of the
obliquity is of about 0.1 degree (Fig. A.2).
![\begin{figure}\par
\includegraphics[width=7.7cm,clip]{figures_pdf/1335figA2} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg327.gif) |
Figure A.2:
Obliquity variation (in degree) versus time resulting from the crossing of the
resonance in the 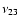 term (solid line).
In the same plot, the dependence of the precession phase is illustrated. for
term (solid line).
In the same plot, the dependence of the precession phase is illustrated. for
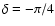 the obliquity offset is null (dashed line)
while it is maximal for
the obliquity offset is null (dashed line)
while it is maximal for
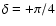 .
The nominal solution (solid line)
corresponds nearly to a maximal decrease of the obliquity. .
The nominal solution (solid line)
corresponds nearly to a maximal decrease of the obliquity.
|
Acknowledgements
J.L. thanks J. Landwehr for providing a copy of Pilgrim's work, A. Vernekar for
a copy of his monograph, and H. Pälike for his comments. This work
benefited from support from INSU-CNRS, PNP-CNRS, and CS, Paris Observatory.
- Adhémar, J. 1842, Révolutions de la mer,
(Paris: Bachelier)
In the text
- Agassiz, L. 1840, Études sur les glaciers
(Paris)
In the text
- Arnold, V. I., Kozlov, V. V., & Neishtadt, A. I. 1988, Mathematical aspects of
classical and celestial mechanics, Dyn. Systems III, ed. V. I. Arnold (New York: Springer)
In the text
- Berger, A. L. 1978, J.
Atmos. Sci., 35, 2362
In the text
- Bills, B. G. 1994, Geophys. Res. Lett., 21(3), 177
In the text
- Bretagnon, P. 1974, A&A, 30, 141
In the text
- Bretagnon, P. 1984, Celest.
Mech., 34, 193
- Bretagnon, P., & Simon, J.-L. 1990, A&A, 239, 387
In the text
- Brouwer, D., & Van Woerkom, A. J. J. 1950, Astron. Papers Am. Ephem., XIII, Part II, 81
In the text
- Chapman, S., & Lindzen, R. S. 1970, Atmospheric tides (Dordrecht: D. Reidel)
In the text
- Chirikov, B. 1979, Phys. Rep., 52, 263
In the text
- Correia, A., & Laskar, J. 2003, J. Geophys. Res., 108(E11), 5123
In the text
- Correia, A., Laskar, J., & Néron de Surgy, O. 2003, Icarus, 163, 1
In the text
- Croll, J. 1890, Climate and Time (London)
In the text
- Darwin, G. H. 1880, Philos. Trans. R. Soc.
London, 171, 713
In the text
- Dickey, J. O., Bender, P. L., Faller, et al. 1994, Science, 265, 182
In the text
- Duriez, L. 1977, A&A, 54, 93
In the text
- Egbert, G. D., & Ray, R. D. 2000, Nature, 405, 775
In the text
- Fienga, A., & Simon, J.-L. 2004,
submitted
In the text
- Forte, A., & Mitrovica, J. X. 1997, Nature, 390, 676
In the text
-
Gradstein, F., Ogg, J., & Smith, A. 2004, A Geologic Time Scale 2004
(UK: Cambridge University Press), in press
- Haretu, S. C. 1885, Annales de l'Observatoire de Paris, 18, I1
In the text
-
Harzer, P. 1895, Die Säcularen veränderungen der bahnen der grossen planeten,
Fürstlich Jablonowski'schen Gesellschaft, Leipzig
In the text
- Hays, J. D., Imbrie, J., & Schackleton, N. J. 1976, Science, 194, 1121
In the text
- Hill, G. 1897, AJ, 17(11), 81
In the text
- Imbrie, J. 1982, Icarus, 50, 408
In the text
- Imbrie, J., & Imbrie, K. P. 1979,
Ice Ages: Solving the Mystery (MA: Harvard University Press)
In the text
- Ito, T., & Tanikawa, K. 2002, MNRAS, 336, 483
In the text
- Ito, T., Masuda, K., Hamano, Y., & Matsui, T. 1995, J. Geophys. Res., 100, 15147
In the text
- Jeffreys, H. 1920, Phil. Trans. R. Soc. London, Ser. A, 221, 239
In the text
- Jeffreys, H. 1976, The Earth,
Its Origin, History, and Physical Constitution, 6th ed.
(Cambridge, UK: Cambridge University Press)
In the text
- Kinoshita, H. 1977, Cel. Mech., 15, 277
In the text
- Lagrange, J. L. 1774, Oeuvres complètes, t. IV, Gauthier-Villars, Paris, 1869, 111
In the text
- Lagrange, J. L. 1776, Oeuvres complètes, t. IV, Gauthier-Villars, Paris, 1869, 255
- Lagrange, J. L. 1777, Oeuvres complètes, t. VI, Gauthier-Villars, Paris, 1873, 633
In the text
- Lagrange, J. L. 1781, Oeuvres complètes, t. V, Gauthier-Villars, Paris, 1870, 125
In the text
- Lagrange, J. L. 1782, Oeuvres complètes, t. V, Gauthier-Villars, Paris, 1870, 211
In the text
- Lambeck, K. 1980, The Earth's variable rotation (UK: Cambridge University Press)
In the text
- Lambeck, K. 1980, Geophysical Geodesy (UK: Oxford University Press)
- Laplace, P. S. 1773-1776, Oeuvres complètes, t. VIII, Gauthier-Villars, Paris, 1891, 199
In the text
- Laplace, P. S. 1776, Oeuvres complètes, t. VIII, Gauthier-Villars, Paris, 1891, 369
In the text
-
Laskar, J. 1984,
Théorie générale planétaire: Eléments orbitaux des planètes sur
1 million d'années, Thèse, Observatoire de Paris
In the text
- Laskar, J. 1985, A&A, 144, 133
In the text
- Laskar, J. 1986, A&A, 157, 59
In the text
- Laskar, J. 1988, A&A, 198, 341
In the text
- Laskar, J. 1989, Nature, 338, 237
In the text
- Laskar, J. 1990, Icarus, 88, 266
In the text
- Laskar, J. 1992, in Chaos, resonance and
collective dynamical phenomena in the solar system, Ferraz-Mello, S. (1) (Kluwer Acad. Publ.), IAU
Symp., 152
- Laskar, J. 1999, Phil. Trans. R. Soc. Lond. A., 357, 1735
In the text
-
Laskar, J. 1999, Introduction to frequency map analysis, in NATO ASI 533
3DHAM95, S'Agaro, Spain, C. Simò (Kluwer), 134
- Laskar, J. : 2001, Astronomical
Solutions for Paleoclimate Studies,. AGU Fall Meeting 2001 Abstracts U11A-01
In the text
- Laskar, J. 2003, Ann. Henri Poincaré, 4, Suppl. 2, S693
-
Laskar, J. 2003,
in Hamiltonian systems and Fourier analysis, ed. Benest et al. (Taylor, Francis), in press
In the text
- Laskar, J., Joutel, F., & Boudin, F. 1993, A&A, 270, 522
In the text
- Laskar, J., & Robutel, P. 2001, Celest. Mech., 80, 39
In the text
- Laskar, J., Correia, A. C. M., Gastineau, M., et al. 2004, Icarus, 170, 343
In the text
-
Le Verrier, U. 1856, Ann. Obs. Paris, II, Mallet-Bachelet, Paris
In the text
- Levrard, B., & Laskar, J. 2003, Journal Geophys. Int., 154, 970
In the text
- Lourens, L. J., Wehausen, R., & Brumsack, H. J. 2001, Nature, 409, 1029
In the text
-
Lourens, L. J., Hilgen, F. J., Shackleton, N. J., Laskar, J., & Wilson, D. 2004, in
The Neogene Period, ed. F. Gradstein, J. Ogg, & A. Smith, A Geologic Time Scale 2004
(UK: Cambridge University Press), in press
In the text
- Lumb, L. I., & Aldridge, K. D. 1991, J. Geomagn. Geoelectr., 43, 93
In the text
-
MacCarthy, D. D. 1992, IERS Standards, IERS Technical note 13, Observatoire de Paris
-
MacCarthy, D. D., & Petit, G. 2004, IERS Standards, IERS Technical note 13, Observatoire de Paris
- Mignard, F. 1979, The Moon and the
Planets, 20, 301
In the text
- Mignard, F. 1980, The Moon and the
Planets, 23, 185
In the text
- Mignard, F. 1981, The Moon and the
Planets, 24, 189
In the text
- Milani, A., Nobili, A. N., & Carpino, M. 1987, A&A, 172, 265
In the text
- Milankovitch, M. 1941,
Kanon der Erdbestrahlung und seine Andwendung auf das Eiszeitenproblem,
Royal Serbian Academy
In the text
- Mitrovica, J. X., & Forte, A. 1995, Geophys. J. Int., 121, 21
In the text
- Néron de Surgy, O., & Laskar, J. 1997, A&A, 318, 975
In the text
- Newhall, X. X., Standish, E. M., & Williams, J. G. 1983, A&A, 125, 150
In the text
- Olsen, P., & Kent, D. 1999, Phil. Trans. R. Soc. London, Ser. A., 357, 1761
In the text
- Pälike, H. 2002, Thesis, University of Cambridge
In the text
- Pälike, H., & Shackleton, N. J. 2001, EPSL, 400, 1029
In the text
-
Pälike, H., Laskar, J., & Shackleton, N. J. 2004,
Geological constraints on the chaotic diffusion of the Solar System,
Geology, in press
In the text
- Pijpers, F. P. 1998, MNRAS, 297, L76
In the text
-
Pilgrim, L. 1904,
Versuch einer rechnerischen behandlung des eiszeitenproblems.
Jahreshefte fur vaterlandische Naturkunde in Wurttemberg, 60
In the text
-
Poincaré, H. 1893,
Méthodes nouvelles de la mécanique céleste,
(Paris: Gauthier-Villars), Vol. II
In the text
- Poincaré, H. 1910, Bull. Astron., 27, 321
In the text
- Pontécoulant, G. de 1834, Théorie Analytique du Système du Monde,
t. III, Bachelier, Paris
In the text
- Quinn, T. R., Tremaine, S., & Duncan, M. 1991, AJ, 101, 2287
In the text
- Rochester, M. G. 1976, Geophys. J. R. A. S., 46, 109
In the text
- Rubincam, D. P. 1990, Science, 248, 720
In the text
- Rubincam, D. P. 1995, Paleoceanography, 10, 365
In the text
- Saha, P., & Tremaine, S. 1994, AJ, 108 (5), 1962
In the text
- Sharav, S. G., & Boudnikova, N. A. 1967a, Bull. I.T.A, XI-4(127), 231
In the text
- Sharav, S. G., & Boudnikova, N. A. 1967b, Trud. I.T.A, XIV, 48
-
Standish, E. M. 1998, JPL planetary and Lunar ephemerides, DE405/LE405. JPL IOM 312.F-98-048,
Pasadena
In the text
- Stockwell, J. N. 1873, Memoir on the secular variations of the elements of the eight principal planets.
Smith. Contr. Knowledge, Washington, 18
In the text
- Sussman, G. J., &
Wisdom, J. 1992, Science, 257, 56
In the text
- Touma, J., & Wisdom, J. 1994, AJ, 108, 1943
In the text
- Varadi, F., Bunnegar, B., & Ghil, M. 2003, ApJ, 592, 620
In the text
- Vernekar 1972, Long-period global variations of incoming solar radiation,
Meteorol. Monogr., 12
In the text
- Volland, H. 1978, Earth's rotation from eons to
days, ed. Brosche and Sündermann (Springer), 62
In the text
- Williams, D. M., Kasting, J. F., & Frakes, L. A. 1998, Nature, 396, 453
In the text
- Williams, J. G., Boggs, D. H., Yoder, C. F., Ratcliff, J. T., & Dickey, J. O. 2001, J. Geophys. Res., 106, 27933
In the text
- Wisdom, J., & Holman, M. 1991, AJ, 102(4), 128
In the text
-
Yoder, C. F. 1995, Astrometric and geodetic properties of Earth and the
Solar System, in ed. T. J. Ahrens, Global Earth Physics: A Handbook
of Physical Constants, American Geophysical Union, Washington
DC, 1
- Zachos, J. C., Shackleton, N. J., Revenaugh, J. S., Pälike, H., & Flower, B. P. 2001, Science, 292, 274
In the text
- Zachos, J. C., Pagani, M., Sloan, L., Thomas, E., & Billups, K. 2001, Science, 292, 686
In the text
Copyright ESO 2004
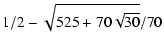
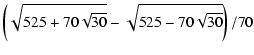
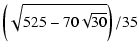
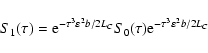
![\begin{figure}\par
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig1}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg98.gif)
![\begin{figure}
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig2}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg99.gif)
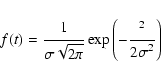
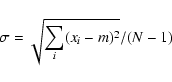
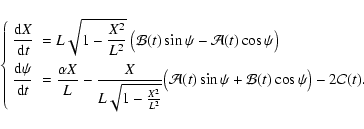
![\begin{displaymath}\left\{ \begin{array}{lll}
{\cal A}(t) &=\displaystyle
\frac...
...2mm]
{\cal
C}(t) &= q\dot p - p\dot q \\
\end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img120.gif)
![$\displaystyle \alpha= {{\displaystyle\strut3G}\over{\displaystyle\strut2\omega}...
...trut3}\over{\displaystyle\strut2}}\sin^2 i_{\rm M}\right) \Bigg] ~ {E_{\rm d}}.$](/articles/aa/full/2004/46/aa1335/img124.gif)
![\begin{displaymath}\left\{\begin{array}{ll}
{{\displaystyle\strut{\rm d}{L}}\ove...
...{2}}} {e_\odot}^2\right) n_\odot\bigg] \\
\end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img130.gif)
![\begin{displaymath}\left\{\begin{array}{l}
{{\displaystyle\strut{\rm d}{L}}\over...
...ight) ~ n_{\rm M}~\cos i_{\rm M}\bigg]. \\ \end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img133.gif)
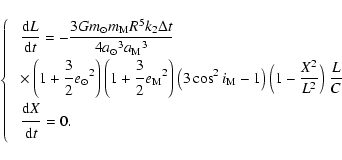
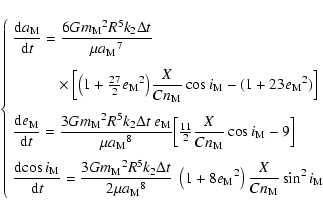
![\begin{displaymath}\left\{
\begin{array}{ll}
{{\displaystyle\strut{\rm d}{a_\odo...
...2}}} {X \over
{C n_\odot}} - 9 \Big] \\
\end{array} \right.
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img137.gif)
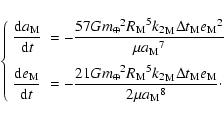
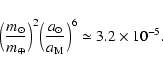
![\begin{figure}
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig4} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg158.gif)
![\begin{figure}\par
\includegraphics[width=13cm,clip]{figures_pdf/1335fig5} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg166.gif)
![\begin{figure}\par
\includegraphics[width=13cm,clip]{figures_pdf/1335fig6}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg167.gif)
![\begin{figure}\par
\includegraphics[width=7.6cm,clip]{figures_pdf/1335fig7} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg168.gif)
![\begin{figure}\par
\includegraphics[width=7.6cm,clip]{figures_pdf/1335fig8} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg170.gif)
![\begin{displaymath}{{\displaystyle\strut{\rm d} [x]}\over{\displaystyle\strut{\rm d}t}} = {i}A [x]
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img172.gif)
![\begin{displaymath}{{\displaystyle\strut{\rm d} [u]}\over{\displaystyle\strut{\rm d}t}} = {i}D [u]
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img177.gif)
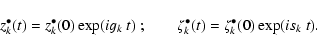
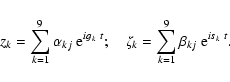
![\begin{displaymath}{{\displaystyle\strut{\rm d} [x]}\over{\displaystyle\strut{\rm d}t}} = {i}A [x] + B(x,\bar x)
\end{displaymath}](/articles/aa/full/2004/46/aa1335/img185.gif)
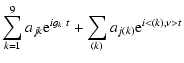
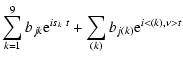
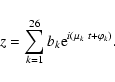
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig9} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg198.gif)
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig10} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg199.gif)
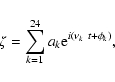
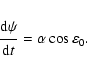
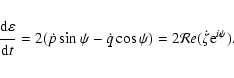
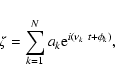
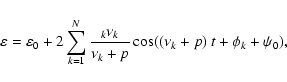
![\begin{figure}\par
\includegraphics[width=14cm,clip]{figures_pdf/1335fig12} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg221.gif)
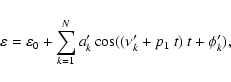
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig13} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg249.gif)
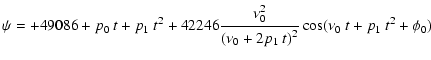
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig15} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg259.gif)
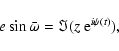
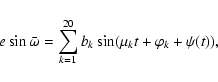
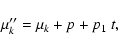
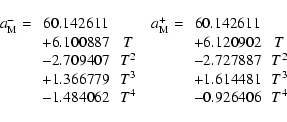
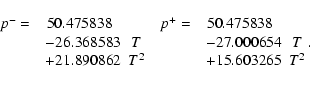
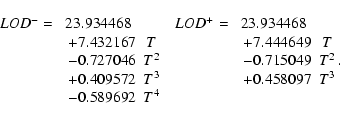
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig16}
\end{figure}](/articles/aa/full/2004/46/aa1335/Timg274.gif)
![\begin{figure}\par
\includegraphics[width=8cm,clip]{figures_pdf/1335fig17} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg275.gif)
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig18} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg276.gif)
![\begin{figure}\par
\includegraphics[width=8.3cm,clip]{figures_pdf/1335fig19} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg277.gif)
![\begin{figure}\par
\includegraphics[width=8.2cm,clip]{figures_pdf/1335fig20} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg278.gif)
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig21} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg282.gif)
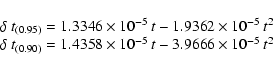
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig22} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg291.gif)
![\begin{figure}\par
\includegraphics[width=7.7cm,clip]{figures_pdf/1335fig23} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg292.gif)
![\begin{figure}\par
\includegraphics[width=8.3cm,clip]{figures_pdf/1335fig24} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg295.gif)
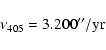
![\begin{figure}\par
\includegraphics[width=8.3cm,clip]{figures_pdf/1335fig25} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg300.gif)
![\begin{figure}\par
\includegraphics[width=8.5cm,clip]{figures_pdf/1335fig26} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg301.gif)
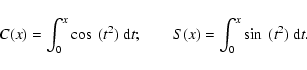
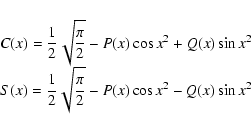
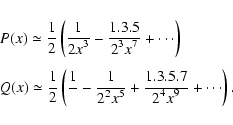
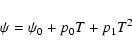

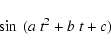
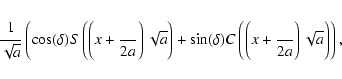
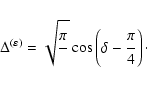
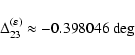
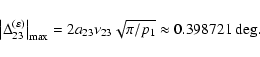
![\begin{figure}\par
\includegraphics[width=7.7cm,clip]{figures_pdf/1335figA2} \end{figure}](/articles/aa/full/2004/46/aa1335/Timg327.gif)