Table 6:
Comparison between two kinds of NG models for four
short-period comets. NG parameters were derived from 8 of 12
detected apparitions for Comet 31P/Schwassmann-Wachmann 2, 8 of 9
detected apparitions for Comet 46P/Wirtanen (the last one were
excluded), 15 of 19 apparitions for Comet 26P/Grigg-Skjellerup and
all available observations (5 apparitions span over 9 perihelion
passages) in the case of Comet 88P/Howell. Standard NG parameters
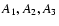 and parameter A (forced
precession model) are given in units of
10-8 AU day-2. The precession factor
and parameter A (forced
precession model) are given in units of
10-8 AU day-2. The precession factor 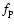 is
in units of 107 day/AU, Subscript "0'' in
is
in units of 107 day/AU, Subscript "0'' in
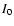 and
and
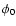 denotes the values for the starting epoch of
integration (Epoch: 2003 12 27). For two comets (31P and 46P) the
assumption about the asymmetry of function g(r) was necessary, and
the time shifts
denotes the values for the starting epoch of
integration (Epoch: 2003 12 27). For two comets (31P and 46P) the
assumption about the asymmetry of function g(r) was necessary, and
the time shifts 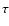 (in days) were derived. The forced
precession model of 26P was taken from Sitarski (2003).
(in days) were derived. The forced
precession model of 26P was taken from Sitarski (2003).
| Name |
Model with constant A
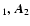 and A
and A
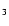 |
Model of a rotating non-spherical nucleus |
| |
|
|
(Forced Precession Model) |
| Observational arc |
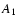 , , |
|
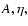 |
|
| No. of apparitions |
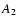 , , |
rms |
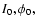 |
rms |
| (No. of obs) |
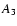 |
|
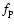 ,
s ,
s |
|
| |
|
|
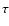 |
|
| 31P/Schwassmann-Wachmann 2 |
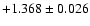 |
|
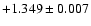 ,
15 ,
15 6 6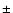 0
0 2 2 |
|
| 1955 05 22-1999 10 08 |
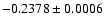 |
5
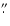 21 21 |
174 1 1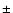 0 0 1, 275 1, 275 1 1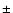 7
7 8 8 |
1
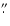 48 48 |
| 8 app (731 obs.) |
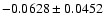 |
|
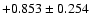 , ,
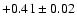 |
|
| |
|
|
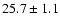 |
|
| 46P/Wirtanen |
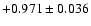 |
|
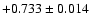 ,
14 ,
14 0 0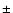 1
1 3 3 |
|
| 1948 01 17-1997 12 30 |
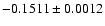 |
16
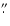 0 0 |
143 1 1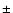 1 1 4, 314 4, 314 4 4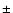 2
2 8 8 |
1
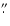 80 80 |
| 8 app (214 obs.) |
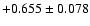 |
|
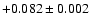 , ,
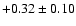 , , |
|
| |
|
|
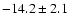 |
|
| 88P/Howell |
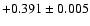 |
|
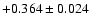 ,
11 ,
11 9 9 0
0 7 7 |
|
| 1955 05 22-1999 10 08 |
 |
2
 31 31 |
113 1 1 2 2 8, 341 8, 341 4 4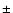 2
2 8 8 |
1
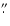 19 19 |
| 5 app (368 obs.) |
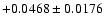 |
|
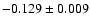 , ,
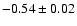 |
|
| 26P/Grigg-Skjellerup |
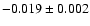 |
|
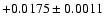 ,
28 ,
28 7 7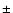 2
2 2 2 |
|
| 1922 05 18-1993 09 17 |
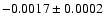 |
5
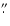 05 05 |
89 9 9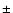 1 1 0, 340 0, 340 7 7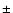 3
3 9 9 |
1
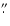 46 46 |
| 15 app (509 obs.) |
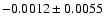 |
|
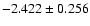 , ,
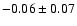 , , |
|
Source LaTeX |
All tables |
In the text