All Tables
- Table 3:
Values of exponents m,n,k, the scale distance
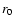 ,
and coefficient
,
and coefficient 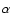 (g(r)-like function,
Eq. (2a)) estimated from observed water sublimation rates for
C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake (Szutowicz et al.
2002a,b).
(g(r)-like function,
Eq. (2a)) estimated from observed water sublimation rates for
C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake (Szutowicz et al.
2002a,b).
- Table 5:
Comparison between mean values of the NG parameters
derived from models with constant
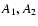 ,
,
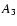 and from models with a rotating spherical nucleus for
the investigated sample of long-period (LP) comets and 20
short-period comets. Comets C/1991 T2 and C/1995 Y1 were excluded
from the basic statistical analysis (17 LP comets) because another
relations of h(r) (g*(r) with k=0 i.e. the power law or
g(r)-like function with
and from models with a rotating spherical nucleus for
the investigated sample of long-period (LP) comets and 20
short-period comets. Comets C/1991 T2 and C/1995 Y1 were excluded
from the basic statistical analysis (17 LP comets) because another
relations of h(r) (g*(r) with k=0 i.e. the power law or
g(r)-like function with
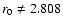 AU) probably are
more adequate for them (see Table 2). Two next two comets
(C/1998 P1 and C/1993 A1) with the greatest NG parameters and
AU) probably are
more adequate for them (see Table 2). Two next two comets
(C/1998 P1 and C/1993 A1) with the greatest NG parameters and
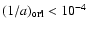 are excluded from the sample of 15 LP
comets. LP models of a rotating spherical nucleus are taken from
Table 4.
are excluded from the sample of 15 LP
comets. LP models of a rotating spherical nucleus are taken from
Table 4.
- Table 1:
General characteristics of the observational material.
The succesive columns signify: comet designation and name (Col. 1)
perihelion time, T, and perihelion distance, q(2), observational arc and number of all observations (3), rms for the pure gravitational orbital fitting to pre-periherlion
(4), post-perihelion (5) and all (6) observations, rms for
the NG orbital fitting to all observations (7), original (8) and
future (9) reciprocals of semimajor axes in units of 10-6 AU-1.
- Table 2:
NG parameters derived from positional observations for
assumed function h(r) (Eq. (5)) represented by: standard function
g(r), g*(r) - modified function g(r),
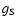 (r)
- Sekanina's function, f(r) - Yabushita's function describing
CO sublimation, respectively. NG parameters
(r)
- Sekanina's function, f(r) - Yabushita's function describing
CO sublimation, respectively. NG parameters
 are given in units of
10-8 AU day-2; these parameters are the standard
are given in units of
10-8 AU day-2; these parameters are the standard
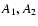 and
and
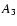 for the NG models
including the standard g(r);
for the NG models
including the standard g(r); 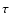 is given in days. First line
for each individual comet shows the NG parameters
is given in days. First line
for each individual comet shows the NG parameters
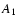 and
and
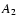 taken from MW Catalogue or Minor Planet Circulars (if
there are). The g*(r) functions for C/1995 O1 Hale-Bopp
(
taken from MW Catalogue or Minor Planet Circulars (if
there are). The g*(r) functions for C/1995 O1 Hale-Bopp
(
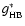 (r)) and C/1996 B2 Hyakutake
(
(r)) and C/1996 B2 Hyakutake
(
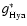 (r)) are described in Table 3. For comet
C/1959 Y1 Burnham the models with displacement, D, of
photometric centre from the gravitational one are also presented;
the values of this displacement (in paranthesis) are given in
units of 10-5 AU. Models with subscript R indicate
solutions based on 37 observations of Comet Burnham made by Roemer
et al. (1966).
(r)) are described in Table 3. For comet
C/1959 Y1 Burnham the models with displacement, D, of
photometric centre from the gravitational one are also presented;
the values of this displacement (in paranthesis) are given in
units of 10-5 AU. Models with subscript R indicate
solutions based on 37 observations of Comet Burnham made by Roemer
et al. (1966).
- Table 4:
Forced precession model for assumed function h(r)
represented by: standard function g(r), f(r), g*(r) -
modified function g(r), respectively. NG parameters
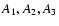 are given in units of
10-8 AU day-2, and precession factor
are given in units of
10-8 AU day-2, and precession factor 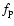 - in
units of 106 day AU-1. Subscript "0'' in
- in
units of 106 day AU-1. Subscript "0'' in
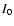 and
and
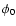 denotes the values on the starting
epoch of integration given in the Col. 1. The g*(r)
functions for C/1995 O1 Hale-Bopp (
denotes the values on the starting
epoch of integration given in the Col. 1. The g*(r)
functions for C/1995 O1 Hale-Bopp (
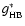 (r)) and
C/1996 B2 Hyakutake (
(r)) and
C/1996 B2 Hyakutake (
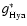 (r)) are described in
Table 3; subscripts (a) and (b) denote
solutions taken from Szutowicz et al. (2002a,b). In the case
of comet Hyakutake models with subscript (a)additionally include the observed comet fragmentation on 1996
March 21.
(r)) are described in
Table 3; subscripts (a) and (b) denote
solutions taken from Szutowicz et al. (2002a,b). In the case
of comet Hyakutake models with subscript (a)additionally include the observed comet fragmentation on 1996
March 21.
- Table 6:
Comparison between two kinds of NG models for four
short-period comets. NG parameters were derived from 8 of 12
detected apparitions for Comet 31P/Schwassmann-Wachmann 2, 8 of 9
detected apparitions for Comet 46P/Wirtanen (the last one were
excluded), 15 of 19 apparitions for Comet 26P/Grigg-Skjellerup and
all available observations (5 apparitions span over 9 perihelion
passages) in the case of Comet 88P/Howell. Standard NG parameters
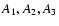 and parameter A (forced
precession model) are given in units of
10-8 AU day-2. The precession factor
and parameter A (forced
precession model) are given in units of
10-8 AU day-2. The precession factor 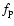 is
in units of 107 day/AU, Subscript "0'' in
is
in units of 107 day/AU, Subscript "0'' in
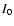 and
and
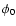 denotes the values for the starting epoch of
integration (Epoch: 2003 12 27). For two comets (31P and 46P) the
assumption about the asymmetry of function g(r) was necessary, and
the time shifts
denotes the values for the starting epoch of
integration (Epoch: 2003 12 27). For two comets (31P and 46P) the
assumption about the asymmetry of function g(r) was necessary, and
the time shifts 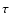 (in days) were derived. The forced
precession model of 26P was taken from Sitarski (2003).
(in days) were derived. The forced
precession model of 26P was taken from Sitarski (2003).