A&A 427, 1117-1126 (2004)
DOI: 10.1051/0004-6361:20041339
M. Królikowska
Space Research Centre of the Polish Academy of Sciences, Bartycka 18A, 00-716, Warsaw, Poland
Received 24 May 2004 / Accepted 24 June 2004
Abstract
The influence of non-gravitational effects on the
motion of long-period comets is analyzed. Investigations were
performed for about 60 nearly-parabolic comets discovered during
the last thirty years. All three non-gravitational parameters
![]() were detected in the motion
of 19 comets on the basis of positional observations only. For
these comets the standard g(r) function as well as some of its
modifications were used to model the ice sublimation from the
cometary nucleus. For 14 of 19 comets the orientation of spin axes
of the nucleus were also determined. Finally, the magnitude of the
non-gravitational effects derived for the long-period comets have
been compared with observed the non-gravitational perturbations on
periodic comets.
were detected in the motion
of 19 comets on the basis of positional observations only. For
these comets the standard g(r) function as well as some of its
modifications were used to model the ice sublimation from the
cometary nucleus. For 14 of 19 comets the orientation of spin axes
of the nucleus were also determined. Finally, the magnitude of the
non-gravitational effects derived for the long-period comets have
been compared with observed the non-gravitational perturbations on
periodic comets.
Key words: solar system: general - comets: general
It is well known that non-gravitational (NG) effects play an essential role in the motion of almost all the short-period comets. The NG solutions have been derived by studying several successive apparitions. Contrary to the short-period comets, the NG orbits have been determined for a very small fraction of the known long-period comets. The first detections of the NG forces in the motion of these comets were reported by Marsden and collaborators in the late 1960s and early 1970s (Marsden 1969; 1970; Marsden et al. 1973). In the Catalogue of Cometary Orbits (Marsden & Williams 2003, hereafter MW Catalogue or MWC) only 23 of 400 nearly parabolic comets have detectable radial and transverse components of the NG force. The problem is obviously observational: the long-period comets are observed on one passage through the inner Solar System. In practice, it turns out that the potential candidates for the detectable NG effects should be observed several months before and after their perihelion passage.
The NG effects are also important for an identification of
hyperbolic comets. The problem of a negative tail in the
distribution of the reciprocals of the original semimajor axis (
![]() )
has been widely discussed in the literature.
Marsden et al. (1973) speculated that the number of hyperbolic
original orbits could be overestimated due to omission of the NG effects. In the 1990s,
Yabushita (1991) and Bolatto et al. (1995)
considered the NG perturbation in a comet's energy per orbital
revolution. They concluded that these perturbations are too small
to explain the negative excess of the original binding energy of
"hyperbolic'' comets. I have investigated this problem in a
separate paper (Królikowska 2001, hereafter Paper I) where the
sample of 33 comets considered as "hyperbolic'' in the sense of a
pure gravitational orbit were analyzed; the radial and transverse
components of the NG accelerations were derived for 16 of them. It
was shown that misleading results are obtained when the same
osculating orbit is used as the initial orbit for backwards
integrations using the NG effects and without these effects. The
differences in the resulting original reciprocals are in this case
significantly smaller than 10-4 AU-1. The respective
differences between two original reciprocal semimajor axes
increase even to about
)
has been widely discussed in the literature.
Marsden et al. (1973) speculated that the number of hyperbolic
original orbits could be overestimated due to omission of the NG effects. In the 1990s,
Yabushita (1991) and Bolatto et al. (1995)
considered the NG perturbation in a comet's energy per orbital
revolution. They concluded that these perturbations are too small
to explain the negative excess of the original binding energy of
"hyperbolic'' comets. I have investigated this problem in a
separate paper (Królikowska 2001, hereafter Paper I) where the
sample of 33 comets considered as "hyperbolic'' in the sense of a
pure gravitational orbit were analyzed; the radial and transverse
components of the NG accelerations were derived for 16 of them. It
was shown that misleading results are obtained when the same
osculating orbit is used as the initial orbit for backwards
integrations using the NG effects and without these effects. The
differences in the resulting original reciprocals are in this case
significantly smaller than 10-4 AU-1. The respective
differences between two original reciprocal semimajor axes
increase even to about
![]() AU-1 when the NG osculating orbit and pure gravitational osculating orbit are
separately used as the initial orbit for the backwards
integrations. Therefore, for 14 of 16 comets with the detectable
NG effects, the original orbits have been changed from hyperbolic
to elliptic, and for the remaining two comets the original orbits
became less hyperbolic as a results of the NG orbit solution. This
tendency to make
AU-1 when the NG osculating orbit and pure gravitational osculating orbit are
separately used as the initial orbit for the backwards
integrations. Therefore, for 14 of 16 comets with the detectable
NG effects, the original orbits have been changed from hyperbolic
to elliptic, and for the remaining two comets the original orbits
became less hyperbolic as a results of the NG orbit solution. This
tendency to make
![]() positive is generated by the
small changes in the orbital osculating eccentricity derived from
the positional observations when the NG effects are taken into
consideration.
positive is generated by the
small changes in the orbital osculating eccentricity derived from
the positional observations when the NG effects are taken into
consideration.
In the present paper the NG motions of individual nearly parabolic comets from the MW Catalogue are carefully examined. Two famous long-period comets, C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake are included in this investigation for comparison with the remaining comets. A more detailed analysis of the motion of these two spectacular objects is described by Szutowicz et al. (2002a,b).
There are important reasons to speculate that the standard g(r)-function could be non-representative for the modelling the NG accelerations detected in the motion of the long-period comets. First, the application of the standard g(r) determined from the photometric studies of the short-period comets to the long-period ones is based on the assumption of the similarity between these two comet families. It is also implicitly assumed that the long-period comets constitute a uniform class of objects. In the third article of his classic series on the NG effects, Marsden (1970) derived the solutions for two long-period comets C/1959 Y1 Burnham and C/1956 R1 Arend-Roland according to his style I NG model. He concluded that the NG forces acting on these two comets "seem to obey something like an inverse-square law, whereas the forces on short-period comets definitely do not''. Recently, the detailed studies of C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake (Szutowicz et al. 2002a,b) show that the g(r)-like forms based on the photometric data are very different for these two objects, and significantly depart from the inverse-square law. The next problem is related to the unacceptably large values of the standard NG parameter A1determined from the observations. This problem also has been known for a long time (Whipple 1977; Yabushita 1991, 1996).
The standard function g(r) is still used to determine
the NG effects in the motion of the long-period comets because the
relevant function has not yet been found. One should stress that
there are strong arguments for the reality of calculated
NG forces. First, the rms of the fitted NG orbits to the
positional data are substantially reduced (Table 1). Second, the
positive value of the radial parameter
![]() determined for
all the comets from the sample (MW Catalogue and Table 2) indicate
that the NG forces are directed radially away from the Sun. The
"vent'' model working also with the negative values of A1, seems
to be inapplicable to those long-period comets that have made only
a few passages through the inner solar system in their dynamical
history. Next, the inclusion of the NG effects in orbit
determinations for dynamically new comets cancels the apparent
hyperbolicity of their orbits, as has been already discussed
(Marsden et al. 1973; Królikowska, Paper I).
determined for
all the comets from the sample (MW Catalogue and Table 2) indicate
that the NG forces are directed radially away from the Sun. The
"vent'' model working also with the negative values of A1, seems
to be inapplicable to those long-period comets that have made only
a few passages through the inner solar system in their dynamical
history. Next, the inclusion of the NG effects in orbit
determinations for dynamically new comets cancels the apparent
hyperbolicity of their orbits, as has been already discussed
(Marsden et al. 1973; Królikowska, Paper I).
The aim of this investigation was to analyze the NG effects based on different forms of NG acceleration as a function of the cometary heliocentric distance.
The preliminary sample of nearly-parabolic comets selected from the MW Catalogue contains the following objects:
The original catalogue orbits of comets selected according to
these criteria are hyperbolic (20 objects) or elliptical (41 objects). The problem of hyperbolic incoming orbits for
single-apparition comets was discussed earlier (Paper I) where all
the 33 comets suspected by Marsden and Williams of hyperbolicity
were investigated. As was mentioned, 16 comets of those 33 objects
have detectable NG effects. For only five of them (C/1959 Y1
Burnham, C/1986 P1A Wilson, C/1995 Y1 Hyakutake, C/1998 P1
Williams and C/1996 E1 NEAT) was the accuracy of all three
NG parameters sufficient for the detailed analysis of their
NG effects. Four of them are listed in the MW Catalogue as comets
with known A1 and
![]() .
.
For the first time the NG effects were determined for six comets among 41 objects with incoming elliptical orbits: C/1975 T1, C/1987 W2, C/1991 B1, C/1991 T1, C/1999 H1, C/1999 J3.
Thus, the final sample consisting of 19 comets with NG effects was investigated in detail (Table 1). Two prominent members of this sample, Comet C/1995 O1 Hale-Bopp and Comet C/1996 B2 Hyakutake, have been treated elsewhere (Szutowicz et al. 2002a,b). Here, these two famous comets are discussed for comparison with the remaining long-period comets with orbits affected by NG forces.
The orbital elements of each comet were recomputed using the archive observations available at the Minor Planet Center (Cambridge, USA). The positional data of comet C/1959 Y1 Burnham were additionally supplemented by 51 observations found in the literature eliminating potential bias which sometimes affects data obtained by a single observer. The observations for individual comets were selected according to the objective criteria elaborated by Bielicki & Sitarski (1991). Table 1 contains characteristics of the observational material for all the considered comets.
In almost all the cases the rms based on all the
observations are significantly larger than the rms obtained
on the basis of pre- or post-perihelion observations alone. In the
numerical calculations it is the first sign that NG forces are
detected in the comet's motion. When the NG force was included in
the cometary equation of motion the rms dropped
significantly, see Col. 7 of Table 1. The listed values of the
rms represent the NG solutions based on the standard g(r)
function (see the next Section). The most spectacular reduction of
the rms was obtained for comets C/1998 P1 Williams (from
4
![]() 58 to 1
58 to 1
![]() 10) and C/1993 A1 Mueller (from 2
10) and C/1993 A1 Mueller (from 2
![]() 79
to 1
79
to 1
![]() 14), the smallest drop - for Comet
C/1991 T2 Shoemaker-Levy (by 0
14), the smallest drop - for Comet
C/1991 T2 Shoemaker-Levy (by 0
![]() 07). However, only three
observations of 1991 T2 were made within a month after the
perihelion passage, and this could explain the small change of the
rms.
07). However, only three
observations of 1991 T2 were made within a month after the
perihelion passage, and this could explain the small change of the
rms.
To calculate the original and future reciprocals of semimajor axes, each comet was followed from its position at a given epoch backwards (orbit before planetary perturbations) and forwards (outgoing orbit) until the comet reached a distance of 250 AU from the Sun. The equations of motion have been integrated in barycentric coordinates using the recurrent power series method (Sitarski 1989, 2002) taking into account the perturbations by all nine planets. All numerical calculations presented here are based on the Warsaw ephemeris DE405/WAW, i.e. the numerical Solar System ephemeris consistent to high accuracy with the JPL ephemeris DE405 (Sitarski 2002).
The respective values of original and future reciprocals of
semimajor axes are given in the last two columns of Table 1. It is
interesting to compare values of
![]() and
and
![]() for the five comets (1959 Y1 Burnham,
1998 P1 Williams, 1996 P1A Wilson, 1996 E1 NEAT and
1993 A1 Mueller) considered in the previous paper (Paper I). It
was shown that the NG effects (described by two standard
parameters
for the five comets (1959 Y1 Burnham,
1998 P1 Williams, 1996 P1A Wilson, 1996 E1 NEAT and
1993 A1 Mueller) considered in the previous paper (Paper I). It
was shown that the NG effects (described by two standard
parameters
![]() and
and
![]() )
are responsible for
small modifications of the pure gravitational osculating elements.
These minute modifications are sufficient, however, to obtain the
elliptic original orbits for comets recognized in the literature
as hyperbolic. The present numerical calculations are based on
different Solar System ephemerides and include also the normal
component of the NG force,
)
are responsible for
small modifications of the pure gravitational osculating elements.
These minute modifications are sufficient, however, to obtain the
elliptic original orbits for comets recognized in the literature
as hyperbolic. The present numerical calculations are based on
different Solar System ephemerides and include also the normal
component of the NG force,
![]() .
Thus,
.
Thus,
![]() and
and
![]() derived here for the NG orbits differ
slightly from that given in Table 1 of Paper I. Nevertheless, the
same tendency is evident. For two comets listed in Table 1,
C/1995 Y1 Hyakutake and C/1959 Y1 Burnham, the original NG orbits
seem be more hyperbolic than the original gravitational orbits.
derived here for the NG orbits differ
slightly from that given in Table 1 of Paper I. Nevertheless, the
same tendency is evident. For two comets listed in Table 1,
C/1995 Y1 Hyakutake and C/1959 Y1 Burnham, the original NG orbits
seem be more hyperbolic than the original gravitational orbits.
In the case of C/1995 Y1 the original NG orbit defined
by
![]() (in the units of
10-6 AU-1 used in this paper) is slightly more
hyperbolic than the pure gravitational orbit characterized by
(in the units of
10-6 AU-1 used in this paper) is slightly more
hyperbolic than the pure gravitational orbit characterized by
![]() ,
where uncertainties of
,
where uncertainties of
![]() are based on the statistical approach to the
orbit determinations (Paper I). In the previous investigations
this object had a slightly elliptical original orbit
are based on the statistical approach to the
orbit determinations (Paper I). In the previous investigations
this object had a slightly elliptical original orbit
![]() (
(
![]() for
NG orbit) and was not classified as a candidate hyperbolic comet.
However, it will be shown that a different form of the NG function
rather than the standard g(r)-function should be used to
adequately describe the NG motion of this comet. The absolute
value of the transverse component
for
NG orbit) and was not classified as a candidate hyperbolic comet.
However, it will be shown that a different form of the NG function
rather than the standard g(r)-function should be used to
adequately describe the NG motion of this comet. The absolute
value of the transverse component
![]() given in the
MW Catalogue for C/1995 Y1 is greater than the radial component
given in the
MW Catalogue for C/1995 Y1 is greater than the radial component
![]() ;
this also suggests another form of the NG function
than the standard g(r).
;
this also suggests another form of the NG function
than the standard g(r).
The elipticity of the original orbit of the second
object, comet C/1959Y1 Burnham, is also uncertain. The NG motion
of this comet has been carefully investigated by many researchers
in the past (van Biesbroeck & Marsden 1963; Sekanina
1968; Matese et al. 1992). It was known as one
of only a few dynamically new comets that had original
gravitational orbit nominally hyperbolic at a level of 5![]() of the formal measured error (Matese et al. 1993; Marsden
et al. 1978). In Paper I only 37 measurements by Roemer et al. (1966) were taken into account. The
of the formal measured error (Matese et al. 1993; Marsden
et al. 1978). In Paper I only 37 measurements by Roemer et al. (1966) were taken into account. The
![]() for the NG orbit was then positive and equaled
for the NG orbit was then positive and equaled
![]() ,
whereas the original gravitational orbit was hyperbolic with
,
whereas the original gravitational orbit was hyperbolic with
![]() .
When 88 positional observations
(covering the same six-month interval as in Roemer et al.) is used
the
.
When 88 positional observations
(covering the same six-month interval as in Roemer et al.) is used
the
![]() are
are
![]() and
and
![]() for the
gravitational and NG orbits, respectively. This example
illustrates that actual uncertainties in some cases could exceed
the formal errors of
for the
gravitational and NG orbits, respectively. This example
illustrates that actual uncertainties in some cases could exceed
the formal errors of
![]() .
Therefore, it is more
advisable to discuss tendencies of the NG orbit to be more eliptic
or more hyperbolic in comparison to the gravitational one (see
also Paper I). It will be shown, however, that assumption of
asymmetric NG acceleration leads to the positive value of
.
Therefore, it is more
advisable to discuss tendencies of the NG orbit to be more eliptic
or more hyperbolic in comparison to the gravitational one (see
also Paper I). It will be shown, however, that assumption of
asymmetric NG acceleration leads to the positive value of
![]() for this object (Sect. 5).
for this object (Sect. 5).
The values of
![]() (Table 1) provide the information
of which comets are dynamically new. From the observed Oort peak
of comets we obtain the canonical rough requirement
(Table 1) provide the information
of which comets are dynamically new. From the observed Oort peak
of comets we obtain the canonical rough requirement
![]() AU-1 for orbits of comets coming
from the Oort cloud. Since most of the comets in the Oort spike
are on their first passage through the inner part of the Solar
System, such comets may contain plenty of volatile ices (CO,
CO
AU-1 for orbits of comets coming
from the Oort cloud. Since most of the comets in the Oort spike
are on their first passage through the inner part of the Solar
System, such comets may contain plenty of volatile ices (CO,
CO
![]() ,
etc.), which should be taken into account in the
modelling of the NG effects. From this point of view seven comets
could be dynamically new: C/1959 Y1 Burnham, C/1990 K1 Levy,
C/1995 Y1 Hyakutake, C/1998 P1 Williams, C/1996 P1A Wilson,
C/1996 E1 NEAT, and C/1993 A1 Mueller. That three of these objects
probably will escape from the Solar System.
,
etc.), which should be taken into account in the
modelling of the NG effects. From this point of view seven comets
could be dynamically new: C/1959 Y1 Burnham, C/1990 K1 Levy,
C/1995 Y1 Hyakutake, C/1998 P1 Williams, C/1996 P1A Wilson,
C/1996 E1 NEAT, and C/1993 A1 Mueller. That three of these objects
probably will escape from the Solar System.
The term "non-gravitational effect'' has been reserved
for the outgassing acceleration of the comet nucleus caused by
anisotropic sublimation of volatiles from the cometary nucleus.
The classical method to determine the NG effects on the orbital
motion of a comet was proposed by Marsden et al. (1973).
Their commonly-used style II model assumes that accelerations are
symmetric about perihelion, and can be expressed by the
semiempirical function g(r):
| (1) |
The form of the dimensionless function g(r) is related to the
empirical water sublimation curve derived by Delsemme & Miller
(1971), and simulates the ice sublimation rate as a function
of the heliocentric distance r:
| (2) | |||
The standard g(r) function can be used to introduce the general
g(r)-like form, g*(r), where exponents
![]() and
parameters
and
parameters ![]() and
and
![]() are determined for each
comet, individually. The general form of the NG acceleration is
defined similarly to Eq. (2):
are determined for each
comet, individually. The general form of the NG acceleration is
defined similarly to Eq. (2):
| (2a) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1339fig1.eps}
\end{figure}](/articles/aa/full/2004/45/aa1339/Timg47.gif) |
Figure 1:
Comparison of different forms of the NG function
h(r) (Eq. (5)) vs. heliocentric distance. Dotted-dashed curves
marked as
|
| Open with DEXTER | |
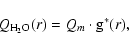 |
(3) |
Therefore, the general form of g*(r) given by
Eq. (2a) was also used here, in the solely orbital calculations for
all the considered long-period comets. It turned out, however,
that the rms determined from the positional data are only
weakly sensitive to exponents m,n and k. Only the scale
distance
![]() could be determined for some comets. Three
possibilities of g*(r) are considered here: (a) the
power law (k=0); (b) the expressions differing from the
standard function g(r) only in the scale distance
could be determined for some comets. Three
possibilities of g*(r) are considered here: (a) the
power law (k=0); (b) the expressions differing from the
standard function g(r) only in the scale distance
![]() ;
and (c) - only the exponent m is fitted. It appears that
only the case (b) can provide better fits to the positional
data. In our calculations we have found seven such g(r)-like
solutions and in Table 2 they are denoted as g(r)
;
and (c) - only the exponent m is fitted. It appears that
only the case (b) can provide better fits to the positional
data. In our calculations we have found seven such g(r)-like
solutions and in Table 2 they are denoted as g(r)
![]() (C/1996 B2, C/1999 H1, C/1995 O1, C/1990 K1, 1999 J3, C/1998 P1,
C/1993 A1). The next two g(r)
(C/1996 B2, C/1999 H1, C/1995 O1, C/1990 K1, 1999 J3, C/1998 P1,
C/1993 A1). The next two g(r)
![]() solutions are given
for comets C/1991 T2 and C/1995 Y1 because they seem to be more
physically realistic than those based on g(r).
solutions are given
for comets C/1991 T2 and C/1995 Y1 because they seem to be more
physically realistic than those based on g(r).
Table 3:
Values of exponents m,n,k, the scale distance
![]() ,
and coefficient
,
and coefficient ![]() (g(r)-like function,
Eq. (2a)) estimated from observed water sublimation rates for
C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake (Szutowicz et al.
2002a,b).
(g(r)-like function,
Eq. (2a)) estimated from observed water sublimation rates for
C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake (Szutowicz et al.
2002a,b).
Yabushita (1996) introduced a convenient form for
the dependence of acceleration on the heliocentric distance based
on sublimations of molecules of CO rather than H2O:
| (4) | |||
To apply Eqs. (2), (2a) and (4) of NG accelerations to asymmetric
cases with respect to perihelion we simply substitute g(r'), g*(r') and
f(r') instead of g(r),
g*(r), f(r), respectively, where
![]() ;
here
;
here ![]() represents the time displacement of the maximum of the
relevant functions with respect to the perihelion.
represents the time displacement of the maximum of the
relevant functions with respect to the perihelion.
Finally, for each comet the following forms of the NG acceleration
were tested:
| (5) | |||
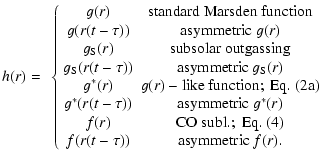 |
Sets of models described by Eq. (5) are presented in Table 2. The
NG parameters
![]() and
and
![]() resulting from the orbital fitting to observations for three
different models including g(r),
resulting from the orbital fitting to observations for three
different models including g(r),
![]() (r) and f(r)
are given. For two comets (C/1991 T2 and C/1995 Y1) the models
with standard g(r) give
(r) and f(r)
are given. For two comets (C/1991 T2 and C/1995 Y1) the models
with standard g(r) give
![]() ,
therefore the
best g*(r) solutions are presented. Asymmetric NG models were
determinable only for five comets: C/1996 B2, C/1959 Y1,
C/1969 Y1, C/1995 O1 and C/1998 P1.
,
therefore the
best g*(r) solutions are presented. Asymmetric NG models were
determinable only for five comets: C/1996 B2, C/1959 Y1,
C/1969 Y1, C/1995 O1 and C/1998 P1.
For most of the investigated comets the NG parameters for the
rotating spherical nucleus were also determined. In such a model
![]() and
and
![]() are now functions
of time by relations:
are now functions
of time by relations:
![]() ,
i=1,2,3, where
Ci(t) are direction cosines for the NG force acting on the
rotating cometary nucleus (Sitarski 1990). Now, three of
the NG parameters are angular parameters:
,
i=1,2,3, where
Ci(t) are direction cosines for the NG force acting on the
rotating cometary nucleus (Sitarski 1990). Now, three of
the NG parameters are angular parameters: ![]() - the lag angle
of the maximum outgassing behind subsolar meridian, I -
equatorial obliquity and
- the lag angle
of the maximum outgassing behind subsolar meridian, I -
equatorial obliquity and ![]() - cometocentric solar longitude
at perihelion. The values of
- cometocentric solar longitude
at perihelion. The values of
![]() and
and ![]() ,
are
presented in Table 4.
,
are
presented in Table 4.
An assumption of a flattened nucleus represents the next step
towards a more realistic cometary model. In this case, the forced
precession of the spin axis could arise due to torque if a vector
of the jet force does not pass through the center of the
nonspherical nucleus. The precession rate is a function of the
nucleus orientation, the lag angle, ![]() ,
the modulus of the
reactive force, A, the nucleus oblateness, s, and the
precession factor,
,
the modulus of the
reactive force, A, the nucleus oblateness, s, and the
precession factor, ![]() ,
which depends on the rotation period and
nucleus size. In such a model the six parameters are derived:
,
which depends on the rotation period and
nucleus size. In such a model the six parameters are derived:
![]() and
and ![]() (Królikowska et al. 1998b).
This procedure could be ambiguous for a one-apparition comet and
it was possible for only three of 19 investigated objects:
C/1993 A1 Mueller, C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake;
the detailed descriptions of forced precession models for the
latter two comets are given by Szutowicz et al. (2002a,b). In the
case of C/1993 A1 the rotating nonspherical model was fully
determinable only for the f(r)-function. For that comet the rms was reduced both for the constant NG parameters (Table 2) and
for the forced precession model (Table 4). All these arguments
indicate that the CO sublimation form described by f(r) is
strongly preferred. This result is also consistent with the small
value of
(Królikowska et al. 1998b).
This procedure could be ambiguous for a one-apparition comet and
it was possible for only three of 19 investigated objects:
C/1993 A1 Mueller, C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake;
the detailed descriptions of forced precession models for the
latter two comets are given by Szutowicz et al. (2002a,b). In the
case of C/1993 A1 the rotating nonspherical model was fully
determinable only for the f(r)-function. For that comet the rms was reduced both for the constant NG parameters (Table 2) and
for the forced precession model (Table 4). All these arguments
indicate that the CO sublimation form described by f(r) is
strongly preferred. This result is also consistent with the small
value of
![]() (Table 1) which implies that the comet
C/1993 A1 Mueller is dynamically young.
(Table 1) which implies that the comet
C/1993 A1 Mueller is dynamically young.
For the next two comets (C/1999 J3 and C/1998 P1) the
best fitted models for the rotating non-spherical nucleus are
given. However, in both cases the values of ![]() and s are
assumed rather than fitted, because it was impossible to determine
all six parameters from the observational data. The case of
C/1999 J3 is very special, because a forced precession model with
the standard g(r) (also with f(r), and
and s are
assumed rather than fitted, because it was impossible to determine
all six parameters from the observational data. The case of
C/1999 J3 is very special, because a forced precession model with
the standard g(r) (also with f(r), and
![]() (r))
gives a negative
(r))
gives a negative ![]() .
Such a solution is physically
unacceptable. This could suggest another g*(r)-like function
with a small value of the exponent m (the similar form as
derived for 1996 B2 Hyakutake). When
.
Such a solution is physically
unacceptable. This could suggest another g*(r)-like function
with a small value of the exponent m (the similar form as
derived for 1996 B2 Hyakutake). When
![]() (r) was
used, the forced precession model gave a positive
(r) was
used, the forced precession model gave a positive ![]() (Table 4)
but parameters
(Table 4)
but parameters ![]() and s could not be determined precisely.
Clearly, the NG behaviour of the rotating nonspherical nucleus of
C/1999 J3 Linear requires further analysis.
and s could not be determined precisely.
Clearly, the NG behaviour of the rotating nonspherical nucleus of
C/1999 J3 Linear requires further analysis.
Table 5:
Comparison between mean values of the NG parameters
derived from models with constant
![]() ,
,
![]() and from models with a rotating spherical nucleus for
the investigated sample of long-period (LP) comets and 20
short-period comets. Comets C/1991 T2 and C/1995 Y1 were excluded
from the basic statistical analysis (17 LP comets) because another
relations of h(r) (g*(r) with k=0 i.e. the power law or
g(r)-like function with
and from models with a rotating spherical nucleus for
the investigated sample of long-period (LP) comets and 20
short-period comets. Comets C/1991 T2 and C/1995 Y1 were excluded
from the basic statistical analysis (17 LP comets) because another
relations of h(r) (g*(r) with k=0 i.e. the power law or
g(r)-like function with
![]() AU) probably are
more adequate for them (see Table 2). Two next two comets
(C/1998 P1 and C/1993 A1) with the greatest NG parameters and
AU) probably are
more adequate for them (see Table 2). Two next two comets
(C/1998 P1 and C/1993 A1) with the greatest NG parameters and
![]() are excluded from the sample of 15 LP
comets. LP models of a rotating spherical nucleus are taken from
Table 4.
are excluded from the sample of 15 LP
comets. LP models of a rotating spherical nucleus are taken from
Table 4.
The principal results and conclusions from the present study of the NG motion of nineteen long-period comets are the following.
1. New comets with detectable NG effects For six comets NG effects were detected in their orbital motion for the first time: C/1999 H1 Lee, C/1991 T2 Shoemaker-Levy, C/1999 J3 Linear C/1975 T1 Mori-Sato-Fujikawa, C/1987 W2 Furuyama, C/1991 B1 Shoemaker-Levy.
2. Normal component A
![]() For most of
the investigated comets the normal component of the
NG acceleration was determined for the first time. It turns out
that only for five comets (C/1959 Y1, C/1995 Y1, C/1993 A1,
C/1999 T1 and C/1991 B1) could this component be neglected in
comparison with the radial and transverse components since
For most of
the investigated comets the normal component of the
NG acceleration was determined for the first time. It turns out
that only for five comets (C/1959 Y1, C/1995 Y1, C/1993 A1,
C/1999 T1 and C/1991 B1) could this component be neglected in
comparison with the radial and transverse components since
![]() .
However, for two of them
(C/1999 T1 and C/1991 B1) the ratio
.
However, for two of them
(C/1999 T1 and C/1991 B1) the ratio
![]() grows when the Sekanina model is used, and for the next two comets
(C/1959 Y1, C/1995 Y1) the normal component increases by a factor
of 10 or more, while the transverse component decreases, if the
asymmetric function g(r') is assumed.
grows when the Sekanina model is used, and for the next two comets
(C/1959 Y1, C/1995 Y1) the normal component increases by a factor
of 10 or more, while the transverse component decreases, if the
asymmetric function g(r') is assumed.
The normal components
![]() are comparable to
or larger than the transverse component
are comparable to
or larger than the transverse component
![]() for eight
comets (C/1996 B2 C/1999 H1, C/1993 Y1, C/1990 K1, C/1998 P1,
C/1986 P1A, C/1998 T1, C/1987 W2). In the extreme case of Comet
C/1993 Y1, the value of
for eight
comets (C/1996 B2 C/1999 H1, C/1993 Y1, C/1990 K1, C/1998 P1,
C/1986 P1A, C/1998 T1, C/1987 W2). In the extreme case of Comet
C/1993 Y1, the value of
![]() is about five times larger
than
is about five times larger
than
![]() .
One should note, however, that in the present
solution the amplitude of
.
One should note, however, that in the present
solution the amplitude of
![]() AU day-2) is much smaller than the value given
in the MW Catalogue, where
AU day-2) is much smaller than the value given
in the MW Catalogue, where
![]() AU day-2 and
AU day-2 and
![]() .
.
3. Transverse component A
![]() In the
majority of cases the sign of the transverse component
In the
majority of cases the sign of the transverse component
![]() does not depend on the assumed symmetric model of
h(r) (see Table 2). For two comets (C/1990 K1 and C/1986 P1A)
does not depend on the assumed symmetric model of
h(r) (see Table 2). For two comets (C/1990 K1 and C/1986 P1A)
![]() is positive, while
is positive, while
![]() derived for
derived for
![]() (r) and f(r) are negative.
(r) and f(r) are negative.
Absolute values of
![]() span a very wide range
and lie between 0.003 (C/1993 Y1) and 2.9 (C/1991 T2) in the units
of 10-8 AU day-2. Similar to the short period
comets, positive and negative values of
span a very wide range
and lie between 0.003 (C/1993 Y1) and 2.9 (C/1991 T2) in the units
of 10-8 AU day-2. Similar to the short period
comets, positive and negative values of
![]() seem to be
equally probable, and generally are an order of magnitude smaller
than the radial component
seem to be
equally probable, and generally are an order of magnitude smaller
than the radial component
![]() .
The mean values of the
.
The mean values of the
![]() ratio are given in Part I of
Table 5.
ratio are given in Part I of
Table 5.
4. Radial component A
![]() The radial
term of the NG acceleration is always greater than the two
remaining components. However, for only one comet in the
sample (C/1986 P1A), the radial component distinctly dominates the
remaining two:
The radial
term of the NG acceleration is always greater than the two
remaining components. However, for only one comet in the
sample (C/1986 P1A), the radial component distinctly dominates the
remaining two:
![]() .
Thus, the simplest model with the only radial component seems to
adequately describe the NG motion of 1986 P1A. Moreover, the
errors of the parameters
.
Thus, the simplest model with the only radial component seems to
adequately describe the NG motion of 1986 P1A. Moreover, the
errors of the parameters
![]() and
and
![]() are of the
same order as the parameters themselves.
are of the
same order as the parameters themselves.
The maximum value of the radial NG force which affected
the cometary motion,
![]() ,
could be calculated from
the
,
could be calculated from
the
![]() parameter according to relation:
parameter according to relation:
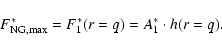
5. Time shift of the maximum of vaporization curve or/and displacement of the photometric center There are two points which should be taken into account in the modelling of the NG effects:
It turns out, however, that the time shift ![]() is
firmly determinable in the NG model with constants
is
firmly determinable in the NG model with constants
![]() for only 5 of 19 long-period comets
(C/1996 B2 Hyakutake, C/1959 Y1 Burnham, C/1969 Y1 Bennett,
C/1995 O1 Hale-Bopp and C/1998 P1 Williams; see Table 2).
for only 5 of 19 long-period comets
(C/1996 B2 Hyakutake, C/1959 Y1 Burnham, C/1969 Y1 Bennett,
C/1995 O1 Hale-Bopp and C/1998 P1 Williams; see Table 2).
The problem of displacement of the photometric center,
![]() ,
from the gravitational one is more complicated because
the shape of a comet's image strongly depends on heliocentric
distance; hence it is an a priori unknown function of r.
Sitarski (1984) fitted the general form of
,
from the gravitational one is more complicated because
the shape of a comet's image strongly depends on heliocentric
distance; hence it is an a priori unknown function of r.
Sitarski (1984) fitted the general form of
![]() ,
where
k=1, 2, 3, 4, 5, to the 37 positional
observations of Comet C/1959 Y1 Burnham made by Roemer et al.
(1966). The best orbit improvement was derived by him for
exponents k=3 and k=4. He concluded that the relation
,
where
k=1, 2, 3, 4, 5, to the 37 positional
observations of Comet C/1959 Y1 Burnham made by Roemer et al.
(1966). The best orbit improvement was derived by him for
exponents k=3 and k=4. He concluded that the relation
![]() ,
similar to the form proposed by
Marsden (1969) as Style I NG effects, represents the best
model of displacement of the photometric center from the center of
mass. Application of this method to the long-period comets
provides ambiguous results. It turns out that only the
observations of comet C/1959 Y1 Burnham indicate that such
displacement could be real. In this case the NG solution with
,
similar to the form proposed by
Marsden (1969) as Style I NG effects, represents the best
model of displacement of the photometric center from the center of
mass. Application of this method to the long-period comets
provides ambiguous results. It turns out that only the
observations of comet C/1959 Y1 Burnham indicate that such
displacement could be real. In this case the NG solution with
![]() (rms = 1
(rms = 1
![]() 12) is the best one in comparison to the
NG solution alone (rms = 1
12) is the best one in comparison to the
NG solution alone (rms = 1
![]() 46) as well as NG solution
including
46) as well as NG solution
including ![]() (rms = 1
(rms = 1
![]() 37) (Table 2). The derived values
of parameters
37) (Table 2). The derived values
of parameters
![]() and D are comparable to those
obtained by Sitarski (1984). The present value of
and D are comparable to those
obtained by Sitarski (1984). The present value of
![]() is significantly different because Sitarski assumed
is significantly different because Sitarski assumed
![]() ,
and in consequence, he obtained the value of
,
and in consequence, he obtained the value of
![]() nearly equal to zero. However, in this case,
observations produced by only one team of observers (Roemer et al.
1966) have been used. When more observations of
comet Burnham were taken into account this discrepancy is
substantially reduced. Thus, the value of D derived from the
observations made by one observer (or one team of observers) could
suffer from large errors and should not be used to determine the
displacement of the photometric center. The appropriate choice
between all reasonable models has a consequence on the shape of
the original orbit. For the symmetric NG model the value of
nearly equal to zero. However, in this case,
observations produced by only one team of observers (Roemer et al.
1966) have been used. When more observations of
comet Burnham were taken into account this discrepancy is
substantially reduced. Thus, the value of D derived from the
observations made by one observer (or one team of observers) could
suffer from large errors and should not be used to determine the
displacement of the photometric center. The appropriate choice
between all reasonable models has a consequence on the shape of
the original orbit. For the symmetric NG model the value of
![]() is negative (see Table 1) whereas for both the
asymmetric model with
is negative (see Table 1) whereas for both the
asymmetric model with ![]() and the symmetric model with assumed
displacement of the photometric center the values of
and the symmetric model with assumed
displacement of the photometric center the values of
![]() are positive and equal to
are positive and equal to
![]() AU-1 and
AU-1 and
![]() AU-1, respectively. An
asymmetric model of comet Burnham was also deduced by Matese &
Whitman (1993).
AU-1, respectively. An
asymmetric model of comet Burnham was also deduced by Matese &
Whitman (1993).
6. Mean values of NG accelerations For the
investigated sample of long-period comets the mean value of a
NG parameter
![]() ,
where
,
where
![]() ,
could also be determined for three assumed forms of h(r):
g(r),
,
could also be determined for three assumed forms of h(r):
g(r),
![]() (r) and f(r) (Table 5).
(r) and f(r) (Table 5).
However, the range of A (and A*) values are broad
(Fig. 2) and covers almost two orders of magnitude from 0.88
(Comet C/1998 T1) to 32.2 (Comet C/1998 P1) in the units of
10-8 AU day-2. Also the errors of A are spread
over a wide range and are distributed between 0.03 and 1.7 (in
the same units). In consequence, the arithmetic mean values of A* (Table 5) differ significantly from the weighted mean value
of A*. Thus, the mean values of
![]() estimated
from the three constant components
estimated
from the three constant components
![]() and
and
![]() should be treated very carefully. Using
should be treated very carefully. Using
![]() or
or
![]() the mean
value of NG acceleration at 1 AU from the Sun,
the mean
value of NG acceleration at 1 AU from the Sun,
![]() ,
could be obtained, where
,
could be obtained, where
![]() cm s-2 is
the solar gravitational acceleration at 1 AU (Table 5).
cm s-2 is
the solar gravitational acceleration at 1 AU (Table 5).
The largest absolute values of the A* parameter (or
radial
![]() parameter) are likely associated with comets
having a large perihelion distance, q, and/or having small
reciprocals of the original semimajor axis,
parameter) are likely associated with comets
having a large perihelion distance, q, and/or having small
reciprocals of the original semimajor axis,
![]() (Fig. 2). Therefore, it is justified to divide the whole sample
in two subgroups with q<1 AU and q>1 AU, respectively. The
values of A for the comets with q greater than 1 AU are
systematically greater and significantly more scattered than the
corresponding distribution for the comets with q smaller than
1 AU (upper panel of Fig. 2). The respective mean values of Acalculated for both samples are:
(Fig. 2). Therefore, it is justified to divide the whole sample
in two subgroups with q<1 AU and q>1 AU, respectively. The
values of A for the comets with q greater than 1 AU are
systematically greater and significantly more scattered than the
corresponding distribution for the comets with q smaller than
1 AU (upper panel of Fig. 2). The respective mean values of Acalculated for both samples are:
![]() (q<1) and
(q<1) and
![]() (q>1) in units of 10-8 AU day-2. A
similar result could be obtained by dividing the whole sample in
two groups with
(q>1) in units of 10-8 AU day-2. A
similar result could be obtained by dividing the whole sample in
two groups with
![]() AU-1 and
AU-1 and
![]() AU-1 (middle panel of
Fig. 2). Then, the mean values are
AU-1 (middle panel of
Fig. 2). Then, the mean values are
![]() and
and
![]() ,
respectively. The correlation between both types of
division is visualized in the bottom panel of Fig. 2. However,
the investigated sample of long-period comets is too small to make
a more detailed statistical analysis.
,
respectively. The correlation between both types of
division is visualized in the bottom panel of Fig. 2. However,
the investigated sample of long-period comets is too small to make
a more detailed statistical analysis.
The mean values of A* for the model of the rotating
spherical nucleus were also determined, using the sample of 14 comets from Table 4. It turns out that the mean values of
![]() estimated from the models of a rotating cometary
nucleus (Part II of Table 5) are similar to previous mean values.
estimated from the models of a rotating cometary
nucleus (Part II of Table 5) are similar to previous mean values.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1339fig2.eps}
\end{figure}](/articles/aa/full/2004/45/aa1339/Timg119.gif) |
Figure 2:
The NG standard parameter
|
| Open with DEXTER | |
It is interesting to compare these mean values with
similar values estimated for short-period comets. Typically,
observations of Jupiter-family comets cover several apparitions
over several dozen years and for some comets even more than one
century. In such cases the models based on constant NG parameters
![]() are fitted significantly less
well to the whole interval of observations than models with a
rotating nonspherical nucleus. It is illustrated by the following
examples. I choose four Jupiter-family comets with different
amplitudes of NG effects: 31P/Schwassmann-Wachmann 2,
46P/Wirtanen, 88P/Howell and 26P/Grigg-Skjellerup. Table 6 gives
the NG solutions for models with constant
are fitted significantly less
well to the whole interval of observations than models with a
rotating nonspherical nucleus. It is illustrated by the following
examples. I choose four Jupiter-family comets with different
amplitudes of NG effects: 31P/Schwassmann-Wachmann 2,
46P/Wirtanen, 88P/Howell and 26P/Grigg-Skjellerup. Table 6 gives
the NG solutions for models with constant
![]() and models with a rotating nonspherical nucleus, i.e.
forced precession models. It is clearly visible that the forced
precession models fit the observations with significantly better
rms than models with constant NG parameters. Thus, the
models with a rotating non-spherical nucleus are the most
appropriate to calculate the mean value of A from positional
observations. Detailed studies of the NG effects that influence
the motion of short-period comets have been undertaken by Sitarski
and collaborators. They showed (Sitarski 1992, 1994;
Królikowska
& Szutowicz 1999; Królikowska et al. 1998a,b,
2001; Szutowicz 1999, 2000) that the forced precession model of
the rotating cometary nucleus successfully describes the long-term
motion of these comets. They obtained NG parameters for 20 short-period comets (some of these models have not been published
yet). The individual values of A have been found to range over 2 orders of magnitude between 0.02 (26P/Grigg-Skjellerup) and 1.4
(31P/Schwassmann-Wachmann 2) in the units of
10-8 AU day2. Table 5 gives the mean values of A,
and models with a rotating nonspherical nucleus, i.e.
forced precession models. It is clearly visible that the forced
precession models fit the observations with significantly better
rms than models with constant NG parameters. Thus, the
models with a rotating non-spherical nucleus are the most
appropriate to calculate the mean value of A from positional
observations. Detailed studies of the NG effects that influence
the motion of short-period comets have been undertaken by Sitarski
and collaborators. They showed (Sitarski 1992, 1994;
Królikowska
& Szutowicz 1999; Królikowska et al. 1998a,b,
2001; Szutowicz 1999, 2000) that the forced precession model of
the rotating cometary nucleus successfully describes the long-term
motion of these comets. They obtained NG parameters for 20 short-period comets (some of these models have not been published
yet). The individual values of A have been found to range over 2 orders of magnitude between 0.02 (26P/Grigg-Skjellerup) and 1.4
(31P/Schwassmann-Wachmann 2) in the units of
10-8 AU day2. Table 5 gives the mean values of A,
![]() and
and
![]() for the sample of 20 short-period comets.
These mean values (fifth column of Table 5) could be directly
compared with the respective mean values obtained for long-period
comets (second column of Table 5). It turns out that the mean
NG parameter A estimated for the long-period comets is at
least 10 times greater than the mean value of A obtained for
short-period comets. This is in very good agreement with the
previous estimates based on the smaller sample of the long-period
comets. Marsden et al. (1973) determined the NG forces described
by
for the sample of 20 short-period comets.
These mean values (fifth column of Table 5) could be directly
compared with the respective mean values obtained for long-period
comets (second column of Table 5). It turns out that the mean
NG parameter A estimated for the long-period comets is at
least 10 times greater than the mean value of A obtained for
short-period comets. This is in very good agreement with the
previous estimates based on the smaller sample of the long-period
comets. Marsden et al. (1973) determined the NG forces described
by
![]() ,
and
,
and
![]() from the sample of 23
short-period and 7 long-period comets. They obtained that the
actual magnitude of the NG forces is typically about 10-5times the solar attraction at 1 AU for short-period comets and
(1-2)
from the sample of 23
short-period and 7 long-period comets. They obtained that the
actual magnitude of the NG forces is typically about 10-5times the solar attraction at 1 AU for short-period comets and
(1-2) ![]() 10-4 of the solar attraction for the long-period
comets.
10-4 of the solar attraction for the long-period
comets.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1339fig3.eps}
\end{figure}](/articles/aa/full/2004/45/aa1339/Timg121.gif) |
Figure 3:
Maximum of NG forces
|
| Open with DEXTER | |
7. Lag angle ![]() The range of
The range of ![]() -
heat lag angles of the maximum outgassing behind the subsolar
meridian - is 6
-
heat lag angles of the maximum outgassing behind the subsolar
meridian - is 6![]() -26
-26![]() for 12 long-period comets (86%
of models of a rotating spherical nucleus). The remaining
solutions yield angles 30
for 12 long-period comets (86%
of models of a rotating spherical nucleus). The remaining
solutions yield angles 30![]() -35
-35![]() (Comet C/1999 H1) and
43
(Comet C/1999 H1) and
43![]() -59
-59![]() (Comet C/1991 T2). In the sample of 20
short-period comets all
(Comet C/1991 T2). In the sample of 20
short-period comets all ![]() angles are below 30
angles are below 30![]() .
Table 5
shows that the mean values of
.
Table 5
shows that the mean values of ![]() calculated for the
long-period comets (Col. 2) somewhat exceed the mean values of
calculated for the
long-period comets (Col. 2) somewhat exceed the mean values of
![]() derived for the short-period comets (Col. 5).
derived for the short-period comets (Col. 5).
8. Which form of h(r) is the most appropriate
for the long-period comets? Effects of the assumed form of
h(r) on the NG parameters derived from the orbital calculations
for the long-period comets have been investigated carefully in the
present analysis. It is also important to examine which form of h(r) is preferable for individual objects, i.e. which form
of h(r) gives the minimum rms in the orbital fitting
procedure. Unfortunately, it is evident that the astrometric
observations alone are not sensitive enough for such an analysis.
Table 2 shows that a g(r)-law fit to the individual long-period
comet gives residuals that are essentially the same as those
obtained from the g(r)-like law (
![]() ,
g*) and those
derived from the f(r)-relation. Nevertheless, I would like to
point to some tendencies which seem to be real.
,
g*) and those
derived from the f(r)-relation. Nevertheless, I would like to
point to some tendencies which seem to be real.
As was discussed in Sect. 2 seven comets from the sample
(C/1959 Y1, C/1990 K1, C/1995 Y1, C/1998 P1, C/1986 P1A,
C/1996 E1, and C/1993 A1) seem to be dynamically new. For three of
them the decrease of rms is visible when the f(r)-law
rather than the g(r)-law is used. For Comet C/1998 P1 Williams
the rms drops from 1
![]() 10 to 1
10 to 1
![]() 02, for
C/1993 A1 Mueller - from 1
02, for
C/1993 A1 Mueller - from 1
![]() 14 to 1
14 to 1
![]() 11, and for
C/1990 K1 Levy - from 1
11, and for
C/1990 K1 Levy - from 1
![]() 21 to 1
21 to 1
![]() 19. For the remaining
12 comets only Comet C/1996 B2 Hyakutake exhibits a similar
decrease of rms from 1
19. For the remaining
12 comets only Comet C/1996 B2 Hyakutake exhibits a similar
decrease of rms from 1
![]() 08 (g(r)-law) to 1
08 (g(r)-law) to 1
![]() 05
(f(r)-law). In the case of these three dynamically young comets
the
05
(f(r)-law). In the case of these three dynamically young comets
the
![]() (r)-law or g(r)-like law with
(r)-law or g(r)-like law with
![]() AU give the same rms as f(r), which further
confuses the issue. However, the extremely large values of
AU give the same rms as f(r), which further
confuses the issue. However, the extremely large values of
![]() for C/1998 P1 Williams and C/1993 A1 Mueller are
unrealistic in terms of the water sublimation (Whipple 1978;
Yabushita 1991). This supports the idea that more volatile
molecules than water play an important role in the orbital
departure from the gravitational path for these two comets.
Furthermore, the detailed investigations of C/1995 O1 Hale-Bopp
and C/1996 B2 Hyakutake show that the g(r)-like forms derived
from the photometric data are very different. This could suggest a
large variety of NG behaviours in the population of the
long-period comets.
for C/1998 P1 Williams and C/1993 A1 Mueller are
unrealistic in terms of the water sublimation (Whipple 1978;
Yabushita 1991). This supports the idea that more volatile
molecules than water play an important role in the orbital
departure from the gravitational path for these two comets.
Furthermore, the detailed investigations of C/1995 O1 Hale-Bopp
and C/1996 B2 Hyakutake show that the g(r)-like forms derived
from the photometric data are very different. This could suggest a
large variety of NG behaviours in the population of the
long-period comets.
The second interesting result is connected with the scale distance
![]() .
Marsden et al. (1973) showed that the value of the
scale distance
.
Marsden et al. (1973) showed that the value of the
scale distance
![]() related to the Bond albedo,
related to the Bond albedo,
![]() ,
and infrared albedo
,
and infrared albedo
![]() ,
is equal to the
standard
,
is equal to the
standard
![]() AU whenever
AU whenever
![]() .
Moreover, the
.
Moreover, the
![]() differs significantly from
2.8 AU, while exponents n, m and k vary only slightly with
the albedos. To investigate this question, I have tested the
family of g(r)-like functions with the same standard values of
exponents n, m and k and different values of
differs significantly from
2.8 AU, while exponents n, m and k vary only slightly with
the albedos. To investigate this question, I have tested the
family of g(r)-like functions with the same standard values of
exponents n, m and k and different values of
![]() :
1.5 AU (
:
1.5 AU (
![]() ), 2.0 AU (
), 2.0 AU (
![]() ), 4 AU (
), 4 AU (
![]() ), 6 AU (
), 6 AU (
![]() ), 8 AU (
), 8 AU (
![]() ). In two cases where the standard g(r) fitted to
observations gave
). In two cases where the standard g(r) fitted to
observations gave
![]() ,
variation of
,
variation of
![]() allowed us to obtain reasonable values of the
NG parameters: for C/1991 T2 with
allowed us to obtain reasonable values of the
NG parameters: for C/1991 T2 with
![]() AU and for
C/1995 Y1 with
AU and for
C/1995 Y1 with
![]() AU (Table 2). For the next
seven comets the better fit to the positional observations is
derived for other values of
AU (Table 2). For the next
seven comets the better fit to the positional observations is
derived for other values of
![]() than the standard
than the standard
![]() AU. For three of those comets (C/1999 H1,
C/1995 O1 Hale-Bopp and C/1999 J3) the smallest rms was
obtained for
AU. For three of those comets (C/1999 H1,
C/1995 O1 Hale-Bopp and C/1999 J3) the smallest rms was
obtained for
![]() AU, for the remaining four
(C/1996 B2, C/1990 K1, C/1998 P1, C/1993 A1) the best fit was
found for the large value of
AU, for the remaining four
(C/1996 B2, C/1990 K1, C/1998 P1, C/1993 A1) the best fit was
found for the large value of
![]() AU. However, as
was discussed above, for three objects from the last group
(C/1990 K1, C/1998 P1, C/1993 A1) the f(r)-function also give a
smaller rms than the standard g(r)-form.
AU. However, as
was discussed above, for three objects from the last group
(C/1990 K1, C/1998 P1, C/1993 A1) the f(r)-function also give a
smaller rms than the standard g(r)-form.
Present investigations show that astrometric observations alone are not sensitive enough to judge which form of h(r) is appropriate in the analysis of the NG effects for individual long-period comets. Therefore, photometric observations are needed to solve this problem. The NG motion of two well-known comets, C/1995 O1 Hale-Bopp and C/1996 B2 Hyakutake, were recently modelled by Szutowicz et al. (2002a,b). They fitted the observed water sublimation rates and the observed light curve collected from the literature to the general g(r)-like form of the water sublimation rate. Since such analysis requires long series of spectroscopic (and/or photometric) observations it could be applied only to a few long-period comets. The g(r)-like functions obtained this way were then applied to determine the NG parameters. It appeared that in the case of comets Hale-Bopp and Hyakutake the coefficients in the g(r)-like law differ significantly (Fig. 1) from theirs canonical values derived by Marsden et al. (1973) (compare Table 3 and Eq. (2)). Similar investigations for the next three long-period comets are in progress.
We also intend to analyze the dynamical evolution of the long-period comets with respect to their NG effects. Some elements of these investigations limited only to NG dynamical evolution described by the g(r)-law are presented by Szutowicz et al. (2002a) and Królikowska (2002).
Acknowledgements
The author thanks Professors Grzegorz Sitarski and Andrzej M. Sotan and Dr. S
awomira Szutowicz for valuable discussions. This work was supported by the Polish Commitee for Scientific Research (the KBN grant 2.P03D.002.09).
Table 1: General characteristics of the observational material. The succesive columns signify: comet designation and name (Col. 1) perihelion time, T, and perihelion distance, q(2), observational arc and number of all observations (3), rms for the pure gravitational orbital fitting to pre-periherlion (4), post-perihelion (5) and all (6) observations, rms for the NG orbital fitting to all observations (7), original (8) and future (9) reciprocals of semimajor axes in units of 10-6 AU-1.
Table 2:
NG parameters derived from positional observations for
assumed function h(r) (Eq. (5)) represented by: standard function
g(r), g*(r) - modified function g(r),
![]() (r)
- Sekanina's function, f(r) - Yabushita's function describing
CO sublimation, respectively. NG parameters
(r)
- Sekanina's function, f(r) - Yabushita's function describing
CO sublimation, respectively. NG parameters
![]() are given in units of
10-8 AU day-2; these parameters are the standard
are given in units of
10-8 AU day-2; these parameters are the standard
![]() and
and
![]() for the NG models
including the standard g(r);
for the NG models
including the standard g(r); ![]() is given in days. First line
for each individual comet shows the NG parameters
is given in days. First line
for each individual comet shows the NG parameters
![]() and
and
![]() taken from MW Catalogue or Minor Planet Circulars (if
there are). The g*(r) functions for C/1995 O1 Hale-Bopp
(
taken from MW Catalogue or Minor Planet Circulars (if
there are). The g*(r) functions for C/1995 O1 Hale-Bopp
(
![]() (r)) and C/1996 B2 Hyakutake
(
(r)) and C/1996 B2 Hyakutake
(
![]() (r)) are described in Table 3. For comet
C/1959 Y1 Burnham the models with displacement, D, of
photometric centre from the gravitational one are also presented;
the values of this displacement (in paranthesis) are given in
units of 10-5 AU. Models with subscript R indicate
solutions based on 37 observations of Comet Burnham made by Roemer
et al. (1966).
(r)) are described in Table 3. For comet
C/1959 Y1 Burnham the models with displacement, D, of
photometric centre from the gravitational one are also presented;
the values of this displacement (in paranthesis) are given in
units of 10-5 AU. Models with subscript R indicate
solutions based on 37 observations of Comet Burnham made by Roemer
et al. (1966).
Table 4:
Forced precession model for assumed function h(r)
represented by: standard function g(r), f(r), g*(r) -
modified function g(r), respectively. NG parameters
![]() are given in units of
10-8 AU day-2, and precession factor
are given in units of
10-8 AU day-2, and precession factor ![]() - in
units of 106 day AU-1. Subscript "0'' in
- in
units of 106 day AU-1. Subscript "0'' in
![]() and
and
![]() denotes the values on the starting
epoch of integration given in the Col. 1. The g*(r)
functions for C/1995 O1 Hale-Bopp (
denotes the values on the starting
epoch of integration given in the Col. 1. The g*(r)
functions for C/1995 O1 Hale-Bopp (
![]() (r)) and
C/1996 B2 Hyakutake (
(r)) and
C/1996 B2 Hyakutake (
![]() (r)) are described in
Table 3; subscripts (a) and (b) denote
solutions taken from Szutowicz et al. (2002a,b). In the case
of comet Hyakutake models with subscript (a)additionally include the observed comet fragmentation on 1996
March 21.
(r)) are described in
Table 3; subscripts (a) and (b) denote
solutions taken from Szutowicz et al. (2002a,b). In the case
of comet Hyakutake models with subscript (a)additionally include the observed comet fragmentation on 1996
March 21.
Table 6:
Comparison between two kinds of NG models for four
short-period comets. NG parameters were derived from 8 of 12
detected apparitions for Comet 31P/Schwassmann-Wachmann 2, 8 of 9
detected apparitions for Comet 46P/Wirtanen (the last one were
excluded), 15 of 19 apparitions for Comet 26P/Grigg-Skjellerup and
all available observations (5 apparitions span over 9 perihelion
passages) in the case of Comet 88P/Howell. Standard NG parameters
![]() and parameter A (forced
precession model) are given in units of
10-8 AU day-2. The precession factor
and parameter A (forced
precession model) are given in units of
10-8 AU day-2. The precession factor ![]() is
in units of 107 day/AU, Subscript "0'' in
is
in units of 107 day/AU, Subscript "0'' in
![]() and
and
![]() denotes the values for the starting epoch of
integration (Epoch: 2003 12 27). For two comets (31P and 46P) the
assumption about the asymmetry of function g(r) was necessary, and
the time shifts
denotes the values for the starting epoch of
integration (Epoch: 2003 12 27). For two comets (31P and 46P) the
assumption about the asymmetry of function g(r) was necessary, and
the time shifts ![]() (in days) were derived. The forced
precession model of 26P was taken from Sitarski (2003).
(in days) were derived. The forced
precession model of 26P was taken from Sitarski (2003).