D. Reese - F. Rincon - M. Rieutord
Laboratoire d'Astrophysique de Toulouse et Tarbes, Observatoire Midi-Pyrénées, 14 avenue É. Belin, 31400 Toulouse, France
Received 29 March 2004 / Accepted 16 July 2004
Abstract
We carry out numerical and mathematical investigations of shear
Alfvén waves inside of a spherical shell filled with an incompressible
conducting fluid, and bathed in a strong dipolar magnetic field. We focus on
axisymmetric toroidal and non-axisymmetric modes, in continuation of a previous
work by Rincon & Rieutord (2003, A&A, 398, 663). Analytical expressions are obtained for
toroidal eigenmodes and their corresponding frequencies at low diffusivities.
These oscillations behave like magnetic shear layers, in which the magnetic
poles play a key role, and hence become singular when diffusivities vanish.
It is also demonstrated that non-axisymmetric modes are split into two
categories, namely poloidal or toroidal types, following similar asymptotic
behaviours as their axisymmetric counterparts when the diffusivities become
arbitrarily small.
Key words: magnetohydrodynamics (MHD) - stars: oscillations - stars: magnetic fields
Numerous astrophysical systems exhibit a pulsating behaviour that can be significantly influenced by the Lorentz force when a strong magnetic field is present. This may for instance be the case in neutron stars and magnetic white dwarfs (Lou 1995). Planetary cores, which are known to sustain a strong dynamo (Stevenson 1983), are also likely to fall into this category.
One of the most exciting examples of couplings between pulsation and
magnetism is given by the seismological activity of roAp stars. This class
of stars, discovered by Kurtz (1978), exhibits several kG (almost)
dipolar magnetic fields and luminosity variations on periods ranging
from 5 to 15 min. These oscillations seem to be well approximated by
a single spherical harmonic ![]() lined up with the magnetic axis,
suggesting a strong mixing between high order p-modes and Alfvénic
type oscillations.
lined up with the magnetic axis,
suggesting a strong mixing between high order p-modes and Alfvénic
type oscillations.
Many different models have been developed to obtain a satisfying picture
of the asteroseismology of these stars. Following theoretical
work by Roberts & Soward (1983); Biront et al. (1982) and Campbell & Papaloizou (1986), Dziembowski & Goode (1996)
have studied acoustic star models enveloped by a layer in which magnetic
effects become dominant. Using a boundary layer approximation, they
came up with an outer boundary condition which was then applied for the
calculation of adiabatic acoustic modes. This model has undergone a lot
of refinements in order to take into account new physical processes. The
latest version, proposed by Bigot & Dziembowski (2002), incorporates
the centrifugal force (a non-axisymmetric effect, since the rotational
and magnetic axis are often tilted in roAp stars) and suggests that
the axis of the modes is not necessarily lined up with the magnetic
axis. In spite of these improvements, there
are still non-negligible discrepancies between the magnetically shifted
eigenfrequencies computed from these models and the observed ones, showing
that the precise coupling mechanism occurring in the surface layers is
likely to be more complex. An important point is that a single ![]() value is
sometimes assumed to be sufficient to describe the oscillations. This
may not be the case, owing to the dipolar structure of the permanent
magnetic field which induces a coupling between spherical harmonics thus
producing a whole spectrum of
value is
sometimes assumed to be sufficient to describe the oscillations. This
may not be the case, owing to the dipolar structure of the permanent
magnetic field which induces a coupling between spherical harmonics thus
producing a whole spectrum of ![]() 's (e.g. Rincon & Rieutord 2003).
's (e.g. Rincon & Rieutord 2003).
Motivated by the observation that chemical peculiarities are observed near the
magnetic poles of roAp stars, Balmforth et al. (2001) have tried to determine what
precise physical phenomena were occurring in the polar and equatorial regions.
Since the magnetic field is almost horizontal near the equator and vertical
near the poles, convection is certainly inhibited in the latter region,
allowing the diffusion of different chemical elements (an excess of helium is
observed on the polar caps). Oscillations triggered by a ![]() -mechanism may
therefore preferentially be observed in this region. This approach stresses the
importance of a global description of the eigenmodes in such stars.
-mechanism may
therefore preferentially be observed in this region. This approach stresses the
importance of a global description of the eigenmodes in such stars.
The work presented here originates partly from the preceding remarks. It continues the study described in Rincon & Rieutord 2003 (hereafter referred to as Paper I) and should be viewed as a preliminary step to obtain global models of the more complex magneto-gravito-acoustic oscillations. We aim at understanding some of the underlying physical mechanisms potentially involved in roAp stars or similar astrophysical objects, by using an approach that rigorously treats the couplings induced by the geometry of the magnetic field. Our highly simplified model consists of a non-rotating spherical shell of incompressible magnetised fluid bathed in a dipolar magnetic field, with small magnetic and kinematic diffusivities. As a consequence of incompressibility, the modes we compute are shear Alfvén waves. In Paper I, a spherical harmonic decomposition of the linearised MHD equations was obtained and results regarding poloidal axisymmetric modes were presented (a short reminder of the classification of modes is given later on in the paper). It was shown that the least-damped modes are near the magnetic poles and exhibit internal shear layers which can potentially play a role in mode selection. In the present study, we focus on the other types of shear Alfvénic oscillations in spherical shells, namely axisymmetric toroidal and non-axisymmetric modes, and characterise numerically and mathematically their geometry, eigenspectrum, and some by-products like boundary layers.
In Sect. 2, we recall the basic physical ingredients of the model and shortly describe our numerical strategy. Section 3 is devoted to the phenomenological description and analytical study of axisymmetric toroidal modes. Section 4 covers non-axisymmetric modes and their resemblance to their axisymmetric counterparts. Finally, Sects. 5 and 6 conclude the paper. Note that most of the mathematical details involved in Sect. 3 are given in Appendices A and B to preserve the clarity of the manuscript.
We first give a brief description of the model that is used in calculating toroidal and non-axisymmetric modes and which was already used in Paper I. More details on the basic equations and their expansion onto the spherical harmonic base are given in Paper I.
The "star'' we work with is a spherical shell of incompressible plasma
of density ![]() ,
with a radius R and an aspect ratio
,
with a radius R and an aspect ratio ![]() .
In all
the numerical examples and figures, we use
.
In all
the numerical examples and figures, we use
![]()
![]() . Within this shell is a dipolar magnetic
field generated in a perfectly conducting core:
. Within this shell is a dipolar magnetic
field generated in a perfectly conducting core:
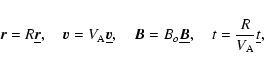
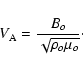 |
(2) |
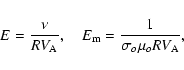 |
(4) |
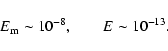
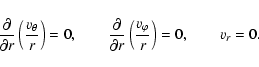 |
(5) |
Equation (3), together with these boundary conditions, defines a
generalised eigenvalue problem, where ![]() is the eigenvalue and
is the eigenvalue and
![]() is the eigenvector which can be computed numerically.
is the eigenvector which can be computed numerically.
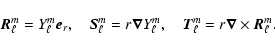
The various eigenmodes fit naturally into different categories. Firstly, as was
already shown in Paper I, there is no coupling between different m's. Hence,
eigenmodes will be made up of only one m. This leads to two types of modes:
axisymmetric oscillations (m=0) and non-axisymmetric ones
![]() .
Secondly, within the axisymmetric category, it is possible to distinguish
between poloidal modes and toroidal ones, as the corresponding equations
fully decouple for m=0 (see Appendix A of Paper I). Poloidal modes are made up
of
.
Secondly, within the axisymmetric category, it is possible to distinguish
between poloidal modes and toroidal ones, as the corresponding equations
fully decouple for m=0 (see Appendix A of Paper I). Poloidal modes are made up
of
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() functions which correspond to
functions which correspond to ![]() and
and
![]() components. Toroidal modes are made up of
components. Toroidal modes are made up of
![]() and
and
![]() functions and are in the
functions and are in the
![]() direction.
direction.
A certain number of symmetries are present in the physical system and lead to a
few simplifications. As was pointed out in Paper I, a parity can be defined
for eigenmodes. However, there was a slight confusion as to the parity of
toroidal components (see Eq. (19) of Paper I) since a mode is called even when
the velocity perturbation is symmetric with respect to the equator and the
magnetic perturbation antisymmetric, and a mode is odd in the reverse
situation. The corrected form for toroidal eigenvectors reads:
| (9) |
| (10) |
If rotation were taken into account, a number of these symmetries would
break down. Apart from the situation where the rotation and magnetic axis are
aligned, different m's become coupled and mode parity is lost.
The symmetry with respect to
![]() is lost even when the rotation axis is lined
up with the magnetic field.
is lost even when the rotation axis is lined
up with the magnetic field.
Eigenmodes and eigenvalues are calculated numerically using two different methods. The first method, based on a QZ algorithm, gives all the eigenvalues (for the discretised problem) whereas the second method is an iterative Arnoldi-Chebyshev algorithm which only computes a selection of eigenvalues and their corresponding eigenmodes.
In our numerical calculations, we use a simplified version of
Eq. (7). Since different m's are
decoupled, we do not have a summation over the azimuthal order. Also,
because the divergence of both perturbations is zero, the functions
![]() and
and
![]() can be expressed in terms of
can be expressed in terms of
![]() and
and
![]() ,
respectively
(see Appendix A of Paper I). Furthermore, in the case of axisymmetric
modes, the summation on
,
respectively
(see Appendix A of Paper I). Furthermore, in the case of axisymmetric
modes, the summation on ![]() will actually start at 1 instead of 0as a result of our boundary conditions. In the non-axisymmetric case,
the summation on
will actually start at 1 instead of 0as a result of our boundary conditions. In the non-axisymmetric case,
the summation on ![]() will start at |m| as expected. Finally, the
sum on the spherical harmonics is truncated at L. This leads to the
following formulas:
will start at |m| as expected. Finally, the
sum on the spherical harmonics is truncated at L. This leads to the
following formulas:
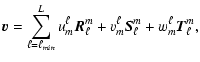 |
|||
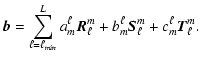 |
(11) |
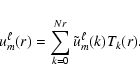
We also define Chebyshev and harmonic spectral coefficients:
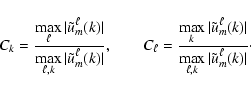
The equations that govern toroidal modes can be simplified. It is no longer
necessary to take the curl of the Navier-Stokes equation to remove the
pressure term, because this term vanishes owing to axisymmetry.
This leads to the following, nearly symmetric system:
In many ways, the eigenvalue spectrum of toroidal modes is similar to that of
the poloidal modes presented in Paper I. The complex eigenvalues are grouped
into "horizontal'' branches, as can be seen in Fig. 1.
These "eigenbranches'', indexed by n, correspond to modes with n nodes in
the radial direction (see Fig. 2). Both
perturbations have n nodes, but in different positions. Depending on
parity, diffusion modes
![]() also appear but these
modes are of little interest to asteroseismology. In all that
follows, we will only consider oscillatory modes.
also appear but these
modes are of little interest to asteroseismology. In all that
follows, we will only consider oscillatory modes.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0539f1.eps}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg104.gif) |
Figure 1:
Eigenvalue spectrum for odd modes and
|
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{c@{\hspace{2cm}}c}
\includegraphics[width=7cm...
...2c.eps} &
\includegraphics[width=7cm,clip]{0539f2d.eps}\end{tabular}\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg105.gif) |
Figure 2:
Axisymmetric toroidal modes with different vertical structures, for
|
| Open with DEXTER | |
A careful look at the eigenvalues along a single branch reveals a regular
structure. These values are remarkably well lined up, much better than their
poloidal counterparts, and they are equally spaced out. This suggests the
following empirical law:
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=7cm]{0539f3a.eps}\\...
...b.eps}\\ [5mm]
\includegraphics[width=7cm]{0539f3c.eps}\end{tabular}\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg111.gif) |
Figure 3: Different modes from the n=3 eigenbranch. From top to bottom, qtakes on the values 1, 3 and 9. |
| Open with DEXTER | |
We can then look at the corresponding eigenmodes. When q increases, two phenomena appear. First of all, for the least-damped modes, the number of nodes in the horizontal direction seems to increase. However, these nodes are not all conspicuous. Secondly, modes that have a higher damping rate gradually depart from the magnetic poles. Figure 3 illustrates both of these phenomena. Care must be taken with highly damped modes: the spectral coefficients indicate that the solutions are convergent, but the corresponding eigenvalues are highly unstable numerically due to round-off errors. This limits the number of modes that can be analysed safely.
The structure of the modes can be understood if one computes
the resonance frequencies of different field lines for
the ideal case
![]() .
As each field line can oscillate at its own
frequency, the resonance frequencies form a continuous spectrum
called the Alfvén continuum. (For our configuration, there will be a continuum
for each value of n.) These eigenvalues are purely imaginary because the
ideal MHD operator which gives the squared eigenvalues
.
As each field line can oscillate at its own
frequency, the resonance frequencies form a continuous spectrum
called the Alfvén continuum. (For our configuration, there will be a continuum
for each value of n.) These eigenvalues are purely imaginary because the
ideal MHD operator which gives the squared eigenvalues ![]() is
self-adjoint.
is
self-adjoint.
For a first approximation of these frequencies, we can apply the same formula
as was used by Alfvén (1945), which is derived from the time it takes for a
wave traveling along a field line to go from one boundary to the other. This
corresponds to a WKB-type approximation, in which the curvature terms have been
neglected:
Taking the variations of ![]() into account, in order to obtain better
results, yields the following equations, which still only apply to individual
field lines:
into account, in order to obtain better
results, yields the following equations, which still only apply to individual
field lines:
| |
Figure 4:
The kinetic energy and dissipation of eigenmode
(n,q) = (1,8) with
resonant field lines superimposed. The diffusivities are
|
| Open with DEXTER | |
We will now give a precise calculation (in the adiabatic case
![]() )
of the resonance frequencies corresponding to the field line
along the magnetic axis. This analysis is motivated by the role of
resonating polar field lines in the asymptotic limit of small diffusivities.
The adiabatic eigenfrequencies will be denoted by the superscript "0''.
)
of the resonance frequencies corresponding to the field line
along the magnetic axis. This analysis is motivated by the role of
resonating polar field lines in the asymptotic limit of small diffusivities.
The adiabatic eigenfrequencies will be denoted by the superscript "0''.
These frequencies are solutions of Eq. (16) with
![]() .
By combining the two first equations and solving for v, we obtain:
.
By combining the two first equations and solving for v, we obtain:
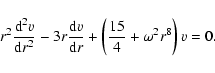 |
(17) |
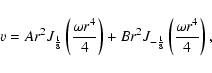 |
(18) |
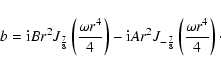 |
(19) |
In order to show the physical meaning of these eigenvalues, we took
an eigenspectrum and prolongated the lines formed by the eigenbranches
(see Fig. 1). The intersections between the lines
and the imaginary axis
![]() correspond to what could be
called "numerical polar eigenfrequencies''. The agreement between
these values and
correspond to what could be
called "numerical polar eigenfrequencies''. The agreement between
these values and
![]() is rather good, as can be seen in
Table 1. This leads to the conclusion that
the polar eigenfrequencies are a good indicator of the eigenbranches'
positions.
is rather good, as can be seen in
Table 1. This leads to the conclusion that
the polar eigenfrequencies are a good indicator of the eigenbranches'
positions.
Table 1:
A comparison between numerical polar eigenfrequencies (Num.),
adiabatic ones (
![]() )
and a WKB approximation. The numerical
values were obtained using a least square method on the eigenvalues
corresponding to
)
and a WKB approximation. The numerical
values were obtained using a least square method on the eigenvalues
corresponding to
![]() and correspond to the intersection between
the eigenbranches and the imaginary axis.
and correspond to the intersection between
the eigenbranches and the imaginary axis.
The next step is to look at the behaviour of eigenmodes and eigenvalues when
the diffusivities E and
![]() approach zero. There are two important reasons
for this. First of all, realistic astrophysical values of E and
approach zero. There are two important reasons
for this. First of all, realistic astrophysical values of E and
![]() are
very small (
are
very small (![]() 10-8) and still out of reach for numerical
solvers. Being able to extrapolate the behaviour of eigenmodes gives an
educated guess as to what they would actually be for low diffusivities. A
second reason is that it may be possible this way to refine analytically the
adiabatic eigenvalues
10-8) and still out of reach for numerical
solvers. Being able to extrapolate the behaviour of eigenmodes gives an
educated guess as to what they would actually be for low diffusivities. A
second reason is that it may be possible this way to refine analytically the
adiabatic eigenvalues
![]() defined by Eq. (20)
to obtain a better approximation of the true eigenvalues.
defined by Eq. (20)
to obtain a better approximation of the true eigenvalues.
We therefore analysed the behaviour of the mode n=1, q=0 for different
values of the diffusivities. Figures 5 and 6 show how its eigenvalue, its position and its
"thickness'' vary. In order to calculate the mode's position and thickness,
we took a profile of the magnetic energy
![]() along a meridional
cut with a fixed radius
along a meridional
cut with a fixed radius![]() of 0.5 and a horizontal extent going from
of 0.5 and a horizontal extent going from
![]() to
to
![]() .
From this profile, we calculated a mean value
.
From this profile, we calculated a mean value
![]() and a standard deviation
and a standard deviation
![]() .
These
correspond to estimates of the mode's position and thickness, respectively.
.
These
correspond to estimates of the mode's position and thickness, respectively.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0539f5.eps}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg146.gif) |
Figure 5:
Behaviour of eigenvalue
(n,q)=(1,0) for different values of E and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0539f6.eps}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg147.gif) |
Figure 6:
Behaviour of an eigenmode for different values of E and
|
| Open with DEXTER | |
From these graphs it is possible to deduce some of the physical phenomena that
are taking place. In the case where
![]() ,
we observe that the eigenvalue
approaches the n=1 polar eigenfrequency given by
Eq. (20). At the same time, the mode seems to get
thinner and closer to the magnetic poles. We observe from
Figs. 5 and 6 that:
,
we observe that the eigenvalue
approaches the n=1 polar eigenfrequency given by
Eq. (20). At the same time, the mode seems to get
thinner and closer to the magnetic poles. We observe from
Figs. 5 and 6 that:
By identifying Eqs. (13) with (22), we find that:
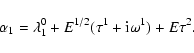 |
(23) |
| (27) |
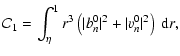 |
|||
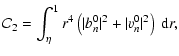 |
|||
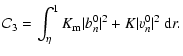 |
(29) |
![\begin{figure}
\par\begin{tabular}{c@{\hspace*{1cm}}c}
\includegraphics[width=8....
...39f7c.eps} &
\includegraphics[width=8.2cm]{0539f7d.eps}\end{tabular}\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg183.gif) |
Figure 7:
Comparison between different numerical profiles of the magnetic field
and theoretical ones. These profiles are calculated along a meridional cut at
a radius
|
| Open with DEXTER | |
A general solution f of Eq. (30) can be expressed via a
linear combination of the following functions:
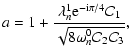 |
(31) |
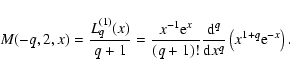 |
(32) |
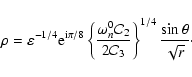 |
(35) |
Table 2:
Comparison between numerical and theoretical first order
eigenvalues (
![]() ). The two sets of numerical values
(Cols. 2 and 3) are based on the numerical eigenspectrum given in
Fig. 1 and are calculated using a least square method.
These values should be very close to each other. The last column is based
on Eq. (33).
). The two sets of numerical values
(Cols. 2 and 3) are based on the numerical eigenspectrum given in
Fig. 1 and are calculated using a least square method.
These values should be very close to each other. The last column is based
on Eq. (33).
To complete our study of axisymmetric toroidal eigenmodes, we also
present some results regarding the existence of boundary layers.
In our case, we expected the presence of Hartmann layers, which are very
thin. Typically their non-dimensional thickness is given by
![]() in which Br is non dimensional (e.g. Pothérat et al. 2002).
This can be penalising for numerical calculations as a high resolution
is needed to properly resolve them.
in which Br is non dimensional (e.g. Pothérat et al. 2002).
This can be penalising for numerical calculations as a high resolution
is needed to properly resolve them.
Two different methods were used to study boundary layers. The first
approach consists in coming up with a highly simplified analytical model.
In this model, developed in Appendix B for clarity reasons,
the permanent magnetic field is constant and vertical, and the fluid
domain is enclosed between two parallel planes. This model leads to the
conclusion that there should be a Hartmann layer on the lower boundary
and nothing on the upper plane. This Hartmann layer only produces
a finite discontinuity of the normal gradient of both perturbations
when the diffusivities vanish (see Eq. (B.3)). The model
also justifies a posteriori the effective boundary conditions
![]() and b(1)=0 (see Eq. (B.9))
which were used in the calculation of polar eigenvalues (see
Sect. 3.4).
and b(1)=0 (see Eq. (B.9))
which were used in the calculation of polar eigenvalues (see
Sect. 3.4).
The second approach is numerical. By looking at the Chebyshev spectral coefficients, we can see the signature of Hartmann layers. Assuming the layer is described by an exponential variation as proposed by Pothérat et al. (2002), it is possible to come up with a corresponding theoretical prediction, which can then be compared with the actual Chebyshev spectral coefficients of the eigenmodes.
![\begin{figure}
\par\includegraphics[width=8cm]{0539f8.eps}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg202.gif) |
Figure 8:
Comparison between numerical
|
| Open with DEXTER | |
Figure 8 shows such a
comparison. The values used for Br are those at the magnetic poles, because
of the mode's localization. In other words, the theoretical inner boundary has
a thickness of
![]() and the outer one a thickness of
and the outer one a thickness of
![]() (see Eq. (1)). The theoretical boundary layers are
multiplied by a constant so as to match the numerical ones. From this figure,
we clearly deduce the presence of two boundary layers, one on the inside and
one on the outside, unlike what was predicted by the analytical model. This is
so probably because in the simplified model, the two outer boundary conditions
become redundant when E and
(see Eq. (1)). The theoretical boundary layers are
multiplied by a constant so as to match the numerical ones. From this figure,
we clearly deduce the presence of two boundary layers, one on the inside and
one on the outside, unlike what was predicted by the analytical model. This is
so probably because in the simplified model, the two outer boundary conditions
become redundant when E and
![]() approach zero, whereas they do not in the
spherical setup.
approach zero, whereas they do not in the
spherical setup.
For larger diffusivities, the agreement between the numerical and theoretical results is not as good. This is not too surprising as the eigenmodes are in general further from the poles. At smaller diffusivities, the radial resolution rapidly becomes insufficient for good comparisons. The theoretical spectral coefficients for the inner boundary diminish very little for the first several hundred Chebyshev components.
A final comment can be made about the numerical approach. By looking at the
relative amplitude of the layer on the boundary, it is possible to determine
what type of discontinuity it produces when both diffusivities approach zero.
In our case, the amplitudes for both the inner and outer layers, obtained by
comparing the numerical and theoretical spectral coefficients, were
proportional to E in the case where
![]() ,
which suggests that there will
be a discontinuity on the gradient of the perturbations when both diffusivities
approach zero. This is the same behaviour as the single boundary layer in the
analytical model.
,
which suggests that there will
be a discontinuity on the gradient of the perturbations when both diffusivities
approach zero. This is the same behaviour as the single boundary layer in the
analytical model.
As was the case for poloidal and toroidal eigenspectra, non-axisymmetric
eigenvalues are located along "horizontal'' branches. However, where there
used to be one branch in the poloidal or toroidal case, there are now two
branches next to each other for each ![]() (see
Fig. 9). This is perhaps not surprising as non-axisymmetric
modes contain poloidal and toroidal components at the same time.
(see
Fig. 9). This is perhaps not surprising as non-axisymmetric
modes contain poloidal and toroidal components at the same time.
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=7.4cm]{0539f9a.eps}...
...}\\ [0.5cm]
\includegraphics[width=7.4cm]{0539f9c.eps}\end{tabular}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg208.gif) |
Figure 9:
Several non-axisymmetric eigenvalue spectra. The diffusivities Eand
|
| Open with DEXTER | |
As diffusivities become small, the two branches start to differ. When compared with poloidal or toroidal branches, it becomes immediately obvious that a first group of eigenvalues resembles the toroidal branch and a second group matches its poloidal counterpart (see Fig. 10).
![\begin{figure}
\par\includegraphics[width=8.3cm]{0539f10.eps}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg209.gif) |
Figure 10:
Comparison between axisymmetric poloidal, axisymmetric toroidal and
non-axisymmetric (m=1) eigenvalues. The diffusivities E and
|
| Open with DEXTER | |
It is then interesting to look at the structure of the corresponding modes. Not surprisingly, modes along the lower branch have a very similar appearance to that of poloidal modes. The radial nodes are in the same positions and the horizontal nodes look the same. As for the modes on the upper branches, it appears that the least-damped ones are poloidal-like, and the most damped toroidal-like. Figure 11 shows a comparison between axisymmetric poloidal and toroidal modes and non-axisymmetric modes with similar appearances. Figure 12 shows the transition from poloidal properties to toroidal ones, when looking at successive modes on the upper branch.
![\begin{figure}
\par\begin{tabular}{c@{\hspace*{2cm}}c}
Poloidal modes & Toroidal...
...eps} &
\includegraphics[width=7.1cm,clip]{0539f11d.eps}\end{tabular}\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg210.gif) |
Figure 11: Comparison between axisymmetric poloidal and toroidal modes and non-axisymmetric modes with similar properties. The axisymmetric modes are above, and the "corresponding'' non-axisymmetric ones below. |
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{c@{\hspace*{2cm}}c}
\includegraphics[width=7....
...539f12d.eps}\\ [4.8mm]
\Large c &\Large d
\end{tabular}\normalsize
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg211.gif) |
Figure 12:
Transition from poloidal to toroidal characteristics in
non-axisymmetric modes. The diffusivities are
|
| Open with DEXTER | |
One way to characterise whether a mode is more poloidal or toroidal is
to calculate the following ratio:
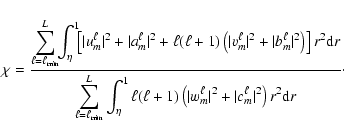 |
(37) |
We can take a more detailed look at the behaviour of an entire pair of branches
for different values of E and
![]() (keeping
(keeping
![]() ), to see whether the
eigenvalues have poloidal or toroidal characteristics. Non-axisymmetric
"poloidal'' eigenvalues appear to obey the following empirical law:
), to see whether the
eigenvalues have poloidal or toroidal characteristics. Non-axisymmetric
"poloidal'' eigenvalues appear to obey the following empirical law:
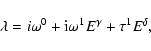 |
(38) |
Non-axisymmetric "toroidal'' eigenvalues behave roughly like their
axisymmetric counterparts. All the values on a single branch seem to converge
toward one frequency, the corresponding polar eigenvalue (see
Eq. (20)). This value is used in
Fig. 13 as the asymptotic frequency of the toroidal modes.
The rate at which eigenvalues converge is about the same as in the
axisymmetric case, namely
![]() .
.
It is also interesting to note that the shape of the toroidal eigenbranch remains more or less the same in the axisymmetric and non-axisymmetric cases (see Fig. 14, bottom). This indicates that the quantization of these modes in the horizontal direction is very similar to the one of the axisymmetric modes. However, the spacing between each mode is not the same (see Fig. 10).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0539f13.eps}
\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg220.gif) |
Figure 13:
Behaviour of |
| Open with DEXTER | |
Table 3: Energy ratios as defined in Eq. (36) for modes shown in Figs. 10 and 12.
![\begin{figure}
\par\includegraphics[width=7.5cm]{0539f14a.eps}\\ [5mm]
\includegraphics[width=7.5cm]{0539f14b.eps}\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg221.gif) |
Figure 14:
Behaviour of non-axisymmetric eigenbranches for different values
of the diffusivities. E(=
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{0539f15.eps}\end{figure}](/articles/aa/full/2004/43/aa0539-04/Timg222.gif) |
Figure 15: Behaviour of non-axisymmetric modes for different values of the diffusivities. The "poloidal'' modes seem to converge toward a non-singular structure. The "toroidal'' ones, on the other hand, do not stop shrinking. The behaviour of their mean position (not shown), however, is much more irregular. |
| Open with DEXTER | |
By looking at the behaviour of the structure of different modes, it is possible
to observe different characteristics (see Fig. 15).
Poloidal-like modes seem to converge toward a non-degenerate structure. In
other words, their widths (
![]() )
do not approach zero, nor do
their positions (
)
do not approach zero, nor do
their positions (
![]() ). Their nodes become more distinct at low
diffusivities.
). Their nodes become more distinct at low
diffusivities.
Toroidal-like modes, on the other hand, exhibit more complex behaviour as the
toroidal character appears only below some given diffusivity. We understand
this behaviour as the consequence of the E1/4-scale of toroidal modes. It
is only when
![]() that the toroidal character may appear but this
condition is not easy to satisfy with non-axisymmetric modes for which the
lowest diffusivities reached yet are
that the toroidal character may appear but this
condition is not easy to satisfy with non-axisymmetric modes for which the
lowest diffusivities reached yet are ![]() 10-5 because of memory storage
requirements.
10-5 because of memory storage
requirements.
The main result of this study is that there are two basic behaviours for shear Alfvén modes, both in the axisymmetric and the non-axisymmetric cases. The first one is the poloidal behaviour, for which modes remain regular as diffusivities approach zero, except for internal shear layers located on resonant field lines. The second one is the toroidal behaviour: these modes become singular as diffusivities approach zero and each branch appears to have only one eigenfrequency in the adiabatic limit.
The toroidal behaviour matches the description of the resistive Alfvén
spectrum given by Kerner et al. (1986) in the context of tokamak-like
configurations. The eigenvalues lie on well-defined curves in the complex
plane which join the endpoints of the ideal Alfvén continua, as is suggested by
Eq. (26). The slope of the eigenbranches is 45° and the
damping rates of the eigenmodes are proportional to
![]() ,
which is in
complete agreement with a quadratic variation of the permanent magnetic field
,
which is in
complete agreement with a quadratic variation of the permanent magnetic field
![]() -profile near the magnetic axis.
-profile near the magnetic axis.
Poloidal modes on the other hand, look like true eigenmodes of the ideal MHD operator with a finite number of resonances in the Alfvén continuum (resonating field lines, see Paper I). Such features are similar to those of "quasimodes" (see Goossens et al. 2002; Poedts & Kerner 1991) which combine a regular and singular behaviour; however, unlike quasimodes, the damping rate of our modes always seem to vanish in the ideal limit (e.g. Figs. 13 or 5 of Paper I).
Presently, we understand the origin of the difference between the toroidal
and poloidal behaviour as the presence or absence of a coupling between
magnetic field lines by total pressure. Indeed, neglecting diffusion
terms, magnetic and velocity perturbations verify:
In this paper we completed the study of shear Alfvén modes of a spherical shell started in Paper I. The global picture that emerges is that both non-axisymmetric and axisymmetric modes can be divided into two subclasses: the toroidal and poloidal ones. In the limit of small diffusivities, relevant for astrophysical objects, only poloidal modes survive since toroidal ones become singular as magnetic shear layers.
However, toroidal modes may play some important role in the excitation process,
especially if rotation is present. Indeed, it is well-known
(e.g. Rieutord 1991) that the Coriolis force induces a coupling between
toroidal and poloidal components, even in the axisymmetric case. This coupling
may not strongly influence the frequency of the modes (except for some
rotational splitting) but may represent a channel by which modes lose energy
through dissipative shear layers; in such a case this mechanism may decide
whether a mode is or is not excited by, say, a ![]() -mechanism.
-mechanism.
For astrophysical applications where the compressibility is an important aspect, pure Alfvén modes coexist with magneto-acoustic modes. The incorporation of these modes will undoubtedly lead to a much more complicated spectrum of eigenvalues as well as a whole new range of physical phenomena. In particular, we can expect new resonances, namely those coming from the interaction of eigenmodes and the slow acoustic, or cusp, continuum (see Sakurai et al. 1991). Taking into account compressibility will however not affect the splitting between pure poloidal and pure toroidal axisymmetric modes; because of the divergence-less nature of purely toroidal modes, we can expect that these modes will not be affected by compressibility and remain unchanged. All the complications will concentrate on the poloidal set of eigenmodes. In the case of non-axisymmetric modes where the poloidal and toroidal characters are mixed, we may expect that only modes with a strong poloidal shape will suffer important changes. However, the importance of these changes, which incorporate the resonances with the cusp continuum, as well as its influence on the shape of the spectrum, can hardly be anticipated and will be investigated in subsequent work.
Acknowledgements
The authors wish to thank the referee for valuable suggestions and comments, which helped to improve this article.
Some of the numerical calculations were carried out on the NEC SX5 of the "Institut du Développement et des Ressources en Informatique Scientifique'' (IDRIS), which is gratefully acknowledged.
We begin with the toroidal Eqs. (12), and express
them explicitly in "semi-dipolar'' coordinates
![]() .
The
coordinate
.
The
coordinate ![]() is equal to
is equal to
![]() ,
and remains constant
along field lines. Choosing
,
and remains constant
along field lines. Choosing ![]() as a coordinate instead of
as a coordinate instead of ![]() simplifies the expression of terms like
simplifies the expression of terms like
![]() .
We
obtain the following system:
.
We
obtain the following system:
![$\displaystyle \lambda b = \displaystyle \sqrt{1- r \nu^2}
\left[ \frac{1}{r^3} \frac{\partial v}{\partial r} - \frac{3v}{2 r^4} \right]
+ E_{{\rm m}}\Delta' b,$](/articles/aa/full/2004/43/aa0539-04/img238.gif) |
|||
![$\displaystyle \lambda v= \displaystyle \sqrt{1- r \nu^2}
\left[ \frac{1}{r^3} \frac{\partial b}{\partial r} + \frac{3b}{2 r^4} \right]
+ E \Delta' v,$](/articles/aa/full/2004/43/aa0539-04/img239.gif) |
(A.1) |
![$\displaystyle \Delta' b = \displaystyle \frac{\partial^2 b}{\partial r^2}
- \fr...
...
+ \frac{1}{\nu} \frac{\partial b}{\partial \nu}
- \frac{b}{\nu^2} \right]\cdot$](/articles/aa/full/2004/43/aa0539-04/img241.gif) |
![\begin{displaymath}\Theta [b] = \frac{\partial^2 b}{\partial \hat{\nu}^2}
+ \f...
...\partial b}{\partial \hat{\nu}}
- \frac{b}{\hat{\nu}^2} \cdot
\end{displaymath}](/articles/aa/full/2004/43/aa0539-04/img250.gif)
| (A.3) |
| (A.4) |
![\begin{displaymath}\left< \left[ \begin{array}{l} u \\ [3mm] w \end{array} \righ...
...^*(r)x(r) + w^*(r) y(r)}{\Vert \vec{B}(r,0) \Vert} ~ {\rm d}r,
\end{displaymath}](/articles/aa/full/2004/43/aa0539-04/img265.gif) |
(A.6) |
![\begin{displaymath}\mathcal{L}_0^{\dag } \left[ \begin{array}{l} u \\ [3mm] w \e...
...ac{\partial u}{\partial r}+\frac{3u}{2r^4}
\end{array}\right].
\end{displaymath}](/articles/aa/full/2004/43/aa0539-04/img268.gif) |
(A.7) |
| (A.8) |
 |
(A.9) |
The model presented here justifies the use of effective boundary conditions
throughout the paper for the adiabatic calculations. In this model, we use
Cartesian coordinates (x,y,z), and the fluid domain is enclosed between two
infinite horizontal planes located at z=0 and z=1. The permanent magnetic
field is constant and in the vertical direction
![]() .
The
perturbations take on the form
.
The
perturbations take on the form
![]() and
and
![]() ,
in order to mimic the toroidal direction
,
in order to mimic the toroidal direction
![]() .
Equation
(3) becomes:
.
Equation
(3) becomes:
| (B.2) |
 |
|||
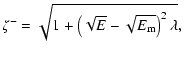 |
|||
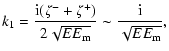 |
|||
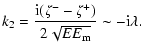 |
(B.4) |
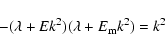 |
(B.5) |
The eigenvalue ![]() must satisfy the following relation:
must satisfy the following relation:
| (B.6) | |||
| (B.7) |
When E and
![]() approach zero, the solutions given in
Eq. (B.3) obey the following effective boundary conditions:
approach zero, the solutions given in
Eq. (B.3) obey the following effective boundary conditions:
When comparing the eigenvalues given in Eq. (B.8) to the ones
given in Eq. (33), we notice that the term
![]() is lacking in the first formula. This is because in the
simplified model, eigenmodes are invariant in the
is lacking in the first formula. This is because in the
simplified model, eigenmodes are invariant in the ![]() direction, thus
removing any quantization in that direction.
direction, thus
removing any quantization in that direction.