- ... shell
![[*]](/icons/foot_motif.gif)
- Appendices are only available in electronic form at http://www.edpsciences.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
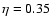
![[*]](/icons/foot_motif.gif)
- This
is the aspect ratio of the Earth's liquid core or that of the radiative
zone of a 3
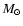 star.
star.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equator
![[*]](/icons/foot_motif.gif)
- In spherical coordinates,
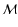 is defined as
follows:
is defined as
follows:
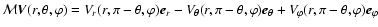 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... operator
![[*]](/icons/foot_motif.gif)
- In
spherical coordinates,
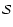 is defined as follows:
is defined as follows:
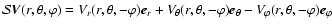 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... radius
![[*]](/icons/foot_motif.gif)
- The choice of this radius is arbitrary. If we
pick different radii, we get approximately the same empirical laws (see
Eq. (22)).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...where
![[*]](/icons/foot_motif.gif)
- When taking the square root of a complex number z, we choose
the root such that
![$\arg(\sqrt{z}) \in ]-\pi/2,\pi/2]$](/articles/aa/full/2004/43/aa0539-04/img294.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.