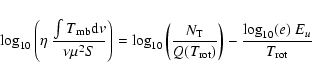A&A 426, 517-521 (2004)
DOI: 10.1051/0004-6361:20047177
The quest for C2N in space
A search with the IRAM 30 m telescope towards IRC+10216
G. W. Fuchs 1 - U. Fuchs1 - T. F. Giesen1 -
F. Wyrowski2
1 - I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937 Köln, Germany
2 -
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
Received 31 January 2004 / Accepted 29 June 2004
Abstract
An extensive search for the linear C2N radical towards the circumstellar envelope IRC+10216
has been performed.
Eight frequency bands of the rotational transitions
J = 7/2-5/2 up to 13/2-11/2 and 17/2-15/2 up to 23/2-21/2 of the C2N molecule
including their 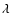 -doubling components have been probed,
using the IRAM 30 m telescope at Pico Veleta, Spain.
However,
there is no evidence for the existence of the C2N radical towards IRC+10216.
Instead, a new upper limit
-doubling components have been probed,
using the IRAM 30 m telescope at Pico Veleta, Spain.
However,
there is no evidence for the existence of the C2N radical towards IRC+10216.
Instead, a new upper limit
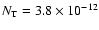 cm-2 for the
column density of C2N was estimated.
Additionally, at least ten yet unidentified lines have been found.
cm-2 for the
column density of C2N was estimated.
Additionally, at least ten yet unidentified lines have been found.
Key words: molecular processes - stars: AGB and post-AGB - stars: carbon - circumstellar matter
The envelope of the carbon star CW Leo/IRC+10216
is well known for its rich chemistry. Already over 50 molecules have been detected in this source
of which many are unsaturated carbon chains. Linear
C3N and C5N were first observed by Guélin & Thaddeus (1977) and Guélin et al. (1998)
in this source and at least C3N has comparable column densities to molecules like HC5N and HNC.
Pauzat et al. (1991) discussed the feasibility of linear
CnN (n=1-7) detection in space and concluded that due to the small dipole moments all CnN members with a
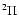 electronic ground state would be poor candidates for interstellar detection. C2N has a
electronic ground state would be poor candidates for interstellar detection. C2N has a 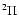 electronic ground state and
recent calculations by Pd & Chandra (2001)
suggest a permanent electric dipole moment of
electronic ground state and
recent calculations by Pd & Chandra (2001)
suggest a permanent electric dipole moment of 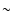 0.425 D,
which is small compared to the
0.425 D,
which is small compared to the 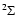 electronic ground state species
C3N and C5N having dipole moments of 2.78 D
(Botschwina et al. 1993) and 3.38 D
(Botschwina 1996), respectively.
Although the dipole moment of a molecule can be crucial for an astronomical detection it is also
important to consider the abundance of the molecule which depends on the local
environment in space.
A study of the formation of C2N was carried out by
Mebel & Kaiser (2002) who found
that the reactions forming CCN, CNC, and c-C2N are strongly endothermic by 52.7, 59.0,
and 99.6 kJ mol-1, respectively. Hence, they concluded that C2N cannot
synthesize in cold molecular clouds where average translational temperatures are only 10-15 K.
Instead, circumstellar envelopes, like IRC+10216, seem to represent ideal targets for C2N because
close to the photosphere of the central star temperatures can reach 4000 K and thus the reaction endothermicity
can be overcome.
In their model a neutral-neutral reaction between C(3Pj) and HCN forms a cyclic HCCN intermediate which can
open up to form linear HCCN or react to H(2S1/2) + C2N (or CNC and cyclo-C2N).
Guelin & Cernicharo (1991) detected
HCCN in the circumstellar envelope of IRC+10216 and also looked at frequencies corresponding to C2N
transitions. They reported a hint of a 0.03 K doublet coincident with the
electronic ground state species
C3N and C5N having dipole moments of 2.78 D
(Botschwina et al. 1993) and 3.38 D
(Botschwina 1996), respectively.
Although the dipole moment of a molecule can be crucial for an astronomical detection it is also
important to consider the abundance of the molecule which depends on the local
environment in space.
A study of the formation of C2N was carried out by
Mebel & Kaiser (2002) who found
that the reactions forming CCN, CNC, and c-C2N are strongly endothermic by 52.7, 59.0,
and 99.6 kJ mol-1, respectively. Hence, they concluded that C2N cannot
synthesize in cold molecular clouds where average translational temperatures are only 10-15 K.
Instead, circumstellar envelopes, like IRC+10216, seem to represent ideal targets for C2N because
close to the photosphere of the central star temperatures can reach 4000 K and thus the reaction endothermicity
can be overcome.
In their model a neutral-neutral reaction between C(3Pj) and HCN forms a cyclic HCCN intermediate which can
open up to form linear HCCN or react to H(2S1/2) + C2N (or CNC and cyclo-C2N).
Guelin & Cernicharo (1991) detected
HCCN in the circumstellar envelope of IRC+10216 and also looked at frequencies corresponding to C2N
transitions. They reported a hint of a 0.03 K doublet coincident with the
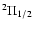 13/2
13/2
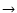 11/2 transition of C2N but could not give a conclusive positive result.
Considering that
the column density ratios
11/2 transition of C2N but could not give a conclusive positive result.
Considering that
the column density ratios 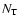 (HC3N/C3N) and
(HC3N/C3N) and 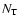 (HC5N/C5N) are of the order
of 10 and assuming that this is also valid for
(HC5N/C5N) are of the order
of 10 and assuming that this is also valid for 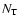 (HC2N/C2N) an astronomical search
seemed to be challenging
since the parent molecule HC2N has already been observed towards IRC+10216 with a column density of
(HC2N/C2N) an astronomical search
seemed to be challenging
since the parent molecule HC2N has already been observed towards IRC+10216 with a column density of
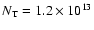 cm-2 (assuming a dipole moment of 3 D for HCCN).
In addition, astro-chemical models by Millar et al. (2000) suggest
the column density of C2N to be
cm-2 (assuming a dipole moment of 3 D for HCCN).
In addition, astro-chemical models by Millar et al. (2000) suggest
the column density of C2N to be
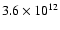 cm-2.
.D..-1
dD.-1
sD..4
SD..7
g[1]D..#1
cm-2.
.D..-1
dD.-1
sD..4
SD..7
g[1]D..#1
Table 1:
Observational parameters.
Using the molecular constants of C2N derived by Ohshima & Endo (1995)
which include their microwave data as well as the constants derived by Kakimoto & Kasuya (1982),
we have recalculated
the millimeter rotational spectrum of C2N![[*]](/icons/foot_motif.gif) and searched for transitions
towards the carbon star envelope IRC+10216 at position ((Eq 1950) RA 09:45:14.8
Dec 13:30:40.0)
close to the center of the star envelope
and searched for transitions
towards the carbon star envelope IRC+10216 at position ((Eq 1950) RA 09:45:14.8
Dec 13:30:40.0)
close to the center of the star envelope![[*]](/icons/foot_motif.gif) .
The search was performed in September 2002 and July 2003 using the IRAM 30 m telescope at Pico Veleta, Spain.
The observations focused on six 500 MHz and two 1 GHz broad frequency bands with their centers
at 83 GHz, 106 GHz, 130 GHz, 154 GHz, 201 GHz, 224 GHz, 248 GHz, and 272 GHz, see Table 1,
thus corresponding to the J= 7/2-5/2 up to 23/2-21/2 (except 15/2-13/2) rotational transitions of C2N.
Figure 1 shows all measured lines during this observation.
The intensities are measured in
.
The search was performed in September 2002 and July 2003 using the IRAM 30 m telescope at Pico Veleta, Spain.
The observations focused on six 500 MHz and two 1 GHz broad frequency bands with their centers
at 83 GHz, 106 GHz, 130 GHz, 154 GHz, 201 GHz, 224 GHz, 248 GHz, and 272 GHz, see Table 1,
thus corresponding to the J= 7/2-5/2 up to 23/2-21/2 (except 15/2-13/2) rotational transitions of C2N.
Figure 1 shows all measured lines during this observation.
The intensities are measured in 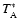 ,
the effective antenna temperature corrected for
spillover losses and atmospheric attenuation, and are then converted to
,
the effective antenna temperature corrected for
spillover losses and atmospheric attenuation, and are then converted to
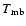 the main beam-averaged source brightness temperature by
the main beam-averaged source brightness temperature by
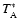 =
=
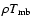 ,
see Table 2.
Here,
,
see Table 2.
Here,
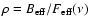 is the 30 m telescope beam efficiency,
see Table 1.
The typical line widths measured in this source are about 30 km s-1.
During the measurements the source had elevations between 40
is the 30 m telescope beam efficiency,
see Table 1.
The typical line widths measured in this source are about 30 km s-1.
During the measurements the source had elevations between 40 and 70
and 70 .
Depending on the frequency the integration time was between 4 and 9 3/4 h and
for most of these bands the rms noise is 2-9 mK
(in
.
Depending on the frequency the integration time was between 4 and 9 3/4 h and
for most of these bands the rms noise is 2-9 mK
(in 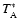 temperature scale).
temperature scale).
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0177fig1.ps}
\end{figure}](/articles/aa/full/2004/41/aa0177-04/Timg24.gif) |
Figure 1:
Lines observed towards IRC+10216 with the IRAM 30 m telescope at a spectral resolution between 0.3 and 1.3 MHz.
The frequency scale is computed for an LSR source velocity of -27 km s-1 and
the ordinate is 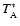 ,
the effective antenna temperature above the atmosphere. The asterisks ( ,
the effective antenna temperature above the atmosphere. The asterisks (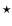 )
mark the transition frequencies of C2N. )
mark the transition frequencies of C2N. |
| Open with DEXTER |
The Grenoble molecular line reduction software CLASS was used to fit the observed lines to a line profile
corresponding to a shell-like emission region.
The frequency scale is computed for a LSR source velocity of -27 km s-1.
Eight rotational transition frequencies of C2N were examined.
Four lines were found at or nearby C2N transition frequencies, none of them have been seen before in any other survey of this source.
However, these lines do not seem to belong to C2N.
The reason that we assign three of these lines to species other than C2N![[*]](/icons/foot_motif.gif) is the fact that the
is the fact that the 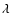 -doublet
components of the rotational transitions of C2N, which should be similar in intensity, are missing and
that the measured intensities fit the expected intensities of the marked (
-doublet
components of the rotational transitions of C2N, which should be similar in intensity, are missing and
that the measured intensities fit the expected intensities of the marked (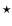 )
species of Table 2.
The remaining line at 82 736.4 MHz, although yet unidentified, is at least 5 MHz away from the calculated C2N transitions at 82 741 to 82 744 MHz and therefore does not belong to CCN.
Also other targeted C2N lines were not detected and only upper limits for their intensities were obtained.
For our calculations of the upper limit of the column density of C2N we used the CCN dipole moment
)
species of Table 2.
The remaining line at 82 736.4 MHz, although yet unidentified, is at least 5 MHz away from the calculated C2N transitions at 82 741 to 82 744 MHz and therefore does not belong to CCN.
Also other targeted C2N lines were not detected and only upper limits for their intensities were obtained.
For our calculations of the upper limit of the column density of C2N we used the CCN dipole moment
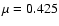 Debye calculated by Pd & Chandra (2001).
The theoretical intensities of the C2N transitions were calculated with
the dpfit and dpcat program written by Herb Pickett.
In the case of small optical depth
the rotational temperature
Debye calculated by Pd & Chandra (2001).
The theoretical intensities of the C2N transitions were calculated with
the dpfit and dpcat program written by Herb Pickett.
In the case of small optical depth
the rotational temperature
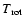 and the total molecular column density
and the total molecular column density
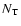 [in cm-2] can be
determined by a least-square fit of
[in cm-2] can be
determined by a least-square fit of![[*]](/icons/foot_motif.gif)
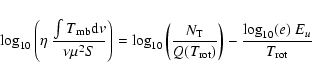 |
(1) |
with
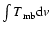 the line integral in (K km s-1),
the line integral in (K km s-1), 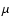 in Debye,
in Debye, 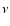 in MHz, S the line strength from
Pickett et al. (1998, Eq. (2)), Q the partition function
in MHz, S the line strength from
Pickett et al. (1998, Eq. (2)), Q the partition function![[*]](/icons/foot_motif.gif) ,
,
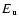 (in K) the energy of the upper level and
(in K) the energy of the upper level and 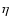 = 1.669813
= 1.669813  1017 a factor to fit the units.
We assumed a line width of 30 km s-1 and after baseline subtraction calculated the intensity by summing over
various un-blended C2N frequency positions.
The large frequency range covered by these measurements allows an estimation of the upper
limit for a variety of
temperatures. We found that if C2N has a rotational temperature of 15 K then
1017 a factor to fit the units.
We assumed a line width of 30 km s-1 and after baseline subtraction calculated the intensity by summing over
various un-blended C2N frequency positions.
The large frequency range covered by these measurements allows an estimation of the upper
limit for a variety of
temperatures. We found that if C2N has a rotational temperature of 15 K then
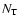
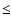 3.5
3.5 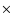 1012 cm-2, if
1012 cm-2, if
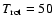 K then
K then
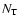
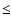 1.8
1.8 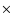 1012 cm-2 and for
1012 cm-2 and for
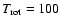 K we find
K we find
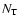
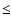 2.3
2.3 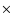 1012 cm-2.
1012 cm-2.
The search for C2N towards IRC+10216 lead to a negative result.
If one assumes that C2N is produced via photo-destruction of HC2N the physical conditions and the region
in which both species are detected should be similar.
Guelin & Cernicharo (1991) detected HCCN towards IRC+10216 using the
IRAM 30 m telescope.
They found that this molecule is essentially present in the outer envelope and has
a rotational temperature of
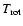 = 12
= 12 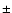 4 K.
If we assume the same physical conditions for C2N as those for HCCN derived by Guelin & Cernicharo (1991),
i.e. same rotational temperature and a spatial molecular distribution mainly in the outer shell so that almost
no beam dilution has to be considered, we get an
upper limit of
4 K.
If we assume the same physical conditions for C2N as those for HCCN derived by Guelin & Cernicharo (1991),
i.e. same rotational temperature and a spatial molecular distribution mainly in the outer shell so that almost
no beam dilution has to be considered, we get an
upper limit of 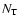 (
(
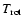 = 12 K) = 3.8
= 12 K) = 3.8 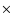 1012 cm-2
1012 cm-2![[*]](/icons/foot_motif.gif) .
The previously published 3
.
The previously published 3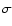 upper limit
upper limit 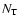 = 5
= 5 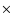 1013 cm-2 byGuelin & Cernicharo (1991)
assumed a dipole moment of 1.3 D for C2N and therefore has to be corrected by
1013 cm-2 byGuelin & Cernicharo (1991)
assumed a dipole moment of 1.3 D for C2N and therefore has to be corrected by
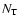 (0.425 D)
(0.425 D) 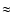 10
10 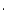
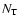 (1.3 D) to be comparable with our new values.
Due to the long integration time our measurements have a significantly lower noise than those of Guélin & Cernicharo
and reveal many new lines even in frequency regions which have already been covered by line surveys
(e.g. Cernicharo et al. 2000).
Therefore the upper limit of
(1.3 D) to be comparable with our new values.
Due to the long integration time our measurements have a significantly lower noise than those of Guélin & Cernicharo
and reveal many new lines even in frequency regions which have already been covered by line surveys
(e.g. Cernicharo et al. 2000).
Therefore the upper limit of
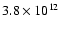 cm-2 presented here
is the most accurate value yet available.
This value is of the same order of magnitude
as the expected column density predicted by Millar et al. (2000).
cm-2 presented here
is the most accurate value yet available.
This value is of the same order of magnitude
as the expected column density predicted by Millar et al. (2000).
Table 2:
Observed lines.
Acknowledgements
We thank J. Cernicharo for his helpful comments and suggestions on the manuscript. We also are grateful to
the IRAM 30 m staff for their hospitality and assistance.
This work was supported by the
Deutsche Forschungsgemeinschaft, DFG project
number SFB 494 and IRAM.
- Botschwina, P. 1996, Chem.
Phys. Lett., 259, 627 [NASA ADS] [CrossRef] (In the text)
- Botschwina, P., Horn,
M., Flugge, J., & Seeger, S. 1993, J. Chem. Soc. Faraday Trans,
89, 2219 [NASA ADS] [CrossRef] (In the text)
- Cernicharo, J.,
Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] (In the text)
- Gensheimer, P., Likkel,
L., & Snyder, L. 1995, ApJ, 439, 445 [NASA ADS] [CrossRef]
- Guélin, M., &
Cernicharo, J. 1991, A&A, 244, L21 [NASA ADS] (In the text)
- Guélin, M., Neininger, N.,
& Cernicharo, J. 1998, A&A, 335, L1 [NASA ADS] (In the text)
- Guélin, M., &
Thaddeus, P. 1977, ApJ, 212, L81 [NASA ADS] [CrossRef] (In the text)
- Kakimoto, M., & Kasuya,
T. 1982, J. Mol. Spectrosc., 94, 380 [NASA ADS] [CrossRef] (In the text)
- Kawaguchi, K., Kasai, Y.,
Ishikawa, S.-I., & Kaifu, N. 1995, PASJ, 47, 853 [NASA ADS]
- Mebel, A. M., &
Kaiser, R. I. 2002, ApJ, 564, 787 [NASA ADS] [CrossRef] (In the text)
- Millar, T., Herbst, E.,
& Bettens, R. 2000, MNRAS, 316, 195 [NASA ADS] [CrossRef] (In the text)
- Müller, H., Thorwirth,
S., Roth, D., & Winnewisser, G. 2001, A&A, 370, L49 [EDP Sciences] [NASA ADS] [CrossRef]
- Ohshima, Y., & Endo, Y.
1995, J. Mol. Spectrosc., 172, 225 [NASA ADS] [CrossRef] (In the text)
- Pauzat, F., Ellinger, Y.,
& McLean, A. 1991, ApJ, 369, L13 [NASA ADS] [CrossRef] (In the text)
- Pd, R., & Chandra, P. 2001,
J. Chem. Phys., 114, 1589 [NASA ADS] [CrossRef] (In the text)
- Pickett, H., Poynter, R.,
Cohen, E., et al. 1998, J. Quant. Spectrosc. Radiat. Transfer,
60, 883 [NASA ADS] [CrossRef] (In the text)
- Turner, B. E. 1991,
ApJS, 76, 617 [NASA ADS] [CrossRef]
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0177fig1.ps}
\end{figure}](/articles/aa/full/2004/41/aa0177-04/Timg24.gif)