- ...N
![[*]](/icons/foot_motif.gif)
- The C2N data are now available
at the Cologne Database for Molecular Spectroscopy (www.cdms.de, see
Müller et al. 2001).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... envelope
![[*]](/icons/foot_motif.gif)
- See for example the SiC2 mapping
of IRC+10216 by Gensheimer et al. (1995).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...N
![[*]](/icons/foot_motif.gif)
- These
are the lines at 129 980.48 MHz, 200 914.8 MHz, and 248 190.2 MHz.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... of
![[*]](/icons/foot_motif.gif)
- The formula was derived using Eq. (1) from Turner (1991).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function
![[*]](/icons/foot_motif.gif)
- The partition function for a temperature T has been calculated by
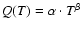 ,
where
,
where
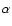 and
and 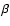 are determined by the Q(Ti) values given by the Pickett program.
For the C2N radical
are determined by the Q(Ti) values given by the Pickett program.
For the C2N radical 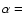 7.1 and
7.1 and 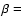 1.2 .
1.2 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...12
![[*]](/icons/foot_motif.gif)
- Taking the temperature uncertainty
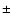 4 K into account we get
4 K into account we get
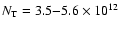 cm-2.
cm-2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.