A&A 426, 151-170 (2004)
DOI: 10.1051/0004-6361:20040400

ISO spectroscopy of disks around Herbig Ae/Be stars^,

B. Acke¹ - M. E. van den Ancker²

1 - Instituut voor Sterrenkunde, KULeuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2 - European Southern Observatory, Karl-Schwarzschild Strasse 2, 85748 Garching bei München, Germany

Received 6 March 2004 / Accepted 22 June 2004

Abstract
We have investigated the infrared spectra of all 46 Herbig Ae/Be stars for which spectroscopic data are available in the ISO data archive. Our quantitative analysis of these spectra focuses on the emission bands at 3.3, 6.2, "7.7'', 8.6 and 11.2 micron, linked to polycyclic aromatic hydrocarbons (PAHs), the nanodiamond-related features at 3.4 and 3.5 micron, the amorphous 10 micron silicate band and the crystalline silicate band at 11.3 micron. We have detected PAH emission in 57% of the Herbig stars in our sample. Although for most of these sources the PAH spectra are similar, there are clear examples of differences in the PAH spectra within our sample which can be explained by differences in PAH size, chemistry and/or ionization. Amorphous silicate emission was detected in the spectra of 52% of the sample stars, amorphous silicate absorption in 13%. We have detected crystalline silicate emission in 11 stars (24% of our sample), of which four (9%) also display strong PAH emission. We have classified the sample sources according to the strength of their mid-IR energy distribution. The systems with stronger mid-infared (20-100 $\mu$m) excesses relative to their near-infrared (1-5 $\mu$m) excess display significantly more PAH emission than those with weaker mid-infrared excesses. There are no pronounced differences in the behaviour of the silicate feature between the two groups. This provides strong observational support for the disk models by Dullemond et al. (2001), in which systems with a flaring disk geometry display a strong mid-infrared excess, whereas those with disks that are strongly shadowed by the puffed-up inner rim of the disk only display modest amounts of mid-infrared emission. Since the silicates are expected to be produced mainly in the warm inner disk regions, no large differences in silicate behaviour are expected between the two groups. In contrast to this, the PAH emission is expected to be produced mainly in the part of the disk atmosphere that is directly exposed to radiation from the central star. In this model, self-shadowed disks should display weaker PAH emission than flared disks, consistent with our observations.

Key words: stars: circumstellar matter - stars: pre-main sequence - stars: planetary systems: protoplanetary disks

1 Introduction

Although the optical-sub-mm energy distribution of Herbig Ae/Be (HAEBE) stars has been well explored by previous authors (e.g., Hillenbrand et al. 1992), the chemical and mineralogical composition of the dust remained poorly studied until the 1995 launch of the Infrared Space Observatory (ISO, Kessler et al. 1996). This first possibility to study the complete infrared spectrum of these objects in detail revealed a large variety in dust properties, from small aromatic hydrocarbons to silicate dust. Moreover, some sources were shown to contain partially crystalline dust grains, similar to those found in comets in our own solar system (Waelkens et al. 1996, Malfait et al. 1998; Meeus et al. 2001; van den Ancker et al. 2000b,a; Malfait et al. 1999).

ISO played a major role in opening up the field of infrared spectroscopy. The emission features at 3.3, 6.2, 7.7, 8.6 and 11.2 micron, found in ISO spectra of many HAEBE stars and previously known as the unidentified infrared (UIR) bands, are generally attributed to polycyclic aromatic hydrocarbons (PAHs, Allamandola et al. 1989; Léger & Puget 1984). PAHs are a large family of molecules, for which the fundamental ingredients are polycyclic benzene rings. PAH molecules are thought to be excited by far-ultraviolet (UV) photons. The absorption of such a photon induces a transition of the PAH molecule to an upper electronic state. The excited molecule then makes rapid transitions to a lower electronic state, leaving most of the initially absorbed energy in the form of vibrational energy in the CC and CH bonds. PAHs cool down by infrared (IR) emission in bands linked to these vibrational modes (Peeters 2002, and references therein). The 3.3 $\mu$m band is due to CH bond stretching vibrations, the 6.2 $\mu$m band is linked to the CC stretching mode and the 7.7 $\mu$m band corresponds to a combination of the CC stretching and the CH in-plane bending modes. The 8.6 and 11.2 $\mu$m features are linked to the CH in-plane and out-of-plane bending modes respectively (Vermeij et al. 2002, and references therein).

In a few sources, emission bands at 3.4 and 3.5 micron are observed. These spectral features are attributed to the CH stretching modes of hydrogenated nanodiamonds (NANs, Guillois et al. 1999; Van Kerckhoven et al. 2002).

The infrared spectra of HAEBEs also contain silicate features. The broad feature at 10 micron has been attributed to the SiO bonds in warm, small amorphous silicate grains like olivine. The feature can appear in emission or in absorption in HAEBE spectra. The spectral signature at 11.3 micron, as well as many features at longer wavelengths which are not included in the analysis presented in this paper, is linked to crystalline silicates (Malfait et al. 1998; van den Ancker et al. 2000b,a; Bouwman et al. 2000,2001; Malfait et al. 1999).

The spectral energy distribution (SED) of HAEBE stars is characterized by the presence of an IR flux excess, due to thermal emission of circumstellar matter. The geometry of the circumstellar dust has been the subject of a long-lasting debate (e.g., Grady et al. 1995; Mannings & Sargent 1997; Böhm & Catala 1994; Grinin et al. 1996; Hartmann et al. 1993; Corcoran & Ray 1998; Hillenbrand et al. 1992; Grinin et al. 1994; Berrilli et al. 1992). For late-B, A and F stars, the evidence for the presence of disk-like geometries is generally accepted. For early-B stars, the matter is less clear. In these systems, the dissipation time scale of the circumstellar spherical envelope is of the order of the pre-main-sequence life time. Disks as well as spherical envelopes might be present.

In their study of the ISO spectra of 14 isolated Herbig Ae/Be stars, Meeus et al. (2001, henceforth M01) classified their sample into two groups, based on the shape of the SED. Group I contains the sources in which a rising mid-IR (20-100 $\mu$m) flux excess is observed; these sources have an SED that can be fitted with a power-law and a black-body continuum. Group II sources have a more modest mid-IR excess; their SEDs can be reconstructed by a power-law only. M01 suggest phenomenologically that this classification represents different geometries of the circumstellar disk: group I sources have flared disks, group II members have flat disks.

Dullemond (2002, henceforth D02) and Dullemond & Dominik (2004, henceforth DD04) have modelled young stellar disks with a self-consistent model based on 2-D radiative transfer coupled to the equation of vertical hydrostatics. The model consists of a disk with an inner hole ($\sim$0.5 AU), a puffed-up inner rim and an outer part. The outer part of the disk can be flared (as in Chiang & Goldreich 1997), but can also lie entirely in the shade of the inner rim. The SEDs of flared disks display a strong mid-IR flux excess, while self-shadowed disks have a much more modest mid-IR excess. D02 explains quantitatively the difference in SED shape in HAEBEs (as expressed by the classification of M01) as the result of a different disk geometry; group I sources have flared disks, group II sources have flat self-shadowed disks.

In this paper we investigate a possible link between the shape of the SED - a proxy for the geometrical distribution of the circumstellar matter - and the strength and profiles of circumstellar infrared emission bands in HAEBE systems. All spectra of HAEBE stars taken by ISO are investigated, amongst others spectra that have never been published before. It is therefore the most complete sample of near-IR spectra of HAEBE stars ever investigated as a whole. Our study is not only qualitative, but contains also, as opposed to many other articles, a quantitative analysis of the infrared spectra of HAEBEs.

2 The data set

2.1 The sample

Our list of HAEBEs is based on the catalogue of Thé et al. (1994, henceforth T94). We restricted ourselves to Tables 1 and 2 of that article. We enlarged the sample with HAEBEs studied by Malfait et al. (1998, henceforth M98), that satisfy the criteria postulated by T94. The resulting list was cross-correlated with the ISO data archive; we selected all objects for which ISO spectra were available with an ISO pointing within a distance of $\pm$5 arcsec of the position given by T94 and M98.

We eliminated some of the remaining sources from the sample; TY CrA was omitted because the infrared emission emanates from the "TY CrA bar'' (Siebenmorgen et al. 2000), which is not directly associated to the star. The object also does not display H$\alpha$ emission, which indicates that this star is no longer actively accreting. From a comparison between the ISO-SWS spectrum of MWC 137 and photometric measurements from the MSX Point Source Catalog (Egan et al. 1997), it appears that there is an offset of 12 $^{\prime \prime }$ between the position indicated in T94 and the position of the infrared source. Only a small portion of the object's flux is seen in the SWS spectrum. We therefore discarded this spectrum from our analysis. A similar problem was encountered for the SWS spectrum of IRAS 12496-7650. A mispointing of the ISO instrument of about 17 $^{\prime \prime }$  compared to the 2MASS point-source-catalogue position (Cutri et al. 2003) caused an anomaly between the ISO SWS-spectra and the IR photometry. However, the PHT-S spectra for this source were not affected due to the larger aperture of the ISO-PHOT instrument (see Sect. 2.2). 51 Oph and MWC 300 were also removed from the list; these are probably evolved objects and not HAEBEs (van den Ancker et al. 2001; Molster et al. 2002, respectively).

The resulting sample of 46 sources is tabulated in Table 1. The columns contain respectively the object's name, the type of ISO spectrum (see Sect. 2.2), the ISO Observation Sequence Number (OSN), the right ascension (RA), the declination (Dec) (both epoch 2000 coordinates), the date and starting time (UT start) of the measurement and the total integration time T in seconds. The objects are sorted by increasing RA. The given coordinates are the pointing coordinates of ISO for that source.

   
2.2 Data reduction

We retrieved all spectra of HAEBE stars present in the ISO data archive. Three types of ISO data were used in this study: ISO-SWS (de Graauw et al. 1996), ISO-PHT (Lemke et al. 1996) and ISO-CAM (Cesarsky et al. 1996).

ISO-SWS was the Short Wavelength Spectrometer aboard ISO (2.38-45.2 $\mu$m). This instrument consisted of 4 sets of 12 detectors. Each set of detectors covered a different wavelength region ([2.38:4.08], [4.08:12.0], [12.0:29.0] and [29.0:45.2] $\mu$m respectively). Not only the material of which the detectors were made differed from band to band, also the aperture sizes were larger at longer wavelengths (from 14 $^{\prime \prime }$$\times$20 $^{\prime \prime }$  around 3 $\mu$m to $20\hbox{$^{\prime\prime}$ }\times 33\hbox{$^{\prime\prime}$ }$ around 30 $\mu$m). The data of different detectors and wavelength regions are calibrated independently.

The source's spectrum was scanned in time, in a way that all 12 detectors of one set scanned through the same wavelength region twice. We only used the SWS data in which the whole spectrum was scanned (scanning mode AOT01). In the standard pipeline reduction, dark currents (residual signal, not related to the actual astrophysical target) are subtracted from the raw data. The detector signal is corrected by multiplication with a responsitivity curve. Furthermore, a wavelength and flux calibration are carried out. We used the resulting product of the latest version of the off-line processing pipeline reduction (OLP 10). After this basic reduction, we manually removed bad data. This includes the suppression of deviating detectors (detectors which measure spectra that are too dissimilar with respect to the spectra observed by the other detectors operating in the same wavelength region) and artefacts like glitches (spikes in intensity, spread out over several data points due to the detector's memory effects). The latter are caused by infalling highly energetic interplanetary particles. A glitch that exceeds the noise level is easily recognizable, since it is only present in one of the two scan directions of the detector and its shape is characteristic.

To diminish the scatter in the data, the calibrated flux levels in a wavelength interval are averaged and all detectors are scaled to this value. The noise distribution is strongly non-Gaussian and asymmetric, among other reasons because of glitches. Since the data will be rebinned and averaged, removal of the outliers is needed. Outliers with a deviation of more than three times the noise in the data were expelled. In the next step the data are rebinned at a spectral resolution of 150 for low flux sources (<10 Jy at 10 $\mu$m) and 500 for high flux sources (>10 Jy at 10 $\mu$m).

Sometimes small differences in flux level are present between the different wavelength regions in the spectrum. The final phase of the data reduction is to correct for these jumps. Since most sources in the sample have low fluxes, jumps are primarily due to errors in the dark current subtraction. Therefore offsets were applied to correct for the flux differences between the wavelength intervals. The shifting was done by adding a constant term - which was computed to minimize the flux difference in the overlap region between two adjacent wavelength regions - to the flux. We took the interval between 3.02 to 3.52 micron as the flux calibration reference and scaled all parts of the spectrum between 2.38 and 12.0 micron to that level. For the region [12.0:29.0] micron, the interval covering [16.5:19.5] micron was used. We discarded the wavelength range longer than 29 micron, since the flux levels in this part of the spectrum were too low to be reliable for many of the sample stars.

The wavelength region around 12 $\mu$m is difficult to interpret, since both the end of the previous and the beginning of the next wavelength range are very noisy and therefore unreliable. For a few spectra, we found it useful to extend the wavelength region of the first interval with respect to the standard pipeline reduction: from 12 to 12.5 $\mu$m. This was done for V376 Cas, HD 31648, Z CMa, HD 95881, HD 104237, HD 139614, HD 142666, HD 150193, T CrA, WW Vul, LkH$\alpha$ 224, HD 200775 and SV Cep. Since we chose to shift the flux levels in [2.38:12.0] $\mu$m, and [12.0:29.0] $\mu$m separately, the overlap region between these two intervals is independent of this post-reduction flux level correction. In this way, we avoid changing the shape of spectrum around this wavelength area too much compared to the original - unshifted - data. Not combining the two intervals in a direct way also prevents the entry of systematic errors in the shape and line flux of the broad, amorphous 10 micron silicate feature. We note that each of the narrower features at 3.3, 3.4, 3.5, 6.2, 7.7, 8.6, 11.2 and 11.3 micron are included within one continuous SWS wavelength interval. Therefore our measurements of line flux and full width at half maximum of those features will be independent of the procedure followed for the alignment of the different wavelength ranges.

For HD 97048, HD 100546, HD 104237, HD 142666, CD-42$^\circ$11721, R CrA, T CrA and MWC 1080, two ISO-SWS spectra were available. We combined the spectra after the reduction to increase the signal-to-noise ratio. For HD 97048 we decided to keep only one of the SWS spectra (OSN 61801318), because the second spectrum was affected by severe instrumental artefacts.

The ISO-PHT instrument was a photo-polarimeter, which had a spectroscopic mode (PHT-S). The spatial resolution of the instrument was $24\hbox{$^{\prime\prime}$ }\times24\hbox{$^{\prime\prime}$ }$. The spectra consist of 127 photometric points, separated into two wavelength intervals ([2.5:4.9] $\mu$m and [5.8:11.6] $\mu$m). For faint sources, PHT-S was able to obtain spectra with a higher S/N ratio than SWS, albeit at much lower spectral resolution ($\sim$90). We retrieved the resulting spectra from the latest version of the off-line processing data reduction (OLP 10). For HD 97048, HD 104237, HD 135344 and WW Vul, two or three PHT-S spectra were available; we merged the spectra.

The ISO-CAM instrument also had a spectrophotometric mode (CAM04). This mode made it possible to take a series of images at variable central wavelengths (between 5 and 15 $\mu$m). We extracted the spectrum by applying synthetic photometry to the images with a circular aperture with a diameter of 15 $^{\prime \prime }$  (comparable with the spatial resolution of SWS and CAM). Only 5 CAM04 spectra are included in this analysis. Again we used the results of the latest version of the off-line processing data reduction pipeline OLP 10.

The resulting spectra of the data reduction are compiled in Figs. 1-3 for ISO-SWS, ISO-PHT and ISO-CAM, respectively.

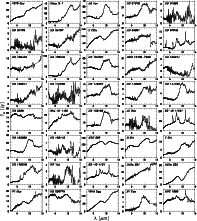	Figure 1: The reduced 2.4-15 $\mu$m SWS spectra of the sample stars.
Open with DEXTER

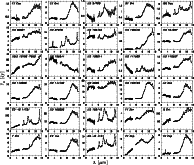	Figure 2: The reduced 2-5-11.6 $\mu$m PHT-S spectra of the sample stars.
Open with DEXTER

	Figure 3: The reduced 5-15 $\mu$m CAM spectra of the sample stars.
Open with DEXTER

2.3 Measurement of the spectral features

In our analysis, we focused on the infrared emission bands at 3.3, 6.2, 7.7, 8.6 and 11.2 micron, attributed to polycyclic aromatic hydrocarbons and the features at 3.4 and 3.5 micron, linked to nanodiamonds. The amorphous silicate feature around 10 micron and the crystalline silicate feature at 11.3 micron were also included in the analysis. The 11.2 and 11.3 micron bands, when present, are blended. Due to the low spectral resolution, we cannot distinguish between the two. Therefore we consider the blend as one complex, which we call the 11 micron feature.

To characterize these features in the spectra, we measured the line flux, full width at half maximum (FWHM), peak wavelength, peak flux, continuum flux at the peak wavelength and the equivalent width (EW).

We wrote an IDL procedure, measfeat.pro, to manipulate the spectra in order to determine the desired measurements. The IDL code allows us to indicate continuum points by hand. Based on these points a spline function is fitted to estimate the continuum. Integrating the continuum subtracted flux, the line flux and EW of the features were computed. We repeated the procedure, indicating an "extreme'' continuum, to estimate the systematic error introduced by the continuum determination. It appears that the uncertainty in the line flux varies from about $\sim$10% for the PAH features and the 10 micron feature, up to $\sim$30% for the 11 micron feature. Furthermore, the IDL program determined the peak position and peak flux by fitting a Gaussian function to the continuum-subtracted line profile. The peak flux was set equal to the maximum of the fit, the peak wavelength is the wavelength of this maximum. When the feature was in absorption, the peak flux was defined as the minimum of the fit. In the latter case the peak wavelength is the wavelength at which this minimum occurred. The value of the continuum flux at the peak wavelength is also recorded. Note that, because of the possible skewness of the features, the peak wavelength in general does not coincide with the centroid wavelength. This may lead to systematic differences between the values used in this paper and values in the literature.

The FWHM was deduced by computing the width at half the peak flux of the smoothed line profile. The smoothing of the spectrum was done to diminish the influence of the noise in the spectrum on this measurement.

When a feature was not detected, we deduced upper limits for its line flux and peak flux, and we computed the continuum flux at the expected central wavelength of the feature. The upper limits were computed in the following manner; we used the averaged spectrum of CD-42$^\circ$11721 and HD 97048 (both sources with fairly typical PAH spectra; Sect. 3.1) as a template spectrum for the PAH emission, the spectrum of HD 97048 for the 3.4 and 3.5 micron NAN emission and the spectrum of HD 150193 as a template for the 10 micron amorphous silicate emission. For non-detections, we assumed a peak emission of 5 times the noise on the spectrum at the theoretical central wavelength of the feature as an upper limit for the peak flux. Scaling the template spectra to this level, we extracted the upper limits for the line flux.

This procedure was applied to the SWS, PHT-S and CAM spectra. Since the spectral resolution of the PHT-S and CAM data is not even 100, only the line flux, EW, peak flux and continuum flux at the theoretical central wavelength were determined for the latter; the other measurements are not meaningful in this case.

2.4 Comparison of SWS, PHT-S and ground-based photometry

For 24 sources, SWS as well as PHT-S spectra were available. We independently measured the desired quantities of the features, when present in both spectra. Comparing these two sets of values, we noticed that there is an offset between the two; the computed PHT-S line fluxes are systematically lower than their SWS counterparts. We attribute this difference to the fact that at 2.8 times the Nyquist sample spacing, the PHT-S data are insufficiently sampled in wavelength to recover the full spectral response. The result of this is that we will lose flux around sharp gradients in the spectra. As an example we show in Fig. 4 the PAH 6.2 feature of HD 100546, as it appears in the SWS and PHT-S spectra. The line flux in the PHT-S spectrum is clearly underestimated. In Table 2 we summarize the ratios of the line flux measured in the PHT-S spectrum over the line flux measured in the SWS spectrum (PHT/SWS) for all detected features. Note that most of the ratios (81%) are smaller than unity, which is consistent with our interpretation. The given errors are the statistical errors on the measurements. Ratios that are larger than one can be due to spatially extended emission or intrinsically varying PAH emission.

Table 2: The ratios of the line flux of the features measured in the PHT-S spectrum over the line flux measured in the SWS spectrum LF $_{{\rm PHT-S}}$/LF $_{{\rm SWS}}$. The given errors are the statistical errors on the measurements.

We calculated the mean ratio of the detected SWS line flux over the PHT-S line flux for each feature. The values of these quantities are 1.18, 1.34, 1.17, 1.16, 1.18, 1.08 and 0.58 for PAH 3.3, NAN 3.4, NAN 3.5, PAH 6.2, PAH 7.7, PAH 8.6 and the 11 micron feature respectively. The PHT-S measurements were adjusted by multiplying with these mean values. The factors were also applied to correct the upper limits.

Note that the amorphous 10 micron silicate feature is only partially sampled in the PHT-S spectra, since the wavelength coverage ends at 11.6 micron. Therefore it is difficult to determine the underlying continuum in the PHT-S spectra. Nevertheless, we indicated the continuum in a consistent manner. Similarly to the PAH features, we computed the line flux ratio of detected 10 micron emission features in both the SWS and the PHT-S spectrum, and computed the mean value. By applying this correction factor (0.86), we compensate for this systematical difference between the measurements of the SWS and PHT-S 10 micron feature.

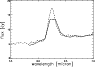	Figure 4: The PAH feature at 6.2 micron of HD 100546 in the SWS spectrum (dashed line) and in the PHT-S spectrum (full line).
Open with DEXTER

The comparison between the CAM and SWS spectra of HD 97048 showed that the results are equal within a 15% range. No corrections for the CAM results were applied. We decided not to use the CAM spectra of HR 5999, HD 179218, HD 200775 and HD 97048 in the analysis; the first two spectra are inhomogeneously covered in wavelength, which leads to insufficiently sampled features. The CAM spectrum of HD 200775 is quite different from the SWS spectrum; the first displays PAH emission, while the latter does not. We relate this to extended emission, visible in the CAM spectrum because the (synthetic) aperture is larger than the aperture for the SWS spectrum at these wavelengths. The CAM spectrum of BD+46$^\circ$3471 is the only spectrum of this source at our disposal. We added the measurements to our data set, even though we noticed unusual features in the spectrum, which could be artefacts (e.g. the "absorption feature'' at 10 micron).

The ISO spectra were compared to space- and ground-based photometric measurements from the literature; we plotted the photometric points from the MSX catalog over the reduced spectra. In general, the mean deviation between the spectra and the photometry is small and non-systematic. Sources where the anomaly exceeds the 20% level are HD 104237, HD 142666, MWC 297, BD+40$^\circ$4124, V645 Cyg and MWC 1080. Except for BD+40$^\circ$4124, the photometric fluxes in these spectra are higher than the SWS or PHT-S fluxes. We attribute the differences to spatially extended emission and different beam/aperture sizes, although we cannot exclude the possibility of intrinsic infrared variability of (some of) our sources.

   
2.5 The final numbers

After the measurements of the features, we condensed the data set into a final set of numbers: one measurement for each star and examined feature. The presence of the features in the HAEBE spectra is summarized in Table 3. The sources are sorted according to their IR-SED classification (see Sect. 2.6).

When only a SWS, PHT-S or CAM spectrum was availaible for a source, those data were taken. For sources with a SWS and a PHT-S spectrum, three possibilities arise; the feature is detected in both spectra, the feature is undetected in both spectra or the feature is detected in only one of the two spectra. In the first case, the data are merged using a weighted average, based on the statistical errors on the measurements. In the second case, the most stringent upper limit for the feature is taken. In the third case, when the measured line flux of the detected feature is lower than the upper limit derived from the other spectrum, the data are consistent and the values of the measurement are selected. In the inconsistent case (the upper limit is lower than the measured line flux), we set a conservative upper limit for the feature. The latter only occurred in 4 cases (out of 192 measured features). This behaviour might be either a result of the different aperture sizes used by SWS and PHT-S, in which case this could indicate the existence of spatially extended emission, or a first indication that the strength of PAH emission may vary with time in some of our sources. We indicated these measurements in Table 3 with $\surd^{ c}$ and $\surd^{ d}$, according to detection in the PHT-S or SWS spectrum respectively.

The computed line fluxes used in the analysis are listed in Table 4. Upper limits are indicated as well. Table 5 summarizes the continuum fluxes at the peak wavelength of each feature.

   
2.6 The SED

To characterize the spectral energy distribution (SED) of the sample sources, several quantities were determined, based on UV to millimetre (mm) photometry from the literature. The photometry consists of ANS and IUE ultraviolet data, ground-based photometry in the Walraven, Johnson/Cousins, and near-IR JHKLM photometric systems, IRAS and MSX data, and single-dish (sub)-mm photometry collected from the literature. The effective temperature $T_{{\rm eff}}$ of each source was determined from its spectral type listed in Table 6, using the calibrations from Schmidt-Kaler (1982). The visual extinction $A_{\rm V}$ and absolute luminosity L of the central star were computed by fitting and integrating a Kurucz (1991) model for the stellar photosphere to the de-reddened photometry, adopting the distance estimates listed in Table 6. The ionising (>13.6 eV) luminosity $L_{{\rm ion}}$ and the UV (2-13.6 eV) luminosity $L_{{\rm uv}}$of the source were computed using this Kurucz model fit. We also computed the IR-excess luminosity $L_{{\rm exc}}$, using a spline fit to the infrared data, and the absorbed luminosity $L_{{\rm abs}}$ of the source, which is the difference between the theoretical Kurucz model and the reddened model. The IR-excess flux in the K band (2.2 $\mu$m), at 60, 850, and 1300 micron was deduced by subtracting the Kurucz model at these wavelengths from the observed fluxes. When no 1300 micron photometry was available, we included 1100 micron measurements, which we then converted into 1300 micron flux values by multiplying with the average 1300/1100 ratio deduced from stars for which we had both measurements. The last parameter used to characterize the SED is the observed bolometric luminosity $L_{{\rm bol}}$, which is the total integrated luminosity of the SED. The latter quantity is not corrected for extinction, as opposed to the stellar luminosity L. The stellar parameters used in this study are listed in Table 6.

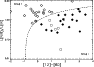Figure 5: Diagram based on van Boekel et al. (2003). The ratio $L_{{\rm NIR}}/L_{{\rm IR}}$ is plotted versus the non-color-corrected IRAS [12]-[60] color. The dashed line represents $L_{{\rm NIR}}/L_{{\rm IR}} = ([12]{-}[60]) + 0.9$. Objects on the left-hand side of this empirical line are defined to be group II members (open diamonds), sources on the right side are either group I (filled diamonds) or group III (squares) members.

Open with DEXTER

The sample sources were classified into different groups, based on the shape of their SED. The quantities used to characterize the infrared spectral energy distribution of HAEBEs are the ratio of $L_{{\rm NIR}}$ (the integrated luminosity derived from the broad-band J, H, K, L and M photometry) and $L_{{\rm IR}}$ (the corresponding quantity derived from IRAS 12, 25 and 60 micron points), and the non-color-corrected IRAS [12]-[60] color (Dullemond et al. 2003; Acke et al. 2004; van Boekel et al. 2003). These parameters compare the near-IR SED, which is expected to be similar in HAEBEs (Natta et al. 2001; de Winter et al. 1995; Hillenbrand et al. 1992), to the mid-IR SED, where the major differences in SED shape occur. M01 group I sources are stronger mid-IR emitters than group II sources. The luminosity ratio $L_{{\rm NIR}}/L_{{\rm IR}}$ represents the strength of the near-IR compared to the mid-IR excess, which is lower for group I than group II sources. The shape of the mid-IR SED of a group I source is "double-peaked'' compared to the SED of a group II member. The IRAS[12]-[60] color index provides a quantitative measure for this difference in SED shape. Group I sources are redder than their group II counterparts. We use the diagram given in Fig. 5 to distinguish between group I and group II in the classification of M01. The dashed line represents $L_{{\rm NIR}}/L_{{\rm IR}} = ([12]{-}[60]) + 0.9$, which empirically provides the best separation between the two groups.

Six of our sample stars display the amorphous 10 micron feature in absorption. These objects are believed to possess disks whose luminosity is dominated by viscous dissipation of energy due to accretion, are deeply embedded systems and hence are fundamentally different from the other sample stars. We therefore classify them in a different group: group III.

BD+40$^\circ$4124, R CrA and LkH$\alpha$ 224 have not been classified based on their appearance in Fig. 5. Confusion with background sources in the IRAS photometry prohibited us from deriving the quantities needed to plot these objects in the diagram. BD+40$^\circ$4124 has been classified as a group I source, because its SED resembles the SED of HD 200775. R CrA and LkH$\alpha$ 224 are both UX Orionis stars according to the definition of Dullemond et al. (2003): both sources have a spectral type later than B9 and optical variations larger than 1 mag on timescales of days to weeks. Therefore we classified them as group II members.

The SEDs of all sample sources are displayed in Fig. 6. The group to which the objects belong is indicated as well. The SEDs are overplotted with the ISO spectra. Squares with error bars indicate photometric measurements from the literature, arrows upper limits.

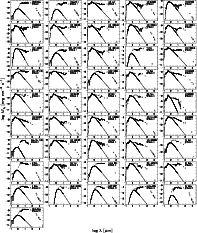	Figure 6: The spectral energy distributions of the sample stars. The squares are the observed photometric data from the literature with error bars. The solid line is the reddened Kurucz model for the stellar photosphere, fitted to the measured UV-optical photometry. The ISO spectra are plotted in the SEDs as well (noisy solid line).
Open with DEXTER

3 Analysis of the ISO spectra

   
3.1 The PAH features

First we investigated the general correlations of the different PAH features in our spectrum. We compared the line fluxes (LF) of the different features, which we normalised by the continuum flux at the peak wavelength (CF), to correct for the distance-to-the-star dependence of the line flux. Figure 7 shows the ratio LF/CF for the PAH 7.7 micron feature versus PAH 6.2 micron; Fig. 8 is a similar plot for the ratio LF/CF of PAH 6.2 micron versus PAH 3.3 micron. The correlation coefficient $\eta$ in the first plot is 0.90, while the data in the second plot are less correlated ( $\eta = 0.58$). The other PAH features display comparable behaviour. It is striking though that PAH features that are linked to the CC bonds (6.2, 7.7 micron) correlate better with each other, as well as the features linked to the CH bonds (3.3, 7.7, 8.6 micron). However, as a first order approximation we can state that the LF/CFratios correlate fairly well over a range of a few orders of magnitude.

Supposing that all HAEBEs have chemically identical PAH molecules, the PAH spectra of this group of stars should be uniform. Two effects that could influence the shape of this "unique'' spectrum are the UV field of the central star and interstellar extinction. If we presume that the wavelength dependence of the first does not vary much from source to source, the dominant source of deviations from a simple linear correlation between the PAH feature-strengths would be extinction. This will have a stronger effect on PAH features that are close to the amorphous 10 micron silicate feature. In Fig. 9 the logarithm of the ratio of the line fluxes of the PAH feature at 8.6 micron over the feature at 6.2 micron, $\log~(LF_{8.6}/LF_{6.2})$, is plotted versus the logarithm of the ratio of the line fluxes of the 3.3 micron PAH feature over the 6.2 feature, $\log~(LF_{3.3}/LF_{6.2})$ (following Hony et al. 2001). To include the extinction effect into the plot, we applied the interstellar extinction law of Fluks et al. (1994) to the line fluxes of MWC 1080 according to the formula

$$LF'_{j}(x) = LF^{{\rm MWC~1080}}_{j} \times 10^{\frac{A_\lambda}{A_{\rm V}} \frac{x}{2.5}}$$

in which x represents the actual visual extinction (in mag) and $A_\lambda / A_{\rm V}$ the interstellar extinction coefficient at the central wavelength $\lambda$ of feature j. The straight line in Fig. 9 represents the ratios of extinction corrected line fluxes for a wide range of visual extinction. If interstellar extinction would be the only effect, all measurements should lie within the observational error bars from this line. This is not the case; sources that deviate significantly are Elias 3-1, AB Aur, RR Tau and CD-42$^\circ$11721. A similar plot based on the PAH 7.7 micron feature instead of the 8.6 micron feature (not in the paper), leads to the same conclusion: the spread cannot be induced by extinction only. Hence, the PAH spectra of HAEBE stars are not identical, indicating differences between PAH molecules in different systems. This spectral variety of PAHs can have several causes.

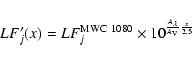
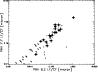	Figure 7: The LF/CF ratio of PAH 7.7 micron versus PAH 6.2 micron. The filled diamonds with error bars indicate detected features, arrows represent upper limits.
Open with DEXTER

	Figure 8: Similar plot as Fig. 7. The LF/CFratio of PAH 6.2 micron versus PAH 3.3 micron.
Open with DEXTER

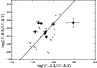Figure 9: The logarithm of the ratio of the line fluxes of the PAH features at 8.6 and 6.2 micron $\log~(LF_{8.6}/LF_{6.2})$ versus the logarithm of the ratio of the line fluxes of the PAH features at 3.3 and 6.2 micron $\log~(LF_{3.3}/LF_{6.2})$ for all program stars. The filled diamonds with error bars indicate detected features, arrows indicate upper limits. The full line represents the line fluxes of MWC 1080 for variable extinction.

Open with DEXTER

1.

As described in the introduction, the different PAH emission bands studied in this analysis are linked to bending and stretching modes in the different bonds of the PAH molecules. Differences in PAH grain sizes will change the ratio of number of CC bonds over number of CH bonds. Larger grains will have a large CC/CH ratio, which may lead to e.g. a smaller LF_3.3/LF_6.2 ratio.

2.

Differences in PAH ionisation can have a strong effect on the intensities of the PAH emission features. The PAH charge is ruled by the photo-ionization rate and the electron recombination rate, and hence depends strongly on local physical conditions, in particular the electron density and the strength of the UV radiation field.

3.

Chemical differences can also affect the PAH emission spectrum. PAH molecules can contain other elements than C and H. This pollution influences the strength and especially the peak position of the feature. The expected shifts in peak position due to this effect are nonetheless too small to be measurable in the available spectra. No definite conclusions on the presence of the latter can be drawn.

4.

Dehydrogenation of PAHs, when the molecules are stripped of their H atoms, is believed not to play a crucial role (Hony et al. 2001). Nevertheless this phenomenon could add to the observed differences in the spectra.

The 6.2 micron feature is the most frequently detected PAH feature in our analysis (25 times out of 46 spectra), followed by the 7.7 micron feature (19/46). This was to be expected, since these two features are both linked to the CC bond, which is an indispensable part of the PAH chemistry. The PAH 3.3 and 8.6 micron features, both linked to the CH bond, are less frequent (12/45 and 16/46 respectively). The mean peak wavelength, FWHM and peak-over-continuum flux ratio of the examined features is given in Table 7. The mean LF ratios of all features are summarized in Table 8.

Table 7: The mean peak wavelength $\lambda _0$, FWHM and peak-over-continuum flux ratio of the detected features.

3.2 The nanodiamond features

Only a small minority of stars in this sample display nanodiamond features in their spectrum. Both examined features (at 3.4 and 3.5 $\mu$m) were detected in the spectra of Elias 3-1 and HD 97048 (as thoroughly described by Van Kerckhoven et al. 2002), but also in the spectrum of BD+40$^\circ$4124. The spectrum of HD 100546 possibly contains the 3.4 micron feature, while the 3.5 micron feature was detected in the spectrum of MWC 297 (see also Terada et al. 2001).

Tables 7 and 8 contain general information about the NAN features. Nevertheless, because of the small number of sources in this sample that display 3.4 or 3.5 micron emission, no stringent conclusions on the conditions needed to see these features can be drawn. We are currently carrying out a ground-based 3.2-3.6 $\mu$m spectroscopic survey of a much larger sample of HAEBEs, which should allow us to draw more definitive conclusions on possible correlations of the NAN and the PAH features in the near future.

   
3.3 The amorphous 10 micron silicate feature

In the sample of HAEBEs presented in this paper, most of the sources (52%) have the amorphous 10 micron silicate feature in emission; 6 out of 46 objects (13%) have the feature in absorption, while it is undetected in the other cases. We note that at least in some cases, the presence of a 10 $\mu$m feature may be masked by the presence of strong PAH emission in the 8.6 and 11.2 micron bands, so the true fraction of sources with amorphous silicates is likely higher than reported here.

The LF/CF correlation coefficients of the 10 micron feature and the PAH features are low. In Fig. 10 the LF/CF ratio of the 10 micron feature is plotted versus that of the PAH 6.2 micron feature. The two ratios correlate poorly, especially when one takes into account the upper limits (arrows) on the left-hand side in the plot. These arrows represent spectra in which the 10 micron feature is present, but where the PAH 6.2 micron feature is undetected. Similar plots in which the other PAH features are plotted against the 10 micron feature show the same result: the strength of the emission of PAHs is uncorrelated with the strength of the amorphous 10 micron silicate feature.

	Figure 10: The LF/CF ratios of the amorphous 10 micron silicate feature (Si 9.7) versus the PAH 6.2 micron feature. Diamonds with error bars indicate detected features, arrows represent upper limits. Sources with the 10 micron feature in absorption have a negative LF/CF ratio.
Open with DEXTER

We now consider the peak-over-continuum flux ratio (PF/CF) of the 10 micron feature in our sample. We plotted this dimensionless quantity for all detected 10 micron emission features in the sample in Fig. 11. The histogram peaks around the average value 1.91, which means that the peak of the 10 micron emission is on average twice as high as the underlying continuum. The minimum and maximum value for the ratio in the sample is 1.21 and 2.69 respectively. There does not seem to be a difference between the 10 micron emission feature in group I and group II sources. The average PF/CFratios for the two groups are 1.85 and 2.03 respectively. Strong as well as more modest amorphous 10 micron silicate features appear in both group I and group II sources. The feature can also be absent in both groups.

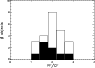	Figure 11: The cumulative histogram of the PF/CF for the amorphous 10 micron silicate feature. The 24 sample stars in which this feature is in emission are included in this plot. The lower filled part of the bars represents group I sources, the upper part group II sources.
Open with DEXTER

Table 8: The mean line-flux ratios of the examined features. Indicated in the table is the mean LF_A/LF_B of all sample stars for which both A and B were detected.

3.4 The 11 micron feature

The 11 micron feature is detected in 48% of the spectra. It is unclear how many of these detected features include the PAH 11.2 micron band, since this feature can be blended with the crystalline silicate feature at 11.3 micron. Figure 12 is similar to Fig. 9. The logarithms of the ratios LF₁₁/LF_6.2 and LF_3.3/LF_6.2 are plotted. Again, the straight line indicates the variable extinction line, based on the line fluxes of MWC 1080. Four sources (AB Aur, Elias 3-1, HD 100546 and HD 179218) lie significantly to the right of this line. This suggests that these sources have an 11 micron feature that contains both PAH and crystalline silicate emission. The presence of crystalline silicates in HD 100546 and HD 179218 was already well-established from longer-wavelength ISO data (Malfait et al. 1998,1999). The detection of crystalline silicates in AB Aur and Elias 3-1 is a new result from our quantitative analysis. We stress that the detection of a stronger than expected 11 micron feature in the four sources mentioned above does not mean that other sources cannot have crystalline silicates; it could just be masked by the presence of strong PAH emission at 11.2 $\mu$m, or the crystalline silicates could be cooler than a few hundred K, causing only very weak emission in our diagnostic band at 11 microns.

When plotting the FWHM of the feature against the ratio $\log(LF_{11}/LF_{6.2})$ (Fig. 13), the same four sources appear to have much higher FWHMs. The horizontal line in the plot indicates the average FWHM (with exclusion of the 4 objects mentioned before). This also points to the presence of 2 blended emission features. Even so, the peak position of the 11 micron feature in AB Aur, Elias 3-1, HD 100546 and HD 179218 is comparable with the average peak wavelength (see Fig. 14). This might indicate that the peak position of the crystalline silicate feature varies, which can be attributed to a variety in its mineorological composition. We stress however that the uncertainties in these determinations are large.

Sample stars that do not display significant PAH emission at 3.3, 6.2, 7.7 or 8.6 micron are not expected to have significant PAH 11.2 micron emission. Hence a detected 11 micron feature in the spectra of these sources is likely to be solely due to crystalline silicate emission. In the present sample HD 142527 (group I), HD 142666, HD 144432, HR 5999, HD 150193, HD 163296 and VV Ser (all group II) meet these requirements. If these objects indeed display the crystalline silicate band in their spectrum, then the number of sources with crystalline silicates in this sample is at least 11 (24%).

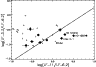	Figure 12: Same type of plot as Fig. 9. The logarithm of the ratio of the line fluxes of the PAH features at 3.3 and 6.2 micron $\log~(LF_{3.3}/LF_{6.2})$ versus the logarithm of the ratio of the line fluxes of the features at 11 and 6.2 micron $\log~(LF_{11}/LF_{6.2})$. Again, the full line represents the line fluxes of MWC 1080 for variable interstellar extinction.
Open with DEXTER

	Figure 13: The FWHM of the 11 micron feature versus the logarithm of the ratio of the line fluxes of the features at 11 and 6.2 micron $\log~(LF_{3.3}/LF_{6.2})$. The dashed line represents the average FWHM (0.214 micron) when excluding the 4 outliers.
Open with DEXTER

The 11 micron complex does not correlate with the PAH 6.2 micron feature, and reaches better agreement with other CH bond related PAHs (3.3, 7.7 micron), which is expected, since the 11.2 micron feature is due to a CH bond itself. The correlation with the PAH 8.6 micron feature, on the other hand, is weak.

In Fig. 15 the ratio LF/CF of the amorphous silicate feature versus the 11 micron complex is plotted. There does not seem to be a correlation between the two features. This can be interpreted in two ways. The 11 micron feature could be mostly dominated by PAH emission in this sample of stars, which leads to a poor correlation with the 10 micron feature like for the other PAH features (see Sect. 3.3). The other possibility is that the crystalline 11.3 micron silicate band - when present in the 11 micron complex - does not correlate with the amorphous 10 micron silicate feature. Note that also the four "crystalline silicate stars'' mentioned above do not display an obvious trent. This could be interpreted in terms of the second explanation.

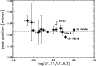	Figure 14: The peak position of the detected 11 micron features versus the ratio of the line fluxes of the 11 micron feature over the 6.2 PAH feature $\log~(LF_{11}/LF_{6.2})$. The dashed line at 11.233 micron indicates the mean peak position of the 11 micron feature.
Open with DEXTER

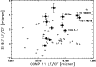	Figure 15: The LF/CF ratios of the amorphous 10 micron silicate feature (Si 9.7) versus the 11 micron feature. Diamonds with error bars indicate detected features, arrows represent upper limits. Sources with the 10 micron feature in absorption have a negative LF/CF ratio.
Open with DEXTER

Except for Z CMa, no crystalline silicate absorption or emission is observed in sources which display amorphous silicate absorption (group III). The spectrum of Z CMa does display a local minimum around 10.7-11.5 micron, which might be due to crystalline silicate absorption. In Fig. 16, the spectrum of Z CMa is plotted. For reasons of clearness it was inverted, making the absorption features appear as emission features. Two sources (HD 144432 and HD 163296) that are likely to display a crystalline silicate emission feature at 11.3 micron, are also plotted as a reference.

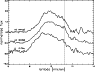Figure 16: The inverted spectrum of Z CMa, and the emission band spectra of HD 144432 and HD 163296. For Z CMa, the figure shows the inverted continuum-divided, continuum-subtracted flux $[\mathcal{F}_{\rm cont}(\lambda) - \mathcal{F}(\lambda)]/ \mathcal{F}_{\rm cont}(\lambda)$. The other two spectra display the continuum-subtracted flux. All three spectra are normalized to a peak flux of 1. An additional offset was applied for the sake of clarity. The dashed line represents $\lambda = 11.3~\mu$m.

Open with DEXTER

4 Correlations between solid-state features and disk properties

4.1 The SED

Using the luminosities and effective temperatures computed in Sect. 2.6, we plot the stars in our sample in a traditional Hertzsprung-Russel (HR) diagram. There is no strong correlation between the classification of the sources and the position in the HR diagram. In Fig. 17, the plotting symbols are proportional to the observed PAH luminosity ( $L_{{\rm PAH}}$; Appendix). In this plot, theoretical pre-main-sequence (PMS) evolutionary tracks of stars with masses M = 1.5, 2, 3 and 5 $M_{\odot }$ are plotted (Bernasconi 1996). Furthermore, the zero-age main sequence (ZAMS) is indicated by a dashed line. Most of the stars lie close to the main sequence (MS), which is represented by the dotted line. Based on this diagram, the masses of the bulk of the sample stars lie between 1.5 and 3 $M_{\odot }$. The strength of the PAH bands does not seem to be strongly correlated with stellar mass or age. Figure 18 is a plot similar to Fig. 17 for the amorphous 10 micron silicate emission feature. The plotting symbols are proportional to the peak-over-continuum flux PF/LF of the feature. The strength of this solid-state band appears to be also uncorrelated with stellar mass and age.

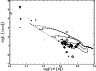Figure 17: The Hertzsprung-Russel diagram for the sample stars. The plotting symbols are proportional to the PAH luminosity. Filled diamonds indicate detected emission, open symbols represent upper limits. The full lines indicate the PMS evolutionary tracks of stars with masses M = 1.5, 2, 3 and 5 $M_{\odot }$ from bottom to top; the dashed and dotted lines represent respectively the ZAMS and the MS (Bernasconi 1996).

Open with DEXTER

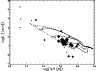	Figure 18: Similar plot as Fig. 17. The plotting symbols are proportional to the peak-over-continuum flux of the amorphous 10 micron silicate emission feature.
Open with DEXTER

One of the main characteristics of HAEBE stars is the IR excess due to thermal emission of circumstellar dust. In Table 6, the ratio of this excess luminosity $L_{{\rm exc}}$ over the stellar luminosity L is included. Ten of the sample sources have an IR-excess luminosity that is larger than the stellar luminosity. This means that these sources cannot have passive reprocessing circumstellar disks. There does not seem to be a link between the classification of the sample stars and their $L_{{\rm exc}}/L$ ratio. The average value for the sources for which the ratio is smaller than unity, is $0.37 \pm 0.21$for group I, $0.39 \pm 0.20$ for group II and $0.09 \pm 0.04$ for group III. Half of the group III objects have a ratio bigger than one, though, which is consistent with the idea that these sources are still actively accreting systems.

In Fig. 19 the logarithm of the IR-excess luminosity $\log~(L_{{\rm exc}})$ is plotted versus the logarithm of the absorbed luminosity $\log~(L_{{\rm abs}})$. The dashed line represents $L_{{\rm exc}} = L_{{\rm abs}}$. Most of the sample stars lie close to this line. Exceptions include the group II source in the upper left corner which represents R CrA and the open diamond at the bottom of the plot, representing HD 141569. The IR excess luminosity of R CrA is due to confusion with the nearby source CrA IRS7 (Choi & Tatematsu 2004). Furthermore, a set of group I sources with low $L_{{\rm abs}}$values, display relatively high $L_{{\rm exc}}$ values. An explanation for this extra IR excess luminosity could be the presence of a late-type companion. Also the orientation of the system can play a role, especially in group I sources, where the flaring of the disk implies that the line of sight to the central star already passes through the disk at fairly low inclinations ( $i \sim 45^\circ$).

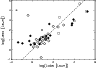	Figure 19: The logarithm of the IR-excess luminosity $\log~(L_{{\rm exc}})$ versus the logarithm of the absorbed luminosity $\log~(L_{{\rm abs}})$. Filled diamonds represent group I, open diamonds group II and squares group III sources. The dashed line is the first bisector. In the left upper corner, the typical error bars are represented by a cross.
Open with DEXTER

4.2 The SED versus the spectral features

The different parameters that characterize the SED were compared to the parameters that describe the infrared solid state bands. In this section we summarize the results.

The UV luminosity of the central star correlates with the PAH luminosities: the absolute PAH luminosity increases with increasing UV radiation. The ratio $L_{{\rm PAH}}/L_{{\rm uv}}$ however decreases with increasing UV luminosity. In Fig. 20, the latter correlation is demonstrated. The dashed line in this figure represents $\log~(L_{{\rm PAH}}/L_{{\rm uv}}) = -0.395 \log~(L_{{\rm uv}}) - 1.99$ or equivalently $L_{{\rm PAH}} = 0.01~L_{{\rm uv}}^{0.6}$. If the emitted PAH luminosity would increase linearly with increasing UV radiation of the central star ( $\log~(L_{{\rm PAH}} \propto L_{{\rm uv}}$), the ratio $L_{{\rm PAH}}/L_{{\rm uv}}$ would have been constant for all $L_{{\rm uv}}$. This is obviously not the case. A higher stellar UV luminosity indeed increases the PAH luminosity, but does this in a sub-linear way: the PAH luminosity increases with  $L_{{\rm uv}}^p$where p=0.6<1. It appears that either the efficiency of the absorption/emission process decreases with increasing UV strength, or that the increasing hardness of the UV photons plays a role. Since hotter stars emit not only more UV photons, but also relatively more high-energy UV photons, the observed trend might be a contrast effect. Short-wavelength UV photons cannot be absorbed by PAHs (no increase of $L_{{\rm PAH}}$), but do contribute to the total UV luminosity $L_{{\rm uv}}$, hence decreasing the luminosity ratio.

It is quite remarkable that some group II sources, even though they have comparable UV luminosities as their group I counterparts, do not display PAH emission. This indicates that the appearance of PAH emission is linked to the group I/II classification of the sources, and does not depend on $L_{{\rm uv}}$ only.

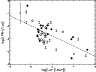Figure 20: The PAH-over-UV luminosity $\log~(L_{{\rm PAH}}/L_{{\rm uv}})$ versus the intensity of the UV radiation field $\log~(L_{{\rm uv}})$. The PAH luminosity is the sum of the luminosities of the PAH features at 3.3, 6.2, 7.7 and 8.6 micron. In the left upper corner, the cross indicates the typical errors. Filled diamonds refer to group I, open diamonds to group II and squares to group III objects. Arrows represent upper limits. The dashed line represents the best linear fit to the data: $\log~(L_{{\rm PAH}}/L_{{\rm uv}}) = -0.395 \log~(L_{{\rm uv}}) - 1.99$.

Open with DEXTER

Suppose that the IR emission is due to PAH molecules that are homogeneously distributed in a spherical, optically thin halo around the star, which has the radius of the ISO-SWS beam (11 $^{\prime \prime }$) at the appropriate distance. It is then possible to estimate the mean particle density of the PAH molecules ($\rho$; see Appendix) in that halo. In Table 9 the computed values are listed. The detected emission of the PAH features at 3.3, 6.2, 7.7 and 8.6 micron has been included. Note that not all emitted PAH flux (e.g. the PAH 11.2 micron flux) is accounted for. This implies that - under the given assumptions - the computed molecule density is a lower limit. For most objects, the resulting values are high compared to the typical ISM PAH density ( $\rho_{{\rm typ}} = 5 \times 10^{-7}~\hbox{cm}^{-3}$; Appendix). We interpret this as an indication that the PAH emission does not emanate from a halo around the central star. For most stars, a denser environment is needed to explain the observed emission.

Table 9: Supposing a homogeneous distribution of the PAH molecules in a halo around the central star, with a radius of the size of the ISO-SWS beam (11 $^{\prime \prime }$) at the appropriate distance, the PAH particle density $\rho$ is computed based on the $L_{{\rm PAH}}/L_{{\rm uv}}$ ratio. All objects in which PAH emission is detected are adopted in this table and are listed according to decreasing PAH-over-UV luminosity.

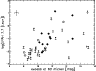	Figure 21: The PAH 7.7 micron luminosity $\log~(L_{{\rm PAH 7.7}})$ versus the excess at 60 micron (in magnitudes). Filled diamonds represent group I, open diamonds group II and squares group III sources. Small symbols indicate undetected features, arrows stand for upper limits. In the left upper corner the typical error bars are displayed.
Open with DEXTER

Habart et al. (2004) have modelled PAH emission in flared circumstellar disks. In their models, they assume PAH molecules containing 40-100 carbon atoms. For PAHs of these sizes, the influence of ionization and photo-evaporation affects the line-flux ratios of the PAH features, in particular the relative strength of the 3.3 micron feature. Even though a clear dependence of the PAH line fluxes on the stellar UV luminosity was observed in our present sample, no correlations between the relative strength of the PAH features and the UV radiation were noted. The line-flux ratio of the 3.3 and 6.2 micron feature - which ranges from 9 to 94% - is independent of the central star's UV field.

The excesses in the K band, at 60, 850 and 1300 micron were compared to the PAH data. Figure 21 shows the luminosity of the PAH 7.7 feature versus the excess at 60 micron. The sources with the faintest 60 micron excesses (by definition mostly group II objects) are those that have the faintest PAH emission. Other PAH features display comparable behaviour.

Notwithstanding these correlations, in general the luminosities of the IR emission bands do not correlate well with the other measured excesses. The lack of correlation between the 850 or 1300 micron excess and the strength of the PAH features shows that the disk mass has no influence on the resulting PAH spectrum. This is consistent with the idea that PAH emission emanates from the surface layers (atmosphere) of the circumstellar disk, which contains only a small fraction of the disk mass. The FWHMs of the IR PAH bands do not correlate with the excesses either.

The Rayleigh-Jeans part of the SED can be modelled with a power law, $\log~(\lambda \mathcal{F}_\lambda) \sim \lambda^{-n}$ in which n is the (sub-)mm spectral index. There is no clear correlation between this index and the strength of the PAH features. The sub-mm slope of the spectrum can be a proxy for the grain size distribution of the cold, large grains in the outer parts and mid-plane of the disk (Acke et al. 2004, henceforth A04). This non-correlation indicates that the grain size distribution of the bulk of the disk's material has no influence on the PAH emission. This is again in agreement with the hypothesis that PAH molecules are excited in and radiate from the disk's atmosphere.

The parameters that describe the amorphous silicate 10 micron feature do not correlate with the IR flux excesses. This indicates that the strength of the 10 micron feature does not depend on the disk mass. The LF and FWHM of the silicate band do not correlate with the sub-mm spectral index either. The grain size distribution of the cold particles in the outer parts of the disk and the warm small silicate grains are independent of each other. Nevertheless, if vertical mixing in the disk is efficient, one may expect that only the smallest grains make it to the surface. Hence the amorphous 10 micron silicate feature may be indicative for the smallest grain sizes (still) present in the disk (A04).

We compared the SEDs of the four stars for which the 11 micron feature is a blend of the PAH 11.2 micron band and the crystalline silicate feature at 11.3 micron (Elias 3-1, AB Aur, HD 100546 and HD 179218) with the SEDs of the other sample stars. The sub-mm spectral index n, 10 micron PF/CF ratio and 1300 micron flux excess of these group I sources make them normal members of this group. The objects AB Aur, HD 100546 and HD 179218 have steep sub-mm slopes ($n\sim4.20$), high 10 micron PF/CF values (larger than the average value 1.91), and intermediate 1300 micron excesses ($\sim$10 mag). The circumstellar material of these sources thus contains cold grains in the outer parts of the disk, significantly smaller than mm-sized (AV04) and small ($\sim$0.1 $\mu$m) warm silicate grains (van Boekel et al. 2003; Bouwman et al. 2001). The estimated disk mass is of the order of 1% of the stellar mass. Elias 3-1 on the other hand is somewhat more peculiar, since n is equal to 3.22 and the 10 micron peak-over-continuum flux ratio is 1.70. The circumstellar matter in this system seems to be more evolved. The disk mass of this source is also high compared to the stellar mass (30%). This is close to the theoretical upper limit for gravitational stability (e.g., Gammie 2001).

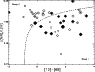Figure 22: Similar plot as Fig. 5. The plotting symbols are scaled proportional to the strength ( $\sum LF/CF$) of the PAH features at 3.3, 6.2, 7.7 and 8.6 micron. The outer limit of the partially filled plotting symbol represents the upper limit for the strength; the filled inner part refers to the part that was actually detected. Diamonds represent group I and group II sources, squares group III objects.

Open with DEXTER

5 Interpretation

We use plotting diagrams like Fig. 5, and include the strength of the IR spectral features by scaling the plotting symbol proportional to LF/CF. In Fig. 22, the sum of the LF/CF ratios of the PAH features at 3.3, 6.2, 7.7 and 8.6 micron is indicated in this manner. The filled diamonds in the plot represent detected features, while open diamonds stand for upper limits. Squares refer to group III sources. The sizes of the diamonds and squares represent the strength of the PAH features on a logarithmic scale. We specifically indicate group III sources since, because of their location in the diagram, they could be confused with group I sources. That group III sources appear in the group I part of the plot is to be expected, since these sources are believed to be in an earlier evolutionary stage; the objects are still highly embedded in the circumstellar environment, which blocks out the stellar light. This makes their SEDs very red and hence they show up in the lower right part of the diagram.

It is striking that the sources that display the strongest PAH emission are mostly group I sources. The Dullemond (2002) model suggests that these objects have circumstellar disks with a flaring geometry. PAH molecules in the atmosphere of the flaring part of these disks are directly irradiated by the UV photons of the central star. This implies that the molecules will be excited and will radiate in the IR, no matter how far out in the disk, as long as the UV field is strong enough. PAH molecules in the atmosphere of the self-shadowed, geometrically flatter disks of group II sources barely see any direct UV radiation, because the puffed-up inner rim blocks out most of the starlight. Hence, in these systems the IR emission bands are expected to be much fainter. Most objects in our sample are consistent with this hypothesis.

Except for MWC 297, no PAH emission is detected in group III sources. The circumstellar matter of these highly embedded objects can probably accurately shield the stellar UV radiation close to the central star. The volume of excited PAH molecules will likely be too small to be observable. Furthermore, the PAH IR radiation has to travel through the dense circumstellar environment. This prohibits the appearance of PAH emission in the group III spectra.

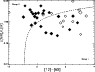	Figure 23: Similar plot as Fig. 22 for the amorphous 10 micron silicate feature. The plotting symbols are scaled proportional to the LF/CF ratio of the feature. The filled diamonds indicate stars with a detected 10 micron emission feature, the open diamonds indicate upper limits.
Open with DEXTER

In Fig. 23 the LF/CF ratio of the amorphous 10 micron silicate feature is plotted in the $L_{{\rm NIR}}/L_{{\rm IR}}$ versus [12]-[60] diagram. Again, the filled diamonds refer to the detected emission features, while the open diamonds represent upper limits. Group III sources, which display amorphous silicate absorption, are not included in this plot. Note that the silicate emission feature appears in both groups. When present, the strength of the emission feature seems to be independent of the classification of the source. Nevertheless, a larger fraction of group I sources have an undetected amorphous silicate feature (10/18 versus 6/22 in group II). M01 suggested that this is probably a selection effect; group II objects that do have 10 micron silicate emission are brighter, and hence are observationally favoured over group II sources without silicate emission. This selection effect plays a smaller role for group I sources, since they are by definition brighter IR emitters.

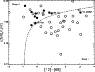	Figure 24: Similar plot as Fig. 5. The filled symbols indicate UXORs, the open symbols are the other HAEBEs in this sample. The 3 UXOR stars that display clear PAH emission are VX Cas, HD 34282 and RR Tau.
Open with DEXTER

According to the definition of Dullemond et al. (2003), 13 of our sample sources are UX Orionis (UXOR) stars. In their paper, the authors argue that the disk geometry of this class of stars must be self-shadowed and hence that UXORs are group II objects. In the present paper we have shown that PAH emission in group II sources is weak. Of the 13 UXORs in our sample, only 3 sources do show significant PAH emission: VX Cas, HD 34282 and RR Tau. They are labelled in Fig. 24. We note that all three lie close to the empirical separation line between groups I and II; they might be transitional objects in which the shadow cast by the inner rim is relatively small. We remind the reader that R CrA and LkH$\alpha$ 224 are not in the plot, and that these sources were classified based on their UXOR behaviour.

In Fig. 25, a selection of 14 of our sample stars shows that the 10 micron emission feature tends to become broader when the peak-over-continuum flux ratio decreases. Small warm silicate grains ($\sim$0.1 $\mu$m) cause a distinct feature that peaks around 9.7 micron, while larger grains ($\sim$2 $\mu$m) induce a broader, less pronounced feature with a peak towards longer wavelengths (Bouwman et al. 2001). van Boekel et al. (2003) interpret this sequence in terms of grain growth in the disk. In Fig. 25 this sequence is reproduced. Our analysis confirms observationally the correlation between the shape and the strength of the amorphous 10 micron silicate band. In their Letter, van Boekel et al. (2003) only plotted group II sources. In this study we have shown that the 10 micron feature is independent of the classification of the objects. Therefore, we also allowed group I sources in Fig. 25. The correlation plot (Fig. 26) of the FWHM versus the PF/CF ratio of the amorphous 10 micron silicate feature shows that indeed the FWHM is larger when the peak-over-continuum flux ratio is lower. Again, no difference is observed between group I and group II sources. The dashed line represents the best fit and has a slope of -0.38 micron.

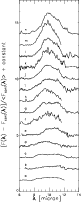Figure 25: The amorphous 10 micron silicate band for 14 of the sample stars. The figure shows the continuum-subtracted flux $\mathcal{F}(\lambda) - \mathcal{F}_{{\rm cont}}(\lambda)$, which was divided by the average value of the underlying continuum $\langle\mathcal{F}_{{\rm cont}}(\lambda)\rangle$. The spectra of the stars are sorted by increasing peak-over-continuum flux from a to n: a- R CrA; b- HR 5999; c- V376 Cas; d- HD 200775; e- T CrA; f- VX Cas; g- HD 104237; h- BF Ori; i- HD 31648; j- HD 163296; k- SV Cep; l- HD 144432; m- UX Ori; n- AB Aur. For clarity, the zero levels of the 14 spectra are shifted.

Open with DEXTER

Van Boekel et al. (2003) suggested the amorphous 10 micron silicate emission originates from the disk's surface. It might appear contradictory that the strength of PAH emission does depend on the shape of the SED (which represents the disk geometry), while the 10 micron feature does not. Nevertheless, the excitation mechanisms for the two emission sources are not the same: the non-equilibrium PAH emission occurs during temperature fluctuations after absorption of a UV photon while the larger silicate grains are in thermal equilibrium with the radiation field of the central star. The models of Habart et al. (2004) show that the PAH emission emanates mostly from the outer parts of the disk ($\sim$100 AU), while the warm silicate emission is confined to the innermost disk regions ($\sim$ a few AU). This reflects the different excitation mechanisms of the small PAH molecules and larger silicate grains, and is in accordance with the observations: spatially resolved PAH emission, on scales of $\sim$10-100 AU, has been detected around HAEBEs by Geers et al. (2004) and van Boekel et al. (2004).

The results of the present paper on both the PAH emission and the silicate emission are consistent with a scenario in which Group I sources have disks that are flaring, whereas Group II sources have flatter disks that are shadowed by the disk's puffed-up inner rim.

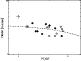	Figure 26: The FWHM of the amorphous 10 micron silicate feature versus the peak-over-continuum flux ratio PF/CF. Filled and open diamonds refer to group I and group II sources respectively. The dashed line represents the best fit to the data; ${\it FWHM} = -0.38 \times {\rm PF/CF} + 3.67$. The typical error bar is indicated in the upper left corner.
Open with DEXTER

6 Conclusions and discussion

We summarize the conclusions which were drawn in the previous sections.

1.

Although in general the PAH emission-line spectrum of HAEBEs is fairly homogeneous, we find clear evidence of differences in size, chemistry and/or ionization for the PAH molecules within the group of Herbig Ae/Be stars.

2.

The 6.2 micron feature is the most frequently detected PAH feature in our analysis. However, in 56% of the spectra where the 6.2 micron feature is detected, the PAH 3.3 micron feature is undetected. Hence the 3.3 micron feature is not a good indicator for the presence of PAH emission, since quite a large fraction of the PAH emitters may be overlooked if one only considers this feature.

3.

PAH emission occurs more frequently, and is stronger in M01 group I sources than in group II sources. If we assume that PAH emission originates in the disk's atmosphere, this result provides strong support for the interpretation of group I sources as sources with flared disks, and group II sources as those with self-shadowed disks.

4.

The strength of the PAH bands is correlated with the strength of the UV radiation of the central star, but the relative strength of the PAH emission decreases with increasing $L_{{\rm uv}}$. This might be due to the fact that the power absorbed by PAHs changes with the spectral energy distribution of the stellar radiation field and decreases with increasing hardness.

5.

Except for MWC 297, no PAH emission is observed in group III sources.

6.

Nanodiamond features were detected in four sample stars, of which three are group I objects and one is group III.

7.

The shape and strength of the 10 micron feature is independent of the M01 classification; strong, weak and even absent emission features are observed in both groups. The 10 micron feature in the spectra of the sample sources indicates that warm amorphous grains are processed in HAEBEs.

8.

Neither the PAH features nor the 10 micron feature depend on disk mass. The masses of the disks are also independent of the classification.

9.

The 11 micron feature does not correlate with the amorphous silicate feature, which could indicate that the PAHs are the dominant ingredient of the feature and/or that crystalline silicates have an independent evolution. The 11 micron complex is in general stronger in group I sources.

10.

Crystalline silicates in emission occur in both types of sources. Z CMa is the only source where the feature is possibly seen in absorption.

We confirm in the present paper that the strongest PAH-emission occurs in group I sources, as was first noted by M01. This is consistent with the idea that group I sources have a flared disk geometry, while group II sources are systems with self-shadowed disks (Dullemond 2002). In a flared disk geometry, the UV photons of the central star can reach the PAH molecules in the surface layers of the disk in a direct way. PAH molecules in the atmosphere of self-shadowed disks are shaded from the UV field by the puffed-up inner rim which casts its shadow over the outer parts of the disk. Therefore, the PAH spectrum of group II sources is expected to be much fainter than that of group I sources. Most sample stars follow this hypothesis.

The amorphous 10 micron silicate feature in this sample of HAEBE stars displays the characteristics of grain growth, independent of the classification of the sources. The small hot silicate grains from which this feature originates seem to have little interaction with the PAH molecules, even though they are believed to radiate from the same locus: the disk atmosphere. Crystallinity seems to be present in more than 1/4 of the stars in our sample.

The global interpretation of the SED of HAEBEs in terms of disk geometry is in many ways consistent with the observations. Future work with new generation IR instruments (e.g., Spitzer) and interferometers (e.g. MIDI/AMBER on the VLTI) will provide the community with new high-quality observations of HAEBE stars, which will offer a good test for the hypotheses suggested in this paper.

Acknowledgements

The authors would like to thank Drs. C. Dullemond, R. van Boekel and R. Waters for many useful discussions that led to significant improvements in the manuscript. We are also indebted to Dr. B. Vandenbussche for his help with the reduction of the ISO-SWS spectra. This publication makes use of data products from the Two micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of the Simbad data base, operated at CDS, Strasbourg, France.

References

• Acke, B., van den Ancker, M. E., Dullemond, C. P., van Boekel, R., & Waters, L. B. F. M. 2004, A&A, 422, 621 [EDP Sciences] [NASA ADS] [CrossRef]
• Allamandola, L. J., Tielens, G. G. M., & Barker, J. R. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef]
• Andersen, J., Lindgren, H., Hazen, M. L., & Mayor, M. 1989, A&A, 219, 142 [NASA ADS]
• Arellano Ferro, A., & Giridhar, S. 2003, A&A, 408, L29 [EDP Sciences] [NASA ADS] [CrossRef]
• Bernasconi, P. A. 1996, A&AS, 120, 57 [NASA ADS] (In the text)
• Berrilli, F., Corciulo, G., Ingrosso, G., et al. 1992, ApJ, 398, 254 [NASA ADS] [CrossRef]
• Bohm, T., & Catala, C. 1993, A&AS, 101, 629 [NASA ADS]
• Böhm, T., & Catala, C. 1994, A&A, 290, 167 [NASA ADS]
• Bouwman, J., de Koter, A., van den Ancker, M. E., & Waters, L. B. F. M. 2000, A&A, 360, 213 [NASA ADS]
• Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [EDP Sciences] [NASA ADS] [CrossRef]
• Cesarsky, C. J., Abergel, A., Agnese, P., et al. 1996, A&A, 315, L32 [NASA ADS] (In the text)
• Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] (In the text)
• Choi, M., & Tatematsu, K. 2004, ApJ, 600, L55 [NASA ADS] [CrossRef] (In the text)
• Cohen, M., & Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef]
• Cohen, M., Kuhi, L. V., Spinrad, H., & Harlan, E. A. 1981, ApJ, 245, 920 [NASA ADS] [CrossRef]
• Corcoran, M., & Ray, T. P. 1998, A&A, 331, 147 [NASA ADS]
• Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, 2246, 0 [NASA ADS] (In the text)
• de Graauw, T., Haser, L. N., Beintema, D. A., et al. 1996, A&A, 315, L49 [NASA ADS] (In the text)
• de Lara, E., Chavarria-K., C., & Lopez-Molina, G. 1991, A&A, 243, 139 [NASA ADS]
• de Winter, D., & Pérez, M. R. 1998, in B[e] stars, ASSL, 233, 269
• de Winter, D., & The, P. S. 1990, Ap&SS, 166, 99 [NASA ADS]
• de Winter, D., van Duuren, R. F., The, P. S., & van den Ancker, M. E. 1995, in Proc. 10th IAP Meet. Circumstellar dust disks and planet formation, ed. R. Ferlet, & A. Vidal-Madjar (Paris: Éditions Frontières), 185
• de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef]
• Drew, J. E., Busfield, G., Hoare, M. G., et al. 1997, MNRAS, 286, 538 [NASA ADS]
• Dullemond, C. P. 2002, A&A, 395, 853 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [EDP Sciences] [NASA ADS] [CrossRef]
• Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] (In the text)
• Dullemond, C. P., van den Ancker, M. E., Acke, B., & van Boekel, R. 2003, ApJ, 594, L47 [NASA ADS] [CrossRef]
• Dunkin, S. K., Barlow, M. J., & Ryan, S. G. 1997, MNRAS, 286, 604 [NASA ADS]
• Dunkin, S. K., & Crawford, I. A. 1998, MNRAS, 298, 275 [NASA ADS] [CrossRef]
• Egan, M. P., Price, S. D., Shipman, R. F., & Tedesco, E. 1997, BAAS, 29, 1294 [NASA ADS] (In the text)
• Finkenzeller, U. 1985, A&A, 151, 340 [NASA ADS]
• Finkenzeller, U., & Mundt, R. 1984, A&AS, 55, 109 [NASA ADS]
• Fluks, M. A., Plez, B., The, P. S., et al. 1994, A&AS, 105, 311 [NASA ADS] (In the text)
• Gammie, C. F. 2001, ApJ, 553, 174 [NASA ADS] [CrossRef] (In the text)
• Geers, V. C., Augereau, J.-C., Pontoppidan, K. M., et al. 2004, Proc. of the ESO Workshop on High Resolution Infrared Spectroscopy in Astronomy (In the text)
• Goodrich, R. W. 1986, ApJ, 311, 882 [NASA ADS] [CrossRef]
• Grady, C. A., Pérez, M. R., Thé, P. S., et al. 1995, A&A, 302, 472 [NASA ADS]
• Gray, R. O., & Corbally, C. J. 1998, AJ, 116, 2530 [NASA ADS] [CrossRef]
• Grinin, V. P., Kozlova, O. V., Thé, P. S., & Rostopchina, A. N. 1996, A&A, 309, 474 [NASA ADS]
• Grinin, V. P., Thé, P. S., de Winter, D., et al. 1994, A&A, 292, 165 [NASA ADS]
• Guillois, O., Ledoux, G., & Reynaud, C. 1999, ApJ, 521, L133 [NASA ADS] [CrossRef]
• Gürtler, J., Friedemann, C., Reimann, H.-G., Splittgerber, E., & Rudolph, E. 1999, A&AS, 140, 293 [NASA ADS]
• Habart, E., Natta, A., & Krügel, E. 2004, A&A, in press [arXiv:astro-ph/0405195] (In the text)
• Hartmann, L., Kenyon, S. J., & Calvet, N. 1993, ApJ, 407, 219 [NASA ADS] [CrossRef]
• Herbig, G. H., & Dahm, S. E. 2002, AJ, 123, 304 [NASA ADS] [CrossRef]
• Hillenbrand, L. A., Strom, S. E., Vrba, F. J., & Keene, J. 1992, ApJ, 397, 613 [NASA ADS] [CrossRef] (In the text)
• Hillenbrand, L. A., Meyer, M. R., Strom, S. E., & Skrutskie, M. F. 1995, AJ, 109, 280 [NASA ADS] [CrossRef]
• Hony, S., Van Kerckhoven, C., Peeters, E., et al. 2001, A&A, 370, 1030 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Houk, N., & Cowley, A. P. 1975, Michigan Catalogue of two-dimensional spectral types for the HD star (Ann Arbor: University of Michigan, Departement of Astronomy)
• Hughes, J. D., Hartigan, P., Graham, J. A., Emerson, J. P., & Marang, F. 1991, AJ, 101, 1013 [NASA ADS] [CrossRef]
• Jaschek, M., Jaschek, C., & Andrillat, Y. 1991, A&A, 250, 127 [NASA ADS]
• Kenyon, S. J., Dobrzycka, D., & Hartmann, L. 1994, AJ, 108, 1872 [NASA ADS] [CrossRef]
• Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] (In the text)
• Kurucz, R. L. 1991, in Stellar Atmospheres-Beyond Classical Models, ed. A. G. Davis Philip, A. R. Upgren, & K. A. Janes (L. Davis press, Schenectady, New York), 441 (In the text)
• Le Bertre, T., Heydari-Malayeri, M., Epchtein, N., Gouiffes, C., & Perrier, C. 1989, A&A, 225, 417 [NASA ADS]
• Léger, A., & Puget, J. L. 1984, A&A, 137, L5 [NASA ADS]
• Lemke, D., Klaas, U., Abolins, J., et al. 1996, A&A, 315, L64 [NASA ADS] (In the text)
• Levreault, R. M. 1988, ApJS, 67, 283 [NASA ADS] [CrossRef]
• Li, A., & Draine, B. T. 2002, ApJ, 572, 232 [NASA ADS] [CrossRef] (In the text)
• Malfait, K., Bogaert, E., & Waelkens, C. 1998, A&A, 331, 211 [NASA ADS]
• Malfait, K., Waelkens, C., Bouwman, J., de Koter, A., & Waters, L. B. F. M. 1999, A&A, 345, 181 [NASA ADS]
• Mannings, V., & Sargent, A. I. 1997, ApJ, 490, 792 [NASA ADS] [CrossRef]
• Marraco, H. G., & Rydgren, A. E. 1981, AJ, 86, 62 [NASA ADS] [CrossRef]
• Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [EDP Sciences] [NASA ADS] [CrossRef]
• Merín, B., Montesinos, B., & Export. 2000, in Disks, Planetesimals, and Planets, ASP Conf. Ser., 219, 399
• Molster, F. J., Waters, L. B. F. M., Tielens, A. G. G. M., Koike, C., & Chihara, H. 2002, A&A, 382, 241 [EDP Sciences] [NASA ADS] [CrossRef]
• Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [EDP Sciences] [NASA ADS] [CrossRef]
• Peeters, E. 2002, Ph.D. Thesis, Rijksuniversiteit Groningen (In the text)
• Piétu, V., Dutrey, A., & Kahane, C. 2003, A&A, 398, 565 [EDP Sciences] [NASA ADS] [CrossRef]
• Rogers, C., Heyer, M. H., & Dewdney, P. E. 1995, ApJ, 442, 694 [NASA ADS] [CrossRef]
• Schmidt-Kaler, T. 1982, Landölt-Bornstein Catalogue, VI/2b (Heidelberg: Springer Verlag) (In the text)
• Shevchenko, V. S., Ezhkova, O. V., Ibrahimov, M. A., van den Ancker, M. E., & Tjin A Djie, H. R. E. 1999, MNRAS, 310, 210 [NASA ADS] [CrossRef]
• Shevchenko, V. S., Ibrahimov, M. A., & Chernysheva, T. L. 1991, Astron. Zh., 68, 466 [NASA ADS] (SvA, 35, 229)
• Shevchenko, V. S., & Yabukov, S. D. 1989a, A. Zh., 66, 718 [NASA ADS]
• Shevchenko, V. S., & Yabukov, S. D. 1989b, SvA, 33, 370 [NASA ADS]
• Shore, S. N., Brown, D. N., Bopp, B. W., et al. 1990, ApJS, 73, 461 [NASA ADS] [CrossRef]
• Siebenmorgen, R., Prusti, T., Natta, A., & Müller, T. G. 2000, A&A, 361, 258 [NASA ADS] (In the text)
• Slettebak, A. 1966, ApJ, 145, 121 [NASA ADS] [CrossRef]
• Terada, H., Imanishi, M., Goto, M., & Maihara, T. 2001, A&A, 377, 994 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Thé, P. S., de Winter, D., & Pérez, M. R. 1994, A&AS, 104, 315 [NASA ADS]
• Tielens, A. G. G. M., Hony, S., van Kerckhoven, C., & Peeters, E. 1999, in The Universe as Seen by ISO, ESA SP-427, 767 (In the text)
• Tjin A Djie, H. R. E., The, P. S., Andersen, J., et al. 1989, A&AS, 78, 1 [NASA ADS]
• Val'tts, I. E., Slysh, V. I., Voronkov, M. A., & Migenes, V. 2002, in Exotic Stars as Challenges to Evolution, ASP Conf. Ser., 279, 279
• van Boekel, R., Waters, L. B. F. M., Dominik, C., et al. 2003, A&A, 400, L21 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• van Boekel, R., Waters, L. B. F. M., Dominik, C., et al., 2004, A&A, 418, 177 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• van den Ancker, M. 1999, Ph.D. Thesis, University of Amsterdam
• van den Ancker, M. E., de Winter, D., & Tjin A Djie, H. R. E. 1998, A&A, 330, 145 [NASA ADS]
• van den Ancker, M. E., Bouwman, J., Wesselius, P. R., et al. 2000a, A&A, 357, 325 [NASA ADS]
• van den Ancker, M. E., Wesselius, P. R., & Tielens, A. G. G. M. 2000b, A&A, 355, 194 [NASA ADS]
• van den Ancker, M. E., Meeus, G., Cami, J., Waters, L. B. F. M., & Waelkens, C. 2001, A&A, 369, L17 [EDP Sciences] [NASA ADS] [CrossRef]
• Van Kerckhoven, C., Tielens, A. G. G. M., & Waelkens, C. 2002, A&A, 384, 568 [EDP Sciences] [NASA ADS] [CrossRef]
• Vermeij, R., Peeters, E., Tielens, A. G. G. M., & van der Hulst, J. M. 2002, A&A, 382, 1042 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Voshchinnikov, N. V. 1981, Astronomicheskij Tsirkulyar, 1200, 1 [NASA ADS]
• Waelkens, C., Waters, L. B. F. M., de Graauw, M. S., et al. 1996, A&A, 315, L245 [NASA ADS] (In the text)
• Whitcomb, S. E., Gatley, I., Hildebrand, R. H., et al. 1981, ApJ, 246, 416 [NASA ADS] [CrossRef]
• Whittet, D. C. B., Kirrane, T. M., Kilkenny, D., et al. 1987, MNRAS, 224, 497 [NASA ADS]
• Whittet, D. C. B., Prusti, T., Franco, G. A. P., et al. 1997, A&A, 327, 1194 [NASA ADS]
• Zinnecker, H., & Preibisch, T. 1994, A&A, 292, 152 [NASA ADS]

 

  
Online Material

Table 1: The sample of HAEBEs used in this study, based on Thé et al. (1994) and Malfait et al. (1998). For each object, the observed ISO spectra are given; S01 refers to SWS AOT01, P40 to PHT-S and C04 to CAM04 spectra.

Table 3: The presence of the PAH features at 3.3, 6.2, 7.7 and 8.6 micron, the NAN features at 3.4 and 3.5 micron, the 11 micron complex (COMP 11) and the amorphous 10 micron silicate feature (Si 9.7) in the spectra of the sample stars. The sources are classified in 3 groups. $\surd$: detection; - : no detection; n.s.: no spectrum available at these wavelengths. $\surd^{ a}$: tentative detection; $\surd^{ b}$: tentative detection in the PHT-S spectrum; $\surd^{ c}$: feature undetected in the SWS spectrum; $\surd^{ d}$: feature undetected in the PHT-S spectrum (see Sect. 2.5). For the amorphous silicate feature, E stands for emission and A for absorption. BD+40$^\circ$4124, R CrA and LkH$\alpha$ 224 have not been classified based on the diagram in Fig. 5, which is indicated by the question mark.

Table 4: The line fluxes LF of the IR features included in this analysis. a(-b) represents $a \times 10^{-b}$.

Table 5: The continuum flux at the peak wavelength of the IR features included in this analysis. When the amorphous 10 micron silicate band was present, the PAH features are superimposed on the band. In this case (flagged by $^\ast$), the silicate feature is regarded as being part of the underlying continuum of the PAH features. Hence the indicated continuum flux of the PAH band is the flux of the silicate feature at the central wavelength of that PAH band.

Table 6: The stellar parameters for the sample sources. The distance d which we used in the analysis and spectral type (Sp. T.) are given. The visual extinction $A_{\rm V}$, the logarithm of the effective temperature $\log T_{{\rm eff}}$, of the stellar luminosity $\log L$, of the stellar UV luminosity $\log L_{{\rm uv}}$ and of the observed bolometric luminosity $\log L_{{\rm bol}}$ are presented as well. The latter quantities are estimated based on the photometric measurements. Furthermore, the ratio of the IR excess luminosity over the stellar luminosity is computed. Ten of the sample sources have a ratio larger than unity, hence are not consistent with a passive reprocessing disk. The last 4 columns contain the IR excess fluxes in K (2.2 $\mu$m), at 60, 850 and 1300 micron. $^\bigstar$ These stars are UX Orionis objects according to the definition of Dullemond et al. (2003). $^{\spadesuit }$ Probable confusion with the nearby source CrA IRS7.

Appendix

We estimate the density of PAH molecules in a spherical, optically thin halo of radius R around the central star, supposing a homogeneous distribution of the PAHs. Furthermore, we assume that all UV radiation absorbed by the PAH molecules is re-emitted in the IR bands.

The cross-section of a single PAH molecule with 50 C atoms is typically $\sigma_{\rm C} = 2.5 \times 10^{-14}~\hbox{cm}^2$ (Li & Draine 2002). The luminosity of the PAH emission $L_{{\rm PAH}}$depends on the number of emitting PAHs $N_{{\rm PAH}}$, the average energy of the absorped UV photons $\langle E_{{\rm uv}} \rangle$, the number of UV photons $N_{{\rm uv}}$ that pass by per second and the cross-section of a single PAH molecule over the average surface S of the sphere:

 

$$L_{{\rm PAH}} N_{{\rm PAH}} \langle E_{{\rm uv}} \rangle N_{{\rm uv}} \frac{\sigma_{\rm C}}{S}$$ =

$$\frac{4\pi}{3} R^3 \rho \times \langle E_{{\rm uv}} \rangle \time... ...rac{L_{{\rm uv}}}{\langle E_{{\rm uv}} \rangle} \times \frac{\sigma_{\rm C}}{S}$$ =

$$\frac{L_{{\rm PAH}}}{L_{{\rm uv}}} 0.37\ \rho\left[\hbox{cm}^{-3}\right]\ R[\hbox{AU}].$$ = (1)

Assuming that all IR PAH emission is observed in the measured PAH bands, the sum of the line fluxes of these features is connected to the PAH luminosity by

  

$$L_{{\rm PAH}} [L_{\odot}] 2.4\times 10^{6} \sum_{{\rm PAH~j}} 4\pi (d[pc])^2 \times LF_j \biggl[ \frac{W}{m^2} \biggr]$$ = (2)

$$\sum_{{\rm PAH~j}} L_{{\rm PAH~j}} [L_{\odot}]$$ = (3)

in which the terms of the sum are the luminosities of the individual PAH features. Hence from formulas 1 and 2, an estimate for $\rho$ can be derived, assuming that the radius of the halo R is equal to the radius of the ISO-SWS beam (11 $^{\prime \prime }$) at the distance d of the source, or

$$R[\hbox{AU}] = 11\ d[\rm pc].$$

A typical value for the ISM abundance of PAHs over H atoms ( $[{\rm PAH}/{\rm H}]=10^{-7}$) can be found in Tielens et al. (1999). Typical ISM electron densities $\rho_{e^-}$ are in the order of 5 cm^-3. Hence a typical value for the ISM density of PAH molecules is

$$\rho_{{\rm typ}} = \biggl[\frac{{\rm PAH}}{{\rm H}}\biggr] \times \rho_{{\rm e}^-} = 5 \times 10^{-7} \hbox{cm}^{-3}.$$ (4)