H. J. Rocha-Pinto 1,4 - C. Flynn 2 - J. Scalo 3 - J. Hänninen 2 - W. J. Maciel 1 - G. Hensler 5
1 - Depart. of Astronomy, IAG/USP,
Rua do Matão 1226, 05508-900 São Paulo, Brazil
2 - Tuorla Observatory, Väisäläntie 20, 21500 Pikkiiö, Finland
3 - Depart. of Astronomy, The University of Texas at Austin, USA
4 -
Depart. of Astronomy, University of Virginia, PO Box 3818, Charlottesville,
VA 22903-0818, USA
5 -
Institut für Theoretische Physik und Astrophysik, Universität
Kiel, 24098 Kiel, Germany
Received 3 November 2003 / Accepted 12 May 2004
Abstract
In this paper, we investigate some chemokinematical properties of the Milky Way
disk, by using a sample composed by 424 late-type dwarfs. We show that the velocity dispersion
of a stellar group correlates with the age of this group, according to a law proportional
to t0.26, where t is the age of the stellar group. The temporal evolution of the vertex
deviation is considered in detail. It is shown that the vertex deviation does not seem to depend
strongly on the age of the stellar group. Previous studies in the literature seem to not have found
it due to the use of statistical ages for stellar groups, rather than individual ages. The
possibility to use the orbital parameters of a star to derive information about its birthplace is
investigated, and we show that the mean galactocentric radius is likely to be the most reliable
stellar birthplace indicator. However, this information cannot be presently used to derive radial
evolutionary constraints, due to an intrinsic bias present in all samples constructed from nearby
stars. An extensive discussion of the secular and stochastic heating mechanisms commonly invoked to
explain the age-velocity dispersion relation is presented. We suggest that the age-velocity
dispersion relation could reflect the gradual decrease in the turbulent velocity dispersion from
which disk stars form, a suggestion originally made by Tinsley & Larson
(1978, ApJ, 221, 554) and
supported by several more recent disk evolution calculations. A test to distinguish between
the two types of models using high-redshift galaxies is proposed.
Key words: stars: late-type - stars: statistics - Galaxy: evolution - Galaxy: solar neighbourhood
The publication of the data from HIPPARCOS (ESA 1997) improved substantially kinematical studies of the solar neighbourhood. Simultaneous measurements of parallaxes and proper motions, made by the astrometric satellite, allow the calculation of tangential velocities for tens of thousands of stars. In spite of it, a complete study of the stellar velocity distribution in the vicinity of the Sun is yet to be made, since the database for radial velocities has not increased in the same proportion, and is still a major problem in stellar kinematic studies.
Table 1: Solar neighbourhood late-type dwarfs (complete table is only available in electronic form at the CDS).
The correlation between kinematical and chemical properties of the disk stars is a classical result of galactic astronomy (Roman 1950, 1952; Eggen et al. 1962; Edvardsson et al. 1993, hereafter Edv93). The knowledge about both the kinematical and chemical properties of the stellar populations gives several clues about the evolution of a galaxy, unveiling the complex processes that concurred in its building.
Recently, we have built a large sample having chromospheric ages and photometric metallicities. This sample was used to study the age-metallicity relation (Rocha-Pinto et al. 2000a, hereafer Paper I) and the star formation history (Rocha-Pinto et al. 2000b, hereafter Paper II). It is interesting to use these data in the study of chemodynamical constraints. Our sample is small, compared to that used in some recent investigations, but it can still be useful for the investigation of some important constraints. Several papers that address constraints between stellar ages and kinematical properties make use of ages calculated by statistical methods, that is, average ages for a group of stars. The advantage of our approach is that we consider absolute ages, and the constraints are expected to give a more accurate description of the galactic kinematics.
This paper is organized as follows. The kinematical sample is described in detail in Sect. 2. The age-velocity dispersion relation (hereafter, AVR) is derived in Sect. 3, where we show that all components of the spatial velocity of the star present a similar AVR. In Sect. 4, we investigate the temporal evolution of the vertex deviation. Section 5 investigates the possibility of using orbital parameters to find the stellar birthplace and age. In Sect. 6, we attempt to use orbital information to derive some radial constraints to chemical evolution parameters. The AVR is readdressed in Sect. 7, where we present a thorough discussion of its interpretation, concluding that secular disk heating mechanisms are incapable of accounting for the large dispersions of old disk stars, and suggesting that a major component of the AVR may be due to disk cooling, as originally suggested by Tinsley & Larson (1978). Our conclusions are presented in Sect. 8.
We have looked for kinematical data in the literature, for the 729 stars of the initial sample and for the 261 of the aditional sample (see Paper I for details). Proper motions were obtained from the HIPPARCOS catalogue or the SIMBAD database. Radial velocities come from several sources: Barbier-Brossat et al. (1994), Duflot et al. (1995a, 1995b), Fehrenbach et al. (1996, 1997), Nordström et al. (1997) and in the SIMBAD database. In total, 459 stars have radial velocities in the literature, from which 424 have chromospheric ages lower than 15 Gyr. In the following, we will use only these 424 stars.
We calculated the spatial velocities U, V and W, in a system pointing to the galactic
anticenter, the direction of the galactic rotation and the direction towards the north galactic
pole, respectively, using the equations of Johnson & Soderblom (1987). The velocities are further
transformed into peculiar velocities with respect to the local standard of rest, u, v and w,
using the basic solar motion![]() (Mihalas & Binney 1981),
(Mihalas & Binney 1981),
![]() .
.
The sample is given in Table 1, available at the CDS,
where we list, respectively, the HD number (or BD number for a few stars),
the chromospheric index
![]() ,
the photometric metallicity [Fe/H],
the radial velocity, the chromospheric age, calculated according to the formalism
described in Paper I, the peculiar velocities u, v and w with their measurement
errors, and some parameters referred to later on.
,
the photometric metallicity [Fe/H],
the radial velocity, the chromospheric age, calculated according to the formalism
described in Paper I, the peculiar velocities u, v and w with their measurement
errors, and some parameters referred to later on.
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{0617f1.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg17.gif) |
Figure 1:
Velocity diagrams |
| Open with DEXTER | |
Spatial velocity distributions are strongly dependent on the mean age of the stellar group studied. We can consider stellar subgroups having different ages, to investigate their velocity distribution. The most direct division in our sample is set by the chromospheric activity levels, since it was constructed from chromospheric activity surveys. Active and inactive stars must present different velocity distributions, that will reflect the mean ages of these subgroups. The active stars are expected to be more concentrated in the velocity space, compared to the inactive stars, as shown by Soderblom (1990) for a sample of 32 active stars. The same result was found by Jeffries & Jewell (1993), from a sample of dwarfs detected in the extreme ultraviolet by ROSAT.
In Fig. 1, we show the velocity diagrams for these two subgroups of chromospheric activity. The diagrams for the active stars are presented in the left panels, and those for the inactive stars in the right panels. The plot confirms the previous conclusions. Active stars present a low velocity dispersion, that is explained by their youth, compared to the inactive stars. Note that some active stars present velocity components typical of an advanced age. Soderblom (1990) has already pointed to this problem. However, in his sample of 32 dwarfs, only 3 showed high velocity components. Rocha-Pinto & Maciel (1998, hereafter RPM98) have increased this number to 10. The present sample contains 29 stars like these. Jahreiß et al. (1999) also mention the existence of chromospherically active high velocity stars. Comparing isochrone, chromospheric and lithium ages of these objects, Rocha-Pinto et al. (2002) concluded that they can be single stars formed out of the coalescence of short-period binaries. The coalescence makes the star look chromospherically younger, because the orbital angular momentum of the former binary is transformed into rotational angular momentum of the newly formed single star; however, since the binary formed some Gyr before the coalescence, the movement of its center of mass around the Galactic center, later inherited by the single star, shows the kinematical signatures of an advanced age. We call these stars CYKOS (chromospherically young, kinematically old stars).
The velocity dispersion of a stellar group is larger, the older is the group. This relation is usually interpreted as a result of gravitational perturbations experienced by the stars during their translations around the galactic center. In spite of the fact that several processes which can cause an increase in the velocity dispersion are relatively well known, it is not completely understood which of them is the main responsible mechanism in this heating, and this comes mainly from the disagreement between the observed dispersions amongst disk dwarfs found by different studies. Several authors have studied this issue (Wielen 1974; Mayor 1974; Cayrel de Strobel 1974; Carlberg et al. 1985; Knude et al. 1987; Strömgren 1987; Meusinger et al. 1991; Wielen et al. 1992; Dehnen & Binney 1998; Fuchs et al. 2001) but their results are quite conflicting. It is not clear whether this was caused by selection effects, a problem which plagues severely kinematical studies, or is an intrinsic property of different stellar classes used by them (see Fridman et al. 1994).
In Fig. 2, we present plots of peculiar velocities as a function of the stellar age. It can be seen clearly that the number of high-velocity stars grows towards older ages. In the middle panel, v clearly shows the asymmetric drift (Binney & Merrifield 1998), that is, the older stars rotate around the galactic center with slower velocities with respect to the local standard of rest.
In order to calculate the velocity dispersion we had to further examine our stellar sample. First of all, there are three clear outliers, as seen in Fig. 2 (solid circles). For these outliers at least one of the velocity components is not typical of thin disk stars. These are all CYKOS, which are not supposed to be real young stars, thus, we have discarded them from this analysis. Furthermore, we have also excluded from the velocity dispersion calculations all the stars with metallicity [Fe/H] < -0.5, since they are likely to belong to the thick disk. This condition excludes 24 stars (empty triangles in Fig. 2), so we are left with 397 stars (crosses) from the 424 star sample.
Each component of the velocity dispersion is calculated in equal star number bins instead of equal
age range bins. Because the sample stars are not evenly distributed in age we have used bins
with equal number of stars (
![]() ). This way we have an equal weight for
each data point when fitting the AVR.
). This way we have an equal weight for
each data point when fitting the AVR.
The AVRs that we have found can be approximated by power laws of the kind
![]() ,
where
,
where ![]() is a time scale for the growth of the velocity
dispersion and t is the stellar age. The exponent x is 0.26
is a time scale for the growth of the velocity
dispersion and t is the stellar age. The exponent x is 0.26 ![]() 0.01, 0.24
0.01, 0.24 ![]() 0.02, 0.30
0.02, 0.30 ![]() 0.03 and 0.34
0.03 and 0.34 ![]() 0.02, for
0.02, for
![]() ,
,
![]() ,
,
![]() and
and ![]() ,
respectively. These exponents can be considered equal within
,
respectively. These exponents can be considered equal within ![]() .
The relation in w is slightly steeper.
.
The relation in w is slightly steeper.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0617f2.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg27.gif) |
Figure 2: Spatial velocities as a function of age. The disk heating can be clearly seen in this picture. Some stars, marked in the plot by solid circles and empty triangles, were discarded from the sample, before the final calculations of the age-velocity dispersion relation (see text). |
| Open with DEXTER | |
Nevertheless, this fitting is very sensitive to the last age bin. If it is removed, we find
![]() for
for
![]() .
If, on the other hand, we use bins equally spaced in age,
we find x equal to 042
.
If, on the other hand, we use bins equally spaced in age,
we find x equal to 042 ![]() 0.04, 0.40
0.04, 0.40 ![]() 0.02, 0.48
0.02, 0.48 ![]() 0.04 and 0.41
0.04 and 0.41 ![]() 0.03, for
0.03, for
![]() ,
,
![]() ,
,
![]() and
and ![]() ,
respectively. The large difference between these exponents and those calculated for equal star number bins reinforces our concerns about the sensitivy of the observed AVR. The equal star number binning was chosen
to avoid many of the uncertainties that arise from the use of age range bins with poor statistics.
,
respectively. The large difference between these exponents and those calculated for equal star number bins reinforces our concerns about the sensitivy of the observed AVR. The equal star number binning was chosen
to avoid many of the uncertainties that arise from the use of age range bins with poor statistics.
Other fitting laws commonly used in the literature were tried.
For a parametrization like
![]() ,
we have
found
,
we have
found
![]()
![]() 0.04,
xu = 0.23
0.04,
xu = 0.23 ![]() 0.04,
xv = 0.37
0.04,
xv = 0.37 ![]() 0.07 and
xw = 0.30
0.07 and
xw = 0.30 ![]() 0.09. For
0.09. For
![]() ,
we have
,
we have
![]()
![]() 0.03,
xu = 0.23
0.03,
xu = 0.23 ![]() 0.04,
xv = 0.28
0.04,
xv = 0.28 ![]() 0.04 and
xw = 0.35
0.04 and
xw = 0.35 ![]() 0.06.
0.06.
Our age-velocity dispersion relations are given in Fig. 3, which shows that our dispersions are considerably higher than those found by Knude et al. (1987), Strömgren (1987) and Meusinger et al. (1991), for the older ages. The agreement is substantially better for the earlier studies by Wielen (1974) and Cayrel de Strobel (1974). The data given by Fuchs et al. (2001) follow closely those of Wielen (1974), and are not shown in the figure.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{0617f3.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg33.gif) |
Figure 3:
Characterization of the kinematical sample with a velocity ellipsoid. The panels a)- d) stand for the relations between the age and the velocity dispersions in the
components u, v, w, and for the total space velocity (
|
| Open with DEXTER | |
The data in Fig. 3 are presented also in Table 2. In this
table, the first column gives the age range considered, and the other columns give, respectively,
![]() and the error in this quantity;
and the error in this quantity; ![]() ,
,
![]() ,
,
![]() ,
and their respective errors, each shown after the corresponding velocity dispersion; the axial
ratios
,
and their respective errors, each shown after the corresponding velocity dispersion; the axial
ratios
![]() and
and
![]() ;
and the asymmetric drift
according to the age of the stellar group.
;
and the asymmetric drift
according to the age of the stellar group.
Although our data agrees at first glance with those given by Fuchs et al. (2001),
the fitted velocity dispersion laws in their work and ours differ considerably. It is important
to understand the cause of this difference. Fuchs et al. have used a sample of late-type
stars based on chromospheric ages, like ours. But they have not taken in consideration
the metallicity dependence of the chromospheric indices (Rocha-Pinto & Maciel 1998),
when calculating the stellar ages. Moreover, they have weighted each star by the modulus of the
vertical velocity,
![]() ,
before calculating the velocity dispersions.
The
,
before calculating the velocity dispersions.
The
![]() weighting was introduced by Wielen (1974) to take into account
the probability for the detection of each star in the local sample, given their vertical
oscillation with respect to the Galactic plane.
weighting was introduced by Wielen (1974) to take into account
the probability for the detection of each star in the local sample, given their vertical
oscillation with respect to the Galactic plane.
By disregarding the metallicity dependence of the chromospheric ages, Fuchs et al. (2001)
are likely to mix hotter older stars with somewhat "warm'' intermediate-age stars. This could boost the velocity dispersion to high values at 4-6 Gyr, resulting in a steeper AVR.
This is illustrated more properly in Fig. 4, for u. We have
investigated this effect with our sample. The chromospheric age was recalculated
using the calibration given by Donahue (1993), that is, without any correction
for the metallicity of the star. The stars were binned by groups of 40, as in the former cases.
For
![]() ,
we have
,
we have
![]()
![]() 0.05,
xu = 0.29
0.05,
xu = 0.29 ![]() 0.05,
xv = 0.39
0.05,
xv = 0.39 ![]() 0.05 and
xw = 0.37
0.05 and
xw = 0.37 ![]() 0.08. This result shows that by disregarding the [Fe/H] dependence in the chromospheric ages, the exponents of the AVR have increased by 6% to 39% from the supposedly real values. This is an important result, since it can shed some light into the different slopes found by different groups, using different star groups. As Fridman et al. (1994) point out, there are two main points of view in the literature for the AVR exponent: Wielen and colleagues
have found higher values than Knude et al. (1987),
Strömgren (1987) and Meusinger et al. (1991). The results by the Heidelberg group
are largely based on chromospheric age estimates that disregard the metallicity dependence of
the chromospheric ages, while the later studies are based on isochrone ages which are free of
this systematic error. Since our results use a corrected cromospheric age scale, we should expect
to find exponents closer to those found from isochrone age studies.
0.08. This result shows that by disregarding the [Fe/H] dependence in the chromospheric ages, the exponents of the AVR have increased by 6% to 39% from the supposedly real values. This is an important result, since it can shed some light into the different slopes found by different groups, using different star groups. As Fridman et al. (1994) point out, there are two main points of view in the literature for the AVR exponent: Wielen and colleagues
have found higher values than Knude et al. (1987),
Strömgren (1987) and Meusinger et al. (1991). The results by the Heidelberg group
are largely based on chromospheric age estimates that disregard the metallicity dependence of
the chromospheric ages, while the later studies are based on isochrone ages which are free of
this systematic error. Since our results use a corrected cromospheric age scale, we should expect
to find exponents closer to those found from isochrone age studies.
Table 2: Velocity dispersions, axial ratios and asymmetrical drift.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0617f4.eps} \end{figure}](/articles/aa/full/2004/32/aa0617/Timg94.gif) |
Figure 4: Increase of the u peculiar velocity with age, for uncorrected (panel a)) and corrected (panel b)) chromospheric ages. The effect of neglecting the [Fe/H] dependence of the chromospheric age calibration is seen in panel a), where the mixing of old hotter stars with intermediate-age stars boosts the velocity dispersion around 4-6 Gyr, yielding a steeper AVR, which otherwise would present a slower increase (panel b)). |
| Open with DEXTER | |
The
![]() weighting also affects considerably the resulting AVR.
For
weighting also affects considerably the resulting AVR.
For
![]() ,
and using the uncorrected chromospheric ages, as above, as in
Fuchs et al. (2001), we have found
,
and using the uncorrected chromospheric ages, as above, as in
Fuchs et al. (2001), we have found
![]()
![]() 0.08,
xu = 0.36
0.08,
xu = 0.36 ![]() 0.09,
xv = 0.49
0.09,
xv = 0.49 ![]() 0.13 and
xw = 0.53
0.13 and
xw = 0.53 ![]() 0.07. Qualitatively similar values are found when we use the
0.07. Qualitatively similar values are found when we use the
![]() weighting with the corrected ages and our preferred heating law
weighting with the corrected ages and our preferred heating law
![]() :
:
![]()
![]() 0.02,
xu = 0.47
0.02,
xu = 0.47 ![]() 0.02,
xv = 0.57
0.02,
xv = 0.57 ![]() 0.04 and
xw = 0.46
0.04 and
xw = 0.46 ![]() 0.03. However, these fits are somewhat worse than the previous ones for which no vertical weight was applied.
0.03. However, these fits are somewhat worse than the previous ones for which no vertical weight was applied.
We have explored the extent to which subgiant and thick disk star contamination can
affect the AVR. Because these stars are expected to come from a hotter Galactic
component, their presence would surely inflate the velocity dispersions of the oldest bins,
making the AVR artificially steeper. Although our adopted metallicity cut [Fe/H] < -0.5
already prevents our AVRs from being severely contaminated by thick disk stars, a proper
separation between the Galactic components can only be made with both kinematical and chemical
data (Nemec & Nemec 1993; Ojha et al. 1996; Chiba & Beers 2000).
This is a classical problem of mixture decomposition that can be reasonably addressed with
a multivariate finite mixture analysis. We have used the EMMIX
program![]() (McLachlan et al.
1999), which fits normal mixture models to multivariate data, using maximum likelihood
through the Expectation-Maximization algorithm (Dempster et al. 1977). An initial group
configuration must be provided to the program, from which it looks for the best partition amongst
the data. The best partition is not very much sensitive to this initial guessing, which can be
either a random grouping or a pre-grouping using a K-means clustering (Hardigan 1975).
The number of groups, n, among which the data will be partitioned must also be provided as
input. Non-parametric tests (e.g., Tarter & Lock 1993) or physical considerations
can be used to select n. Since we are mostly interested in singling out eventual thick-disk
contaminators, we will assume n=2. We applied the partitioning algorithm to our initial sample
of 424 stars, in the four-dimensional space defined by [Fe/H], u, v and w. The average
properties of the two best-partitioned groups are shown in Table 3.
The statistical decomposition yields a young, kinematically-cold, metal-rich group and a
predominantly old, kinematically-hot, metal-poor group. It is reasonable to identify this later
group with a different, contaminant population, although its
(McLachlan et al.
1999), which fits normal mixture models to multivariate data, using maximum likelihood
through the Expectation-Maximization algorithm (Dempster et al. 1977). An initial group
configuration must be provided to the program, from which it looks for the best partition amongst
the data. The best partition is not very much sensitive to this initial guessing, which can be
either a random grouping or a pre-grouping using a K-means clustering (Hardigan 1975).
The number of groups, n, among which the data will be partitioned must also be provided as
input. Non-parametric tests (e.g., Tarter & Lock 1993) or physical considerations
can be used to select n. Since we are mostly interested in singling out eventual thick-disk
contaminators, we will assume n=2. We applied the partitioning algorithm to our initial sample
of 424 stars, in the four-dimensional space defined by [Fe/H], u, v and w. The average
properties of the two best-partitioned groups are shown in Table 3.
The statistical decomposition yields a young, kinematically-cold, metal-rich group and a
predominantly old, kinematically-hot, metal-poor group. It is reasonable to identify this later
group with a different, contaminant population, although its
![]() is somewhat
lower than typical thick disk metallicities, suggesting that old thin disk stars may have
interloped this group. EMMIX outputs the a posteriori probability, pi, of each star being
member of group i. To avoid thin-disk interlopers, we have considered a likely contaminator
every star with
is somewhat
lower than typical thick disk metallicities, suggesting that old thin disk stars may have
interloped this group. EMMIX outputs the a posteriori probability, pi, of each star being
member of group i. To avoid thin-disk interlopers, we have considered a likely contaminator
every star with
![]() .
After discarding these stars from the sample, the AVR
was calculated with and without the
.
After discarding these stars from the sample, the AVR
was calculated with and without the
![]() weighting, using the law
weighting, using the law
![]() .
The resulting exponents can be found in Table 4, together with a summary of all other
fitted AVRs. We have found that the presence of thick-disk and subgiant contaminators in the
sample can increase the exponent of the power-law AVR by up to 40%, in all velocity components.
This caveat must be taken into account in every AVR investigation, especially
in face of the growing evidence supporting the singularity of the thick disk
(Robin et al. 1996; Gratton et al. 2000).
.
The resulting exponents can be found in Table 4, together with a summary of all other
fitted AVRs. We have found that the presence of thick-disk and subgiant contaminators in the
sample can increase the exponent of the power-law AVR by up to 40%, in all velocity components.
This caveat must be taken into account in every AVR investigation, especially
in face of the growing evidence supporting the singularity of the thick disk
(Robin et al. 1996; Gratton et al. 2000).
Table 3: Properties of the best-partition groups.
Table 4: Fitted age-velocity dispersion relations.
In Figs. 3e and 3f, we present the value of the ratio between the semiaxes of the velocity ellipsoid,
![]() and
and
![]() .
The values we have found are closer to those in Wielen (1974) and in Cayrel de Strobel (1974), as well as those found by Dehnen (1998), for the 14369 HIPPARCOS stars. The axial ratios seem to be nearly constant, in opposition to the findings by Knude et al. (1987), according
to which the young groups have a velocity ellipsoid with a substantially high
.
The values we have found are closer to those in Wielen (1974) and in Cayrel de Strobel (1974), as well as those found by Dehnen (1998), for the 14369 HIPPARCOS stars. The axial ratios seem to be nearly constant, in opposition to the findings by Knude et al. (1987), according
to which the young groups have a velocity ellipsoid with a substantially high
![]() ,
that decreases for old groups. This behaviour, as well as the very high values for
,
that decreases for old groups. This behaviour, as well as the very high values for
![]() found by Meusinger et al. (1991) could reflect basically selection effects in the data samples.
Finally, in panel g we show the asymmetric drift, which is the trend of the rotational velocity of a stellar population lagging behind more and more slowly
the LSR, the larger its velocity dispersions (Gómez & Mennessier 1977;
Binney & Merrifield 1998).
found by Meusinger et al. (1991) could reflect basically selection effects in the data samples.
Finally, in panel g we show the asymmetric drift, which is the trend of the rotational velocity of a stellar population lagging behind more and more slowly
the LSR, the larger its velocity dispersions (Gómez & Mennessier 1977;
Binney & Merrifield 1998).
In spite of the apparent constancy of the velocity axial ratios, a sudden jump is seen in both
![]() and
and
![]() at 1.2 Gyr ago, amongst our data as well as in the
analysis of Wielen (1974), Knude et al. (1987) and Meusinger et al. (1991). We presently do not have an explanation for this. If this feature is real, as these different analyses suggest, this could be an important constraint to the AVR theory.
at 1.2 Gyr ago, amongst our data as well as in the
analysis of Wielen (1974), Knude et al. (1987) and Meusinger et al. (1991). We presently do not have an explanation for this. If this feature is real, as these different analyses suggest, this could be an important constraint to the AVR theory.
The stars show a velocity distribution that can be characterized by a velocity ellipsoid
(Schwarzschild 1907; Mihalas & Binney 1981), with semiaxes
![]() ,
,
![]() and
and
![]() ,
that correspond to the principal velocity dispersions of the stellar group. The
semiaxes of the ellipsoid generally do not correspond to the coordinate axes used for the
calculation of the spatial velocities (i.e., u, v and w), and some calculations must be
done for the determination of these axes. In practice, it is known that the semiaxes
,
that correspond to the principal velocity dispersions of the stellar group. The
semiaxes of the ellipsoid generally do not correspond to the coordinate axes used for the
calculation of the spatial velocities (i.e., u, v and w), and some calculations must be
done for the determination of these axes. In practice, it is known that the semiaxes
![]() and
and
![]() are in the galactic plane (for instance, see Dehnen & Binney 1998), and the problem is restricted to the determination of the angle
are in the galactic plane (for instance, see Dehnen & Binney 1998), and the problem is restricted to the determination of the angle ![]() that indicates the galactic
longitude towards which the principal major axis of the velocity ellipsoid points. This
angle is called vertex deviation. Once determined, the peculiar velocity dispersions can be
calculated with respect to the semiaxes of the velocity ellipsoid.
that indicates the galactic
longitude towards which the principal major axis of the velocity ellipsoid points. This
angle is called vertex deviation. Once determined, the peculiar velocity dispersions can be
calculated with respect to the semiaxes of the velocity ellipsoid.
The vertex deviation ![]() is defined by
is defined by
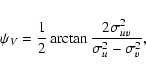 |
(1) |
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{0617f5.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg141.gif) |
Figure 5: Projection of the velocity ellipsoid of the stars younger than 1 Gyr onto the uv-plane. The tilted ellipsis with respect to the coordinate axes illustrates the vertex deviation of the data points. |
| Open with DEXTER | |
Figure 5 presents the data points used for the youngest age bin used in this analysis. The dashed ellipsis is the projection of the velocity ellipsoid onto the uv-plane. The vertex deviation amongst these youngs stars is clearly seen by the tilt of the ellipsis with respect to the coordinate axes.
The classical behaviour for the vertex deviation can be found in Delhaye (1965).
The vertex deviation is negative (-50
![]() )
amongst O and B stars, but positive (
)
amongst O and B stars, but positive (![]()
![]() )
amongst young dwarfs (mainly A type stars). Later dwarfs also present positive vertex deviations, but considerably smaller. The vertex deviation for very red and old stars is quoted as nearly zero. This relation between vertex deviation and spectral type have led many
investigations to assume an implicit relation between the age of the stellar group
and its vertex deviation (e.g., Oblak 1983; Oblak & Crézé 1985), since later dwarfs have a higher average age than early dwarfs.
)
amongst young dwarfs (mainly A type stars). Later dwarfs also present positive vertex deviations, but considerably smaller. The vertex deviation for very red and old stars is quoted as nearly zero. This relation between vertex deviation and spectral type have led many
investigations to assume an implicit relation between the age of the stellar group
and its vertex deviation (e.g., Oblak 1983; Oblak & Crézé 1985), since later dwarfs have a higher average age than early dwarfs.
Surprisingly, we do not find a similar behaviour in our data, as can be seen from Table 5. Either using all the stars in our sample or just those with vertical velocity smaller than 15 km s-1, there is weak indication of an evolutive trend in the vertex deviation, if any. Moreover, the greatest vertex deviation is not seen amongst the youngest stars.
Almost all of the former studies in the literature that tried to measure the dependence of the vertex deviation on the age used groups of stars with several ages. An average age for the group was calculated from the observed properties of stars, and this average age was used in the derivation of the function ![]() .
The main difference between this approach and ours is that the former can
only measure integrated kinematical properties of a stellar group (as a function of spectral type or colour). They are cumulative kinematical properties. In our approach, since we have ages for
individual stars, we can consider the kinematical properties in each age bin, in a differential
approach.
.
The main difference between this approach and ours is that the former can
only measure integrated kinematical properties of a stellar group (as a function of spectral type or colour). They are cumulative kinematical properties. In our approach, since we have ages for
individual stars, we can consider the kinematical properties in each age bin, in a differential
approach.
Table 5: Vertex deviation.
There are few studies in the literature that do use a differential approach for the study of the vertex deviation. Their results give some support to our findings, regardless of their authors conclusion on the contrary. Byl (1974) has used evolutionary isochrones to calculate
average stellar ages of nine stellar groups ranging from 0.38 to 10.50 Gyr old. The evolution of
the vertex deviation amongst these groups does not show the implicit smooth trend expected
from the classical theory, although much of the scatter could be blamed on the small number of stars in each of the nine groups. Wielen (1974) has also found high values for ![]() at advanced ages, and a variation uncorrelated with age. Moreover, Wielen has also
argued that the near zero vertex deviation found amongst late-type dwarfs could be a selection
effect: classic vertex deviation studies usually limited the samples to those stars with
orbital eccentricity smaller than a given value, to avoid the contamination of the sample with
high-velocity stars. By doing this, they sample the phase space within an ellipsis with
semi-axes pointing to the main Galactic plane axes, thus biasing the sample. For old, late-type
stars, which have large velocity dispersions, this bias would favour low
at advanced ages, and a variation uncorrelated with age. Moreover, Wielen has also
argued that the near zero vertex deviation found amongst late-type dwarfs could be a selection
effect: classic vertex deviation studies usually limited the samples to those stars with
orbital eccentricity smaller than a given value, to avoid the contamination of the sample with
high-velocity stars. By doing this, they sample the phase space within an ellipsis with
semi-axes pointing to the main Galactic plane axes, thus biasing the sample. For old, late-type
stars, which have large velocity dispersions, this bias would favour low ![]() measurements.
By using a less biasing selection criteria,
measurements.
By using a less biasing selection criteria,
![]() km s-1 and
km s-1 and
![]() km s-1, Wielen showed that
km s-1, Wielen showed that ![]() in the range 10
in the range 10
![]() to 30
to 30
![]() could be found amongst stellar groups thought to have nearly zero deviation. We have tested both selection criteria with our sample. The vertex deviation amongst our stars using the classical selection criteria (orbital eccentricity
could be found amongst stellar groups thought to have nearly zero deviation. We have tested both selection criteria with our sample. The vertex deviation amongst our stars using the classical selection criteria (orbital eccentricity ![]() 0.15 and
0.15 and
![]() km s-1) and after
applying Wielen's selection criteria are given in Table 5.
These data were calculated within each of the original bins, using only the stars that
passed the selection criteria. Since the number of stars passing the Wielen criteria at the oldest age bin was very small, we combined the two oldest age bins.
The result is somewhat close to the expected bias pointed by Wielen. However, it is clear that the
value
km s-1) and after
applying Wielen's selection criteria are given in Table 5.
These data were calculated within each of the original bins, using only the stars that
passed the selection criteria. Since the number of stars passing the Wielen criteria at the oldest age bin was very small, we combined the two oldest age bins.
The result is somewhat close to the expected bias pointed by Wielen. However, it is clear that the
value ![]() varies substantially depending on the selection criteria used. Same order variations
in the measured
varies substantially depending on the selection criteria used. Same order variations
in the measured ![]() have also been reported when the sample is limited by a coordinate
range (Oblak 1983; Núñez & Figueras 1984).
have also been reported when the sample is limited by a coordinate
range (Oblak 1983; Núñez & Figueras 1984).
This variation could be caused by statistical errors in the calculation of ![]() .
If we consider
only the error propagation from the velocity errors (taking as
.
If we consider
only the error propagation from the velocity errors (taking as ![]()
![]() 2 km s-1 for each star), through a Monte Carlo simulation, we have
2 km s-1 for each star), through a Monte Carlo simulation, we have
![]() .
But the error also depends on the Poisson noise due to sample size. We have run a bootstrap routine to randomly select stars in each bin (so that some stars were counted twice or more and some were neglected from a given bin) and calculated the vertex deviation. This bootstrap selection was performed 1000 times. We have found that the average error in
.
But the error also depends on the Poisson noise due to sample size. We have run a bootstrap routine to randomly select stars in each bin (so that some stars were counted twice or more and some were neglected from a given bin) and calculated the vertex deviation. This bootstrap selection was performed 1000 times. We have found that the average error in ![]() is
is ![]()
![]() .
This indicates that statistical errors alone cannot explain the variations we have found.
.
This indicates that statistical errors alone cannot explain the variations we have found.
Even non-differential analyses have not made a strong case for a smooth vertex deviation-age
relation. The data compiled by Mayor (1972) shows a large scatter in the value of ![]() for each, adopted coeval, stellar groups. Particularly interesting is the fact that active HK dwarfs in his sample present a smaller vertex deviation (12
for each, adopted coeval, stellar groups. Particularly interesting is the fact that active HK dwarfs in his sample present a smaller vertex deviation (12
![]() )
than inactive HK dwarfs (20
)
than inactive HK dwarfs (20
![]() ), a
result that bears resemblance with the entries of Table 5. Mayor concludes that
large vertex deviations are observed amongst stars of all ages, provided that their orbital eccentricity is low. Recently, Ratnatunga & Upgren (1997) used a maximum-likelihood analysis in a sample of more than 700 Vyssotsky K and M dwarfs and showed that their vertex deviation is significantly non-zero, amounting to
), a
result that bears resemblance with the entries of Table 5. Mayor concludes that
large vertex deviations are observed amongst stars of all ages, provided that their orbital eccentricity is low. Recently, Ratnatunga & Upgren (1997) used a maximum-likelihood analysis in a sample of more than 700 Vyssotsky K and M dwarfs and showed that their vertex deviation is significantly non-zero, amounting to
![]()
![]()
![]() .
.
The existence of a smooth decreasing vertex deviation-age relation could provide an important clue about the cause of the vertex deviation. Theoretical work on this subject are generally split between those theories that propose the vertex deviation is a reflection of the initial conditions, which we will call congenital scenario, and those, which explain it as the effect of perturbations in the local Galactic potential, here called perturbation scenario.
Congenital scenarios proposed include the natural evolution of the original stellar configuration at birthplace taken as a spiral arm (Wooley 1970; Yuan 1971), the launching of stars recently formed at the spiral arms with postshock velocity (Hilton & Bash 1982) or emerging from an expanding shell (Moreno et al. 1999), a temporary arrangement in the phase space due to the epicycles (Byl & Ovenden 1973; Bassino et al. 1986) or oscillations in the stellar orbits (House & Innanen 1975) and the superposition of macroscopic motions over the Galactic rotation (Kato 1970). Perturbation scenarios address the effects of non-axisymmetry in the Galactic potential (Sanz & Catalá 1987; Cubarsí 1990) and gravitational perturbations caused by the spiral arms (Mayor 1970, 1972).
So far, none of these hypotheses can explain satisfactorily the vertex deviation phenomenon in all spectral classes. Some of the explanations are particularly suitable for the earlier stars, like the launching of recently formed stars by spiral arms or expanding shells, while other are more appropriate to explain the deviation found amongst late-type stars.
A third class of explanation has gained momentum in the last years. The substantial improvement
in the observational techniques has allowed the investigation of the velocity phase space of the
solar neighbourhood with unprecedented resolution. These studies have showed very convincingly
that the velocity phase space is not homogeneous, but punctuated by small scale structures and
moving groups (e.g., Dehnen 1998; Skuljan et al. 1999).
Dehnen (1998) has shown that these moving groups themselves are the main responsible for
the vertex deviation, and it is easy to understand this: Clumpy structures in the phase space
puts a large weight on
![]() ,
yielding a larger
,
yielding a larger ![]() .
This idea was first
raised by Palous (1986), who argues that the Hyades and Sirius superclusters
contaminate local samples, imprinting on their velocity distribution the vertex deviation.
Moreno et al. (1999) present a similar reasoning for the explanation of the negative
vertex deviation amongst OB stars.
.
This idea was first
raised by Palous (1986), who argues that the Hyades and Sirius superclusters
contaminate local samples, imprinting on their velocity distribution the vertex deviation.
Moreno et al. (1999) present a similar reasoning for the explanation of the negative
vertex deviation amongst OB stars.
This could explain why the vertex deviation varies so widely depending on the selection
criteria used and the coordinate range of the stars used in its determination.
These different
criteria would discard totally or partially some moving groups from the phase
space, and this
could induce to uncorrelated variations of
![]() .
In this case, the
vertex deviation
problem would be reduced to explaining the surviving of old moving groups and
their peculiar velocities. A very original and promising idea was introduced
by Dehnen (2000) and further developed by Fux (2001) and
Mühlbauer & Dehnen (2003), according
to which several features of the velocity phase space can be explained by
the kinematic interaction
between the outer disk and the Galactic central bar.
.
In this case, the
vertex deviation
problem would be reduced to explaining the surviving of old moving groups and
their peculiar velocities. A very original and promising idea was introduced
by Dehnen (2000) and further developed by Fux (2001) and
Mühlbauer & Dehnen (2003), according
to which several features of the velocity phase space can be explained by
the kinematic interaction
between the outer disk and the Galactic central bar.
From its spatial velocities and distance, it is possible to calculate the orbit of a star around the
galactic center. The orbit is characterized by some parameters: perigalactic and apogalactic distance, ![]() and
and ![]() ,
average galactocentric distance, Rm, orbital eccentricity, e, and maximum height above the galactic plane,
,
average galactocentric distance, Rm, orbital eccentricity, e, and maximum height above the galactic plane,
![]() .
When a star is born from a molecular cloud, e and
.
When a star is born from a molecular cloud, e and
![]() are nearly zero. With time, due to the orbital diffusion, both parameters will grow, and the stellar orbit will become less circular. The orbits were integrated in a galactic potential, consisting of an exponential thin disk, a spherical bulge and a dark halo, as described in Flynn et al. (1996). The value for the orbital parameters were calculated for 380 of the 459 stars in the kinematical sample, which correspond to the number of stars that follow the some additional criteria used in Table 2 of Paper I, that is, stars should be closer than 80 pc to avoid substantial reddening in the photometric indices, brighter than 8.3 mag in V magnitude, less active than
are nearly zero. With time, due to the orbital diffusion, both parameters will grow, and the stellar orbit will become less circular. The orbits were integrated in a galactic potential, consisting of an exponential thin disk, a spherical bulge and a dark halo, as described in Flynn et al. (1996). The value for the orbital parameters were calculated for 380 of the 459 stars in the kinematical sample, which correspond to the number of stars that follow the some additional criteria used in Table 2 of Paper I, that is, stars should be closer than 80 pc to avoid substantial reddening in the photometric indices, brighter than 8.3 mag in V magnitude, less active than
![]() and have nominal chromospheric age lower than 15 Gyr.
and have nominal chromospheric age lower than 15 Gyr.
Let us consider the problem of the determination of the stellar birthplace. Wielen (1977) claims that it is impossible to know with accuracy the galactocentric radius of the stellar birthplace from its orbit, due to the diffusion of stellar orbits in phase space caused by local fluctuations of the Galactic gravitational field. In each epicycle, the star would be scattered in random directions, and this would destroy any information about the origin of the star.
Grenon (1987) proposed that, even if the present stellar position cannot be taken as an indicative of its birthplace, the average radius of its orbit, Rm, is kept close to the initial galactocentric radius of the stellar birthplace. This would make possible the use of Rm in the derivation of radial constraints, like the abundance gradients and radial variation of the age-metallicity relation.
Wielen et al. (1996) criticized this conclusion, pointing that Rm must also be
considerably modified due to the orbital diffusion. Due to irregularities produced by, for instance, giant molecular clouds and spiral arms, the average galactocentric radius of a stellar orbit Rm, at time t, would not be directly linked with the galactocentric radius where the star was born, Rm(0). Wielen et al. have described the star scattering process due to the orbital diffusion, and have shown that after some Gyr it is impossible to know where the star was born, from Rm, with a accuracy better than some kpc. Also, to explain the high metallicity dispersion in Edv93 data, these authors suggest that the Sun and some other nearby stars were born closer to the galactic center, and have migrated to their present location due to the orbital diffusion. Supposing a very well mixed ISM, the authors propose that the stellar birthplace, Ri, can be roughly estimated from the age and metallicity of a star, by the equation
![\begin{figure}
\par\includegraphics[width=5.3cm,clip]{0617f6.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg163.gif) |
Figure 6: Comparison between two proposed birthplace indicators. The solid line shows the prediction by Wielen et al. (1996). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{0617f7.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg164.gif) |
Figure 7: Correlation between two proposed birthplace indicators. Panel a), Rm versus age for our sample; panel b), Ri versus age for our sample; panel c), Rm versus age for the sample of Edv93; panel d), Ri versus age for the sample of Edv93. The dashed line indicates the present galactocentric radius of the Sun. |
| Open with DEXTER | |
Our sample can be used to test whether Ri and Rm present the same behaviour predicted by Wielen et al. (1996). In Fig. 6 we show a plot with values for Ri and Rm. The solid line indicates the predictions by Wielen et al. (1996). The scattering is too large to allow a significant conclusion. Moreover, the small range of Rm in our sample makes difficult the comparison with the theory.
Nevertheless, if Ri (or Rm) are good indicators of the stellar birthplace, we must find a relation between these parameters and the stellar age, since a finite time is necessary for a star to be able to move from its birthplace to the present galactocentric radius of the Sun. Thus, we expect to find stars born at several galactocentric radii only amongst the oldest stars, since the youngest would not have had time to migrate radially 1 or 2 kpc from its initial position.
In Fig. 7, we show how these parameters are linked with age. Panel a presents Rm
as a function of the stellar age, while panel b presents Ri. The data are for our sample.
Rm presents a well-marked correlation with age. It is clear that young objects have all
![]() ,
and that older stars present a higher proportion of objects coming from different galactocentric radii. If we assume that Ri represents the stellar birthplace radius, we do not find the same behaviour. It is difficult to understand how a star with less than 1 Gyr could come from galactocentric radii much smaller than
,
and that older stars present a higher proportion of objects coming from different galactocentric radii. If we assume that Ri represents the stellar birthplace radius, we do not find the same behaviour. It is difficult to understand how a star with less than 1 Gyr could come from galactocentric radii much smaller than ![]() .
Panels c and d present the same comparisons, for the sample by Edv93. The same conclusion can be taken from them. The comparison for Ri is even worse than for our sample.
.
Panels c and d present the same comparisons, for the sample by Edv93. The same conclusion can be taken from them. The comparison for Ri is even worse than for our sample.
This figure shows that Eq. (2) is not suitable to calculate the stellar birthplace radius. However, it does not imply that the outwards migration of the Sun has not occurred. The formalism by Wielen et al. is developed for a well-mixed interstellar medium, in which the metallicity dispersion seen amongst the stars is produced by the orbital diffusion. However, if there is instead a non-negligible metallicity dispersion in the gas, at each galactocentric radius, the straightforward use of the stellar age and [Fe/H] in Eq. (2) will only give a rough estimate for the birthplace radius.
We have also tested this idea with a simulation of the stellar orbits diffusion. We have inserted tracer stars in an exponential disk under the 3D model for the Galaxy, as described in Flynn et al. (1996). New stars are born each time step, simulating a constant SFR. The stars are given small random kicks in their velocities at each time step. Stars near the solar circle get sufficient kicks for being heated up to have values of the velocity dispersion ellipsoid similiar to the observed one. Closer to the galactic center, the heating is greater, increasing exponentially inward with the same scale length as the disk light distribution (circa 4 kpc), with less heating in the outer disk. Inside 2 kpc, the heating is cut off, to simulate less molecular clouds there and to simplify the computation. Indeed, such stars are not expected to be deflected onto orbits which eventually take them out to the solar circle over the disk lifetime.
At the end of the simulation, we find all stars which are on or near to the solar circle. We have
computed the mean guiding radius of their present orbit, Rm and compared it with the a priori
known birth radius Ri. The relationship found between them is
![]() as expected by the theoretical considerations performed
by Wielen et al. (1996).
as expected by the theoretical considerations performed
by Wielen et al. (1996).
The problem does indeed come when one tries to recover the relationship from the data. The only way we have of recovering Ri from the data is to use [Fe/H]. The disk gradient is only about 0.1 dex/kpc, and the scatter in the local metallicities is (intrinsically) of the same order or larger (e.g., Edv93; Paper I). Here, by scatter, we mean the width of the [Fe/H] distribution. In our sample, Rm lies in the range 6 to 10 kpc, so that the birth radii of the stars lie in the range 7 to 9 kpc. Over such a short range in the disk, the mean metallicity of the stars changes by only 0.1 dex in either direction, whereas the intrinsic dispersion (over all ages) is 0.12-0.3 dex.
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{0617f8.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg167.gif) |
Figure 8: Comparison of constraints for two samples, one internal to the solar radius, and the other external to it. Panel a), age-metallicity relation; panel b), metallicity distribution; panel c), age distribution. |
| Open with DEXTER | |
Our results show that Rm can surely give some information about the birthplace radii
of the stars. But this information can be used only in a statistical sense, according
to Eq. (3), due to the intrinsic scatter in the Rm relation introduced by the orbital
diffusion. This must be kept in mind, when interpreting the results from the next section.
Edv93 have used Rm to investigate the radial variation of some chemical constraints, like the abundance ratios and the age-metallicity relation. We decided to use our data sample to derive constraints to the age-metallicity relation, the radial variation of the metallicity distribution, the star formation rate and the abundance gradient in the disk.
Due to the narrow range of Rm in our data, we have divided the sample in only two bins according to their galactocentric radius: stars with Rm<8 kpc and stars with Rm>8 kpc, which corresponds to stars born internally and externally to the solar galactocentric radius, respectively. These groups are composed by 158 and 222 stars, respectively, adding up to 380 objects.
Ideally, it should be possible to derive such constraints from a large data sample as ours. However, a close look at Fig. 7a shows that there is an intrinsic bias in the Rm distribution.
The younger objects were born in the vicinity of ![]() ,
and are badly represented for
,
and are badly represented for
![]() .
Any attempt to derive radial constraints are affected by this bias.
.
Any attempt to derive radial constraints are affected by this bias.
Let us consider three possible constraints: the age-metallicity relation, the radial variation of the metallicity distribution, and the star formation history (from the age distribution), shown in Fig. 8. At first glance, there is no radial variation in the age-metallicity relation (Fig. 8a), in opposition to the conclusions by Edv93, that the most inner parts of the Galaxy have evolved more rapidly. However, from Fig. 8c we see that the sample internal to the solar radius does not comprise many young stars, since that have had not time to migrate to the solar vicinity. Since the younger stars are generally richer, the radial variation presented in this figure cannot be considered real. This explains why the metallicity distribution of the inner sample presents a paucity of metal rich stars, compared to the metallicity distribution of the outer sample (see Fig. 8b). The different age distributions in Fig. 8c also must not be interpreted as radial variation of the star formation history, because our sample does not have an homogeneous Rm distribution as a function of the stellar age.
In Fig. 9 we show the metallicity as a function of the birthplace (upper panel). The different symbols separate the objects according to their age, namely: stars with ages lower than 1 Gyr (filled squares), stars with ages of 1-3 Gyr (open circles), stars with ages from 3 to 6 Gyr (dotted triangles), and stars with ages greater than 6 Gyr (upside down triangles). We can see that the metal-rich objects are those that were born in the vicinity of the Sun, whereas the metal-poor objects come from several galactocentric radii. The same behaviour is present in Edv93 data (lower panel).
The present sample is not particularly useful in the study of radial abundance gradients, in view of the uncertainties in the determination of Rm and the magnitude of the gradients, which is comparable to the average dispersion in the abundances as taken in the whole range of galactocentric radii. However, it is interesting to note that an average [Fe/H] gradient of -0.07 to -0.09 dex/kpc as adopted by Maciel (2002) for open cluster stars fits rather nicely our data points with ages under 6 Gyr as shown by the filled squares, open circles and dotted triangles in the upper panel of Fig. 9.
The conclusion by Edv93, that the inner parts of the Galaxy have experienced a more rapid enrichment, seems somewhat premature. There is no unbiased coverage in Rm and [Fe/H] in their sample to allow such conclusion, just like in our sample. Although radial constraints are extremely needed for the understanding of the chemical evolution of the Galaxy, presently there is no sample of late-type dwarfs that can be used in their derivation.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{0617f9.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg169.gif) |
Figure 9: Metallicity-Rm diagram. Upper panel: our data; lower panel, Edv93's data. The symbols indicate: filled squares, stars having ages lower than 1 Gyr; open circles, stars aging 1-3 Gyr; dotted triangles, stars having ages from 3 to 6 Gyr; upside down triangles, stars with ages greater than 6 Gyr. |
| Open with DEXTER | |
Our results for the AVR, while fairly consistent with independent work, add to the growing evidence
that heating by scattering by GMCs, spiral structures, and accretion, are insufficient to explain
the observations. Here we summarize the problem, and suggest that a different interpretation
of the AVR should be re-investigated. In the following, we mostly consider velocity dispersions
with respect to a cylindrical coordinate system, where r, ![]() and z represent the radial,
azimuthal and vertical components of the space velocity, respectively. For Solar neighbourhood stars, we can adopt
and z represent the radial,
azimuthal and vertical components of the space velocity, respectively. For Solar neighbourhood stars, we can adopt
![]() .
.
Our major results are:
Perhaps the discrepancy is due to the many approximations made in the Fokker-Planck theory, which
are well-summarized by Villumsen (1985). Villumsen presented numerical simulations
that overcame many of these shortcomings. After a brief initial period of fairly rapid increase
of heating, the velocity dispersions flatten out to give
![]() (in agreement
with Lacey's analytical treatment), and
(in agreement
with Lacey's analytical treatment), and
![]() .
By the end of the simulations
(
.
By the end of the simulations
(![]() 5
5 ![]() 109 yr) the ratios of velocity dispersions were
109 yr) the ratios of velocity dispersions were
![]() .
Thus the velocity dispersion is too round, although not as round as
found by Lacey's (1984) analytic result. Judging from the papers cited above, transient
spiral arms would reduce the
.
Thus the velocity dispersion is too round, although not as round as
found by Lacey's (1984) analytic result. Judging from the papers cited above, transient
spiral arms would reduce the
![]() ratio, but the addition of disk
accretion should increase it again, by an unknown amount. Extrapolating Villumsen's
velocity dispersions to 1010 yr indicates that the total dispersion will not exceed 40 km s-1, while
ratio, but the addition of disk
accretion should increase it again, by an unknown amount. Extrapolating Villumsen's
velocity dispersions to 1010 yr indicates that the total dispersion will not exceed 40 km s-1, while ![]() will only reach
will only reach ![]() 15 km s-1, compared to about 70 and 30 km s-1, respectively, found here for the oldest stellar group. A major approximation made by Villumsen (1985) is that the number of clouds in the simulations was greatly reduced to 200 for computational reasons while the masses of the clouds were reduced by the square root of this factor to compensate. It is not known how the diffusion argument on which this scaling is based might affect the results. However, recent high-accuracy simulations of
15 km s-1, compared to about 70 and 30 km s-1, respectively, found here for the oldest stellar group. A major approximation made by Villumsen (1985) is that the number of clouds in the simulations was greatly reduced to 200 for computational reasons while the masses of the clouds were reduced by the square root of this factor to compensate. It is not known how the diffusion argument on which this scaling is based might affect the results. However, recent high-accuracy simulations of
![]() GMC heating by some of us (Hänninen & Flynn 2002) give an even weaker increase of the velocity dispersion with time, although the velocity ellipsoid is flatter.
GMC heating by some of us (Hänninen & Flynn 2002) give an even weaker increase of the velocity dispersion with time, although the velocity ellipsoid is flatter.
The situation may actually be worse than this. In a pair of little-cited papers, Yasutomi
& Fujimoto (1989, 1991) presented a significantly more sophisticated
treatment of the star-cloud scattering problem, including the non-Keplerian potential of
individual clouds (assumed Plummer), the nonlinear part of the background disk gravitational
field (neglected in earlier work which assumed harmonic oscillation through the linear
epicyclic approximation), the galactic shear of stars and gas clouds, and the non-uniform
distribution of massive molecular clouds in the Galactic plane (annulus-like 4-8 kpc ring and
spiral-like distributions), but restricted to two dimensions. The main approximation made is
that stars only interact with their nearest gas cloud. The major effect discovered
was that statistically anisotropic encounters (direct and catching-up encounters)
lead to important systematic accelerations and decelerations of the stars, corresponding to
dynamical friction. This leads to very slow growth of the velocity dispersion for times
![]() 1 Gyr, with
1 Gyr, with ![]() 0.20 for a uniform distribution of clouds, and even
smaller values
0.20 for a uniform distribution of clouds, and even
smaller values ![]() 0.10 to 0.15 for clouds distributed in an annulus or spiral arms.
In all cases the maximum total velocity dispersion was only 30 to 50 km s-1, a value reached
quickly (
0.10 to 0.15 for clouds distributed in an annulus or spiral arms.
In all cases the maximum total velocity dispersion was only 30 to 50 km s-1, a value reached
quickly (![]() 1 Gyr), before dynamical friction effects become important. These results
led Yasutomi & Fujimoto to suggest that if a scattering process is to account for the
observations, either gas clouds must have been more massive and numerous billions of years
ago (Semenzato 1987), and/or there must exist a high surface density of
massive dark objects, such as the
1 Gyr), before dynamical friction effects become important. These results
led Yasutomi & Fujimoto to suggest that if a scattering process is to account for the
observations, either gas clouds must have been more massive and numerous billions of years
ago (Semenzato 1987), and/or there must exist a high surface density of
massive dark objects, such as the
![]() black holes proposed by Lacey &
Ostriker (1985). The generalization of these calculations to three
dimensions by Yasutomi & Fujimoto (1991) showed that the general results are robust.
In none of their models did the total velocity dispersion reach values in excess of 35 km s-1, and in fact slowly decreased with time due to the dynamical friction effect, after
the initial transient heating episode for models with a uniform spatial distribution of clouds.
Furthermore, they quote a result for the velocity ellipsoid
black holes proposed by Lacey &
Ostriker (1985). The generalization of these calculations to three
dimensions by Yasutomi & Fujimoto (1991) showed that the general results are robust.
In none of their models did the total velocity dispersion reach values in excess of 35 km s-1, and in fact slowly decreased with time due to the dynamical friction effect, after
the initial transient heating episode for models with a uniform spatial distribution of clouds.
Furthermore, they quote a result for the velocity ellipsoid
![]() ,
clearly too round compared to the results found here or in earlier work.
,
clearly too round compared to the results found here or in earlier work.
Kokubo & Ida (1992) reexamined the problem using direct integrations
of epicycle orbits to obtain probability distributions for the change in orbital
parameters, but obtained results similar to the other methods. After an initial
rapid increase, the later phases gave x = 0.25 for all three velocity
dispersion components (smaller than our result) and
![]() (slightly larger than our result). For GMC masses of
(slightly larger than our result). For GMC masses of
![]() ,
the
total velocity dispersion only reaches about 30 km s-1 while
,
the
total velocity dispersion only reaches about 30 km s-1 while ![]() only
reaches 10 km s-1 after 1010 yr. Kokubo & Ida find that if the GMC mass is increased to
only
reaches 10 km s-1 after 1010 yr. Kokubo & Ida find that if the GMC mass is increased to
![]() ,
,
![]() increases to about 50 km s-1, while
increases to about 50 km s-1, while ![]() reaches about 20 km s-1. Kokubo & Ida's claim to the contrary, these values are still significantly smaller than found here and elsewhere.
reaches about 20 km s-1. Kokubo & Ida's claim to the contrary, these values are still significantly smaller than found here and elsewhere.
Thus the current situation is that none of the above investigations of
scattering/heating models can account for either x,
![]() or the total or vertical velocity dispersions found here and elsewhere for
older stars, even when shear motions are included. Including more physical
realism has apparently only exacerbated or accentuated the problems in earlier work.
or the total or vertical velocity dispersions found here and elsewhere for
older stars, even when shear motions are included. Including more physical
realism has apparently only exacerbated or accentuated the problems in earlier work.
The ratio
![]() has also been estimated for at least two other disk galaxies,
NGC 488 (Gerssen et al. 1997) and NGC 2985 (Gerssen et al. 2000). The values that they found (0.70
has also been estimated for at least two other disk galaxies,
NGC 488 (Gerssen et al. 1997) and NGC 2985 (Gerssen et al. 2000). The values that they found (0.70 ![]() 0.19 and 0.85
0.19 and 0.85 ![]() 0.1, respectively) are larger than found in the solar annulus, although still significantly less
than unity. The existence of a broad range in this ratio among disk galaxies would significantly
complicate the interpretation, especially since there are several different mechanisms for producing
a ratio of a given value and uncertainty in the result for each mechanism. We therefore concentrate
on the absolute values of the velocity dispersions themselves, and confine our interpretation to
the solar annulus where the data is probably most accurate.
0.1, respectively) are larger than found in the solar annulus, although still significantly less
than unity. The existence of a broad range in this ratio among disk galaxies would significantly
complicate the interpretation, especially since there are several different mechanisms for producing
a ratio of a given value and uncertainty in the result for each mechanism. We therefore concentrate
on the absolute values of the velocity dispersions themselves, and confine our interpretation to
the solar annulus where the data is probably most accurate.
One possibility is that the lifetimes of the clouds were assumed to be too large (infinite).
Fujimoto (1980), using a significantly different stochastic approach to the problem
(theory of random walks in the field of a harmonic oscillator), assumed that GMC lifetimes are small, ![]() 107 yr. At the time of this work, the large lifetimes (
107 yr. At the time of this work, the large lifetimes (![]() 3
3 ![]() 108 yr) suggested by Solomon et al. (1979), based on coagulation requirements, were popular, and so several papers dismiss Fujimoto's calculations as unrealistic because of the small adopted cloud lifetimes. However subsequent work has strongly suggested smaller lifetimes about equal to what Fujimoto adopted for "GMC''s (see Elmegreen 2000; Hartmann et al. 2001, and references therein). The effect of the short lifetimes is
significant because it provides a strong fluctuating force component which is missing
in all other work. Kroupa (2002), unaware of Fujimoto's work, independently pointed
out how the small cloud lifetimes would add a fluctuating acceleration to stars because they
experience a time-varying potential on the timescale of their passage by each cloud. However,
Fujimoto obtained total velocity dispersions and vertical velocity dispersions of only 40 km s-1 and 6 km s-1 after 1010 yr. This result must be partly related to Fujimoto's small assumed GMC mass of 2
108 yr) suggested by Solomon et al. (1979), based on coagulation requirements, were popular, and so several papers dismiss Fujimoto's calculations as unrealistic because of the small adopted cloud lifetimes. However subsequent work has strongly suggested smaller lifetimes about equal to what Fujimoto adopted for "GMC''s (see Elmegreen 2000; Hartmann et al. 2001, and references therein). The effect of the short lifetimes is
significant because it provides a strong fluctuating force component which is missing
in all other work. Kroupa (2002), unaware of Fujimoto's work, independently pointed
out how the small cloud lifetimes would add a fluctuating acceleration to stars because they
experience a time-varying potential on the timescale of their passage by each cloud. However,
Fujimoto obtained total velocity dispersions and vertical velocity dispersions of only 40 km s-1 and 6 km s-1 after 1010 yr. This result must be partly related to Fujimoto's small assumed GMC mass of 2 ![]()
![]() ,
but the scaling of the heating rate with GMC mass derived by Kokubo & Ida (1992) suggests that even this short-lifetime effect will be insufficient to provide the large velocity dispersions of the older stars.
,
but the scaling of the heating rate with GMC mass derived by Kokubo & Ida (1992) suggests that even this short-lifetime effect will be insufficient to provide the large velocity dispersions of the older stars.
In order to use heating to account for the AVR, it may be necessary to invoke very massive
black holes (Lacey & Ostriker 1985). Simulations by Hänninen
& Flynn (2002) show that if the total mass of the halo consists of
![]() black holes, the disk could be heated from a present veloci
ty dispersion of 18 km s-1 to 80 km s-1 in about 8 Gyr (i.e., for an 8 Gyr old population), but if the present velocity
dispersion is 10 km s-1, the disk would only be heated to about 60 km s-1 even for 15 Gyr old populations. Only a combination of GMCs and
black holes, the disk could be heated from a present veloci
ty dispersion of 18 km s-1 to 80 km s-1 in about 8 Gyr (i.e., for an 8 Gyr old population), but if the present velocity
dispersion is 10 km s-1, the disk would only be heated to about 60 km s-1 even for 15 Gyr old populations. Only a combination of GMCs and
![]() black holes comprising half the halo could heat the disk sufficiently in 12 Gyr, but in that case
black holes comprising half the halo could heat the disk sufficiently in 12 Gyr, but in that case
![]() ,
somewhat larger than found here, although marginally consistent with other results.
,
somewhat larger than found here, although marginally consistent with other results.
Another mechanism which could plausibly result in a velocity dispersion-age relation is the stochastic heating due to minor mergers of the Galactic disk with satellite galaxies or passage of dark matter substructure through the disk. The dynamical friction force exerted by the disk converts a fraction of the satellite kinetic energy into vertical disk energy. Older stars should have suffered more events, either from more satellites and dark matter substructure, or repeated orbital passages of an individual object until it is tidally stripped, resulting in a velocity dispersion-age correlation. This process has been studied analytically and numerically by a large number of authors (see Velázquez & White 1999; Font et al. 2001; Taylor & Babul 2001; Benson et al. 2003, and references therein). Unfortunately most of this work was aimed at the problems of disk disruption, and then matching the scale heights of present-day disk galaxies. The problem is made more difficult by the uncertain partitioning of energy deposited in the disk between disk heating and global modes such as warping and bars (which themselves could heat the disk). Font et al. (2001) used simulations of disks heated by the ensemble of subhalos in CDM model halos to infer that the disk heating rate (as measured by an estimated diffusion coefficient) is less than the rate required to match observations of the solar neighborhood, although the discrepancy is not very large, and depends somewhat on the adopted distribution of satellite orbits and especially the mass distribution of the CDM subhalos. Benson et al. (2003) used similar ensembles of halos with a wide range of masses to show that the predicted scale height distribution of present-day models (i.e. after billions of years of heating) compares favorably with the distribution of scale heights determined by Bizyaev & Mitronova (2002) for a complete sample of 60 edge-on galaxies, but only when some molecular cloud scattering is included to avoid a low-scale height tail of the distribution. However they did not give information concerning how the velocity dispersion increases with time, its absolute value, or the ratio of vertical to radial velocity dispersion. After 4 Gyr of the orbit of a single satellite, the disk vertical energy increases by about 10% to 80% for various models of Benson et al. (2003). As a velocity dispersion increase (i.e. square root of energy increase), this is very small compared to the factor of 2 or so increase that the Milky Way exhibits over a similar time, but the number of discrete satellite bodies could be large, at least initially (about 100 in the Font et al. models).
One problem we see with this model is that tidal stripping by the disk continually decreases the flux of bombarding subhalo structures, so one expects that eventually the velocity dispersion-age relation should flatten out at ages less than some value, or at least show a change of slope due to the decreasing effectiveness of this process at more recent times. Such a flattening is seen in the velocity dispersion-age relations shown in Font et al. (2001). No such feature is seen in the observations presented here, supporting their conclusion that heating by merger with subhalos is unlikely to account for the relations.
We cannot rule out the possibility that minor mergers could have imprinted sudden changes in the slope of the AVR, especially given the cumulative observational evidence that the Milky Way faced and is presently facing mergers with some dwarf satellites (e.g., Ibata et al. 1994; Gilmore et al. 2002; Newberg et al. 2002; Yanny et al. 2003; Rocha-Pinto et al. 2003; Majewski et al. 2003). It is tempting to ask whether slope changes in the AVR could be used to recover the past merging history of the Galaxy. Mergers could also trigger star formation bursts in the disk, as Paper II suggests. Nevertheless, we have found no clear correlation between the star formation history (derived in Paper II) and the AVR.
Similarly, it appears that vertical heating of a galactic disk by bending instability (Sotnikova & Rodionov 2003), while possibly important due to the relatively long saturation timescale of the instability, appears to give significant "shelves'' in the velocity dispersion-time relation. These features appear at the time of maximum amplitude of the nonaxisymmetric and then symmetric bending, at relatively small times (0.5 to 1.5 Gyr in the models of Sotnikova & Rodionov), followed by a flat velocity dispersion-time relation. Again, such saturation is not seen in the observations, although it is uncertain if the mechanism, in conjunction with the other mechanisms discussed, could avoid the saturation. However the radial velocity dispersion component actually decreases in time due to this mechanism, again suggesting that it may be important, but would need to be combined with other mechanisms to explain the observations. The results for heating by the bending of a bar presented by Sotnikova & Rodionov are similar (except that the radial dispersion increases somewhat with time), with a factor of 2-3 increase in the vertical dispersion produced in about 1.5 Gyr.
A very different, but entirely plausible, way for dissipative gas systems to account for the AVR that was first proposed by Tinsley & Larson (1978). They showed, in the context of Larson's (1976) two-fluid models for disk galaxy formation and evolution, that the gradual dissipation and settling of the gas into a thinner and cooler layer naturally results in a reduction of the vertical velocity dispersion from about 50 km s-1 at age 3 Gyr when the disk becomes well-defined, to about 15 to 12 km s-1 for ages between 10 and 15 Gyr. The stellar velocity dispersion just reflects the evolution of the combined internal velocity dispersion and (for the older stars) the vertical motion of the gas disk.
Advantages of the Tinsley & Larson dissipation model are:
Later fluid models for the settling of initial hot protogalactic gas into the equatorial
plane have become more detailed in input physics making use of the chemodynamical
prescription of galaxy evolution, including different forms of star-formation feedback,
a number of heating and cooling processes, and an accounting of the multi-phase character
of the interstellar medium. Although more parameters are naturally required to accommodate the
increased number of processes, their choice is not arbitrary but formulated from plasmaphysical
and astrophysical studies. It can also be demonstrated that even if the parametrization
of the star-formation rate is taken arbitrarily in the chemodynamical prescription it will
install a dependence on density and temperature of the warm gas phase in a very narrow
range because of self-regulation processes (Köppen et al. 1995, 1998).
Burkert et al. (1992) provide a useful example, although only the
vertical dependence is included in their one-dimensional fluid model. The results are
very similar to Tinsley & Larson, with the velocity dispersion decreasing from ![]() 40 km s-1 to
40 km s-1 to ![]() 20 km s-1 after about 5 Gyr. Although they ascribe this decrease to a decline in the star formation rate (hereafter, SFR) by a factor of 10 due to gas depletion (they assumed the SFR varies with the square of the gas density), this is equivalent to
Tinsley & Larson's gaseous dissipation effect, since it is the SFR that drives the
"cloud'' or "turbulent'' motions of the gas from which the stars form in both cases.
Besides the advantages mentioned above, the work of Burkert et al. (1992) shows
that their models can account for the observed vertical distribution of stellar
density and velocity dispersion.
20 km s-1 after about 5 Gyr. Although they ascribe this decrease to a decline in the star formation rate (hereafter, SFR) by a factor of 10 due to gas depletion (they assumed the SFR varies with the square of the gas density), this is equivalent to
Tinsley & Larson's gaseous dissipation effect, since it is the SFR that drives the
"cloud'' or "turbulent'' motions of the gas from which the stars form in both cases.
Besides the advantages mentioned above, the work of Burkert et al. (1992) shows
that their models can account for the observed vertical distribution of stellar
density and velocity dispersion.
An extension of this chemodynamical model to two dimensions and more physical processes
has been presented by Samland et al. (1997). A notable result of the
Samland et al. models (their Fig. 3) is that, although the total (halo + bulge + disk)
SFR has an early peak at ![]() 2 Gyr and then declines by a factor of five or so,
the disk SFR is actually fairly flat. As explained by Samland et al., this is
because the disk has only become a relatively discrete entity after about 7-8 Gyr, while
the total duration of the model is 15 Gyr. This slow disk formation in their models can be
traced back to the large cloud collision (i.e. dissipation) timescales adopted.
Even beginning at 7 Gyr, the disk SFR appears to only decrease by a factor
of three or so, suggesting that the velocity dispersion will not decrease
much with time.
2 Gyr and then declines by a factor of five or so,
the disk SFR is actually fairly flat. As explained by Samland et al., this is
because the disk has only become a relatively discrete entity after about 7-8 Gyr, while
the total duration of the model is 15 Gyr. This slow disk formation in their models can be
traced back to the large cloud collision (i.e. dissipation) timescales adopted.
Even beginning at 7 Gyr, the disk SFR appears to only decrease by a factor
of three or so, suggesting that the velocity dispersion will not decrease
much with time.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{0617f10.eps}\end{figure}](/articles/aa/full/2004/32/aa0617/Timg196.gif) |
Figure 10: Temporal evolution of the vertical velocity dispersion of the cloudy gas phase in the solar vicinity (at 8.5 kpc galactocentric distance) as the result of the chemodynamical Milky Way model by Samland et al. (1997), adapted from Samland (1995). |
| Open with DEXTER | |
Figure 10 shows the time history of the vertical velocity dispersion of the cloudy
gas phase in the solar vicinity (at 8.5 kpc galactocentric distance) obtained in the chemo-dynamical Milky Way model by Samland et al. (1997). Since stars are formed from the cool phase this also
represents the velocity dispersion of the newly formed stars. One can discern that the
vertical dispersion has early oscillations between 45 and 65 km s-1, when gas starts to
accumulate in the equatorial plane and partly cools dissipatively but is still heated
due to the continuing collapse. Then, after the disk has formed about 8 Gyr ago (in the model),
the vertical velocity dispersion declines, flattening out at about 25-30 km s-1 over the
past 5 Gyr. For the comparison of this value with observed solar vicinity stars, one has to
realize that the result is derived as an average over a few vertical grid cells and thus only
represents a thick disk component of almost 700 pc height because of its coarse spatial
resolution. The ratio
![]() is about 0.5 at most radii in the late-time
model, in good agreement with our empirical result.
is about 0.5 at most radii in the late-time
model, in good agreement with our empirical result.
Other models for disk galaxies that include dark matter and cosmologically-motivated
initial conditions have tended to concentrate on chemical evolution and/or high-redshift
properties, and have used SPH + N-body methods rather than fluid models, making it
difficult to estimate velocity dispersions at late times when small SFRs mean that
the number of newly-formed star particles is small. However, the
velocity dispersion behavior of such models, when available, are very similar
to those discussed above. For example, Steinmetz & Müller (1995)
state that for stars in age intervals [3, 8.5], [1, 3], and (indirectly)
<1 Gyr, the velocity dispersions fall from 80 to 40 to 20 km s-1, respectively, at ![]() kpc. Their Fig. 8b suggests that at late times
kpc. Their Fig. 8b suggests that at late times
![]() over most of the model galaxy that is relevant to the solar neighborhood,
but small number fluctuations and artificial heating by scattering from the
model dark matter particles make the results difficult to interpret. Once
again, the agreement with the density distribution and chemical properties
(e.g. metallicity gradients, see Steinmetz & Müller 1994) of
real galaxies makes this cooling interpretation of the
over most of the model galaxy that is relevant to the solar neighborhood,
but small number fluctuations and artificial heating by scattering from the
model dark matter particles make the results difficult to interpret. Once
again, the agreement with the density distribution and chemical properties
(e.g. metallicity gradients, see Steinmetz & Müller 1994) of
real galaxies makes this cooling interpretation of the ![]() correlation
attractive from the point of view of "Occam's razor''.
correlation
attractive from the point of view of "Occam's razor''.
More recent SPH/N-body models of disk galaxies by Berczik (1999,
2000), which include more stellar components and different
parameterization of stellar energy feedback, as well as a different star formation rate
prescription (basically a virial theorem condition on the SPH particles rather than
either a density dependence or a density threshold) do not give the
time-dependence of the stellar velocity dispersion, but indicates that final values are
![]() km s-1 over the whole disk, with
km s-1 over the whole disk, with
![]() near the sun (see Berczik 1999, Figs. 6-8).
near the sun (see Berczik 1999, Figs. 6-8).
Thus the time dependence of the disk velocity dependence and its absolute scale seems robust over a fairly wide range of independent models, agreeing overall with Larson's (1976) early work. It is unfortunate that the relevant kinematic information from the detailed disk evolution models of Raiteri et al. (1996) and Friedli & Benz (1995) are not available to test this robustness further. The published star formation rates suggest that the behavior will be similar, although there are larger apparent temporal fluctuations in the late disk SFRs and presumably in the stellar velocity dispersions.
However unlike the scattering models, which have great trouble accounting for the large velocity dispersion of older stars, the cooling models have a problem in producing small enough velocity dispersions at late times: Instead of power law cooling, the velocity dispersion approaches a nearly constant value. Larson's early models apparently gave the smallest present day velocity dispersions of 12-15 km s-1, while all the other models discussed above tend to flatten out at about 20-35 km s-1. In fact Tinsley & Larson (1978) and Larson (1979) were aware of this problem, and suggested that turbulent dissipation within the disk layer (rather than settling of the disk itself on larger scales) could lead to the requisite small velocity dispersion. The reason this does not occur in the disk formation models is that at late times the SFR is small, so that the star formation uses available gas on a long timescale, leading to a relatively constant SFR. Since the models tend toward self-regulating equilibrium, with dissipation balancing SF (see Köppen et al. 1995, for one-zone models), the gas and hence stellar velocity dispersion cannot decrease.
Nevertheless, one reason for the apparent large velocity dispersions in all the disk formation models at late times might be lack of spatial resolution, such that the calculation is yielding an average velocity dispersion over a height much larger than that of the thin disk.
A likely more important aspect of these models is that they all use some form of sub-grid (unresolved) dissipation whose timescale is essentially a parameter in the models. For example, in the chemo-dynamical collapse models, the dissipation comes through cloud collisions, but the dissipation timescale is set to about an order of magnitude larger than the cloud collision timescale based on the geometric cross section. This allows for slow early collapse, but also forces the gas to resist a reduction in velocity dispersion below about 20 km s-1. It is relatively easy to show using one-zone analytic models that the self-regulated gas velocity dispersion will scale with the SFR as (SFR)1/3 - see Scalo & Chappell (1999). In fact a number of independent simulations of interstellar MHD turbulence indicate that the dissipation time is rapid, of order a crossing time (Mac Low et al. 1998; Mac Low 1999; Ostriker et al. 1999), even in the presence of stellar heating sources (Avila-Reese & Vázquez-Semadeni 2001). Thus we ascribe the inability of collapse models to settle to a small-enough velocity dispersion to an underestimation of the dissipation rate. If the dispersion were really set by an equilibrium between SF and dissipation, this model would be unable to account for the continued decrease in velocity dispersion at relatively recent times (<1 Gyr). We think the problem is not serious, since, moving away from one-zone models, more detailed turbulence simulations show that the turbulence dissipates rapidly in spatial regions between star-forming events (Avila-Reese & Vázquez-Semadeni 2001), and new stars will form from this gas.
In fact it is obvious that this model has no problem in accounting for the low velocity dispersion of young stars, since the velocity dispersion of the interstellar gas is observed to have about the same value as that for the stars. The only problem involves understanding why the existing simulations do not dissipate turbulence sufficiently to match the observed present-day gas velocity dispersions.
In the future it may be possible to empirically distinguish between the dissipation
and heating models by comparing the models with observations of
![]() in disk galaxies. Shapiro et al. (2003) have used
major- and minor-axis kinematics to estimate
in disk galaxies. Shapiro et al. (2003) have used
major- and minor-axis kinematics to estimate
![]() for a number
of disk galaxies of various Hubble types. The resulting values of
for a number
of disk galaxies of various Hubble types. The resulting values of
![]() are in the range 0.5 to 0.8 with considerable uncertainties, and are consistent with no
trend with Hubble type at the
are in the range 0.5 to 0.8 with considerable uncertainties, and are consistent with no
trend with Hubble type at the ![]() level, or with a marginally
significant trend of decreasing
level, or with a marginally
significant trend of decreasing
![]() with later Hubble type.
with later Hubble type.
Unfortunately, it is not yet possible to test these results with
predictions of the two models. Simulations by Jenkins & Binney (1990)
seem to predict a decrease with increasing molecular gas fraction and
spiral arm strength, so with advancing Hubble type. The uncertainties
in the empirical ratios are large enough that such a trend cannot be
uncovered at the ![]() level. The galaxy collapse models can produce
level. The galaxy collapse models can produce
![]() ratios in the observed range, but the inability of the
models to predict the ratio at late times, and the lack of modeling of
disks of different Hubble types, preclude a prediction of any trend.
Hopefully further models of disk kinematics in galaxy formation models
that result in a range of Hubble types will yield such information.
One trend that could in principle be tested is that
ratios in the observed range, but the inability of the
models to predict the ratio at late times, and the lack of modeling of
disks of different Hubble types, preclude a prediction of any trend.
Hopefully further models of disk kinematics in galaxy formation models
that result in a range of Hubble types will yield such information.
One trend that could in principle be tested is that
![]() varies from 0.6 in the dense inner regions to 0.48 in the outermost
region in the model of Samland et al. (1997). It is not known whether
this variation is generic for the dissipation model.
varies from 0.6 in the dense inner regions to 0.48 in the outermost
region in the model of Samland et al. (1997). It is not known whether
this variation is generic for the dissipation model.
Following our former investigations on the age-metallicity relation and the star formation history, we have used the chromospheric ages for a sample of late-type dwarfs to investigate the chemokinematical properties of the solar vicinity. The use of chromospheric ages warrants an almost complete coverage of the galactic disk history with a sample consisting of stars in the same colour range, something that cannot be achieved from other methods.
The exponents for the AVR that we have found frustrantingly seem to span the whole
range of values which can be used to constrain the theory on the disk heating.
Nevertheless, after taking into account a statistically more meaningful binning and
metallicity corrections to the chromospheric age, we arrive at an exponent ranging
from 0.26 to 0.31, for
![]() .
.
We have shown that the vertex deviation of solar neighbourhood late-type stars varied irregularly between the present time and 10 Gyr ago. No clear dependence of the vertex deviation on the age of the stellar group was found in our analysis. The vertex deviation also varies substantially when different selection criteria are applied to the sample. We give support to Palous (1986) idea that the vertex deviation is caused by the contamination of the sample by superclusters and moving groups stars.
Our sample was used to test the idea that there is a statistical relation between the average orbital galactocentric distance and the galactocentric radius where the star was born. While our simulations provide support to Wielen et al. (1996) results, we have found that local data does not have a good coverage in orbital galactocentric distance to allow a empirical testing of this relation. Nevertheless, the relation between Rm and age that we have found supports Edv93's use of Rm as a reasonable indicator of the stellar birthplace radius.
Nevertheless, since young stars born at a galactocentric radius different from ![]() have not had time to scatter into the solar neighbourhood at representative numbers,
we believe that there is no possibility to find the radial variation of the age-metallicity
relation or star formation rate using local stars only. A much larger data sample, as that
expected to be provided by GAIA, could solve this problem.
have not had time to scatter into the solar neighbourhood at representative numbers,
we believe that there is no possibility to find the radial variation of the age-metallicity
relation or star formation rate using local stars only. A much larger data sample, as that
expected to be provided by GAIA, could solve this problem.
A consideration of numerous results of theoretical studies of secular heating mechanisms, most involving gravitational scattering from large inhomogeneities in the gas or star system, indicates that none of these is capable of explaining satisfactorily the large velocity dispersions of the oldest disk stars. The problem is especially serious when one considers the dynamical friction effect found by Yasutomi & Fujimoto (1989, 1991).
Stochastic heating mechanisms involving satellite interactions are possible, but should (and do) give an AVR that flattens out for relatively young (few Gyr) stars, a feature that is not observed. Instead, we suggest that a very plausible alternative is the one suggested long ago by Tinsley & Larson (1978), that the velocity dispersion of stars just reflects the velocity dispersion of the gas from which they formed, and that the turbulent motions of this gas has been declining continually since the formation of the disk. We cite a number of more recent disk evolution papers that find similar behaviour.
While all the models successfully account for the dispersion of the older stars, we are unable to say whether the simulations produce the low velocity dispersions observed for young stars, due to a combination of resolution effects and uncertainties in input physics. However this is obviously only a problem for the simulations, and not for the idea itself: the real observed interstellar medium does have a velocity dispersion that is similar to the velocity dispersion of the youngest stars, so we are assured that the model must give the correct result at the present time. Hopefully future studies of disk evolution will improve the situation.
There is a straightforward way to test and distinguish the heating and cooling models if stellar and gas velocity dispersions for face-on high redshift galaxies can be obtained in the future. The heating model predicts that the stellar velocity dispersion should be small at such early times, while the cooling models predict that the gas velocity dispersion should be large. We think it unlikely that both conditions can occur simultaneously.
Acknowledgements
We have made extensive use of the SIMBAD database, operated at CDS, Strasbourg, France. Part of this research was made possible by the use of the multivariate decomposition software EMMIX, freely distributed to the scientific community by Geoff McLachlan and collaborators. Markus Samland kindly provided us with data from chemodynamical models. This work was partially supported by FAPESP and CNPq to W.J.M. and H.J.R.-P., NASA Grant NAG 5-3107 to JMS, the Finnish Academy to C.F. and J.H., and the Deutsche Forschungsgemeinschaft to G.H. under grant HE1487/5. H.J.R.-P. also acknowledges generous support from Frank Levinson and Wynnette LaBrosse through the Celerity Foundation.