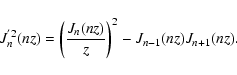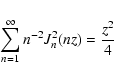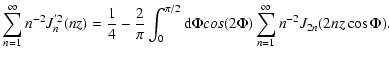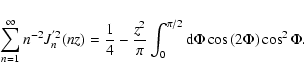A&A 420, 799-808 (2004)
DOI: 10.1051/0004-6361:20034304
Cosmic ray transport in anisotropic magnetohydrodynamic
turbulence
III. Mixed magnetosonic and Alfvénic turbulence![[*]](/icons/foot_motif.gif)
A. Shalchi1,2 - R. Schlickeiser1
1 - Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum, Germany
2 -
now at: Bartol Research Institute, University of Delaware,
Newark, DE 19716, USA
Received 10 September 2003 / Accepted 2 February 2004
Abstract
Observations of interstellar turbulence imply that
the power spectrum of the wave turbulence must
be highly anisotropic. This anisotropy has to be included
when transport of high energy cosmic rays in
the Galaxy is discussed. Here we evaluate the relevant cosmic ray
transport parameters in the presence of anisotropic plasma wave
turbulence, consisting of
a mixture of shear Alfvén waves and fast magnetosonic waves.
By averaging the respective Fokker-Planck coefficient over the particle
pitch-angle we calculate the momentum and spatial diffusion
coefficients for
different anisotropy parameters.
For strongly perpendicular turbulence (
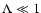 )
we obtain that
the momentum
diffusion coefficient is proportional to
)
we obtain that
the momentum
diffusion coefficient is proportional to
![$\Lambda ^{-1/2} \left[ \ln
\epsilon^{-1} + \ln \Lambda ^{1/2} \right]$](/articles/aa/full/2004/24/aa0304/img43.gif) ,
whereas for strongly parallel turbulence (
,
whereas for strongly parallel turbulence (
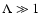 )
the momentum
diffusion
coefficient is a constant.
We also calculate the anisotropy dependence of the spatial diffusion
coefficient and
the parallel mean free path for the mixed turbulence.
For all coefficients we discuss the rigidity dependence for
different cosmic ray particles.
)
the momentum
diffusion
coefficient is a constant.
We also calculate the anisotropy dependence of the spatial diffusion
coefficient and
the parallel mean free path for the mixed turbulence.
For all coefficients we discuss the rigidity dependence for
different cosmic ray particles.
Key words: magnetohydrodynamics (MHD) - plasmas - turbulence - ISM:
cosmic rays - ISM: magnetic fields - acceleration of particles
Observations of interstellar scintillations (Rickett 1990;
Spangler
1991), general theoretical considerations (Goldreich & Sridhar
1995), and comparison of interstellar radiative cooling in
HII-regions
and in the diffuse interstellar medium with linear Landau damping
estimates for
fast-mode decay (Lerche & Schlickeiser 2001a), all strongly
imply that
the power spectrum of wave turbulence in the interstellar medium must
be highly anisotropic. It is not clear from the observations whether
the
turbulence spectrum is oriented mainly parallel or mainly perpendicular
to the
ambient magnetic field, either will satisfy the needs of balancing wave
damping
energy input against radiative cooling.
This anisotropy must be included when transport of high energy cosmic
rays in
the Galaxy is discussed (Chandran 2001; Yan & Lazarian 2002).
In the first paper of this series (Lerche & Schlickeiser
2001b, hereafter referred to LS) we have started to evaluate
the relevant cosmic ray
transport parameters in the presence of anisotropic fast
magnetosonic plasma wave turbulence. All technical details of the
calculation of Fokker-Planck coefficients and their relation
to the transport parameters of the cosmic ray diffusion-convection
equation
(as the parallel mean free path, the rate of adiabatic deceleration and
the momentum diffusion coefficient) were presented there (see LS
Sects. 2 and 3).
In the second paper of this series (Teufel et al.
2003,
hereafter referred to TLS) we continued to evaluate the relevant cosmic
ray
transport parameters in the presence of anisotropic shear Alfvén
waves.
However, in order to calculate these transport parameters in the
interstellar medium
we must calculate also the influence of the anisotropy parameter on
the Fokker-Planck coefficients for the mixed turbulence, because
interstellar plasma turbulence most probably is a mixture of fast
magnetosonic waves and
shear Alfvén waves. This analysis is the subject of the present
paper. In order to
avoid unnecessary repititions we will use the same notation and will
frequently refer to equations in papers LS and TLS.
The organisation of the paper is as follows: in Sect. 2 we summarize
the results
for shear Alfvén waves of TLS. In Sect. 3 we present improved (in
comparison to LS)
calculations for fast magnetosonic waves. In Sect. 4 we
use these new
results together with the shear Alfvén wave results to calculate the
Fokker-Planck
coefficients and transport parameters for the mixed turbulence. In
Sect. 5 we calculate
the rigidity dependence of the transport parameters for heliospheric
parameters for shear
Alfvén waves, fast magnetosonic waves and the mixed turbulence.
To calculate the transport parameters in the mixed turbulence we need
the Fokker-Planck coefficients
for shear Alfvén and fast magnetosonic waves. Because the mixed
momentum diffusion coefficient
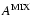 can be written as the sum of the momentum diffusion coefficients
can be written as the sum of the momentum diffusion coefficients
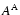 and
and 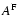 ,
we write down
the Fokker-Planck coefficients and transport parameters of shear
Alfvén waves. To do this
we can use the results of TLS. For all Fokker-Planck coefficients and
transport parameters
we have made the assumption that
,
we write down
the Fokker-Planck coefficients and transport parameters of shear
Alfvén waves. To do this
we can use the results of TLS. For all Fokker-Planck coefficients and
transport parameters
we have made the assumption that
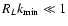 .
Therefore we
cannot use our results
for high rigidities. We also assume that 1 < s < 2 for the inertial
range spectral index.
.
Therefore we
cannot use our results
for high rigidities. We also assume that 1 < s < 2 for the inertial
range spectral index.
For the momentum diffusion coefficient 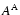 for pure shear Alfvén
waves we obtain from TLS(25)
for pure shear Alfvén
waves we obtain from TLS(25)
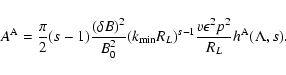 |
(1) |
In Eq. (1) we used the ratio of the turbulent fields and
the magnetic
background field
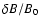 ,
the particle speed v and momentum
p. The parameter
RL is the gyroradius and
,
the particle speed v and momentum
p. The parameter
RL is the gyroradius and 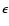 is the ratio
is the ratio
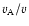 where
where
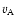 is the
Alfvén speed. The parameter
is the
Alfvén speed. The parameter 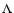 is the anisotropy parameter.
This parameter
allows us to change the turbulence geometry. For
is the anisotropy parameter.
This parameter
allows us to change the turbulence geometry. For
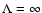 we
obtain the
often considered case of a slab geometry.
we
obtain the
often considered case of a slab geometry. 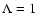 is equivalent to
isotropic and
is equivalent to
isotropic and
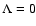 is equivalent to 2D geometry (see Bieber et al. 1994; Shalchi &
Schlickeiser 2004).
In Eq. (1) we also used the function
is equivalent to 2D geometry (see Bieber et al. 1994; Shalchi &
Schlickeiser 2004).
In Eq. (1) we also used the function 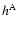 which can be
approximated
as follows:
which can be
approximated
as follows:
In Table 1 we compare for the special case s=5/3 the
numerical values
of the anisotropy function calculated from these asymptotics with the
values calculated from
the exact form of the anisotropy function from TLS.
To obtain the results above, we use the Fokker-Planck coefficients of
shear Alfvén waves
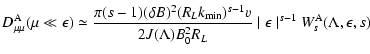 |
|
|
(3) |
with
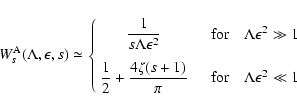 |
(4) |
and
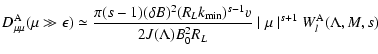 |
|
|
(5) |
with
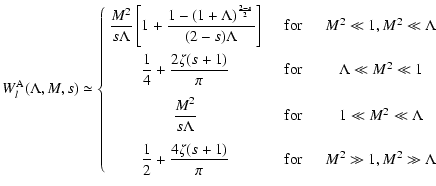 |
|
|
(6) |
where
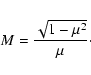 |
(7) |
For the function
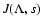 we have
we have
Table 1:
Anisotropy function 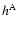 for Alfvén waves and for
s=5/3.
for Alfvén waves and for
s=5/3.
Here we use the results from TLS again to obtain
 |
(9) |
with the function
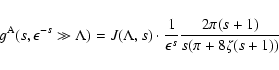 |
(10) |
if
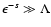 ,
and
,
and
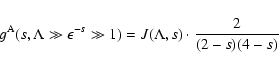 |
(11) |
if
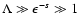 .
In Table 2 we show the
values of the
function
.
In Table 2 we show the
values of the
function 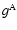 for the special case s=5/3.
for the special case s=5/3.
Table 2:
The function 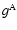 for Alfvén waves and for s=5/3.
for Alfvén waves and for s=5/3.
To calculate the transport parameters for the mixed turbulence we also
need the parameters for fast magnetosonic waves.
For these waves the momentum diffusion coefficient is the sum of the
gyroresonance
contribution 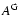 and the transit-time damping contribution
and the transit-time damping contribution 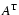 ,
,
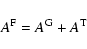 |
(12) |
because we know that
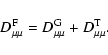 |
(13) |
To calculate 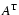 we use the results from LS that
we use the results from LS that
and
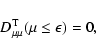 |
(15) |
respectively, where we introduce
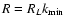 and define the two
functions
and define the two
functions
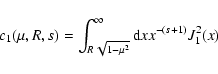 |
(16) |
and
In this paper we restrict our analysis to
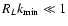 .
Then
the approximation
.
Then
the approximation
holds, and we obtain for the momentum diffusion coefficient of the
transit-time damping
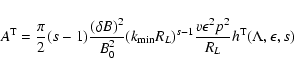 |
(19) |
with the anisotropy function 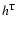 listed in Table 3.
listed in Table 3.
Table 3:
Anisotropy function 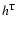 for fast magnetosonic waves. In
this table we introduced the functions
for fast magnetosonic waves. In
this table we introduced the functions
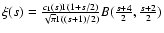 with
the generalized
with
the generalized 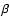 -function B(x,y) and
-function B(x,y) and
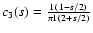 .
.
The Fokker-Planck coefficient for the gyroresonance contribution has
also been
calculated in LS, but it is possible
to derive improved approximations using Kapteyn series, as is shown in
Appendix C.
For small pitch angles
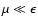 and for
and for
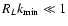 we obtain from Appendix B
we obtain from Appendix B
with
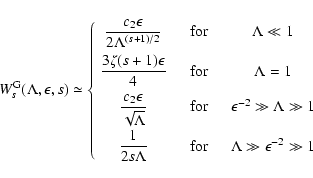 |
(21) |
where we introduced
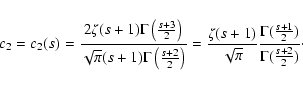 |
(22) |
For large pitch angles
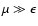 and
and
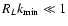 we
obtain from Appendix A
we
obtain from Appendix A
with
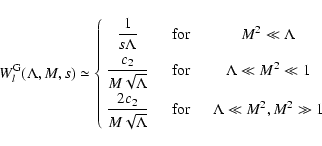 |
(24) |
and with
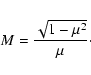 |
(25) |
With the definition of the momentum diffusion coefficient A(Eq. LS(9)) we find for cosmic rays with gyroradii
much less than
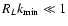
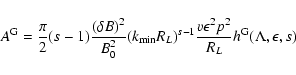 |
(26) |
with the anisotropy function
This anisotropy function can again be simplified for different limits
of
the anisotropy parameter
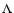 .
We discuss the different limits in turn.
With the results of Appendix A it is easy to determine
.
We discuss the different limits in turn.
With the results of Appendix A it is easy to determine
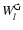 in this
case:
in this
case:
 |
(28) |
For 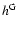 we use
we use
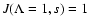 and split the integral as
and split the integral as
These integrals are elementary and we obtain to lowest order in 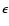
In this case we obtain from Appendix A:
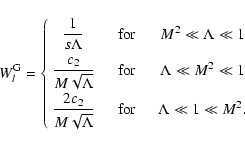 |
(31) |
For 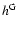 we now find
we now find
Again these integrals are elementary, so that
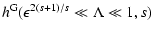 |
= |
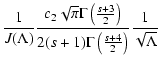 |
(33) |
to lowest order in 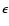 .
With
.
With
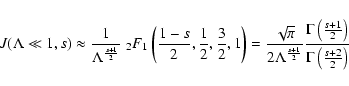 |
(34) |
we find for the anisotropy function 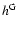
 |
(35) |
The calculations are similar as before. Here we find:
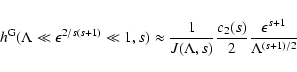 |
(36) |
and therefore
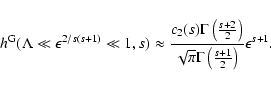 |
(37) |
Because
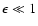 this implies very small
values of
this implies very small
values of
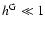 .
In this case we obtain:
.
In this case we obtain:
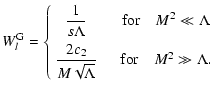 |
|
|
(38) |
For 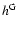 we now find to lowest order in
we now find to lowest order in 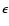
Like in the cases before the integrals are elementary and we obtain
![\begin{displaymath}h^{\rm G}(\epsilon^{-2} \gg \Lambda \gg 1, s) \approx {1 \ove...
... s \Lambda} \left[ {1 \over s } - { 1 \over s+2 } \right]\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img155.gif) |
(40) |
With
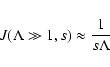 |
(41) |
we finally find
 |
(42) |
In this case we have:
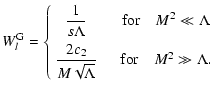 |
|
|
(43) |
For 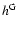 we then find
we then find
and to lowest order in 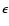 we find the same result as in the
case before.
we find the same result as in the
case before.
 |
(45) |
The combined result for the case
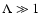 therefore is
therefore is
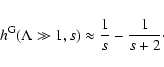 |
(46) |
In Table 4 we list the results for the different cases of
anisotropy for
the special turbulence spectral index value s=5/3.
We also calculate the three cases numerically from the exact
expression.
As can be seen, the agreement is very good in cases one and three
and
acceptable in the second case.
Table 4:
Anisotropy function 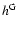 for fast magnetosonic waves.
for fast magnetosonic waves.
Knowing the variation of the two anisotropy functions from transit-time
damping (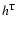 )
and
gyroresonant interactions (
)
and
gyroresonant interactions (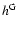 ), we are now able to calculate
), we are now able to calculate
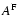 :
:
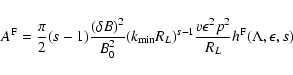 |
(47) |
with
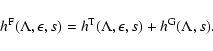 |
(48) |
The behaviour of the function
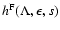 is
summarized
in Table 5:
for the cases
is
summarized
in Table 5:
for the cases
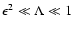 and
and
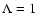 the
momentum
diffusion coefficient
the
momentum
diffusion coefficient 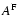 can be approximated solely by the transit-time damping contribution
can be approximated solely by the transit-time damping contribution
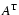 ,
whereas for the case
,
whereas for the case
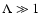 (parallel turbulence) the
gyroresonance contribution
dominates the sum, because of the lack of perpendicular waves which are
essential for
transit-time damping.
(parallel turbulence) the
gyroresonance contribution
dominates the sum, because of the lack of perpendicular waves which are
essential for
transit-time damping.
Table 5:
Anisotropy function 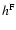 for fast magnetosonic waves.
for fast magnetosonic waves.
We restrict our analysis to
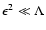 .
From LS we know
that
.
From LS we know
that
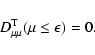 |
(49) |
With the function
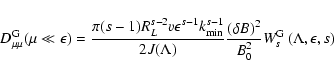 |
(50) |
from Appendix B we obtain for the spatial diffusion coefficient
which can be written as
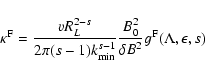 |
(52) |
where we introduced the function
with the functions
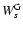 ,
,
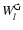 and
and
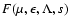 defined in
Eqs. (21), (24) and (17), respectively.
These integrals can be solved analytically for special cases of
defined in
Eqs. (21), (24) and (17), respectively.
These integrals can be solved analytically for special cases of
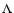 again.
Here we find
again.
Here we find
where we have used
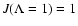 .
It is easy to see that the second
and
third integral are of higher order in
.
It is easy to see that the second
and
third integral are of higher order in
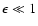 ,
so that
the function
,
so that
the function 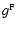 is determined by the first integral:
is determined by the first integral:
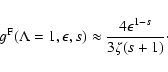 |
(55) |
For this case we find
With
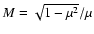 this can be written as
this can be written as
Now we use
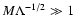 in the second and third integral
and
in the second and third integral
and
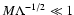 in the last integral.
To lowest order in
in the last integral.
To lowest order in 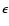 and for
and for
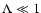 we find that
the first term dominates
we find that
the first term dominates
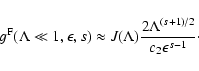 |
(58) |
With
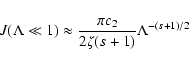 |
(59) |
we then obtain
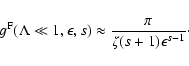 |
(60) |
Here we obtain
With
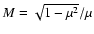 this can be written as
this can be written as
We use
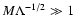 in the first integral and
in the first integral and
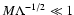 in the second integral.
To lowest order in
in the second integral.
To lowest order in 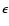 and for
and for
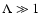 we find
we find
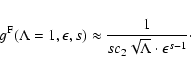 |
(63) |
For this case we find
which can be written as
Table 6 summarizes the derived asymptotic behaviour.
Table 6:
Anisotropy function 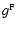 for fast magnetosonic turbulence.
for fast magnetosonic turbulence.
After having derived the individual momentum diffusion coefficients
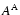 ,
,
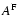 and the Fokker-Planck coefficients, it is straightforward to determine
the transport
parameters for the mixed turbulence once the relevant plasma parameters
are specified.
As an illustrative example
we assume equal intensity and identical plasma and anisotropy
parameters for
shear Alfvén waves and fast magnetosonic waves, i.e.
and the Fokker-Planck coefficients, it is straightforward to determine
the transport
parameters for the mixed turbulence once the relevant plasma parameters
are specified.
As an illustrative example
we assume equal intensity and identical plasma and anisotropy
parameters for
shear Alfvén waves and fast magnetosonic waves, i.e.
The application to other plasma turbulence mixtures is obvious.
In case of the illustrative example (66) the
Fokker-Planck coefficient
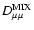 can be written as a sum of
the Fokker-Planck
coefficients from shear Alfvén waves and fast magnetosonic waves
can be written as a sum of
the Fokker-Planck
coefficients from shear Alfvén waves and fast magnetosonic waves
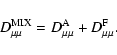 |
(67) |
With Eq. (67) we obtain
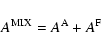 |
(68) |
which can be written as
 |
(69) |
with
With 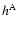 from Table 1 and
from Table 1 and 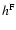 from Table 5 we
find for the function
from Table 5 we
find for the function
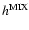 the results listed in Table 7. As can be seen
the results listed in Table 7. As can be seen
If
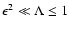 the main contribution to momentum
diffusion in
mixed turbulence (66) comes from transit-time damping of
fast magnetosonic waves,
whereas for
the main contribution to momentum
diffusion in
mixed turbulence (66) comes from transit-time damping of
fast magnetosonic waves,
whereas for
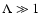 the two gyroresonance contributions
are dominant.
the two gyroresonance contributions
are dominant.
Table 7:
Anisotropy function
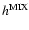 for mixed turbulence.
for mixed turbulence.
The spatial diffusion coefficient in the mixed turbulence
(66)
can be written as
| |
|
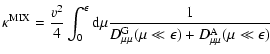 |
|
| |
|
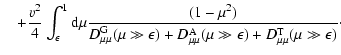 |
(72) |
Now we restrict our calculations to
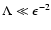 .
To continue we must compare the Fokker-Planck coefficient for Alfvén
waves
.
To continue we must compare the Fokker-Planck coefficient for Alfvén
waves
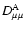 with the
gyroresonance contribution from the Fokker-Planck coefficient for fast
magnetosonic waves
with the
gyroresonance contribution from the Fokker-Planck coefficient for fast
magnetosonic waves
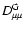 .
.
We start with the case
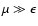 .
Here we have (see Sect. 2):
.
Here we have (see Sect. 2):
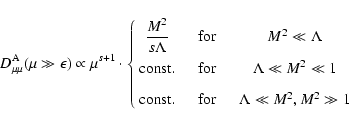 |
(73) |
and according to Sect. 3:
| |
|
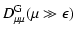 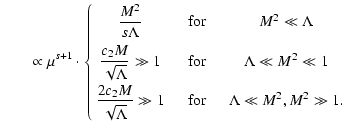 |
(74) |
Therefore it is easy to see that for all cases of 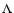 and M we
have
and M we
have
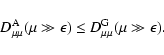 |
(75) |
Comparing the Fokker-Planck coefficients for the case
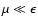 ,
we can
use (see Sect. 2)
,
we can
use (see Sect. 2)
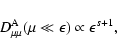 |
(76) |
and according to Sect. 3
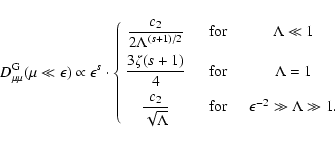 |
(77) |
Consequently, for all cases
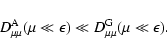 |
(78) |
Hence, we obtain for the spatial diffusion coefficient in the mixed
turbulence
(66)
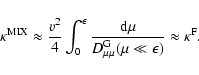 |
(79) |
The contribution from shear Alfvén waves and the transit-time damping
contribution from
fast magnetosonic waves are negligibly small in all cases.
The spatial diffusion coefficient
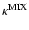 is dominated by the
gyroresonance contribution from fast magnetosonic turbulence.
Here we calculate the rigidity dependence of the transport parameters.
We introduce the rigidity r and the parameter r0
is dominated by the
gyroresonance contribution from fast magnetosonic turbulence.
Here we calculate the rigidity dependence of the transport parameters.
We introduce the rigidity r and the parameter r0
| |
|
 |
|
| |
|
 |
(80) |
so that
| |
|
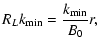 |
|
| |
|
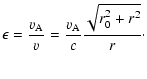 |
(81) |
The restriction
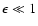 implies
implies
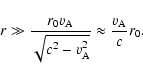 |
(82) |
For electrons and positrons
r0 = 0.511 MV, while for protons
r0 =
938 MV.
If we adopt
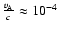 the rigidity
restriction reads
the rigidity
restriction reads
| |
|
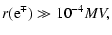 |
|
| |
|
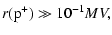 |
(83) |
which are assumed in the following analysis. Moreover, the assumption
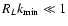 becomes
becomes
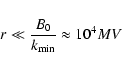 |
(84) |
for all particles, if we use
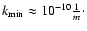 For Alfvén waves we use the results from TLS where we have shown that
For Alfvén waves we use the results from TLS where we have shown that
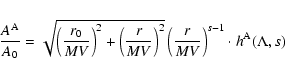 |
(85) |
with
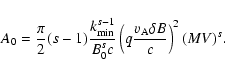 |
(86) |
If we do the corresponding calculations for fast magnetosonic waves
we find a similar result, but there the anisotropy function h is also
a
function of 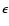 ,
and therefore through Eq. (81) also a
function of particle rigidity r. It is possible to write for all
turbulence models
,
and therefore through Eq. (81) also a
function of particle rigidity r. It is possible to write for all
turbulence models
 |
(87) |
where A0 is the same function for all models. For 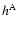 we can use
Table 1, for
we can use
Table 1, for 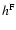 we can use Table 5 and for
we can use Table 5 and for
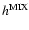 we can use Table 7. In Fig. 1 we show the resulting
momentum diffusion coefficients for shear Alfvén waves and in Fig. 2
for fast magnetosonic waves, respectively.
we can use Table 7. In Fig. 1 we show the resulting
momentum diffusion coefficients for shear Alfvén waves and in Fig. 2
for fast magnetosonic waves, respectively.
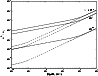 |
Figure 1:
The momentum diffusion coefficient for shear Alfvén waves 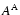 for protons (solid lines),
electrons and positrons (dashed lines). We show the results for different values of the
anisotropy parameter
for protons (solid lines),
electrons and positrons (dashed lines). We show the results for different values of the
anisotropy parameter 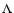 . . |
| Open with DEXTER |
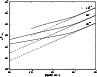 |
Figure 2:
The momentum diffusion coefficient for fast magnetosonic
waves 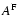 for protons (solid lines),
electrons and positrons (dashedlines). We show the results for different values of the
anisotropyparameter
for protons (solid lines),
electrons and positrons (dashedlines). We show the results for different values of the
anisotropyparameter 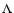 . . |
| Open with DEXTER |
Restricting our analysis to
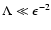 we have
we have
 |
(88) |
with
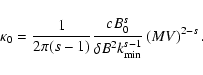 |
(89) |
For 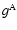 we can use Table 2, for
we can use Table 2, for 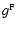 we can use Table 6 and we know that
we can use Table 6 and we know that
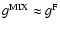 .
In Fig. 3 we show the spatial diffusion coefficient for shear Alfvén
waves and in
Fig. 4 for fast magnetosonic waves, which also gives the spatial
diffusion coefficient in
case for the mixed turbulence (66).
.
In Fig. 3 we show the spatial diffusion coefficient for shear Alfvén
waves and in
Fig. 4 for fast magnetosonic waves, which also gives the spatial
diffusion coefficient in
case for the mixed turbulence (66).
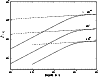 |
Figure 3:
The parallel spatial diffusion coefficient for shear Alfvén waves
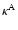 for protons (solid lines),
electrons and positrons (dashedlines). We show the results for different values of the
anisotropyparameter
for protons (solid lines),
electrons and positrons (dashedlines). We show the results for different values of the
anisotropyparameter 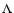 . . |
| Open with DEXTER |
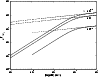 |
Figure 4:
The parallel spatial diffusion coefficient for fast magnetosonic
waves
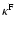 for protons (solid lines),
electrons and positrons (dashedlines). We show the results for different values of the
anisotropyparameter
for protons (solid lines),
electrons and positrons (dashedlines). We show the results for different values of the
anisotropyparameter 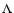 . . |
| Open with DEXTER |
The parallel mean free path is given by
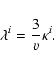 |
(90) |
This can be written as
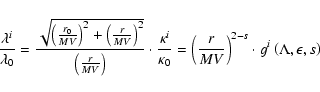 |
(91) |
with
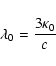 |
(92) |
and we know that
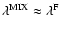 .
Figure 5 shows the
parallel mean free path for shear
Alfvén waves, while in Fig. 6 the mean free path for fast
magnetosonic waves and therefore
for the mixed turbulence (66) is shown.
.
Figure 5 shows the
parallel mean free path for shear
Alfvén waves, while in Fig. 6 the mean free path for fast
magnetosonic waves and therefore
for the mixed turbulence (66) is shown.
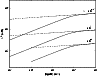 |
Figure 5:
The parallel mean free path for shear Alfvén waves
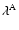 for protons (solid lines),
electrons and positrons (dashed lines). We show the results for different values of the
anisotropy parameter
for protons (solid lines),
electrons and positrons (dashed lines). We show the results for different values of the
anisotropy parameter 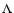 . . |
| Open with DEXTER |
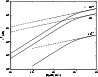 |
Figure 6:
The parallel mean free path for fast magnetosonic waves
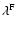 for protons (solid lines),
electrons and positrons (dashed lines). We show the results for different values of the
anisotropy parameter
for protons (solid lines),
electrons and positrons (dashed lines). We show the results for different values of the
anisotropy parameter 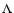 . . |
| Open with DEXTER |
We have continued to evaluate the relevant cosmic ray
transport parameters in the presence of anisotropic plasma wave
turbulence. Using the estimates of the anisotropy parameter in the
strongly
parallel and perpendicular regimes, based on linear Landau damping
balancing
radiative loss in the diffuse interstellar medium,
we have calculated the Fokker-Planck coefficients,
the momentum (A) and parallel spatial diffusion coefficient (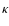 )
and the
parallel mean free path (
)
and the
parallel mean free path (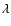 )
of cosmic ray particles for a mixed plasma
turbulence of shear Alfvén
waves and fast magnetosonic waves. We elaborated in detail on the case
of equal intensity,
plasma and anisotropy parameters of shear Alfvénic and magnetosonic
turbulence, but our formalism easily allows generalization to any intensity ratio of these
plasma waves.
)
of cosmic ray particles for a mixed plasma
turbulence of shear Alfvén
waves and fast magnetosonic waves. We elaborated in detail on the case
of equal intensity,
plasma and anisotropy parameters of shear Alfvénic and magnetosonic
turbulence, but our formalism easily allows generalization to any intensity ratio of these
plasma waves.
In the equal intensity case, regarding the influence of the anisotropy
parameter 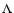 ,
we find that
for strongly perpendicular turbulence (
,
we find that
for strongly perpendicular turbulence (
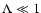 )
)
![$A \sim \Lambda ^{-1/2} \left[ \ln \epsilon^{-1} + \ln \Lambda ^{1/2}
\right]$](/articles/aa/full/2004/24/aa0304/img288.gif) and
and
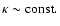 whereas for strongly
parallel turbulence (
whereas for strongly
parallel turbulence (
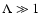 )
we obtain
)
we obtain
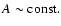 and
and
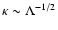 .
Moreover, for the momentum diffusion coefficient we show that for a
non-slab-like geometry the transit-time damping of the fast
magnetosonic waves is dominant. In slab-like turbulence (
.
Moreover, for the momentum diffusion coefficient we show that for a
non-slab-like geometry the transit-time damping of the fast
magnetosonic waves is dominant. In slab-like turbulence (
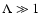 )
both gyroresonance
contributions are equal and dominate over transit-time damping.
For the spatial diffusion coefficient and the mean free path we find
that the Alfvén contribution can be neglected. The gyroresonance
contribution
of the fast magnetosonic waves controls the spatial diffusion
coefficient and the
parallel mean free path.
)
both gyroresonance
contributions are equal and dominate over transit-time damping.
For the spatial diffusion coefficient and the mean free path we find
that the Alfvén contribution can be neglected. The gyroresonance
contribution
of the fast magnetosonic waves controls the spatial diffusion
coefficient and the
parallel mean free path.
We established that the rigidity dependences of the momentum and
parallel spatial diffusion coefficients for general values of
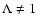 are the same as in the case of isotropic (
are the same as in the case of isotropic (
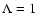 )
turbulence discussed
earlier by Schlickeiser & Miller (1998); however, the absolute values of these
transport parameters are strongly dependent on the value of
)
turbulence discussed
earlier by Schlickeiser & Miller (1998); however, the absolute values of these
transport parameters are strongly dependent on the value of 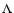 .
As indicated above the value of momentum diffusion coefficient
increases
.
As indicated above the value of momentum diffusion coefficient
increases 
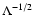 for strongly perpendicular (
for strongly perpendicular (
 )
turbulence, whereas the value of the parallel diffusion coefficient
decreases
)
turbulence, whereas the value of the parallel diffusion coefficient
decreases 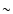
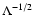 for strongly parallel
(
for strongly parallel
(
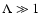 )
turbulence.
)
turbulence.
We also demonstrated that in general the parameter 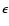 has a strong
influence on the results of transport parameters. Therefore the plasma wave dispersion
relation and the turbulent electrical fields cannot be neglected if one
calculates spatial and momentum diffusion coefficients in anisotropic turbulence
geometry.
has a strong
influence on the results of transport parameters. Therefore the plasma wave dispersion
relation and the turbulent electrical fields cannot be neglected if one
calculates spatial and momentum diffusion coefficients in anisotropic turbulence
geometry.
Our results have direct implications for the cosmic ray transport
parameters inferred from the observations of galactic cosmic rays:
in particular the cosmic ray anisotropy and the diffusive cosmic ray escape
time, inferred from the decay of radioactive cosmic ray isotopes and the
secondary-to-primary-ratio, are related to the spatial diffusion coefficients,
while the rate of stochastic acceleration is determined by the momentum diffusion
coefficient. However, a detailed discussion of these implications is premature, before
the role of perpendicular spatial diffusion in the mixed plasma wave turbulence
fields has been clarified.
Moreover, it also is useful to extend our study to arbitrary intensity ratios
of Alfvénic and magnetosonic waves and to investigate the effect of steeper
(s>2) turbulence power spectra.
A further future study concerns the cosmic ray rigidity range.
For all the calculations done sofar in the three papers of this
series we used the restriction
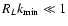 .
But it is also very
important to consider the opposite limit (
.
But it is also very
important to consider the opposite limit (
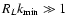 )
for
ultrahigh cosmic
ray energies. These topics will be the subject of future work.
)
for
ultrahigh cosmic
ray energies. These topics will be the subject of future work.
Acknowledgements
This work was partially supported by the Deutsche
Forschungsgemeinschaft through
Sonderforschungsbereich 591. A.S. acknowledge support by the National
Science Foundation
under grant ATM-0000315.
- Abramowitz, M., &
Stegun, I. A. 1972, Handbook of Mathematical Functions, National
Bureau of Standards, Washington
(In the text)
- Bieber, J. W.,
Matthaeus, W. H., Smith, C. W., et al. 1994, ApJ, 420, 294 [NASA ADS] [CrossRef] (In the text)
- Chandran, B. 2001, Phys.
Rev. Lett., 85, 4656 [NASA ADS] [CrossRef] (In the text)
- Goldreich, P., &
Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] (In the text)
- Lerche, I., &
Schlickeiser, R. 2001a, A&A, 366, 1008 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Lerche, I., &
Schlickeiser, R. 2001b, A&A, 378, 279 [EDP Sciences] [NASA ADS] [CrossRef] (LS)
(In the text)
- Magnus, W.,
Oberhettinger, F., & Soni, R. P. 1966, Formulas and Theorems
for the Special Functions of Mathematical Physics (Berlin,
Heidelberg, New York: Springer-Verlag)
(In the text)
- Rickett, B. J. 1990,
ARA&A, 28, 561 [NASA ADS] (In the text)
- Schlickeiser, R., &
Miller, J. A. 1998, ApJ, 492, 352 [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R. 2002, Cosmic
Ray Astrophysics (Berlin Heidelberg: Springer-Verlag)
- Shalchi, A.,
& Schlickeiser, R. 2004, ApJ, 604, 861 [CrossRef] (In the text)
- Spangler, S. R. 1991, ApJ,
376, 540 [NASA ADS] [CrossRef] (In the text)
- Teufel, A., Lerche, I.,
& Schlickeiser, R., 2003, A&A, 397, 777 [EDP Sciences] [NASA ADS] [CrossRef] (TLS)
(In the text)
- Yan, H., & Lazarian,
A. 2002, Phys. Rev. Lett., 89, 1102 [NASA ADS] (In the text)
- Watson, G. N. 1966, A
treatise on the Theory of Bessel Functions (Cambridge University
Press)
(In the text)
Online Material
From LS we know that
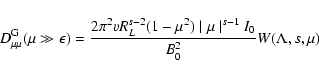 |
(A.1) |
with
![$\displaystyle W_l^{\rm G} (\Lambda, s, \mu) = \sum_{n=1} ^{\infty} \int _{0} ^{...
... + \Lambda x]^{(s+2)/2}}
\left[ J'_{n} \left( n M \sqrt{x} \right) \right] ^{2}$](/articles/aa/full/2004/24/aa0304/img297.gif) |
|
|
(A.2) |
and with
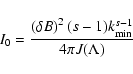 |
(A.3) |
under the condition
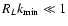 .
We split the integral as
.
We split the integral as
and approximate the two sums.
To approximate the first sum we use the Kapteyn series from Appendix C
 |
(A.5) |
so that
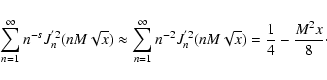 |
(A.6) |
The second sum can be approximated with
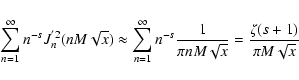 |
(A.7) |
where we neglect the oscillating part in the approximation of the
Bessel
function for large arguments
(Abramowitz & Stegun 1972). We then obtain
We write this as
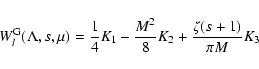 |
(A.9) |
with the integrals
![\begin{displaymath}K_{1} = \int_{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1} {1 \over \left[ 1 +
\Lambda x \right] ^{(s+2)/2}},
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img310.gif) |
(A.10) |
![\begin{displaymath}K_{2} = \int_{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1} {x \over \left[ 1 +
\Lambda x \right] ^{(s+2)/2}}
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img311.gif) |
(A.11) |
and
![\begin{displaymath}K_{3} = \int_{M^{-2}} ^{\infty} {\rm d}x {x+2 \over x+1} {x^{-1/2} \over
\left[ 1 + \Lambda x \right] ^{(s+2)/2}}\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img312.gif) |
(A.12) |
We consider the three integrals in the limits of small and large M2 and
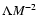 in turn.
Here
in turn.
Here
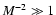 so that
so that
| K1 |
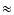 |
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img316.gif) |
|
| |
= |
![$\displaystyle {4 \over s \Lambda} \left[ 1 - \left(1 + \Lambda M^{-2} \right)^{-s/2} \right]$](/articles/aa/full/2004/24/aa0304/img317.gif) |
(A.13) |
| K2 |
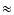 |
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img318.gif) |
|
| |
= |
 |
(A.14) |
| K3 |
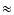 |
![$\displaystyle \int _{M^{-2}} ^{\infty} {{\rm d}x \over \sqrt{x}} \left[ 1
+ \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img320.gif) |
|
| |
= |
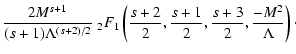 |
(A.15) |
For
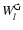 we then obtain approximately
we then obtain approximately
In the limit
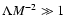 we find
we find
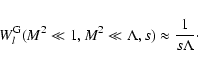 |
(A.17) |
To derive the last equations we have used the following approximations
and relations for the hypergeometric functions (Magnus et al. 1966):
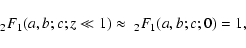 |
(A.18) |
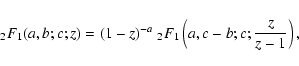 |
(A.19) |
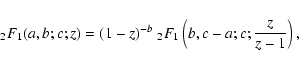 |
(A.20) |
and if c > a+b
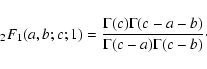 |
(A.21) |
Here we obtain for
 approximately
approximately
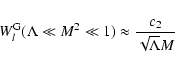 |
(A.22) |
with
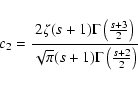 |
(A.23) |
where we have used the same relations and approximations (Eqs. (A.18)-(A.21))
as in the last case.
In this case
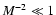 is a small quantity and the three integrals
are approximately
is a small quantity and the three integrals
are approximately
| K1 |
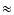 |
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img316.gif) |
|
| |
= |
![$\displaystyle {4 \over s \Lambda} \left[ 1 - \left(1 + \Lambda M^{-2} \right)^{-s/2} \right]$](/articles/aa/full/2004/24/aa0304/img317.gif) |
(A.24) |
| K2 |
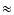 |
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img318.gif) |
|
| |
= |
 |
(A.25) |
| K3 |
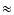 |
![$\displaystyle 2 \int _{M^{-2}} ^{\infty} {{\rm d}x \over \sqrt{x}} \left[
1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img334.gif) |
|
| |
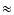 |
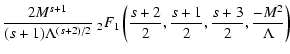 |
(A.26) |
and we then obtain
in the limit
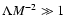 and
and
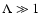 .
With Eqs. (A.18)-(A.21)
we obtain
.
With Eqs. (A.18)-(A.21)
we obtain
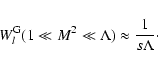 |
(A.28) |
In the last case we find for Wl approximately
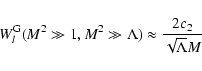 |
(A.29) |
where we have used the same relations and approximations as in the
first three cases.
From LS we know that
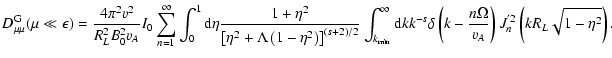 |
|
|
(B.1) |
Now we restrict our analysis to
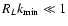 .
With Eq. (A.3) we then find
.
With Eq. (A.3) we then find
 |
(B.2) |
with
With the same approximations for the sums of Bessel functions as used
in Appendix A we obtain
We can express these integrals in terms of hypergeometric functions:
Now we consider special cases for 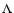 and
and
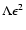 :
Here we find with Eqs. (A.18)-(A.21) that
:
Here we find with Eqs. (A.18)-(A.21) that
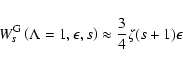 |
(B.6) |
to lowest order in 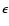 .
Here we obtain approximately
.
Here we obtain approximately
| |
|
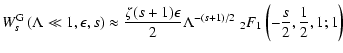 |
|
| |
|
 |
(B.7) |
If we use
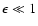 and
and
 we find for this case
we find for this case
 |
(B.8) |
In this case we can use approximations for the hypergeometric functions
again to find that
| |
|
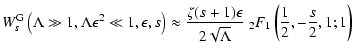 |
|
| |
|
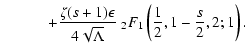 |
(B.9) |
We can express the hypergeometric functions through  -functions
and in the
limit
-functions
and in the
limit
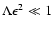 we obtain
we obtain
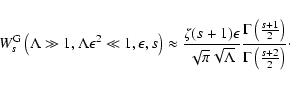 |
(B.10) |
Here we find
and we obtain for this case
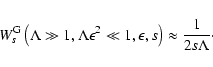 |
(B.12) |
With the Bessel function identities
![\begin{displaymath}\left[ 2 J'_{n} (nz) \right] ^{2} = \left[ J_{n-1} (nz) - J_{n+1} (nz)
\right]^{2}
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img372.gif) |
(C.1) |
and
![\begin{displaymath}\left[ {2 n J_{n} (nz) \over nz } \right] ^{2} = \left[ J_{n-1} (nz) +
J_{n+1} (nz) \right]^{2}
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img373.gif) |
(C.2) |
we find
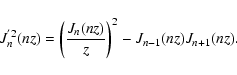 |
(C.3) |
Therefore we obtain for the series
 |
|
|
(C.4) |
With the Kapteyn series (Watson 1966)
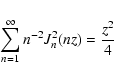 |
(C.5) |
and with (Watson 1966)
 |
(C.6) |
we obtain
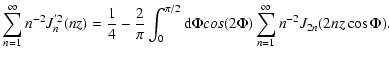 |
|
|
(C.7) |
With (Watson 1966)
 |
(C.8) |
we find
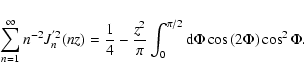 |
(C.9) |
It is very easy to solve this integral and we finally find
 |
(C.10) |
if
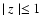 .
.
Copyright ESO 2004
![]() )
we obtain that
the momentum
diffusion coefficient is proportional to
)
we obtain that
the momentum
diffusion coefficient is proportional to
![]() ,
whereas for strongly parallel turbulence (
,
whereas for strongly parallel turbulence (
![]() )
the momentum
diffusion
coefficient is a constant.
We also calculate the anisotropy dependence of the spatial diffusion
coefficient and
the parallel mean free path for the mixed turbulence.
For all coefficients we discuss the rigidity dependence for
different cosmic ray particles.
)
the momentum
diffusion
coefficient is a constant.
We also calculate the anisotropy dependence of the spatial diffusion
coefficient and
the parallel mean free path for the mixed turbulence.
For all coefficients we discuss the rigidity dependence for
different cosmic ray particles.
![]() for pure shear Alfvén
waves we obtain from TLS(25)
for pure shear Alfvén
waves we obtain from TLS(25)
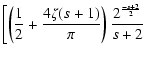
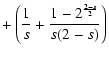
![$\displaystyle \times \left. \left( {1 \over s} - {2^{-s/2} \over s} + {2^{-{s+2} \over 2} \over
s+2} - {1 \over s+2} \right) \right],$](/articles/aa/full/2004/24/aa0304/img57.gif)
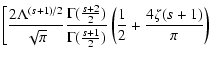
![$\displaystyle \times \left. {1 \over 2 (s+2)} \left( 1 + {1 \over 2^{(s+2)/2}} \right) \right],$](/articles/aa/full/2004/24/aa0304/img60.gif)
![$\displaystyle \left[ {1 \over s} - {1 \over s+2}
\right] \cdot$](/articles/aa/full/2004/24/aa0304/img62.gif)
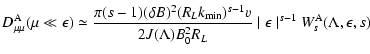
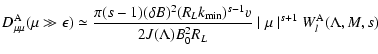
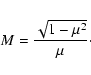
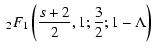
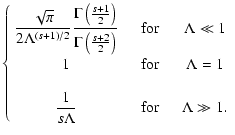
![]() for Alfvén waves and for
s=5/3.
for Alfvén waves and for
s=5/3.
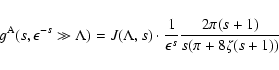
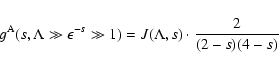
![]() for Alfvén waves and for s=5/3.
for Alfvén waves and for s=5/3.
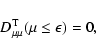
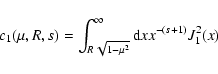
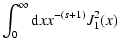
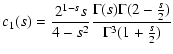
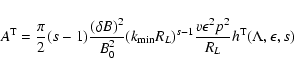
![]() for fast magnetosonic waves. In
this table we introduced the functions
for fast magnetosonic waves. In
this table we introduced the functions
![]() with
the generalized
with
the generalized ![]() -function B(x,y) and
-function B(x,y) and
![]() .
.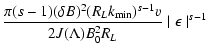
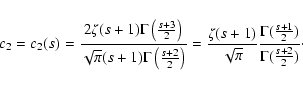
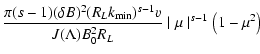
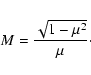
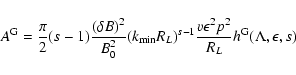
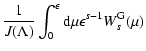
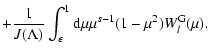

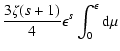
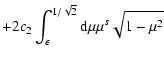
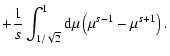
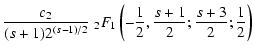
![$\displaystyle + {1 \over s} \left[ {1 \over s} - {1 \over s+2} - {1 \over s
2^{s/2}} + {1 \over (s+2) 2^{(s+2)/2}} \right]\cdot$](/articles/aa/full/2004/24/aa0304/img135.gif)
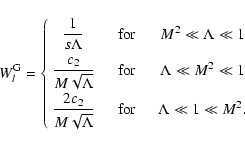
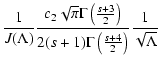
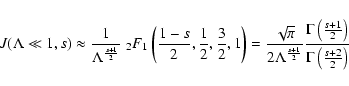

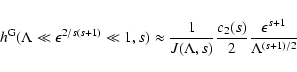
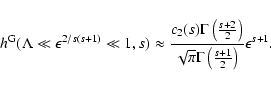
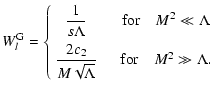
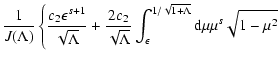
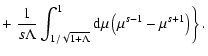
![\begin{displaymath}h^{\rm G}(\epsilon^{-2} \gg \Lambda \gg 1, s) \approx {1 \ove...
... s \Lambda} \left[ {1 \over s } - { 1 \over s+2 } \right]\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img155.gif)
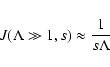

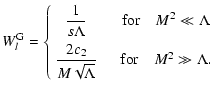
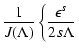
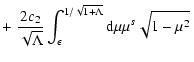
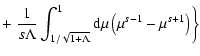

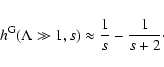
![]() for fast magnetosonic waves.
for fast magnetosonic waves.![]() )
and
gyroresonant interactions (
)
and
gyroresonant interactions (![]() ), we are now able to calculate
), we are now able to calculate
![]() :
:
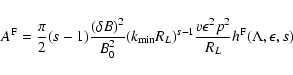
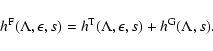
![]() for fast magnetosonic waves.
for fast magnetosonic waves.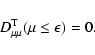
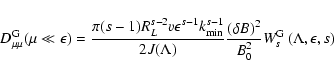
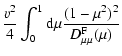
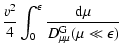
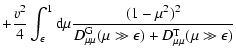
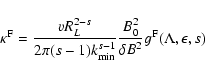
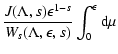
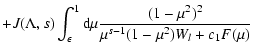
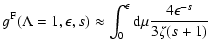
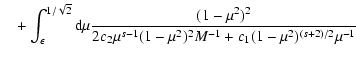
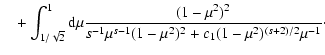
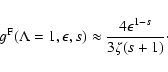
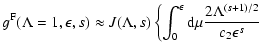
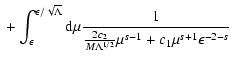
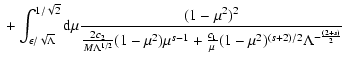
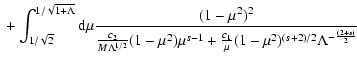
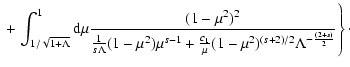
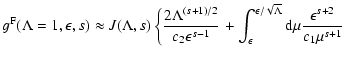
![$\displaystyle \quad + \int_{\epsilon/\sqrt{\Lambda}}^{1/\sqrt{2}} {\rm d} \mu
{...
...u^{s+1} \left[ 2 c_2 M \Lambda^{-1/2} + c_1
M^{s+2} \Lambda^{-(2+s)/2} \right]}$](/articles/aa/full/2004/24/aa0304/img198.gif)
![$\displaystyle \quad + \int_{1/\sqrt{2}}^{1/\sqrt{1+\Lambda}} {\rm d} \mu
{ (1-\...
...\mu^{s+1} \left[ c_2 M \Lambda^{-1/2} + c_1 M^{s+2}
\Lambda^{-(2+s)/2} \right]}$](/articles/aa/full/2004/24/aa0304/img199.gif)
![$\displaystyle \quad + \left. \int_{1/\sqrt{1+\Lambda}}^{1} {\rm d} \mu
{ (1-\mu...
...s^{-1} M^2 \Lambda^{-1} + c_1
M^{s+2} \Lambda^{-(2+s)/2} \right]} \right\}\cdot$](/articles/aa/full/2004/24/aa0304/img200.gif)
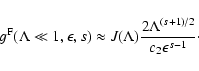
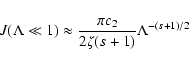
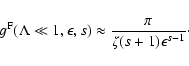
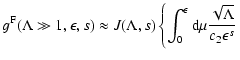
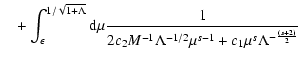
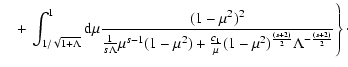
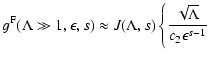
![$\displaystyle \quad + \int_{\epsilon}^{1/\sqrt{1+\Lambda}} {\rm d} \mu {1
\over...
...^{s+1} \left[ 2 c_2 M \Lambda^{-1/2} + c_1 M^{s+2}
\Lambda^{-(s+2)/2} \right] }$](/articles/aa/full/2004/24/aa0304/img210.gif)
![$\displaystyle \quad + \left. \int_{1/\sqrt{1+\Lambda}}^1 {\rm d} \mu {(1-\mu^2)...
...s^{-1} M^2 \Lambda^{-1} + c_1 M^{s+2}
\Lambda^{-(s+2)/2} \right]} \right\}\cdot$](/articles/aa/full/2004/24/aa0304/img211.gif)
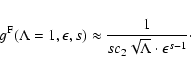
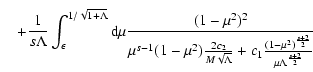
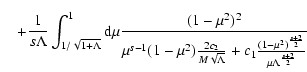
![]() for fast magnetosonic turbulence.
for fast magnetosonic turbulence.![]() can be written as a sum of
the Fokker-Planck
coefficients from shear Alfvén waves and fast magnetosonic waves
can be written as a sum of
the Fokker-Planck
coefficients from shear Alfvén waves and fast magnetosonic waves

![]() for mixed turbulence.
for mixed turbulence.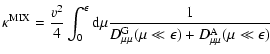
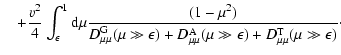
![]() .
Here we have (see Sect. 2):
.
Here we have (see Sect. 2):

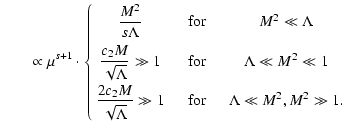
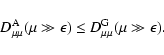
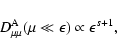
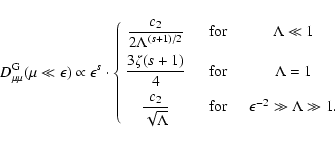
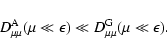
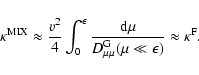

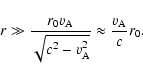
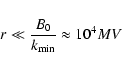
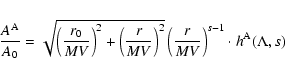
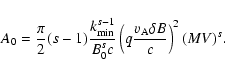




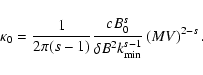


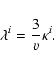
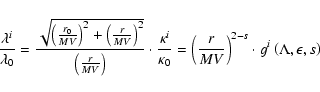
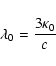


![]() ,
we find that
for strongly perpendicular turbulence (
,
we find that
for strongly perpendicular turbulence (
![]() )
)
![]() and
and
![]() whereas for strongly
parallel turbulence (
whereas for strongly
parallel turbulence (
![]() )
we obtain
)
we obtain
![]() and
and
![]() .
Moreover, for the momentum diffusion coefficient we show that for a
non-slab-like geometry the transit-time damping of the fast
magnetosonic waves is dominant. In slab-like turbulence (
.
Moreover, for the momentum diffusion coefficient we show that for a
non-slab-like geometry the transit-time damping of the fast
magnetosonic waves is dominant. In slab-like turbulence (
![]() )
both gyroresonance
contributions are equal and dominate over transit-time damping.
For the spatial diffusion coefficient and the mean free path we find
that the Alfvén contribution can be neglected. The gyroresonance
contribution
of the fast magnetosonic waves controls the spatial diffusion
coefficient and the
parallel mean free path.
)
both gyroresonance
contributions are equal and dominate over transit-time damping.
For the spatial diffusion coefficient and the mean free path we find
that the Alfvén contribution can be neglected. The gyroresonance
contribution
of the fast magnetosonic waves controls the spatial diffusion
coefficient and the
parallel mean free path.
![]() are the same as in the case of isotropic (
are the same as in the case of isotropic (
![]() )
turbulence discussed
earlier by Schlickeiser & Miller (1998); however, the absolute values of these
transport parameters are strongly dependent on the value of
)
turbulence discussed
earlier by Schlickeiser & Miller (1998); however, the absolute values of these
transport parameters are strongly dependent on the value of ![]() .
As indicated above the value of momentum diffusion coefficient
increases
.
As indicated above the value of momentum diffusion coefficient
increases ![]()
![]() for strongly perpendicular (
for strongly perpendicular (
![]() )
turbulence, whereas the value of the parallel diffusion coefficient
decreases
)
turbulence, whereas the value of the parallel diffusion coefficient
decreases ![]()
![]() for strongly parallel
(
for strongly parallel
(
![]() )
turbulence.
)
turbulence.
![]() has a strong
influence on the results of transport parameters. Therefore the plasma wave dispersion
relation and the turbulent electrical fields cannot be neglected if one
calculates spatial and momentum diffusion coefficients in anisotropic turbulence
geometry.
has a strong
influence on the results of transport parameters. Therefore the plasma wave dispersion
relation and the turbulent electrical fields cannot be neglected if one
calculates spatial and momentum diffusion coefficients in anisotropic turbulence
geometry.
![]() .
But it is also very
important to consider the opposite limit (
.
But it is also very
important to consider the opposite limit (
![]() )
for
ultrahigh cosmic
ray energies. These topics will be the subject of future work.
)
for
ultrahigh cosmic
ray energies. These topics will be the subject of future work.
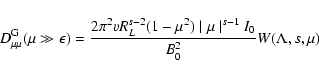
![$\displaystyle W_l^{\rm G} (\Lambda, s, \mu) = \sum_{n=1} ^{\infty} \int _{0} ^{...
... + \Lambda x]^{(s+2)/2}}
\left[ J'_{n} \left( n M \sqrt{x} \right) \right] ^{2}$](/articles/aa/full/2004/24/aa0304/img297.gif)
![$\displaystyle \int _{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1}
{1 \over [1 + \Lambda x]^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img300.gif)
![$\displaystyle \times \sum_{n=1} ^{\infty} \left[ J'_{n} \left( n M \sqrt{x} \right) \right]^{2}$](/articles/aa/full/2004/24/aa0304/img301.gif)
![$\displaystyle + \int _{M^{-2}} ^{\infty} {\rm d}x {x+2 \over x+1} {1 \over [1 + \Lambda x]^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img302.gif)
![$\displaystyle \times \sum_{n=1} ^{\infty} \left[ J'_{n} \left( n M \sqrt{x} \right) \right]^{2}$](/articles/aa/full/2004/24/aa0304/img301.gif)

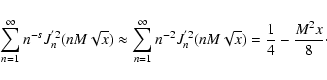
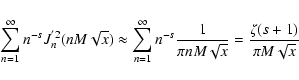
![$\displaystyle {1 \over 4} \int_{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1} {1 \over \left[ 1 +
\Lambda x \right] ^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img306.gif)
![$\displaystyle - {M^{2} \over 8} \int_{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1} {x \over
\left[ 1 + \Lambda x \right] ^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img307.gif)
![$\displaystyle + { \zeta{(s+1)} \over \pi M} \int_{M^{-2}} ^{\infty} {\rm d}x {x+2 \over
x+1} {x^{-1/2} \over \left[ 1 + \Lambda x \right] ^{(s+2)/2}}\cdot$](/articles/aa/full/2004/24/aa0304/img308.gif)
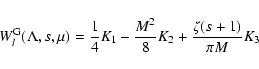
![\begin{displaymath}K_{1} = \int_{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1} {1 \over \left[ 1 +
\Lambda x \right] ^{(s+2)/2}},
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img310.gif)
![\begin{displaymath}K_{2} = \int_{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1} {x \over \left[ 1 +
\Lambda x \right] ^{(s+2)/2}}
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img311.gif)
![\begin{displaymath}K_{3} = \int_{M^{-2}} ^{\infty} {\rm d}x {x+2 \over x+1} {x^{-1/2} \over
\left[ 1 + \Lambda x \right] ^{(s+2)/2}}\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img312.gif)
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img316.gif)
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img318.gif)

![$\displaystyle \int _{M^{-2}} ^{\infty} {{\rm d}x \over \sqrt{x}} \left[ 1
+ \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img320.gif)
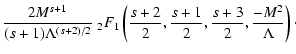
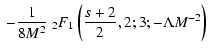
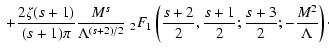
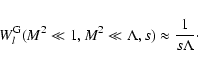
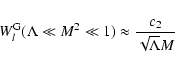
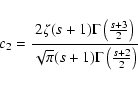
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img316.gif)
![$\displaystyle 2 \int _{0} ^{M^{-2}} {\rm d}x x \left[ 1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img318.gif)

![$\displaystyle 2 \int _{M^{-2}} ^{\infty} {{\rm d}x \over \sqrt{x}} \left[
1 + \Lambda x \right] ^{-{s+2 \over 2}}$](/articles/aa/full/2004/24/aa0304/img334.gif)
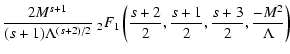
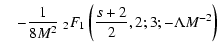
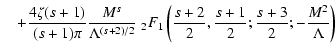
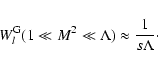
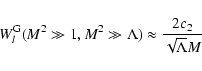
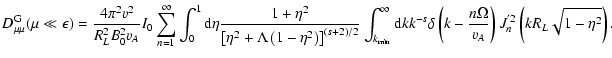

![$\displaystyle \int _{0} ^{\sqrt{1 -
\epsilon^{2}}} {\rm d} \eta {1 + \eta ^{2} \over\left[ \eta ^{2} + \Lambda
\left(1 - \eta ^{2} \right) \right] ^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img344.gif)
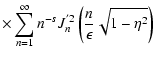
![$\displaystyle + \int _{\sqrt{1 - \epsilon^{2}}} ^{1} {\rm d} \eta {1 + \eta ^{2} \over
\left[ \eta ^{2} + \Lambda \left(1 - \eta ^{2} \right) \right]^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img346.gif)
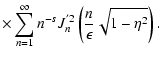
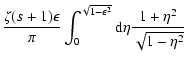
![$\displaystyle + {1 \over 8} \int _{\sqrt{1 - \epsilon^{2}}} ^{1} d \eta {1 + \e...
...over \left[ \eta ^{2} + \Lambda \left(1 - \eta ^{2} \right)
\right] ^{(s+2)/2}}$](/articles/aa/full/2004/24/aa0304/img350.gif)
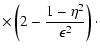
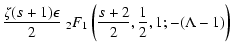
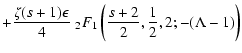
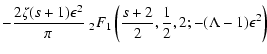
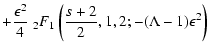
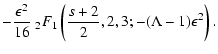
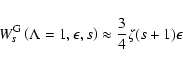
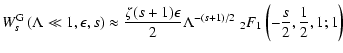


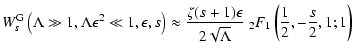
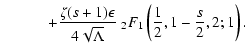
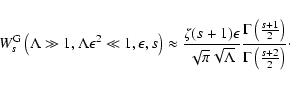
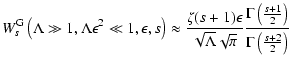
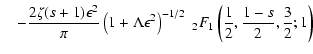
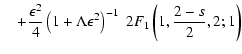
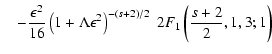
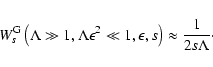
![\begin{displaymath}\left[ 2 J'_{n} (nz) \right] ^{2} = \left[ J_{n-1} (nz) - J_{n+1} (nz)
\right]^{2}
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img372.gif)
![\begin{displaymath}\left[ {2 n J_{n} (nz) \over nz } \right] ^{2} = \left[ J_{n-1} (nz) +
J_{n+1} (nz) \right]^{2}
\end{displaymath}](/articles/aa/full/2004/24/aa0304/img373.gif)