A&A 420, 1025-1032 (2004)
DOI: 10.1051/0004-6361:20034180

Meissner effect and vortex dynamics in quark stars

A model for soft gamma-ray repeaters

R. Ouyed 1 - Ø. Elgarøy 2,3 - H. Dahle 3 - P. Keränen 2


1 - Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4 Canada
2 - Nordic Institute for Theoretical Physics, Blegdamsvej 17, 2100 Copenhagen, Denmark
3 - Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern, 0315 Oslo, Norway

Received 12 August 2003 / Accepted 11 March 2004

Abstract
We present a new model for soft gamma-ray repeaters based on a quark star born with temperatures above the critical value ($T_{\rm c}$) for the onset of the colour-flavor locked superconductivity. The quark star then quickly cools below $T_{\rm c}$, expelling a fraction of the surface magnetic field via the Meissner effect. We show that if a small fraction ($\leq$$10\%$) of the surface magnetic field ( $10^{14}{-}10^{15}~ {\rm G}$) is expelled, it quickly decays via magnetic reconnection and heats up the quark star surface to temperatures > $10^9~{\rm K}$. Created $({\rm e}^{+},{\rm e}^{-})$ pairs annihilate into gamma rays emitted in a giant burst (the first burst in our model), with a luminosity of $\sim$ $10^{45}~ {\rm erg}~ {\rm s}^{-1}$. Subsequent bursts result from the restructuring of the surface magnetic field following the formation and relaxation of a vortex lattice which confines the internal magnetic field. During this phase, energy is sporadically released as a consequence of magnetic reconnection events in the entangled surface magnetic field as it evolves into a smooth, more stable, configuration. The star eventually enters a quiescent phase in which energy is continuously supplied by vortex annihilation at the surface. As the star spins down, the outermost vortex lines will be pushed to the surface where they annihilate and release their confined magnetic field. We show that the corresponding luminosity is $L_v \sim 10^{36}~ {\rm erg}~ {\rm s}^{-1}$ for a typical soft gamma-ray repeater spinning with a period of $8~ {\rm s}$ and a surface magnetic field not exceeding $10^{15}~ {\rm G}$. Our model can be applied to any situation where a $T > T_{\rm c}$ quark star is generated. We discuss the connection between anomalous X-ray pulsars and soft gamma-ray repeaters in the context of our model.

Key words: gamma rays: bursts - X-rays: stars - stars: magnetic fields - stars: neutron - stars: quark star

1 Introduction

Soft $\gamma$-ray repeaters (SGRs) are sources of recurrent, short ( $t \sim 0.1$ s), intense ( $L \sim 10^3{-}10^4~L_{\rm Edd}$) bursts of $\gamma$-ray emission with a soft energy spectrum. The normal pattern of SGR activity are intense activity periods which can last weeks or months, separated by quiescent phases lasting years or decades. The five known SGRs are located in our Galaxy, or, in the case of SGR 0526-66, in the Large Magellanic Cloud. The two most intense SGR bursts ever recorded were the 5 March 1979 giant flare of SGR 0526-66 (Mazets et al. 1979) and the similar 27 August 1998 giant flare of SGR 1900+14. The peak luminosities of these events ($\sim$ $10^6{-}10^7~L_{\rm Edd}$) exceeded the peak luminosities of "normal'' SGR bursts by a factor >103. In Table 1 we summarize the burst properties of these giant flares.

Table 1: Giant burst properties.

Several SGRs have been found to be X-ray pulsars with an unusually high spin down rate of $\dot{P} / P \sim 10^{-10}$ s-1, usually attributed to magnetic braking caused by a super-strong magnetic field B > 1014 G, which implies that SGRs are magnetars (Golenetskij et al. 1979; Duncan & Thompson 1992; Kouveliotou et al. 1998, 1999). In the magnetar model, the magnetic field is the likely provider of the burst energy, since it is the dominant source of free energy in the star. A common scenario is that stresses build up in the magnetic field and create a quake in the crust of the neutron star which ejects hot plasma Alfvén waves through its rigid magnetosphere (Thompson & Duncan 1995, 1996). The magnetic field of such a star would have grown to magnetar-scale strengths because of strong convection during the collapse of the proto-neutron star core (Duncan & Thompson 1992; Thompson & Duncan 1993).

In this paper, we propose an alternative model where the SGR activity is produced by phenomena occurring in a hot ( $T > T_{\rm c}$) quark star. In Sect. 2 we discuss the cooling timescales of the quark star and the onset of colour superconductivity. In Sect. 3 we show how giant flares such as the 5 March 1979 event could be powered by the expulsion of a fraction of the magnetic field due to the Meissner effect after the onset of superconductivity. We also calculate the light curve and temperature evolution for such a burst in our model. The remaining magnetic field in the star is confined to vortices, which will evolve into a lattice configuration, as discussed in Sect. 4. Subsequent weaker SGR bursts may be due to the reorganization of the external magnetic field, and the luminosity of SGRs in their quiescent phase may be mostly powered by the annihilation of vortices at the stellar surface, as detailed in Sect. 5. After decades of quiescence, a crust may form, leading to occasional crustquakes which could power later burst events, and additional events could be due to rare impacts; such events are discussed in Sect. 6. In Sect. 7, we briefly discuss known SGRs within our model, and in Sect. 8 we discuss the suggested connection SGRs have with anomalous X-ray pulsars (AXPs) in relation to our model. Finally, we conclude in Sect. 9.

   
2 Cooling timescale and onset of colour superconductivity: The CFL star

Present estimates of the critical temperature for onset of colour-flavor locked (CFL) superconductivity suggest $T_{\rm c} \sim 10^{12}\;{\rm K}$ (Rajagopal & Wilczek 2000) whereas early estimates indicated $T_{\rm c} \sim 10^{9}\;{\rm K}$ (Bailin & Love 1984). The quark star we take to be born with an effective temperature higher than $T_{\rm c}$. Once formed, the quark star will cool rapidly through neutrino emission. Using the result of Haensel (1991) for the neutrino emissivity,

 \begin{displaymath}\varepsilon_\nu = 2.2 \times 10^{26} \alpha_{\rm c} Y_{\rm e}... ...}(n_{\rm b}/n_0) T_9^6 \;{\rm erg}~{\rm cm}^{-3}~{\rm s}^{-1}, \end{displaymath} (1)

where $\alpha_{\rm c} = g^2/4\pi$ is the QCD fine structure constant, g is the quark-gluon coupling constant, $Y_{\rm e} = n_{\rm e} / n_{\rm b}$ is the ratio of electron and baryon numbers, $n_0 \simeq 1.7\times 10^{38}\;{\rm cm}^{-3}$ is the nuclear matter saturation density, T9 is the temperature in units of $10^9\;{\rm K}$, and taking the specific heat per volume as (Iwamoto 1982)

 \begin{displaymath}C_q = 2.5 \times 10^{20}(n_{\rm b}/n_0)^{2/3}T_9\;{\rm erg}~{\rm cm}^{-3} ~{\rm K}^{-1}, \end{displaymath} (2)

we can estimate the timescale for neutrino cooling from an initial temperature $T_{9,\rm i}$ to a final temperature $T_{9,\rm f} \ll T_{9,\rm i}$:

 \begin{displaymath}\tau_{\rm cool} \simeq 3\times 10^2\alpha_{\rm c}^{-1}Y_{\rm ... ...(\frac{n_{\rm b}}{n_0}\right)^{-1/3}T_{9,\rm f}^{-4}\;{\rm s}. \end{displaymath} (3)

According to this estimate a critical temperature of, say, $T_{\rm c} \sim 10^{11}\;K$ will be reached within $\tau_{\rm cool} \sim 0.4\;{\rm ms}$. Thus, the star will rapidly undergo a phase transition to a colour superconducting state (except in the cores of the vortices formed in response to the rotation of the star; see Sect. 4).

   
3 Giant Burst: Expulsion and decay of the magnetic field

In an ordinary superconductor there is a thermodynamical critical field $H_{\rm c}$ (or $H_{\rm c1}$ for type II superconductors), determined by the free-energy difference between the normal and superconducting states in zero field, below which a magnetic field will be screened from the interior of the superconductor: this is the Meissner effect. The existence of the magnetic Meissner effect in colour superconductors is a matter of some debate (Alford et al. 2000; Sedrakian et al. 2001; Iida & Baym 2002) but we will proceed on the assumption that there is a Meissner effect in the CFL phase, and that at least part of the magnetic field is expelled from the surface layers of the star.

The model we consider assumes that the star intially consists of uniform density strange quark matter with an associated surface electric field Alcock et al. (1986). In this situation the calculations of Page & Usov (2002) show that the surface of the star cools faster than the core because of thermal emission of photons and ${\rm e}^+~ {\rm e}^-$-pairs from the surface. Therefore the CFL phase transition occurs first in a thin layer of thickness $\delta \ll R$ (R is the radius of the star) close to the surface. The magnetic field decay discussed later will thus heat the surface leading to thermal emission of photons.

The penetration depth $\lambda$ for the magnetic field is of the order 1 fm (see Iida & Baym 2002) so the magnetic field is negligible throughout the superconducting layer provided that $\delta \gg \lambda \sim \;{\rm fm}$. Note that the thermodynamical critical field is $H_{\rm c}\sim 10^{19}\;{\rm G}$ (Iida & Baym 2002), much larger than the field strengths of interest to us.

3.1 Expulsion timescale

The time scale for the expulsion is determined by the conductivity of the normal, non-superconducting state according to

 \begin{displaymath}\tau_{\rm exp} = \frac{4\pi \sigma_{\rm el} d^2}{\pi c^2}\left(\frac{B}{H_{\rm c}}\right)^2, \end{displaymath} (4)

where $\sigma_{\rm el}$ is the electrical conductivity in the normal state while B, c and d are the magnetic field strength, the speed of light and the thickness of the superconducting layer, respectively. For quarks, this quantity was found by Heiselberg & Pethick (1993) to be given by

 \begin{displaymath}\sigma_{\rm el,quark} \simeq (\alpha_s T_9)^{-5/3}\left(\frac{\mu}{300\;{\rm MeV}}\right)^{8/3} \times 10^{19}\;{\rm s}^{-1}, \end{displaymath} (5)

where $\mu$ is the quark chemical potential. For $\alpha_s=0.1$ (strong coupling constant), $\sigma_{\rm el}$ varies from $\sim$ $10^{17}\;{\rm s}^{-1}$ for $T=10^{11}\;{\rm K}$ to $\sim$ $ 10^{14}\;{\rm s}^{-1}$ for $T=10^{13}\;{\rm K}$. The electron contribution to the electrical conductivity can be estimated from the classical result

 \begin{displaymath}\sigma_{\rm el,electron} \simeq \frac{8\pi\alpha n_{\rm e} \ell_{\rm e}}{m_{\rm e}\overline{v}_{\rm e}}, \end{displaymath} (6)

where $\alpha\simeq 1/137$ is the QED fine structure constant, $n_{\rm e}$ is the electron number density ($m_{\rm e}$ is the electron mass), $\ell_{\rm e}$ is the electron mean free path, $\overline{v}_{\rm e}$ their mean thermal velocity, and taking the ultrarelativistic limit where $\overline{v}_{\rm e} \sim c$ and $m_{\rm e}$ is replaced by T, using $\ell_{\rm e} \sim n_{\rm e}^{-1/3}$ as a crude estimate, this gives

 \begin{displaymath}\sigma_{\rm el} \simeq 7.1\times 10^{21} \left(\frac{Y_{\rm e... ...ight)^{2/3} \left(\frac{1\;{\rm MeV}}{T}\right)\;{\rm s}^{-1}. \end{displaymath} (7)

More refined estimates (Baym & Heiselberg 1997; Arnold et al. 2000; Shovkovy & Ellis 2003) give $\sigma_{\rm el}\sim 10^{23}$- $10^{24}\;{\rm s}^{-1}$. With $H_{\rm c} = 10^{19}\;{\rm G}$ we obtain

 \begin{displaymath}\tau_{\rm exp} \simeq 10^{-6}\left(\frac{\sigma_{\rm el}}{10... ...}}\right)^2\left(\frac{B}{10^{15}\;{\rm G}}\right)^2\;{\rm s}, \end{displaymath} (8)

so a reasonable estimate is $\tau_{\rm exp}$ of the order of a few seconds or less since $\delta_{\rm max}\sim R\sim 10$ km.

3.2 Energetics

The expelled magnetic field would quickly lead to magnetic reconnection in the magnetosphere. Since reconnection typically occurs at a fraction of the Alfvén velocity, the growth time of the instability can be estimated to be $\sim$ 10-5-10-4 s which is comparable to the $\sim$ $ 2\times 10^{-4}$ s rise time of the March 5 event (Mazets et al. 1979; Paczynski 1992). The long expulsion time (see Eq. (8) for $\delta_{\rm max}\sim R$) implies that the reconnection events continued for many times the Alfvén time scale which we suggest could account for the longer duration of the hard transient phase of the burst.

The energy released is

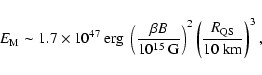\begin{displaymath}E_{\rm M} \sim 1.7 \times 10^{47}~ {\rm erg}~ \left(\frac{\be... ...}}\right)^{2}\left(\frac{R_{\rm QS}}{10~ {\rm km}}\right)^{3}, \end{displaymath} (9)

where $\beta$ is the fraction of the surface magnetic field expelled with the subsequent reconnection events (the subscript "M" stands for main). Locally we expect the energy from the magnetic reconnection event to be rapidly converted to a thermal photon-pair plasma (e.g. Thompson & Duncan 1995, Sect. 3) which heats up the surface. The cooling is defined by the rate at which the photons escape this heated region. However, since these reconnection events occur very close to the surface of the star, we expect the photons to be trapped, and the cooling time to be long enough to allow for thermalization. The corresponding thermal temperature is

 \begin{displaymath}T_{\rm M} \sim 4.0\times 10^{9}~ {\rm K} \left(\frac{\beta B... ...t)^{1/2} \left(\frac{R_{\rm QS}}{10~ {\rm km}}\right)^{1/4} , \end{displaymath} (10)

which is the maximum surface temperature that can be reached. Even smaller surface temperatures (when cooling is faster than heating) are enough to trigger the mechanism of thermal emission, as we discuss next.

3.3 Light curve

Usov (2001) showed that creation of ${\rm e}^+{\rm e}^-$ pairs by the Coulomb barrier at the quark star surface is the main mechanism of thermal emission from their surface at the temperature $T_{\rm S} < 5\times 10^{10}$ K. Created ${\rm e}^+{\rm e}^-$ pairs mostly annihilate in the vicinity of the quark star into $\gamma$-rays, and Usov (2001) argued that the light curves of the March 5, 1979 and August 27, 1998 events may be explained in a model where the burst radiation is produced by the bare surfaces of such stars heated up to $\sim$ $ 2\times 10^{9}$ K by impacts of massive cometlike objects. He also points out that any other mechanism which quickly heats up the surface can explain the events, so Eq. (10) indicates that the Meissner effect and subsequent decay of the expelled magnetic field can power a burst. To give further evidence for this we have computed the light curves in our model.

We consider a thin layer of thickness $\delta \ll R$ close to the surface of the star which is heated by the release of magnetic energy $E_{\rm dec}$ from the decaying magnetic field. The temperature in the layer (taken to be isothermal) is governed by the equation

 \begin{displaymath}V_\delta C \frac{{\rm d}T}{{\rm d}t} = Q - V_{\delta}\tilde{\epsilon}_\nu, \end{displaymath} (11)

where $V_\delta = 4\pi R^2 \delta$ is the volume of the layer, and Q for times $0 < t < \tau_{\rm dec}$ is given by the energy released per unit time by the decay of the magnetic field, $Q \simeq E_{\rm dec} / \tau_{\rm dec}$, while for times $ t > \tau_{\rm dec}$ it is given by the luminosity of the ${\rm e}^+{\rm e}^-$ pair emission, $Q = - 4\pi R^2 \epsilon_\pm f_\pm$, where $\epsilon_\pm = m_{\rm e} c^2 + kT $ is the mean energy of the electron-positron pairs created,

 \begin{displaymath}f_\pm = 1.6 \times 10^{39}T_9^3 \exp\left(-\frac{11.9}{T_9}\right) J(\zeta)\;{\rm cm}^{-2}~{\rm s}^{-1} , \end{displaymath} (12)

is the flux of pairs per unit surface area,

 \begin{displaymath}J(\zeta) = \frac{1}{3}\frac{\zeta^3\ln(1+2\zeta^{-1})}{(1+0.074\zeta)^3} +\frac{\pi ^5}{6}\frac{\zeta^4}{(13.9+\zeta)^4}, \end{displaymath} (13)

and $\zeta = 20 / T_9$. The specific heat per unit volume C is the sum of the contribution from the electrons (Blaschke et al. 2001)

 \begin{displaymath}C_{\rm e} \simeq 5.7\times 10^{19}Y_{\rm e}^{2/3}(n_{\rm b}/n_0)^{2/3}T_9\;{\rm erg} ~{\rm cm}^{-3}~{\rm K}^{-1}, \end{displaymath} (14)

and the heat capacity of the quarks in the CFL phase is modified from Eq. (2) according to

 \begin{displaymath}\tilde{C}_q = C_qf(T/T_{\rm c}), \end{displaymath} (15)

where Cq is given by Eq. (2) and

 \begin{displaymath}f(x) = \frac{3.2}{x}\exp\left(\frac{1}{0.57x}\right)(2.5-1.5x+3.6x^2), \end{displaymath} (16)

see Horvath et al. (1991). Also, the neutrino luminosity (1) is suppressed in the CFL phase by the Boltzmann factor $\exp(-\Delta/k_{\rm B}T)$, where $\Delta$ is the energy gap, i.e.

 \begin{displaymath}\tilde{\epsilon}_\nu = \epsilon_\nu g(T/T_{\rm c}), \end{displaymath} (17)

where

 \begin{displaymath}g(x) = \exp\left(-\frac{\sqrt{1-x}}{0.57x}\right), \end{displaymath} (18)

and we have assumed that the temperature dependence of the energy gap is $\Delta(T) = \Delta(T=0)(1-T/T_{\rm c})^{1/2}$ (e.g., Carter & Reddy 2000), and used the standard relation $k_{\rm B}T_{\rm c} \simeq 0.57\Delta(T=0)$.

We have solved Eq. (11) numerically with the initial condition $T = 10^8\;{\rm K}$. For the parameters we used the values $\alpha_{\rm c}=0.1$, $n_{\rm b}=5n_0$, $Y_{\rm e}=10^{-4}$, $R=10^6\;{\rm cm}$, $\delta = 10^3\;{\rm cm}$, $B = 10^{15}\;{\rm G}$, $\tau_{\rm dec}=0.1$. We varied the fraction of the magnetic field expelled by the partial Meissner effect, using $\beta = 0.5$, 0.2, 0.1 and 0.05 as representative values. The light curves are shown in Fig. 2. The maximum luminosity for $\beta = 0.1$ is $5\times 10^{45} \;{\rm erg}~{\rm s}^{-1}$, so the decay of 10% of a surface magnetic field of $10^{15}\;{\rm G}$ is enough to power the main burst. The light curve and time evolution of the surface temperature for this case are shown in Fig. 3.

We note that since the CFL phase transition occurs only once, there will be only one giant burst in our model. We also note that our model is too simplistic to reproduce the periodic pattern (e.g. the 8.0 s period in the March 5 event) overimposed to a smooth exponential decay. However, given the partial Meissner effect and the resulting random reconnection fronts we expect isolated spots on the surface of the star to be heated and release energy as described above. These hot spots would pulse at the same rate as the rotation of the star, and thus, would appear periodic. We further note that a few of these hot spots could appear simultaneously at random locations on the surface of the star. This means that each of the pulses (superimposed on the smooth curve) could consist of even smaller subpulses. Multiple small hot spots should produce many harmonics in the lightcurve. In other words, if our model is a correct representation of SGRs, observations could constrain the number of hot spots.

Finally, we note that given the rapid cooling time scale of a quark star, as discussed in Sect. 2, the CFL phase transition should happen immediately after the formation of the quark star. However, this does not necessarily mean that the giant burst will follow immediately after the core collapse in a supernova since the quark star can in principle be formed also much later.

   
4 Subsequent bursts: Vortex lattice dynamics

4.1 Vortex formation and relaxation

The CFL front quickly expands to the entire star followed by the formation of rotationally induced vortices, analogously to rotating superfluid He3 (the vortex lines are parallel to the rotation axis; Tilley & Tilley 1990). Via the Meissner effect, the magnetic field is partially screened from the regions outside the vortex cores. The system now consists of alternating regions of superconducting material with a screened magnetic field and the vortices where most of the magnetic field resides.

The vortex relaxation time, which is within an order of magnitude similar to the random diffusion timescale, can be estimated to be

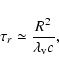\begin{displaymath}\tau_r \simeq \frac{R^{2}}{\lambda_{\rm v} c} , \end{displaymath} (19)

where $\lambda_{\rm v} = (\pi R^{2} / N_{\rm v})^{1/2}$ is the vortex mean free path, and $N_{\rm v}$ is the number of vortices in the entire star,
                                   $\displaystyle N_{\rm v}$ = $\displaystyle \frac{2}{3} \mu R^2 \Omega$  
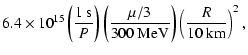  $\textstyle \simeq$ $\displaystyle 6.4 \times 10^{15} \left(\frac{1~ {\rm s}}{P}\right) \left(\frac{\mu / 3}{300~ {\rm MeV}}\right) \left(\frac{R}{10 ~{\rm km}}\right)^2 ,$ (20)

(Iida & Baym 2002), where $\mu$ is the quark chemical potential related to the density. Using the above values, we thus estimate a relaxation timescale of $\sim$11 min for $P = 5\;{\rm s}$. Note that this is within an order of magnitude consistent with the relation between lattice formation time and rotation period found in numerical simulations of vortices in rotating Bose-Einstein condensates (Tsubota et al. 2002).

4.2 Magnetic field restructuration and reorganization

Given the complicated structure of the resulting surface magnetic field, following relaxation, the latter may then suffer from frequent magnetic reconnections and thus account for the subsequent bursts. This phase could last for days or months, depending on the magnetic field strength, the period and the fraction of the field which remained entangled in the period immediately following the giant burst. These random reconnection events would bear many (temporal and spectral) similarities to the main burst but we expect them to be less energetic as the magnetic field slowly decays and weakens. Eventually, the magnetic field evolves into a stable configuration (see Fig. 1) after which the star enters a quiescent phase.


  \begin{figure} \par\includegraphics[height=7.5cm,width=8.5cm,clip]{0180fig1.eps} \end{figure} Figure 1: Schematic view of the initial and final stages in the development of the SGR in our model. The QS, born with $T > T_{\rm c}$ quickly cools into a CFL star. In the early stages of this transition, a fraction of the surface magnetic field is expelled by the Meissner effect, inducing magnetic reconnection events leading to the main burst. In the late stage, once the vortices form (parallel to the rotation axis), the system evolves into a configuration where most of the magnetic field is confined to the vortex lines. Magnetic reconnection events between the complex surface magnetic field and the external part of the magnetic field coupled to the vortex lines lead to occasional flares (subsequent bursts). In the SGR quiescent phase, magnetic energy is released as vortex lines are being continuously pushed to the surface and annihilate there. In the more general case where the magnetic field is not aligned with the rotation axis, we expect an even more complex behaviour/evolution of the field leading to more reconnection events.
Open with DEXTER

   
5 Quiescent phase: Vortex annihilation

The number of vortices decreases with the spin-down of the star, and can be formulated as (extrapolating from results established for cylindrically rotating superfluids):[*]

\begin{displaymath}\frac{{\rm d}N_{\rm v}}{{\rm d}\Omega} = \frac{N_0}{\Omega} \... ...c{\lambda_{\rm v}}{R} \right] \simeq \frac{N_0}{\Omega} \cdot \end{displaymath} (21)

As the star spins down, the outermost vortex line will be pushed to the surface and annihilate there (Ruutu et al. 1997). The corresponding luminosity is

 \begin{displaymath}L_{\rm v} = \frac{{\rm d}E_{\rm v}}{{\rm d}t} = \epsilon_{\rm... ...{\rm d}t} = \epsilon_{\rm v} N_0 \frac{\dot{\Omega}}{\Omega} , \end{displaymath} (22)

where $\epsilon_{\rm v} = \epsilon_0 + \epsilon_{\rm m} \simeq \epsilon_{\rm m}$, is the energy density per vortex which consists of the rest mass energy ( $\epsilon_0$) and the confined magnetic energy ( $\epsilon_{\rm m}$). This means $\epsilon_{\rm v} N_0 \simeq E_{\rm mag} \simeq 1.7 \times 10^{47}~ {\rm erg} \left(B/10^{15}~{\rm G}\right)^2 \left(R/10~ {\rm km}\right)^3$ (recall that most of the magnetic field/energy resides in the vortex and that $\epsilon_{\rm m}\gg\epsilon_{\rm v}$). The star continues to loose rotational energy due to the electromagnetic radiation losses which allow us to write in the simplest approximation,
 
                               $\displaystyle \frac{\dot{\Omega}}{\Omega}$ = $\displaystyle - \frac{4 B^2 R^6 \Omega^2}{9 I c^3} \simeq 3.24 \times 10^{-10} ~{\rm s}^{-1}$  
    $\displaystyle \times \left(\frac{B}{10^{15}~ {\rm G}}\right)^2 \left(\frac{R}{1... ...left(\frac{1~ {\rm s}}{P}\right)^2 \left(\frac{M_{\hbox{$\odot$ }}}{M}\right) ,$ (23)

where I is the star's moment of inertia (Manchester & Taylor 1977).
  \begin{figure} \par\includegraphics[width=8cm,clip]{0180fig2.eps} \end{figure} Figure 2: The light curve expected in our model. The four curves (from top to bottom) correspond to $\beta = 0.5$, 0.2, 0.1, and 0.05.
Open with DEXTER


  \begin{figure} \par {\includegraphics[width=8.cm,clip]{0180fig3_1.eps} } \par\vspace*{5mm} \par {\includegraphics[width=8.cm,clip]{0180fig3_2.eps} }\end{figure} Figure 3: Upper panel: the light curve for $\beta = 0.1$. Lower panel: the corresponding time evolution of the surface temperature.
Open with DEXTER

Combining Eqs. (22) and (23), the luminosity induced by vortex annihilation is

 
                                $\displaystyle L_{\rm v}$ = $\displaystyle 5.51 \times 10^{37}~ {\rm erg}~ {\rm s}^{-1}$  
    $\displaystyle \times \left(\frac{B}{10^{15}~{\rm G}}\right)^4 \left(\frac{R}{10... ...t(\frac{1~ {\rm s}}{P}\right)^2 \left(\frac{M_{\hbox{$\odot$ }}}{M}\right)\cdot$ (24)

This can be compared to the luminosity from the dipole radiation,
 
                                $\displaystyle L_{\rm dip}$ = $\displaystyle - \frac{4 B^2 R^6 \Omega^4}{9 c^3} \simeq 2.6 \times 10^{36}~ {\rm erg}~ {\rm s}^{-1}$  
    $\displaystyle \times \left(\frac{B}{10^{15}~ {\rm G}}\right)^2 \left(\frac{R}{10~ {\rm km}}\right)^6 \left(\frac{1 ~{\rm s}}{P}\right)^4\cdot$ (25)

We note that for $P > 1~{\rm s}$ we can still account for the observed SGR quiescent luminosity with $B \leq 10^{15}~ {\rm G}$ while much higher fields are required to power the luminosity with dipole radiation (Fig. 4).


  \begin{figure} \par {\includegraphics[width=8.cm,clip]{0180fig4.ps} }\end{figure} Figure 4: The X-ray luminosity versus period for the four SGRs for which these values have been measured (from Kaplan 2000, and references therein). The solid lines are predictions given by Eq. (24) for stars with magnetic fields of $10^{15}~ {\rm G}$ (upper curve) and $10^{14}~ {\rm G}$, for $R = 10~ {\rm km}$ and $M = 1~M_{\hbox{$\odot$ }}$. The dashed lines are predictions given by Eq. (25) for stars with magnetic fields of $10^{15}~ {\rm G}$ (upper curve) and  $10^{14}~ {\rm G}$, for $R = 10~ {\rm km}$.
Open with DEXTER

In our model, the quiescent phase emission consists of two sources of energy, related to vortex annihilation and dipole radiation. It would be interesting to compute the corresponding spectra and compare them to the now well-established best fit model of SGR spectra which is a composite of blackbody and power-law emission (Kaplan 2002; Kulkarni et al. 2003). This is beyond the scope of this paper and is left as an avenue for future work.

   
6 Later bursts: Crustquakes and debris impacts

6.1 Crust formation and crustquakes

A crust of hadronic matter suspended above the quark star surface (Alcock et al. 1986) might eventually form, leading to possible starquakes. Since known SGRs are solitary objects, such a crust should have formed due to fall-back of supernova ejecta. Also in the Quark-Nova (Ouyed et al. 2002) picture, where a hot quark star is formed, high accretion rates are expected from the fallback material (Keränen & Ouyed 2003). Later bursts could be driven by energy released during crust fractures that result from magnetic stresses as described in Thompson & Duncan (2001). In the case of the neutron star crust, the corresponding energy is

 
                              $\displaystyle \delta E_{\rm mag}$ $\textstyle \simeq$ $\displaystyle 10^{44}~ \left({\psi^2\over (10^{-2})^2}\right)~ \left({B\over 10^{15}\ {\rm G}}\right)^{-2}$  
    $\displaystyle \times\left({\rho_{\rm crust}\over 0.6~\rho_{\rm N}}\right)^{1.6}~ \left({\Delta R_\mu\over 0.3~{\rm km}}\right)^2\hbox{erg} ,$ (26)

where $\psi$ is the shear strain, $\rho_{\rm N}$ the nuclear saturation density and $\Delta R_\mu$ is the extent of the fracture in the crust. If a similar phenomenon can be expected for quark star crusts, we expect later (crust induced) bursts with energies as high as $\sim$1040 erg (the maximum density for a quark star crust is close to the neutron drip value, $\rho_{\rm crust}\sim 4\times 10^{11}$ g cm-3 see e.g., Glendenning 1997).

6.2 Hard emission bursts

Rare (<1%) subsequent bursts of hard emission (Woods et al. 1999) could be due to random debris impacts. Again, as an example, such debris could naturally result during disk (and the subsequent planetary) formation around the quark star following an expulsion of the crust (Keränen & Ouyed 2003).

   
7 SGRs in our model

7.1 SGR 0526-66

Applying our model to the SGR responsible for the famous 1979 March 5 giant burst, and for $P = 8~ {\rm s}$, we find the luminosity in the quiescent phase to be $8.6 \times 10^{35}~ {\rm erg}~ {\rm s}^{-1}$ for $B = 10^{15}~ {\rm G}$. The corresponding minimum age, making use of Eq. (23), is  $\sim$ $ 3~ {\rm kyr}$. Hence, our model does not require extreme magnetic fields (> $10^{15}~ {\rm G}$) and predicts ages of at least a few kyr, in accordance with age estimates of the nearby SNR N49 (e.g., Vancura et al. 1992). However, we note that the association with SNR N49 is tenuous, and the large offset between the two objects would still be a challenge if the CFL phase transition occurred as recently as 1979 (see Sect. 8.4). Following its long quiescent phases SGR 0526-66 could have acquired a thin crust (Sect. 6) which could explain why it currently shows X-ray characteristics similar to AXPs (Kulkarni et al. 2003), two decades after becoming quiescent. We speculate that the 1979 March 5 giant burst, detailed in Table 1, could have been a signature of a CFL phase transition and associated physical processes, as described in Sect. 3. This SGR, displaying a giant burst and a subsequent active phase followed by a long quiescence, fits best within the picture outlined in this paper.

7.2 SGR 1900+14

Because of the presence of SGR burst activity prior to the main event (Hurley et al. 1999), the 1998 August 27 event in SGR 1900+14 would be best explained by, e.g., restructuring of the magnetic field (Sect. 4), crustquakes or debris impact (Sect. 6).

   
8 Discussion

8.1 The suggested SGR-AXP connection

It has been debated whether anomalous X-ray pulsars (AXPs) and SGRs are connected, with both classes of systems being magnetars (e.g., Chatterjee et al. 2000; Gavriil et al. 2002). AXPs display persistent strong X-ray emission with $P \sim 6{-}12$ s pulsations. The term "anomalous'' comes from the fact that the X-ray emission is not powered by rotational energy or by accretion from a companion star (AXPs are solitary objects). The likely association of three AXPs with supernova remnants indicate that they are young (t < 104 yr) systems with unusually fast spin-down rates (Gaensler et al. 2001). Like SGRs, the AXPs are rare objects (five confirmed cases are currently known), and they have a similar distribution of rotational periods.

If AXPs are magnetars, their emission is most likely powered by the decaying magnetic field. Recent observational results have suggested a link between the two classes of objects: Gavriil et al. (2002) report SGR-like X-ray bursts from the AXPs 1E 1048.1-5937 and 1E 2259.1+586, and Kaspi et al. (2003) report a major SGR-like X-ray outburst from 1E 2259.1+586. Furthermore, Kulkarni et al. (2003) report Chandra observations of SGR 0526-66 in a quiescent phase showing that the object has X-ray properties similar to an AXP. These similarities have been suggested to favour a common magnetar model for AXPs and SGRs (see Kaspi 2004 for a recent discussion). However, it remains to be seen if these two classes of objects are similar physical systems that could perhaps be linked through a simple evolutionary model, or whether they are in fact disparate.

In our model, SGRs are strange matter quark stars that have undergone the phase transition into a colour superconducting state. Based on this, we cannot identify a simple connection between AXPs and SGRs, but our model merely suggests that they are not closely connected. We discuss below how missing glitch activity and inferred transverse velocities of SGRs could hint in favour of our picture.

8.2 Glitches in our model

Glitch activity is apparent in AXPs, but seems to be absent in SGRs, see Woods et al. (2003a,b) and Kaspi et al. (2003). Vortices are a natural outcome of the CFL phase transition, and the interaction between the vortices and the crust could in principle lead to glitch activity (see Alpar 1991). If only a tiny crust is expected for a CFL star, glitches would be unlikely unless a glitch mechanism which does not involve the crust-core interaction is involved. A possibility for such a mechanism has been suggested by Alford et al. (2001). They propose that in a certain range of densities quarks may form Cooper pairs with nonzero momentum, leading to pairing energy gaps which vary periodically in a crystalline pattern, and this structure opens up the possibility of vortex pinning. However, the details of this mechanism have not yet been worked out. Thus we do not expect glitch activity to occur in SGRs in our model except maybe in a case where a sizeable crust has been formed. This might be possible e.g. if the hadron-quark phase transition has happened very quickly after the supernova explosion and the crust has been formed from the possible fall-back matter of the supernova ejecta.

8.3 Transverse velocities

At least half of the AXPs are now confirmed to be located near the centers of supernova remnants (SNRs) (see discussion by Gaensler 2002). This infers transverse velocities of $\le$ $ 500~ {\rm km}~ {\rm s}^{-1}$ and an age of $\le$ $ 10~ {\rm kyr}$. Furthermore, three out of the five confirmed SGRs are located near SNRs, but the SGR separation from the SNR centers and the SNR ages imply transverse velocities of order $\geq$ $ 1000~ {\rm km}~ {\rm s}^{-1}$, which is higher than what would be expected from a SN explosion alone. In our model, an neutron star undergoes a phase transition into quark matter. This phase transition is accompanied by a neutrino emission (see e.g., Iwamoto 1980). If the neutrino emission is not fully isotropic, this may lead into a high transverse velocity of the quark star, explaining the large offsets between some SGRs and apparently associated nearby young SNRs.

   
8.4 Formation scenarios

The transition from hadronic matter into quark matter can in principle happen immediately during or after the supernova explosion, but also very much later than that. If formed quickly after the supernova occurred, the emitted gamma rays would be absorbed by the expanding supernova ejecta, and there would be no detectable gamma-ray signature of the transition from neutron star matter into quark matter. In this case, the resulting quark star would be born in a relatively dense evironment and might form a crust from accreted material. We would then expect subsequent SGR-type bursting behaviour to be caused by mechanisms discussed in Sect. 6. As discussed above, because of the crust, the star could show glitch activity and could in this respect have characteristics more similar to AXPs than other SGRs.

The hadron-quark transition may also happen much later than the supernova explosion. Quark star formation can, for example, happen as a result of accretion or spin-down of a neutron star. In this case, the CFL phase transition should be accompanied by an observable gamma ray emission (as a giant burst in our picture), as we speculate is the case for SGR0526-66. In this second scenario, the quark star would remain bare or have only a thin crust due to low accretion (since the objects are solitary). Therefore there would be no glitch activity. However, if indeeed SGR0526-66 is a CFL star, the late formation and a resulting recent boost of the transverse velocity would not explain its current offset from the nearby young SNR N49: even if the neutrino emission had been anisotropic, the SGR can not have moved very far during a few decades, and so the late formation scenario would suggest that there is no physical association between SNR N49 and SGR0526-66. In any case, there is currently no compelling observational evidence for such an association (Gaensler 2002).

It is important to notice that the CFL phase transition will occur only once, so the model discussed in this paper predicts that there will be only one giant burst. Also, note that the probability of observing such an event is small, since the mean time between supernovae is about 100 years and formation of a quark star is maybe even rarer. This should be compared to the short time we have had gamma-ray observatories.

It has been demonstrated that CFL stars with very short rotation periods should not exist, because they are prone to so-called r-mode instabilities (Madsen 2000). Since the CFL star we consider has a rotation period of the order of a few seconds, this should not be a problem for our model.

Finally, the era of decaying vortices can be estimated to last 103 to 105 years in our model. Even if the formation of the quark star happens immediately after (or during) the supernova explosion, the SGR should remain active long enough to account for the observed $\sim$ $ 10\;{\rm s}$ periods. A fast spin down occurs if the magnetic field is initially large as our model assumes.

   
9 Conclusion

We presented an alternative model for explaining SGRs where a newly born quark star experiences bursting activity as it cools below the critical temperature for the onset of CFL. In our model, the subsequent magnetic field expulsion and reorganization are crucial ingredients in explaining the giant bursts and the subsequent weaker ones; magnetic field strength and period alone cannot be responsible for the unusual properties of SGRs according to our model. We also discuss the relation between AXPs and SGRs which in our model are separate objects.

Acknowledgements
The research of R.O. is supported by grants from the Natural Science and Engineering Research Council of Canada (NSERC). H.D. is funded by a post-doctoral fellowship from the Research Council of Norway. H.D., Ø.E. and R.O. acknowledge the hospitality of Nordita and P.K. and R.O. the hospitality of the University of Oslo.

References


Copyright ESO 2004