... superfluids):

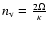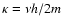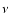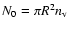In rotating superfluids the density of vortex lines in equilibrium rotation is $n_{\rm v} = \frac{2 \Omega}{\kappa}$, where $\kappa = \nu h / 2 m$ is the circulation of a vortex with quantization number $\nu$ for atoms of mass m (Ruutu et al. 1997); h is the planck's constant. In the continuum limit a totally filled cylindrical container with radius R would have $N_0 = \pi R^2 n_{\rm v}$ lines. Interactions with the lateral walls give rise to an annular vortex-free region along the wall. 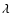Its width $\lambda$ is of order the intervortex distance 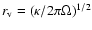$r_{\rm v} = (\kappa / 2 \pi \Omega )^{1/2}$ (expressed here as the radius of the Wigner-Seitz unit cell of the vortex lattice). 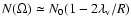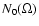As a result, the total line number $N (\Omega ) \simeq N_0 (1 - 2 \lambda_{\rm v} / R)$ is always less than $N_0 ( \Omega )$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.