A&A 419, 801-810 (2004)
DOI: 10.1051/0004-6361:20040097
G. Siemieniec-Ozieb![]() o - A. Woszczyna
o - A. Woszczyna
Astronomical Observatory, Jagellonian University, Faculty of Mathematics, Physics and Computer Science, ul. Orla 171, 30-244 Kraków, Poland
Received 20 December 2002 / Accepted 23 February 2004
Abstract
The transition from acoustic noise in the radiation-dominated universe to the
density structures in the matter dominated epoch is considered. The initial
state is a stochastic field of sound waves moving in different directions. The
construction of the initial state is compatible with the hyperbolic type of
propagation equation for density perturbations, and parallel to the theory of
stochastic background of gravitational waves. Instantaneous transition between the
cosmological epochs is assumed, and Darmois-Israel joining
conditions
are applied to match solutions for sound waves with growing or decaying modes at the
decoupling. As a result a substantial amplification of the low scale structures
is obtained.
Key words: cosmology: theory - cosmology: miscellaneous - cosmology: large-scale structure of the universe
For scalar or electrodynamic fields, as well as for gravitational waves the
amplification can be measured by Bogolubov coefficients (Birrell &Davies 1982).
These fields are governed by hyperbolic partial differential equations in each
of discussed epochs and the changes in the equation of state - the change in the
background dynamics - result in a specific relations between Fourier modes in
the in and out state, respectively. For some
frequencies, counter-propagating waves are substantially amplified (creation of
pairs of particles with opposite momentum) - the so called back scattering
effect (Parker 1972) comes into play![]() . Similar effects may occur in acoustic
field (Lukash 1999). Fields enhancement on non static background is generally
referred to parametric amplification (Grishchuk 1995).
. Similar effects may occur in acoustic
field (Lukash 1999). Fields enhancement on non static background is generally
referred to parametric amplification (Grishchuk 1995).
Neither parametric amplification nor particle creation theories provide appropriate language to describe the growth of density perturbations in the transition to matter-dominated epoch. The scalar perturbations form waves (Sachs &Wolfe 1967; White 1973; Field &Shepley 1968) (in quantum phonon-approach Lukash 1980; Chibisov &Mukhanov 1982) only in the epochs of non vanishing pressure, but they transform into non-travelling ingomogeneities (growing and decaying modes) in the matter dominated epoch (p=0). The change then is two-fold: 1) the transition modifies the background dynamics; 2) the propagation equation change its differential type. Bogolubov coefficients lose their physical meaning. Yet, the general scheme of the field propagation throughout the transition epoch is the same: for the scalar or electrodynamic fields the continuity of each field and its time derivative must be satisfied at the transition, for metric perturbations (both scalar and tensor) the first and the second fundamental forms must be continuous (Darmois-Israel conditions).
Classical perturbations in the cosmological models with sharp transitions have been investigated by Kodama & Sasaki (1984) or Hwang &Vishniac (1991). These authors limit themselves to the standing wave solutions and to regime of low frequencies. A similar task for a universe with the radiation and dust mixture has been undertaken by Mukhanov et al. (1992) also in the long wave limit. In quantum theories the radiation to matter transition has been extensively discussed by Grishchuk (1994) as a part of a more complex cosmological model including an inflationary stage. Large scale perturbations where investigated there in the context CMBR temperature fluctuations. Relatively little is known about the low scale inhomogeneities.
In this paper we present exact formulae for density perturbations in the universe with sharp transition in a full range of frequencies. We start with acoustic noise in the radiation era and investigate its transition to density structures in the matter dominated epoch. We employ the autocorrelation function as a measure of structure, or equivalently its Fourier transform - the spatial spectrum of inhomogeneities. This measure agrees well with what other authors propose in cosmology. However, despite the cosmological practice we do not limit the basis of elementary solutions to "growing modes''. Instead, we take into account the complete basis of Fourier modes, adequate to the hyperbolic character of the propagation equation and in full analogy to a stochastic description of gravitational waves (Allen et al. 2000) and quantum (phonon) theories (Lukash 1980; Chibisov &Mukhanov 1982; Grishchuk 1994). Since we disregard inflation, there is no squeezing mechanism (Grishchuk 1995) for the acoustic field. We examine the spatial power spectrum without being limited to standing waves, and show that substantial amplification occurs in the high frequency regime, which has not been investigated till now.
The structure of the paper is the following: in Sect. 2 we discuss exact solutions to the perturbation equations in both radiation and matter eras employing orthogonal gauge. In the Sect. 3 we construct the 2-epoch model with the instantaneous transition in the equation of state, by use of the Darmois-Israel conditions. The Sect. 4 is devoted to the stochastic properties of the acoustic field. Finally, we investigate the time evolution of the spatial spectrum of cosmological inhomogeneities.
There are several independent methods to describe scalar perturbations in a
gauge-invariant way
(Olson 1976;
Bardeen 1980;
Brandenberger et al. 1983;
Lyth &Stewart 1990;
Ellis &Bruni 1989).
For the universe filled
with an ideal fluid![]() with arbitrary non-
vanishing pressure p all of them lead to the same result: under appropriate choice
of the perturbation variables, the propagation equations converge to the wave
equation (Sachs &Wolfe 1967; Field &Shepley 1968; Chibisov &Mukhanov 1982; Golda &Woszczyna 2001).
The density perturbations form travelling waves. Below we
consider rotationless fluid, hence the hypersurfaces orthogonal to the fluid
flow can be globally defined, and therefore, the orthogonal gauge
(Lyth &Mukherjee 1988; Lyth &Stewart 1990; Padmanabhan 1993)
is naturally applied.
with arbitrary non-
vanishing pressure p all of them lead to the same result: under appropriate choice
of the perturbation variables, the propagation equations converge to the wave
equation (Sachs &Wolfe 1967; Field &Shepley 1968; Chibisov &Mukhanov 1982; Golda &Woszczyna 2001).
The density perturbations form travelling waves. Below we
consider rotationless fluid, hence the hypersurfaces orthogonal to the fluid
flow can be globally defined, and therefore, the orthogonal gauge
(Lyth &Mukherjee 1988; Lyth &Stewart 1990; Padmanabhan 1993)
is naturally applied.
The linear corrections to the energy density and the expansion rate
evolve according to
Let us assume now that the universe is filled by the single fluid with the
equation of state
![]() ,
where the value of wdetermines both the evolution of the background metric (unperturbed universe) and
the sound velocity for small perturbations. We express the energy density and the
expansion rate as the composition of the background energy values
,
where the value of wdetermines both the evolution of the background metric (unperturbed universe) and
the sound velocity for small perturbations. We express the energy density and the
expansion rate as the composition of the background energy values
![]() ,
,
![]() and the small inhomogeneous correction
and the small inhomogeneous correction
![]() ,
,
![]()
The propagation equations for small perturbations (5), (6) (and
consequently (7) below) do not contain the gravitational constant G, which means that inhomogeneities do not self-gravitate unless the linear
regime breaks down. They evolve as acoustic waves in the expanding gas medium
(compare Sachs &Wolfe 1967; Stone 2000). All the perturbation equations
obtained in different gauge invariant formalisms can be reduced to an equation of
the form (5) by suitable changes of variables (and with different
meaning of the variable ![]() and the time parameter) (Golda &Woszczyna 2001).
The necessary changes reads (in the notation:
and the time parameter) (Golda &Woszczyna 2001).
The necessary changes reads (in the notation:
![]() )
(Sakai 1969):
)
(Sakai 1969):
![]() ;
;
(Bardeen 1980):
![]() ;
;
(Kodama &Sasaki 1984, Chap. IV):
![]() ;
;
(Lyth &Mukherjee 1988):
![]() ;
;
(Padmanabhan 1993):
![]() ;
;
(Brandenberger et al. 1983):
![]() ;
;
(Ellis et al. 1990):
![]() .
.
Transformations of these equations to conformal time (if parameterized
differently) are necessary.
In the universe filled with highly relativistic matter, the scale factor ![]() evolves as a linear function of the conformal time:
evolves as a linear function of the conformal time:
![]() ,
and preserves
,
and preserves
![]() as the constant of motion.
Equation (6) expressed in conformal time takes the canonical form
(independent of first derivatives)
as the constant of motion.
Equation (6) expressed in conformal time takes the canonical form
(independent of first derivatives)
In the epoch of matter dominance
![]() is the constant of
motion and the scale factor evolves as
is the constant of
motion and the scale factor evolves as
![]() .
The
propagation equation expressed in orthogonal gauge (in all formalism mentioned
above) reads
.
The
propagation equation expressed in orthogonal gauge (in all formalism mentioned
above) reads
Consider now the two-epoch cosmological model composed of both, the radiation epoch
(governed by the equation of state
![]() ), and the succeeding epoch of
matter domination (with p=0). Below, the quantities related to these two epochs
will appear with the indices (1) and (2), respectively. We assume that the
transition between the epochs is instantaneous and occurs on the hypersurface
), and the succeeding epoch of
matter domination (with p=0). Below, the quantities related to these two epochs
will appear with the indices (1) and (2), respectively. We assume that the
transition between the epochs is instantaneous and occurs on the hypersurface ![]() orthogonal to the four velocity
orthogonal to the four velocity ![]() of the matter
content.
of the matter
content.
The initial Cauchy conditions are unique and consistent on the hypersurface ![]() if the first and the second fundamental forms are equal
(Darmois 1927; Hawking &Ellis 1973)
if the first and the second fundamental forms are equal
(Darmois 1927; Hawking &Ellis 1973)
In the gauge-orthogonal formalism conditions ((16), (17))
can be rewritten to directly join the density and expansion perturbations in both
epochs, before and after the transition. From Eqs. ((16), (17)) one
can
easily find that the energy density ![]() and the expansion rate
and the expansion rate ![]() are continuous on
are continuous on ![]() .
Indeed, the energy density
.
Indeed, the energy density ![]() is
related to the induced curvature R(3) and the second fundamental form by
(Hawking &Ellis 1973)
is
related to the induced curvature R(3) and the second fundamental form by
(Hawking &Ellis 1973)
The starting point for the investigations of acoustic fields and the structures they produce
in the two-epoch universe is the analysis of a single monochromatic wave (a
single Fourier mode)
The acoustic field in the early universe is shaped by thermodynamic or quantum
phenomena acting prior to and during the radiation era. Their probabilistic
nature leads to stochastic description. We restrict ourselves to stochastic
processes homogeneous in the broad sense, called also weakly
homogeneous processes, which keep their mean value and variance (standard
deviation) invariant under translations. The two-point autocorrelation functions
for them are functions of the distance between points solely - not of these
points' positions (Loeve 1963).
Processes homogeneous in the broad sense have their Fourier
representations (Loeve 1963; Sobczyk 1991; Yaglom 1961)
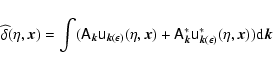 |
(33) |
The relations (34), (35) have a clear physical meaning. The first
of them expresses the statistical independence of waves with different wave-vectors.
The second means that phases of perturbations at any moment and any place are
statistically independent. Altogether they assure statistical independence of
waves moving in different directions.
This stochastic process can be also expressed in terms of the
![]() variable. With
help of the random Fourier coefficients
variable. With
help of the random Fourier coefficients
![]() satisfying
satisfying
Modes
![]() while regularly extended across the transition
hypersurface
while regularly extended across the transition
hypersurface ![]() define a stochastic structure (by means of integral
(38)) in the matter dominated universe. The commonly used measure of this
structure is the two-point autocorrelation function
define a stochastic structure (by means of integral
(38)) in the matter dominated universe. The commonly used measure of this
structure is the two-point autocorrelation function
| |
= | ||
| = | 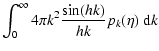 |
(40) |
It is important to clearly distinguish between pk and Pk, and understand
their roles in the cosmological context. As defined above, pk is the Fourier transform of the
two-point autocorrelation function.
In the cosmological literature it is called the power spectrum![]() by analogy to
similar concept known in the analysis of time series (Anderson 1971),
but its physical dimension is different.
On the other hand, Pk defined by Eq. (36) is the genuine power spectrum of
the acoustic field (with the same physical sense as the Planck power spectrum
of the electromagnetic radiation),
and can be obtained from Hamiltonian description (Lukash 1980). Although in
cosmology one cannot directly observe Pk, this quantity defines the physical
state of acoustic field. This is Pk not pk, which should be either guessed, or
inferred from fundamental laws of physics (Chibisov &Mukhanov 1982). The shape
of Pk is not precised in this paper.
by analogy to
similar concept known in the analysis of time series (Anderson 1971),
but its physical dimension is different.
On the other hand, Pk defined by Eq. (36) is the genuine power spectrum of
the acoustic field (with the same physical sense as the Planck power spectrum
of the electromagnetic radiation),
and can be obtained from Hamiltonian description (Lukash 1980). Although in
cosmology one cannot directly observe Pk, this quantity defines the physical
state of acoustic field. This is Pk not pk, which should be either guessed, or
inferred from fundamental laws of physics (Chibisov &Mukhanov 1982). The shape
of Pk is not precised in this paper.
The time factor
![]() converts the acoustic spectrum Pkinto the spatial-spectrum
converts the acoustic spectrum Pkinto the spatial-spectrum ![]() .
(It is numerically equal to
.
(It is numerically equal to ![]() for the white noise acoustic field:
for the white noise acoustic field:
![]() .). Factor
.). Factor
![]() contains the entire time dependence of cosmological
inhomogeneities. Employing extended modes (31), (32), we find
contains the entire time dependence of cosmological
inhomogeneities. Employing extended modes (31), (32), we find
In the radiation era, perturbations greater than the sound horizon decrease,
while the low scale ones maintain constant amplitude. This can be seen directly
from Eq. (42). The result qualitatively agrees with quantum theories (see
Mukhanov et al. 1992 Part III, formula 20.6). Quantitative
difference comes from the different gauge choice![]() . It should be emphasized that the spectrum Pk, the
spatial spectrum pk and the parameter
. It should be emphasized that the spectrum Pk, the
spatial spectrum pk and the parameter ![]() are invariant under unitary
transformations. Therefore, the result is physically well defined - it is not the
effect of any particular choice of the Fourier basis.
are invariant under unitary
transformations. Therefore, the result is physically well defined - it is not the
effect of any particular choice of the Fourier basis.
In the matter era the perturbations (32) are a specific mixture
of growing and decaying solution (compare
Ellis et al. 1990; Liang 1977). Therefore, despite vanishing
pressure, their evolution
depend on their length-scales. The dominant growing term
![]() in Eq. (43) is multiplied by
in Eq. (43) is multiplied by
![]() ,
which
means strong amplification of short waves.
,
which
means strong amplification of short waves.
A peculiar velocity field can be measured by the deviation
![]() from the homogeneous Hubble flow
from the homogeneous Hubble flow
![]() .
Modes of the fluid
compression
.
Modes of the fluid
compression![]() are
associated to the density modes (12), (27). On the strength of
Eq. (26) we obtain
are
associated to the density modes (12), (27). On the strength of
Eq. (26) we obtain
To express the perturbation enhancement relative to its initial amplitude we introduce the ratio
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3437F1a.eps}
\end{figure}](/articles/aa/full/2004/21/aa3437/Timg189.gif) |
Figure 1:
The spectrum transfer function
|
| Open with DEXTER | |
| |
Figure 2:
The density spectrum transfer function
|
| Open with DEXTER | |
As already mentioned, the large scale inhomogeneities (those, which are larger than the local sound
horizon
![]() )
decay in the radiation era (
)
decay in the radiation era (
![]() ). In
this case, the term
). In
this case, the term
![]() is dominant in
the time factor
is dominant in
the time factor
![]() and strongly
decreases with time. Decay of the large scale component
is a generic feature of acoustic noise on the expanding radiation dominated
homogeneous background. In other words, the homogeneity of the radiation filled
universe is a stable property at least as long as the generic perturbations
are taken into account. Similar phenomenon of large-scale wave
extinction is observed in scalar field theory (Stebbins &Veerarghavan 1993).
Although the large-scale inhomogeneities change substantially during the radiation
era, their response to the change in the equation of state is very weak. Their
wave character vanishes at
and strongly
decreases with time. Decay of the large scale component
is a generic feature of acoustic noise on the expanding radiation dominated
homogeneous background. In other words, the homogeneity of the radiation filled
universe is a stable property at least as long as the generic perturbations
are taken into account. Similar phenomenon of large-scale wave
extinction is observed in scalar field theory (Stebbins &Veerarghavan 1993).
Although the large-scale inhomogeneities change substantially during the radiation
era, their response to the change in the equation of state is very weak. Their
wave character vanishes at
![]() ,
but the spatial spectrum itself is
insensitive to the transition (see Fig. 2).
,
but the spatial spectrum itself is
insensitive to the transition (see Fig. 2).
The low scale perturbations produce a different scenario. Their amplitudes kept
constant during the radiation dominated-epoch to increase by several orders of
magnitude at the transition. For inhomogeneities of galactic scale
(
![]() )
the time factor
)
the time factor![]() is of 108, which means a 104 times
amplitude enhancement. The pressure discontinuity excites low-scale
perturbations and their contribution to the spatial-spectrum becomes dominant
shortly after the transition.
is of 108, which means a 104 times
amplitude enhancement. The pressure discontinuity excites low-scale
perturbations and their contribution to the spatial-spectrum becomes dominant
shortly after the transition.
As opposed to the density perturbations, the velocity magnitude does not change
significantly at the transition. An analogue of the transfer function
![]() constructed for the
expansion spectrum is shown in Fig. 3. The expansion contrast increases
systematically during the radiation era and smoothly enters the matter era,
keeping nearly the same growth rate before and after the transition. A
substantial change in the velocity field relates to its phase. Figure 4
shows the difference in arguments of the density and expansion modes
constructed for the
expansion spectrum is shown in Fig. 3. The expansion contrast increases
systematically during the radiation era and smoothly enters the matter era,
keeping nearly the same growth rate before and after the transition. A
substantial change in the velocity field relates to its phase. Figure 4
shows the difference in arguments of the density and expansion modes
![]() .
In the radiation era large frequency modes,
(both
.
In the radiation era large frequency modes,
(both
![]() and
and
![]() )
are shifted to each other by
)
are shifted to each other by ![]() (compare also Eqs. (46)
and (27)). This effect is the generic perturbation property in
the radiation dominated fluid (Ellis et al. 1990), and is an artefact
of their acoustic character. Similar relation of phases can be also obtained on
the ground of binding energy analysis (Liang 1977). After the transition the
arguments of the density and velocity modes differ by
(compare also Eqs. (46)
and (27)). This effect is the generic perturbation property in
the radiation dominated fluid (Ellis et al. 1990), and is an artefact
of their acoustic character. Similar relation of phases can be also obtained on
the ground of binding energy analysis (Liang 1977). After the transition the
arguments of the density and velocity modes differ by ![]() so their maxima are
anti-correlated. Smallest expansion occurs in the regions of highest density.
Decreasing modes have decayed and fluid flow becomes potential
(Peebles 1980). (Slightly more complex is the behaviour of the low frequency
modes. Solutions like that hardly achieve the phase of potential flow (the
argument shift is different from
so their maxima are
anti-correlated. Smallest expansion occurs in the regions of highest density.
Decreasing modes have decayed and fluid flow becomes potential
(Peebles 1980). (Slightly more complex is the behaviour of the low frequency
modes. Solutions like that hardly achieve the phase of potential flow (the
argument shift is different from ![]() ).)
).)
| |
Figure 3:
The expansion spectrum transfer
|
| Open with DEXTER | |
| |
Figure 4: Phases of perturbations. |
| Open with DEXTER | |
From the hydrodynamic point of view, the transition from the radiation
to the matter-dominated epoch breaks down the acoustic approximation.
The sound velocity instantly falls from
![]() to zero, and in
consequence, the fluid velocity formally becomes greater than the sound
velocity at each point in space. (In this way the structure formation
has some aspects characteristic for formation of acoustic shocks -
compare Montenegro et al. 1999; Khoperskov &Khrapov 1999). The growth of inhomogeneities is
based on acoustic instability - the self-gravitation processes do not
switch on until the linear regime fails. In both cases - the density
and expansion fields - the spectrum transfer function monotonically increases with the
wave number k. In particular the phenomenon of acoustic peaks is
absent
to zero, and in
consequence, the fluid velocity formally becomes greater than the sound
velocity at each point in space. (In this way the structure formation
has some aspects characteristic for formation of acoustic shocks -
compare Montenegro et al. 1999; Khoperskov &Khrapov 1999). The growth of inhomogeneities is
based on acoustic instability - the self-gravitation processes do not
switch on until the linear regime fails. In both cases - the density
and expansion fields - the spectrum transfer function monotonically increases with the
wave number k. In particular the phenomenon of acoustic peaks is
absent![]() . The absence of peaks is
characteristic feature of the random field composed of the
statistically independent moving waves (Grishchuk 1995). The
spectrum transfer function may substantially change in the small
k-regime when the universes undergoes more than one phase transition
(some classical ones, like
the change in the sound velocity, or semiclassical like the transition
from inflationary to radiation dominated universe). In these cases the
squeezed states in the acoustic field appear on large scales, which are
an alternative explanation of the CMBR temperature spectrum
(Bose &Grishchuk 2002).
. The absence of peaks is
characteristic feature of the random field composed of the
statistically independent moving waves (Grishchuk 1995). The
spectrum transfer function may substantially change in the small
k-regime when the universes undergoes more than one phase transition
(some classical ones, like
the change in the sound velocity, or semiclassical like the transition
from inflationary to radiation dominated universe). In these cases the
squeezed states in the acoustic field appear on large scales, which are
an alternative explanation of the CMBR temperature spectrum
(Bose &Grishchuk 2002).
When considering instantaneous transition to the matter dominated universe
authors limit
themselves to the large scale perturbation regime. In this regime the growing mode amplitude after the phase
transition is entirely dominated by that before the phase transition and
there is no chance of generating a growing mode out of a decaying mode
(Kodama &Sasaki 1984). Although the short perturbations
do not produce the same scenario![]() the decaying modes
of any length-scale are commonly neglected
at the beginning of the matter dominated era.
the decaying modes
of any length-scale are commonly neglected
at the beginning of the matter dominated era.
By abandoning all the decaying terms in the formula (43) one obtains
![]() ,
and consequently, the spatial spectrum of
the density contrast
,
and consequently, the spatial spectrum of
the density contrast
While the pure growing modes increase ten times
in the interval
![]() ,
the mixture of growing and decaying
low scale modes is enhanced by several orders of magnitude
(compare Figs. 1 and 5).
The enhancement of this mixture depends on the
wave number k. Substantial magnification of the low scale modes
(Fig. 1) means that the low-scale
structures may enter the nonlinear regime first.
,
the mixture of growing and decaying
low scale modes is enhanced by several orders of magnitude
(compare Figs. 1 and 5).
The enhancement of this mixture depends on the
wave number k. Substantial magnification of the low scale modes
(Fig. 1) means that the low-scale
structures may enter the nonlinear regime first.
When the decaying modes are taken into account the scale-independence breaks
down. Decaying modes "remember'' perturbations' past. In our case the
admixture of decaying modes defined by the joining conditions (23), (24) is an imprint of the acoustic (travelling wave) character of the
density perturbations in the radiational era. Consequently, the radiational era
affects the structure formation processes occurring latter on, when matter
dominates. Instability of perturbations is the genuine feature of the
entire cosmological evolution rather than the property of separate
cosmological epochs.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{3437F3.eps}
\end{figure}](/articles/aa/full/2004/21/aa3437/Timg209.gif) |
Figure 5: The density spectrum transfer function for perturbations composed of pure growing modes. |
| Open with DEXTER | |
Although our primary goal is to discuss the role of decaying solutions in the formation of the small-scale structures, it is worth checking the models consistence with data presently available for larger scales.
Data coming from the large galaxy surveys (SDSS, 2dFGRS and others) probe the large-scale mass distribution at late epochs, while the WMAP experiment reports the density fluctuations at the last scattering surface. These two categories of data potentially allow reconstruction of the spectrum transfer function i.e. the scale of inhomogeneity enhancement after decoupling.
To examine the spectrum transfer function (51) we focus on the LSS spectral estimations,
with the scale range of some 100 Mpc, that at the same time overlaps the right
end of the range (![]() few
few
![]() )
probed by WMAP experiment. As
an example we take two close length-scales,
)
probed by WMAP experiment. As
an example we take two close length-scales,
![]() and
and
![]() ,
for which the values of
,
for which the values of ![]() contrast (Fig. 3 in Wu et al. 1999) are
respectively,
contrast (Fig. 3 in Wu et al. 1999) are
respectively, ![]() 10-2 and
10-2 and ![]() 10-3. These scales correspond to
10-3. These scales correspond to
![]() in the CMB spectrum and may be considered as the intermediate length-scales.
The spectrum transfer function
in the CMB spectrum and may be considered as the intermediate length-scales.
The spectrum transfer function
![]() in this scales is given in
Fig. 6. The curves are drawn for the constant
in this scales is given in
Fig. 6. The curves are drawn for the constant ![]() -surfaces between
-surfaces between
![]() (the
lowest) and
(the
lowest) and ![]() - 31 - corresponding roughly to redshift
- 31 - corresponding roughly to redshift ![]() 0. The
increase of the model spectrum transfer function (51) are roughly of the order of 103 and 102 at the scales under discussion, and reproduce the current density
contrast, from the initial density contrast of the order
0. The
increase of the model spectrum transfer function (51) are roughly of the order of 103 and 102 at the scales under discussion, and reproduce the current density
contrast, from the initial density contrast of the order ![]() 10-5. In
spite of the high idealization, we obtain rough agreement with observations
in the
10-5. In
spite of the high idealization, we obtain rough agreement with observations
in the
![]() regime.
regime.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3437F4.eps}
\end{figure}](/articles/aa/full/2004/21/aa3437/Timg218.gif) |
Figure 6:
The spectrum transfer function
|
| Open with DEXTER | |
Spectrum transfer function is substantially more difficult view in the context of extremely
low, or extremely large scales. In the large scale limit the spectrum transfer function
(51) becomes insensitive to changes in the equation of state. This
confirms that the large scale perturbations are "fossils'' of the past,
which is interesting in the context of their quantum or semiclassical
origin. The recently reported (e.g. Oliveira-Costa et al. 2003; Hannestad 2003)
discrepancy between the WMAP observational spectrum and that coming from the
inflationary paradigm for scales
![]() challenges some revisions
of the initial perturbation spectrum theory. On the other hand the
interpretation of measurements also deserves careful examination. The
perturbations and the resulting temperature fluctuations are commonly related to
each other by means of the Sachs-Wolfe formula - an integral over gravitational
potential performed along the photon path (Sachs &Wolfe 1967; Peebles 1980).
The formula is true in the absence or neglect of the decaying modes at the last
scattering surface (Sachs &Wolfe 1967). For the density perturbation matched to
the acoustic field the decaying modes cannot be neglected, particularly the low
multipoles, where discrepancies become substantial
challenges some revisions
of the initial perturbation spectrum theory. On the other hand the
interpretation of measurements also deserves careful examination. The
perturbations and the resulting temperature fluctuations are commonly related to
each other by means of the Sachs-Wolfe formula - an integral over gravitational
potential performed along the photon path (Sachs &Wolfe 1967; Peebles 1980).
The formula is true in the absence or neglect of the decaying modes at the last
scattering surface (Sachs &Wolfe 1967). For the density perturbation matched to
the acoustic field the decaying modes cannot be neglected, particularly the low
multipoles, where discrepancies become substantial![]() . To understand properly the measured
. To understand properly the measured ![]() coefficients at
low-l limit we need the exact formula for the temperature
fluctuation. (In the discussed model the exact formula can be found, but is beyond the scope of this paper.)
coefficients at
low-l limit we need the exact formula for the temperature
fluctuation. (In the discussed model the exact formula can be found, but is beyond the scope of this paper.)
Violent formation of fine scale structures in the transient epoch, the
characteristic feature of the model, enables inhomogeneities to enter the nonlinear
regime soon after decoupling. The model qualitatively supports observations of
highly developed structures at high redshifts z. However, the WMAP angular
resolution limit rules out any quantitative estimations for the structures less
than
![]() .
Expecting more relevant data from the forthcoming Planck
mission we anticipate, on the strength of the spectrum transfer function (51), that the CMBR
temperature fluctuations in the fine-scale regime may have relatively low
amplitude.
.
Expecting more relevant data from the forthcoming Planck
mission we anticipate, on the strength of the spectrum transfer function (51), that the CMBR
temperature fluctuations in the fine-scale regime may have relatively low
amplitude.
Generic density perturbations in the radiation-dominated universe propagate in
the same way as sounds propagate in air or electromagnetic waves in vacuum. As
shown by Sachs &Wolfe (1967) and White (1973) perturbations form
waves travelling with the same speed
![]() independently of
their scales or profiles, hence gravitationally bound structures cannot form.
Perturbations do not self-gravitate in the linear regime, so gravity may affect
their evolution merely by affecting the dynamics of the homogeneous background.
The wave character of the density perturbations (independent of their scales) is
confirmed in the Hamiltonian formalism (Lukash 1980; Chibisov &Mukhanov 1982).
independently of
their scales or profiles, hence gravitationally bound structures cannot form.
Perturbations do not self-gravitate in the linear regime, so gravity may affect
their evolution merely by affecting the dynamics of the homogeneous background.
The wave character of the density perturbations (independent of their scales) is
confirmed in the Hamiltonian formalism (Lukash 1980; Chibisov &Mukhanov 1982).
The hyperbolic type of propagation equation requires appropriate perturbation statistics, where acoustic waves travelling in different directions are statistically independent. This kind of statistics form a classical limit for quantum theories (Lukash 1980; Chibisov &Mukhanov 1982; Grishchuk 1995) and is compatible with the gravitational waves theory (Abbott &Harari 1986; Allen 1996; Allen &Romano 1999; Maggiore 2000). Probability and appropriate expectation values may depend on the wave frequency, but not on the direction of propagation, neither the wave phase at any time or position. A random choice of plane waves guarantees that the perturbations and their canonical momenta are statistically independent and uncorrelated quantities at any time. This finally results in the stability of homogeneous expanding environment. Perturbations larger than the sound horizon decay during the radiation era, while those well inside the horizon keep their magnitude constant in time. This property, although contradicting Jeans conjecture, confirms results obtained in other gauges: synchronous (Grishchuk 1994; Golda &Woszczyna 2001), longitudinal (Mukhanov et al. 1992 Part III) and in Hamiltonian formalism (Chibisov &Mukhanov 1982). Similar decrease in amplitude occurs for the large scale component of the scalar field (Stebbins & Veerarghavan 1993).
Cosmic structure formation naturally occurs at the transition from the
radiational to matter domination era. To match the acoustic field at the
decoupling, the growing and decaying modes contribute in the short wave limit
with nearly opposite phases, and therefore, compensate each other at ![]() .
After the transition both modes "decouple" and the resulting superposition grows
explosively. Physically it means that the pressure decay from
.
After the transition both modes "decouple" and the resulting superposition grows
explosively. Physically it means that the pressure decay from
![]() to
p=0 excite perturbations much lower than horizon scale, while leave
untouched the amplitude of those, which substantially exceed
horizon
to
p=0 excite perturbations much lower than horizon scale, while leave
untouched the amplitude of those, which substantially exceed
horizon![]() . For growth of inhomogeneities the break down
of the acoustic approximation is responsible, i.e. the same group of physical
phenomena that may excite shock waves in the interstellar medium. This kind of
instabilities cannot be described by any formalism, which a priori
neglects the role of decaying modes, no matter how realistic are the models for
physics of recombination and decoupling, which are used.
. For growth of inhomogeneities the break down
of the acoustic approximation is responsible, i.e. the same group of physical
phenomena that may excite shock waves in the interstellar medium. This kind of
instabilities cannot be described by any formalism, which a priori
neglects the role of decaying modes, no matter how realistic are the models for
physics of recombination and decoupling, which are used.
This is obvious that the sharp transition between cosmological eras is not a realistic model for decoupling or recombination. In reality these phenomena are continuous, take some cosmologically substantial time, and involve a number of complex physical processes. The recombination and decoupling do not coincide. One can hardly expect that the realistic situation can be described by simple analytical solutions as presented in this paper. Eventually one have to apply numerical codes involving multi fluid hydrodynamics or magnetohydodynamics. Still, the problem of the initial state remains. The physical meaning of the obtained numerical results strongly depends on their stability against initial condition and on the physical relevance of the initial state assumed at early epochs. Most of hydrodynamical codes are ready to work with travelling waves, therefore, the complete numerical analysis of random acoustic fields in the expanding universe - without neglecting a priori the role of "decaying modes'' - is basically possible. On the other hand, simple but nontrivial analytic solutions presented in this paper may easily be used to verify numeric procedures.
Acknowledgements
We thank Zdzisaw Golda for valuable critical comments. This work was partially supported by State Committee for Scientific Research, project No. 2 P03D 014 17.