... play[*]
For low frequency gravitational standing waves of substantial amplitude may appear (squeezed state of gravitational field, Grishchuk 1996). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... fluid[*]
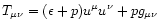With the diagonal energy momentum tensor $T_{\mu\nu}=(\epsilon+\P)u^{\mu}u^{\nu}+\P g_{\mu\nu}$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... velocity[*]
This is not the case of open or closed universes, where sound is dispersed on the space curvature (Golda &Woszczyna 2001). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... spectrum[*]
In this context we consequently use the name spatial power spectrum. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... choice[*]
The quadratic behaviour of the decreasing term is characteristic for the orthogonal gauge. In the synchronous system of reference this term decays as 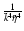$\frac{1}{\tilde{k}^4\tilde{\eta}^4}$. It can be easily derived in the Field-Shepley formalism, see formula (5.3) of (Chibisov &Mukhanov 1982) after substituting solutions of Eq. (4.7) and evaluating the integral over $\eta$. Equivalently, it can be proved directly in the original Lifshitz formalism (Golda &Woszczyna 2001). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... compression[*]
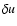The orthogonal gauge realizes the comoving system of reference, where the four velocity is globally chosen as u=(1,0,0,0), therefore one cannot describe the peculiar velocity field directly by $\delta u$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... absent[*]
The same effect appears in more sophisticated transition models investigated numerically (Press &Vishniac 1980), if they include the complete basis of solutions. On the other hand, as shown in (), peaks may appear in a pure radiation-filled universe model without evoking complicated recombination processes, if one limits to growing modes (standing waves) with specific phase correlation. These phenomena have also been discussed in (Fang &Wu 1996; Riazuelo &Deruelle 2000). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... scenario[*]
(...) the general relation among the amplitudes (...) would be too complicated to extract any physical information out of it (Kodama &Sasaki 1984). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... substantial[*]
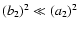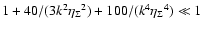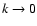To neglect decaying modes one needs $(b_2)^2\ll(a_2)^2$. After employing (30) this condition is $1+40/(3 k^2 {\eta_\Sigma}^2)+100/(k^4 {\eta_\Sigma}^4)\ll 1$, and is false for any k. Particularly, in the $k\rightarrow 0$ the error becomes arbitrarily large. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... horizon[*]
This behaviour is opposite to that of tensor perturbations. A similar transition in the equation of state will amplify large scale gravitational waves not affecting the small scale ones. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Copyright ESO 2004