A&A 419, 405-417 (2004)
DOI: 10.1051/0004-6361:20034375

Protostellar mass accretion rates from gravoturbulent fragmentation

S. Schmeja - R. S. Klessen

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 19 September 2003 / Accepted 4 February 2004

Abstract
We analyse protostellar mass accretion rates $\dot{M}$ from numerical models of star formation based on gravoturbulent fragmentation, considering a large number of different environments. To within one order of magnitude, $\dot{M} \approx M_{\rm J} / \tau_{\rm ff}$ with $M_{\rm J}$ being the mean thermal Jeans mass and $\tau_{\rm ff}$ the corresponding free-fall time. However, mass accretion rates are highly time-variant, with a sharp peak shortly after the formation of the protostellar core. We present an empirical exponential fit formula to describe the time evolution of the mass accretion and discuss the resulting fit parameters. There is a positive correlation between the peak accretion rate and the final mass of the protostar. We also investigate the relation of $\dot{M}$ with the turbulent flow velocity as well as with the driving wavenumbers in different environments. We then compare our results with other theoretical models of star formation and with observational data.

Key words: hydrodynamics - accretion, accretion disks - stars: formation - ISM: kinematics and dynamics - methods: numerical

   
1 Introduction

Stars are born in dense cores of interstellar molecular clouds. Despite recent observational and theoretical progress, the initial conditions and physical processes that determine the formation of stars are still not fully understood.

In the so-called "standard theory of star formation'' (Shu et al. 1987) stars are formed by the inside-out collapse of a singular isothermal sphere that is initially in quasistatic equilibrium, supported against gravity by magnetic and thermal pressure and evolves only due to slow ambipolar diffusion processes. This model predicts protostellar mass accretion rates that are constant with time and only depend on the isothermal sound speed (Shu 1977). This hypothesis, however, has been challenged from several sides (see Larson 2003 or Mac Low & Klessen 2004 for a summary). It only is applicable to isolated, single stars, while it is known that the majority of stars form in small aggregates or large clusters (Adams & Myers 2001; Lada & Lada 2003). Furthermore, there is both observational evidence (Crutcher 1999; André et al. 2000; Bourke et al. 2001) and theoretical reasoning (e.g. Nakano 1998) showing that most observed cloud cores do not have magnetic fields strong enough to support against gravitational collapse. Similarly, the long lifetimes implied by the quasi-static phase of evolution in the model are difficult to reconcile, e.g., with observational statistics of cloud cores (Taylor et al. 1996; Lee & Myers 1999; Visser et al. 2002) and with chemical age considerations (van Dishoeck & Blake 1998; Langer et al. 2000).

Molecular clouds appear to actually be transient objects with lifetimes of a few million years that form and dissolve in the larger-scale turbulent flow of the Galactic disc (Ballesteros-Paredes et al. 1999b; Elmegreen 2000; Hartmann et al. 2001; Hartmann 2003; Vázquez-Semadeni et al. 2004). Observations of self-similar structure in molecular clouds (e.g. Mac Low & Ossenkopf 2000; Ossenkopf & Mac Low 2002) indicate that interstellar turbulence is driven on scales substantially larger than the clouds themselves. These large-scale turbulent flows compress and cool gas. At sufficiently high densities atomic gas is then quickly converted into molecular form (Hollenbach et al. 1971). These same flows will continue to drive the turbulent motions observed within the newly formed cloud. Some combination of turbulent flow, free expansion at the sound speed of the cloud and dissociating radiation from internal star formation will then be responsible for their destruction on a timescale of 5-10 Myr. The most likely source of such large-scale interstellar turbulence in the Milky Way is the combined energy and momentum input from supernovae explosions. They appear to overwhelm all other possibilities. In the outer reaches of the Galaxy and in low surface brightness galaxies, on the other hand, the situation is not so clear, with magnetorotational or gravitational instabilities being most likely to drive the observed flows (Mac Low 2002; Mac Low & Klessen 2004).

Modern star formation theory, therefore, considers supersonic interstellar turbulence as the controlling agent for stellar birth, rather than mediation by magnetic fields (Mac Low & Klessen 2004). This turbulence typically carries sufficient energy to counterbalance gravity on global scales. On small scales, however, it may actually provoke localised collapse (Hunter & Fleck 1982; Elmegreen 1993; Padoan 1995; Ballesteros-Paredes et al. 1999a; Klessen et al. 2000; Padoan & Nordlund 1999, 2002). This apparent paradox can be resolved when considering that supersonic turbulence establishes a complex network of interacting shocks, where converging flows generate regions of enhanced density. The system becomes highly filamentary, with elongated structures caused either by shear motions or by compression at the intersection of shocked layers of gas. At some locations the density enhancement can be sufficiently strong for gravitational instability to set in. The stability criteria for filaments and sheets have been derived and discussed in the context of star formation, e.g., by Larson (1985), Lubow & Pringle (1993) and Clarke (1999). However, the same random flow that creates density enhancements may disperse them again. For local collapse to result in stellar birth, it must progress fast enough for the region to "decouple'' from the flow.

The efficiency of protostellar core formation, the growth rates and final masses of the protostars and essentially all other properties of nascent star clusters then depend on the intricate interplay between gravity on the one hand side and the turbulent velocity field in the cloud on the other. The star formation rate is regulated not just at the scale of individual star-forming cores through ambipolar diffusion balancing magnetostatic support, but rather at all scales (Elmegreen 2002), via the dynamical processes that determine whether regions of gas become unstable to prompt gravitational collapse. The presence of magnetic fields does not alter that picture significantly (Mac Low et al. 1998; Stone et al. 1998; Padoan & Nordlund 1999; Heitsch et al. 2001b). In particular, it cannot prevent the decay of interstellar turbulence.

Clusters of stars build up in molecular cloud regions where self-gravity overwhelms turbulence, either because such regions are compressed by a large-scale shock, or because interstellar turbulence is not replenished and decays on short timescales. Then, many gas clumps become gravitationally unstable and synchronously go into collapse. If the number density is high, contracting protostellar cores interact and may merge to produce new cores which now contain multiple protostars. Close encounters drastically alter the trajectories of the protostars, thus changing their mass accretion rates. This has important consequences for the final stellar mass spectrum (Bonnell et al. 1997, 2001a,b; Klessen & Burkert 2000, 2001; Klessen 2001b; Bate et al. 2002).

Inefficient, isolated star formation will occur in regions that are supported by turbulence carrying most of its energy on very small scales. This requires an unrealistically large number of driving sources and appears at odds with the measured velocity structure in molecular clouds which in almost all cases is dominated by large-scale modes (Mac Low & Ossenkopf 2000; Ossenkopf & Mac Low 2002).

In this paper we extend the analysis of protostellar mass accretion rates from a single case (Klessen 2001a) to a large series of numerical models of turbulent molecular cloud fragmentation that covers the entire spectrum of observed star-forming regions, ranging from inefficient and isolated star formation to the fast and efficient build-up of stellar clusters. These calculations, their numerical realisation and the adopted parameters are described in Sect. 2. In Sect. 3 we discuss our findings. We investigate the mass growth history of all protostars in our set of models and present a simple analytic fit formula for the accretion rate $\dot{M}$. We discuss our study in relation to previous analyses and observational data in Sects. 4 and 5, respectively. In Sect. 6 we summarise our results.

   
2 The models

To adequately describe the fragmentation of turbulent, self-gravitating gas clouds and the resulting formation and mass growth of protostars, we need to resolve the dynamical evolution of collapsing cores over several orders of magnitude in density. Due to the stochastic nature of supersonic turbulence, it is not known in advance where and when this local collapse occurs. Hence, SPH (smoothed particle hydrodynamics) is used to solve the equations of hydrodynamics. It is a Lagrangian method, where the fluid is represented by an ensemble of particles and flow quantities are obtained by averaging over an appropriate subset of the SPH particles (Benz 1990; Monaghan 1992). The method is able to resolve large density contrasts as particles are free to move and so naturally the particle concentration increases in high-density regions. We use the same smoothing procedure for gravity and pressure forces. This is needed to prevent artificial fragmentation (Bate & Burkert 1997). Because it is computationally prohibitive to treat the cloud as a whole, we concentrate on subregions within the cloud and adopt periodic boundary conditions (Klessen 1997). Once the central region of a collapsing protostellar core exceeds a density contrast of ${\sim} 10^5$, it is replaced by a "sink'' particle (Bate et al. 1995), which has the ability to accrete gas from its surrounding while at the same time keeping track of mass and linear and angular momentum. By adequately replacing high-density cores with sink particles we can follow the dynamical evolution of the system over many free-fall times.

Table 1: Overview of our models (see text for details).

The suite of models consists of two globally unstable models that contract from Gaussian initial conditions without turbulence (for details see Klessen & Burkert 2000, 2001) and of 22 models where turbulence is maintained with constant rms Mach numbers $\cal M$, in the range $0.1 \le {\cal M} \le 10$. We distinguish between turbulence that carries its energy mostly on large scales, at wavenumbers $1 \le k \le 2$, on intermediate scales, i.e. $3 \le k \le 4$, and on small scales with $7 \le k \le 8$. The corresponding wavelengths are $\ell = L/k$, where L is the total size of the computed volume. The models are labelled mnemonically as M$\cal M$kk, with rms Mach number $\cal M$ and wavenumber k, while G1 and G2 denote the two Gaussian runs. The main parameters are summarised in Table 1. To have well defined environmental conditions given by $\cal M$ and k, $\cal M$ is required to be constant throughout the evolution. However, turbulent energy dissipates rapidly, roughly on a free-fall timescale (Mac Low et al. 1998; Stone et al. 1998; Padoan & Nordlund 1999). We therefore apply a non-local driving scheme that inserts energy at a given rate and at a given scale k. We use Gaussian random fluctuations in velocity. This is appealing because Gaussian fields are fully determined by their power distribution in Fourier space. We define a Cartesian mesh with 643cells, and for each three-dimensional wave number $\vec{k}$ we randomly select an amplitude from a Gaussian distribution around unity and a phase between zero and $2\pi$. We then transform the resulting field back into real space to get a "kick-velocity'' in each cell. Its amplitude is determined by solving a quadratic equation to keep $\cal M$ constant (Mac Low 1999; Klessen et al. 2000). The "kick-velocity'' is then simply added to the speed of each SPH particle located in the cell. We adopted this method for mathematical simplicity. In reality, the situation is far more complex. Still, our models of large-scale driven clouds contain many features of molecular clouds in supernovae-driven turbulence (e.g. Ballesteros-Paredes & Mac Low 2002; Mac Low et al. 2003). Conversely, our models of small-scale turbulence bear certain resemblance to energy input on small scales provided by protostellar feedback via outflows and winds.

Our models neglect the influence of magnetic fields, because their presence cannot halt the decay of turbulence (Mac Low et al. 1998; Stone et al. 1998; Padoan & Nordlund 1999) and does not significantly alter the efficiency of local collapse for driven turbulence (Heitsch et al. 2001a). More importantly, we do not self-consistently consider feedback effects from the star formation process itself (like bipolar outflows, stellar winds, or ionising radiation from new-born O or B stars). Our analysis of protostellar mass accretion rates focuses solely on the interplay between turbulence and self-gravity. This is also the case in the Shu (1977) theory of isothermal collapse. Hence, our findings can be directly compared to the "standard theory of star formation''.

The models are computed in normalised units using an isothermal equation of state. Scaled to physical units we adopt a temperature of 11.3 K corresponding to a sound speed $c_{\rm s} = 0.2~$km s-1, and we use a mean density of $n({\rm H}_2) = 10^5~$cm-3, which is typical for star-forming molecular cloud regions (e.g. in $\rho$ Ophiuchi, see Motte et al. 1998). The total mass contained in the computed volume in the two Gaussian models is 220 $~M_{\hbox{$\odot$ }}$ and the size of the cube is 0.34 pc. This corresponds to 220 thermal Jeans masses. The turbulent models have a mass of 120 $~M_{\hbox{$\odot$ }}$ within a volume of ( $0.28~{\rm pc})^3$, equivalent to 120 thermal Jeans masses[*]. The mean thermal Jeans mass in all models is thus $\langle M_{\rm J} \rangle = 1~M_{\hbox{$\odot$ }}$, the global free-fall timescale is $\bar{\tau}_{\rm ff} = 10^5~$yr, and the simulations cover a density range from $n({\rm H}_2) \approx 100~$cm-3 in the lowest density regions to $n({\rm H}_2) \approx 10^9~$cm-3 where collapsing protostellar cores are identified and converted into "sink'' particles in the code. This coincides in time with the formation of the central protostar to within ${\sim}10^3~$yr (Wuchterl & Klessen 2001). The resolution limit for each model, requiring that the local Jeans mass is always resolved by at least 100 gas particles (Bate & Burkert 1997), is given in Col. 5 of Table 1.

In the subsequent protostellar phase of evolution, we determine accretion rates $\dot{M}$ by measuring the amount of mass as a function of time that falls into a control volume defined by each "sink'' particle. Its diameter is fixed to 560 AU. Entering gas particles pass through several tests to check if they remain bound to the "sink'' particle (Bate et al. 1995) before they are considered accreted. As all gas particles have the same mass and as accretion events occur at random times, the resulting accretion rates are mass-binned and we smooth over a few consecutive accretion events to get a description of the time evolution of $\dot{M}$. We cannot resolve the evolution in the interior of the control volume. Because of angular momentum conservation most of the matter that falls in will assemble in a protostellar disc. There it is transported inwards by viscous and possibly gravitational torques. The latter will be provided by spiral density waves that develop when the disc becomes too massive, which happens when mass is loaded onto the disc faster than it is removed by viscous transport. Altogether, the disc will not prevent or delay material from accreting onto the protostar for long. It acts as a buffer and smoothes eventual accretion spikes. For the mass range considered here feedback effects are too weak to halt or delay accretion. With typical disc sizes of the order of several hundred AU, the control volume therefore fully encloses both star and disc, and the measured core accretion rates are good estimates of the actual stellar accretion rates. Deviations may be expected only if the protostellar core forms a binary star, where the infalling mass must then be distributed over two stars, or if very high-angular momentum material is accreted, where a certain mass fraction may end up in a circumbinary disc and not accrete onto a star at all.

In the prestellar phase, i.e. before the central protostar forms, we determine the accretion history by computing the change of mass inside the control volume centered on the SPH particle that turns into a "sink'' during the later evolution. Turbulent compression leads to mass growth, i.e. $\dot{M}>0$, while expansion will result in mass loss and $\dot{M}<0$. Appreciable mass growth, however, is only achieved when gravity takes over and the region goes into collapse.

   
3 Discussion

3.1 First approximation to $\dot{M}$

The entire process of molecular cloud collapse and build-up of the stellar cluster lasts several global free-fall times ( $\bar{\tau}_{\rm ff} = 10^5$ yr). Likewise, the accretion process of a protostellar core takes place on a timescale of a few $\bar{\tau}_{\rm ff}$, comparable to most other models of star formation.

A simple approximation of the accretion rate can be achieved by dividing the local Jeans mass by the local dynamical timescale:

 \begin{displaymath}\dot{M} \approx M_{\rm J}/\tau_{\rm ff}. \end{displaymath} (1)

By substituting

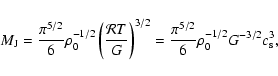\begin{displaymath}M_{\rm J} = \frac{\pi^{5/2}}{6} \rho_0^{-1/2} \left(\frac{\ma... ...2} = \frac{\pi^{5/2}}{6} \rho_0^{-1/2} G^{-3/2} c_{\rm s}^3, \end{displaymath} (2)

where $\rho_0$ denotes the initial density, T the temperature and $c_{\rm s}$the isothermal sound speed, and

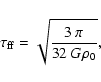\begin{displaymath}\tau_{\rm ff} = \sqrt{\frac{3~\pi}{32~G \rho_0}}, \end{displaymath} (3)

Eq. (1) can be written as

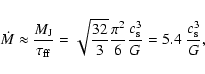\begin{displaymath}\dot{M} \approx \frac{M_{\rm J}}{\tau_{\rm ff}} = \sqrt{\frac... ...c{\pi^2}{6} \frac{c_{\rm s}^3}{G} = 5.4~\frac{c_{\rm s}^3}{G}, \end{displaymath} (4)

depending only on the isothermal sound speed (or temperature). For a sound speed $c_{\rm s} = 0.2~{\rm km~s^{-1}}$ we obtain $\dot{M} = 10^{-5}~{M_{\hbox{$\odot$ }}~\rm yr^{-1}}$. This is higher than the accretion rate for the collapse of a singular isothermal sphere: $\dot{M} = 0.975~c_{\rm s}^3/G$ (Shu 1977). However, the accretion rates in our models vary with time. Typical peak accretion rates are roughly in the range $(3{-}50)~c_{\rm s}^3/G$or $5 \times 10^{-6}$ to $10^{-4}~{M_{\hbox{$\odot$ }}~\rm yr^{-1}}$. The values exceed the approximated value $M_{\rm J}/\tau_{\rm ff}$due to external compression in the turbulent flow.


  \begin{figure} \par\includegraphics[width=15.6cm,clip]{0375fig1.eps} \end{figure} Figure 1: Mass accretion rates of nine randomly selected protostellar cores of three different models. Left panel: $\dot{M}$ versus time for a Gaussian collapse (G2; upper row), a turbulent model driven on a large scale (M6k2a; middle row), and a turbulent model driven on a small scale (M6k8b; lower row). The thin line represents the actual simulation, the thick line the fit as described in the text. The deviation $\sigma $ as given by Eq. (6) is indicated for each object. The dotted line shows the constant accretion rate that would be expected from the classical Shu (1977) scenario. The dashed line stands for the assumed transition from Class 0 to Class I. The right panel shows the same protostellar cores as on the left side plotted versus the ratio of accreted to final mass. The final masses (in $M_{\hbox {$\odot $ }}$) are also given.
Open with DEXTER

3.2 Time-varying mass accretion rates

We analyse the full mass growth history of all protostellar cores in our models and we find that mass accretion rates from gravoturbulent fragmentation are highly time-variable. Several examples of the accretion rate $\dot{M}$ are displayed in Fig. 1, plotted versus time (left panel) and the ratio of accreted to final mass (right panel), respectively. The maximum accretion rate is reached rather rapidly and is then followed by a somewhat slower decline. In some cases this decline is interrupted by one or more secondary peaks. As shown above, the maximum accretion rate is significantly higher than the constant rate predicted by the classical isothermal collapse model (plotted as dotted line in Fig. 1), but it falls below that value in later stages. Due to the dynamical interaction and competition between protostellar cores, the mass accretion rates of cores in a dense cluster are different from those of isolated cores. In the first stage a core accretes local gas from its immediate vicinity. Once the local reservoir is depleted, the core may accrete fresh gas streaming in from farther away or by encounters with non-collapsed gas clumps (see discussion in Klessen & Burkert 2000). This results in secondary accretion peaks that are also visible in the right panel of Fig. 1, where one would expect a single bump in the case of an isolated core. For example, the central graph of the right panel of Fig. 1 clearly shows that this particular protostar accretes only about half of the final mass from its direct environment (first bump), while the rest comes from later accretion events.

The transition phase between Class 0 and Class I protostars is believed to take place when about half of the final mass has been accumulated (André et al. 2000). This time is indicated by the dashed line in Fig. 1. Typically it takes place during or at the end of the peak accretion phase. It determines the lifetime of Class 0 objects, which will be discussed below.

We define a mean accretion rate $\langle \dot{M} \rangle$ by averaging $\dot{M}$ in the mass range $0.1 \le M/M_{\rm end} \le 0.8$, with $M_{\rm end}$being the final mass of the protostar. This phase typically lasts only a few 104 years. This is short compared to the full accretion history. The bulk of stellar material is therefore accumulated in the short time interval while the system is close to maximum accretion.


  \begin{figure} \par\includegraphics[width=16.3cm,clip]{0375fig2.eps} \par\end{figure} Figure 2: Mean accretion rates $\langle \dot{M} \rangle$ versus final mass ( upper panel) and versus time of core formation ( lower panel) for the same models as in Fig. 1. The zero point of the timescale coresponds to the time when gravity is "switched on''. Note the different timescales on which the formation of the cluster takes place.
Open with DEXTER

In Fig. 2, we plot the mean accretion rates versus final star mass $M_{\rm end}$ and versus time of core formation $t_{\rm form}$, respectively, for the same models as in Fig. 1. Not surprisingly, $\langle \dot{M} \rangle$ increases with increasing stellar mass, and decreases when the core forms later, although this second correlation is not as clear. In other words, more massive stars have higher mass accretion rates and start to form first. They can grow large, because on average they form in the high-density regions of the cluster centre where they are able to maintain relatively high accretion rates over a long time as more and more gas falls in from the cluster outskirts.

3.3 An empirical fit formula for $\dot{M}$

One of our aims is to find a simple-to-use fit formula to approximate the accretion process. The protostellar mass growth history in our models can be fitted empirically in the lin-log diagram by the function

 \begin{displaymath}\log \dot{M}(t) = \log \dot{M}_0~\frac{{e}}{\tau}~t~{\rm e}^{-t/\tau}% \end{displaymath} (5)

with time t and the fit parameters $\log \dot{M}_0$ and $\tau $. This holds for the following conditions: we shift the ordinate by $\Delta \log \dot{M}/({M_{\hbox{$\odot$ }}\rm ~yr^{-1}}) = +7$and we consider accretion when $\log \dot{M} \ge -7$. The zero point of the timescale is determined once the accretion rate exceeds $\log \dot{M} = -7$. The fitted curves are plotted as thick lines in Fig. 1. Note that the ordinate displays the original values without the applied shift. If there are secondary accretion peaks, they are typically ignored and levelled out by the routine. The overall quality of the fit can be estimated by the standard deviation

 \begin{displaymath}\sigma = \sqrt{\frac{1}{n-1} \sum_{t=0}^{n} \left[ \dot{M}_{\rm fit}(t) - \dot{M}(t) \right]^2} \end{displaymath} (6)

where $\dot{M}(t)$ is the actual value of $\dot{M}$ at the time t from our simulation, while $\dot{M}_{\rm fit}(t)$ denotes $\dot{M}$ calculated using Eq. (5) for the same time. The mean value of $\sigma $ for each model is given in Col. 9 of Table 1. Prestellar cores where the fit routine fails or where $\sigma > 1$ are not taken into account in our subsequent analysis. This concerns a wide variety of cores; there is no correlation with the final mass or the time of formation. However, they represent only a small fraction of the total number of objects. The actual numbers of fitted cores are listed in Col. 8 of Table 1.

When interpreting the fit parameter $\log \dot{M}_0$, the applied shift has to be taken into account. Thus, $\log \dot{M}_{\rm max}^{\rm fit} = \log \dot{M}_0 - 7$ gives the real value of the peak accretion. This parameter is plotted for all protostellar cores and all models versus the respective final mass (Fig. 3). A correlation with $M_{\rm end}$ is obvious. We apply a linear fit in the log-log diagram, which is indicated by the straight line. The fitted peak accretion rates show the same behaviour as the mean accretion rates $\langle \dot{M} \rangle$.

The parameter $\tau $ indicates the time of the maximum of the accretion curve. It is plotted for all protostellar cores in Fig. 4. In almost all models $\tau $ shows a correlation with the final mass. The parameter indicates how fast the gas falls in onto the core, therefore we expect it to be related to the local free-fall time and, thus, to the local density at the onset of collapse. It lies in the range $10^4 \la \tau \la 10^5$ yr, which is less than the global free-fall time $\bar{\tau}_{\rm ff}$. If we take an average value $\langle \tau \rangle \approx \bar{\tau}_{\rm ff}/3$, this suggests an initial overdensity of almost a factor of ten in the collapsing regions.


  \begin{figure} \par\includegraphics[width=16.7cm,clip]{0375fig3.eps} \end{figure} Figure 3: Peak accretion rates ( $\log \dot{M}_{\rm max}^{\rm fit}$) versus $M_{\rm end}$ for all our models, sorted by Mach number ${\mathcal M}$ ( top to bottom) and wave number k ( left to right). The straight line shows the applied linear fit. Details of the models can be found in Table 1.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{0375fig4.eps} \end{figure} Figure 4: The time of maximum accretion $\tau $ for all models, arranged analogous to Fig. 3.
Open with DEXTER

3.4 Class 0 lifetimes and the effect of the turbulent medium


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{0375fig5.eps} \end{figure} Figure 5: The assumed duration of Class 0 phase versus $M_{\rm end}$ for all models, arranged analogous to Fig. 3. The dotted lines confine the range of this parameter according to observations (André et al. 2000).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{0375fig6.eps} \end{figure} Figure 6: Averaged mean accretion rates $\langle \dot{M} \rangle$ $_{\rm mean}$ of all models versus Mach number. For the sake of clarity the upper panel is split into mass bins, while the lower panel shows the same, separated according to the wave numbers.
Open with DEXTER

We calculate the transition times from Class 0 to Class I, assumed as described above. This gives the duration of the Class 0 phase for each protostar; the values are plotted versus the corresponding final masses in Fig. 5. The duration of the Class 0 phase increases with increasing final mass. Thus, a massive star is marked not only by a higher peak accretion rate but also by a longer time spent in Class 0 phase.

The mean accretion rates $\langle \dot{M} \rangle$ of all individual protostellar cores of one model are averaged in four mass bins: $0 < M_{\rm end}/{M_{\hbox{$\odot$ }}} \le 0.7$ (bin1), $0.7 < M_{\rm end}/{M_{\hbox{$\odot$ }}} \le 1.5$ (bin2), $1.5 < M_{\rm end}/{M_{\hbox{$\odot$ }}} \le 3$ (bin3), and $M_{\rm end}/{M_{\hbox{$\odot$ }}} > 3$ (bin4). The values are given in Cols. 10 to 13 of Table 1. Figure 6 shows the relation of the averaged mean mass accretion rate $\langle \dot{M} \rangle$ $_{\rm mean}$ to the Mach number for all models, split into mass bins and wave numbers, respectively. Three conclusions can be drawn from the figure: there is a trend that $\langle \dot{M} \rangle$ $_{\rm mean}$decreases with increasing Mach number. This means that the mean accretion rate is lower, when the rms velocity dispersion (i.e. the turbulent Mach number) of the medium is increased. The stronger support of the turbulent medium against gravitational collapse typically results in a lower mass accretion rate. Secondly, $\langle \dot{M} \rangle$ $_{\rm mean}$ is higher for higher mass bins. This is consistent with the findings for the individual mean and maximum accretion rates ( $\langle \dot{M} \rangle$ and  $\dot{M}_{\rm max}^{\rm fit}$) discussed above. Finally, though, there is no correlation of $\langle \dot{M} \rangle$ $_{\rm mean}$ with the wavenumber. Apparently the scale of the driving energy has no influence on the accretion rate.

  
4 Comparison with other theoretical models

In the standard theory of isolated star formation (Shu 1977), which takes a singular isothermal sphere as initial condition, the mass accretion rate is constant in time: $\dot{M} = 0.975~c_{\rm s}^3/G$. Note that also the Larson-Penston solution (Larson 1969; Penston 1969), considering constant-density initial perturbations, gives a time-independent accretion rate, however, at a higher level of $47~c_{\rm s}^3/G$. The first numerical collapse calculations were reported by Bodenheimer & Sweigart (1968), Larson (1969) and Hunter (1977). Models with more realistic initial density profiles generally predict accretion rates that decline with time: the models of Hunter (1977; $\dot{M}_{\rm max}$  $\approx 36~c_{\rm s}^3/G$ from numerical integrations of isothermal collapses), Foster & Chevalier (1993; $\dot{M}_{\rm max}$  $\approx 47~c_{\rm s}^3/G$ from numerical hydrodynamic simulations), Tomisaka (1996; $\dot{M}_{\rm max}$ = $(4{-}40)~c_{\rm s}^3/G$ from numerical MHD models), Basu (1997; $\dot{M}_{\rm max}$ = $13~c_{\rm s}^3/G$ from a semi-analytical model), Ogino et al. (1999; $\dot{M}_{\rm max}$ $\approx (30{-}230)~c_{\rm s}^3/G$ from numerical hydrodynamic simulations), Masunaga & Inutsuka (2000; radiation hydrodynamic numerical codes), Whitworth & Ward-Thompson (2001) and Motoyama & Yoshida (2003; $\dot{M}_{\rm max}$  $\ga 42~c_{\rm s}^3/G$) predict mass accretion rates that peak shortly after the formation of the protostar and decrease with time. This shows better agreement with observational data than constant accretion rates (see Sect. 5). Our results display the same behaviour and our values of $\dot{M}_{\rm max}$  $\approx (3{-}50)~c_{\rm s}^3/G$coincide quite well with those findings. In contrast, some models yield mass accretion rates that increase with time (McLaughlin & Pudritz 1997; Bonnell et al. 2001a; Behrend & Maeder 2001).

Theoretical models of star formation usually are scale-free. Thus, the results strongly depend on the adopted physical scaling, e.g. the choice of the initial density or temperature. The comparison of numerical values of accretion rates therefore requires some care. Again, in most cases the maximum accretion rates scale approximately as a few times $M_{\rm J}/\tau_{\rm ff}$.

Whitworth & Ward-Thompson (2001) presented an analytical model for protostellar collapse using a Plummer-like density profile as initial condition. They successfully modelled the prestellar core L1544 in good agreement with observations. Their $\dot{M}_{\rm max}$  $\approx 8.1 \times 10^{-5}\ M_{\hbox{$\odot$ }}~{\rm yr^{-1}}$ corresponds quite well to our Gaussian collapse cases for the same stellar mass (G1, G2). However, the accretion history of the collapsing Plummer sphere cannot be matched with our fit formula (5). The increase is steeper, while the decrease is slower compared to any of our models. The slow decline might be due to the fact that Whitworth & Ward-Thompson (2001) use a non-truncated, infinite density profile, while our models have finite sizes. A similar model was used by Motoyama & Yoshida (2003) who examined the hypothesis that very high mass accretion rates exceeding $ 10^{-4}\ M_{\hbox{$\odot$ }}{\rm ~yr^{-1}}$ require external triggering, as inferred from some observations. They find that the maximum accretion rate is proportional to the momentum given to the cloud core in their perturbed collapse model. A momentum of ${\ga} 0.1\ {M_{\hbox{$\odot$ }}~\rm km~s^{-1}}$ causes an accretion rate of ${\ga} 10^{-4}\ M_{\hbox{$\odot$ }}{\rm ~yr^{-1}}$.

Smith (1999, 2000) presented a formula for the mass accretion rate with a sharp exponential rise and a power law decrease in time. This model provides an early peak in which $\dot{M} \approx 10^{-4}\ {M_{\hbox{$\odot$ }}~\rm yr^{-1}}$ for 104 years and eventually becoming $\dot{M} \approx 10^{-7}\ {M_{\hbox{$\odot$ }}~\rm yr^{-1}}$ for 106 years. However, his formula (Eq. (6) in Smith 2000) applies to our models only when choosing parameters completely different to those suggested, otherwise his accretion curve has a more rapid increase but a slower decline than our models.

Bonnell et al. (2001a) analysed competitive accretion in embedded stellar clusters by means of SPH simulations. They find that accretion in a cluster is highly non-uniform and that the accretion rate is higher for stars near the cluster centre. We do not see this in our results, likely because the protostars in our model are at different stages of evolution at a certain time, so this effect, if existent, is covered by the strongly time-dependent variation in the accretion rate. Also the evolution of $\dot{M}$ with time in their models differs from our results: the mean accretion rate reported by Bonnell et al. (2001a), determined from all protostars in the cluster, increases with time until near the end of the simulation when the gas is significantly depleted. The difference is probably caused by the different assumptions (e.g. lack of turbulence, clustered potential). Indeed, the recent models of Bonnell et al. (2003) produce nearly constant accretion rates onto the most massive stars in the cluster. The difference might be due to the fact that the accretion rates are determined by the accretion onto the cluster from outside, while in the models of Bonnell et al. (2001a) all the mass was already in the cluster.

Reid et al. (2002) used a logatropic equation of state as the basis for their hydrodynamical simulations of isolated star formation. Their accretion rate depends on the size of the core. It increases cubically and reaches maximum when the expansion wave leaves the core, then it falls steadily. With the adopted scaling, $\dot{M}_{\rm max}$ is one to two orders of magnitude smaller than in our models. Consequently the whole accretion process lasts much longer, several 106 years, which is in contradiction to estimates of rapid star formation (Elmegreen 2000; Hartmann et al. 2001; Hartmann 2003; Mac Low & Klessen 2004).

Wuchterl & Tscharnuter (2003) find, from models based on radiation hydrodynamics, time-varying accretion rates of a few $10^{-6}\ {M_{\hbox{$\odot$ }}\rm ~yr^{-1}}$ for the phase ${<} 0.8~M_{\rm end}$, which is about an order of magnitude lower than our values, especially for Gaussian collapse or large-scale turbulence. The reason may be that protostellar cores in our models form by external compression before gravity takes over. This results in enhanced accretion rates relative to cores that begin contraction close to hydrostatic equilibrium.

Hennebelle et al. (2003) performed numerical simulations where the collapse is triggered by a steady increase in the external pressure. $\dot{M}_{\rm max}$ is reached immediately after the formation of the central protostar (i.e. during Class 0 phase), followed by a steady decrease to the Class I phase. The more rapid and the more prolonged the increase in external pressure, the higher is  $\dot{M}_{\rm max}$, ranging from $6.5 \times 10^{-6}\ {M_{\hbox{$\odot$ }}\rm ~yr^{-1}}$ to $2.6 \times 10^{-5}\ {M_{\hbox{$\odot$ }}\rm ~yr^{-1}}$, corresponding to ${\sim} (4{-}16)~c_{\rm s}^3/G$. The qualitative behaviour of the accretion process does not differ much from our models, but the peak accretion rates are slightly smaller except in their models with the most rapid compression.

  
5 Comparison with observations

It is very difficult to measure mass accretion rates directly from observations (e.g. from inverse P Cygni profiles), instead they often have to be inferred indirectly based on the spectral energy distributions (SEDs) of protostars or using outflow characteristics (Hartigan et al. 1995; Bontemps et al. 1996). The correlation between accretion rates and outflow strength, however, is still subject of strong debate (Wolf-Chase et al. 2003). For Class 0 objects typical mass accretion rates are estimated in the range $10^{-5} \la \dot{M}/{ M_{\hbox{$\odot$ }}~\rm yr^{-1}} \la 10^{-4}$ (Hartmann 1998; Narayanan et al. 1998; André et al. 1999; Ceccarelli et al. 2000; Jayawardhana et al. 2001; Di Francesco et al. 2001; Maret et al. 2002; Beuther et al. 2002a,b). The growth rate of Class I objects is believed to be about an order of magnitude smaller (Henriksen et al. 1997; André et al. 2000), with observational values between ${\sim} 10^{-7}$ and ${\sim} 5 \times 10^{-6}\ {M_{\hbox{$\odot$ }}~\rm yr^{-1}}$ (Brown & Chandler 1999; Greene & Lada 2002; Boogert et al. 2002; Yokogawa et al. 2003; Young et al. 2003).

Bontemps et al. (1996) studied the outflow activities in a sample of 45 low-mass embedded young stellar objects. They estimate that the observed decline of CO outflow momentum fluxes with time results from a decrease of the mass accretion rate from ${\sim} 10^{-5}\ {M_{\hbox{$\odot$ }}\rm ~yr^{-1}}$ for the youngest Class 0 protostars to ${\sim} 10^{-7}\ {M_{\hbox{$\odot$ }}\rm ~yr^{-1}}$ for the most evolved Class I objects. Furthermore, they propose a simple exponential dependency of the accretion rate with time: $\dot{M} = (M_{\rm env}^0 / \tau) {\rm e}^{-t/\tau}$with initial mass of the dense clump $M_{\rm env}^0$ and a characteristic time $\tau \approx 9 \times 10^4~{\rm yr}$. This is comparable to our Eq. (5). A similar exponential equation is also used by Myers et al. (1998), while Henriksen et al. (1997) describe the accretion rate by an equation that asymptotically approaches a power-law dependence at late times.

Brown & Chandler (1999), who determined an upper limit of $\dot{M}\la (2{-}4) \times 10^{-7}\ { M_{\hbox{$\odot$ }}~\rm yr^{-1}}$ for two Class I protostars in Taurus, also conclude that the accretion rate is not constant in time and likely is much higher in the early phase. On the other hand, Hirano et al. (2003) observed a dozen of deeply embedded young stellar objects of both Class 0 and I and derived the same mass accretion rates of $(1{-}5) \times 10^{-6}\ {M_{\hbox{$\odot$ }}\rm ~yr^{-1}}$for all of them. Unlike other authors, they argue that there is no significant difference in $\dot{M}$ between Class 0 and Class I sources.

The values given above correspond to the accretion rates derived for the model of gravoturbulent star formation discussed here. They also decrease from 10-5 to $ 10^{-4}\ M_{\hbox{$\odot$ }}{\rm ~yr^{-1}}$during the Class 0 phase to less than $10^{-7}\ { M_{\hbox{$\odot$ }}~\rm yr^{-1}}$ in later stages. However, the supposed transition between Class 0 and Class I still takes place during the peak accretion phase. The accretion rates in our models typically do not decline significantly until about 80% of the final mass has been accreted (Fig. 1). This is unlike e.g. the model of Reid et al. (2002), where $\dot{M}$begins to fall off when about half of the mass of the core has been accreted. Given the uncertainties of the mass estimate for the Class 0/I transition we do not consider this a large discrepancy.

According to observations, Class 0 objects have an estimated lifetime of ${\sim} (1 {-} 3) \times 10^4$ yr (André et al. 2000). In our models this parameter is widely spread, ranging from ${\sim} 10^4$ to > 105 yr, but for a 1  $M_{\hbox {$\odot $ }}$ star it lies roughly in the range deduced from observations (see Fig. 5).

   
6 Summary

We have studied protostellar mass accretion rates from numerical models of star formation based on gravoturbulent fragmentation. Twenty-four models covering a wide range of environmental conditions from low to high turbulent velocities and different driving scales with a total number of 1325 protostellar cores have been investigated. Our main results may be summarised as follows:

1.
An order-of-magnitude estimate for mass accretion rates resulting from gravoturbulent fragmentation is given by $\dot{M} \approx M_{\rm J} / \tau_{\rm ff}$ with $M_{\rm J}$being the mean thermal Jeans mass and $\tau_{\rm ff}$ the corresponding free-fall time.

2.
However, protostellar mass accretion is a highly time-variant process. It can be approximated by the empirical function $\log \dot{M}(t) = \log \dot{M}_0~({e}/\tau)~t~{\rm e}^{-t/\tau}$. The peak accretion rate is reached during the Class 0 stage, shortly after the formation of the core; its value ranges between about $5 \times 10^{-6}$ and $10^{-4}\ {M_{\hbox{$\odot$ }}~\rm yr^{-1}}$. The maximum accretion rate is approximately one order of magnitude higher than the constant rate predicted by the collapse of a classical singular isothermal sphere.

3.
Around the peak accretion phase the mass accretion rates are roughly constant. The mean accretion rates increase with increasing final mass. More massive stars have higher mass accretion rates and tend to form first.

4.
The same applies to the fitted peak accretion rates, which are also proportional to the final stellar mass.

5.
There is a similar correlation between the duration of Class 0 phase (assuming that half of the final mass is accreted in this phase) and the final mass.
6.
$\langle \dot{M} \rangle$ $_{\rm mean}$ decreases with increasing Mach number of the turbulent environment, but is not correlated with the driving wavenumber.

Our results agree well with many other models treating the time evolution of the mass accretion process and the value of the peak accretion rate. In particular, the accretion rates from our models show an exponential decline, as also proposed by Bontemps et al. (1996), Myers et al. (1998) and Smith (1999, 2000). They also match observational findings like the supposed decline of the mass accretion rate from the Class 0 to Class I phase. We conclude that a theory of star formation based on gravoturbulent fragmentation of molecular clouds is an adequate approach to describe stellar birth in the Milky Way.

Acknowledgements
This work was supported by the Emmy Noether Programme of the Deutsche Forschungsgemeinschaft (grant No. KL1358/1). We are grateful to Dirk Froebrich and Philippe André for helpful remarks. We also wish to thank the referee Ian Bonnell for his insightful comments and suggestions.

References


Copyright ESO 2004