We use a spherical definition of the
Jeans mass,
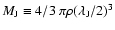 ,
with density
,
with density 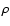 and Jeans length
and Jeans length
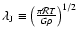 and where G and
and where G and
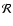 are the gravitational and the gas constant. The mean Jeans
mass
are the gravitational and the gas constant. The mean Jeans
mass
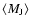 is then determined from the average
density in the system
is then determined from the average
density in the system
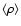 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.