A&A 418, 151-162 (2004)
DOI: 10.1051/0004-6361:20040057

Are dust shell models well-suited to explain interferometric data of late-type stars in the near-infrared?

P. Schuller1,2 - P. Salomé3 - G. Perrin4 - B. Mennesson5 - G. Niccolini6 - P. de Laverny6 - S. T. Ridgway4,7 - V. Coudé du Foresto4 - W. A. Traub2


1 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
2 - Harvard-Smithsonian Center for Astrophysics, MS-20, 60 Garden Street, Cambridge, MA 02138, USA
3 - Observatoire de Paris, LERMA, 61 avenue de l'Observatoire, 75014 Paris, France
4 - Observatoire de Paris, LESIA, 5 place Jules Janssen, 92195 Meudon, France
5 - Jet Propulsion Laboratory, MS 306-388, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
6 - Observatoire de la Côte d'Azur, Département Fresnel UMR 6528, BP 4229, 06304 Nice, France
7 - National Optical Astronomy Observatories, PO Box 26732, Tucson, AZ 85726, USA

Received 13 March 2003 / Accepted 15 January 2004

Abstract
Recently available near-infrared interferometric data on late-type stars show a strong increase of diameter for asymptotic giant branch (AGB) stars between the K ( $2.0{-}2.4~{\rm\mu m}$) and L ( $3.4{-}4.1~{\rm\mu m}$) bands. Aiming at an explanation of these findings, we chose the objects $\alpha $ Orionis (Betelgeuse), SW Virginis, and R Leonis, which are of different spectral types and stages of evolution, and which are surrounded by circumstellar envelopes with different optical thicknesses. For these stars, we compared observations with spherically symmetric dust shell models. Photometric and  $11~{\rm\mu m}$ interferometric data were also taken into account to further constrain the models. - We find the following results. For all three AGB stars, the photosphere and dust shell model is consistent with the multi-wavelength photometric data. For $\alpha $ Orionis the model dust shell has a very small optical depth (0.0065 at $11~{\rm\mu m}$); the visibility data and model in K and L are essentially entirely photospheric with no significant contribution from the dust, and the visibility data at $11~{\rm\mu m}$ show a strong dust signature which agrees with the model. For SW Virginis the model dust shell has a small optical depth (0.045 at  $11~{\rm\mu m}$); in K the visibility data and model are essentially purely photospheric, in L the visibility data demand a larger object than the photosphere plus dust model allows, and at  $11~{\rm\mu m}$ there was no data available. For R Leonis the model dust shell has a moderate optical depth (0.1 at  $11~{\rm\mu m}$); in K and L the visibility data and model situation is similar to that of SW Vir, and at  $11~{\rm\mu m}$ the visibility data and model are in agreement. - We conclude that AGB models comprising a photosphere and dust shell, although consistent with SED data and also interferometric data in K and at $11~{\rm\mu m}$, cannot explain the visibility data in L; an additional source of model opacity, possibly related to a gas component, is needed in L to be consistent with the visibility data.

Key words: techniques: interferometric - radiative transfer - infrared: stars - stars: late-type - stars: circumstellar matter - stars: individual: $\alpha $ Orionis, SW Virginis, R Leonis

  
1 Introduction

Supergiant stars and stars on the Asymptotic Giant Branch (AGB) are surrounded by a dust envelope coupled with gas; for example, see Habing (1996) for a review of these objects, Willson (2000) for a review of mass loss, and Tsuji (2000) for evidence of H2O shells around supergiants.

AGB stars are subject to pulsation and other surface phenomena (shock waves, acoustic waves etc., see Lafon & Berruyer 1991) that levitate matter above the stellar photosphere. Dust grains appear in the envelope at altitudes where the temperature falls below the condensation temperature. The radiation pressure drives the dust grain overflow far from the star up to distances of a thousand stellar radii causing mass-loss.

The mechanism for mass loss in supergiants is not so clear. The main difference compared to Mira stars is that due to the larger luminosity of supergiants the atmosphere is much more extended and has a much greater pressure scale height. Therefore, the mass loss may have a different driving force although pulsation may also play a role.

Both kinds of stars are characterised by their large diameter and strong luminosity and are consequently very good candidates for infrared interferometry. In the next section, we briefly present the instruments which were used to acquire the interferometric data discussed in this paper, namely FLUOR in the K band ( $2.0{-}2.4~{\rm\mu m}$) and TISIS in the L band ( $3.4{-}4.1~{\rm\mu m}$). We selected three particular stars of three different types for which we have a substantial set of data: the supergiant $\alpha $ Ori, the semi-regular SW Vir, and the Mira-type star R Leo. Furthermore, their envelopes have quite differing optical thicknesses. It appears that for the objects with large optical depth (SW Vir and R Leo) the observed diameters in L are considerably larger than the respective K band diameters (see Sect. 2.3). Measurements in the L band are more sensitive to cooler material above the stellar photosphere than are the K band data. The question is: what is the physical nature of these layers? One possibility might be astronomical dust. Dust reprocesses the star radiation, in particular in the infrared. Depending on the dust abundance, the star's L band radiation might be superposed by a dust contribution that probes the inner region of the dust envelope at a few stellar radii away from the star. The measured L band radius might consequently be increased compared to the K band, which is mainly fed by stellar emission.

In Sect. 3, the modelling of the dust envelopes around these stars by a radiative transfer code is explained and the parameters of the model are described. In Sect. 4, we compare the model output with the interferometric and photometric data. Finally, in Sect. 5 we discuss the limits of such models and the questions they raise about the L band observations.

  
2 Observations and data reduction

  
2.1 Instruments used

The stars discussed here were observed with the IOTA (Infrared-Optical Telescope Array) interferometer operating (at that time) with two telescopes (Traub 1998). IOTA is located at the Smithsonian Institution's Whipple Observatory on Mount Hopkins, Arizona. It offers multiple baseline observations providing visibilities at different spatial frequencies. This enables a model-fit to the visibility data to obtain information on the spatial intensity distribution of the sources. The beams were combined with FLUOR (Fiber Linked Unit for Optical Recombination) in the K band (Coudé du Foresto et al. 1998) and with its extension to the L band TISIS (Thermal Infrared Stellar Interferometric Set-up, Mennesson et al. 1999). Beam combination with FLUOR is achieved by a single-mode fluoride glass triple coupler. The fibres filter the wavefronts corrugated by the atmospheric turbulence. The phase fluctuations are traded against photometric fluctuations which are monitored for each beam to correct for them a posteriori. The accuracy on visibility estimates measured by FLUOR is usually better than 1% for most sources (Perrin et al. 1998) and can be as good as 0.2% (Perrin 2003).

TISIS is the extension of FLUOR to the thermal infrared ( $3.4{-}4.1~{\rm\mu m}$). A single coupler is used as beam combiner and photometric signals are not monitored. Approximate correction of turbulence-induced flux fluctuations is achieved with the low-frequency part of the interferometric signal. Accuracy in the L band is therefore not as good as in the K band, but still better than without spatial filtering by fibres. The acquisition protocol is also different from that of the K band, since ground-based interferometric observations encounter a new difficulty at  $3.6~{\rm\mu m}$. Thermal background emission produces a fluctuating photometric offset which must be correctly subtracted in order to achieve a good calibration. Hence each source observation must be bracketed by a sky background measurement (chopping) that reduces the instrument efficiency.

  
2.2 Data selection

Table 1: Some basic parameters of the studied objects taken from the General Catalogue of Variable Stars (Kholopov et al. 1998). The distances come from the HIPPARCOS catalogue (Perryman et al. 1997).

We chose to include three stars in our study which span different spectral types and stages of evolution, namely the supergiant $\alpha $ Orionis (Betelgeuse), the semi-regular variable SW Virginis, and the Mira star R Leonis. Some basic parameters of these objects are compiled in Table 1. These stars are also some of the most observed in our sample. The L band data are extracted from Chagnon et al. (2002) - we have used the data from the February-March 2000 observations. The K band data for $\alpha $ Orionis were presented in Perrin et al. (2003a) and observations cover the period February 1996 to March 1997. The K band data for SW Virginis were collected in May 2000 and are presented in Perrin (2003). Lastly, the K band data for R Leonis were published in Perrin et al. (1999) and were collected in April 1996 and March 1997. Except for SW Virginis, there is a large time difference between the dates of the L band and K band data acquisitions. We believe this to not be a major issue - although these stars are known to be variable, the effects we want to analyse are slower than the periodic changes of stars and larger in amplitude.

In order to get the best constraints on the dust shell model spatial distribution, we have included interferometric data acquired with ISI (Infrared Spatial Interferometer, Hale et al. 2000) at $11.15~{\rm\mu m}$ as published by Danchi et al. (1994).

A journal of all used data points is given in Table 2.

Table 2: Journal of interferometric data. K band (FLUOR) data for $\alpha $ Orionis have been presented in Perrin et al. (2003a), for SW Virginis in Perrin (2003), and for R Leonis in Perrin et al. (1999). All L band (TISIS) data were taken from Chagnon et al. (2002). The ISI data points for $\alpha $ Orionis and R Leonis were extracted from Danchi et al. (1994) using the DEXTER online tool at ADS (2003). No exact position angle was given along with the ISI data, therefore we indicated the basic geographic orientation of the baselines used. Where known for the objects, the phase $\Phi $ of the visual variability was indicated.

  
2.3 Uniform disk diameters

The visibilities Vi, and their standard deviations $\sigma_i$, in the K and L bands were fitted by a uniform disk model by minimising the quantity:

 \begin{displaymath} \chi^{2} = \sum_{i=1}^{n} \frac{\left(V_{i}-M({{\phi_{\rm UD}},S_{i}})\right)^{2}}{\sigma_{i}^{2}} \end{displaymath} (1)

where n is the number of available measurements in the respective band. M is the uniform disk model:

 \begin{displaymath} M({{\phi_{\rm UD}}, S_{i}}) = \left\vert\frac{2J_{1}(\pi\phi_{\rm UD} S_{i})}{\pi\phi_{\rm UD}S_{i}}\right\vert, \end{displaymath} (2)

with Si the spatial frequency and $\phi_{\rm UD}$ the uniform disk diameter. J1 is the Bessel function of first order.

The best fit uniform disk radii, and standard deviations, are listed in Table 3. The last column is the ratio of the L band and K band diameters. It is very close to 1 in the case of Betelgeuse, but the difference is 20-30% for the other two stars.

In the next sections, we investigate the possibility that dust envelopes around the star may be the cause for the diameter variations from K to L.

Table 3: Uniform disk radii $\phi $ in the L and K bands.

  
3 Modelling of the dust envelope

The models used in this paper are based on a radiative transfer code maintained at the Observatoire de la Côte d'Azur in Nice, France. A description of the code is presented by Niccolini et al. (2003). We discuss hereafter the main hypotheses and parameters of this model.

  
3.1 Description of the radiative transfer code

The code is based on the modelling of stellar radiation and circumstellar dust envelope interaction by a Monte Carlo method, assuming thermal equilibrium. The star is assumed to be a blackbody whose emitted energy is split in a number of packets, or "photons''. These photons can either pass the envelope directly, or they are scattered once or more in the envelope, or the photons are absorbed and then thermally re-emitted by the dust grains. A grid over the dust envelope is defined with radial zones and angular sections, with the resolution accounting for expected temperature gradients. From the resulting temperature profile, the code derives the spectral energy distribution (SED) for the three individual photon flux contributions mentioned above. Initially, the stellar radius is left as scaling factor. Assigning a specific stellar radius, the total SED can be compared to photometric data in order to constrain the model. Absorption, emission, and scattering by gaseous components are not taken into account.

Furthermore, the spatial flux distribution at a given wavelength can be derived, i.e., a model image of the object at this wavelength can be created. The Fourier transform of the model image can be compared to visibilities measured at that wavelength which yields a further constraint to the model. For the purpose of producing the image, the code allows a zooming factor while the image dimensions are always fixed at  $300\times 300$ pixels.

  
3.2 Parameters of the envelope

The code offers several parameters that can be chosen. The size distribution s(a) of spherical dust particles having the radius a was set as  $s(a) \sim a^{-3.5}$, according to the interstellar medium (Mathis et al. 1977) and independent of the distance from the star. The radius a was contained in the range $0.005{-}0.25~{\rm\mu m}$.

The particle density distribution n(r) of the dust grains that was used in this study includes acceleration effects on dust by radiation pressure and gas drag (see Appendix A). The resulting density distribution is much more peaked at the inner edge of the envelope than is a r-2 distribution.

For our study, the dust particle material was constrained to astronomical silicates. Their complex dielectric function (respectively complex refractive index) is given by Draine & Lee (1984). It was sampled at 37 wavelengths between  $0.1~{\rm\mu m}$ and  $300~{\rm\mu m}$, with the sample points considering local extrema.

The previously mentioned parameters were chosen in consistency with the relevant subset of studies reported by Danchi et al. (1994). They were set and fixed in this study. To fit the model to the data, the following input parameters were adjusted. The stellar radius $R_\star $ and the stellar effective temperature $T_\star $ govern the flux radiated by the star. Spherical symmetry was assumed for a dust shell around the star with an inner radius $r_{\rm i}$ and an outer radius $r_{\rm o}$, in units of $R_\star $. Furthermore, the envelope is characterised by its optical depth, $\tau_\lambda$, which is defined for overall extinction (absorption and scattering). It can be chosen at a given wavelength, $\lambda$, expressed in $\mu$m.

Since the code, as used for this study, does not take into account possible changes of the dust properties when heated beyond the dust condensation temperature, the temperature map has to be checked accordingly for each set of parameters. As condensation temperature for silicates, we adopted $T_{\rm cond}\approx 1000~{\rm K}$ (Gail & Sedlmayr 1998).

   
4 Comparison between model and observations

We now study the case of three particular stars. The question is whether a simple spherical dust shell model can account for the large diameter differences observed in the K and L bands. The goal is to find the stellar parameters for which visibility points in the K and L bands and at  $11~{\rm\mu m}$ are compatible and simultaneously in agreement with the photometric data.

  
4.1 A supergiant: $\alpha $ Orionis

Betelgeuse is a Semi-Regular (SRc) variable star of spectral type M 1I. It is a late-type supergiant star with a 2335-day period (see Table 1).

The mass-loss rate $\dot{M}$ of $\alpha $ Orionis is moderate. Knapp et al. (1998) estimate a mass-loss rate from CO emission measurements of  $3.1\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$ at HIPPARCOS distance and with an outflow velocity  $v_{\rm o}=14.2~{\rm km}~{\rm s}^{-1}$. Throughout this study, we adopt terminal outflow velocities from their work. For a distance d of  $150~{\rm p }$ and an outflow velocity  $v_{\rm o}=15~{\rm km}~{\rm s}^{-1}$, Danchi et al. (1994) yield a mass-loss rate of $17\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$. With the HIPPARCOS parallax of  $7.63~{\rm mas}$ yielding a distance of  $131~{\rm pc}$, and  $\dot{M}\propto v_{\rm o}~ d$, their mass-loss rate is updated to  $14\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$, which is given in Table 4.

Table 4: Mass-loss rate comparison. The values for $v_{\rm o}$ come from Knapp et al. (1998). Data from Danchi et al. were re-evaluated at HIPPARCOS distance (see Table 1) following $\dot{M}\propto v_{\rm o}~ d$.

Observational data

We used low spectral resolution data from different catalogues available at the SIMBAD (2003) Astronomical Database to constrain the SED over a large range of wavelengths. The TD1 catalogue provides fluxes around  $0.2~{\rm\mu m}$. UBV measurements are reported in the GEN and UBV catalogues. Fluxes in the UBVRIJHKL bands are taken from the JP11 Johnson catalogue. The 12, 25, 60, and  $100~{\rm\mu m}$ fluxes are from the IRAS catalogue, and Danchi et al. (1994) provide flux curves from 8 to  $22~{\rm\mu m}$.

For Betelgeuse, having slight luminosity variations, we can easily compare visibility points from different epochs. This assumption will be fully justified by the fit we obtain.

Parameters

Danchi et al. (1994) propose a spherical dust shell model to account for ISI data in the thermal infrared. This shell is supposed to have a small extent ( $r_{\rm i}=45.9~R_\star$, $r_{\rm o}=48.2~R_\star$) quite far away from the central star and to be optically very thin ( $\tau _{11}=0.0065$). It seems to indicate an episodic mass-loss process, leading to an empty area between the star and its envelope. We used these parameters (see Table 5) to reproduce the shorter wavelength visibility points given by FLUOR and TISIS.

Table 5: Parameters adjusted for modelling (see Sect. 3.2). $T_\star $: stellar temperature; $R_\star $: stellar radius; $r_{\rm i}, r_{\rm o}$: inner respectively outer radius of dust shell; $\tau _{11}$: optical depth of shell at $11~{\rm\mu m}$. In all cases, an accelerated dust density profile was used.

The effective stellar temperature of $3640~{\rm K}$ used by Danchi et al. (1994) is fully consistent with the evaluation by Perrin et al. (2003a) giving $3640~{\rm K}$ and  $3690~{\rm K}$ depending on models. The stellar radius used in that model is $21.8~{\rm mas}$, satisfactorily accounting for both the photometric data and interferometric data in the three bands. This radius is close to the uniform disk model radii in the K and L bands of $21.6~{\rm mas}$ and $21.4~{\rm mas}$, respectively.

Results


  \begin{figure} \par\includegraphics[width=8cm,height=7.5cm,clip]{3722-f1a}\hspac... ...ce*{2mm} \includegraphics[width=8.5cm,height=7.5cm,clip]{3722-f1d} \end{figure} Figure 1: Model output for $\alpha $ Ori. From top left to bottom left: modelled visibility curve with interferometric data for the bands K, L, and N; bottom right: modelled spectral energy distribution with photometric data. Model parameters (see Table 5): $T_\star=3640~{\rm K}$, $R_\star=21.8~{\rm mas}$, $r_{\rm i}=45.9~R_\star$, $r_{\rm o}=48.2~R_\star$, and $\tau _{11}=0.0065$.
Open with DEXTER

The SED of the model is shown in Fig. 1. Apart from the total flux from the object, the plot also contains the contributions of the stellar flux attenuated by the circumstellar shell, the distribution of the flux scattered by the dust grains in the shell (maximum at short wavelength), and the thermal emission of the grains (maximum at longer wavelength). As the SED shows, stellar radiation is prominent over a large wavelength range. Flux emitted by dust becomes prominent only in a small band around $10~{\rm\mu m}$.

Visibility curves are also plotted in Fig. 1. The K and L band visibility curves from the dust shell model resemble each other and show good superposition with the respective visibility curves of the uniform disk model. Apparently, the same structure is seen in these two bands. The SED plot indicates that this should be the stellar photosphere since in these two bands the direct stellar flux is roughly 103 times larger than the scattered part and about 105 times larger than the dust emission. One can conclude that the dust envelope, having a very small optical depth, has little influence on the intensity distribution at these wavelengths. The dust shell is transparent in K and L and the star is seen through the dust at these wavelengths. As a consequence, the dust shell model derived from the ISI data is fully consistent with the FLUOR and TISIS measurements.

As a further consistency check, yet with minor priority, we computed a mass-loss rate $\dot{M}$ from our model parameters by a method similar to Danchi et al. (1994) (see Appendix A for details). With the set of parameters for $\alpha $ Ori, we obtain a mass-loss rate of $17\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$, consistent with Danchi et al. (1994) and roughly a factor of 5 higher than that of Knapp et al. (1998).

Although $\alpha $ Ori has the lowest optical depth of the studied objects, its mass-loss rate seems to be the highest. The parameters used here indicate an episodic event in the past. Yet, since this event the dust shell has expanded, with its enlarged inner radius entering the computation. For a further discussion of the mass-loss event see Danchi et al. (1994).

We now study the case of stars with circumstellar envelopes at higher optical depths.

  
4.2 A semi-regular variable: SW Virginis

The pulsation period of this M 7III semi-regular (SRb) variable star is 150 days. Its main characteristics are recapitulated in Table 1. The mass-loss rate is estimated by Knapp et al. (1998) to $1.7\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$.

Observational data

Photometric data are retrieved from the IRC catalogue for the I and K bands, from the UBV catalogue in the respective filters, from the IRAS catalogue at 12, 60, $100~{\rm\mu m}$, and from Monnier et al. (1998) in the 8 to  $13~{\rm\mu m}$ range. The M band flux at  $5~{\rm\mu m}$ comes from Wannier & Sahai (1986).

To date, no 11- ${\rm\mu m}$ interferometric data is available for SW Virginis. Benson et al. (1989) report observations by speckle interferometry in the N band at spatial frequencies below $2\times 10^{5}~{\rm rad^{-1}}$. Since they do not provide measured data directly, but rather give some model parameters, this has not been considered here. It is therefore not possible to assess the consistency of the spatial model between all bands for this object.

Parameters

For SW Vir, Perrin et al. (1998) give an effective temperature of $2921\pm 100~{\rm K}$, as derived from the bolometric flux and the limb-darkened diameter. Consistent with this value, the effective temperature was set to  $2800~{\rm K}$. For the parameters of the dust shell we chose to adopt $r_{\rm i}=15.0~R_\star$ and $r_{\rm o}=1000~R_\star$, as proposed by van der Veen et al. (1995) on the basis of sub-mm observations. Applying an optical depth  $\tau _{11}=0.045$ and assuming a stellar radius of  $8.65~{\rm mas}$ then accounts for flux data at low spectral resolution.

Danchi et al. (1994) make a distinction between two classes of objects. The first class has a cold circumstellar envelope far from the star (beyond 10 stellar radii), while objects of the second class are surrounded by a warmer dust envelope, near the star (at about 2 or 3 stellar radii). The mass-loss process is different for these two classes. For the second class, the mass-loss process is more continuous than for the first one. SW Virginis has been classified in the past as a Mira star, hence with a somewhat regular mass-loss. Yet, its current classification as a semi-regular variable, possibly a precursor of a Mira star, makes its mass-loss more likely to be irregular, consistently with its irregular photometric variations. It is therefore very tempting to identify it as a member of the first class. The preferred set of parameters obtained for this star is summarised in Table 5. A large optical depth and a large shell extent are necessary to reproduce the photometric contribution of dust at large wavelengths.

Results


  \begin{figure} \par\includegraphics[width=8cm,height=7.5cm,clip]{3722-f2a}\hspac... ...ce*{2mm} \includegraphics[width=8.5cm,height=7.5cm,clip]{3722-f2d} \end{figure} Figure 2: Model output for SW Vir. Top left and right: modelled visibility curve with interferometric data for the K and L bands; bottom left: expected visibility curve for the N band; bottom right: modelled spectral energy distribution with photometric data. Model parameters (see Table 5): $T_\star=2800~{\rm K}$, $R_\star=8.65~{\rm mas}$, $r_{\rm i}=15.0~R_\star$, $r_{\rm o}=1000~R_\star$, and $\tau _{11}=0.045$.
Open with DEXTER

As Fig. 2 shows, the contribution of dust emission to the SED in the K and L bands of SW Virginis is more important than in the case of $\alpha $ Ori, i.e., it is higher in relation to the direct flux. This can be attributed to the larger optical depth. SW Virginis has some infrared excess that requires a dust shell. However, the dust cannot be too warm, otherwise it would produce a much larger infrared excess than is compatible with the SED.

From this model, visibility curves were derived. Although comparatively few visibility measurements are available for this object, it is obvious that the single dust shell model is not simultaneously compatible with the K and L band data. Again, model visibility curves are similar in K and L which lets us assume that we see the same structure, i.e. the stellar photosphere. This is also reflected by the SED for which a similar reasoning applies like in the case of $\alpha $ Ori. Indeed, the dust being quite far away from the photosphere, the K band data are well reproduced by the visibility model. However, the dust is too cold and optically too thin to lead to a significant increase of the diameter at larger wavelengths compatible with the L band data. A simple dust shell model, therefore, cannot account for both the interferometric and the photometric data. Unfortunately, no ISI data are available for this star. They would have been very useful to help model the dust shell and place stronger constraints on it.

The mass-loss rate we obtain from our parameters is $1.4\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$, which is roughly consistent with the one of Knapp et al. (1998).

  
4.3 A Mira-type variable: R Leonis

R Leonis is a Mira-type long-period variable with a period of $\sim$310 days and of late spectral type M 8IIIe (see Table 1). Its mass-loss rate is indicated by Knapp et al. (1998) as $0.94\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$, whereas the estimate by Danchi et al. (1994) can be updated to $0.60\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$.

R Leonis is known to have a very strong infrared excess and very steady pulsations which makes it very different from SW Virginis. R Leonis shows large photometric variations, especially at short wavelengths. The problem here is to synthesise a low spectral resolution SED, as well as visibility curves, for a star with large photometric variations. Nevertheless, we decided to include all available data points (both photometric and interferometric) into the plots despite the object variability which will allow a larger range of acceptable model parameters.

Observational data

For R Leonis, UBV measurements can be found in the GEN and UBV catalogues. The JP11 Johnson catalogue provides magnitudes in the BVRIJKL bands. Strecker et al. (1978) observed this object between 1.2 and  $4.0~{\rm\mu m}$. The fluxes at 12, 20, 60 and  $100~{\rm\mu m}$ are from IRAS, and fluxes between 8 and  $20~{\rm\mu m}$ come from Danchi et al. (1994).

  
Parameters

The effective temperature that accounts for the photometric data is about  $2500~{\rm K}$, a bit more than the temperature of  $2000~{\rm K}$ assumed by Danchi et al. (1994) for their model containing only silicate dust around R Leo. The stellar radius is clearly smaller ( $14.9~{\rm mas}$ instead of  $19.8~{\rm mas}$). However, we have estimated these two parameters with all data combined (interferometric data in the K and N bands and the spectro-photometric data), and they show good consistency (in as much as the star is neither a perfect blackbody nor a uniform disk) with those derived from the K band interferometric data alone by Perrin et al. (1999), who give uniform disk radii of at most $\sim$ $15~{\rm mas}$ and photosphere effective temperatures closer to  $3000~{\rm K}$ rather than  $2000~{\rm K}$. Our effective temperature is larger than that of Danchi et al. which is not surprising since in their case only photometric data above  $8~{\rm\mu m}$ was used, i.e., in a range of wavelengths very sensitive to cool dust emission. This also explains why their stellar radius is larger: for a given bolometric flux, the stellar diameter increases with decreasing temperature.

As in Danchi et al. (1994), we consider a large circumstellar envelope near the central star. But instead of 2 $R_\star $ for the inner edge of the dust shell, we chose 3.5 $R_\star $ to keep the temperature of the grains close to  $1000~{\rm K}$, the assumed temperature of grain condensation. The overall parameters are summarised in Table 5.

Results


  \begin{figure} \par\includegraphics[width=8cm,height=7.5cm,clip]{3722-f3a}\hspac... ...ce*{2mm} \includegraphics[width=8.5cm,height=7.5cm,clip]{3722-f3d} \end{figure} Figure 3: Model output for R Leo. From top left to bottom left: modelled visibility curve with interferometric data for the bands K, L, and N; bottom right: modelled spectral energy distribution with photometric data. Model parameters (see Table 5): $T_\star=2500~{\rm K}$, $R_\star=14.9~{\rm mas}$, $r_{\rm i}=3.5~R_\star$, $r_{\rm o}=140~R_\star$, and  $\tau _{11}=0.1$.
Open with DEXTER

The fit of the photometric data described in the previous section is displayed in Fig. 3. The contribution of the envelope dominates beyond  $10~{\rm\mu m}$ up to about  $30~{\rm\mu m}$. With a quite large extent, up to 140 $R_\star $, and an optical depth  $\tau _{11}=0.1$the dust shell accounts for IRAS and Danchi et al. (1994) observations in the long wavelength range. As can be noticed in the graph, scattered flux and thermal dust emission are even more important than for SW Vir. This is apparently due to the larger optical depth and the smaller inner radius of the envelope. These parameters lead to a mass-loss rate of  $0.77\times 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$, which is of the same order of and intermediate between the values published by Danchi et al. (1994) and Knapp et al. (1998) (see Table 4).

Visibility curves gained from this model are also shown in Fig. 3 for the K, L, and N bands respectively. The stellar radius derived from our model is  $14.9~{\rm mas}$, much smaller than the $19.8~{\rm mas}$ of Danchi et al. (1994). Since our study is based on interferometric data spanning a wider range of wavelengths, the parameters we derive are different from that of Danchi et al. (1994) The ISI data are better suited to characterise the dust, yet the shorter-wavelength data bring more accurate stellar parameters, hence explaining the discrepancies between the two studies. The dust envelope structure may be considered as stationary with little sensitivity to stellar pulsation. FLUOR observations at phase 0.28 (March 1997) in K band give a uniform disk radius of  $15.34~{\rm mas}$ (Perrin et al. 1999). In principle, the K band measurements are more sensitive to regions very close to the photosphere. It therefore seems that the radius of R Leonis should be smaller than the evaluations by Danchi et al. (1994) and the difference between our estimate and that of Danchi et al. cannot be attributed to the star pulsation. This difference must be attributed to the difference of effective temperatures.

We now compare interferometric data in the K and L band and that of ISI. Our parameters are still consistent with the ISI visibility points at  $11~{\rm\mu m}$ and account for FLUOR observations in the K band at low spatial frequencies. It is to be noticed that, since the ISI visibility data are at low spatial frequencies, they are not as sensitive to the different models as are the visibilities at shorter wavelengths. This explains why they are consistent with both the Danchi et al. (1994) and our model. On the other hand, in the L band our model overestimates the measured visibility values. As in the case of SW Vir, it appears that the large structure seen in the L band is not well accounted for by a simple dust shell model, despite the even larger optical depth. Also the SED shows that contributions from the dust shell are at least a factor 102 below the direct stellar flux. A larger radius could explain both  $3.6~{\rm\mu m}$ and  $11~{\rm\mu m}$ observations, but would disagree with K band measurements and the SED.

  
5 Discussion

  
5.1 Obtained results

From what we have seen so far, the best consistency between the multiple band data and the dust shell model is obtained for $\alpha $ Ori. The model described by Danchi et al. (1994) has a stellar radius close to the K and L radii estimated with a uniform disk model. Yet, in this case the influence of the envelope is not very important because of its small thickness and low opacity. Nevertheless, model parameters for ISI data from Danchi et al. are consistent with what we see both for K and L bands.

One may note, however, that Weiner et al. (2000) report further ISI data on $\alpha $ Ori which are not fully consistent with the model of Danchi et al. based on observations at low spatial frequencies. Weiner et al. took their measurements at higher spatial frequencies where the dust shell is fully resolved. Its contribution to the visibility is therefore negligible and the observed data are governed by radiation coming directly from the star or from its close environment. Like the L band data of SW Vir and R Leo (see below), the data of Weiner et al. are overestimated by the dust shell model. These findings are further discussed in Perrin et al. (2003a).

For AGB stars with later types like SW Vir and R Leo, for which we measure large diameter differences between  $2.15~{\rm\mu m}$ and  $3.77~{\rm\mu m}$ (the approximate effective wavelengths of the FLUOR and TISIS instruments), a simple dust shell model cannot account for these differences. However, the shape of near-infrared visibility curves for SW Vir and R Leo seem to show a trend. L band visibility points are systematically overestimated by a simple dust shell model meaning the source is larger than predicted by the model. This shows that the stellar environment mainly seen at this wavelength is much more complex than suggested by a model that takes into account only the star and its dust envelope.

Indeed, the temperature of this area is close to the temperature at which grains form. Consequently, we must also take the presence of gas into account in modelling. Doing this will radically change the radiation transfer behaviour. Recently, spectroscopic detection of SiO, OH, and H2O masers in late-type star envelopes have revealed the necessity of modelling the gas to explain large diameters seen in L band. ISO/SWS and other studies (Tsuji 2000; Yamamura et al. 1999; Tsuji et al. 1997) brought up the existence of molecular layers of warm and cold H2O, SiO, and CO2 around AGB stars. Such layers in AGB stars certainly exist and have an impact on the stellar radiation which is observed by infrared interferometers. Strong molecular scattering by H2O and CO were suggested to account for K band visibility measurements of R Leo by FLUOR in 1997 (Perrin et al. 1999) and seem to explain more easily the near-infrared measurements (Perrin et al. 2003b; Mennesson et al. 2002). It is very likely that dust needs to be coupled with gas to produce a more reliable model of these sources and that dust alone cannot be the only cause of the measurements taken in a wide range of wavelengths. The inclusion of a detailed photospheric model with line opacity due to gas would improve the agreement of the SED, particularly in the blue, and would improve the discrimination between stellar and shell components.

  
5.2 Data used

Certain aspects of our study can be further weighed. Simultaneous interferometric data would certainly help constrain models more accurately. Same epoch measurements are needed because of the large diameter variations of AGB stars. At least for the position angles it can be noted, though, that they are fairly close in range, which leaves little possibility that the discrepancy we see may be explained by an elliptical shape (see below). Furthermore, 11.15- ${\rm\mu m}$ data would have been very useful to see whether our SW Vir dust model parameters are correct since the envelope has more impact on the model at this wavelength. Such data might be provided in the near future by single-dish instruments on 10-m class telescopes or by upcoming mid-infrared interferometers like MIDI at the VLTI.

  
5.3 Model code parameters

A limitation of the model as used for this study is that it does not consider heterogeneous grain size distributions s(a) depending upon the distance from the star or temporal effects (like grain formation, growth, or destruction). Also, different limits of the grain radius a might have affected the fit of the SED in the UV and the far-infrared. Yet, varying the grain size range from $0.005{-}0.25~{\rm\mu m}$ to  $0.005{-}2.5~{\rm\mu m}$ and  $0.05{-}2.5~{\rm\mu m}$ for R Leo as a study case, the resulting diagrams showed only small changes. It appeared that, in the modelled visibility curves for the K and L bands, the contribution of spatial frequencies below  $20\times 10^5~{\rm rad}^{-1}$ were somewhat increased. Above all, neither the star nor the envelope are ideal blackbodies which adds to these deviations.

Concerning the particle density distribution n(r), Suh (1999) questions the necessity of assuming a distribution which is peaked at the inner edge. Indeed, comparing results of calculations with two sets of parameters that differ only in n(r) showed only minor changes in K and L bands. For  $11.15~{\rm\mu m}$, changes were somewhat clearer, whereby for $\alpha $ Ori and R Leo the accelerated version fitted ISI data better. Other issues are the possible existence of smaller structures in the envelope like clumps or aspherical dust distributions, as they were investigated, for example, by Lopez et al. (1997). These have not been tested here and require more intense visibility modelling. This would be definitely required if sources showed systematic asymmetric effects, yet which are likely to produce ringing features on top of a visibility curve compared to the more basic effect of radiative transfer in spherical shells. Nevertheless, closure phase observations could help test for asymmetries.

As for the dust particle material, slightly differing optical properties were proposed by several authors. See, for example, Suh (1999) for a comparison of optical properties of silicate dust grains in the envelopes around AGB stars. We chose the ones of Draine & Lee (1984) which are widely used. Using optical properties suggested by Suh (1999) for comparison made it necessary to choose different dust shell parameters in order to achieve reasonable consistency with ISI data. Yet, L band data were still overestimated, similar to Fig. 3. Another issue might be the dust composition. For example, for R Leo, Danchi et al. (1994) tested also a mixture of silicates and graphites. Yet, this led to a required stellar radius in the dust shell model almost twice as large as observed in the K band, which is supposedly sensitive to the region close to the stellar photosphere. Therefore, this has not been further investigated here. A third aspect might be the condensation temperature  $T_{\rm cond}$ that we adopted. Some authors chose higher  $T_{\rm cond}$, see, for example, Willson (2000) for an overview. Taking R Leo as study case, we set $r_{\rm i} = 2~R_\star$ and chose $r_{\rm o}$ and an optical depth $\tau _{11}$ so that also ISI data were well fitted. The output of the model showed a somewhat increased IR excess around  $11~{\rm\mu m}$, and the temperature at the inner radius turned out to be about  $1400~{\rm K}$. Still, while the SED, K band, and ISI data were reasonably well fitted, the modelled visibility curve in the L band was clearly higher than the measured data, similar to Fig. 3.

In summary, we do not believe the aspects mentioned above to affect our conclusions significantly.

  
6 Conclusions

High angular resolution techniques give important constraints on spatial intensity distribution of late-type stars. Using diameter measurements in the K and L bands, we have tried to explain both K and L observations for three stars surrounded by circumstellar envelopes with different optical depths. We applied a model with a single dust shell and consistent with low resolution photometric data as well as thermal infrared interferometry data from ISI when available.

For the supergiant Betelgeuse, the optically very thin dust shell has little influence on what is seen and is transparent in the K and L bands. The observed diameters are almost equal. In contrast, the AGB stars SW Vir and R Leo show bigger diameters in the L band than in the K band. Here, the optical depths of the shells are larger and near-infrared model visibilities react quite sensitively on changes of the dust shell parameters. Yet, the models we find in agreement with the SED, K band interferometry, and the specially dust-sensitive  $11~{\rm\mu m}$ interferometry cannot reproduce the observed diameter differences.

Our study leads to the conclusion of the insufficiency of a simple shell model with dust only or without more complex structures. New observations at several wavelengths from visible to far-infrared would help understand better external envelopes of AGB stars. A denser coverage of the spatial frequency plane will also be very useful to strongly constrain models. Interferometric observations with higher spectral resolution could enable to localise molecular components of these envelopes and certainly help explain differences between K and L band.

Acknowledgements
P. Sch. appreciated support by the European Community through a Marie Curie Training Fellowship for an extended stay at the Observatoire Paris-Meudon. It also allowed the collaboration with the Observatoire de la Côte d'Azur. - The authors are solely responsible for the information communicated.

This publication made use of NASA's Astrophysics Data System (ADS) Bibliographic Services (http://cdsads.u-strasbg.fr/) and of the SIMBAD database, operated at the Centre de Donné astronomiques de Strasbourg (CDS), Strasbourg, France (http://simbad.u-strasbg.fr/).

We thank the referee and Lee Anne Willson for helpful comments.

  
Appendix A: Evaluation of the mass-loss rate

Let $\dot{M}_{\rm dust}$ be the constant mass-loss rate of dust ejected from the star, $m_{\rm d}$ the average single dust grain mass, and n(r) the dust particle density, then at the inner edge $r_{\rm i}$ of the dust shell it holds that

 \begin{displaymath} \dot{M}_{\rm dust} = \frac{4\pi {r^2_{\rm i}} {\rm d}r \cd... ...\rm d}t} = 4\pi {r^2_{\rm i}} v_{\rm i} m_{\rm d} n_{\rm i}, \end{displaymath} (A.1)

where $v_{\rm i}$ is the dust outflow velocity and $n_{\rm i}=n(r_{\rm i})$ the particle density.

In the dust shell, the particle density of grains is assumed as (Schutte & Tielens 1989; Danchi et al. 1994)

 \begin{displaymath} n(r) = n_{\rm i} \cdot f(r) = n_{\rm i} \cdot \frac{r_{\rm i}^2}{r^2}\cdot \frac{1}{(1-A\cdot r_{\rm i}/r)^{1/2}} \end{displaymath} (A.2)

where the parameter

 \begin{displaymath} A = 1-(v_{\rm i}/v_{\rm o})^2 \end{displaymath} (A.3)

can be adapted to different cases. It is zero, if $v_{\rm i}$ is assumed to equal the terminal outflow velocity $v_{\rm o}$ of the dust far away from the star. In this case, the particle density simply follows  $n(r) \propto r^{-2}$. For taking into account acceleration of the dust by radiation pressure and coupling with the gas, $v_{\rm o}$ will be higher than $v_{\rm i}$. The parameter A will then be larger than in the first case and the particle density much more pronounced at $r_{\rm i}$. In the present study we chose A = 0.99, which applies for typical conditions (Danchi et al. 1994).

The optical depth $\tau_\lambda$ of the envelope is determined by

 
                         $\displaystyle \tau_{\lambda}$ = $\displaystyle \int_{r_{\rm i}}^{r_{\rm o}} C_{\rm ext}(\lambda) n(r)~{\rm d}r$  
  = $\displaystyle C_{\rm ext}(\lambda)~n_{\rm i} \int_{r_{\rm i}}^{r_{\rm o}} f(r)~{\rm d}r,$ (A.4)

where n(r) was replaced by (A.2). $C_{\rm ext}$ is the average extinction mean section of the dust grains. Replacing $n_{\rm i}$ in (A.1) by expression (A.4) yields a relation for the mass-loss rate by dust:

 \begin{displaymath} \dot{M}_{\rm dust} = \frac{4\pi {r^2_{\rm i}} v_{\rm i} m_... ...xt}(\lambda)\int_{r_{\rm i}}^{r_{\rm o}}{f(r)~{\rm d}r}}\cdot \end{displaymath} (A.5)

In the previous two expressions, $r_{\rm i}$, $r_{\rm o}$, and  $\tau_\lambda$ are the chosen model parameters. $C_{\rm ext}$ is calculated in the modelling code for a given grain size distribution from the optical properties of the dust by Mie theory (Niccolini et al. 2003). Likewise, the integral in (A.5) is performed by the code. The dust grain mass $m_{\rm d}$ has to be estimated by averaging the size distribution s(a) and defining the mass density. For the presently considered silicate dust, we chose as  $\rho_{\rm d}=3.3~{\rm g}~{\rm cm}^{-3}$ (also used by Draine & Lee 1984 and Danchi et al. 1994). The terminal velocity of the shell particles is taken from high-spectral resolution observations of CO lines (Knapp et al. 1998).

Furthermore, for the total mass-loss rate also the gas has to be taken into account, i.e.,

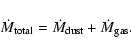\begin{displaymath}\dot{M}_{\rm total} = \dot{M}_{\rm dust}+\dot{M}_{\rm gas}. \end{displaymath} (A.6)

Gas-to-dust mass ratios are not well known and differ quite a lot. We adopted here, as typical value and assuming dust and gas to have the same terminal velocities (Schutte & Tielens 1989; Habing 1996; Danchi et al. 1994),

 \begin{displaymath} \dot{M}_{\rm gas} \approx 250~ \dot{M}_{\rm dust}. \end{displaymath} (A.7)

This means that most of the mass-loss is carried by gas. For  $\dot{M}_{\rm gas}$, an expression analogous to (A.1) can be given where $v_{\rm o}$ enters for $v_{\rm i}$. Considering (A.7), and therefore neglecting the mass-loss carried by dust, the total mass-loss rate is eventually

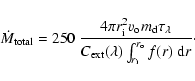\begin{displaymath}\dot{M}_{\rm total} = 250~ \frac{4\pi {r^2_{\rm i}} v_{\rm ... ...xt}(\lambda)\int_{r_{\rm i}}^{r_{\rm o}}{f(r)~{\rm d}r}}\cdot \end{displaymath} (A.8)

References


Copyright ESO 2004