A&A 417, 235-246 (2004)
DOI: 10.1051/0004-6361:20034203

Analysis of $\alpha$ Centauri AB including seismic constraints

P. Eggenberger¹ - C. Charbonnel^1,2 - S. Talon³ - G. Meynet¹ - A. Maeder¹ - F. Carrier¹ - G. Bourban¹

1 - Observatoire de Genève, 51 chemin des Maillettes, 1290 Sauverny, Suisse
2 - Laboratoire d'Astrophysique de Toulouse, CNRS UMR 5572, OMP, 14 Av. E. Belin, 31400 Toulouse, France
3 - Département de Physique, Université de Montréal, CP 6128, Station centre-ville, 2900 Bld. Édouard-Montpetit, Montréal PQ H3C 3J7, Canada

Received 15 August 2003 / Accepted 6 December 2003

Abstract
Detailed models of $\alpha$ Cen A and B based on new seismological data for $\alpha$ Cen B by Carrier & Bourban (2003) have been computed using the Geneva evolution code including atomic diffusion. Taking into account the numerous observational constraints now available for the $\alpha$ Cen system, we find a stellar model which is in good agreement with the astrometric, photometric, spectroscopic and asteroseismic data. The global parameters of the $\alpha$ Cen system are now firmly constrained to an age of $t=6.52 \pm 0.30$ Gyr, an initial helium mass fraction $Y_{{\rm i}}=0.275 \pm 0.010$ and an initial metallicity $(Z/X)_{{\rm i}}=0.0434 \pm 0.0020$. Thanks to these numerous observational constraints, we confirm that the mixing-length parameter $\alpha$ of the B component is larger than the one of the A component, as already suggested by many authors (Noels et al. 1991; Fernandes & Neuforge 1995; Guenther & Demarque 2000): $\alpha_{{\rm B}}$ is about 8% larger than $\alpha_{{\rm A}}$ ( $\alpha_{{\rm A}}=1.83 \pm 0.10$and $\alpha_{{\rm B}}=1.97 \pm 0.10$). Moreover, we show that asteroseismic measurements enable to determine the radii of both stars with a very high precision (errors smaller than 0.3%). The radii deduced from seismological data are compatible with the new interferometric results of Kervella et al. (2003) even if they are slightly larger than the interferometric radii (differences smaller than 1%).

Key words: stars: binaries: visual - stars: individual: $\alpha$ Cen - stars: evolution - stars: oscillations

   
1 Introduction

The $\alpha$ Cen system is the ideal target to test our knowledge of stellar physics in solar-like stars, due to its proximity which allows precise determination of the fundamental parameters of the two stars. As a result, numerous theoretical analysis of $\alpha$ Cen A and B have already been performed.

Flannery & Ayres (1978) were the first to compute models of the $\alpha$ Cen system. They found that stellar models constructed by assuming a solar composition for $\alpha$ Cen A and B were not able to reproduce the astrometric and photometric data. They concluded that the $\alpha$ Cen system is more metal-rich than the Sun ( $Z_{\alpha~{\rm Cen}}/Z_{\odot} \sim 2$).

Following the report of a possible detection of p-mode oscillations on $\alpha$ Cen A (Fossat et al. 1984), Demarque et al. (1986) investigated the astrometric and physical properties of the $\alpha$ Cen system. Firstly, they deduced the masses of the components ( $1.09 \pm 0.01$ and $0.90 \pm 0.01$ $M_\odot$ for $\alpha$ Cen A and B respectively) from orbital measurements and ground-based parallax. Secondly, they computed stellar models of $\alpha$ Cen A in order to confront theoretical predicted p-mode frequencies to observed ones. They concluded that the observed frequencies were inconsistent with p-mode spectra constructed from standard theoretical models.

Noels et al. (1991) introduced a calibration procedure which is based on the simple principle that the four observables (two luminosities and two effective temperatures) will determine the four unknowns of the modelisation (Z, Y, age and mixing-length parameter $\alpha$, which is assumed to be identical for both stars). Using the masses deduced by Demarque et al. (1986), they found Z=0.04, Y=0.32, $\alpha=1.6$ and an age of 5 Gyr.

Contrary to Noels et al. (1991), Edmonds et al. (1992) relaxed the hypothesis of a unique mixing-length parameter for both stars by considering the observed metallicity as an additional constraint. They were also the first to include the effects of helium diffusion. They found $Y=0.300 \pm 0.005$, an age of $4.6 \pm 0.4$ Gyr, and a mixing-length parameter for $\alpha$ Cen A slightly smaller than for $\alpha$ Cen B, but did not include an uncertainty analysis to determine if this difference was significant. Edmonds et al. also computed the theoretical p-mode frequencies of $\alpha$ Cen A and B; they predicted a mean large spacing (for $\ell=0$) of 108 $\mu$Hz and 179 $\mu$Hz and a mean small spacing of 6.2 $\mu$Hz and 12.6 $\mu$Hz for $\alpha$ Cen A and B respectively.

Neuforge (1993) revisited the study by Noels et al. (1991) using OPAL opacities. She obtained a solution which favours a high value for the metallicity ( $Z_{\alpha~{\rm Cen}}/Z_{\odot} \sim 2$) and a unique convection parameter for both stars.

The $\alpha$ Cen system was also studied in order to test the modelisation of convection. Lydon et al. (1993) constructed a series of models of $\alpha$ Cen A and B for the purpose of testing the effects of convection modeling both by means of the mixing-length theory and by means of parametrization of energy fluxes based upon numerical simulations of turbulent compressible convection. They found that their formulation of convection produced models with theoretical radii compatible with the observed ones. They were thus able to correctly modelize a star using a formulation of convection which does not include an adjustable free parameter to determine the radius.

Fernandes & Neuforge (1995) also studied the $\alpha$ Cen system to test stellar models based upon the mixing-length theory of convection and models using the Canuto & Mazzitelli formulation (Canuto & Mazzitelli 1991, 1992). Their calibration suggested that the mixing-length parameter for $\alpha$ Cen B is larger that the one for $\alpha$ Cen A if the mass fraction of heavy elements Z is smaller than 0.038; if Z is larger than this threshold, the two mixing-length parameters become very similar. However, because of the uncertainties in the observational constraints, these differences could not be firmly established.

Kim (1999) calibrated the $\alpha$ Cen system using the observational constraint [Z/X] of Neuforge-Verheecke & Magain (1997). His study, which took into account the helium diffusion, gave an age of about 5.4 Gyr and showed that both stars may have the same mixing-length ratio ( $1.6 \sim 1.7$). Kim also computed the p-mode frequencies of the $\alpha$ Cen system and predicted a mean large spacing of 104 and 171 $\mu$Hz for $\alpha$ Cen A and B respectively.

The different calibrations mentioned previously used the masses derived by Demarque et al. (1986): $1.09 \pm 0.01$ and $0.90 \pm 0.01$ $M_\odot$ for $\alpha$ Cen A and B respectively. Pourbaix et al. (1999) performed a simultaneous least-squares adjustment of all visual and spectroscopic observations of the $\alpha$ Cen system with precise radial velocities measurements. They derived new consistent values of the orbital parallax, sum of masses, mass ratio and individual masses. They found masses of $1.16 \pm 0.031$ $M_\odot$ and $0.97 \pm 0.032$ $M_\odot$ for $\alpha$ Cen A and B respectively. The differences between the masses derived by Pourbaix et al. (1999) and the ones obtained by Demarque et al. (1986) mainly result from the lower parallax found by Pourbaix et al. ( $737.0 \pm 2.6$ mas instead of $750.6 \pm 4.6$ mas for Demarque et al.). In order to investigate the consequences of these new masses, Pourbaix et al. constructed new models of the $\alpha$ Cen system and found a significantly smaller age than previous estimates (2.7 Gyr).

Guenther & Demarque (2000) calculated detailed models of $\alpha$ Cen A and B based on three different parallaxes: the parallax from Hipparcos ( $742.12 \pm 1.40$ mas), the parallax of $750.6 \pm 4.6$ mas obtained by Demarque et al. (1986) and the value of $747.1 \pm 1.2$ mas determined by Söderhjelm (1999). Using the orbital data from Heintz (1982) and the mass ratio of Kamper & Wesselink (1978) they thus deduced different masses of $\alpha$ Cen A and B for each parallax: $M_{\rm A}=1.1238\pm 0.008$ $M_\odot$ and $M_{\rm B}=0.9344\pm 0.007$ $M_\odot$ for the parallax from Hipparcos, $M_{\rm A}=1.0844\pm 0.008$ $M_\odot$ and $M_{\rm B}=0.9017\pm 0.007$ $M_\odot$ for the parallax of Demarque et al., and $M_{\rm A}=1.1015\pm 0.008$ $M_\odot$ and $M_{\rm B}=0.9159\pm 0.007$ $M_\odot$ for the parallax determined by Söderhjelm. For each pair of masses, Guenther & Demarque calculated models of $\alpha$ Cen A and B including helium and heavy-element diffusion which had to reproduce the observed effective temperatures, luminosities (which are slightly different for each pair of masses due to the different parallaxes) and surface metallicities. They found that self-consistent models of the $\alpha$ Cen system could be produced for each pair of masses and thus that the parallax from Demarque et al. as well as the Hipparcos parallax could not be ruled out, because observational uncertainties in other parameters, such as composition, dominated the uncertainties. To investigate in details the effect of uncertainties in mass, luminosity, effective temperature, helium aboundance and metallicity on the models, they chose the models based on the most recent determination of the parallax (the parallax of Söderhjelm). For these models, p-mode frequencies were also computed. Guenther & Demarque found an initial helium mass fraction $Y_{\rm ZAMS}\cong 0.28$ and an age of the system which depends critically on whether or not $\alpha$ Cen A has a convective core. If it does, the system has an age of $7.6~ \pm~ 0.8$ Gyr. If $\alpha$ Cen A does not have a convective core (corresponding to $Z_{\rm ZAMS}\lesssim 0.3$), $\alpha$ Cen A and B are $6.8~ \pm~ 0.8$ Gyr old. They also found that the mixing-length parameter of $\alpha$ Cen A is about 10% smaller that the one of the B component. However, they pointed out that the effect of composition and surface temperature uncertainties on $\alpha$ is greater than this difference. Concerning the pulsation analysis of their models, they concluded that the large spacing provides a very precise means of determining the radius of the star, uncontaminated to any significant degree by uncertainties in the star's composition. They also pointed out that, because $\alpha$ Cen A and B have the same age and initial composition, the small spacing may be useful as an age indicator. They predicted an average large and small spacing of $101\pm 3$ $\mu$Hz and $4.6 \pm 0.4$ $\mu$Hz for $\alpha$ Cen A, and $173\pm 6$ $\mu$Hz and $15\pm 1$ $\mu$Hz for $\alpha$ Cen B.

Morel et al. (2000) calculated detailed evolutionary models of the $\alpha$ Cen system based on the new masses of $1.16 \pm 0.031$ $M_\odot$ and $0.97 \pm 0.032$ $M_\odot$ for $\alpha$ Cen A and B respectively (Pourbaix et al. 1999). Contrarily to previous works they also chose to use the spectroscopic gravities instead of the luminosity derived from the photometry, bolometric correction and parallax. The evolutionary code they used included microscopic diffusion. With the mixing-length theory of convection, Morel et al. found that the $\alpha$ Cen system has an age of 2.71 Gyr (in very good agreement with Pourbaix et al. 1999), an initial chemical composition $Y_{{\rm i}}=0.284$ and $(Z/X)_{{\rm i}}=0.0443$, and values of the convection parameters which are almost the same for both stars. Including overshooting of convective cores, they found a larger age of the system (3.53 Gyr), an initial chemical composition almost the same as without overshooting ( $Y_{{\rm i}}=0.279$ and $(Z/X)_{{\rm i}}=0.0450$), and mixing-length parameters almost identical for both components. Morel et al. also performed a calibration of the $\alpha$ Cen system using the Canuto and Mazzitelli convection theory. They found that this formulation of the convection changed the results of the calibration. Indeed, the age of the $\alpha$ Cen system is larger with the Canuto and Mazzitelli convection theory than with the mixing-length theory (4.086 Gyr instead of 2.71 Gyr). The initial composition derived using the Canuto and Mazzitelli formulation is $Y_{{\rm i}}=0.271$ and $(Z/X)_{{\rm i}}=0.0450$. The convection parameters of both components were also almost identical and close to unity. Morel et al. also calculated models using the observational constraints adopted by Guenther & Demarque (2000). This calibration gave a smaller age (5.64 Gyr) and a larger initial helium mass fraction ( $Y_{{\rm i}}=0.300$) than obtained by Guenther & Demarque (2000). Finally, Morel et al. calculated the p-mode frequencies of their models based on the masses of Pourbaix et al. (1999). They predicted large and small spacings of about 107-108 $\mu$Hz and 7.5-9.1 $\mu$Hz for $\alpha$ Cen A and 154-157 $\mu$Hz and 12 $\mu$Hz for $\alpha$ Cen B.

The detection and identification of p-modes in $\alpha$ Cen A by Bouchy & Carrier (2002) brought strong additional constraints. These measurements were not fully in agreement with the theoretical calibrations quoted above, which were based on non-asteroseismic observables. Moreover, Pourbaix et al. (2002) studied in detail the masses of the $\alpha$ Cen system. Thanks to the accurate estimate of the parallax (Söderhjelm 1999) and new radial velocities, they determined very precise masses of $1.105 \pm 0.0070$ $M_\odot$ and $0.934 \pm 0.0061$ $M_\odot$ for $\alpha$ Cen A and B respectively.

Consequently, new calibrations of the $\alpha$ Cen system were performed by Thévenin et al. (2002) and Thoul et al. (2003) in order to find a model reproducing the asteroseismic observations of the A component as well as the new masses of Pourbaix et al. (2002). The analysis of these two theoretical groups led to different results. Thévenin et al. found a model with an age of 4.85 Gyr which is not able to reproduce the astrometric mass of Pourbaix et al. (2002) of $\alpha$ Cen B, whereas Thoul et al. proposed an older model (6.41 Gyr) which matches astrometric masses of both stars. The main difference between these two analysis results from the inclusion of atomic diffusion. Indeed, the evolution code used by Thoul et al. does not include the diffusion of helium and other heavy elements which cannot be neglected in order to obtain accurate stellar models of stars in the mass range of $\alpha$ Cen A and B. On the other hand, Thévenin et al. included the atomic diffusion in their evolution code and assumed the mixing-length parameter of the two components to be the same. Moreover, Thévenin et al. used the luminosity derived from the photometry, bolometric correction and parallax contrary to Thoul et al. who used the spectroscopic surface gravities to constrain the system. Both studies mentioned that, even if the p-mode frequencies of $\alpha$ Cen A bring strong constraints for the calibration of the $\alpha$ Cen system, asteroseismic measurements of $\alpha$ Cen B are needed to unambiguously determine the fundamental parameters of $\alpha$ Cen A and B.

Recently, Carrier & Bourban (2003) detected solar-like oscillations in $\alpha$ Cen B with the CORALIE echelle spectrograph and identified twelve individual frequencies. Thanks to these new asteroseismic measurements, there are now enough observational constraints to determine an accurate model for the $\alpha$ Cen system. Moreover, Kervella et al. (2003) recently measured the angular diameters of $\alpha$ Cen A and B. These results enable us to test the consistency between interferometric and asteroseismic observations.

The whole observational constraints available for the $\alpha$ Cen system are presented in Sect. 2. The physics of the stellar models and the calibration method are described in Sect. 3, while the results are given in Sect. 4. Finally Sect. 5 contains the comparison of our results with previous studies and the conclusion is given in Sect. 6.

   
2 Observational constraints

2.1 Astrometric data

The parallax and the orbital elements of the $\alpha$ Cen binary system are difficult to determine accurately due to the high luminosity and large separation of the stellar components. This results in various values for the parallax published in the literature (see the introduction and Table 10 of Kervella et al. 2003). In this work we consider the accurate parallax obtained by Söderhjelm (1999) that combines Hipparcos and ground-based observations, $747.1 \pm 1.2$ mas.

Pourbaix et al. (2002) improved the precision of the orbital parameters of the $\alpha$ Cen system by adding new radial velocity measurements of $\alpha$ Cen A and B obtained in the framework of the Anglo-Australian Planet Search programme as well as in the CORALIE programme to those by Endl et al. (2001). Adopting the parallax of Söderhjelm (1999), they determined precise masses of $1.105 \pm 0.0070$ $M_\odot$ and $0.934 \pm 0.0061$ $M_\odot$ for $\alpha$ Cen A and B respectively. Note that the mass ratio they determined is compatible with the one obtained by Kamper & Wesselink (1978). These new masses constitute the most recent and accurate values now available for $\alpha$ Cen A and B. Consequently, we consider them as true observables which have to be reproduced by a consistent model of the $\alpha$ Cen system.

   
2.2 Effective temperatures and chemical composition

Many spectroscopic measurements of both components of the system can be found in the literature. A summary of published values is given in Table 3 of Morel et al. (2000).

Concerning the effective temperatures, Thévenin et al. (2002) and Thoul et al. (2003) used the same value for $\alpha$ Cen B. In this work, we considered the same effective temperature of $\alpha$ Cen B of $5260 \pm 50$ K. For the A component, we note a small discrepancy between the value of Neuforge-Verheecke & Magain (1997) used by Thoul et al. and the temperature derived by Morel et al. (2000) and used by Thévenin et al. We thus adopted an effective temperature of $5810 \pm 50$ K for $\alpha$ Cen A in order to encompass the intervals of temperatures used by Thévenin et al. and Thoul et al.

For the metallicities, we adopted $[{\rm Fe/H}]_{{\rm A}}=0.22~ \pm~ 0.05$ dex for $\alpha$ Cen A and $[{\rm Fe/H}]_{{\rm B}}=0.24 \pm 0.05$ dex for $\alpha$ Cen B. These values lie between the ones used by Thévenin et al. and those adopted by Thoul et al., with larger error boxes which appear to us more realistic in view of the different values found in the literature.

   
2.3 Luminosities

From 1978 to 1981, both components of the $\alpha$ Cen system have been measured in the GENEVA photometric system (Golay 1980) with the photoelectric photometer P7 (Burnet & Rufener 1979) installed on the 40 cm Swiss telescope in La Silla (ESO, Chile). Six measurements were obtained for both stars (see Table 1) using a mask on the telescope in order to reduce the flux of these stars; the photometric reduction procedure is described by Rufener (1964, 1985). Combining the mean magnitudes $\langle V_{{\rm A}}\rangle = -0.003 \pm 0.006$ and $\langle V_{{\rm B}}\rangle = 1.333 \pm 0.014$ mag, the parallax of Söderhjelm (1999), the solar absolute bolometric magnitude $M_{{\rm bol},~\odot}=4.746$(Lejeune et al. 1998) and the bolometric corrections from Flower's (1996) $BC_{{\rm A}} = -0.074 \pm 0.009$ and $BC_{{\rm B}} = -0.207 \pm 0.017$ mag determined from the effective temperatures, luminosities are calculated and have values of $L_{{\rm A}} = 1.522 \pm 0.030$ $L_{\odot}$and $L_{{\rm B}} = 0.503 \pm 0.020$ $L_{\odot}$.

Table 1: Geneva photometric measurements of $\alpha$ Cen A and B. P corresponds to the weight which varies from 0 to 4 according to the quality of the nights (4 for the best nights and 0 for the worst).

2.4 Angular diameters

Recently Kervella et al. (2003) measured the angular diameters of $\alpha$ Cen A and B using the VINCI instrument installed at ESO's VLT Interferometer. They found limb darkened angular diameters $\theta_{\rm A}=8.511 \pm 0.020$ mas and $\theta_{\rm B}=6.001 \pm 0.034$ mas for the A and B component respectively. The radius of each star can then be deduced by using the following simple relation between the angular diameter $\theta$ (in mas), the radius of the star R (in $R_{\odot}$) and the parallax $\pi$(in mas): $\theta=9.305 \times 10^{-3} (2R) \pi$. By taking into account the error on the parallax of Söderhjelm (1999), we obtained a radius of $1.224 \pm 0.003$ $R_{\odot}$ for $\alpha$ Cen A and $0.863 \pm 0.005$ $R_{\odot}$ for $\alpha$ Cen B.

   
2.5 Asteroseismic constraints

Solar-like oscillations in $\alpha$ Cen A have been detected by Bouchy & Carrier (2002) with the CORALIE echelle spectrograph. Twenty-eight oscillation frequencies were identified in the power spectrum between 1.8 and 2.9 mHz with amplitudes in the range 12 to 44 cm s^-1. The radial orders of these modes with angular degrees $l \leq 2$ lie between 15 and 25. According to the asymptotic theory (Tassoul 1980) the oscillation spectrum can be characterized by two frequency separations, the large and the small spacing. The large frequency spacing $\Delta \nu_{l} \equiv \nu_{n,l}- \nu_{n-1,l}$ corresponds to differences between frequencies of modes with the same angular degree l and consecutive radial order. For high frequency oscillation modes, this spacing remains approximately constant with a mean value $\Delta \nu_{0}$ proportional to the square root of the star's mean density. Thus $\Delta \nu_{0}$ puts strong constraints on the value of the radius of the star and enables us to test the consistency between interferometric measurements and asteroseismic data. The small spacing $\delta \nu_{l,l+2} \equiv \nu_{n+1,l}- \nu_{n,l+2}$ is the difference between the frequencies of modes with an angular degree l of same parity and with consecutive radial order. This small spacing is very sensitive to the structure of the core and mainly to its hydrogen content, i.e. to its evolutionary status. Unlike the large spacing, $\delta \nu_{l,l+2}$ can vary sensitively with the frequency. This fact has to be taken into account when one compares theoretical value of this mean small spacing with asteroseismic results. Bouchy & Carrier determined the averaged large and small spacing of $\alpha$ Cen A by a least square fit of the asymptotic relation with their twenty-eight oscillations frequencies identified. They found a mean large spacing $\Delta \nu_{0}^{{\rm A}}=105.5 \pm 0.1$ $\mu$Hz and a mean small spacing between l=2 and l=0 modes $\delta \nu_{02}^{{\rm A}}=5.6 \pm 0.7$ $\mu$Hz. Note that their fit also gives the value of a third parameter, $\epsilon$, which is sensitive to the reflexion conditions near the surface of the star. Given that the exact values of the frequencies depend on the details of the star's atmosphere, where the pulsation is non-adiabatic, we will not use this parameter to constrain our stellar models. Indeed, a linear shift of a few $\mu$Hz between theoretical and observational frequencies is perfectly acceptable.

Table 2: Observational constraints for $\alpha$ Cen A and B. References: (1) Söderhjelm (1999), (2) Pourbaix et al. (2002), (3) this paper, (4) derived from the other observational measurements (see text), (5) Kervella et al. (2003), (6) Bouchy & Carrier (2002) and (7) Carrier & Bourban (2003).

Recently, Carrier & Bourban (2003) detected solar-like oscillations in $\alpha$ Cen B with the CORALIE echelle spectrograph. They identified twelve modes between 3 and 4.6 mHz with amplitudes in the range 8.7 to 13.7 cm s^-1. From these twelve frequencies they deduced a large spacing $\Delta \nu_{0}^{{\rm B}}=161.1 \pm 0.1$ $\mu$Hz and a mean small spacing $\delta \nu_{02}^{{\rm B}}=8.7 \pm 0.8$ $\mu$Hz.

All the observational constraints are listed in Table 2.

3 Stellar models

3.1 Input physics

The stellar evolution code used for these computations is the Geneva code, described several times in the literature (see Meynet & Maeder 2000 for more details). We used the OPAL opacities, the MHD equation of state (Däppen et al. 1988; Hummer & Mihalas 1988; Mihalas et al. 1988), the NACRE nuclear reaction rates (Angulo et al. 1999) and the standard mixing-length formalism for convection.

Our models have been computed including atomic diffusion on He, C, N, O, Ne and Mg using the routines developed for the Geneva-Toulouse version of our code (see for example Richard et al. 1996) recently updated by Richard (private communication). The diffusion coefficients are computed with the prescription by Paquette et al. (1986). We included the diffusion due to the concentration and thermal gradients, but the radiative acceleration was neglected as it is negligible for the structure of the low-mass stellar models with extended convective envelopes (Turcotte et al. 1998).

3.2 Calibration method

Basically, the calibration of a binary system consists in finding the set of stellar modeling parameters which best reproduces all observational data available for both stars. For a given stellar mass the characteristics of a stellar model (luminosity, effective temperature, surface metallicity, frequencies of oscillation modes, etc.) depend on four modeling parameters: the age of the star (noted t in the following), the mixing-length parameter $\alpha \equiv l/H_{{\rm p}}$ for convection and two parameters describing the initial chemical composition of the star. For these two parameters, we chose the initial helium abundance $Y_{{\rm i}}$ and the initial ratio between the mass fraction of heavy elements and hydrogen $(Z/X)_{{\rm i}}$. Assuming that this ratio is proportional to the abundance ratio [Fe/H], we can directly relate (Z/X) to [Fe/H] by using the solar value $(Z/X)_{\odot}=0.0230$ given by Grevesse & Sauval (1998). Thus, any characteristic A of a given stellar model has the following formal dependences with respect to modeling parameters: $A=A(t,\alpha,Y_{{\rm i}},(Z/X)_{{\rm i}})$.

The binary nature of the system provides three constraints: $t_{{\rm A}}=t_{{\rm B}}$, $Y_{{\rm i}}^{{\rm A}}=Y_{{\rm i}}^{{\rm B}}$ and $(Z/X)_{{\rm i}}^{{\rm A}}=(Z/X)_{{\rm i}}^{{\rm B}}$. Consequently, we have to determine a set of five modeling parameters (t, $\alpha_{{\rm A}}$, $\alpha_{{\rm B}}$, $Y_{{\rm i}}$ and $(Z/X)_{{\rm i}}$) instead of eight (four for each star). Note that we do not assume that the mixing-length value is identical for $\alpha$ Cen A and B. This assumption was often used in the past (Noels et al. 1991) as an additional constraint needed to close the system, because the only observed values were the effective temperatures, the masses and the luminosities of both stars. We no longer need this assumption because we now have enough observational data to strongly constrain the models. Moreover, one of the applications of asteroseismology is to determine whether or not a single mixing-length parameter is applicable to all stars regardless of mass, composition and age.

   
3.2.1 Non-asteroseismic constraints

Once assuming that the masses of $\alpha$ Cen A and B are those determined by Pourbaix et al. (2002), the determination of the set of modeling parameters (t, $\alpha_{{\rm A}}$, $\alpha_{{\rm B}}$, $Y_{{\rm i}}$ and $(Z/X)_{{\rm i}}$) leading to the best agreement with the observational constraints is made in two steps. First, we only consider non-asteroseismic observations and construct a grid of models with positions of the two components in the HR diagram in agreement with the observational values of the luminosities, effective temperatures and radii listed in Table 2. The boxes in the HR diagram for $\alpha$ Cen A and B are shown in Fig. 1. To construct the grid of models with positions of the two components lying in the observational boxes, we proceed in the following way: for a given chemical composition (i.e. a given set $Y_{{\rm i}}$, $(Z/X)_{{\rm i}}$) the mixing-length coefficient of each star is adjusted in order to match the observational position in the HR diagram. Note that because of the uncertainties on the effective temperature, different values of the mixing-length parameter $\alpha$ enable to match the observational box in the HR diagram. Thus, for each component and for a given initial chemical composition, we obtain different models corresponding to different value of $\alpha$ between the smallest value of $\alpha$ needed to match the observational box (denoted $\alpha_{{\rm min}}$) and the largest value ( $\alpha_{{\rm max}}$). The uncertainty of 50 K on the effective temperature of both stars leads to a typical difference between $\alpha_{{\rm min}}$ and $\alpha_{{\rm max}}$of about 0.1.

Figure 1: Observational constraints in the HR diagram for $\alpha$ Cen A and B. The dashed lines indicate the boxes delimited by the observed luminosities and effective temperatures (with their respective 1-sigma errors). The continuous lines denote the boxes delimited by the observed radii with their 1-sigma errors, while the dotted line correspond to the same observed radii with errors of 2 sigma. The positions in the HR diagram of $\alpha$ Cen A and B for the M1 model is indicated by the two triangles, while the dots correspond to the positions of the M2 model. Note that for $\alpha$ Cen B the dot and the triangle are partly superimposed, because the M1 model is only slightly hotter and less luminous than the M2 model.

Open with DEXTER

Once the positions in the HR diagram of the two components agree with the observed values, the surface metallicity of the two stars is compared to the observed one. If the surface metallicity of one of the component is out of the metallicity intervals listed in Table 2, the models are rejected and the procedure is repeated with another choice of $Y_{{\rm i}}$ and $(Z/X)_{{\rm i}}$. Note that the surface metallicities [Fe/H] $_{{\rm s}}$ are almost identical for the models with the same initial composition and different mixing-length parameters $\alpha$. Moreover, the [Fe/H] $_{{\rm s}}$ of the models are mainly sensitive to $(Z/X)_{{\rm i}}$ and less to $Y_{{\rm i}}$. As a result, the values of $(Z/X)_{{\rm i}}$ are directly constrained by the observed surface metallicities; we found that the models matching the observed metallicities have $(Z/X)_{{\rm i}}$ ranging from about 0.038 to 0.048 (i.e. an initial metallicity [Fe/H] $_{{\rm i}}$ between 0.22 and 0.32).

If the metallicities of both stars agree with the observed values, we then compare their ages. All the models of $\alpha$ Cen A with different values of the mixing-length parameters between $\alpha_{{\rm min}}$ and $\alpha_{{\rm max}}$ are considered. For all these models, whose position in the HR diagram as well as the surface metallicity are in agreement with the observational values, the smallest ( $t_{{\rm min}}^{{\rm A}}$) and the highest ages ( $t_{{\rm max}}^{{\rm A}}$) are determined. Note that, given the shape of the observational box in the HR diagram (see Fig. 1), the youngest model has $\alpha= \alpha_{{\rm min}}$ and the oldest has $\alpha= \alpha_{{\rm max}}$. In the same way, $t_{{\rm min}}^{{\rm B}}$ and $t_{{\rm max}}^{{\rm B}}$ are determined for the B component. If $t_{{\rm min}}^{{\rm A}} > t_{{\rm max}}^{{\rm B}}$ or $t_{{\rm max}}^{{\rm A}} < t_{{\rm min}}^{{\rm B}}$the models of $\alpha$ Cen A are not compatible in age with the models of the B component; they are rejected and the procedure is repeated with another choice of $Y_{{\rm i}}$ and $(Z/X)_{{\rm i}}$. Otherwise, all the models of $\alpha$ Cen A and B with the same age (with a difference smaller than 0.01 Gyr) are considered as models of the $\alpha$ Cen system which reproduce all the non-asteroseismic constraints. The whole procedure is then repeated with a new choice of $Y_{{\rm i}}$ and $(Z/X)_{{\rm i}}$.

In this way, we obtained a grid of models with various sets of modeling parameters (t, $\alpha_{{\rm A}}$, $\alpha_{{\rm B}}$, $Y_{{\rm i}}$ and $(Z/X)_{{\rm i}}$) which satisfied all the non-asteroseismic observational constraints, namely the effective temperatures, the luminosities, the radii and the surface metallicities. The second step in determining the best model of the binary system $\alpha$ Cen is to consider the asteroseismic measurements for both stars. Note that if no asteroseismic observations were available for the $\alpha$ Cen system, we would not be able to discriminate between these stellar models. Indeed, asteroseismic observations are needed to differentiate models with different internal structures located in the same region of the HR diagram, which is absolutely necessary in order to determine the age of the system for instance.

   
3.2.2 Pulsation analysis

For each stellar model of the grid constructed as explained above, low-l p-mode frequencies were calculated using the Aarhus adiabatic pulsation package (Christensen-Dalsgaard 1997). Following the observations, frequencies of modes of degree $l \leq 2$ were calculated for a radial order n ranging from 15 to 25 for $\alpha$ Cen A and from 17 to 27 for $\alpha$ Cen B. The determination of the large and small spacings was carried out exactly as in Bouchy & Carrier (2002) and Carrier & Bourban (2003). For the models of $\alpha$ Cen A, we selected the theoretical modes corresponding to the twenty-eight frequencies identified by Bouchy & Carrier and fitted the asymptotic relation to obtain the mean values $\Delta \nu_0^{{\rm A}}$ and $\delta \nu_{02}^{{\rm A}}$. In the same way, we selected the theoretical modes of the $\alpha$ Cen B models corresponding to the twelve frequencies identified by Carrier & Bourban and fitted the asymptotic relation to obtain $\Delta \nu_0^{{\rm B}}$ and $\delta \nu_{02}^{{\rm B}}$.

Once the asteroseismic characteristics of all the relevant models were determined, we performed a $\chi^2$ minimization in order to deduce the set of parameters (t, $\alpha_{{\rm A}}$, $\alpha_{{\rm B}}$, $Y_{{\rm i}}$, $(Z/X)_{{\rm i}}$) leading to the best agreement with the observations. Therefore we defined the $\chi^2_{{\rm tot}}$ functional

 

$$\chi^2_{{\rm tot}} \equiv \sum_{{\rm A}, {\rm B}} \sum_{i=1}^{6} \left( \frac{C_i^{{\rm theo}}-C_i^{{\rm obs}}}{\sigma C_i^{{\rm obs}}} \right)^2 ,$$ (1)

where the vectors $\vec{C}$ contains all the observables for one star:

$$\vec{C} \equiv (L/L_{\odot},T_{{\rm eff}},R/R_{\odot}, [{\rm Fe/H}]_{{\rm s}},\Delta \nu_0,\delta \nu_{02}) .$$

The vector $\vec{C}^{{\rm theo}}$ contains the theoretical values of these observables for the model to be tested, while the values of $\vec{C}^{{\rm obs}}$ are those listed in Table 2. The vector $\sigma \vec{C}$ contains the errors on these observations which are also given in Table 2.

To better test the agreement between models and asteroseismic observations, we defined a second functional $\chi^2_{{\rm astero}}$ which directly compares individual theoretical frequencies to the observed ones instead of using the mean large and small spacings. As mentioned in Sect. 2.5, a linear shift of a few $\mu$Hz between theoretical and observational frequencies is perfectly acceptable, because the exact values of the frequencies depend on the details of the star's atmosphere, where the pulsation is non-adiabatic. To take this fact into account, we defined the mean value of the differences between the theoretical and observed frequencies:

$$\langle D_{\nu}\rangle \equiv \frac{1}{N} \sum_{i=1}^N (\nu_i^{{\rm theo}}-\nu_i^{{\rm obs}}) ,$$

where N is the number of observed frequencies ( $N_{{\rm A}}=28$ for $\alpha$ Cen A and $N_{{\rm B}}=12$ for $\alpha$ Cen B). The functional $\chi^2_{{\rm astero}}$ can then be defined as

 

$$\chi^2_{{\rm astero}} \equiv \frac{1}{N_{{\rm A}}} \sum_{i=1}^{N_... ...i^{{\rm obs}} - \langle D_{\nu}\rangle_{{\rm B}}}{\sigma_{{\rm B}}} \right)^2 ,$$ (2)

where $\sigma_{{\rm A}}=0.46$ $\mu$Hz and $\sigma_{{\rm B}}=0.47$ $\mu$Hz are the errors on the observed frequencies for $\alpha$ Cen A and B respectively.

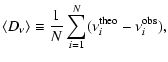The determination of the best set of parameters (t, $\alpha_{{\rm A}}$, $\alpha_{{\rm B}}$, $Y_{{\rm i}}$, $(Z/X)_{{\rm i}}$) was based on the minimization of the functional defined in Eq. (1) which includes four non-asteroseismic and two asteroseismic observational constraints for each star. Once the model with the smallest $\chi^2_{{\rm tot}}$ was determined, we refined the grid in the vicinity of this preliminary solution in order to find the best solution which minimizes at the same time $\chi^2_{{\rm tot}}$ and  $\chi^2_{{\rm astero}}$.

   
4 Results

Table 3: Models for $\alpha$ Cen A and B. The upper part of the table gives the observational constraints used for the calibration. The middle part of the table presents the modeling parameters with their confidence limits, while the bottom part presents the global parameters of the two stars. The mean large and small spacings and their respective errors are calculated exactly as in Bouchy & Carrier (2002) and Carrier & Bourban (2003).

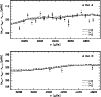	Figure 2: Large spacing versus frequency for $\alpha$ Cen A and B for the model with 1-sigma error boxes on the observed radii (model M1). The dots indicate the observed values of the large spacing with an uncertainty on individual frequencies estimated to half the time resolution (0.46 and 0.47 $\mu$Hz for $\alpha$ Cen A and B respectively).
Open with DEXTER

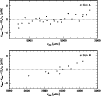	Figure 3: Differences between calculated and observed frequencies for the model with 1-sigma error boxes on the observed radii (model M1). The systematic shifts for $\alpha$ Cen A and B are $\langle D_{\nu}\rangle_{{\rm A}}=-11.5$ $\mu$Hz and $\langle D_{\nu}\rangle_{{\rm B}}=13.7$ $\mu$Hz (see text for more details).
Open with DEXTER

4.1 Model M1: 1-sigma error on the observed radii

We first computed a grid of models reproducing all non-asteroseismic constraints within their one-sigma error boxes as described in Sect. 3.2.1. The positions in the HR diagram for $\alpha$ Cen A and B are given by their luminosities, effective temperatures and radii (see Fig. 1). Of course, these independent measurements are not fully consistent with each other; for instance, the radius determined by interferometry has not exactly the same value as the one deduced from the luminosity and the effective temperature of the star.

Once this grid of models was computed, we performed the $\chi^2$ minimization described above to find the set of modeling parameters which best reproduced all observational constraints. In this way, we found the solution $t=6.50 \pm 0.20$ Gyr, $\alpha_{{\rm A}}=1.83 \pm 0.10$, $\alpha_{{\rm B}}=1.99 \pm 0.10$, $Y_{{\rm i}}=0.275 \pm 0.010$ and $(Z/X)_{{\rm i}}=0.0435 \pm 0.0020$. The position in the HR diagram of this model of $\alpha$ Cen A and B (denoted model M1 in the following) is given in Fig. 1. The characteristics of this model are reported in Table 3. The confidence limits of each modeling parameter given in Table 3 are estimated as the maximum/minimum values which fit the observational constraints when the other calibration parameters are fixed to their medium value. The asteroseismic features of this solution are given in Figs. 2 and 3. These two figures show that this solution is not in complete agreement with the asteroseismic observations. Indeed, the theoretical mean large spacing $\Delta \nu_{0}$ of $\alpha$ Cen A and B are respectively $4 \sigma$ and $6 \sigma$ larger than the observed ones. This can be seen in Fig. 2 which exhibits the large spacing versus frequency for both stars, but is more clearly shown in Fig. 3 where differences between calculated and observed frequencies are plotted. In fact, the differences between calculated and observed frequencies increase with frequency. This trend, which is more pronounced for $\alpha$ Cen B than for $\alpha$ Cen A, results directly from the too large values of the theoretical large spacings. The solution which minimized the $\chi^2$ functional implies that the two stars lie in the upper border of their respective boxes in radius (see Fig. 1). Given that the large spacing $\Delta \nu$ of a star is proportional to the square root of its mean density, we find that the radii observed by interferometry are slightly smaller that the ones needed to reproduce the asteroseismic observations of $\alpha$ Cen A and B.

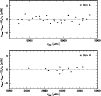	Figure 4: Differences between calculated and observed frequencies for the model with 2-sigma error boxes on the observed radii (model M2). The systematic shifts between theoretical and observed frequencies for $\alpha$ Cen A and B are $\langle D_{\nu}\rangle_{{\rm A}}=-19.0$ $\mu$Hz and $\langle D_{\nu}\rangle_{{\rm B}}=0.7$ $\mu$Hz (see text for more details).
Open with DEXTER

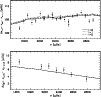	Figure 5: Large and small spacings versus frequency for $\alpha$ Cen A for the model with 2-sigma error boxes on the observed radii (model M2). The dots indicate the observed values of the large and small spacings with an uncertainty on individual frequencies estimated to half the time resolution (0.46 and 0.47 $\mu$Hz for $\alpha$ Cen A and B respectively).
Open with DEXTER

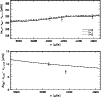	Figure 6: Large and small spacings versus frequency for $\alpha$ Cen B for the M2 model. The dots indicate the observed values of the large and small spacings with an uncertainty on individual frequencies estimated to 0.46 and 0.47 $\mu$Hz for $\alpha$ Cen A and B respectively.
Open with DEXTER

   
4.2 Model M2: 2-sigma error on the observed radii

In order to determine a model of $\alpha$ Cen A and B which is in better agreement with the asteroseismic measurements, we decided to repeat the above calibration considering larger values for the errors on the observed radii. We thus took an error on the observed radii of two sigma instead of the one-sigma error considered previously: $R=1.224 \pm 0.006$  $R_{\odot}$ for $\alpha$ Cen A and $R=0.863 \pm 0.010$ $R_{\odot}$ for $\alpha$ Cen B. For the other observational constraints, we kept the same values as the previous ones. These new intervals in radius defined a larger region in the HR diagram which is shown in Fig. 1. With these new constraints on the radii, we found the solution $t=6.52 \pm 0.30$ Gyr, $\alpha_{{\rm A}}=1.83 \pm 0.10$, $\alpha_{{\rm B}}=1.97 \pm 0.10$, $Y_{{\rm i}}=0.275 \pm 0.010$ and $(Z/X)_{{\rm i}}=0.0434 \pm 0.0020$. The position of $\alpha$ Cen A and B in the HR diagram for this model (noted model M2 in the following) is denoted by a dot in Fig. 1. The characteristics of this model are given in Table 3. Note that the radii of $\alpha$ Cen A and B for this solution are only 1.7 and 1.4 sigma larger than the observed values. Table 3 and Fig. 4 clearly show that the mean large spacings of the M2 model are in perfect accordance with the observed values. Indeed, the trend visible for the M1 model in Fig. 3 is no longer present in the M2 model. The variations of the large and small spacing with the frequency for $\alpha$ Cen A and B are given in Figs. 5 and 6. One can see that the M2 model perfectly reproduces the observed large spacings. It is interesting to notice that asteroseismic observations enable an accurate determination of the radii of both stars. Indeed, one can see that the M1 model with a radius of 1.227 $R_{\odot}$ for $\alpha$ Cen A and 0.868 $R_{\odot}$ for $\alpha$ Cen B is not compatible with the observed large spacings, while the M2 model with slightly larger radii (1.229 $R_{\odot}$ for $\alpha$ Cen A and 0.870 $R_{\odot}$ for $\alpha$ Cen B) is in perfect agreement with the observed large spacings. Consequently, we deduce that the asteroseismic measurements enable to determine the radii of both stars with a very high precision (errors smaller than 0.3%).

Concerning the small spacings $\delta \nu_{02}$, we note that the agreement with the observed values is not as good as for the large spacings. For $\alpha$ Cen A, the theoretical mean small spacing is compatible with the observational measurement but remains slightly smaller than the observed value of 5.6 $\mu$Hz. For $\alpha$ Cen B, this is exactly the opposite: the theoretical mean small spacing is higher than the observed one. Since the small spacing $\delta \nu_{02}$ is very sensitive to the hydrogen content of the core of a main-sequence star, i.e. mainly to its age and its initial chemical composition, we conclude that the age of about 6.5 Gyr given by the calibration constitutes the best compromise to reproduce at the same time the small spacing of $\alpha$ Cen A and that of $\alpha$ Cen B. Note that the observed mean small spacing of $\alpha$ Cen B is not strongly constrained since it is deduced from only two points (see Fig. 6). The point at low frequency is perfectly reproduced by the model, contrary to the value at higher frequency which is smaller than predicted by the model. As a result, the theoretical decrease of $\delta \nu_{02}$ with frequency for $\alpha$ Cen B is smaller than observed. If this trend for $\alpha$ Cen B can be thought to be artificial given that it is deduced from only two observational points, it is interesting to mention that this trend is also present for $\alpha$ Cen A (see Fig. 5). Note that for $\alpha$ Cen A this discrepancy is always present even for stellar models with quite different ages (see Fig. 2 of Thévenin et al. 2002 and Fig. 4 of Thoul et al. 2003) and remains therefore difficult to explain.

Previous analysis of the $\alpha$ Cen system made without the asteroseismic constraints on the B component disagreed on the presence of a convective core in $\alpha$ Cen A. Thévenin et al. (2002) found a model with a convective core, while Thoul et al. (2003) proposed a model without a convective core. Our model of $\alpha$ Cen A does not have a convective core. However, it is important to note that $\alpha$ Cen A lies very close to the boundary between models with and without convective core. Thus small changes in the observational constraints adopted to calibrate the system can lead to models of $\alpha$ Cen A with or without a convective core. Moreover, the asteroseismic measurements of $\alpha$ Cen A are not precise enough to allow a direct discrimination on this characteristic. As can indeed be seen on Fig. 7, the spacing $\delta \nu_{01}=\nu_{n+1,l=0}+ \nu_{n,l=0}- 2\nu_{n,l=1}$for our best model of $\alpha$ Cen A is very similar to the spacing $\delta \nu _{01}$ of a model with a convective core (see Fig. 3 of Thévenin et al. 2002). Therefore it cannot be used to discriminate models with and without a convective core.

	Figure 7: $\delta \nu _{01}$ spacing versus frequency for $\alpha$ Cen A for the M2 model. The uncertainty on the observed individual frequencies is estimated to 0.46 $\mu$Hz.
Open with DEXTER

Finally, we compare the theoretical p-mode frequencies of our best model (model M2) to the observed frequencies by plotting the echelle diagrams of the two stars. Figure 8 shows the echelle diagram of $\alpha$ Cen A, while that of $\alpha$ Cen B is given in Fig. 9. In these two figures, the systematic differences between theoretical and observed frequencies ( $\langle D_{\nu}\rangle_{{\rm A}}=-19.0$ $\mu$Hz and $\langle D_{\nu}\rangle_{{\rm B}}=0.7$ $\mu$Hz for $\alpha$ Cen A and B) have been taken into account. These two figures show the good agreement between our model of the $\alpha$ Cen system and the asteroseismic observations. The theoretical frequencies for $\alpha$ Cen A and B are given in Table 4.

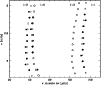Figure 8: Echelle diagram of $\alpha$ Cen A for the best model of the $\alpha$ Cen system (model M2), with a large spacing $\Delta \nu =105.5$ $\mu$Hz. Open symbols refer to theoretical frequencies, while the filled circles correspond to the frequencies observed by Bouchy & Carrier (2002). Open circles are used for modes with l=0, triangles for l=1, squares for l=2 and pentagons for l=3 (see text for more details).

Open with DEXTER

Figure 9: Echelle diagram of $\alpha$ Cen B for the best model of the $\alpha$ Cen system (model M2), with a large spacing $\Delta \nu =161.1$ $\mu$Hz. Open symbols refer to theoretical frequencies, while the filled circles correspond to the frequencies observed by Carrier & Bourban (2003). Open circles are used for modes with l=0, triangles for l=1, squares for l=2 and pentagons for l=3 (see text for more details).

Open with DEXTER

Table 4: Low degree p-mode frequencies (in $\mu$Hz) for the best model (model M2) of $\alpha$ Cen A and B. The observations are from Bouchy & Carrier (2002) for $\alpha$ Cen A and from Carrier & Bourban (2003) for $\alpha$ Cen B.

5 Comparison with previous studies

We initially consider the calibrations made without seismic constraints and in particular the two recent detailed studies by Guenther & Demarque (2000) and Morel et al. (2000). Contrary to our calibration, Guenther & Demarque (2000) did not use the masses of Pourbaix et al. (2002) which were of course not available at the time. However, they considered three different parallaxes which led to masses for the $\alpha$ Cen system very close to the ones of Pourbaix et al. (2002). Indeed, they used masses contained between 1.0844 and 1.1238 $M_\odot$ for $\alpha$ Cen A and 0.9017 and 0.9344 $M_\odot$ for $\alpha$ Cen B (see Sect. 1 for more details). Given that these masses are similar to the ones we used for our calibration and that the input physics of both evolution codes is similar (mixing-length theory for convection and helium and heavy-element diffusion), one expects good agreement between their results and ours. This is indeed the case. First of all, the initial helium aboundance of our models ( $Y_{{\rm i}}=0.275 \pm 0.010$) is in good agreement with the value of about 0.28 obtained by Guenther & Demarque. Secondly, Guenther & Demarque found an age of $6.8 \pm0.8$ Gyr if $\alpha$ Cen A does not have a convective core. As explained in Sect. 4.2, our model of $\alpha$ Cen A lies very close to the boundary between models with and without a convective core, but does not exhibit a convective core. Thus, the age of $6.52 \pm 0.30$ Gyr of our M2 model is perfectly compatible with the results of Guenther & Demarque. Finally, Guenther & Demarque found that the mixing-length parameter of $\alpha$ Cen A is about 10% smaller that the one of the B component. However, they pointed out that this difference may not be significant, because the observables available at the time of their studies were not sufficient to strongly constrain the models. Thanks to the asteroseismic results of Bouchy & Carrier (2002) and Carrier & Bourban (2003), we obtained a model of the $\alpha$ Cen system which is now firmly constrained. As a result, we confirm that a single mixing-length parameter cannot be found for both components of the system, as already suggested by many authors (Noels et al. 1991; Fernandes & Neuforge 1995; Guenther & Demarque 2000). Indeed, our results show that this parameter is about 8% larger for $\alpha$ Cen B than for $\alpha$ Cen A, in perfect agreement with the value of about 10% determined by Guenther & Demarque. Note that, at first sight, we would expect this parameter, if physically meaningful, to be the same for all stars regardless of mass, composition and age. However, as shown by models with rotational mixing or mixing by magnetic instability, many more effects act, to the first order, as a change of the mixing-length parameter. Thus, differences in $\alpha \equiv l/H_{{\rm p}}$ must rather be considered as a measure of our ignorance in the internal stellar hydrodynamics, rather than only a difference stricto sensu of the mixing-length parameter. Note also that the mixing-length parameter of the A component is only slightly larger than the solar calibrated mixing-length parameter ( $\alpha_{\odot}=1.7$).

The calibration of Morel et al. (2000) was based on the masses obtained by Pourbaix et al. (1999): $M_{{\rm A}}=1.16 \pm 0.031$ $M_\odot$ and $M_{{\rm B}}=0.97 \pm 0.032$ $M_\odot$. These masses are larger than the ones considered by Guenther & Demarque (2000) and the new masses of Pourbaix et al. (2002) that we used for our models. Accordingly, the results obtained by Morel et al. (2000) are quite different. For example, Morel et al. found an age of only 2.71 Gyr (for their model with the mixing-length theory and without overshooting). They also found values of the convection parameter that are almost equal for both stars. All these differences are mainly due to the different masses used. Note also that Morel et al. used the spectroscopic gravities to constrain the models instead of the luminosities derived from the photometry. This results in different error boxes in the HR diagram that have to be matched by the models and thus also influences the results of the calibration.

The first study of the $\alpha$ Cen system which took into account the asteroseismic measurements of the A component (Bouchy & Carrier 2002) was made by Thévenin et al. (2002). At first sight, one can think that our results are incompatible with this study, since Thévenin et al. pointed out that they were unable to produce a model of $\alpha$ Cen A and B compatible with the non-asteroseismic constraints and the data of Bouchy & Carrier (2002) using the masses of Pourbaix et al. (2002). To understand why we are able to determine a model of the $\alpha$ Cen system which is in good agreement with all observables now available for these stars, one has to compare the non-asteroseismic constraints used by the two groups. As explained in Sect. 2.2, we adopted the same effective temperature as Thévenin et al. for $\alpha$ Cen B, while we increased the uncertainty on the effective temperature of $\alpha$ Cen A ( $5810~ \pm~ 50$ K) in order to encompass the intervals of temperature used by Thévenin et al. and Thoul et al. (2003). In the same way, we adopted $[{\rm Fe/H}]_{{\rm A}}=0.22~ \pm~ 0.05$ dex for $\alpha$ Cen A and $[{\rm Fe/H}]_{{\rm B}}=0.24 \pm 0.05$ dex for $\alpha$ Cen B; these values lie between the ones used by Thévenin et al. and those adopted by Thoul et al., with larger error boxes which appear to us more realistic in view of the different values found in the literature. Finally, Thévenin et al. determined the luminosities of both stars from the Geneva photometry using mean values with errors which do not take into account the quality of the night. We also used the Geneva photometric system, but calculated the mean magnitudes using the individual values listed in Table 1 and taking into account the quality of the night. As a result, the luminosities used by Thévenin et al. are very similar to our luminosities but with smaller uncertainties. It is important to underline these small differences, because they can explain the different results found by the two studies. Indeed, our model of the $\alpha$ Cen system gives a luminosity of $\alpha$ Cen B which is in good agreement with our adopted observational constraints, but not with the small error box in the HR diagram adopted by Thévenin et al. Consequently, it is not surprising that Thévenin et al. did not find the solution we obtained. Moreover, the input physics of the evolution code used by Thévenin et al. differs from the input physics of our code. The main difference concerns the modelisation of convection: Thévenin et al. used the Canuto and Mazzitelli formulation while we used the mixing-length theory. These two different formulations can lead to significant different results, as shown by Morel et al. (2000). Another important difference concerns the hypothesis of a unique convection parameter for both stars. Indeed, Thévenin et al. assumed the convection parameters to be the same for both components. As aforesaid, we found that a single mixing-length parameter is not applicable for both components of the system, in good agreement with Thévenin et al.

We also notice that the model proposed by Thévenin et al. is not in good agreement with the new asteroseismic measurements of $\alpha$ Cen B (Carrier & Bourban 2003) due to theoretical large and small spacings that are higher than observed. Besides, Kervella et al. (2003) slightly changed the masse and the mixing-length parameter of the B component in order to obtain a model of $\alpha$ Cen B with a slightly larger radius than the one found by Thévenin et al. which is compatible with the interferometric radius. This larger radius for $\alpha$ Cen B certainly improves the agreement between their model and the observed mean large spacing. It is perhaps possible to obtain a model based on the masses derived by Thévenin et al. which is also compatible with the observed mean small spacing by redoing the whole calibration in the same way as Thévenin et al., but with the asteroseismic measurements of $\alpha$ Cen B as additional constraints. However, we consider the observed masses as true observables which have to be reproduced by a consistent model of the $\alpha$ Cen system.

Finally, we compare our results to the second calibration of $\alpha$ Cen A and B which took into account the asteroseismic observations of $\alpha$ Cen A (Thoul et al. 2003). At first sight, one can think that the study by Thoul et al. is in good agreement with our work, since they determined a model of the $\alpha$ Cen system which reproduced the observed p-mode frequencies as well as the masses of Pourbaix et al. (2002). Moreover, they found an age of 6.41 Gyr which is in good agreement with our value of $6.52 \pm 0.30$ Gyr. However, we have to notice that the non-asteroseismic observational constraints they used are quite different from ours. Indeed, Thoul et al. used the spectroscopic surface gravities, while we used the luminosities derived from the photometry, bolometric correction and parallax. We chose to use the luminosities instead of the surface gravities to constrain the models, because the luminosities are determined with higher accuracy than the surface gravities. Consequently, our error boxes in the HR diagram are smaller than the ones adopted by Thoul et al. As a result, we see that our model of $\alpha$ Cen B lies within the error box adopted by Thoul et al., whereas the model of $\alpha$ Cen B determined by Thoul et al. is not included in our error boxes; this simply means that our model is also in perfect agreement with the surface gravities, whereas the solution obtained by Thoul et al. is not compatible with the observed luminosity of $\alpha$ Cen B. Another main difference between both studies concerns the input physics of the evolution code. Indeed, the evolution code used for our calibration includes a detailed treatment of the atomic diffusion of helium and heavy elements, contrary to Thoul et al. who neglect it. This fact can also explain certain discrepancies between the results found by Thoul et al. and our results, and in particular the fact that they obtained an identical mixing-length parameter for both stars.

6 Conclusion

The aim of this work was to determine the best model for the $\alpha$ Cen system using the Geneva evolution code including atomic diffusion. This model had to reproduce all observational constraints available for $\alpha$ Cen A and B, namely the masses, the luminosities, the effective temperatures, the metallicities, the radii and the low degree p-mode frequencies of both stars. First, we used all non-asteroseismic constraints with one-sigma error boxes and found the solution $t=6.50 \pm 0.20$ Gyr, $\alpha_{{\rm A}}=1.83 \pm 0.10$, $\alpha_{{\rm B}}=1.99 \pm 0.10$, $Y_{{\rm i}}=0.275 \pm 0.010$ and $(Z/X)_{{\rm i}}=0.0435 \pm 0.0020$. However, this model, which is in perfect agreement with all non-asteroseismic measurements, was found to have large spacings $\Delta \nu_{0}$ slightly larger than observed ( $105.9 \pm 0.1$ $\mu$Hz instead of $105.5 \pm 0.1$ $\mu$Hz for $\alpha$ Cen A and $161.7~ \pm~ 0.1$ $\mu$Hz instead of $161.1~ \pm~ 0.1$ $\mu$Hz for $\alpha$ Cen B). These small discrepancies indicate that the radii observed by interferometry are slightly smaller than the ones deduced from asteroseismic measurements. Accordingly, we increased the error boxes on the observed radii from one to two sigma and found the following solution: $t=6.52 \pm 0.30$ Gyr, $\alpha_{{\rm A}}=1.83 \pm 0.10$, $\alpha_{{\rm B}}=1.97 \pm 0.10$, $Y_{{\rm i}}=0.275 \pm 0.010$ and $(Z/X)_{{\rm i}}=0.0434 \pm 0.0020$. Note that the radii of this solution are still in good agreement with the interferometric results of Kervella et al. (2003) since they are only 0.4% and 0.8% larger than the observed radii for $\alpha$ Cen A and B respectively.

To sum up, we point out that we obtained a model of the $\alpha$ Cen system which correctly reproduce all the numerous observational constraints now available for both stars. Thanks to the recent asteroseismic measurements of both components (Bouchy & Carrier 2002; Carrier & Bourban 2003), this model is firmly constrained. We therefore conclude that asteroseismic measurements are needed to determine accurate stellar parameters of a given star as well as to test the physics used in the stellar evolution codes. Indeed, non-asteroseismic constraints are not able to discriminate stellar models with similar positions in the HR diagram but different internal structures. It is however worthwhile to recall that asteroseismic measurements by themselves are not sufficient to obtain a reliable model of a given star nor to test the physics of stellar models. Indeed, the analysis of $\alpha$ Cen A and B shows that the combination of asteroseismic and non-asteroseismic constraints is the only way to obtain interesting and accurate results. Consequently, the determination of precise non-asteroseismic parameters like the luminosity, the effective temperature or the metallicity of a given star is needed. For this purpose, the analysis of a visual binary system constitutes an ideal target for future asteroseismic measurements, since it is the guarantee to obtain reliable non-asteroseismic parameters and additional constraints as the same initial chemical composition and age for both stars.

Acknowledgements

We would like to thank J. Christensen-Dalsgaard for providing us with the Aarhus adiabatic pulsation code. We also thank D. Pourbaix for helpful advices. This work was partly supported by the Swiss National Science Foundation.

References

• Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [CrossRef] (In the text)
• Bouchy, F., & Carrier, F. 2002, A&A, 390, 205 [EDP Sciences] (In the text)
• Burnet, M., & Rufener, F. 1979, A&A, 74, 54 (In the text)
• Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [CrossRef] (In the text)
• Canuto, V. M., & Mazzitelli, I. 1992, ApJ, 389, 724 [CrossRef] (In the text)
• Carrier, F., & Bourban, G. 2003, A&A, 406, L23 [EDP Sciences] [CrossRef] (In the text)
• Christensen-Dalsgaard, J. 1997, http://www.obs.aau.dk/~jcd/ adipack.n/ (In the text)
• Däppen, W., Mihalas, D., Hummer, D. G., & Mihalas, B. W. 1988, ApJ, 332, 261 [CrossRef] (In the text)
• Demarque, P., Guenther, D. B., & van Altena, W. F. 1986, ApJ, 300, 773 [CrossRef] (In the text)
• Edmonds, P., Cram, L., Demarque, P., et al. 1992, ApJ, 394, 313 [CrossRef] (In the text)
• Endl, M., Kürster, M., Els, S., Hatzes, A. P., & Cochran, W. D. 2001, A&A, 374, 675 [EDP Sciences] [CrossRef] (In the text)
• Fernandes, J., & Neuforge, C. 1995, A&A, 295, 678 (In the text)
• Flannery, B. P., & Ayres, T. R. 1978, ApJ, 221, 175 [CrossRef] (In the text)
• Flower, P. 1996, ApJ, 469, 355 [CrossRef] (In the text)
• Fossat, E., Grec, G., Gelly, B., & Decanini, Y. 1984, C. R. Acad. Sci. Paris, Sér. 2, 229, 17 (In the text)
• Golay, M. 1980, Vist. Astron., 24, 141 (In the text)
• Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [CrossRef] (In the text)
• Guenther, D. B., & Demarque, P. 2000, ApJ, 531, 503 [CrossRef] (In the text)
• Heintz, W. D. 1982, The Observatory, 102, 42 (In the text)
• Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794 [CrossRef] (In the text)
• Kamper, K. W., & Wesselink, A. J. 1978, AJ, 83, 1653 [CrossRef] (In the text)
• Kervella, P., Thévenin, F., Ségransan, D., et al. 2003, A&A, 404, 1087 [EDP Sciences] [CrossRef] (In the text)
• Kim, Y.-C. 1999, JKAS, 32, 119 (In the text)
• Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 (In the text)
• Lydon, T. J., Fox, P. A., & Sofia, S. 1993, ApJ, 413, 390 [CrossRef] (In the text)
• Meynet, G., & Maeder, A. 2000, A&A, 361, 101 (In the text)
• Mihalas, D., Däppen, W., Hummer, D. G. 1988, ApJ, 331, 815 [CrossRef] (In the text)
• Morel, P., Provost, J., Lebreton, Y., & Berthomieu, G. 2000, A&A, 363, 675 (In the text)
• Neuforge, C. 1992, A&A, 268, 650 (In the text)
• Neuforge-Verheecke, C., & Magain, P. 1997, A&A, 328, 261 (In the text)
• Noels, A., Grevesse, N., Magain, P., et al. 1991, A&A, 247, 91 (In the text)
• Paquette, C., Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJ, 61, 177 [CrossRef] (In the text)
• Pourbaix, D., Neuforge-Verheecke, C., & Noels, A. 1999, A&A, 344, 172 (In the text)
• Pourbaix, D., Nidever, D., McCarthy, C., et al. 2002, A&A, 386, 280 [EDP Sciences] [CrossRef] (In the text)
• Richard, O., Vauclair, S., Charbonnel, C., & Dziembowski, W. A. 1996, 312, 1000 (In the text)
• Rufener, F. 1964, Publ. Obs. Genève, A, 66, 413 (In the text)
• Rufener, F. 1985, in Calibration of Fundamental Stellar Quantities, ed. D. S. Hayes, L. E. Pasenetti, & A. G. Davis Philip (Dordrecht: Reidel Publ. Co.), IAU Symp., 111, 253 (In the text)
• Söderhjelm, S. 1999, A&A, 341, 121 (In the text)
• Tassoul, M. 1980, ApJS, 43, 469 [CrossRef] (In the text)
• Thévenin, F., Provost, J., Morel, P., et al. 2002, A&A, 392, L9 [EDP Sciences] [CrossRef] (In the text)
• Thoul, A., Scuflaire, R., Noels, A., et al. 2003, A&A, 402, 293 [EDP Sciences] [CrossRef] (In the text)
• Turcotte, S., Richer, J., Michaud, G., et al. 1998, ApJ, 504, 539 [CrossRef] (In the text)