A&A 416, 191-212 (2004)
DOI: 10.1051/0004-6361:20031704
On the internal structure of starless cores
I. Physical conditions and the distribution of CO, CS, N2H+,
and NH3 in L1498 and L1517B
M. Tafalla 1 - P. C. Myers 2 - P. Caselli 3 - C. M. Walmsley 3
1 - Observatorio Astronómico Nacional, Alfonso XII 3, 28014 Madrid,
Spain
2 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge,
MA 02138, USA
3 -
Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125
Firenze, Italy
Received 16 June 2003 / Accepted 24 November 2003
Abstract
We have characterized the physical structure and chemical composition of two
close-to-round starless cores in Taurus-Auriga,
L1498 and L1517B. Our analysis is based
on high angular resolution observations in
at least two transitions of NH3, N2H+, CS,
C34S, C18O, and C17O, together with maps of the 1.2 mm
continuum. For both cores, we derive radial profiles of constant
temperature and constant turbulence, together
with density distributions close to those
of non-singular isothermal spheres. Using these physical
conditions and a Monte Carlo radiative transfer
model, we derive abundance profiles for all species
and model the strong chemical differentiation
of the core interiors. According to our
models, the NH3 abundance increases toward the core centers
by a factor of several 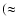 5) while N2H+has a constant abundance over most of the cores. In contrast, both
C18O and CS (and isotopomers) are strongly depleted in the core
interiors, most likely due to their freeze out
onto grains at densities of a few 104 cm-3. Concerning the
kinematics of the dense gas, we find (in addition to constant turbulence)
a pattern of internal motions at the level of 0.1 km s-1.
These motions seem
correlated with asymmetries in the pattern of molecular depletion,
and we interpret them as residuals of core contraction.
Their distribution and size suggest that
core formation occurs in a rather irregular manner
and with a time scale of a Myr. A comparison of our derived core
properties with those predicted by
supersonic turbulence models of core formation
shows that our Taurus cores are much more quiescent than representative predictions from these models. In two appendices at the end of the paper
we present a simple and accurate approximation to the density profile
of an isothermal (Bonnor-Ebert) sphere, and a Monte Carlo-calibrated
method to derive gas kinetic temperatures using NH3 data.
5) while N2H+has a constant abundance over most of the cores. In contrast, both
C18O and CS (and isotopomers) are strongly depleted in the core
interiors, most likely due to their freeze out
onto grains at densities of a few 104 cm-3. Concerning the
kinematics of the dense gas, we find (in addition to constant turbulence)
a pattern of internal motions at the level of 0.1 km s-1.
These motions seem
correlated with asymmetries in the pattern of molecular depletion,
and we interpret them as residuals of core contraction.
Their distribution and size suggest that
core formation occurs in a rather irregular manner
and with a time scale of a Myr. A comparison of our derived core
properties with those predicted by
supersonic turbulence models of core formation
shows that our Taurus cores are much more quiescent than representative predictions from these models. In two appendices at the end of the paper
we present a simple and accurate approximation to the density profile
of an isothermal (Bonnor-Ebert) sphere, and a Monte Carlo-calibrated
method to derive gas kinetic temperatures using NH3 data.
Key words: ISM: abundances - ISM: clouds -ISM: molecules -
stars: formation - ISM: individual objects: L1498, L1517B
Dense cores like those in Taurus and other nearby dark clouds
represent the simplest environments where stars form. Their study holds
the
promise of revealing the basic physics of star formation, but despite
their apparent simplicity, dense cores
remain mysterious in their internal structure,
formation and evolution, and in the manner in which they collapse under gravity
(see, e.g., Myers 1999; Evans 1999 for recent reviews). Part of this
mystery results from a number of contradictions between
observations of different dense gas tracers (see, e.g., Zhou et al. 1989),
which have so far precluded a self consistent description of the core internal
properties. Fortunately,
multi-molecular and continuum observations over the last few years
have started to suggest that most contradictions arise from
cores not being chemically homogeneous, as initially assumed,
but having strongly differentiated interiors (Kramer et al. 1999; Kuiper et al. 1996; Willacy et al. 1998; Alves et al. 1999; Tafalla et al. 2002; Bergin et al. 2002,2001; Bacmann et al. 2002; Jessop & Ward-Thompson 2001; Caselli et al. 1999).
Understanding and characterizing the chemical structure
of dense cores has therefore become a top priority for star formation
studies, as solving this problem may finally produce
a coherent picture of dense cores, from which
their star forming evolution may be inferred.
If cores have strong chemical composition gradients,
in addition to density gradients, their description cannot
rely on average parameters, as often assumed.
It is necessary to use spatially-variable abundances, and these
need to be derived from the data
through a realistic modeling of the radiative transfer.
This approach, unfortunately, involves a number of uncertainties, one of
the largest being
our ignorance of the exact (3D) geometry of a core, which
is not well constrained either by theory or 2D images (e.g.,
compare Jones & Basu 2002 with Curry 2002). To minimize
this effect, it is convenient to concentrate on cores with relatively
simple geometries, and for this reason, we have selected L1498 and L1517B
as subjects of the present study.
L1498 and L1517B are two dense cores in the Taurus-Auriga
cloud complex, and were first identified by Myers et al. (1983) from the
inspection of Palomar Sky Atlas prints. They are not associated with
IRAS point sources (Beichman et al. 1986) or 1.2 mm point
sources (Tafalla et al. 2002), and can therefore be considered starless.
Over the last decade, L1498 has been the subject of a number of
detailed studies: Lemme et al. (1995) mapped its C18O and CS emission, Kuiper et al. (1996) first identified it as a chemically differentiated system,
and further details of its chemical structure have been presented by Wolkovitch et al. (1997) for CCS and Willacy et al. (1998) for CO. More recently, Langer & Willacy (2001) have presented an estimate of the core density profile from
FIR data and Levin et al. (2001) have estimated an upper limit to
its magnetic field of 100 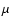 G from Zeeman observations.
Tafalla et al. (2002, TMCWC hereafter) presented line and
continuum observations of L1498,
L1517B, and three other dense cores, and found a systematic pattern
of chemical differentiation: species like CS and CO
are almost absent from
the core interiors while NH3 and N2H+ are present even in
the densest parts. In this paper, we improve the study of
L1498 and L1517B using new multiline, high angular resolution observations
and creating for each core a model of the internal conditions
that simultaneously explains all our C18O,
C17O, CS, C34S, N2H+, and NH3 data.
As a result, we confirm the presence of a systematic
abundance pattern, and show that the two cores are very close to
isothermal spheres both in their density profiles and
physical parameters (temperature and turbulence). At the same time, we
infer that the core contraction history has been asymmetrical,
both from the internal kinematics and the chemical composition.
In a follow-up
paper (Tafalla et al. 2004, in preparation) we will present a full
chemical survey of these two cores.
G from Zeeman observations.
Tafalla et al. (2002, TMCWC hereafter) presented line and
continuum observations of L1498,
L1517B, and three other dense cores, and found a systematic pattern
of chemical differentiation: species like CS and CO
are almost absent from
the core interiors while NH3 and N2H+ are present even in
the densest parts. In this paper, we improve the study of
L1498 and L1517B using new multiline, high angular resolution observations
and creating for each core a model of the internal conditions
that simultaneously explains all our C18O,
C17O, CS, C34S, N2H+, and NH3 data.
As a result, we confirm the presence of a systematic
abundance pattern, and show that the two cores are very close to
isothermal spheres both in their density profiles and
physical parameters (temperature and turbulence). At the same time, we
infer that the core contraction history has been asymmetrical,
both from the internal kinematics and the chemical composition.
In a follow-up
paper (Tafalla et al. 2004, in preparation) we will present a full
chemical survey of these two cores.
We observed L1498 and L1517B in the 1.2 mm continuum with the IRAM 30 m
telescope in 1999 December and 2000 December. We used the MAMBO 1
bolometer array (Kreysa et al. 1998) in on-the-fly mode with a scanning speed of
4'' s-1, a wobbler period of 0.5 s, and a wobbler throw of 53''.
The data were corrected for atmospheric
extinction using sky dips done before and after
each individual map, and they were reduced using the NIC software (Broguière et al. 1996).
A global calibration factor of 15 000 counts per Jy beam-1
was estimated for both 1999 and 2000 epochs from observations of Uranus.
The bolometer central frequency is 240 GHz and the
telescope beam size is approximately 11''. (The 1999 data have already
been presented in Tafalla et al. 2002.)
We observed L1498 and L1517B in C18O(1-0), C18O(2-1),
C17O(2-1), CS(2-1), CS(3-2), C34S(2-1), C34S(3-2),
and N2H+(1-0) with the IRAM 30 m telescope in 2000 October. L1498 was
mapped in all lines and L1517B was mapped in all but C34S(2-1)
and C34S(3-2), which were so weak that only the central position
was observed. Additional N2H+(3-2) observations were carried out
in 2001 April. All data were taken in frequency switching mode
with frequency throws of approximately 7 or 14 MHz. As a backend we
used the facility autocorrelator, split into several windows to achieve
velocity resolutions between 0.03 and 0.06 km s-1. The
telescope pointing was corrected using frequent cross scans of continuum
sources, and the total errors were found to be smaller than 4'' (rms).
The data were calibrated using the standard chopper wheel method
and converted to the main beam brightness temperature scale. The full
width at half maximum (FWHM) of the telescope beam is inversely
proportional to the frequency, and ranges from approximately
26'' at the (lowest) frequency of N2H+(1-0) to 11'' at the (highest)
frequency of N2H+(3-2).
As stressed in previous studies (Tafalla et al. 2002; Lee et al. 2001), the modeling
and interpretation of
the very narrow spectral lines from starless cores like L1498 and L1517B
(FWHM
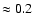 km s-1
km s-1 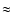 70 kHz at 100 GHz) requires using
rest frequency values more accurate
than those in standard compilations. Fortunately, current laboratory
work is starting to produce frequency determinations with uncertainties
of the order of 1 kHz, and whenever such a measurement exists we have
preferred it over any other value, including our own previous astronomical
determinations (Lee et al. 2001). The rest frequencies used in this paper are
indicated in Table 1.
70 kHz at 100 GHz) requires using
rest frequency values more accurate
than those in standard compilations. Fortunately, current laboratory
work is starting to produce frequency determinations with uncertainties
of the order of 1 kHz, and whenever such a measurement exists we have
preferred it over any other value, including our own previous astronomical
determinations (Lee et al. 2001). The rest frequencies used in this paper are
indicated in Table 1.
Table 1:
Rest frequencies.
![\begin{figure}
\par\includegraphics[clip,width=15.1cm]{4112.f1}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg27.gif) |
Figure 1:
1.2 mm continuum maps of L1498 ( left) and L1517B ( right).
Note the central concentration and symmetry of the emission. In order to
enhance the sensitivity, each map has been convolved with
a 20'' Gaussian. First contour and contour spacing are 2 mJy/11''-beam,
and central coordinates are
(
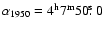 , ,
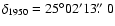 )
for L1498 and
( )
for L1498 and
(
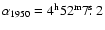 , ,
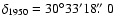 )
for L1517B. )
for L1517B. |
| Open with DEXTER |
In contrast with the molecules, whose emissivity is highly
sensitive to excitation and chemistry (see below), the dust
in a starless core is expected to have an emissivity approximately constant
with radius (see also below for caveats). This property allows
a rather straightforward conversion
of the observed continuum emission into a density profile
(e.g., André et al. 1996; Ward-Thompson et al. 1994; Evans et al. 2001), and for
this reason, we start our analysis of L1498 and L1517B by
studying their dust emission.
Figure 1 presents 1.2 mm continuum maps of L1498 and L1517B, and shows
that in both cores the mm emission
is centrally concentrated. In L1498, the emission appears slightly
elongated SE-NW, while L1517B is rounder with a weak extension to the SW
(and a weaker one to the NE). Neither of the cores presents evidence for
an unresolved point-like component, indicative of an embedded object, so
they appear as bona fide starless cores.
To estimate the density distributions of L1498 and L1517B from the
data shown in Fig. 1, we follow the same procedure as in
TMCWC (where the December 1999 part of this dataset was presented).
Thus, we approximate each core as a spherical system, and derive
a continuum radial profile by taking an azimuthal average of
its map. As L1498
is slightly elongated, we average the data of this source
in ellipses of position
angle 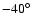 and aspect ratio b/a=0.6, while for the rounder L1517B,
we average the data in circles. These radial profiles are
presented in Fig. 2 both in linear and log-log scales. (Core centers are assumed to be at (10'', 0) and (-15'', -15'') for L1498 and L1517B, respectively.)
and aspect ratio b/a=0.6, while for the rounder L1517B,
we average the data in circles. These radial profiles are
presented in Fig. 2 both in linear and log-log scales. (Core centers are assumed to be at (10'', 0) and (-15'', -15'') for L1498 and L1517B, respectively.)
To model each continuum radial profile we need to assume
a dust temperature law. Theoretical models of
the dust temperature in cores
predict a slight inward decrease (Zucconi et al. 2001; Mathis et al. 1983; Evans et al. 2001), which for the case of
the L1498 and L1517B cores is estimated to range between
11 K in the outer layers and 8 K in the innermost part (Evans et al. 2001, their model for L1512). Here, for
simplicity (and from our NH3 analysis in Sect. 3.3),
we will assume that both cores have a constant dust
temperature of 10 K, and we will use this value to estimate their
density radial profiles (see also Langer & Willacy 2001).
In addition, we assume a constant dust emissivity of
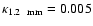 cm2 g-1, for consistency with previous
work (e.g., André et al. 1996). Following TMCWC, we fit the
data using a density profile of the form
cm2 g-1, for consistency with previous
work (e.g., André et al. 1996). Following TMCWC, we fit the
data using a density profile of the form
where n0 is the central density, r0 is the radius of the
inner "flat'' region
(2 r0 is the full width at half maximum), and 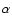 is
the asymptotic power index. For each choice of n0, r0,
and
is
the asymptotic power index. For each choice of n0, r0,
and 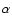 ,
we calculate the emergent
continuum distribution by integrating the equation of radiative
transfer in the optically thin case, and simulate an
on-the-fly bolometer observation of such a distribution
using the same instrumental parameters as those used at the telescope.
The radial profile of this simulated observation is compared
with the measured radial profile, and the free parameters n0, r0,
and
,
we calculate the emergent
continuum distribution by integrating the equation of radiative
transfer in the optically thin case, and simulate an
on-the-fly bolometer observation of such a distribution
using the same instrumental parameters as those used at the telescope.
The radial profile of this simulated observation is compared
with the measured radial profile, and the free parameters n0, r0,
and 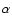 are modified until model and data agree.
As shown by the solid lines in Fig. 2, the final choice of free parameters
(Table 2)
gives very reasonable fits for both cores, and indicates that L1517B
is twice as dense at its center than L1498, while it has a FWHM
approximately half that of L1498 (so both cores have similar
central column densities:
are modified until model and data agree.
As shown by the solid lines in Fig. 2, the final choice of free parameters
(Table 2)
gives very reasonable fits for both cores, and indicates that L1517B
is twice as dense at its center than L1498, while it has a FWHM
approximately half that of L1498 (so both cores have similar
central column densities:
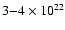 cm-2).
We note that the fit for L1517B is the same as derived in TMCWC,
while the fit for L1498 is only slightly different (by less than
10% for radii smaller than 110'' and by less than 30%
in the range 110-150'').
cm-2).
We note that the fit for L1517B is the same as derived in TMCWC,
while the fit for L1498 is only slightly different (by less than
10% for radii smaller than 110'' and by less than 30%
in the range 110-150'').
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f2}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg33.gif) |
Figure 2:
Radial profiles of 1.2 mm continuum emission (from the
maps in Fig. 1).
The squares represent observed data and the lines are the
predictions from two density models: the solid line is a simple
analytic model and the dashed line is an isothermal model (see text).
Both linear-linear and log-log plots are shown. |
| Open with DEXTER |
Although our analytical density distributions
accurately fit the continuum data, their motivation is purely
phenomenological. As detailed in Appendix A, however,
a particular choice of parameters in this density family
provides an excellent approximation
to an isothermal function (or Bonnor-Ebert sphere), and this choice
happens to be the best fit for L1517B (see Appendix A for further details).
This "coincidence'' motivated us to explore isothermal
fits to the L1517B and L1498 radial profiles
as an alternative to the analytical models presented before. For this,
we have used the numerical solution to the isothermal function
by Chandrasekhar & Wares (1949), and searched for the best fit to each core
by varying the central
density and the isothermal sound speed as independent free parameters.
In this procedure, we have followed the steps explained in the fitting with
analytical models including the on-the-fly simulation, and
the best fit parameters are given in Table 2. As can be seen in
Fig. 2, the isothermal models (dashed lines) provide reasonable
fits to the observed continuum data, especially for the rounder L1517B,
where the isothermal and analytic models are
indistinguishable (see also Appendix A). For the more elongated L1498 core,
the isothermal model does not
fit the radial profile as well as the analytic function,
but its deviation from the data is never very large (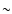 25% at the
center), and is less than the deviation of this core from
spherical geometry (about 40%). Our fits of L1498 and L1517B, therefore,
add to recent evidence that the density profiles of
starless cores can be modeled exactly or approximately
by isothermal spheres (Alves et al. 2001; Evans et al. 2001; Bacmann et al. 2000).
25% at the
center), and is less than the deviation of this core from
spherical geometry (about 40%). Our fits of L1498 and L1517B, therefore,
add to recent evidence that the density profiles of
starless cores can be modeled exactly or approximately
by isothermal spheres (Alves et al. 2001; Evans et al. 2001; Bacmann et al. 2000).
As shown by Ebert (1955) and Bonnor (1956), a self gravitating isothermal
sphere is stable only if it is bounded from the outside
and its center-to-edge density contrast does not exceed a
limiting value close to 14, or equivalently, its dimensionless radius
(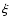 )
does not
exceed the critical value 6.45. Although neither L1498
nor L1517B show a clear boundary at which the core merges with
an external medium, we can assess possible core stability
by calculating the critical radius for each core.
For the less centrally concentrated L1498 core, the
critical radius occurs at 150'', which is at the very edge of our map
(defined by the sensitivity of our continuum measurements).
For L1517B, the critical radius occurs at 100''; so if the isothermal
core continues to the edge of our map, the core would seem unstable.
This situation is similar to that found by Bacmann et al. (2000) in their
study of a sample of starless cores with ISOCAM. We defer further discussion
of the isothermal model and its stability to Sect. 4.1.
)
does not
exceed the critical value 6.45. Although neither L1498
nor L1517B show a clear boundary at which the core merges with
an external medium, we can assess possible core stability
by calculating the critical radius for each core.
For the less centrally concentrated L1498 core, the
critical radius occurs at 150'', which is at the very edge of our map
(defined by the sensitivity of our continuum measurements).
For L1517B, the critical radius occurs at 100''; so if the isothermal
core continues to the edge of our map, the core would seem unstable.
This situation is similar to that found by Bacmann et al. (2000) in their
study of a sample of starless cores with ISOCAM. We defer further discussion
of the isothermal model and its stability to Sect. 4.1.
Table 2:
Density fits from continuum data.
![\begin{figure}
\par\includegraphics[clip,width=10.3cm]{4112.f3}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg35.gif) |
Figure 3:
Integrated intensity maps for continuum and lines
observed toward L1498 and L1517B. Note the systematic
dichotomy between centrally-peaked and centrally-depressed
morphologies. For each core, the top row shows the maps of
centrally-peaked tracers, 1.2 mm continuum, N2H+, and NH3, and
the two lower rows present the maps of centrally-depressed species,
isotopomers of CO ( middle row) and isotopomers of CS ( bottom row).
In each map, the lowest contour and the contour interval are equal, and
for each line, the same contour choice has been used for both L1498
and L1517B. Lowest contours are (in K km s-1): 0.15 for C18O(1-0)
and (2-1), 0.05 for C17O(2-1), 0.25 for N2H+(1-0), 1.5 for
NH3(1, 1), 0.15 for CS(2-1), 0.1 for CS(3-2), and 0.05 for C34S(2-1).
Continuum maps and central positions as in Fig. 1.
The C17O(2-1) data have been convolved with a 35'' ( FWHM) Gaussian
to improve S/N. |
| Open with DEXTER |
To derive the temperature, kinematics, and chemical structure of L1498
and L1517B, we now analyze their molecular emission. Before
starting the detailed radiative transfer modeling, we first present a
comparison between the integrated maps of all species and identify
the most general trends. As Fig. 3 shows (see also TMCWC), the maps
of each core
display a striking dichotomy - almost to the point of anti correlation -
between the distribution of the different tracers:
the 1.2 mm continuum, N2H+, and
NH3 emission on the one hand
are compact and centrally concentrated, while the CO and CS isotopomer
emission on the other hand
are extended and almost ring-like. In the larger L1498 core, the
CO/CS ring is well resolved spatially, and it appears fragmented with
a bright peak toward the SE. In the more compact L1517B core,
the CO isotopomers form a well-defined half ring toward the west, while
the CS emission is more concentrated, although it is still offset toward
the west from the 1.2 mm/N2H+ maximum.
As modeled in detail in the next sections,
the ring distributions of the CO and CS isotopomers result from a
sharp drop in the abundances of these molecules toward the dense centers
of the cores, most likely caused by the freeze out of
these molecules onto dust grains (for additional cases, see Kramer et al. 1999; Kuiper et al. 1996; Bergin et al. 2001; Bacmann et al. 2002; Jessop & Ward-Thompson 2001; Willacy et al. 1998; Caselli et al. 1999; Alves et al. 1999; TMCWC).
N2H+ and NH3, on the other hand, seem immune to this process
at typical core densities
and they are
present in the gas phase all throughout the core.
The goal of the following sections is to derive self consistent models
of the internal structure of
L1498 and L1517B that fit simultaneously all line observations.
For this, we model the cores as spherically symmetric systems and
predict the emission from each molecule with a Monte Carlo
radiative transfer code based on that of Bernes (1979). The physical
properties of these models are fully defined by radial profiles of density,
temperature, turbulent velocity, and systematic velocity, and the same
parameters are used to model all molecular lines. As core density
profiles, we use the analytic functions derived from the continuum data,
and the rest of the gas parameters are derived from the molecular line data.
In our derivation of these parameters we have favored simplicity over
detailed fine tuning, and here we summarize the main results (see following
sections for more details and Table 3 for a parameter list). To derive
gas temperature profiles, we have used the NH3 data, and we have found
that this parameter is
constant with radius in both cores (Sect. 3.3). The turbulent profiles
are also derived from the NH3 data, and they are constant with
radius, as indicated by the radial profiles of linewidth (Sect. 3.7.1).
The profiles of systematic velocity have been derived
from the combined fit to all line shapes, as different species
trace the gas velocity at different radii depending on optical
depth. For both L1498 and L1517B, we find that the velocity field in
the core central part
is constant, as indicated by the NH3 data, and that there is a
slight gradient toward the outside traced by the velocity of
the CS self absorptions
(Sect. 3.6). For simplicity we have modeled this outer gradient with a
linear function.
When modeling the self absorbed lines of CS (Sect. 3.6), HCO+, and
HCN (Tafalla et al. 2004 in preparation), the shape of the profiles
depends very sensitively on the gas conditions at very large radii
(>
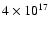 cm
cm
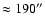 ). These conditions, however,
cannot
be safely extrapolated from our dust continuum or NH3 data, as they
correspond more to the ambient cloud or envelope than to the dense
core itself, and favoring again simplicity, we have modeled
them using constant gas parameters determined from an approximate fit to the
line self absorptions of different molecules. For both L1498 and L1517B,
we have introduced a discontinuity in the density profile at
). These conditions, however,
cannot
be safely extrapolated from our dust continuum or NH3 data, as they
correspond more to the ambient cloud or envelope than to the dense
core itself, and favoring again simplicity, we have modeled
them using constant gas parameters determined from an approximate fit to the
line self absorptions of different molecules. For both L1498 and L1517B,
we have introduced a discontinuity in the density profile at
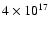 cm, where both cores reach a density of approximately
cm, where both cores reach a density of approximately
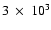 cm-3, and we have extended these profiles with
envelopes of constant density equal to 103 cm-3 up to
a radius of
cm-3, and we have extended these profiles with
envelopes of constant density equal to 103 cm-3 up to
a radius of
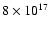 cm. To match the self absorption
features, we have set the velocity of this envelope equal to zero
for L1517B and to 0.35 km s-1 for L1498 (inward motion), and the
turbulent component equal to 4 and 5 times the central turbulence, for
L1517B and L1498 respectively. As we will see below, the inward-moving
envelope component in L1498 seems only present in the front part of
the cloud and most likely represents an unrelated foreground cloud,
so we have neglected the contribution of the back side of the
envelope in this object. It should be stressed that our parameterization
of the cloud envelopes is highly simplified
and it has been carried out with the only purpose of fitting the shape of
the self absorbed lines. These envelopes have no effect on the
emission of the thin lines used to determine the abundance profiles
of each species, so their role in the modeling is almost cosmetic. Detailed
mapping of the environment surrounding the cores is necessary to
further constrain the envelope properties.
cm. To match the self absorption
features, we have set the velocity of this envelope equal to zero
for L1517B and to 0.35 km s-1 for L1498 (inward motion), and the
turbulent component equal to 4 and 5 times the central turbulence, for
L1517B and L1498 respectively. As we will see below, the inward-moving
envelope component in L1498 seems only present in the front part of
the cloud and most likely represents an unrelated foreground cloud,
so we have neglected the contribution of the back side of the
envelope in this object. It should be stressed that our parameterization
of the cloud envelopes is highly simplified
and it has been carried out with the only purpose of fitting the shape of
the self absorbed lines. These envelopes have no effect on the
emission of the thin lines used to determine the abundance profiles
of each species, so their role in the modeling is almost cosmetic. Detailed
mapping of the environment surrounding the cores is necessary to
further constrain the envelope properties.
Having fixed the physical parameters of the cores (summarized in Table 3),
the only free parameter left to fit the emission of each species is
the radial profile of its abundance. To determine this profile,
we have searched for Monte Carlo solutions of the radiative transfer
that fit simultaneously the radial profile of integrated
intensity and the central spectrum of each observed transition.
This approach is similar to that of TMCWC, with the
novelty that the present analysis uses higher
spatial resolution observations, and that for each
species we simultaneously model multiple transitions.
This new analysis results in a more detailed and accurate
derivation of the physical and chemical structure of the cores.
Table 3:
Monte Carlo model fits.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f4}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg64.gif) |
Figure 4:
Radial profiles of gas kinetic temperature for L1498 and L1517B
derived from NH3. The squares represent real data and
the solid lines
represent the result of applying the same NH3 analysis used
for the data to spectra generated with a Monte Carlo model
having constant temperature (10 K for L1498 and 9.5 K for L1517B).
The dashed lines are the expected NH3-derived 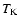 profile
for two temperature equilibrium models (see text for details).
profile
for two temperature equilibrium models (see text for details). |
| Open with DEXTER |
TMCWC used NH3 data to determine the gas kinetic temperature
of several cores including L1498 and L1517B. Given the importance
of this parameter and the recent
calculations of the expected temperature structure of dense cores (Galli et al. 2002; Zucconi et al. 2001; Evans et al. 2001), here we present an improved NH3 analysis using the new density profiles
of Sect. 3.1 and a more accurate temperature determination method.
Our new method is an updated version of the
classical analysis (e.g., Walmsley & Ungerechts 1983) calibrated
with Monte Carlo radiative transfer models, and as detailed in
Appendix B, it provides accurate temperature determinations
for realistic core conditions. With its help, we first
estimate the L1498 and L1517B temperature profiles directly from
the NH3 data,
and then use the full Monte Carlo model to fit the observed
radial profiles and spectra deriving NH3 abundance profiles
(and demonstrating the self consistency of the temperature determination).
To derive the temperature profiles of L1498 and L1517B, we first
estimate the
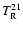 rotation temperature for each observed
position using the NH3 lines.
This involves fitting the hyperfine (hf) structure of
the NH3(1, 1) spectra (where we find that the
hf components are in LTE), fitting single Gaussians
to the NH3(2, 2) spectra, and estimating the ratio between the
(2, 2) and (1, 1) populations (see Bachiller et al. 1987 for details).
Then, we use the analytical expression derived in Appendix B
to convert each rotation temperature into a gas kinetic
temperature. The resulting temperature radial profiles,
presented in Fig. 4, show that in each core
the gas kinetic temperature is to very good approximation constant
with radius and almost equal to 10 K with an rms of about 1 K.
rotation temperature for each observed
position using the NH3 lines.
This involves fitting the hyperfine (hf) structure of
the NH3(1, 1) spectra (where we find that the
hf components are in LTE), fitting single Gaussians
to the NH3(2, 2) spectra, and estimating the ratio between the
(2, 2) and (1, 1) populations (see Bachiller et al. 1987 for details).
Then, we use the analytical expression derived in Appendix B
to convert each rotation temperature into a gas kinetic
temperature. The resulting temperature radial profiles,
presented in Fig. 4, show that in each core
the gas kinetic temperature is to very good approximation constant
with radius and almost equal to 10 K with an rms of about 1 K.
The temperature profiles in Fig. 4 represent line-of-sight
averages spatially smoothed with a 40'' Gaussian (telescope resolution). To
test the possibility that a realistic non-constant temperature
distribution could mimic the constant temperature profile
of our NH3 analysis,
we have run a Monte Carlo NH3 model for L1517B using the temperature
law recently calculated by Galli et al. (2002) (and kindly adapted to L1517B
by Daniele Galli). The synthetic NH3 spectra from this model have been
analyzed as the real data and used to compute an NH3-derived temperature
profile. As the upper dashed line in Fig. 4
shows, a model with the "standard'' cosmic ray ionization rate of
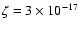 s-1 (Goldsmith 2001), overestimates the
core temperature at all radii (in fact, it overestimates the (2, 2) intensity by
more than a factor of 2). However, reducing
s-1 (Goldsmith 2001), overestimates the
core temperature at all radii (in fact, it overestimates the (2, 2) intensity by
more than a factor of 2). However, reducing 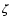 by a
factor of 5 (lower dashed curve) produces a temperature profile consistent
with the observations (such a low
by a
factor of 5 (lower dashed curve) produces a temperature profile consistent
with the observations (such a low 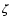 value is also favored by
the chemical models of the L1544 core in Taurus by Caselli et al. 2002b,
but see McCall et al. 2003 for the opposite conclusion in a nearby cloud).
This low
value is also favored by
the chemical models of the L1544 core in Taurus by Caselli et al. 2002b,
but see McCall et al. 2003 for the opposite conclusion in a nearby cloud).
This low 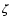 temperature profile is in fact almost
constant, as it has a maximum-to-minimum variation of less than
1.5 K in the region of interest. We thus conclude that the gas
kinetic temperature in the L1498 and L1517B cores is constant within
about 10%, and that this property is consistent with a realistic
treatment of the heating and cooling of dense gas (assuming a low
temperature profile is in fact almost
constant, as it has a maximum-to-minimum variation of less than
1.5 K in the region of interest. We thus conclude that the gas
kinetic temperature in the L1498 and L1517B cores is constant within
about 10%, and that this property is consistent with a realistic
treatment of the heating and cooling of dense gas (assuming a low 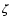 value).
value).
![\begin{figure}
\par\includegraphics[clip,width=17.6cm]{4112.f5}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg67.gif) |
Figure 5:
Radial profiles of integrated intensity and central spectra
of NH3(1, 1) and (2, 2) towards L1498 and L1517B. The squares in the
radial profiles and the histograms in the spectra represent real data.
The solid lines represent the results of Monte Carlo radiative transfer
models with constant temperature and a central NH3 abundance
enhancement (see text). Note how they simultaneously fit the radial profiles
and the central spectra (they also fit the NH3-derived temperature
profiles, see previous figure). The dashed lines in the radial profiles are
models with constant NH3 abundance, chosen to fit the
observations at large radius (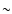 60''). Note how these flatter profiles
cannot fit the observed central emission.
The velocity scale in L1517B has been shifted by 2 km s-1 for
presentation purposes.
(Note that the 1-sigma uncertainty in the
integrated intensity points is of the order of 0.2 K km s-1for NH3(1, 1) and 0.8 K km s-1 for NH3(2, 2) multiplied by 20,
and it is therefore similar to the size of the squares.) 60''). Note how these flatter profiles
cannot fit the observed central emission.
The velocity scale in L1517B has been shifted by 2 km s-1 for
presentation purposes.
(Note that the 1-sigma uncertainty in the
integrated intensity points is of the order of 0.2 K km s-1for NH3(1, 1) and 0.8 K km s-1 for NH3(2, 2) multiplied by 20,
and it is therefore similar to the size of the squares.) |
| Open with DEXTER |
Given the above results, we model both L1498 and L1517B as
having constant temperature, and for each core, we search for the NH3
abundance profile that fits simultaneously the observed (1, 1) and (2, 2) radial profiles of integrated intensity together with the
central spectra of both transitions. We do this by using our full non LTE
Monte Carlo radiative transfer analysis, and convolve the results with
a 40'' Gaussian to simulate an observation with the Effelsberg antenna
(see Appendix B for details). For L1517B, our best model is identical
to that in TMCWC, as we use the same density profile.
This means that the gas temperature has a constant
value of 9.5 K and that the para-NH3abundance increases inwards following the law
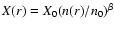 ,
where
,
where
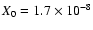 and
and 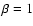 (the above expression is only valid for
X > 10-9).
Our best fit model for L1498
is slightly different from that in TMCWC because of our improved
density profile and core peak determination from the new continuum
data. This model has a constant temperature of 10 K and a para-NH3
abundance that increases inwards following the same law as in L1517B,
but this time with
(the above expression is only valid for
X > 10-9).
Our best fit model for L1498
is slightly different from that in TMCWC because of our improved
density profile and core peak determination from the new continuum
data. This model has a constant temperature of 10 K and a para-NH3
abundance that increases inwards following the same law as in L1517B,
but this time with
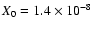 and
and 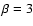 ,
and
again with a 10-9 threshold.
(Note that if the ortho-to-para ratio of NH3 equals 1,
the total NH3 abundance is 2 times the
measured para-NH3 abundance.)
As Fig. 5 shows, these NH3 models fit simultaneously the radial
profile of integrated intensity and the central
emergent spectra for both NH3(1, 1) and (2, 2). They also fit
NH3-derived temperature profiles of Fig. 4 (see solid lines).
,
and
again with a 10-9 threshold.
(Note that if the ortho-to-para ratio of NH3 equals 1,
the total NH3 abundance is 2 times the
measured para-NH3 abundance.)
As Fig. 5 shows, these NH3 models fit simultaneously the radial
profile of integrated intensity and the central
emergent spectra for both NH3(1, 1) and (2, 2). They also fit
NH3-derived temperature profiles of Fig. 4 (see solid lines).
Although initially unexpected, the higher central NH3 abundance in
L1498 and L1517B is a necessary element of the radiative transfer models. To
illustrate this point, we also
present in Fig. 5 (dashed lines) the results of constant abundance models
chosen to fit the emission at intermediate radii (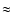 70''). As can
be seen in the figure, these models predict radial profiles that are too
flat for both NH3(1, 1) and (2, 2), and are therefore inconsistent with
the data. The higher central abundance, thus, is unavoidable,
and sets apart the NH3 molecule among all other observed species
(see Tafalla et al. 2004, in preparation, for an extensive
chemical survey of L1498 and L1517B). In Sect. 4.2 we discuss the
possible origin of this behavior.
70''). As can
be seen in the figure, these models predict radial profiles that are too
flat for both NH3(1, 1) and (2, 2), and are therefore inconsistent with
the data. The higher central abundance, thus, is unavoidable,
and sets apart the NH3 molecule among all other observed species
(see Tafalla et al. 2004, in preparation, for an extensive
chemical survey of L1498 and L1517B). In Sect. 4.2 we discuss the
possible origin of this behavior.
Like NH3, N2H+ presents centrally peaked distributions in
our maps of Fig. 3, and this suggests that the N2H+ abundance
does not vary greatly over the core interiors.
In this section we quantify this impression
by solving the N2H+ radiative transfer with our Monte Carlo code.
This code now needs to take
into account the hyperfine structure introduced by the two N atoms,
because (in contrast with the almost thermalized NH3) the N2H+
hyperfine structure affects the line trapping and the level excitation.
Unfortunately, an exact treatment of the N2H+ radiation transfer
with hf structure is not yet possible for two reasons. First,
the collision rates between the individual hf components are not known,
and only approximate hf-averaged values are available (see below). Second, the
hf structure introduces the possibility
of partial overlap between lines, complicating the problem.
TMCWC
presented a simplified solution of the N2H+ transfer which ignored
the hf structure in the excitation calculation but considered it in the
computation of the emergent spectrum. As mentioned there, the main
problem with this approach is that it neglects the decrease in trapping
caused by the splitting. Here, to take this effect into account, we improve
the model and treat explicitly the hf splitting in the low J transitions
(up to J=2), where the trapping decrease is expected to be important,
while we assume the rest of transitions are degenerate (up to J=6). This
improved approach requires increasing the number of levels considered in
the Monte Carlo code to 23 and the number of transitions to 44 (no
line overlaps are considered). For collision rates, we
use the HCO+-H2 rates from Flower (1999) and derive the individual
coefficients between N2H+ hf components by assuming that
collisions do not distinguish between hf levels. By using these
simplified collision rates and neglecting line overlaps we lose the
ability to reproduce the non LTE excitation known to occur in the
J=1-0 line (Caselli et al. 1995). This excitation anomaly, however, seems to be a
10% effect in the level population, and therefore is of little
consequence for our abundance estimate.
![\begin{figure}
\par\includegraphics[clip,width=17.6cm]{4112.f6} %
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg73.gif) |
Figure 6:
Radial profiles of integrated emission ( left) and central emerging
spectra ( right) for N2H+(1-0) toward L1498 and L1517B. Observed
data are represented by squares in the radial profiles (sum of all
hf components) and by histograms in the spectra (main beam brightness
temperature). The solid lines represent the results from best fit
Monte Carlo models: for L1517B, the model has a constant
N2H+ abundance of
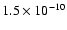 ,
and for L1498
the model has a constant abundance of ,
and for L1498
the model has a constant abundance of
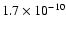 with a drop of a factor of 3 for radii larger than with a drop of a factor of 3 for radii larger than
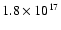 cm.
The dashed line in the radial profile of L1498 shows the expected emission
for a constant abundance model without outer drop.
The velocity scale in L1517B has been shifted by 2 km s-1 for
presentation purposes.
(Note that the 1-sigma uncertainty in the
integrated intensity points
is of the order of 0.05 K km s-1and it is therefore smaller than the size of the squares.) cm.
The dashed line in the radial profile of L1498 shows the expected emission
for a constant abundance model without outer drop.
The velocity scale in L1517B has been shifted by 2 km s-1 for
presentation purposes.
(Note that the 1-sigma uncertainty in the
integrated intensity points
is of the order of 0.05 K km s-1and it is therefore smaller than the size of the squares.) |
| Open with DEXTER |
To better constrain the N2H+ abundance profiles, we fit simultaneously
the N2H+(1-0) radial profile of integrated intensity and the
emergent spectra toward the core center for both N2H+(1-0)
and N2H+(3-2). We start our analysis by exploring models with
constant abundance, which we find fit the data rather well.
As illustrated in Figs. 6 and 7, a constant abundance model with X(N2H
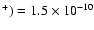 fits automatically all L1517B observations
and no additional change is required in the abundance profile
to fit this source. (Note that our model spectra are slightly brighter
than the observations despite having the same integrated area because the
real N2H+ lines seem to have additional broadening, most likely
caused by unresolved hyperfine structure, see Sect. 3.7.1.) For
L1498, a constant abundance model with X(N2H
fits automatically all L1517B observations
and no additional change is required in the abundance profile
to fit this source. (Note that our model spectra are slightly brighter
than the observations despite having the same integrated area because the
real N2H+ lines seem to have additional broadening, most likely
caused by unresolved hyperfine structure, see Sect. 3.7.1.) For
L1498, a constant abundance model with X(N2H
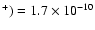 fits well both the J=1-0 and 3-2 spectra (not shown) and
almost fits the J=1-0 radial profile, although it tends to
overestimate the intensity at large radius (dashed lines in Fig. 6).
To improve this fit, we have modified the constant abundance model
by introducing an abundance drop of a factor of 3 for
radii larger than
fits well both the J=1-0 and 3-2 spectra (not shown) and
almost fits the J=1-0 radial profile, although it tends to
overestimate the intensity at large radius (dashed lines in Fig. 6).
To improve this fit, we have modified the constant abundance model
by introducing an abundance drop of a factor of 3 for
radii larger than
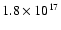 cm (85'' at 140 pc). This
new model fits all L1498 data rather well, as can be seen by the
solid lines in Figs. 6 and 7 (the slight deviation from flat top
at the center of L1498 probably arises from a similar deviation in our density
profile, see Fig. 2).
cm (85'' at 140 pc). This
new model fits all L1498 data rather well, as can be seen by the
solid lines in Figs. 6 and 7 (the slight deviation from flat top
at the center of L1498 probably arises from a similar deviation in our density
profile, see Fig. 2).
In contrast with our conclusion that the N2H+ abundance is
constant or close-to-constant
at the centers of L1498 and L1517B, Bergin et al. (2002) find
a factor of 2 drop in the N2H+ abundance
at the center of the B68 core. Such a significant drop seems excluded
in L1517B or L1498, not just from our modeling but from the
lack of any significant drop in the N2H+ emission near the
continuum peak (see maps in Fig. 3).
This contrast with the behavior in B68 is especially significant
in the case of L1517B, as both B68 and L1517B
have central densities of about
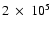 cm-3 and are
well fitted by isothermal models (Alves et al. 2001, our Sect. 3.1).
Given the importance of N2H+ as a tracer of dense gas, further
work should be carried out to understand the discrepancy between
these cores.
cm-3 and are
well fitted by isothermal models (Alves et al. 2001, our Sect. 3.1).
Given the importance of N2H+ as a tracer of dense gas, further
work should be carried out to understand the discrepancy between
these cores.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f7}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg77.gif) |
Figure 7:
Observed N2H+(3-2) spectra (histograms) and
predictions (lines) for the same models shown in Fig. 6.
The models derived to fit the 1-0 transition also fit the 3-2 spectra.
(Note that the multiple peaks in the spectra arise from hyperfine structure, and
do not represent multiple velocity components.) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[clip,width=15cm]{4112.f8}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg78.gif) |
Figure 8:
Radial profiles of integrated emission ( left) and central emerging
spectra ( right) for C18O(1-0), C18O(2-1), C17O(1-0),
and C17O(2-1) toward L1498 and L1517B. Observed
data are represented by squares in the radial profiles
and by histograms in the spectra (main beam brightness
temperature). The dashed lines represent constant abundance models
chosen to fit the emission at radius 100''(
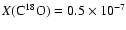 in L1498 and
in L1498 and
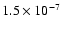 in L1517B) and, as the figure shows,
they fail to fit the central emission by a large margin.
The solid lines are models with the same abundance value for large radii but
having a central hole with no molecules ( in L1517B) and, as the figure shows,
they fail to fit the central emission by a large margin.
The solid lines are models with the same abundance value for large radii but
having a central hole with no molecules (
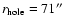 for L1498 and
83'' for L1517B). These models fit simultaneously all transitions
at all radii. A C18O/C17O isotopic ratio
of 3.65 is assumed in both cores. (Note that the 1-sigma uncertainty
in the integrated intensity points is of the order of 0.03 K km s-1
and it is therefore similar to the size of the squares.)
for L1498 and
83'' for L1517B). These models fit simultaneously all transitions
at all radii. A C18O/C17O isotopic ratio
of 3.65 is assumed in both cores. (Note that the 1-sigma uncertainty
in the integrated intensity points is of the order of 0.03 K km s-1
and it is therefore similar to the size of the squares.) |
| Open with DEXTER |
The central holes in the CO isotopomer maps of Fig. 3 indicate graphically
that the abundance of these species drops systematically toward
the peak of both L1498 and L1517B. To determine
quantitatively these abundance drops, we use again
the Monte Carlo radiative transfer model to fit the observations
with a variable abundance profile
(for further details on the Monte Carlo modeling, see TMCWC).
To better constrain the abundances
and to provide a self consistency check to our calculations, we use
simultaneously all the CO isotopomer data we have available. Thus,
in addition to fitting the C18O(1-0), C18O(2-1),
and C17O(2-1) data from the IRAM 30 m telescope, we use the
lower angular resolution C17O(1-0) data from FCRAO already
presented in TMCWC. Also, taking into account previous
work on isotopic abundances in the ISM, we assume a constant
C18O/C17O abundance ratio of 3.65 (Penzias 1981). In this way,
our determination of the CO isotopomer abundances reduces for each core
to finding a single abundance profile that fits simultaneously
four radial profiles of integrated intensity and four emergent spectra.
Before attempting to reproduce the observations, we test
the conclusion that constant abundance models cannot fit
the data from neither L1498 nor L1517B. To do this, we fix the
C18O abundance so that the models fit the observations at a radius
of 100'', and compare the model predictions with the
observations at smaller radii. As the dashed lines in the radial profiles
of Fig. 8 show, the constant abundance models fail to fit the data for all
CO isotopomers in both L1498 and L1517B. They do so by a wide margin
(more than a factor of 2), and this proves that constant abundance
C18O/C17O models are inconsistent with observations.
A sharp drop of abundance toward the center is therefore required.
To model the CO central abundance drop, we have explored different
abundance profiles, starting with the exponential forms introduced
by TMCWC (
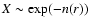 ). Our higher angular resolution
data, however, suggest that these forms do not provide
a fast enough abundance drop to fit the integrated
intensity near the core centers, and that faster decreases
are needed to reproduce the data (note that because of the central
flattening of the density profiles, the exponential forms do not
necessarily result in dramatic abundance drops). Thus, we have explored
alternative abundance profiles, like squares of the exponential forms
or central holes. Unfortunately, if the abundance toward the core
center is low enough that the emission is dominated by the outer layers
(order of magnitude drop),
the exact form of the abundance profile is not very critical.
Given this degeneracy of the solution, we have
chosen the simplest form, a (step) central hole, and
used it as basic model for the CO (and CS) abundance profiles
in L1498 and L1517B.
Although in some cases a slightly different abundance profile may produce
a better fit to the integrated intensity
radial profile (as in the case of CS in L1517B, see
below), we have preferred for consistency and inter-comparability to fit
all the abundance drops with central holes.
). Our higher angular resolution
data, however, suggest that these forms do not provide
a fast enough abundance drop to fit the integrated
intensity near the core centers, and that faster decreases
are needed to reproduce the data (note that because of the central
flattening of the density profiles, the exponential forms do not
necessarily result in dramatic abundance drops). Thus, we have explored
alternative abundance profiles, like squares of the exponential forms
or central holes. Unfortunately, if the abundance toward the core
center is low enough that the emission is dominated by the outer layers
(order of magnitude drop),
the exact form of the abundance profile is not very critical.
Given this degeneracy of the solution, we have
chosen the simplest form, a (step) central hole, and
used it as basic model for the CO (and CS) abundance profiles
in L1498 and L1517B.
Although in some cases a slightly different abundance profile may produce
a better fit to the integrated intensity
radial profile (as in the case of CS in L1517B, see
below), we have preferred for consistency and inter-comparability to fit
all the abundance drops with central holes.
Figure 8 shows a comparison between the central hole models (solid lines)
and the observations for both L1498 and L1517B. These models are
characterized by
just two parameters (external abundance and hole radius, see Table 3)
and provide a simultaneous fit to the four integrated intensity radial
profiles and the four central spectra of C18O and C17O.
Their ability to fit the data shows that the central abundance drop
in each core is sudden and deep, and that the data are consistent with
both L1498 and L1517B having no CO molecules in their innermost
region (r<70''). Although the radius of the
central hole is not uniquely determined by the observations (it is
slightly coupled to the initial abundance estimate), the true values cannot
be very far from our estimates. Thus, we
combine the radius of the abundance drop (Table 3) with the
density profiles (Table 2) in order to estimate that the density at which
CO molecules disappear from the gas phase is
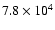 cm-3 for L1498 and
cm-3 for L1498 and
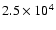 cm-3 for L1517B.
cm-3 for L1517B.
Our radiative transfer analysis has assumed spherical symmetry, and
our Monte Carlo models have been used to fit azimuthal averages of the observed
emission. This means that our radial profiles with a central abundance drop
represent spherical averages of the distribution of CO molecules in each core.
As the maps in Fig. 3 show, however,
the distribution of CO emission
in both L1517B and L1498 is not fully circular (or elliptical), and superposed
upon the central emission drop, there is a pattern of secondary peaks
and valleys. In L1517B, for example, the CO emission is brighter toward
the west, and in L1498 there are bright spots toward the southeast and the west.
The asymmetries in the CO emission appear in all transitions but
do not have counterparts
in the continuum or NH3 emission (Fig. 3). This suggests that they
do not arise from
asymmetries in the distribution of density or temperature, but that they result
from true non-azimuthal asymmetries in the distribution of CO abundance.
The detailed modeling of these asymmetries is outside the scope
of our spherically symmetric radiative transfer analysis, but a simple
inspection of the maps in Fig. 3 suggests that the abundance variations
needed to produce them
are at the level of a factor of two. These variations, therefore,
are only perturbations on the (order of magnitude) drop
in abundance at high densities,
but as we will see in Sect. 4.3, they offer interesting clues concerning
the process of core formation.
![\begin{figure}
\par\includegraphics[clip,width=15.1cm]{4112.f9}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg82.gif) |
Figure 9:
Radial profiles of integrated emission ( left) and central emerging
spectrum ( right) for CS(2-1), CS(3-2), C34S(2-1),
and C34S(3-2) toward L1498 and L1517B. Observational
data are represented by squares in the radial profiles
and by histograms in the spectra (main beam brightness
temperature). The dashed lines represent constant abundance models
chosen to fit the emission at radius 100''(X(CS)
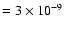 in both L1498 and
L1517B) and, as the figure shows,
they fail to fit the central emission by a large margin.
The solid lines are models with the same abundance value for large radii but
having a central hole with no molecules (
in both L1498 and
L1517B) and, as the figure shows,
they fail to fit the central emission by a large margin.
The solid lines are models with the same abundance value for large radii but
having a central hole with no molecules (
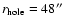 for L1498 and
55'' for L1517B). These models fit simultaneously all transitions
at all radii. A CS/C34S isotopic ratio
of 22.7 is assumed in both cores. (Note that the 1-sigma uncertainty
in the integrated intensity points
is of the order of 0.03 K km s-1and it is therefore similar to the size of the squares.)
for L1498 and
55'' for L1517B). These models fit simultaneously all transitions
at all radii. A CS/C34S isotopic ratio
of 22.7 is assumed in both cores. (Note that the 1-sigma uncertainty
in the integrated intensity points
is of the order of 0.03 K km s-1and it is therefore similar to the size of the squares.) |
| Open with DEXTER |
We finish our abundance analysis studying the distribution of
the CS molecule. Unfortunately, its emission is more difficult to model
because the CS lines from both cores are very optically thick and
strongly self absorbed. This
can be seen in Fig. 9, where the main CS isotopomer lines appear
asymmetric and double-peaked while the spectra of the rare C34S
species are single Gaussians. These self absorbed spectra depend strongly
on the physical parameters of the low-excitation outermost layers
that give rise to the absorption (r>0.1 pc) and for which we have very
little information in terms of density and temperature. Thus, although
the Monte Carlo code can treat accurately the transfer of radiation
under optically thick conditions, our CS modeling is limited by
our ignorance of the gas properties in the outer core regions.
If these properties deviate
from the extrapolation of our simple models, the radiative transfer
solution for the main isotopomer of CS is compromised. To minimize this
effect, we have complemented our CS observations with C34S data.
As with CO, we test the CS models simultaneously against our full CS
isotopomer data set, which consists of maps and spectra of CS(2-1) and
CS(3-2), and central spectra of C34S(2-1) and C34S(3-2)
(plus a full C34S(2-1) map of L1498). To minimize the
number of free parameters, we set the
CS/C34S isotopic ratio to its solar value of 22.7, since this number
seems consistent with ISM determinations (Lucas & Liszt 1998). An acceptable
abundance curve, therefore, must fit simultaneously the 4 emergent spectra
and 2 radial profiles (3 in L1498) shown in Fig. 9.
Our first set of Monte Carlo models have spatially constant CS abundance,
set to a value that fits the integrated intensity radial profile
at a radius of 100 ''. As the dashed lines in Fig. 9 show, these
constant abundance models predict a significant concentration of the emission
toward the core center, which is not seen in the data. This is
more evident in L1517B because of its higher central density concentration,
but is also clear in the flatter and more CS-opaque L1498 core,
especially in the
thinner C34S(2-1) line, where the central deviation between model
and data is of at least a factor of two. The failure of the constant
abundance models to fit the data proves that the CS abundance must
drop toward the centers of both L1498 or L1517B
(in agreement with previous lower resolution results, see Kuiper et al. 1996 and TMCWC).
To model the central decrease of the CS abundance,
we have again explored different families of abundance profiles.
Models with a central hole, for example, seem slightly
superior to exponential drop models
in the case of L1498, although both models fit the data in L1517B.
Unfortunately, a detailed comparison between the different
forms of the central abundance drop is difficult
because of the dependence of the results
on the CS self absorption, and for this reason, we only present the results
of models with a central hole. These models provide reasonable
fits to the observations, as illustrated in Fig. 9,
which shows that central hole models (solid lines)
match simultaneously for each core all radial
profiles of integrated intensity and all central spectra.
The simultaneous fit of both the self absorbed CS lines and the Gaussian
C34S spectra is a critical test for the models.
The CS self absorption arises as a natural consequence
of the combination of high optical depth and subthermal excitation
in the model low-density outer layers, and this makes this
feature the most sensitive
tracer of the velocity field in the outer core (as mentioned in
Sect. 3.2). The red shifted CS selfabsorption in L1498 indicates a
contraction motion, while the blue shifted self absorption in L1517B
requires expansion (in agreement with
previous work, see Lee et al. 1999; Kuiper et al. 1996, and TMCWC).
These velocity gradients, however, do not continue all the way to
the core center, since otherwise the central C34S spectra would
not have the same linewdith (within the noise) as the N2H+ and
NH3 lines. Thus, we have parametrized the velocity field
as constant up to a
radius of
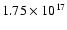 cm (83'') in L1498 and
cm (83'') in L1498 and
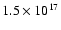 cm (71'') in L1517B, and then as increasing/decreasing
linearly with radius for larger distances (Table 3).
To fit the broader CS(2-1) self absorption and the slight wing in L1498,
we have additionally
required that the CS abundance increases by a factor of 5
in the outer envelope (
cm (71'') in L1517B, and then as increasing/decreasing
linearly with radius for larger distances (Table 3).
To fit the broader CS(2-1) self absorption and the slight wing in L1498,
we have additionally
required that the CS abundance increases by a factor of 5
in the outer envelope (
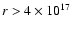 cm
cm
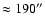 ).
As mentioned in Sect. 3.2, however, this
envelope most likely represents
a foreground red component that also gives rise to a
red wing in the C18O spectra (Fig. 8, see also Lemme et al. 1995).
Foreground contamination, in fact, may also be the cause of
the blue shifted self absorption in L1517B, as the nearby L1517A core
is slightly blue shifted with respect to L1517B (Benson & Myers 1989). Thus, the
velocity gradients traced with the CS self absorption most likely reflect the
conditions in the region where the cores meet the extended ambient
cloud (r>0.1 pc) and not an intrinsic core velocity pattern.
Although these motions affect strongly the shape of the
CS spectra, they seem to involve only the core outermost layers and
not the dense (probably star-forming) part.
Their interpretation as global core contraction
or expansion patterns seems therefore not warranted.
).
As mentioned in Sect. 3.2, however, this
envelope most likely represents
a foreground red component that also gives rise to a
red wing in the C18O spectra (Fig. 8, see also Lemme et al. 1995).
Foreground contamination, in fact, may also be the cause of
the blue shifted self absorption in L1517B, as the nearby L1517A core
is slightly blue shifted with respect to L1517B (Benson & Myers 1989). Thus, the
velocity gradients traced with the CS self absorption most likely reflect the
conditions in the region where the cores meet the extended ambient
cloud (r>0.1 pc) and not an intrinsic core velocity pattern.
Although these motions affect strongly the shape of the
CS spectra, they seem to involve only the core outermost layers and
not the dense (probably star-forming) part.
Their interpretation as global core contraction
or expansion patterns seems therefore not warranted.
The reasonable fit provided by the central-hole models shows that the
CS abundance drop in L1498 and L1517B is as dramatic as that of CO.
This implies that the centers of these two cores may
lack CS molecules for radii smaller than 48'' in L1498
and 55'' in L1517B (Table 3), and that the CS emission in these systems
only traces the outer core layers. As with CO, we can convert the
radius of the central hole into a critical density above which
CS molecules disappear from the gas phase. Using the density profiles
of Sect. 3.1, we derive a maximum density of
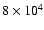 cm-3for L1498 and
cm-3for L1498 and
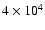 cm-3 in L1517B, which are similar to
but slightly larger than those measured for the CO isotopomers.
Thus, CS seems to freeze-out from the gas phase at slightly larger
densities than CO, and therefore traces slightly more central
parts of cores. The innermost core regions, however, are totally
invisible in CS, even when observed with optically thin C34S emission.
cm-3 in L1517B, which are similar to
but slightly larger than those measured for the CO isotopomers.
Thus, CS seems to freeze-out from the gas phase at slightly larger
densities than CO, and therefore traces slightly more central
parts of cores. The innermost core regions, however, are totally
invisible in CS, even when observed with optically thin C34S emission.
A look at the maps of Fig. 3 shows that the CS emission presents the
same azimuthal asymmetries found in CO: relative maxima
toward the SE and W in L1498 and toward the W in L1517B. This similarity
with the pattern of C18O asymmetries and the fact
that in L1498 the asymmetry
can also be seen in the thinner C34S(2-1) emission strongly
suggest that these features are real and not the result
of self absorption effects. Thus, following
the arguments presented in the study
of CO (Sect. 3.5.1), we conclude that in each core the distribution
of CS abundance is not azimuthally symmetric.
As in CO, this azimuthal asymmetry probably arises from
changes in the abundance of a factor of a few and is superposed upon the
order-of-magnitude central abundance drop. A full discussion
of its possible origin in terms of core formation history is
deferred to Sect. 4.3.
Our modeling of the line profiles toward the center of L1498 and L1517B
has sampled the gas velocity field along the central line of sight of
each core. This field has been found to have a turbulent component
approximately constant with radius, with a possible increase in the
outer part of L1498 (but most likely due to another velocity
component). The line-of-sight systemic velocity seems also constant
over the center of the cores, although it presents gradients
in the outer layers: contraction in L1498 and expansion in L1517B.
In this section, we turn our attention to the 2-dimensional (plane of the sky)
velocity field as a complement to the analysis of the
central line-of-sight. To do this,
we make Gaussian fits to the spectra at all
positions and we study the spatial variations of the fit results.
As only N2H+ and NH3 are
sensitive to the core dense gas, we only use these
species in our velocity study. Both N2H+ and NH3 have the
additional advantage of having hyperfine structure, which
allows for correction of optical depth effects in the linewidth
determination.
We study the spatial distribution of the gas turbulent component
using the intrinsic linewidths derived from the hf fits
and determining their radial profiles as we have done before with the
integrated line intensities. As the intrinsic linewidth is the sum
in quadrature of a thermal and a non thermal component (e.g., Myers 1983), and the thermal part is constant because the
gas kinetic temperature is constant (Sect. 3.3),
any spatial variation of the intrinsic
linewidth has to result from an equivalent spatial variation
of the non-thermal (turbulent) part.
Figure 10 presents the radial profiles of the NH3(1, 1) and N2H+(1-0)
intrinsic linewidths 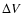 for both L1498 and L1517B. A simple
inspection of these profiles suggests that there is no significant
trend of increase or decrease of linewidth as a function of radius,
meaning that any non thermal component is also spatially constant over
both cores.
To test for the presence of a hidden slope in the linewidth distribution,
we have fitted the points in Fig. 10 with a function of the form
for both L1498 and L1517B. A simple
inspection of these profiles suggests that there is no significant
trend of increase or decrease of linewidth as a function of radius,
meaning that any non thermal component is also spatially constant over
both cores.
To test for the presence of a hidden slope in the linewidth distribution,
we have fitted the points in Fig. 10 with a function of the form
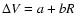 ,
where R is the radius in arcseconds and
a and b are two free parameters.
In three out of four cases the b coefficient is smaller
than its rms, hence the fit is consistent with b=0and the distribution of
,
where R is the radius in arcseconds and
a and b are two free parameters.
In three out of four cases the b coefficient is smaller
than its rms, hence the fit is consistent with b=0and the distribution of 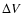 is independent of radius.
In the fourth case (L1517B N2H+ data), the slope is negative, and
the linewidth slightly decreases with radius (only by 30% in
100''). This slight decrease, which can be seen in the data at large radii,
is most likely due to errors in the N2H+ hfs fit (see below)
and has no counterpart in the NH3 linewidth distribution.
We therefore conclude that the non thermal component of the velocity field
in both L1498 and L1517B is constant with radius for as far as we can measure.
is independent of radius.
In the fourth case (L1517B N2H+ data), the slope is negative, and
the linewidth slightly decreases with radius (only by 30% in
100''). This slight decrease, which can be seen in the data at large radii,
is most likely due to errors in the N2H+ hfs fit (see below)
and has no counterpart in the NH3 linewidth distribution.
We therefore conclude that the non thermal component of the velocity field
in both L1498 and L1517B is constant with radius for as far as we can measure.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f10}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg88.gif) |
Figure 10:
Radial profiles of intrinsic linewidth
for L1498 and L1517B from NH3and N2H+ hyperfine-structure fits.
Note the lack of systematic variations and the extremely low dispersion.
The long-dashed horizontal lines indicate the average value for each
core and molecule (very close to 0.20 km s-1 in all cases). The
short-dashed lines indicate the N2H+linewidth expected when adding the nonthermal component derived from
NH3 to a thermal N2H+ component at 10 K (see text for details).
To maximize sensitivity, only points with integrated intensity larger than
1.3, 1, 0.6, and 0.6 K km s-1 are presented for L1498 NH3,
L1517B NH3, L1498 N2H+, and L1517B N2H+, respectively.
(As indicated in the text, the 1-sigma uncertainty of the
linewidth estimates, both from NH3 and N2H+, is of
the order of 0.01 km s-1,
and it is therefore smaller than the size of the squares.) |
| Open with DEXTER |
The finding of constant linewidth in L1498 and L1517B agrees
with the results of Barranco & Goodman (1998), who found the
same behavior in the interior of four other dense
cores. These authors, however, suggested that linewidths may increase
at the largest observed radii, a behavior not seen in our data.
Even if we include the low sensitivity points at very large radii, the
constant linewidth trend of Fig. 10 remains unchanged, and the scatter due to
noise dominates the plots.
We therefore conclude that the linewidth does not increase with radius,
or if it does, it starts increasing at a larger radius than suggested by Barranco & Goodman (1998).
A puzzling result from our hf analysis is that the
N2H+(1-0) and NH3(1, 1) linewidths are almost equal
(very close to 0.20 km s-1). This is unexpected because
the N2H+ molecule is 1.7 times heavier than NH3 and thus
its thermal
component is 1.3 times smaller. If both molecules are tracing the same
gas, their turbulent components should be equal, and the lighter NH3should always present broader lines. To quantify this problem, we have
assumed that the NH3 hf fit returns the true linewidth (thermal plus
turbulent), and we have derived its nonthermal part by
subtracting a thermal component at 10 K. When this nonthermal component
is added to the N2H+ thermal part, we find that the N2H+
linewidths derived from the hf fit are approximately 20% larger than
expected, as illustrated in Fig. 10, where the dotted
line is the expected N2H+ linewidth.
The origin of the larger N2H+ non-thermal component is unclear.
Different linewidths for ions and neutrals are expected
in the presence of magnetic fields, but the observed trend
in both L1498 and L1517B (larger non-thermal component in the ion line)
is opposite to what is expected theoretically (Houde et al. 2000).
A more likely explanation is that the N2H+ hf fit overestimates
the linewidth by about 20%. This is so because the hf analysis
of both molecules assumes
LTE among hf components, but this is only correct for the NH3 lines.
N2H+ is notorious for showing non-LTE excitation among its
components (Caselli et al. 1995), and this violates a main assumption of the
analysis. In addition, as our data show and was first noticed by Caselli et al. (1995), there is a discrepancy between the N2H+ linewidth
derived from the hf fit and the linewidth measured by a Gaussian fit to
the thinnest (reddest) component. This component appears slightly (5-10%)
narrower than the hf-fit linewidth, contrary to what would be expected
if the hf fit truly corrected for optical
depth broadening. This suggests that N2H+ linewidths derived from
standard hf fits may be slightly overestimated (20%), either because
of a failure in the LTE analysis or because of the presence of additional
hyperfine splitting due to magnetic spin-rotation interaction of
the H atom (the latter option seems less likely according to recent
estimates of the splitting, Luca Dore private communication).
Of course, this suggestion does not contradict our conclusion that the
linewidth is constant in L1498 and L1517B, as it is confirmed independently
(with even less scatter) by the more reliable NH3 analysis (Fig. 10).
According to this analysis, the mean intrinsic (NH3) linewidth is
0.204 km s-1 in L1498 and 0.196 km s-1 in L1517. Subtracting
thermal components of 10 K for L1498 and 9.5 K for L1517B (Sect. 3.3),
we estimate non thermal turbulent (FWHM) linewidths of 0.121 km s-1
in L1498 and 0.113 km s-1 in L1517B (note that our Monte Carlo
models use 0.125 km s-1 as a compromise to fit both NH3and the broader N2H+).
Even if the turbulent linewidth is constant with radius on average, it
may still present random variations
across each core, and to explore this possibility we
compare the measured rms
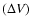 of N2H+ and NH3(
of N2H+ and NH3(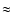 10-2 km s-1)
with the value expected from the noise level in the
data. To calculate this expected rms, we have created at each L1498 and
L1517B position a pair of simulated
N2H+ and NH3 spectra with the correct intensity and noise level,
but with all positions having the same linewidth. These
simulated data result from averaging all spectra of each molecule
and core, creating a high S/N spectrum which has then been scaled
for each position to match the observed integrated intensity,
with noise added to match the observed noise level
(the averaging process broadens the line due to velocity fields,
but by less than 10%). This artificial
data set has then been subject to the same hf analysis as the real data,
so its rms
10-2 km s-1)
with the value expected from the noise level in the
data. To calculate this expected rms, we have created at each L1498 and
L1517B position a pair of simulated
N2H+ and NH3 spectra with the correct intensity and noise level,
but with all positions having the same linewidth. These
simulated data result from averaging all spectra of each molecule
and core, creating a high S/N spectrum which has then been scaled
for each position to match the observed integrated intensity,
with noise added to match the observed noise level
(the averaging process broadens the line due to velocity fields,
but by less than 10%). This artificial
data set has then been subject to the same hf analysis as the real data,
so its rms
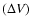 provides a direct measure of the effect of noise
on the measured linewidth. Comparing this rms
provides a direct measure of the effect of noise
on the measured linewidth. Comparing this rms
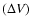 with that
measured from the real data, we find that
rms
with that
measured from the real data, we find that
rms
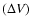 of the real data
is
of the real data
is
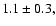 times the rms
times the rms
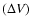 of the simulated
data, which means that the observed dispersion is consistent with
noise, and that there is no evidence for an additional
source of linewidth variations. This result, which agrees
with the line-of-sight analysis of the Monte Carlo modeling,
indicates that the data are consistent with a single
of the simulated
data, which means that the observed dispersion is consistent with
noise, and that there is no evidence for an additional
source of linewidth variations. This result, which agrees
with the line-of-sight analysis of the Monte Carlo modeling,
indicates that the data are consistent with a single 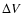 value in the inner core (r<0.05 pc) within better than
0.01 km s-1 (5%).
value in the inner core (r<0.05 pc) within better than
0.01 km s-1 (5%).
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f11}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg91.gif) |
Figure 11:
Radial profiles of line center velocity
for L1498 and L1517B derived from NH3
and N2H+ hyperfine-structure fits.
The dispersion of the points indicates the presence of bulk
internal motions. Intensity threshold as in Fig. 10.
(As indicated in the text, the 1-sigma uncertainty of the
velocity estimates, both from NH3 and N2H+, is of
the order of 0.005 km s-1,
and it is therefore smaller than the size of the squares.) |
| Open with DEXTER |
The other kinematic parameter derived from the hf fit of the
NH3 and N2H+ spectra is
the line center velocity. As with the linewidth, we have
made radial profiles of the line center velocity for
both NH3 and N2H+ in L1498 and L1517B, and they are
presented in Fig. 11. These radial profiles are flat on average,
and their scatter around
the mean is larger than the scatter in linewidth by a about a
factor of 2. This larger scatter of the line center velocity
is significant according to the model
of simulated spectra used in the previous section, because
the hf analysis is more sensitive to the line center velocity
than to the linewidth, especially for N2H+. Comparing the data
with the model, we estimate that the observed
scatter in the line center velocity is approximately 0.03 km s-1, or
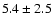 times larger
than it should be if all positions had exactly the same velocity. This
implies that the
times larger
than it should be if all positions had exactly the same velocity. This
implies that the
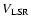 variations seen in the radial profiles of Fig. 11
correspond to real changes in the gas velocity across the core
and not just to noise.
variations seen in the radial profiles of Fig. 11
correspond to real changes in the gas velocity across the core
and not just to noise.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f12}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg93.gif) |
Figure 12:
Gradients of
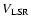 from N2H+ hf fits. The arrows indicate
both the direction (from low to high
from N2H+ hf fits. The arrows indicate
both the direction (from low to high
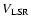 )
and intensity of the
gradient (the arrows in the bottom left corners represent
gradients of 3 km s-1 pc-1). The contours are N2H+integrated intensity maps. )
and intensity of the
gradient (the arrows in the bottom left corners represent
gradients of 3 km s-1 pc-1). The contours are N2H+integrated intensity maps. |
| Open with DEXTER |
To study the origin of the velocity changes, we first determine their
spatial distribution. Using a program similar to that of Caselli et al. (2002a),
we have calculated at
each map position the local velocity gradient, both in modulus and
direction, by comparing the
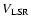 velocity of each point with that
of its neighbors. A graphical representation of the N2H+
results is shown in Fig. 12, and similar plots, but with fewer points,
were derived for NH3 (their similarity confirms that the velocity
fluctuations represent real velocity variations). As these maps
show, both the direction and modulus of the velocity gradient
change across both L1498 and L1517B, indicating that the gradients do
not originate from simple global velocity patterns like rotation. This lack
of global patterns, however, does not imply that the velocity
variations are completely random, because the gradients
are correlated over areas larger than the telescope beam (26'')
or the area used to measure individual velocity gradients (40''). They
therefore have to arise from bulk gas motions that affect
sizeable fractions of the core material.
velocity of each point with that
of its neighbors. A graphical representation of the N2H+
results is shown in Fig. 12, and similar plots, but with fewer points,
were derived for NH3 (their similarity confirms that the velocity
fluctuations represent real velocity variations). As these maps
show, both the direction and modulus of the velocity gradient
change across both L1498 and L1517B, indicating that the gradients do
not originate from simple global velocity patterns like rotation. This lack
of global patterns, however, does not imply that the velocity
variations are completely random, because the gradients
are correlated over areas larger than the telescope beam (26'')
or the area used to measure individual velocity gradients (40''). They
therefore have to arise from bulk gas motions that affect
sizeable fractions of the core material.
As a first estimate of the importance of
these motions, we calculate the average
velocity gradient for each core. Both N2H+ and NH3give consistent results, especially for the position
angle (-20 and -75 degrees for L1498 and L1517B, respectively).
For the modulus of the gradient, the NH3 data give a slightly
lower value (10% for L1498 and 40% for L1517B), so we average
the N2H+ and NH3 values and derive
0.75 and 1.1 km s-1 pc-1 for L1498 and L1517B, respectively.
These values are similar to those found by Goodman et al. (1993) in
other cores, again an indication that L1498 and L1517B are
representative Taurus cores. Our value for L1498, in addition,
is in excellent agreement with a similar estimate by Caselli et al. (2002a).
The gradients
measured in this manner, however, are strict lower limits, as in
addition to the average across the sky required to estimate
the mean gradient, the velocity estimate at each position already
represents an average along the line of sight. This average necessarily
cancels spatial variations of the velocity, given the lack
of coherence over scales of a core diameter (Fig. 12). Unfortunately, this
effect cannot be corrected without a full model of the core kinematics, and
as a simple alternative for estimating the velocity
differences between parts of the core, we measure the spread of
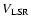 in Fig. 11, which is approximately 0.1 km s-1 (=
in Fig. 11, which is approximately 0.1 km s-1 (=
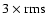 ). The noise
contribution to this spread is negligible according to our synthetic spectra
model (
). The noise
contribution to this spread is negligible according to our synthetic spectra
model (
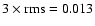 km s-1), so we can consider that
the scatter represents true velocity variations. It is possible
that part of this dispersion arises from a global component
(e.g., rotation), but the results in Fig. 12 show that this
component cannot be dominant. Crudely assuming
equipartition, we estimate the internal
core motions to be at least 0.05 km s-1, although they can be as
high as 0.1 km s-1.
km s-1), so we can consider that
the scatter represents true velocity variations. It is possible
that part of this dispersion arises from a global component
(e.g., rotation), but the results in Fig. 12 show that this
component cannot be dominant. Crudely assuming
equipartition, we estimate the internal
core motions to be at least 0.05 km s-1, although they can be as
high as 0.1 km s-1.
Although the gas motions are small and subsonic (sound speed is 0.19 km s-1 for 10 K), and therefore have little effect on the
core energy budget,
their presence indicates that the cores have not yet attained
a state of perfect hydrostatic equilibrium. How these motions originate
is unclear, but several indications suggest that they are
related to the process of core formation. First, the motions
are similar in magnitude to the inward motions
observed in other cores (Lee et al. 2001,1999), and these are believed
to be associated with
core contraction (note that L1498 has also infall asymmetry, while
L1517B has the opposite). Second, the
time scale of these motions is of the order
of 1 Myr (0.05 km s-1 over 0.05 pc or 75''), a typical
starless core lifetime (Lee & Myers 1999). Finally, and more important,
there is a correlation between
some velocity components and the non azimuthal asymmetries in the
abundance of the depleted molecules (CS and CO). These abundance asymmetries
are most likely related to different contraction times of different
parts of the core (Sect. 4.3), and thus their correlation with the velocity
pattern suggests that the pattern is related to contraction.
To show this, we present in Fig. 13 (left panels)
the distribution of "high velocity'' N2H+ emission (blue for L1498
and red for L1517B) superposed upon the integrated N2H+
emission (see caption for details). As the right panels in
the figure show, these "high velocity'' N2H+ components have
distributions remarkably close to the distribution of bright
CS/C34S spots (more so than to CO probably because CS and
N2H+ are sensitive to similar densities), which we have seen most
likely arise from differences in the amount of CS freeze-out.
The similar distributions
are more remarkable because CS and CO hardly coexist
with N2H+, as they deplete at radii for which N2H+is non-detectable, and suggest a correlation of high CS
abundance with the "high velocity'' components.
As we will see below, these high CS-abundance spots most likely arise
from material that has been recently acquired by
the core and has therefore been at high density
for shorter time than the rest (i.e., it is "younger'' and less depleted,
see also Kuiper et al. 1996).
A peculiar velocity in this material is exactly what would have been
expected if this interpretation is correct.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f13}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg96.gif) |
Figure 13:
Comparison of "high velocity'' N2H+ emission to C34S or
CS emission showing their similar distribution. This is an
indication that the gas velocity structure is
related to the deviations from spherical symmetry
in the pattern of molecular freeze out, probably due
to asymmetries in the core contraction history (see text). The solid lines in
the left panels are N2H+ integrated intensity maps
for velocity intervals 0.2 km s-1 (one linewidth, see Fig. 10)
away from the line center velocity (towards blue for L1517B and towards
red for L1498) and 0.2 km s-1 wide. The C34S or CS maps
in the right panels and
the full integrated N2H+ map (dashed) are as in Fig. 3. |
| Open with DEXTER |
We have seen that the systematic internal motions in both L1498 and
L1517B are of the order of 0.1 km s-1 and therefore subsonic
for gas at 10 K (sound speed is 0.19 km s-1).
This suggests that both cores are close to a state of hydrostatic
equilibrium in which the core self gravity is balanced by internal
forces. Given the core parameters we have derived in previous
sections, we now analyze whether such an equilibrium state is possible
and whether it is consistent with the observed core structure.
The simplest support component in each core is the thermal pressure
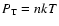 ,
where n is the gas density,
k is the Boltzmann constant, and T the gas kinetic temperature.
This pressure may be supplemented by a
non-thermal component
,
where n is the gas density,
k is the Boltzmann constant, and T the gas kinetic temperature.
This pressure may be supplemented by a
non-thermal component
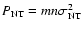 if the non-thermal linewidth arises from turbulent supporting motions
(m is the mean particle mass and
if the non-thermal linewidth arises from turbulent supporting motions
(m is the mean particle mass and
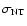 is the non thermal velocity
dispersion, related to the non thermal FWHM by
is the non thermal velocity
dispersion, related to the non thermal FWHM by
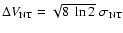 ). The relative
importance of these two supporting components is given by the
ratio
). The relative
importance of these two supporting components is given by the
ratio
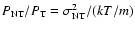 ,
which can
be easily estimated from the core parameters derived in previous sections.
As both
,
which can
be easily estimated from the core parameters derived in previous sections.
As both
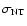 and T are constant over the central
0.1 pc of L1498 and L1517B, the pressure ratio is constant, and has a value of
0.07 for
and T are constant over the central
0.1 pc of L1498 and L1517B, the pressure ratio is constant, and has a value of
0.07 for
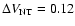 km s-1 and T=10 K (Sects. 3.3 and 3.7.1). This low ratio indicates that the non thermal motions contribute
negligibly to the core support over at least the central 0.1 pc
(see also Fuller & Myers 1993), and that in the absence of
support by an ordered magnetic field, thermal pressure is
the main supporting agent in both L1498 and L1517B
(a similar conclusion for the case of B68 has been recently
obtained by Lada el al. 2003).
km s-1 and T=10 K (Sects. 3.3 and 3.7.1). This low ratio indicates that the non thermal motions contribute
negligibly to the core support over at least the central 0.1 pc
(see also Fuller & Myers 1993), and that in the absence of
support by an ordered magnetic field, thermal pressure is
the main supporting agent in both L1498 and L1517B
(a similar conclusion for the case of B68 has been recently
obtained by Lada el al. 2003).
If thermal pressure dominates core support and the gas temperature is
constant, the equation of core hydrostatic equilibrium reduces to the
isothermal case, which has a classical solution for spherical geometry (Chandrasekhar 1939). The addition of a constant non-thermal contribution
implies only a simple generalization of the isothermal case and
does not change the solution significantly (e.g.,
Appendix Aof McLaughlin & Pudritz 1996). As we have seen in Sect. 3.1,
the density profiles derived from the dust continuum emission do in fact
have shapes very close to those expected for isothermal
spheres, especially in the case of L1517B. To check whether
these profiles are consistent with equilibrium between self gravity
and internal (thermal plus non thermal) pressure, we can compare the measured
velocity dispersion 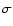 (=0.185 km s-1 for gas at 9.5 K
and
(=0.185 km s-1 for gas at 9.5 K
and
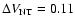 km s-1) with the velocity dispersion
required by the isothermal fit to the dust emission (Sect. 3.1).
Unfortunately, the fit only constrains the combined parameter
km s-1) with the velocity dispersion
required by the isothermal fit to the dust emission (Sect. 3.1).
Unfortunately, the fit only constrains the combined parameter
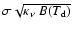 ,
making impossible a full check
without independent estimates of the dust emissivity
,
making impossible a full check
without independent estimates of the dust emissivity
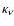 and
temperature
and
temperature 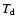
![[*]](/icons/foot_motif.gif) .
To take into account this dependence, we
re-write the velocity dispersions required from the continuum fits
in Table 1 (where we assumed
.
To take into account this dependence, we
re-write the velocity dispersions required from the continuum fits
in Table 1 (where we assumed
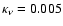 cm2 g-1
and
cm2 g-1
and
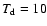 K) as
K) as
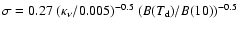 km s-1for L1517B and
km s-1for L1517B and
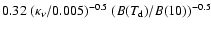 km s-1 for L1498. These values show that if
km s-1 for L1498. These values show that if
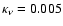 cm2 g-1 and
cm2 g-1 and
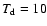 K,
there is either an extra pressure contribution
which does not affect the observed linewidth or the cores should be
contracting under their own gravity.
K,
there is either an extra pressure contribution
which does not affect the observed linewidth or the cores should be
contracting under their own gravity.
Although a state
of slow contraction is likely in both L1498 and L1517B (Sect. 3.7.2),
we cannot rule out that at least part of
the velocity dispersion mismatch reflects a wrong choice
of dust parameters. For example, the value of
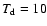 K, chosen so it equals the well-measured gas temperature,
may in fact be a slight overestimate. This is suggested by the
models of Galli et al. (2002) (their Fig. 3), which show that although
dust and gas are thermally coupled at core densities the dust is
cooler by about 2 K. A lower dust temperature requires a larger
K, chosen so it equals the well-measured gas temperature,
may in fact be a slight overestimate. This is suggested by the
models of Galli et al. (2002) (their Fig. 3), which show that although
dust and gas are thermally coupled at core densities the dust is
cooler by about 2 K. A lower dust temperature requires a larger
 ,
and this makes the pressure unbalance more severe, although only by a
small margin: a dust temperature of 8 K requires a 1.2 increase in
,
and this makes the pressure unbalance more severe, although only by a
small margin: a dust temperature of 8 K requires a 1.2 increase in
 .
More critical in the balance argument is the choice of
the dust emissivity
.
More critical in the balance argument is the choice of
the dust emissivity
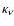 ,
as this parameter is considered to
be uncertain by a factor of 2. In L1517B, for example,
if
,
as this parameter is considered to
be uncertain by a factor of 2. In L1517B, for example,
if
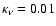 cm2 g-1, the gas will be in hydrostatic
equilibrium assuming
cm2 g-1, the gas will be in hydrostatic
equilibrium assuming
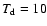 K. This higher
K. This higher
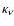 value
is not too far from the 0.008 cm2 g-1 recommended by Ossenkopf & Henning (1994) for a standard gas-to-dust ratio of 100
and dust in regions of density
value
is not too far from the 0.008 cm2 g-1 recommended by Ossenkopf & Henning (1994) for a standard gas-to-dust ratio of 100
and dust in regions of density 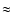 105 cm-3, which is
typical of the L1517B center, and recent observations do in fact suggest
a systematic increase of
105 cm-3, which is
typical of the L1517B center, and recent observations do in fact suggest
a systematic increase of
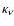 at high densities (Bianchi et al. 2003; Kramer et al. 2003).
Thus, it is still
possible that L1517B is exactly or very close to
a state of hydrostatic equilibrium
where its (mostly thermal) pressure balances its self gravity.
This higher
at high densities (Bianchi et al. 2003; Kramer et al. 2003).
Thus, it is still
possible that L1517B is exactly or very close to
a state of hydrostatic equilibrium
where its (mostly thermal) pressure balances its self gravity.
This higher
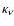 value, however, will not bring L1498 to
a state of equilibrium, and this is also consistent with the non spherical
shape of this core.
value, however, will not bring L1498 to
a state of equilibrium, and this is also consistent with the non spherical
shape of this core.
The abundance profiles of NH3, N2H+, and
the isotopomers of CO and CS can be qualitatively understood
as the result of the selective freeze out of molecules onto
cold dust grains as the gas becomes centrally concentrated during
core formation. The lower binding energy of N2 to grain surfaces
makes this species relatively overabundant at high densities,
and this in turn favors the presence of molecules composed of N and H
(like NH3 and N2H+) in the core interiors. This selective freeze
out of molecules during core contraction and its resulting chemistry
has been modeled in detail by a number of authors over the last few years (Bergin & Langer 1997; Charnley 1997; Caselli et al. 1999; Nejad & Wagenblast 1999; Aikawa et al. 2001, 2003; Shematovich et al. 2003; Li et al. 2002), and their results
are in general agreement with the observations and analysis
presented here. A detailed comparison between models and data, however,
reveals some differences between observed molecular behavior and theoretical
expectations, and in this section we comment on the possible origin of these
differences.
The main disagreement between our observations and the published models
involves the behavior of NH3 and N2H+ near the
core centers. As seen in Sects. 3.3 and 3.4, both L1498 and L1517B
present the same pattern of constant N2H+ abundance
together with a factor-of-a-few central NH3 increase, and this
pattern seems also present in other starless cores (see TMCWC).
Most chemical models, however, predict that NH3 and N2H+ will behave
in a similar fashion given that they have N2 as a common parent.
This is qualitatively correct in that the two species trace
the same regions but the quantitative differences noted above
require explanation. Aikawa et al. (2003) have made a detailed
attempt to fit observations of L1544 (their Fig. 8). Their best
model (a delayed collapse with N initially molecular and a high
CO binding energy) has an essentially constant NH3/N2H+ abundance
ratio as a function of radius.
It is unclear which processes cause
the NH3 and N2H+ abundances to follow
different trends at high densities
and produce the relative enhancement of NH3. Both have
their origins in molecular nitrogen and hence their abundance
ratio should be independent of the N2 abundance. Their
formation involves reactions with He+ (in the case of
NH3) and H+3 (in the case of N2H+) and
thus their abundance ratio is sensitive to the abundance ratio
of these ions. The ionic abundances
are certainly sensitive to the depletion
of CO and other molecules and hence uncertainties in key rates determining
the abundances of He+ and H3+ may be responsible for
variations in the NH3/N2H+ abundance ratio. Apart from this,
we note that while N2H+ is likely mainly destroyed
by recombination with electrons and reactions with CO,
it is rather unclear what the main destruction mechanism for
NH3 is in regions where CO (and hence carbon compounds in
general) is sufficiently depleted that reactions with ions
such as C+ become negligible. The answers to these questions
may provide the explanation for the observed gradient in
the NH3/N2H+ ratio.
Although it is clear that dense
cores contract from the lower density gas of their
surrounding molecular clouds, how this process occurs and
how long it takes is still a matter of much uncertainty (see, e.g., Shu et al. 1987 and Hartmann et al. 2001 for two opposing views).
This state of affairs results in part because it is not yet possible
to infer a core contraction history directly from observations,
as we lack reliable time markers to assess the evolutionary state
of different cores. Fortunately, the time and density dependence of the
freeze out process may offer the possibility of shedding some
light on the core contraction history by allowing us to
correlate the molecular abundances of volatile species with the
evolutionary state of the gas in a core. Here we present a first
(and preliminary)
application of these ideas to the case of the L1498 and L1517B cores.
Both L1498 and L1517B appear highly symmetric in their distribution
of N2H+, NH3, and dust continuum (Fig. 3), which are
the most reliable tracers of the dense core gas. L1498,
especially in the density-sensitive N2H+, presents an evident
bilateral symmetry with respect to a NE-SW axis, and L1517B has
an almost perfect circular symmetry with only minor deviations.
These symmetries in the emission of the most robust tracers most likely
reflect a high degree of symmetry in the underlying distributions of
matter in the cores, in agreement with their state close to hydrostatic
equilibrium.
In contrast with the symmetric distributions of
N2H+, NH3, and dust continuum, the distributions
of CS and CO emission in L1498 and L1517B are highly asymmetric (Fig. 3).
As we have seen in Sects. 3.5 and 3.6,
these asymmetries arise from a pattern of
non axisymmetric abundance variations that is
superposed to
the central abundance drop due to molecular freeze out.
These non axisymmetric variations are
located at radii where freeze out is already
prevalent, so they very likely represent
variations in the amount of freeze out, in the sense that
the bright spots to the SE and E of L1498 and to the W of L1517B
are places where this process is less severe and therefore
the CO and CS abundances are higher.
This interpretation is supported by the fact that the same regions have
at the same time
bright CO, CS, and other molecules that freeze out at similar densities
(Tafalla et al.
2004 in preparation), indicating that the process responsible for the
asymmetry is not
limited to one particular chemical species.
As molecular freeze out is very sensitive to
the time the gas has spent at high density (e.g., Bergin & Langer 1997), the
simplest explanation of the lower freeze out at the CO and CS
bright spots is that these regions
have somehow stayed at high density
less time than other regions with similar radius
(and therefore similar present density). (Pre-existing chemical
inhomogeneities seem unlikely because of the small scale.)
For this to happen, the contraction of the gas in L1498 and
L1517B has to have been non spherically symmetric, with the gas
at the CO and CS bright spots being "younger''
(less processed) and therefore more recently accreted.
This interpretation is consistent with the correlation between
enhanced CO/CS abundance and "high'' velocity N2H+ and NH3
found in
Sect. 3.7.2 (see Fig. 13), as the younger portions of the core will
have not yet attained
perfect equilibrium and thus retain a fraction of their contraction speed.
Kinematics and chemical composition, therefore, agree in suggesting that
L1498 and L1517B have formed from non spherical contraction
of cloud material. The time scale of this contraction seems to be
of the order of a few Myr (Sect. 3.7.2).
The above time scale, although short, is not enough to discriminate
between the different scenarios of star formation. On
the one hand, the value is
consistent with a picture of relatively rapid star formation (Hartmann et al. 2001; Elmegreen 2000), but on the other,
it is also consistent with ambipolar diffusion models
that start with an initially not highly subcritical
cloud (Li 1999; Ciolek & Basu 2001).
In Paper 2, we will revisit the time scale issue based on
the analysis of the freeze out process of a large number of molecular
species. Here we note that if the magnetically-mediated scenario
is correct,
the fastest gas motions are expected to occur along the
magnetic field axis, and this would imply a correlation of the
observed abundance anisotropies with the magnetic field direction.
Observations of the polarization direction in the submillimeter continuum
should be able to test this prediction.
More conclusive than the kinematic estimate of the contraction
time scale is the measurement of the (low) turbulence level
inside the cores. Our observations
of L1498 and L1517B (Fig. 10, top) appear to be inconsistent with
typical expectations from the supersonic
turbulence scenario (see Mac Low & Klessen 2004 for a recent review). Ballesteros-Paredes et al. (2003) have recently argued that density profiles similar to
those of hydrostatic equilibrium systems can appear fortuitously in
model simulations of supersonic turbulence, showing that the shape of the
density profile is not a reliable indication of a core equilibrium state.
Although it is true that the cores in the Ballesteros-Paredes et al. (2003) simulations
can mimic the density profiles of systems like L1498 and L1517B,
their internal velocity fields clearly betray their "hydrostatic
disguise.'' Turbulent model cores in the simulations of Ballesteros-Paredes et al. (2003) present velocity profiles with internal changes larger than
the speed of sound, and on the order of 0.5-1 km s-1in cases of driven turbulence (their Figs. 9-11). Our observations
rule out such strong velocity changes by about an order of
magnitude, and not only in the plane of
the sky (from our radial profiles of line center velocity, see
Fig. 11), but also along any given line of sight (our linewidth measurements,
see Fig. 10).
The problem of the supersonic turbulence scenario
is unlikely to be restricted to L1498 and L1517B, as these objects
seem representative of the
Taurus core population in, for example, having narrow lines
(e.g., Fuller & Myers 1993). This problem points to the need of any model
of core formation for producing condensations which appear
thermally dominated and extremely quiescent. How these
close to hydrostatic equilibrium configurations can be achieved
in the relatively short time of a few Myr seems to
pose a challenge to most core formation models.
We have presented detailed models of the internal structure of two
close-to-round starless cores in the nearby Taurus-Auriga star formation
complex, L1498 and L1517B. Our models have been constrained from the
simultaneous fit of the spatial distribution and the central emerging
spectrum of at least two transitions of NH3, N2H+, CS,
C34S, C18O, and C17O, together with maps of the 1.2 mm
continuum. The main conclusions of this work are:
1. Both cores present gas temperature distributions consistent with
a constant value (10 K for L1498 and 9.5 K for L1517B) and a very
small rms (1 K). No evidence for radial temperature gradients
is found in the central 0.1 pc.
2. Assuming constant dust temperature and emissivity, we derive density
profiles for both L1498 and L1517B of the form
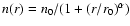 ,
where n0, r0, and
,
where n0, r0, and 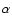 are free parameters. For L1517B, the
are free parameters. For L1517B, the
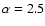 best fit is
indistinguishable from an isothermal sphere fit, and for L1498
the
best fit is
indistinguishable from an isothermal sphere fit, and for L1498
the
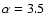 best fit is close to the isothermal fit.
best fit is close to the isothermal fit.
3. From the combination of radiative transfer modeling and hyperfine
fitting of the NH3 and N2H+ spectra, we determine that in
both L1498 and L1517B the
non thermal component of the linewidth is constant with radius
over at least the central 0.1 pc. This component
is smaller than the thermal linewidth and has a FWHM of about 0.12 km s-1 in both cores. Its scatter in the radial profiles
is extremely small (<5%), and it is consistent with
the measurement uncertainty.
4. Using a Monte Carlo radiative transfer code and
the radial profiles of density, temperature, and linewidth,
we determine radial profiles of molecular abundance for all observed
species. For NH3, the abundance at the core centers is a
factor of a few higher than at intermediate radii (0.05 pc). For N2H+,
a constant abundance model fits well the emission at all radii
in L1517B, while a drop by
a factor of 3 at large radii is preferred in L1498. For both CO
and CS (and isotopomers), constant abundance models fail dramatically
to fit the emission, and an abrupt central abundance drop is needed
to explain the data. The abundance drop of these two species is so severe
that the emission can be modeled with step functions and no
molecules at the center.
5. The central abundance drop of CO and CS
seems to arise from the freeze out of these molecules onto cold
dust grains at densities of a few 104 cm-3. The simultaneous
survival of
N2H+ and NH3 seems related to the
lower binding energy to grains of N2, which allows
the production of these two species
at the core centers. The relative increase of the NH3 abundance
over N2H+ probably results from a combination of a more
efficient NH3 production in the highly CO-depleted core interiors
and a decrease in the ion fraction with density, although further
modeling is required to understand this behavior.
6. Superposed to the pattern of radial abundance gradients
there is a weaker pattern of non axially symmetric abundance
variations in both CO and CS.
This pattern results from asymmetries in the
distribution of CO and CS freeze out, and its
presence indicates that
the process responsible for the freeze out has not been
spherically symmetric. As gas contraction to form the cores
is the likely cause of the central freeze out, the asymmetry suggests
that core formation has occurred in a non spherically symmetric way.
7. The analysis of the line center velocities of the freeze-out resistant
N2H+ and NH3reveals spatial variations at the level of 0.1 km s-1in both L1498 and L1517B. The spatial distribution of these variations is
complex and cannot be explained with a simple pattern
like rotation. It most likely represents internal bulk motions
in the core gas. Some gas at anomalous velocities has a spatial
distribution similar to the gas with anomalously high
CO and CS abundance in the pattern of non axisymmetric freeze out.
This similarity suggests that part of the observed bulk motions
result from residual core contraction. If so, the contraction time is
of the order of 1 Myr.
8. We have used the model physical parameters to study the stability of
L1498 and L1517B. The small non thermal linewidth
indicates that any turbulent pressure support is negligible in both cores
(<10%), and that in the absence of magnetic fields,
thermal pressure is the only stabilizing agent. Although the density profiles
have the shape expected for isothermal equilibrium, the mass estimated from
the continuum is larger than what could be held in equilibrium. Either
our choice of dust parameters is incorrect, there is additional magnetic
support, or the cores are in state of (slow) contraction.
In any case, the observed velocity and linewidth profiles
in both L1498 and L1517B are inconsistent with representative predictions
of supersonic turbulence models
that generate density profiles similar to those of an isothermal sphere.
Acknowledgements
We thank the IRAM 30 m staff for help during the observations,
Carl Gottlieb for communicating new frequency measurements
prior to publication,
Daniele Galli for providing us with model gas temperature
profiles for L1517B,
Zhi-Yun Li for advise on ambipolar diffusion models,
and Alexander Lapinov for bringing to our attention
recent work on approximations to the isothermal sphere.
We also thank the referee, Ted Bergin, for comments that
helped clarifying the manuscript.
M.T. acknowledges partial support from grant AYA2000-0927 of
the Spanish DGES. P.C. and C.M.W. acknowledge support from the MIUR project "Dust
and Molecules in Astrophysical Environments".
This research has made use of NASA's Astrophysics Data System
Bibliographic Services and the SIMBAD database, operated at CDS,
Strasbourg, France.
In TMCWC we fitted the volume density profiles of 5 dense cores using an
analytical expression of the form
with n0, r0, and  as free parameters. The motivation of this
choice was purely empirical, based on the ability of these profiles
to fit the observed radial distribution of dust continuum emission.
A later hydrostatic equilibrium analysis of these profiles (unpublished)
showed that for
as free parameters. The motivation of this
choice was purely empirical, based on the ability of these profiles
to fit the observed radial distribution of dust continuum emission.
A later hydrostatic equilibrium analysis of these profiles (unpublished)
showed that for
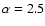 an almost perfect balance between isothermal
plus constant turbulence pressure and self gravity was achieved. Intrigued
by this "coincidence,'' especially because an
an almost perfect balance between isothermal
plus constant turbulence pressure and self gravity was achieved. Intrigued
by this "coincidence,'' especially because an
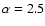 profile lacks
the proper asymptotic behavior for an isothermal sphere (1/r2), we
carried out a point-by-point
comparison between this profile and the numerical solution of the isothermal
function given by Chandrasekhar & Wares (1949). These authors calculated
numerically the mass density profile for an isothermal sphere normalized to
the central density (
profile lacks
the proper asymptotic behavior for an isothermal sphere (1/r2), we
carried out a point-by-point
comparison between this profile and the numerical solution of the isothermal
function given by Chandrasekhar & Wares (1949). These authors calculated
numerically the mass density profile for an isothermal sphere normalized to
the central density (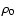 ),
which can be written as
),
which can be written as
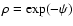 with
with 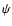 being the solution of
being the solution of
and
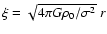 (see Chandrasekhar 1939 for a
full discussion). To compare our
(see Chandrasekhar 1939 for a
full discussion). To compare our
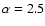 profile with this function, we
normalize it and require that it reaches the half maximum density at the same
radius as the isothermal solution (
profile with this function, we
normalize it and require that it reaches the half maximum density at the same
radius as the isothermal solution (
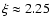 ), and this
completely fixes the profile as:
), and this
completely fixes the profile as:
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.fa1}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg124.gif) |
Figure A.1:
Top: numerical solution of the isothermal function from Chandrasekhar & Wares (1949) (squares) compared to our simple
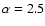 analytic model (line). Bottom: relative error of several
analytic approximations to the isothermal sphere. The solid line
represents the analytic model (line). Bottom: relative error of several
analytic approximations to the isothermal sphere. The solid line
represents the
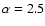 profile presented here, the long-dashed lines
is the modified Hubble law, and the dotted line is model b from
Nataranjan & Lynden-Bell (1997). Note how the
profile presented here, the long-dashed lines
is the modified Hubble law, and the dotted line is model b from
Nataranjan & Lynden-Bell (1997). Note how the
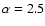 profile remains
within 10% of the exact solution to higher
profile remains
within 10% of the exact solution to higher 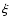 values than the other
profiles (although it finally diverges while the Nataranjan & Lynden-Bell (1997)
curve converges to the right solution at large
values than the other
profiles (although it finally diverges while the Nataranjan & Lynden-Bell (1997)
curve converges to the right solution at large 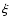 ). ). |
Figure A.1 shows (top) a comparison between the
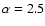 profile
and the numerical solution from Chandrasekhar & Wares (1949).
For additional comparison, we also present the classical modified Hubble law
approximation (Binney & Tremaine 1987)
and the recent simple approximation
proposed by Nataranjan & Lynden-Bell (1997) (their case b). As can be seen,
the
profile
and the numerical solution from Chandrasekhar & Wares (1949).
For additional comparison, we also present the classical modified Hubble law
approximation (Binney & Tremaine 1987)
and the recent simple approximation
proposed by Nataranjan & Lynden-Bell (1997) (their case b). As can be seen,
the
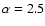 profile remains within 10% from the exact solution
up to a larger
profile remains within 10% from the exact solution
up to a larger 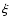 value than the other solutions (although
the Nataranjan & Lynden-Bell (1997) profile finally converges to the
exact solution for large
value than the other solutions (although
the Nataranjan & Lynden-Bell (1997) profile finally converges to the
exact solution for large 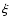 ). In fact, the
). In fact, the
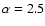 solution
is accurate within 10% for
solution
is accurate within 10% for
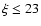 ,
more than 3.5 times the instability radius (Ebert 1955; Bonnor 1956),
and over this range, the density varies by more than a factor 300.
The associated instability point of this solution (
,
more than 3.5 times the instability radius (Ebert 1955; Bonnor 1956),
and over this range, the density varies by more than a factor 300.
The associated instability point of this solution (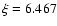 )
is
within 0.25% of the exact solution (
)
is
within 0.25% of the exact solution (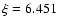 , Hunter 1977).
This shows that the
, Hunter 1977).
This shows that the
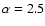 profile can be used to approximate
any stable Bonnor-Ebert sphere within 10%.
profile can be used to approximate
any stable Bonnor-Ebert sphere within 10%.
The lack of allowed radiative transitions between the (J, K)=(2, 2) and
(1, 1) levels
of NH3 makes their relative population (described by the rotational
temperature
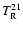 )
highly sensitive to collisions, and therefore a
good estimator of the gas kinetic temperature. In the traditional NH3analysis, the (1, 1) and (2, 2) populations are calculated from the
spectra assuming LTE
conditions, and the derived
)
highly sensitive to collisions, and therefore a
good estimator of the gas kinetic temperature. In the traditional NH3analysis, the (1, 1) and (2, 2) populations are calculated from the
spectra assuming LTE
conditions, and the derived
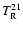 rotational temperature is converted
into an estimate of the gas kinetic temperature TK (Walmsley & Ungerechts 1983).
To test this procedure and to calibrate the
rotational temperature is converted
into an estimate of the gas kinetic temperature TK (Walmsley & Ungerechts 1983).
To test this procedure and to calibrate the
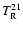 -
-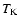 relation using realistic radiative transfer and
cloud conditions, we have run a series of Monte Carlo models
and produced synthetic (1, 1) and (2, 2) spectra. These spectra
have been analyzed using the standard NH3 procedure, and the derived
gas parameters have been compared with those used in the models.
relation using realistic radiative transfer and
cloud conditions, we have run a series of Monte Carlo models
and produced synthetic (1, 1) and (2, 2) spectra. These spectra
have been analyzed using the standard NH3 procedure, and the derived
gas parameters have been compared with those used in the models.
Our NH3 Monte Carlo model has been described in TMCWC and is based on that
of Bernes (1979), adapted to handle NH3. It includes the 6 lowest
levels of para-NH3, which contain more than 99.9% of the molecules at
10 K (typical core gas temperature). It assumes that the relative hf
sub-populations of the meta-stable
levels are in LTE (as required by observations), and calculates the
relative populations between the (1, 1), (2, 1), and (2, 2) levels
in a self-consistent manner. It uses
the collision coefficients with H2 of Danby et al. (1988), which seems to
be the most accurate set available, according to recent laboratory
measurements (Willey et al. 2002). As cloud
parameters, we use the density profiles derived from dust emission for L1498
(L1498-models) and L1517B (L1517B-models), and assume a constant
gas temperature (given the results of Sect. 3.3), which we have varied from
5 to 20 K.
In all 9 models we have run we find that while both the (1, 1) and (2, 2)
excitation temperatures vary with radius by a factor of several
(as a result of the core density gradient),
the
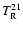 rotational temperature stays constant over the
core within 2% or less. This makes
the derivation of
rotational temperature stays constant over the
core within 2% or less. This makes
the derivation of
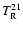 using the standard NH3 analysis
(e.g., Bachiller et al. 1987) rather accurate, despite of violating
one of its basic assumptions: that of a single excitation temperature
for both (1, 1) and (2, 2). In fact, our models show that in the range
of kinetic temperatures we
have explored (5-20 K),
using the standard NH3 analysis
(e.g., Bachiller et al. 1987) rather accurate, despite of violating
one of its basic assumptions: that of a single excitation temperature
for both (1, 1) and (2, 2). In fact, our models show that in the range
of kinetic temperatures we
have explored (5-20 K),
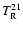 estimates using the standard analysis
agree within 5% with the real values, and that the
agreement is at the 1% level for temperatures around 10 K or lower.
Thus,
estimates using the standard analysis
agree within 5% with the real values, and that the
agreement is at the 1% level for temperatures around 10 K or lower.
Thus,
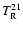 can be easily and accurately
determined from observations for realistic core conditions.
can be easily and accurately
determined from observations for realistic core conditions.
![\begin{figure}
\par\includegraphics[clip,width=7.05cm]{4112.fb1}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg128.gif) |
Figure B.1:
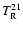 versus
versus 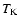 derived using Monte Carlo models.
derived using Monte Carlo models.
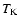 is the (constant) gas kinetic temperature and
is the (constant) gas kinetic temperature and
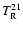 is the (2, 2)-to-(1, 1) rotation temperature derived by applying the
standard NH3 analysis to the Monte Carlo spectra. Filled triangles
and open squares represent
models having the analytic density profile derived in Sect. 3.1 for L1517B and L1498, respectively (see Table 2). Multiple
points at the same is the (2, 2)-to-(1, 1) rotation temperature derived by applying the
standard NH3 analysis to the Monte Carlo spectra. Filled triangles
and open squares represent
models having the analytic density profile derived in Sect. 3.1 for L1517B and L1498, respectively (see Table 2). Multiple
points at the same 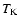 represent values measured at radii equal
0, 10, 30, 60, 100, and 150 arcsec (data convolved to the 40''resolution of the Effelsberg 100 m telescope). The solid line is the
analytic expression proposed in the text to derive
represent values measured at radii equal
0, 10, 30, 60, 100, and 150 arcsec (data convolved to the 40''resolution of the Effelsberg 100 m telescope). The solid line is the
analytic expression proposed in the text to derive 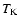 using
the
using
the
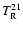 estimate from the standard NH3 analysis.
estimate from the standard NH3 analysis. |
The critical part of the NH3 analysis is the conversion of the
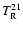 estimate into an estimate of the gas kinetic temperature
estimate into an estimate of the gas kinetic temperature 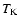 ,
as
this step requires a full solution of the radiative transfer
equation. Walmsley & Ungerechts (1983) have presented a simple analytic
expression derived under simplifying assumptions and using an old
version of the NH3-H2 collision coefficients from Green (1981).
In order to derive a revised expression using realistic radiative
transport and the new collision coefficients of Danby et al. (1988),
we compare the
,
as
this step requires a full solution of the radiative transfer
equation. Walmsley & Ungerechts (1983) have presented a simple analytic
expression derived under simplifying assumptions and using an old
version of the NH3-H2 collision coefficients from Green (1981).
In order to derive a revised expression using realistic radiative
transport and the new collision coefficients of Danby et al. (1988),
we compare the 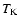 inputs in the Monte Carlo models
with the
inputs in the Monte Carlo models
with the
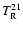 values derived from the above analysis.
As can be seen in Fig. B.1, for any given
values derived from the above analysis.
As can be seen in Fig. B.1, for any given 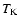 between 5 and 20 K, the
L1498-models and L1517B-models predict the same
between 5 and 20 K, the
L1498-models and L1517B-models predict the same
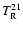 within
5% or better, and this shows that at least for our conditions, the
within
5% or better, and this shows that at least for our conditions, the
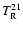 -
-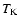 relation is almost independent of the
details of core density, size, etc.
To derive an analytic expression for this relation, we use as
inspiration Eq. (2) of Walmsley & Ungerechts (1983), although we look
for the inverse function of theirs
because we want to predict
relation is almost independent of the
details of core density, size, etc.
To derive an analytic expression for this relation, we use as
inspiration Eq. (2) of Walmsley & Ungerechts (1983), although we look
for the inverse function of theirs
because we want to predict 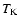 given the
given the
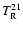 value determined with the standard NH3 analysis. After some
experimentation, we have found that the following expression
value determined with the standard NH3 analysis. After some
experimentation, we have found that the following expression
![\begin{displaymath}T_{\rm K} = {T_{\rm R}^{21}\over 1-{T_{\rm R}^{21}\over 42}\; \ln\left[1+1.1\exp(-16/T_{\rm R}^{21})\right]}
\end{displaymath}](/articles/aa/full/2004/10/aa4112/img129.gif)
fits the points in the range
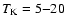 K to better than 5%, and therefore
provides an accurate gas temperature estimate based on
easy-to-measure quantities. We recommend this relation to derive
K to better than 5%, and therefore
provides an accurate gas temperature estimate based on
easy-to-measure quantities. We recommend this relation to derive
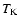 in dense, cold cores at temperatures lower than or around 20 K
(extrapolation to higher temperatures requires further modeling).
in dense, cold cores at temperatures lower than or around 20 K
(extrapolation to higher temperatures requires further modeling).
- Aikawa, Y., Ohashi, N., Inutsuka, S.,
Herbst, E., & Takakuwa, S. 2001, ApJ, 552, 639
In the text
NASA ADS
- Aikawa, Y., Ohashi, N., & Herbst, E.
ApJ, 593, 906
In the text
NASA ADS
- Alves, J., Lada, C. J., & Lada, E. A. 1999,
ApJ, 515, 265
In the text
NASA ADS
- Alves, J., Lada, C. J., & Lada, E. A. 2001,
Nature, 409, 159
In the text
NASA ADS
- André, P., Ward-Thompson, D., &
Motte, F. 1996, A&A, 314, 625
In the text
NASA ADS
- Bachiller, R., Guilloteau, S.,
& Kahane, C. 1987, A&A, 173, 324
In the text
NASA ADS
- Bacmann, A., André, P., Puget, J. -L.,
et al. 2000, A&A, 361, 558
In the text
- Bacmann, A., Lefloch, B.,
Ceccarelli, C., et al. 2002, A&A,
389, L6
In the text
NASA ADS
- Ballesteros-Paredes, J.,
Klessen, R. S., & Vázquez-Semadeni, E. 2003, ApJ, 592, 188
In the text
- Barranco, J. A., & Goodman, A. A.
1998, ApJ, 504, 207
In the text
NASA ADS
- Beichman, C. A., Myers, P. C., Emerson,
J. P., et al. 1986, ApJ,
307, 337
In the text
NASA ADS
- Bergin, E. A., & Langer, W. D. 1997,
ApJ, 486, 316
In the text
NASA ADS
- Bergin, E. A., Ciardi, D. R., Lada, C. J.,
Alves, J., & Lada, E. A. 2001, ApJ, 557, 209
In the text
NASA ADS
- Bergin, E. A., Alves, J., Huard, T.,
& Lada, C. J. 2002, ApJ, 570, L101
In the text
NASA ADS
- Bernes, C. 1979, A&A, 73, 67
In the text
NASA ADS
- Benson, P. J., & Myers, P. C. 1989,
ApJS, 71, 89
In the text
NASA ADS
- Bianchi, S., Gonçalves, J.,
Albrecht, M., et al. 2003, A&A,
399, L43
In the text
NASA ADS
- Binney, J., & Tremaine, S. 1987
Galactic Dynamics (Princeton: Princeton University Press)
In the text
- Bonnor, W. B. 1956, MNRAS, 116, 351
In the text
NASA ADS
- Broguière, D., Neri, R., &
Sievers, A. 1996, IRAM Tech. Report
In the text
- Caselli, P., Myers, P. C., & Thaddeus,
P. 1995, ApJ, 455, L77
In the text
NASA ADS
- Caselli, P., Walmsley, C. M., Tafalla,
M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165
In the text
NASA ADS
- Caselli, P., Benson, P. J.,
Myers, P. C., & Tafalla, M. 2002a, ApJ, 572, 238
In the text
NASA ADS
- Caselli, P., Walmsley, C. M.,
Zucconi, A., et al. 2002, ApJ, 565, 344
In the text
NASA ADS
- Caselli, P., Walmsley, C. M.,
Zucconi, A., et al. 2002, ApJ, 565, 331
NASA ADS
- Cazzoli, G., Dore, L., Puzzarini, C.,
& Beninati, S. 2002, Phys. Chem. Chem. Phys., 4, 3575
- Chandrasekhar, S. 1939, An
Introduction to the Study of Stellar Structure (Chicago: Univ. Chicago Press)
In the text
- Chandrasekhar, S., & Wares,
G. W. 1949, ApJ, 109, 551
In the text
NASA ADS
- Charnley, S. B. 1997, MNRAS, 291, 455
In the text
NASA ADS
- Ciolek, G. E., & Basu, S. 2001, ApJ,
547, 272
In the text
NASA ADS
- Curry, C. 2002, ApJ, 576, 849
In the text
NASA ADS
- Danby, G., Flower, D. R., Valiron, P.,
Schilke, P., & Walmsley, C. M. 1988, MNRAS, 235, 229
In the text
NASA ADS
- Ebert, R. 1956, Z. Astrophys., 37, 216
In the text
- Elmegreen, B. G. 1979, ApJ, 232, 729
NASA ADS
- Elmegreen, B. G. 2000, ApJ, 530, 277
In the text
NASA ADS
- Evans, N. J. II 1999, ARA&A, 37, 311
In the text
NASA ADS
- Evans, N. J. II, Rawlings, J. M. C.,
Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193
In the text
NASA ADS
- Flower, D. R. 1999, MNRAS, 305, 651
In the text
NASA ADS
- Fuller, G. A., & Myers, P. C. 1993,
ApJ, 418, 273
In the text
NASA ADS
- Galli, D., Walmsley, M., & Gonçalves, J.
2002, A&A, 394, 275
In the text
NASA ADS
- Goldsmith, P. F. 2001, ApJ, 557, 736
In the text
NASA ADS
- Goodman, A. A., Benson, P. J., Fuller,
G.A., & Myers, P. C. 1993, ApJ, 406, 528
In the text
NASA ADS
- Goodman, A. A., Barranco, J. A.,
Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223
NASA ADS
- Gottlieb, C. A., Myers, P. C.,
& Theddeus, P. 2003, ApJ, 588, 655
NASA ADS
- Green, S. 1981, NASA Tech. Memo., 83869
In the text
- Hartmann, L., Ballesteros-Paredes, J.,
& Bergin, E. 2001, ApJ, 562, 852
In the text
NASA ADS
- Hotzel, S., Harju, J., & Juvela, M.
2002, A&A, 395, L5
NASA ADS
- Houde, M., Bastien, P., Peng, R., Phillips, T. G.,
& Yoshida, H. 2000, ApJ, 536, 857
In the text
NASA ADS
- Hunter, C. 1977, ApJ, 218, 834
In the text
NASA ADS
- Jessop, N. E.,
& Ward-Thompson, D. 2001, MNRAS, 323, 1025
In the text
NASA ADS
- Jones, C. E., & Basu, S. 2002, ApJ,
569, 280
In the text
NASA ADS
- Kramer, C., Alves, J., Lada, C. J.,
et al. 1999, A&A, 342, 257
In the text
NASA ADS
- Kramer, C., Richer, J., Mookerjea, B.,
Alves, J., & Lada, C. 2003, ApJ, 399, 1073
In the text
- Kreysa, E., Gemuend, H. -P., Grombe, J., et al. 1998, SPIE, 3357, 319
In the text
- Kukolich, S. G. 1966, Phys. Rev., 156, 83
- Kuiper, T. B. H., Langer, W. D., &
Velusamy, T. 1996, ApJ, 468, 761
In the text
NASA ADS
- Lada, C. J., Bergin, E. A., Alves, J. F.,
& Huard, T. R. 2003, ApJ, 586, 286
In the text
NASA ADS
- Langer, W. D., & Willacy, K. 2001,
ApJ, 557, 714
In the text
NASA ADS
- Lee, C. W. & Myers, P. C. 1999, ApJS, 123,
233
In the text
NASA ADS
- Lee, C. W., Myers, P. C., & Tafalla, M. 1999,
ApJ, 526, 788
In the text
NASA ADS
- Lee, C. W., Myers, P. C., & Tafalla, M. 2001,
ApJS, 136, 703
In the text
NASA ADS
- Lemme, C., Walmsley, C. M.,
Wilson, T. L., & Muders, D. 1995 A&A, 302, 509
In the text
NASA ADS
- Levin, S. M., Langer, W. D., Velusamy,
T., Kuiper, T. B. H., & Crutcher, R. M. 2001, ApJ, 555, 850
In the text
NASA ADS
- Li, Z.-Y. 1999, ApJ, 526, 806
In the text
NASA ADS
- Li, Z.-Y., Shematovich, V. I., Wiebe, D. S., &
Shustov, B. M. 2002, ApJ, 569, 792
In the text
NASA ADS
- Lucas, R., & Liszt, H. 1998, A&A,
337, 246
In the text
NASA ADS
- Mac Low, M.-M., & Klessen, R. S.
2004, Rev. Mod. Phys., 76, 125
In the text
NASA ADS
- Mathis, J. S., Mezger, P. G.,
& Panagia, N. 1983, A&A, 128, 212
In the text
NASA ADS
- McCall, B. J., Huneycutt, A. J., Saykally, R. J., et al. 2003, Nature, 422, 500
In the text
NASA ADS
- McLaughlin, D. E., & Pudritz,
R. E. 1996, ApJ, 469, 194
In the text
NASA ADS
- Müller, H. S. P., Thorwirth, S.,
Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49
NASA ADS
- Myers, P. C. 1983, ApJ, 270, 105
In the text
NASA ADS
- Myers, P. C., Linke, R. A., & Benson,
P. J. 1983, ApJ, 264, 517
In the text
NASA ADS
- Myers, P. C. 1999, in The Physics and
Chemistry of
the Interstellar Medium, ed. V. Ossenkopf, J. Stutzki, & G. Winnewisser
(Herdecke: GCA-Verlag), 227
In the text
- Myers, P. C., Fuller, G. A., Mathieu, R. D.,
et al. 1987, ApJ,
319, 340
NASA ADS
- Nataranjan, P., &
Lynden-Bell, D. 1997, MNRAS, 286, 268
In the text
NASA ADS
- Nejad, L. A. M., & Wagenblast, R.
1999, A&A, 350, 204
In the text
NASA ADS
- Ossenkopf, V., & Henning, T.
1994, A&A, 291, 943
In the text
NASA ADS
- Penzias, A. A. 1981, ApJ, 249, 518
In the text
NASA ADS
- Shematovich, V. I., Wiebe, D. S.,
Shustov, B. M., & Li, Z.-Y. 2003, ApJ, 588, 894
In the text
NASA ADS
- Shu, F. H., Adams, F. C., & Lizano S. 1987,
ARA&A, 25, 23
In the text
NASA ADS
- Tafalla, M., Mardones, D., Myers, P. C.,
et al. 1998, ApJ, 504, 900
NASA ADS
- Tafalla, M., Myers, P. C.,
Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815
In the text
NASA ADS
- Walmsley, C. M., & Ungerechts,
H. 1983, A&A, 122, 164
In the text
NASA ADS
- Ward-Thompson, D.,
André, P., & Kirk, J. M. 2002, MNRAS, 329, 257
NASA ADS
- Ward-Thompson, D., Scott, P. F.,
Hills, R. E., & André, P. 1994, MNRAS, 268, 276
In the text
NASA ADS
- Willacy, K., Langer, W. D., &
Velusamy, T. 1998, ApJ, 507, L171
In the text
NASA ADS
- Willey, D. R., Timlin, R. E., Merlin, J. M.,
Sowa, M. M., & Wesolek, D. M. 2002, ApJS, 139, 191
In the text
NASA ADS
- Wolkovitch, D., Langer, W. D.,
Goldsmith, P. F., & Heyer, M. 1997, ApJ, 477, 241
In the text
NASA ADS
- Zhou, S., Wu, Y., Evans, N. J. II, Fuller,
G. A., & Myers, P. C. 1989, ApJ, 346, 168
In the text
NASA ADS
- Zucconi, A., Walmsley, C. M., & Galli,
D. 2001, A&A, 376, 650
In the text
NASA ADS
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[clip,width=15.1cm]{4112.f1}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg27.gif)
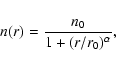
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f2}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg33.gif)
![\begin{figure}
\par\includegraphics[clip,width=10.3cm]{4112.f3}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg35.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f4}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg64.gif)
![\begin{figure}
\par\includegraphics[clip,width=17.6cm]{4112.f5}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg67.gif)
![\begin{figure}
\par\includegraphics[clip,width=17.6cm]{4112.f6} %
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg73.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f7}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg77.gif)
![\begin{figure}
\par\includegraphics[clip,width=15cm]{4112.f8}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg78.gif)
![\begin{figure}
\par\includegraphics[clip,width=15.1cm]{4112.f9}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg82.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f10}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg88.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f11}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg91.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f12}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg93.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.f13}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg96.gif)
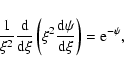
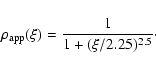
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{4112.fa1}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg124.gif)
![\begin{figure}
\par\includegraphics[clip,width=7.05cm]{4112.fb1}
\end{figure}](/articles/aa/full/2004/10/aa4112/Timg128.gif)
![\begin{displaymath}T_{\rm K} = {T_{\rm R}^{21}\over 1-{T_{\rm R}^{21}\over 42}\; \ln\left[1+1.1\exp(-16/T_{\rm R}^{21})\right]}
\end{displaymath}](/articles/aa/full/2004/10/aa4112/img129.gif)