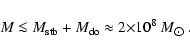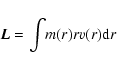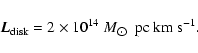A&A 416, 67-78 (2004)
DOI: 10.1051/0004-6361:20031709
The rotating visible outflow in M 82
A. Greve
Institut de Radio Astronomie Millimétrique,
300 rue de la Piscine, 38406 St. Martin d'Hères, France
Received 21 March 2003 / Accepted 26 November 2003
Abstract
M 82's minor axis outflow is seen at visible wavelengths as more or
less regular hollow cones on both sides of the galactic disk. The outflowing
material is expected to entrain the rotation, or part of the rotation, of the
disk where the outflow originates. From the conservation of angular momentum
it is furthermore expected that the outflowing material continues to rotate at
large distances from the disk, although probably with smaller velocity because
of radial divergence of the cones. We provide evidence of this kinematic
picture from long-slit spectra of the cone wall H ,
[NII] and [SII]
emission lines taken at
,
[NII] and [SII]
emission lines taken at  20'' (
20'' ( 300 pc) and
300 pc) and

 40'' (
40'' (
 600 pc) distance from the center and
parallel to the minor axis, from data extracted from the literature, and from
a cone model fit of the data. The angular momentum which is entrained in the
outflow and eventually dissipated is a small fraction of the total angular
momentum associated with the stars and gas in the central part of the disk.
600 pc) distance from the center and
parallel to the minor axis, from data extracted from the literature, and from
a cone model fit of the data. The angular momentum which is entrained in the
outflow and eventually dissipated is a small fraction of the total angular
momentum associated with the stars and gas in the central part of the disk.
We compare our observation of the visible outflow with the outflow of
dragged-out material investigated in mm-wavelength CO by other observers. It
seems that the material observed at visible wavelengths is confined to narrow
cones, and blows out at velocities larger than the escape velocity of the
galaxy. The dragged-out material moves at slower velocities and on wider
cones, and may fall back into the galaxy.
Key words: galaxies: individual: M 82 - galaxies: structure - galaxies:
ISM
The supernova explosions and stellar winds of M 82's starburst produce an
outflow of 107-108 K hot gas along the minor axis on both
sides of the galactic disk. This tenuous hot gas is collimated by the
molecular gas ring and moves into the halo in the form of more or less
regular cones. Because of M 82's favourable edge-on orientation (inclination
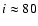
 ,
seen from below), the X-ray emission of the hot
material inside the cones is seen to a distance of several kpc above and below
the galactic plane (Bregman et al. 1995; Strickland et al. 1997). At the
boundary between the hot gas and the disk and the halo, the outflow material
shocks with swept-out material of the disk and with material of the halo, and
cools to a temperature of
,
seen from below), the X-ray emission of the hot
material inside the cones is seen to a distance of several kpc above and below
the galactic plane (Bregman et al. 1995; Strickland et al. 1997). At the
boundary between the hot gas and the disk and the halo, the outflow material
shocks with swept-out material of the disk and with material of the halo, and
cools to a temperature of  104 K. At this temperature the
ionized gas (
104 K. At this temperature the
ionized gas (
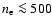 cm-3) emits the (forbidden)
recombination lines of H
cm-3) emits the (forbidden)
recombination lines of H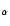 ,
[NII], [SII]. This visible
filamentary emission, confined to the cone walls, is seen to a height of
1-2 kpc on both sides of the disk with typical double
velocity-split line profiles. The position-velocity analysis of the visible
emission has revealed that the cones have opening angles of
,
[NII], [SII]. This visible
filamentary emission, confined to the cone walls, is seen to a height of
1-2 kpc on both sides of the disk with typical double
velocity-split line profiles. The position-velocity analysis of the visible
emission has revealed that the cones have opening angles of
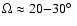 (full angle) (Burbidge et al. 1964; Axon &
Taylor 1978; Amirkhanyan et al. 1982, 1985; Bland & Tully 1988
[BT-88]; Götz et al. 1990; McKeith et al. 1995 [M-95]; Shopbell
& Bland-Hawthorn 1998 [SBH-98]), although also considerably wider
cones of
(full angle) (Burbidge et al. 1964; Axon &
Taylor 1978; Amirkhanyan et al. 1982, 1985; Bland & Tully 1988
[BT-88]; Götz et al. 1990; McKeith et al. 1995 [M-95]; Shopbell
& Bland-Hawthorn 1998 [SBH-98]), although also considerably wider
cones of
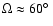 opening angle have been proposed
(Heckman et al. 1990 [HAM-90]). At the height of
opening angle have been proposed
(Heckman et al. 1990 [HAM-90]). At the height of  10 kpc, at the
NW side of the disk, the outflowing gas apparently bow-shocks with
intergalactic gas and emits H
10 kpc, at the
NW side of the disk, the outflowing gas apparently bow-shocks with
intergalactic gas and emits H (Devine & Bally 1999; Lehnert et al. 1999). Detection at visible wavelengths of rotation of cone wall material
at large distances from the disk was mentioned by Bland & Tully and
Shopbell & Bland-Hawthorn. Spectra taken by Heckathorn (1972) parallel to
the major axis to a distance of 675 pc below and 410 pc above the galactic
plane have sloped tracks in the position-velocity diagrams and by this
clearly illustrate rotation of the visible outflow material, in the same
direction as the material of the disk and with decreasing velocity for
increasing distances from the disk. These and other imaging and spectroscopic
observations were used to determine the geometry and kinematics of the
visible outflow material; for a recent analysis and summary see SBH-98 and
Table 1. Models of this type of starburst-driven outflow are published by
Chevalier & Clegg (1985), Tomisaka & Ikeuchi (1988), Umemura et al.
(1988), Heckman et al. (1990), Yokoo et al. (1993), Tenorio-Tagle &
Muñoz-Tuñon (1997), Strickland & Stevens (2000), and others.
(Devine & Bally 1999; Lehnert et al. 1999). Detection at visible wavelengths of rotation of cone wall material
at large distances from the disk was mentioned by Bland & Tully and
Shopbell & Bland-Hawthorn. Spectra taken by Heckathorn (1972) parallel to
the major axis to a distance of 675 pc below and 410 pc above the galactic
plane have sloped tracks in the position-velocity diagrams and by this
clearly illustrate rotation of the visible outflow material, in the same
direction as the material of the disk and with decreasing velocity for
increasing distances from the disk. These and other imaging and spectroscopic
observations were used to determine the geometry and kinematics of the
visible outflow material; for a recent analysis and summary see SBH-98 and
Table 1. Models of this type of starburst-driven outflow are published by
Chevalier & Clegg (1985), Tomisaka & Ikeuchi (1988), Umemura et al.
(1988), Heckman et al. (1990), Yokoo et al. (1993), Tenorio-Tagle &
Muñoz-Tuñon (1997), Strickland & Stevens (2000), and others.
The observations indicate also that at the base, and probably mainly at the
periphery of the visible cones, the outflow drags cool gas and dust out of
the disk into the halo. At visible wavelengths (H ,
[NII]) this
dragged-out gas and dust is clearly seen in the images published by
Ohyama et al. (2002 [OEA-02]). The dust in the halo is also seen to a
height of
,
[NII]) this
dragged-out gas and dust is clearly seen in the images published by
Ohyama et al. (2002 [OEA-02]). The dust in the halo is also seen to a
height of  1-2 kpc as scattered optical continuum emission of
radiation apparently originating in the disk (BT-88), and by its optical
polarization (Scarrott et al. 1991). Dragged-out dust is seen to a
height of
1-2 kpc as scattered optical continuum emission of
radiation apparently originating in the disk (BT-88), and by its optical
polarization (Scarrott et al. 1991). Dragged-out dust is seen to a
height of 
 800 pc in 1.2 mm, 0.85 mm and 0.45 mm continuum
observations
800 pc in 1.2 mm, 0.85 mm and 0.45 mm continuum
observations![[*]](/icons/foot_motif.gif) (Alton et al. 1999; Thuma et al. 2000).
Dragged-out molecular gas is seen in mm-wavelength CO emission to a height
of approximately 0.5-1 kpc above and below the disk (Nakai et al. 1987;
Loiseau et al. 1990; Sofue et al. 1992). Loiseau et al. and Sofue et al. find
that the molecular gas at the height between 0.5 kpc and 1 kpc rotates in
the same direction as the disk, though with gradually smaller velocity at
greater distances from the disk. The recent JCMT observation by Seaquist &
Clark (2001 [SC-01]) confirms without doubt CO material and its
rotation up to a distance of
(Alton et al. 1999; Thuma et al. 2000).
Dragged-out molecular gas is seen in mm-wavelength CO emission to a height
of approximately 0.5-1 kpc above and below the disk (Nakai et al. 1987;
Loiseau et al. 1990; Sofue et al. 1992). Loiseau et al. and Sofue et al. find
that the molecular gas at the height between 0.5 kpc and 1 kpc rotates in
the same direction as the disk, though with gradually smaller velocity at
greater distances from the disk. The recent JCMT observation by Seaquist &
Clark (2001 [SC-01]) confirms without doubt CO material and its
rotation up to a distance of  900 pc, on both sides of the disk.
However, SC-01 find that the CO material moves out from the disk at a
significantly smaller velocity than the visible cone wall material, that the
CO material does not show velocity-split line profiles, and that the outflow
of the molecular gas forms cones of a much wider opening angle of
900 pc, on both sides of the disk.
However, SC-01 find that the CO material moves out from the disk at a
significantly smaller velocity than the visible cone wall material, that the
CO material does not show velocity-split line profiles, and that the outflow
of the molecular gas forms cones of a much wider opening angle of
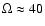 -90
-90
 .
They argue also that the molecular material flows
out under conservation of angular momentum, as already proposed by Nakai et al. (1987) and Sofue et al. (1992). Seaquist & Clark conclude that
the motion of the hot visible gas and of the cool dragged-out CO gas are
distinctly different aspects of the outflow phenomenon. Further evidence of
cool material being dragged-out in a cone-like form, at least at the SE side
of the disk, comes from CO (1-0) observations made with the OVRO and
IRAM 30 m telescopes by Walter et al. (2002 [WWS-02]). They find CO with
.
They argue also that the molecular material flows
out under conservation of angular momentum, as already proposed by Nakai et al. (1987) and Sofue et al. (1992). Seaquist & Clark conclude that
the motion of the hot visible gas and of the cool dragged-out CO gas are
distinctly different aspects of the outflow phenomenon. Further evidence of
cool material being dragged-out in a cone-like form, at least at the SE side
of the disk, comes from CO (1-0) observations made with the OVRO and
IRAM 30 m telescopes by Walter et al. (2002 [WWS-02]). They find CO with
 100 km s-1 velocity splitting at the SE side of the disk to a
distance of
100 km s-1 velocity splitting at the SE side of the disk to a
distance of  600 pc below the plane, flowing out at the
velocity of 230 km s-1 and forming a cone of
600 pc below the plane, flowing out at the
velocity of 230 km s-1 and forming a cone of  55
55
 opening
angle. They do not find a similar cone-like outflow at the NW side of the
disk. Their published position-velocity diagrams of CO at a distance of
350 pc SE and NW from the disk show clearly rotation. Discussions on the
energy and temperature of outflows and observational evidence of dragged-out
material have led to the theory of mass-loaded outflows, as published by
Tomisaka & Bregman (1993), Suchkov et al. (1994, 1996), Hartquist et al.
(1997), Strickland & Stevens (2000), and others. For a sketch of these
outflow phenomena see Fig. 1 in HAM-90, Fig. 5 in Alton et al. (1999), and
especially Fig. 6 in OEA-02. In the terminology used by Ohyama et al. the
cone walls are the ridge component, the dragged-out dust and gas component
in the halo, outside the cones, is the diffuse component. The different
spatial distributions are evident from their published pictures.
opening
angle. They do not find a similar cone-like outflow at the NW side of the
disk. Their published position-velocity diagrams of CO at a distance of
350 pc SE and NW from the disk show clearly rotation. Discussions on the
energy and temperature of outflows and observational evidence of dragged-out
material have led to the theory of mass-loaded outflows, as published by
Tomisaka & Bregman (1993), Suchkov et al. (1994, 1996), Hartquist et al.
(1997), Strickland & Stevens (2000), and others. For a sketch of these
outflow phenomena see Fig. 1 in HAM-90, Fig. 5 in Alton et al. (1999), and
especially Fig. 6 in OEA-02. In the terminology used by Ohyama et al. the
cone walls are the ridge component, the dragged-out dust and gas component
in the halo, outside the cones, is the diffuse component. The different
spatial distributions are evident from their published pictures.
In this picture of a minor axis outflow the material of the visible cone walls
is expected to rotate. We present new observations which trace in long-slit
spectra parallel to the minor axis the rotation of the visible outflow
material to a distance of 1-1.2 kpc above and below the galactic plane.
In the observations, distances are originally measured in angular scale
( ). To be consistent with our earlier publication (M-95), we adopt
that 1'' is equivalent to 15 pc at the distance of M 82 (3.1 Mpc; see
Freedman et al. 1994 and Sakai & Madore 1999 for a somewhat larger
distance of 3.2-3.9 Mpc). The position angle of M 82's major axis is
). To be consistent with our earlier publication (M-95), we adopt
that 1'' is equivalent to 15 pc at the distance of M 82 (3.1 Mpc; see
Freedman et al. 1994 and Sakai & Madore 1999 for a somewhat larger
distance of 3.2-3.9 Mpc). The position angle of M 82's major axis is
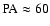 -65
-65
 ,
of the minor axis
,
of the minor axis
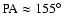 ,
as for
instance extracted from the deep image published by Devine & Bally (1999)
but not represented by the warped central CO distribution (Shen & Lo 1995;
Neininger et al. 1998). The Western side (
,
as for
instance extracted from the deep image published by Devine & Bally (1999)
but not represented by the warped central CO distribution (Shen & Lo 1995;
Neininger et al. 1998). The Western side (
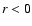 )
of M 82's disk moves
towards the observer, the Eastern side (
)
of M 82's disk moves
towards the observer, the Eastern side (
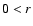 )
moves away (Neininger
et al. 1998; Greve et al. 2002): emission from the Western side is
blue-shifted, from the Eastern side red-shifted. We note also that at
visible wavelengths we do not necessarily observe the rotation of the disk
core region (McKeith et al. 1993), which is hidden behind dust, but the
rotation of material which lies mainly in front of the molecular ring of
600-800 pc diameter (Shen & Lo 1995; Neininger et al. 1998;
Weiß et al. 2001), or even further out. For this reason we do not discuss
the optical emission inside
)
moves away (Neininger
et al. 1998; Greve et al. 2002): emission from the Western side is
blue-shifted, from the Eastern side red-shifted. We note also that at
visible wavelengths we do not necessarily observe the rotation of the disk
core region (McKeith et al. 1993), which is hidden behind dust, but the
rotation of material which lies mainly in front of the molecular ring of
600-800 pc diameter (Shen & Lo 1995; Neininger et al. 1998;
Weiß et al. 2001), or even further out. For this reason we do not discuss
the optical emission inside 
 200 pc distance from the galactic
plane.
200 pc distance from the galactic
plane.
Simultaneous observations of the H 6563 Å, [NII] 6548,
6583 Å and [SII] 6716, 6731 Å emission lines were made with the
2.5 m Isaac Newton Telescope (La Palma, Spain) at a spectral resolution of
6563 Å, [NII] 6548,
6583 Å and [SII] 6716, 6731 Å emission lines were made with the
2.5 m Isaac Newton Telescope (La Palma, Spain) at a spectral resolution of
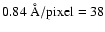 km s-1/pixel (grating of 1200 grooves/mm) and
a spatial resolution of
km s-1/pixel (grating of 1200 grooves/mm) and
a spatial resolution of
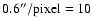 pc/pixel. The seeing was
pc/pixel. The seeing was
 1'', i.e.
1'', i.e.  15 pc. The slit of 3' (2.7 kpc) length was
placed along the minor axis (
15 pc. The slit of 3' (2.7 kpc) length was
placed along the minor axis (
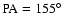 ), passing approximately through
the center of M 82 defined by the 2.2
), passing approximately through
the center of M 82 defined by the 2.2 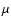 m
peak
m
peak![[*]](/icons/foot_motif.gif) , and subsequently
placed parallel to the minor axis at
, and subsequently
placed parallel to the minor axis at
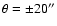 (
(
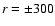 pc) and
pc) and
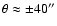 (
(
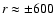 pc) radial distance from the center (in linear scale
denoted by r). Because of the narrow cone opening and small base of the
outflow, the on-axis spectrum and the
pc) radial distance from the center (in linear scale
denoted by r). Because of the narrow cone opening and small base of the
outflow, the on-axis spectrum and the  20'' spectra show clear line
splitting and allow the determination of the cone angle, the outflow
velocity(ies) and acceleration, and the rotation; the
20'' spectra show clear line
splitting and allow the determination of the cone angle, the outflow
velocity(ies) and acceleration, and the rotation; the  40'' spectra
are taken more or less along the cone edge where line splitting disappears
and rotation is clearly observed.
40'' spectra
are taken more or less along the cone edge where line splitting disappears
and rotation is clearly observed.
The velocities of the emission components are extracted from 50 pc-binned
spectra (z-direction) by Gaussian profile fits; the accuracy of the
velocity determination (peak of the Gaussian profile) is

 10 km s-1 (
10 km s-1 ( 1/3 pixel). The width of the lines
(FWHP) varies from
1/3 pixel). The width of the lines
(FWHP) varies from  100 km s-1 to occasionally
200-250 km s-1, as also seen by other observers.
We do not interpret the line widths of the fitted Gaussian profiles because of
insufficient spectral resolution (FWHP of skylines
100 km s-1 to occasionally
200-250 km s-1, as also seen by other observers.
We do not interpret the line widths of the fitted Gaussian profiles because of
insufficient spectral resolution (FWHP of skylines 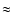 instrumental
profile
instrumental
profile 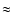 1-
1-
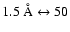 -70 km s-1). Confidence in the reality of faint emission
features, and of the Gaussian component decomposition, is obtained from the
similarity of the results deduced independently from the H
-70 km s-1). Confidence in the reality of faint emission
features, and of the Gaussian component decomposition, is obtained from the
similarity of the results deduced independently from the H ,
[NII]
and [SII] lines.
,
[NII]
and [SII] lines.
The results are presented as position-velocity [p-v]
diagrams in which the systemic velocity (200 km s-1 [ 11],
Götz et al. 1990) has been subtracted. Figure 1a is the p-v diagram at -20'' to the West (r = - 300 pc) of the
center; Fig. 1b the p-v diagram at 20'' to the East
(r = 300 pc) of the center. Line splitting is observed, although
a very regular flow pattern is at some places absent. Figure 1 shows as
reference the p-v diagram along the minor axis (
11],
Götz et al. 1990) has been subtracted. Figure 1a is the p-v diagram at -20'' to the West (r = - 300 pc) of the
center; Fig. 1b the p-v diagram at 20'' to the East
(r = 300 pc) of the center. Line splitting is observed, although
a very regular flow pattern is at some places absent. Figure 1 shows as
reference the p-v diagram along the minor axis (
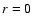 )
obtained in this observation and the earlier observation by M-95.
)
obtained in this observation and the earlier observation by M-95.
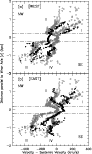 |
Figure 1:
a) BLUE-shifted outflow (solid dots) measured
parallel to the minor axis at
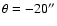 (
(
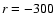 pc) to the West of the center. The gray symbols (open circles:
M-95) represent the outflow along the minor axis ( pc) to the West of the center. The gray symbols (open circles:
M-95) represent the outflow along the minor axis (
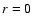 ). The
dashed-dotted lines indicate a galactic disk of ). The
dashed-dotted lines indicate a galactic disk of  200 pc thickness.
The projected rotation of the disk is 200 pc thickness.
The projected rotation of the disk is
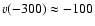 km s-1, as seen at visible wavelengths.
b) RED-shifted outflow (solid dots) measured parallel to
the minor axis at km s-1, as seen at visible wavelengths.
b) RED-shifted outflow (solid dots) measured parallel to
the minor axis at
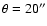 (
(
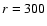 pc) to the East of the
center. The projected rotation of the disk is pc) to the East of the
center. The projected rotation of the disk is
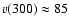 km s-1, as seen at visible wavelengths. km s-1, as seen at visible wavelengths. |
| Open with DEXTER |
Figure 2 shows the p-v diagram parallel to the minor axis at
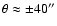 (
(
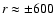 pc) distance
from the center. Emission of the cone walls is still visible at this distance
from the center (contrary to a very thin cone for instance shown in Fig. 9
by Strickland & Stevens 2000) and the emission extends continuously to a
height of
pc) distance
from the center. Emission of the cone walls is still visible at this distance
from the center (contrary to a very thin cone for instance shown in Fig. 9
by Strickland & Stevens 2000) and the emission extends continuously to a
height of 
 1 kpc from the disk. This leads us to conclude
that the width of the outflow is
1 kpc from the disk. This leads us to conclude
that the width of the outflow is 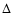
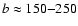 pc.
At the SE side of the disk we do not observe line splitting which confirms
that we observe the edge, or regions close to the edge, of the visible cone.
The outflow at the NW side of the disk observed to the East from the center
(
pc.
At the SE side of the disk we do not observe line splitting which confirms
that we observe the edge, or regions close to the edge, of the visible cone.
The outflow at the NW side of the disk observed to the East from the center
(
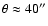 )
shows some velocity splitting. This gives the
impression that the NW cone is tilted in the plane perpendicular to the
line-of-sight in the direction East, as already mentioned by Lynds &
Sandage (1963) and also seen in the image taken by Deharveng & Pellet
(1970). However, our observation is not sufficient to quantify this tilt. The
literature contains a spectrogram of the H
)
shows some velocity splitting. This gives the
impression that the NW cone is tilted in the plane perpendicular to the
line-of-sight in the direction East, as already mentioned by Lynds &
Sandage (1963) and also seen in the image taken by Deharveng & Pellet
(1970). However, our observation is not sufficient to quantify this tilt. The
literature contains a spectrogram of the H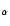 line taken with the slit
parallel to the Northern part of the minor axis at
line taken with the slit
parallel to the Northern part of the minor axis at  50'' to the East
of the center (Devine & Bally 1999, their Fig. 5). This spectrogram shows
a velocity splitting of
50'' to the East
of the center (Devine & Bally 1999, their Fig. 5). This spectrogram shows
a velocity splitting of  200-300 km s-1, up to the distance
of
200-300 km s-1, up to the distance
of  1 kpc or more. Some of this velocity-split emission is probably
seen in our observation at a similar velocity separation (Fig. 2).
1 kpc or more. Some of this velocity-split emission is probably
seen in our observation at a similar velocity separation (Fig. 2).
Figures 1 and 2 show that the outflow breaks out of the disk at a distance
of 
 200 pc from the galactic plane. Line splitting is seen
above this height and can be traced to a distance of
200 pc from the galactic plane. Line splitting is seen
above this height and can be traced to a distance of  1-1.5 kpc
on both sides of the galactic plane.
1-1.5 kpc
on both sides of the galactic plane.
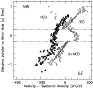 |
Figure 2:
Red-shifted outflow (dots) measured parallel to the
minor axis at
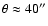 (
(
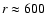 pc)
to the East of the center, and Blue-shifted outflow (triangles)
measured at pc)
to the East of the center, and Blue-shifted outflow (triangles)
measured at 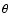
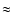 - 40'' (
- 40'' (
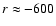 pc) to the West of the center. The dashed-dotted lines indicate
a galactic disk of pc) to the West of the center. The dashed-dotted lines indicate
a galactic disk of  200 pc thickness. The projected rotation velocity
of the disk is 200 pc thickness. The projected rotation velocity
of the disk is
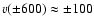 km s-1.
The velocity difference between the Western and Eastern branch at the SE
and NW side of the disk can be taken as evidence of rotation. For the straight
lines on the SE and NW side see Sect. 6.4. km s-1.
The velocity difference between the Western and Eastern branch at the SE
and NW side of the disk can be taken as evidence of rotation. For the straight
lines on the SE and NW side see Sect. 6.4. |
| Open with DEXTER |
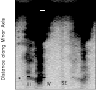 |
Figure 3:
H 6563 Å ( left) and [NII] 6583 Å ( right)
emission lines observed (4.2 m WHT) parallel and close to the minor axis
( 6563 Å ( left) and [NII] 6583 Å ( right)
emission lines observed (4.2 m WHT) parallel and close to the minor axis
(  
 5''). The spatial direction is vertical,
NW is at the top, SE at the bottom; the wavelength (velocity) direction is
horizontal. The profiles show on the SE side at
5''). The spatial direction is vertical,
NW is at the top, SE at the bottom; the wavelength (velocity) direction is
horizontal. The profiles show on the SE side at
 kpc
distance some emission between the velocity-split cone sections (*). Note the
breakout from cone wall III (SE side, blue-shifted) close to the galactic
disk (+). kpc
distance some emission between the velocity-split cone sections (*). Note the
breakout from cone wall III (SE side, blue-shifted) close to the galactic
disk (+). |
| Open with DEXTER |
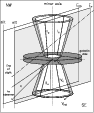 |
Figure 4:
Illustration of an idealized outflow cone on the SE and NW side of
the galactic disk. E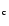 :
plane of the slit along the minor axis
through the center of the galaxy, producing the velocity branches
(I, II, III, IV) :
plane of the slit along the minor axis
through the center of the galaxy, producing the velocity branches
(I, II, III, IV)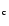 (on-axis profile in Fig. 1); E20: plane
of the slit parallel to the minor axis at
(on-axis profile in Fig. 1); E20: plane
of the slit parallel to the minor axis at
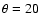 '' to the East of the
center, producing the velocity branches (I, II, III, IV) '' to the East of the
center, producing the velocity branches (I, II, III, IV)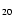 (Fig. 1b) (similar for
(Fig. 1b) (similar for
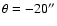 ,
West). The rotation of the
disk ,
West). The rotation of the
disk 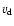 and of the halo material
and of the halo material
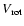 is shown.
is shown.
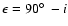 is the tilt of the galaxy. For a
similar schematic see HAM-90.
is the tilt of the galaxy. For a
similar schematic see HAM-90. |
| Open with DEXTER |
In the discussion of superwind outflows we may distinguish between a
cone-like geometry or a bubble-like geometry. Using a simple description,
a cone-like outflow has a broad base in the disk, no top, and is open;
line splitting is seen up to the top (for instance M 82, NGC 253). A
bubble-like outflow has a small base in the disk, a top, and is closed, at
least partially; line splitting disappears at the top (for instance
NGC 3097, NGC 1482). Our observations, and in particular the observation
along or close to the minor axis shown in Figs. 1 and 3, give some indication
of emission at a distance of  1-1.5 kpc at the SE side of the
disk which fills the gap between the velocity-split branches III-IV (for the branches see Fig. 4). These observations
give the impression of a bubble, at least at the SE side of the disk. The
closed velocity structure was noticed by BT-88 on the SE and NW side
at
1-1.5 kpc at the SE side of the
disk which fills the gap between the velocity-split branches III-IV (for the branches see Fig. 4). These observations
give the impression of a bubble, at least at the SE side of the disk. The
closed velocity structure was noticed by BT-88 on the SE and NW side
at  900 pc distance from the disk; it is also indicated in the
observation by HAM-90 (their Fig. 10) where the SE and NW cones seem
to be closed at the top. A similar impression of closure, or partial closure,
of the SE cone at a distance of
900 pc distance from the disk; it is also indicated in the
observation by HAM-90 (their Fig. 10) where the SE and NW cones seem
to be closed at the top. A similar impression of closure, or partial closure,
of the SE cone at a distance of  2 kpc below the disk is obtained from
the optical image shown by Deharveng & Pellet (1970) and the Fabry-Perot
images published by SBH-98. The H
2 kpc below the disk is obtained from
the optical image shown by Deharveng & Pellet (1970) and the Fabry-Perot
images published by SBH-98. The H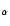 image published by OEA-02
gives at the NW side of the disk the impression of an outflow of diffuse
material with some bubble-like structure extending to
image published by OEA-02
gives at the NW side of the disk the impression of an outflow of diffuse
material with some bubble-like structure extending to  2.5 kpc
distance from the disk, and on the SE side of the disk the impression of more
or less cylindrical cones (as earlier mentioned by Lynds & Sandage 1963).
The CO observation by WWS-02 shows at the SE side of the disk an outflow cone
and at
2.5 kpc
distance from the disk, and on the SE side of the disk the impression of more
or less cylindrical cones (as earlier mentioned by Lynds & Sandage 1963).
The CO observation by WWS-02 shows at the SE side of the disk an outflow cone
and at  660 pc distance from the disk emission which fills the
velocity branches (however, at this position there is confusion with a
sidelobe in the interferometer observation; Weiß, priv. comm.). The
closure seems also to be indicated in the X-ray observations. Bregman et al.
(1995) note that the X-ray cone at the SE side of the disk shows a
significant change from a wide cone angle (
660 pc distance from the disk emission which fills the
velocity branches (however, at this position there is confusion with a
sidelobe in the interferometer observation; Weiß, priv. comm.). The
closure seems also to be indicated in the X-ray observations. Bregman et al.
(1995) note that the X-ray cone at the SE side of the disk shows a
significant change from a wide cone angle (
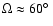 )
to a
narrow cone angle (
)
to a
narrow cone angle (
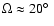 )
at the distance of
)
at the distance of
 1.7 kpc.
1.7 kpc.
We adopt, despite this apparently bubble-like velocity feature, a cone-like
outflow geometry, also since there exists collimated emission at a larger
distance than the apparent closure. In addition to these observations, we note
that according to SBH-98 there exists no acceptable model of a bubble which
fits the observations, at least at the SE side of the disk.
An idealized picture of the outflow cones, and of the selected slit positions,
is shown in Fig. 4. The geometry of the outflow uses the parameters:
the inclination of M 82: i  80
80
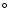 (Lynds & Sandage
1963); the direction of the inclination: the northern side of the galaxy is
tipped away from the observer; the distance
(Lynds & Sandage
1963); the direction of the inclination: the northern side of the galaxy is
tipped away from the observer; the distance
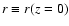 measured along the major axis (
measured along the major axis (
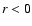 :
West,
:
West,
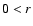 :
East) and parallel to the major axis,
r(z), at the distance z from the disk; the distance z
above and below the galactic plane (
:
East) and parallel to the major axis,
r(z), at the distance z from the disk; the distance z
above and below the galactic plane (
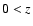 :
direction NW,
:
direction NW,
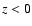 :
direction SE), and
:
direction SE), and
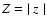 ;
the
thickness of the galactic disk: 2 H (
;
the
thickness of the galactic disk: 2 H (
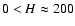 pc); the diameter at the base of the cone:
pc); the diameter at the base of the cone:
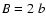 ;
the thickness of the cone wall:
;
the thickness of the cone wall: 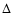 b; the
full opening angle of the SE cone and NW cone:
b; the
full opening angle of the SE cone and NW cone: 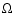
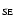 and
and
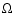
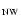 ;
the tilt of the SE cone and NW cone in the direction of
the line-of-sight:
;
the tilt of the SE cone and NW cone in the direction of
the line-of-sight: 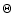
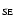 and
and 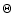
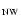 ;
and the
tilt in the plane perpendicular to the line-of-sight:
;
and the
tilt in the plane perpendicular to the line-of-sight: 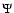
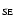 and
and 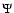
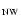 .
We do not distinguish between the true distance
(z*) and the projected distance (z) along the minor axis
since z* = z/sin(
.
We do not distinguish between the true distance
(z*) and the projected distance (z) along the minor axis
since z* = z/sin(
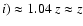 .
.
The kinematics of the outflow uses the parameters:
the distance measured along the cone walls: 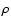 ;
the true (de-projected)
blowout velocities at the base of the cone and at the edge of the disk
(at
;
the true (de-projected)
blowout velocities at the base of the cone and at the edge of the disk
(at
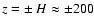 pc):
pc):
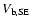 and
and
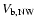 ;
the true gradient (increase) of the outflow velocity along the
cone wall:
;
the true gradient (increase) of the outflow velocity along the
cone wall: 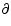
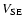 (
(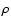 )/
)/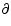
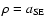 (
(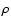 )
and
)
and 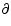
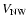 (
(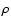 )/
)/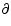
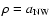 (
(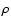 ); and the tangential component of the rotation of cone
wall gas:
); and the tangential component of the rotation of cone
wall gas:
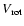 (r,z) at the distance r from
the minor axis and z from the disk. The tangential component of the
rotation of disk material is v(r). Only the component of a velocity
perpendicular to the plane of the sky can be measured.
(r,z) at the distance r from
the minor axis and z from the disk. The tangential component of the
rotation of disk material is v(r). Only the component of a velocity
perpendicular to the plane of the sky can be measured.
For the true outflow velocity along the cone walls (distance 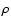 )
at the
SE and NW side of the disk we use
)
at the
SE and NW side of the disk we use
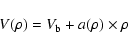 |
(1) |
with 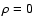 at the edge of the disk at
at the edge of the disk at
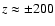 pc.
The blowout velocity
pc.
The blowout velocity 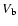 and the acceleration a(
and the acceleration a(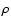 )
may be
different at the SE and NW side of the disk. Following the notation of M-95
(their Figs. 2, 5), the projected velocity components of the front side and
rear side of the SE cone are V
)
may be
different at the SE and NW side of the disk. Following the notation of M-95
(their Figs. 2, 5), the projected velocity components of the front side and
rear side of the SE cone are V
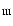 and V
and V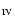 ,
respectively, and equivalent V
,
respectively, and equivalent V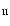 and V
and V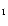 for the
NW cone. Using
for the
NW cone. Using
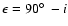 ,
,
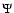
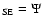
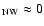 because of lack of observational
information, and
because of lack of observational
information, and 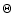
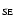 and
and 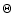
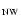 counted positive
if the respective cone is tilted towards the observer, the projected
velocities measured with the slit centered along the minor axis are for the SE
cone
counted positive
if the respective cone is tilted towards the observer, the projected
velocities measured with the slit centered along the minor axis are for the SE
cone
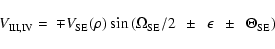 |
(2) |
with the upper sign for branch III, the lower sign for branch IV. For the
NW cone
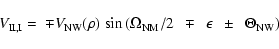 |
(3) |
with the upper sign for branch II, the lower sign for branch I. At a selected
height
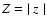 ,
the distances
,
the distances 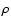 in Eqs. (2) and (3)
where the line-of-sight intersects the walls of the SE (III, IV) cone and
the NW (I, II) cone, are
in Eqs. (2) and (3)
where the line-of-sight intersects the walls of the SE (III, IV) cone and
the NW (I, II) cone, are
![\begin{displaymath}{\rho}_{\rm III,IV} = [{Z + D}_{\rm III,IV}]/{\rm cos}
\left(...
...SE}/2\ \ \pm\ \ {\epsilon}\ \ \pm\ \
{\Theta}_{\rm SE}\right)
\end{displaymath}](/articles/aa/full/2004/10/aa3753/img102.gif) |
(4) |
![\begin{displaymath}{\rho}_{\rm II,I} = [{Z + D}_{\rm II,I}]/{\rm cos}
\left({\Om...
...NW}/2\ \ \mp\ \ {\epsilon}\ \ \pm\ \
{\Theta}_{\rm NW}\right)
\end{displaymath}](/articles/aa/full/2004/10/aa3753/img103.gif) |
(5) |
with
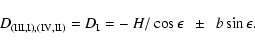 |
(6) |
The projected velocities Eqs. (2) and (3) measured along the minor axis do not
reveal rotation; for this slit position a possibly entrained galactic
rotation is expected to be perpendicular to the line-of-sight and thus
not visible. Primarily spectra taken along the minor axis were used by
HAM-90, M-95 and SBH-98 to derive the geometry of the outflow.
Figure 4 shows also the situation of a slit parallel to the minor axis
(
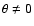 ). At the base of the outflow the radius of the cone is
b*, at the height
). At the base of the outflow the radius of the cone is
b*, at the height
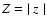 its radius is
its radius is
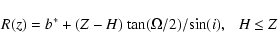 |
(7) |
with 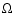 either
either 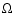
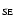 or
or 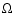
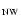 ,
and
,
and
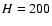 pc. For idealized cones, Eq. (7) holds throughout the thickness of the
cone wall, i.e. for material inside b -
pc. For idealized cones, Eq. (7) holds throughout the thickness of the
cone wall, i.e. for material inside b - 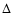 b/2
b/2
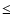 b*
b* 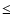 b +
b + 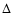 b/2, where
b/2, where
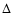 b is of the order of 150-200 pc (Table 1).
b is of the order of 150-200 pc (Table 1).
Table 1:
Cone opening angle(s) 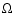 ,
diameter of the outflow base
B = 2 b, and cone wall thickness
,
diameter of the outflow base
B = 2 b, and cone wall thickness 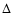 b determined in
earlier optical observations and recent radio observations.
b determined in
earlier optical observations and recent radio observations.
We assume that the rotation
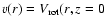 )
of the disk at the off-center position
)
of the disk at the off-center position
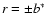 ,
or a part of this rotation, is entrained by
the outflow. We assume also that the visible material (ridge material) flows
out primarily along the cone walls, with little diffusion in perpendicular
radial direction (see Fig. 3). If the rotation
,
or a part of this rotation, is entrained by
the outflow. We assume also that the visible material (ridge material) flows
out primarily along the cone walls, with little diffusion in perpendicular
radial direction (see Fig. 3). If the rotation
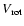 (r, z)
at the distance r(z) from the minor axis and distance z from
the disk is known, then the line-of-sight velocity
(r, z)
at the distance r(z) from the minor axis and distance z from
the disk is known, then the line-of-sight velocity
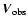 measured at the off-center slit position (
measured at the off-center slit position (
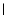 r
r 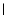 )
is
)
is
with
![\begin{displaymath}{\sin}[{\varphi}({\it z})] = \sqrt{{R(}{\it z})^{2} - {\it r}...
...{\it z)},\ \ {\cos}[{\varphi}({\it z})] = {\it r}/{R(}{\it z)}
\end{displaymath}](/articles/aa/full/2004/10/aa3753/img117.gif) |
(9) |
and
 for the velocity branch under discussion. The minus
sign in Eq. (8) refers to the Western side (blue-shifted) of the center, the
plus sign to the Eastern side (red-shifted) of the center. The relation (8)
shows that the observed velocity V
for the velocity branch under discussion. The minus
sign in Eq. (8) refers to the Western side (blue-shifted) of the center, the
plus sign to the Eastern side (red-shifted) of the center. The relation (8)
shows that the observed velocity V
 consists of the
components V
consists of the
components V
 and V
and V
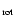 .
In order to derive
the rotation V
.
In order to derive
the rotation V
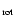 it is convenient to eliminate the outflow
component V
it is convenient to eliminate the outflow
component V
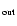 from the observation. This can for instance be
done by taking the difference of the velocities
V
from the observation. This can for instance be
done by taking the difference of the velocities
V
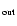 (r, z) and
V
(r, z) and
V
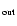 (-r, z) observed at opposite sides of the cone,
or at the edges.
(-r, z) observed at opposite sides of the cone,
or at the edges.
Table 1 reviews the geometry of the cones as determined in and from earlier
optical investigations and the recent radio observations. Some of the earlier
observers (until  1990) assumed that the outflow originates from a
small volume at the center of the galaxy so that the cone-like outflow has a
vertex (called "pointed'' in Table 1). From Table 1 we adopt, for the time
being, for the visible outflow cones on both sides of the disk that
1990) assumed that the outflow originates from a
small volume at the center of the galaxy so that the cone-like outflow has a
vertex (called "pointed'' in Table 1). From Table 1 we adopt, for the time
being, for the visible outflow cones on both sides of the disk that
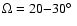 ,
,
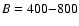 pc, and
pc, and
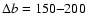 pc. We extract from our on-axis observation (
pc. We extract from our on-axis observation (
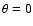 )
primarily the geometry (
)
primarily the geometry (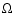 ,
b), the outflow velocity
(
,
b), the outflow velocity
(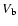 ), and the acceleration (a). These values are used in
the off-axis observations (
), and the acceleration (a). These values are used in
the off-axis observations (
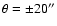 )
to investigate the
rotation of the outflow.
)
to investigate the
rotation of the outflow.
A collision-free outflow conserves mass and angular momentum. The combination
of both laws of conservation provides the theoretical rotation velocity
V
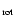 (r, z) as function of radial distance (r)
from the minor axis and distance (z) from the disk, to be used in
Eq. (8). As illustrated in Fig. 5, we assume that the mass
(r, z) as function of radial distance (r)
from the minor axis and distance (z) from the disk, to be used in
Eq. (8). As illustrated in Fig. 5, we assume that the mass
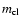 of an
individual cloud (filament, particle) does not change and that its angular
momentum L is conserved while the material follows a trajectory along
the gradually increasing radius R(z) of the cone walls. The relevant
relations are
of an
individual cloud (filament, particle) does not change and that its angular
momentum L is conserved while the material follows a trajectory along
the gradually increasing radius R(z) of the cone walls. The relevant
relations are
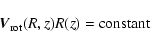 |
(10) |
since
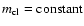 .
The distance R(z) as function of distance z is given by Eq. (7). We use the angular momentum L
.
The distance R(z) as function of distance z is given by Eq. (7). We use the angular momentum L
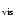 for visible cone wall material with
for visible cone wall material with
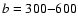 pc,
pc,
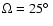 ,
and the angular momentum L
,
and the angular momentum L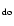 for dragged-out
material with b = 300 pc,
for dragged-out
material with b = 300 pc,
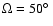 .
Evidently, at the
base of the outflow
.
Evidently, at the
base of the outflow
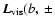
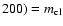 b*v(b*), and similarly for
L
b*v(b*), and similarly for
L .
.
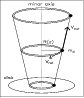 |
Figure 5:
Momentum conservation of outflow material moving outwards along the
cone walls (a tangential element is shown). The arrow indicates the trajectory
of the outflowing material. |
| Open with DEXTER |
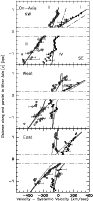 |
Figure 6:
Illustration of the agreement between the observation and the
adopted cone model (Table 2). The displayed data are the averages of the
velocities determined from the H ,
[NII] and [SII] lines. Open
circles: front sides of the cone; dots: rear sides. The solid lines represent
the calulated velocity branches when
rotation around the minor axis with angular momentum conservation
L ,
[NII] and [SII] lines. Open
circles: front sides of the cone; dots: rear sides. The solid lines represent
the calulated velocity branches when
rotation around the minor axis with angular momentum conservation
L
 is applied. Note that in the on-axis observation
(top) the rotation velocity is perpendicular to the line-of-sight
and hence not seen. The dashed lines show the calculated velocity
branches without rotation around the minor axis. Observation West at
is applied. Note that in the on-axis observation
(top) the rotation velocity is perpendicular to the line-of-sight
and hence not seen. The dashed lines show the calculated velocity
branches without rotation around the minor axis. Observation West at
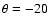 '' from the center, observation East at '' from the center, observation East at
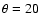 ''
from the center. The dashed-dotted line in the on-axis observation
(top) is a calculation without the velocity shift of
-100 km s-1 of the cone at the NW side. ''
from the center. The dashed-dotted line in the on-axis observation
(top) is a calculation without the velocity shift of
-100 km s-1 of the cone at the NW side. |
| Open with DEXTER |
We agree with the other investigators that the visible outflow at the SE side
has to a large extent the geometry of a cone; however, contrary to SBH-98
and in agreement with our earlier observation (M-95) we find that the outflow
at the NW side is also cone-like. The parameters of the adopted best-fit
cone model as derived from the presented observation are summarized in
Table 2; the correspondingly calculated velocity branches I-IV for
the slit along the minor axis, or parallel to the minor axis
(
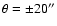 ), are shown in Fig. 6.
), are shown in Fig. 6.
In general we obtain an acceptable fit of the observations if we adopt for
M 82's inclinitation the value
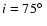 ,
instead of
,
instead of
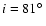 derived by Lynds & Sandage (1963). We note that the inclination
of the velocity branches I-IV in the respective p-v diagrams can only be explained by accelerated motion of the outflow; the
values are given in Table 2. It is also important to note that a fit of the
NW cone is only obtained if we introduce an additional line-of-sight
velocity shift of -100 km s-1 towards the observer, as given in
Table 2 and illustrated in Fig. 6 (top panel). We have searched for
an explanation other than a velocity shift by varying the base of the outflow,
the cone angle, the blowout velocity, and the tilt of the cone, however,
without finding an acceptable solution. For the time being we accept this
velocity shift, knowing that further confirmation is required.
derived by Lynds & Sandage (1963). We note that the inclination
of the velocity branches I-IV in the respective p-v diagrams can only be explained by accelerated motion of the outflow; the
values are given in Table 2. It is also important to note that a fit of the
NW cone is only obtained if we introduce an additional line-of-sight
velocity shift of -100 km s-1 towards the observer, as given in
Table 2 and illustrated in Fig. 6 (top panel). We have searched for
an explanation other than a velocity shift by varying the base of the outflow,
the cone angle, the blowout velocity, and the tilt of the cone, however,
without finding an acceptable solution. For the time being we accept this
velocity shift, knowing that further confirmation is required.
Table 2:
Parameters of the Adopted Cone Model (shown in Fig. 6) for
an inclination of M 82 of i = 75
 ,
b = 300 pc, and
,
b = 300 pc, and
 b = 150-200 pc.
b = 150-200 pc.
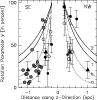 |
Figure 7:
Values of the rotation parameter 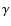 (Eqs. (11) and (12)) above (NW)
and below (SE) the disk as derived from observations of CO material and
visible cone wall material. We assume that the disk rotates homogeneously
within
(Eqs. (11) and (12)) above (NW)
and below (SE) the disk as derived from observations of CO material and
visible cone wall material. We assume that the disk rotates homogeneously
within 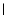 z z 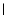
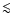
 H H 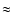
 200 pc.
Radio data based on the CO observations by Sofue et al. (1992) and
Loiseau et al. (1990): triangles; based on CO observations by Seaquist &
Clark (2001): dots; based on CO observations by Walter et al. (2002):
squares.
Optical data based on H 200 pc.
Radio data based on the CO observations by Sofue et al. (1992) and
Loiseau et al. (1990): triangles; based on CO observations by Seaquist &
Clark (2001): dots; based on CO observations by Walter et al. (2002):
squares.
Optical data based on H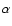 , [NII] and [SII] slit spectra parallel
to the major axis by Heckathorn (1972): open circles; this paper: shaded
circles.
The lines represent the parameter , [NII] and [SII] slit spectra parallel
to the major axis by Heckathorn (1972): open circles; this paper: shaded
circles.
The lines represent the parameter 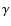 calculated for outflow with angular
momentum conservation L
calculated for outflow with angular
momentum conservation L
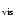 of cone wall gas with
of cone wall gas with
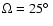 and b = 300 pc (1) and b = 400 pc (2) as appropriate
for visible material. The dashed lines refer in a similar way to angular
momentum conservation L
and b = 300 pc (1) and b = 400 pc (2) as appropriate
for visible material. The dashed lines refer in a similar way to angular
momentum conservation L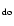 of CO cone wall gas with
of CO cone wall gas with 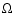 =
50
=
50
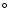 and
and
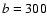 pc (a) and pc (a) and 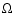 = 90
= 90
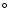 and b =
300 pc (b), as suggested by Seaquist & Clark (2001) and Walter et al.
(2002).
and b =
300 pc (b), as suggested by Seaquist & Clark (2001) and Walter et al.
(2002). |
| Open with DEXTER |
Any rotation entrained by the visible outflow material, or the dragged-out
material, originates from the rotation of disk material. Since the visible
outflow is seen to at least a distance of  600 pc
600 pc 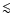 r
from the center (Fig. 2), we are concerned with rotation of disk material
inside this region. For the rotation of the disk material we use the
rotation curves published by McKeith et al. (1993) and Greve et al. (2002).
We have shown (Greve et al. 2002) that M 82 contains a stellar bar within
r
from the center (Fig. 2), we are concerned with rotation of disk material
inside this region. For the rotation of the disk material we use the
rotation curves published by McKeith et al. (1993) and Greve et al. (2002).
We have shown (Greve et al. 2002) that M 82 contains a stellar bar within
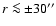 (
(
 500 pc) and that the bar
contains the dominant mass of this region. The stars move on elliptical
x1 and x2 orbits, which is apparently also the case for the
dominant part of the (molecular) gas, as evident from the CO observations by
Shen & Lo (1995) and Neininger et al. (1998). The starburst OB stars, which
eventually produce the material of the outflow by supernova explosions, may
follow similarly ordered orbits. Because of the low ellipticity of the stellar
orbits (0.6-0.9; see Achterman & Lacy 1995; Wills et al. 2000), we
assume that the outflow material moves inside and outside the disk in more or
less circular orbits.
500 pc) and that the bar
contains the dominant mass of this region. The stars move on elliptical
x1 and x2 orbits, which is apparently also the case for the
dominant part of the (molecular) gas, as evident from the CO observations by
Shen & Lo (1995) and Neininger et al. (1998). The starburst OB stars, which
eventually produce the material of the outflow by supernova explosions, may
follow similarly ordered orbits. Because of the low ellipticity of the stellar
orbits (0.6-0.9; see Achterman & Lacy 1995; Wills et al. 2000), we
assume that the outflow material moves inside and outside the disk in more or
less circular orbits.
Information on the rotation of material above and below the disk (
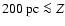 )
is available from mm-wavelength CO observations. From the
observation by Sofue et al. (1992) it appears that the CO above and below the
disk rotates in the same direction as the disk, and that the rotation of the
disk of v(
)
is available from mm-wavelength CO observations. From the
observation by Sofue et al. (1992) it appears that the CO above and below the
disk rotates in the same direction as the disk, and that the rotation of the
disk of v(
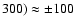 km s-1 at the distance
km s-1 at the distance
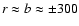 pc from the center (McKeith
et al. 1993; Greve et al. 2002) decreases to
pc from the center (McKeith
et al. 1993; Greve et al. 2002) decreases to
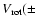
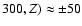 km s-1 at the distance
km s-1 at the distance
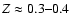 kpc; to
kpc; to
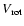 (
(
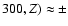 20-30 km s-1 at the distance
20-30 km s-1 at the distance
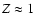 kpc; and
that the CO and the rotation disappear at the distance
kpc; and
that the CO and the rotation disappear at the distance
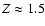 kpc.
Seaquist & Clark (their Fig. 5) provide CO rotation curves at different
distances above and below the disk, up to a distance of
kpc.
Seaquist & Clark (their Fig. 5) provide CO rotation curves at different
distances above and below the disk, up to a distance of
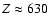 pc.
These curves confirm that the CO rotates in the same direction as the disk,
and that the rotation decreases with increasing distance from the disk.
Globally, the steepest part of the rotation curves is observed between
opposite sides at
pc.
These curves confirm that the CO rotates in the same direction as the disk,
and that the rotation decreases with increasing distance from the disk.
Globally, the steepest part of the rotation curves is observed between
opposite sides at
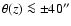
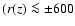 pc) distance from the minor axis, for all heights where CO
rotation curves are determined. The CO rotation curves show slow(er) rotation,
or even a reversed rotation, between 40
pc) distance from the minor axis, for all heights where CO
rotation curves are determined. The CO rotation curves show slow(er) rotation,
or even a reversed rotation, between 40
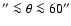 (
(
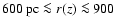 pc) and -60
pc) and -60
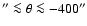 (-900 pc
(-900 pc 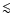 r(z)
r(z) 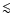 -600 pc) distance from the minor axis. These outer regions are apparently
located at the periphery of the visible cones, although this interpretation
needs further observational confirmation.
-600 pc) distance from the minor axis. These outer regions are apparently
located at the periphery of the visible cones, although this interpretation
needs further observational confirmation.
To quantify the decrease of rotation with distance from the disk, we have
derived the steepness of the CO rotation curves [km s-1/''] as
function of distance from the galactic plane, i.e.
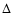 V in Eq. (11) is the velocity difference of the CO emission measured at
corresponding opposite positions at the Eastern side [r1(z)]
and Western side [r2(z)] of the minor axis
(
V in Eq. (11) is the velocity difference of the CO emission measured at
corresponding opposite positions at the Eastern side [r1(z)]
and Western side [r2(z)] of the minor axis
(
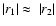 ),
separated by the distance
),
separated by the distance
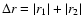 .
The values
.
The values 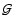 are normalized to the value
are normalized to the value
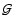 (0) measured in the galactic plane, i.e.
(0) measured in the galactic plane, i.e.
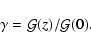 |
(12) |
As evident from Eq. (11), the parameter 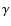 eliminates the outflow
component V
eliminates the outflow
component V
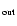 but contains the factor cos
but contains the factor cos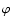 (r, z)
which relates the positions (r1, z) and
(r2, z) to the cone axis and the projection of the velocity of
rotation to this direction of the line-of-sight. Figure 7 shows the values
(r, z)
which relates the positions (r1, z) and
(r2, z) to the cone axis and the projection of the velocity of
rotation to this direction of the line-of-sight. Figure 7 shows the values
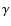 /
/
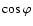 as function of distance from the galactic plane. In this
figure the factor
as function of distance from the galactic plane. In this
figure the factor
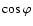 ,
based on the cone parameters of CO material
(Table 1), has been considered as far as possible. The values
,
based on the cone parameters of CO material
(Table 1), has been considered as far as possible. The values 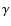 derived
from the p-v diagrams of CO measured by WWS-02 at
derived
from the p-v diagrams of CO measured by WWS-02 at  330 pc
distance from the disk are also shown in Fig. 7. The data suggests a faster
decrease of CO rotation at the SE side of the disk, as pointed out by SC-01.
330 pc
distance from the disk are also shown in Fig. 7. The data suggests a faster
decrease of CO rotation at the SE side of the disk, as pointed out by SC-01.
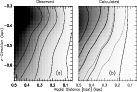 |
Figure 8:
Momentum conserved rotation of the eastern part of the visible
outflow material at the SE side of the disk; plotted as grayscale and lines of
values L = V
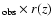 = constant =
5, 15, 30, 45, 60 kpc
= constant =
5, 15, 30, 45, 60 kpc  km s-1 (from the minor axis to the
outside). a) based on optical line observations by Heckathorn (1972)
and this paper; b) calculated from the adopted model of Table 2. The
solid lines show the calculated values
V
km s-1 (from the minor axis to the
outside). a) based on optical line observations by Heckathorn (1972)
and this paper; b) calculated from the adopted model of Table 2. The
solid lines show the calculated values
V
 = constant; the dashed lines show
the calculated values V
= constant; the dashed lines show
the calculated values V
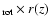 = constant,
in which the outflow velocity V
= constant,
in which the outflow velocity V
 has been removed.
has been removed. |
| Open with DEXTER |
The spectra of visible cone wall material taken by BT-88,
HAM-90 and SBH-98 parallel to the major axis well below the disk
(
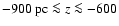 pc) do not allow a quantitative
estimate of rotation around the minor axis, although BT-88 and SBH-98
mention that rotation is seen. The spectra taken by Heckathorn (1972) parallel
to the major axis to a distance
pc) do not allow a quantitative
estimate of rotation around the minor axis, although BT-88 and SBH-98
mention that rotation is seen. The spectra taken by Heckathorn (1972) parallel
to the major axis to a distance
 pc above and below the disk have
sloped tracks in the corresponding p-v diagrams (his Figs. 2-17)
and by this provide evidence of rotation of the visible cone wall material. As
to be expected, the visible cone wall material rotates in the same direction
as the disk, and the rotation decreases with increasing distance from the
disk. As seen in Heckathorn's Fig. 18, the optical observations
(H
pc above and below the disk have
sloped tracks in the corresponding p-v diagrams (his Figs. 2-17)
and by this provide evidence of rotation of the visible cone wall material. As
to be expected, the visible cone wall material rotates in the same direction
as the disk, and the rotation decreases with increasing distance from the
disk. As seen in Heckathorn's Fig. 18, the optical observations
(H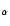 ,
[NII], [SII]) produce a less regular velocity pattern than the
CO observations, and it is impossible to find data at corresponding opposite
sides of the minor axis (r1, r2) from which the
parameter
,
[NII], [SII]) produce a less regular velocity pattern than the
CO observations, and it is impossible to find data at corresponding opposite
sides of the minor axis (r1, r2) from which the
parameter 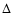 V/
V/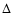 r can be determined. The values
r can be determined. The values
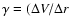 )/
)/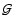 (0) obtained from Heckathorn's
observation for irregular sections parallel to the major axis are shown in
Fig. 7. This figure contains also the values
(0) obtained from Heckathorn's
observation for irregular sections parallel to the major axis are shown in
Fig. 7. This figure contains also the values 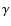 extracted from our
observation at
extracted from our
observation at  20'' (r1, r2) from the center and
the front side (branch III) of the SE cone. The optical emission of the NW
cone is too irregular to provide usefull data.
20'' (r1, r2) from the center and
the front side (branch III) of the SE cone. The optical emission of the NW
cone is too irregular to provide usefull data.
If we assume that we observe in Fig. 2 at the SE side of the disk the edge of
the outflow cone (no velocity splitting), then the velocity difference between
the Eastern (red-shifted) and Western (blue-shifted) branch is  2 times the rotation velocity of the cone wall material. Taking the straight
lines inserted in Fig. 2 as a first approximation of the outflow, the rotation
velocity is
2 times the rotation velocity of the cone wall material. Taking the straight
lines inserted in Fig. 2 as a first approximation of the outflow, the rotation
velocity is
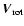 (600,
(600,
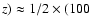 -150) = 50-75 km s-1.
-150) = 50-75 km s-1.
Using the model of Table 2, the synthetic profiles of the branches I-IV
inserted in Fig. 6 show that rotation of the visible cone wall material is
required to obtain an acceptable interpretation of the data. The heavy lines
in this figure include angular momentum conserved rotation of the cone wall
material (L
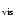 ). The dashed lines are the branches I-IV
calculated without rotation, i.e.
). The dashed lines are the branches I-IV
calculated without rotation, i.e.
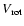 (r,
(r,
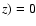 at
all distances z. This gives a poorer fit to the data.
at
all distances z. This gives a poorer fit to the data.
We have inserted in Fig. 7 the calculated parameter 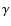 (Eqs. (11) and (12)) of
visible material moving with conserved angular momentum L
(Eqs. (11) and (12)) of
visible material moving with conserved angular momentum L
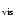 on a narrow cone (
on a narrow cone (
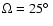 )
as well as the calculated
parameter
)
as well as the calculated
parameter 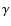 of dragged-out material moving with conserved angular
momentum L
of dragged-out material moving with conserved angular
momentum L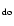 on a wider cone (
on a wider cone (
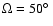 and
90
and
90
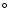 ). The data shown in Fig. 7
provide evidence of rotation, but unfortunately no clear distinction between
visible material on a narrow cone and CO material on a wider cone. The figure
suggests, to some extent, that the visible material of the SE cone follows
first the rotation of the narrow visible cone, but diverts into a wider cone
at greater distances from the disk. The large scatter of the data is probably
due to the fact that in the construction of Fig. 7 we have used measurements
at opposite sides of the minor axis in order to eliminate the outflow velocity
Visin
). The data shown in Fig. 7
provide evidence of rotation, but unfortunately no clear distinction between
visible material on a narrow cone and CO material on a wider cone. The figure
suggests, to some extent, that the visible material of the SE cone follows
first the rotation of the narrow visible cone, but diverts into a wider cone
at greater distances from the disk. The large scatter of the data is probably
due to the fact that in the construction of Fig. 7 we have used measurements
at opposite sides of the minor axis in order to eliminate the outflow velocity
Visin .
These opposite positions are separated by several
100 pc or even a kpc; the irregularities which exists in the outflow over
such large distances may produce the large scatter.
.
These opposite positions are separated by several
100 pc or even a kpc; the irregularities which exists in the outflow over
such large distances may produce the large scatter.
As known from Heckathorn's (1972, his Fig. 18) investigation, the outflow
in the Eastern quadrant at the SE side of the disk shows the most regular
velocity pattern. Using Heckathorn's observation and the data of this
publication, we derived for this section of the SE outflow the diagram of
constant values
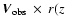 )
(in which the outflow velocity Visin(
)
(in which the outflow velocity Visin(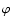 )
is not eliminated).
As displayed in Fig. 8, the contours of constant momentum calculated for the
adopted model (Table 2) and momentum conservation L
)
is not eliminated).
As displayed in Fig. 8, the contours of constant momentum calculated for the
adopted model (Table 2) and momentum conservation L
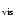 agree
with the contours derived from the observations. This figure illustrates
the existence of momentum conserved rotation of the visible outflow
material.
agree
with the contours derived from the observations. This figure illustrates
the existence of momentum conserved rotation of the visible outflow
material.
We summarize the result of this investigation and comment on the collimation
of the outflow, the escape of the outflow material, the dissipation in the
outflow of angular momentum, and the NW-SE asymmetry of the outflow.
(1) The outflow of the visible material occurs along the walls of
cones, on both sides of the disk. The parameters of the visible outflow cones
are summarized in Table 2. This is an idealized, though physically
acceptable picture of the visible cone walls despite evidence of an irregular
geometry, velocity, and density.
(2) The outflow builds up inside the central  600-1000 pc of the
disk and breaks out of the disk at the height of
600-1000 pc of the
disk and breaks out of the disk at the height of 
 200 pc on the
SE and NW side. Our observation detects the visible outflow at
200 pc on the
SE and NW side. Our observation detects the visible outflow at  300 pc
and
300 pc
and  600 pc radial distance from the center so that the base over which
the visible outflow extends is of the order of B
600 pc radial distance from the center so that the base over which
the visible outflow extends is of the order of B 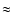 600-1200 pc diameter. This is larger than the base of
600-800 pc diameter considered so far.
600-1200 pc diameter. This is larger than the base of
600-800 pc diameter considered so far.
(3) At the height of 
 200 pc above and below the disk exists a
sharp discontinuity (
200 pc above and below the disk exists a
sharp discontinuity ( 50 pc extent) of the outflow; below this height
the outflow builds up, above this height the outflow appears to be cone-like
with double-split emission lines, on the SE and NW side of the disk. At the
discontinuity the de-projected blowout velocity is
50 pc extent) of the outflow; below this height
the outflow builds up, above this height the outflow appears to be cone-like
with double-split emission lines, on the SE and NW side of the disk. At the
discontinuity the de-projected blowout velocity is
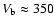 -400 km s-1, on both sides of the disk. The discontinuity is
probably the location of the sonic surface beyond which the outflow moves at
super-sonic speed (Heckman et al. 1990). This view is supported by the fact
that the sound velocity in the tenuous gas is
-400 km s-1, on both sides of the disk. The discontinuity is
probably the location of the sonic surface beyond which the outflow moves at
super-sonic speed (Heckman et al. 1990). This view is supported by the fact
that the sound velocity in the tenuous gas is
 200-300 km s-1 (Tomisaka & Bregman 1983; Strickland
& Stevens 2000). The height of the discontinuity is similar to the vertical
distribution of the stars (K image of
200-300 km s-1 (Tomisaka & Bregman 1983; Strickland
& Stevens 2000). The height of the discontinuity is similar to the vertical
distribution of the stars (K image of 
 10
10
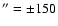 pc
extent above and below the plane (Telesco et al. 1991; Larkin et al. 1994)).
pc
extent above and below the plane (Telesco et al. 1991; Larkin et al. 1994)).
(4) The visible SE and NW cones have small opening angles of
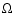
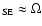
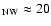 -30
-30
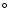 .
The shape of these cones is jet-like, in the terminology of Suchkov et al.
(1996), and predicted in model calculations assuming a thick disk. The
spectroscopic observations show that the visible emission follows the cone
walls in a nearly continuous way, with little interruptions and breakout,
which gives the impression of a nearly continuous outflow from the disk.
.
The shape of these cones is jet-like, in the terminology of Suchkov et al.
(1996), and predicted in model calculations assuming a thick disk. The
spectroscopic observations show that the visible emission follows the cone
walls in a nearly continuous way, with little interruptions and breakout,
which gives the impression of a nearly continuous outflow from the disk.
(5) The double velocity-split visible emission lines originate in the walls
of the cone-like outflow on the SE and NW side of the disk. The absence, to a
large extent, of emission between the velocity branches I-IV
(Fig. 3) is evidence of a finite thickness of the cone walls, estimated to be
of the order of 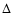
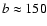 -250 pc. A similar cone
wall thickness is seen in the outflow of NGC 253, which has an opening angle
of
-250 pc. A similar cone
wall thickness is seen in the outflow of NGC 253, which has an opening angle
of
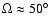 and a base of
and a base of
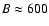 pc
diameter (Schulz & Wegner 1992). The absence of velocity splitting,
at least of the SE cone, when investigated at
pc
diameter (Schulz & Wegner 1992). The absence of velocity splitting,
at least of the SE cone, when investigated at 
 600 pc radial
distance (Fig. 2), indicates that in this region the edge of
the visible cone is located.
600 pc radial
distance (Fig. 2), indicates that in this region the edge of
the visible cone is located.
(6) The outflow velocity of the visible cone wall material increases more or
less linearly along the cone walls, at least up to the distance of
 1 kpc. The velocity increase is
1 kpc. The velocity increase is
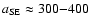 km s-1 kpc-1 at the SE side of the disk and
km s-1 kpc-1 at the SE side of the disk and
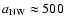 -800 km s-1 kpc-1 at the NW side
of the disk. The small inclinations of the velocity branches I-IV above
and below
-800 km s-1 kpc-1 at the NW side
of the disk. The small inclinations of the velocity branches I-IV above
and below  1 kpc distance from the disk suggests that the cone wall
material continues to flow out at a more or less constant velocity (Fig. 1).
A similar velocity feature is probably seen in the off-center spectrogram
published by Devine & Bally (1999).
1 kpc distance from the disk suggests that the cone wall
material continues to flow out at a more or less constant velocity (Fig. 1).
A similar velocity feature is probably seen in the off-center spectrogram
published by Devine & Bally (1999).
(7) The visible cone wall material rotates in the direction of the galactic
disk and with decreasing velocity at greater distances above and below the
galactic plane. The rotation seems to conserve angular momentum, as also
indicated by the CO observations of Seaquist & Clark (2001) and Walter et al. (2002). The rotation velocity is small and of the order of
50 km s-1 at the height of  0.5 kpc. A complete rotation of the
cone wall material at
0.5 kpc. A complete rotation of the
cone wall material at  0.5 kpc distance from the disk requires
0.5 kpc distance from the disk requires
 10 Myr. If we assume that the lifetime of the visible clumps and
filaments is small, then the visible outflow material is seen as
straight-line streamers rather than helical-type streamers. The rotation
of the outflowing material entrains angular momentum. The entrained and
eventually dissipated angular momentum is a small fraction of the angular
momentum of the central part of the disk.
10 Myr. If we assume that the lifetime of the visible clumps and
filaments is small, then the visible outflow material is seen as
straight-line streamers rather than helical-type streamers. The rotation
of the outflowing material entrains angular momentum. The entrained and
eventually dissipated angular momentum is a small fraction of the angular
momentum of the central part of the disk.
(8) Dust continuum observations (Alton et al. 1999) and molecular line (CO)
observations by Seaquist & Clark (2001) and Walter et al. (2002) indicate
that the outflow drags cool material out of the disk. The observations show
that the outflow of visible cone wall material occurs within significantly
narrower cones (
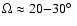 )
than the outflow of
dragged-out material (
)
than the outflow of
dragged-out material (
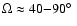 ). The cones of
dragged-out CO material are (presently) only detected to a height of
). The cones of
dragged-out CO material are (presently) only detected to a height of
 650 pc (Seaquist & Clark 2001), and apparently only on the SE
side (Walter et al. 2002), while CO material itself is seen at larger
distances from the disk (
650 pc (Seaquist & Clark 2001), and apparently only on the SE
side (Walter et al. 2002), while CO material itself is seen at larger
distances from the disk ( kpc).
kpc).
We obtain from the earlier and present optical observations the picture of a
highly collimated jet-like outflow (in the terminology of Suchkov et al.
1996) of M 82's visible material. This collimation is assumed to be due
to the molecular ring of  600 pc inner diameter (B), of
approximately 300 pc radial extent (
600 pc inner diameter (B), of
approximately 300 pc radial extent ( r), and of approximately
r), and of approximately
 150 pc thickness in z-direction (
150 pc thickness in z-direction ( z) (Neininger
et al. 1998; Mao et al. 2000; Weiß et al. 2001). The collimation of
M 82's outflow may be explained by the favourable "confinement'' ratio
z) (Neininger
et al. 1998; Mao et al. 2000; Weiß et al. 2001). The collimation of
M 82's outflow may be explained by the favourable "confinement'' ratio
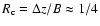 and the relatively
high local "compactness'' (i.e. high filling factor) of the molecular ring and
dust material. This is well seen in the H
and the relatively
high local "compactness'' (i.e. high filling factor) of the molecular ring and
dust material. This is well seen in the H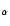 Fabry-Perot image of the
outflow published by SBH-98 (their Fig. 9) where the Eastern side of the SE
outflow is sharply confined (collimated) by a prominent dust lane which
extends nearly perpendicular out of the disk.
Fabry-Perot image of the
outflow published by SBH-98 (their Fig. 9) where the Eastern side of the SE
outflow is sharply confined (collimated) by a prominent dust lane which
extends nearly perpendicular out of the disk.
Strickland & Stevens (2000) discuss the collimation efficiency of outflows,
in particular of the outflow in M 82, and conclude from hydrodynamic
calculations that a starburst in a thin disk produces an outflow with
wide cone angle (
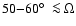 ), a starburst in a
thick disk an outflow with narrow cone angle (
), a starburst in a
thick disk an outflow with narrow cone angle (
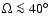 ).
We emphasize that the present investigation confirms the highly collimated
visible outflow but also that the base of the outflow extends over
).
We emphasize that the present investigation confirms the highly collimated
visible outflow but also that the base of the outflow extends over
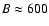 -1200 pc (
-1200 pc (
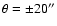 of Fig. 1;
of Fig. 1;
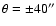 of Fig. 2). This fact may solve part of the discrepancy that
for M 82 the hydrodynamic model calculations (Tomisaka & Bregman 1993;
Suchkov et al. 1994; Strickland & Stevens 2000) predict a base of
of Fig. 2). This fact may solve part of the discrepancy that
for M 82 the hydrodynamic model calculations (Tomisaka & Bregman 1993;
Suchkov et al. 1994; Strickland & Stevens 2000) predict a base of
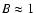 kpc diameter, or even larger. This is significantly larger than
the until now adopted base of the visible outflow of
kpc diameter, or even larger. This is significantly larger than
the until now adopted base of the visible outflow of
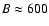 pc, assumed to be comparable in size to the inner diameter of the
molecular ring. The presented observations indicate that the base of the
visible outflow is as large as the outer diameter of the molecular ring
(Table 1). However, we cannot exclude the possibility that we observe
at this large radial distance some ionized material which is dragged-out of
the disk.
pc, assumed to be comparable in size to the inner diameter of the
molecular ring. The presented observations indicate that the base of the
visible outflow is as large as the outer diameter of the molecular ring
(Table 1). However, we cannot exclude the possibility that we observe
at this large radial distance some ionized material which is dragged-out of
the disk.
The presented observation shows that at  0.5 kpc (
0.5 kpc ( )
above
and below the disk the visible cone wall material moves outward along the cone walls at
the true velocity of 500-800 km s-1. This velocity is larger
than the escape velocity from the disk of
)
above
and below the disk the visible cone wall material moves outward along the cone walls at
the true velocity of 500-800 km s-1. This velocity is larger
than the escape velocity from the disk of
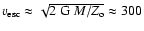 km s-1, derived for the
stellar mass of
km s-1, derived for the
stellar mass of
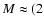 -
-
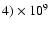
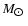 concentrated
within
concentrated
within 
 1000 pc radial distance from the center (for the mass
of M 82 see Götz et al. 1990; Förster Schreiber et al. 2001; Greve et al.
2002). Most of the visible cone wall material, and probably a major part of
the inner tenuous gas, is therefore eventually dispersed into interglactic
space. The recent observations (Seaquist & Clark 2001; Walter et al. 2002)
show that the CO material flows out at a significantly smaller velocity than
of the visible material, i.e.
1000 pc radial distance from the center (for the mass
of M 82 see Götz et al. 1990; Förster Schreiber et al. 2001; Greve et al.
2002). Most of the visible cone wall material, and probably a major part of
the inner tenuous gas, is therefore eventually dispersed into interglactic
space. The recent observations (Seaquist & Clark 2001; Walter et al. 2002)
show that the CO material flows out at a significantly smaller velocity than
of the visible material, i.e.
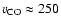 km s
km s
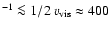 km s-1. The velocity
km s-1. The velocity
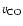 is probably not exceeding the escape velocity so that the
major part of the dragged-out material may eventually fall back into
the disk at a large radial distance, like in a fountain. Dust at a large
distance from the disk showing this fountain-like behaviour is probably seen
in the observation by Ichikawa et al. (1994) and Alton et al. (1999). In this
picture it is understandable that the cone angle of the fan-like (in the
terminology of Suchkov et al. 1996) dragged-out material is significantly
larger than the cone angle of the visible cone wall material, i.e.
is probably not exceeding the escape velocity so that the
major part of the dragged-out material may eventually fall back into
the disk at a large radial distance, like in a fountain. Dust at a large
distance from the disk showing this fountain-like behaviour is probably seen
in the observation by Ichikawa et al. (1994) and Alton et al. (1999). In this
picture it is understandable that the cone angle of the fan-like (in the
terminology of Suchkov et al. 1996) dragged-out material is significantly
larger than the cone angle of the visible cone wall material, i.e.
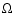
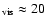 -30
-30
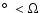
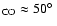 ,
or even larger. The dragged-out material is probably
located mostly at the periphery of the visible cones.
,
or even larger. The dragged-out material is probably
located mostly at the periphery of the visible cones.
M 82's rotating and partially escaping outflow dissipates matter and
angular momentum which, however, is only a small amount of the angular
momentum of the material of the disk and hence of little consequence for the
kinematic evolution of the galaxy. This can be
seen from the comparison of the angular momentum L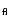 dissipated
in the outflow during the time of the recent starburst of
dissipated
in the outflow during the time of the recent starburst of
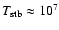 years (O'Connell et al. 1995) with the
angular momentum L
years (O'Connell et al. 1995) with the
angular momentum L
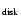 of the material inside the disk of
2
of the material inside the disk of
2
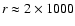 pc diameter. In order to calculate
pc diameter. In order to calculate
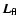 we assume that the material inside the cones and the cone
walls was and is the major part of the material ejected in the supernova
explosions of the heavy stars created in the starburst. We assume that this
outflowing material rotates, as known to be the case of the molecular material
and shown above to be the case of the visible material. The ejected material
eventually escapes. The amount of angular momentum L
we assume that the material inside the cones and the cone
walls was and is the major part of the material ejected in the supernova
explosions of the heavy stars created in the starburst. We assume that this
outflowing material rotates, as known to be the case of the molecular material
and shown above to be the case of the visible material. The ejected material
eventually escapes. The amount of angular momentum L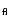 dissipated by this material during the starburst time is
dissipated by this material during the starburst time is
The mass M in relation (13) is derived under the assumption that the
star formation rate
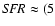 -
-
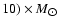 yr-1
(O'Connell et al. 1995) has persisted throughout the starburst time, and that
the heavier stars of some
yr-1
(O'Connell et al. 1995) has persisted throughout the starburst time, and that
the heavier stars of some
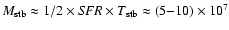
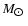 total mass have ended in supernova
explosions and that their material has escaped in the outflow. A somewhat
lower value is obtained if we assume a constant supernova rate
total mass have ended in supernova
explosions and that their material has escaped in the outflow. A somewhat
lower value is obtained if we assume a constant supernova rate
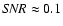 SN yr-1 (Kronberg & Sramek 1985; Muxlow et al. 1994) throughout
the starburst time and if the exploded stars had an average mass of
SN yr-1 (Kronberg & Sramek 1985; Muxlow et al. 1994) throughout
the starburst time and if the exploded stars had an average mass of
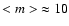
 .
Under these assumptions
.
Under these assumptions
 .
In addition, the outflow drags material out of
the disk and this material transports angular momentum which is partially
dissipated. The mass of the dragged-out material (H2), presently
residing in the halo, is estimated to be
.
In addition, the outflow drags material out of
the disk and this material transports angular momentum which is partially
dissipated. The mass of the dragged-out material (H2), presently
residing in the halo, is estimated to be 
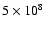
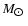 (Seaquist & Clark 2001). However, only a fraction of the dragged-out
material may escape while the major part falls back into the halo. If we
assume the fraction of the escaping mass to be
(Seaquist & Clark 2001). However, only a fraction of the dragged-out
material may escape while the major part falls back into the halo. If we
assume the fraction of the escaping mass to be
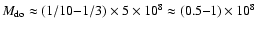
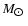 ,
we obtain for
the mass M in relation (13)
,
we obtain for
the mass M in relation (13)
In relation (13) the average distance of the outflow material from the minor
axis is assumed to be
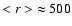 pc, the average
rotation velocity
pc, the average
rotation velocity
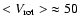 km s-1.
km s-1.
On the other hand, the angular momentum L
 is obtained when
using in the relation
is obtained when
using in the relation
the mass distribution m(r) derived by Götz et al. (1990; see also
Förster Schreiber et al. 2001) and the galactic rotation v(r)
derived by Greve et al. (2002; see also McKeith et al. 1993). In this way we
obtain
Allowing for a large uncertainty in this estimate, the ratio
L /L
/L
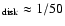 -1/100 indicates
that during the
-1/100 indicates
that during the  107 years of the starburst only a small amount
of angular momentum of the central part of the disk has been dissipated in the
outflow.
107 years of the starburst only a small amount
of angular momentum of the central part of the disk has been dissipated in the
outflow.
There exists in the optical and the CO observations of M 82 an asymmetry
between the outflow at the NW and SE side of the disk. This asymmetry is not
due to
the fact that on the NW side the line-of-sight passes through a more
extended layer of visual extinction because of M 82's inclination in this
direction![[*]](/icons/foot_motif.gif) . The asymmetry exists even at larger distances from the disk since
wide-field deep optical images (for instance Lynds & Sandage 1963; Devine
& Bally 1999) show that the NW outflow is much wider than the SE outflow,
and that the axes of the cones are not co-linear (for instance Deharveng &
Pellet 1970). In addition, our observation seems to indicate that the visible
NW cone has a significant velocity component in the direction of the observer
and also a significantly larger acceleration along the cone walls. Finally,
the CO distribution and the CO outflow kinematics is significantly different
at the SE and NW side of the disk (Seaquist & Clark 2001; Walter et al.
2002) which, however, in this case may be due to an irregular distribution of
material produced in the tidal interaction between M 81 and M 82 (Cottrell
1986; Yun et al. 1994). It is important to perform a closer study of the
origin of this asymmetry and of a possible build-up of this asymmetry inside
the disk.
. The asymmetry exists even at larger distances from the disk since
wide-field deep optical images (for instance Lynds & Sandage 1963; Devine
& Bally 1999) show that the NW outflow is much wider than the SE outflow,
and that the axes of the cones are not co-linear (for instance Deharveng &
Pellet 1970). In addition, our observation seems to indicate that the visible
NW cone has a significant velocity component in the direction of the observer
and also a significantly larger acceleration along the cone walls. Finally,
the CO distribution and the CO outflow kinematics is significantly different
at the SE and NW side of the disk (Seaquist & Clark 2001; Walter et al.
2002) which, however, in this case may be due to an irregular distribution of
material produced in the tidal interaction between M 81 and M 82 (Cottrell
1986; Yun et al. 1994). It is important to perform a closer study of the
origin of this asymmetry and of a possible build-up of this asymmetry inside
the disk.
Acknowledgements
Part of the observations at RGO, La Palma (Spain),
were made in service time. I thank the observatory for efficient assistence.
A. Weiß made a copy of the publication WWS-02 available prior to
publication. I appreciated the discussion with D. Downes (IRAM). I thank the
referee for his comments, his clarification of momentum conservation,
and his advice to throw out the straw while keeping the oats.
-
Achtermann, J. M., & Lacy, J. H. 1995, ApJ, 439, 163
In the text
NASA ADS
-
Alton, P. B., Davies, J. I., & Bianchi, S. 1999, A&A, 343, 51
In the text
NASA ADS
-
Amirkhanyan, A. S., Gagen-Torn, V. A., & Reshetnikov, V. P. 1982, Astrofizica,
18, 31
NASA ADS
-
Amirkhanyan, A. S., Gagen-Torn, V. A., & Reshetnikov, V. P. 1985, Astrofizica, 22, 239
In the text
NASA ADS
-
Axon, D. J., & Taylor, K. 1978, Nature, 274, 37
In the text
NASA ADS
-
Bland, J., & Tully, R. B. 1988, Nature, 334, 43 (BT-88)
In the text
NASA ADS
-
Bregman, J. N., Schulman, E., & Tomisaka, K. 1995, ApJ, 439, 155
In the text
NASA ADS
-
Burbidge, E. M., Burbidge, G. R., & Rubin, V. C. 1964, ApJ, 140, 942
In the text
NASA ADS
-
Chevalier, R. A., & Clegg, A. W. 1985, Nature, 317, 44
In the text
NASA ADS
-
Cottrell, G. A. 1977, MNRAS, 178, 577
NASA ADS
-
Deharveng, J. M., & Pellet, A. 1970, A&A, 9, 181
In the text
NASA ADS
-
Devine, D., & Bally, J. 1999, ApJ, 510, 197
In the text
NASA ADS
-
Dietz, R. D., Smith, J., Hackwell, J. A., Gehrz, R. D., & Grasdalen, G. L. 1986, AJ, 91, 758
NASA ADS
-
Freedman, W. L., Hughes, S. M., Madore, B. F., et al. 1994, ApJ, 427, 628
In the text
NASA ADS
-
Förster Schreiber, N. M., Genzel, R., Lutz, D., et al. 2001, ApJ, 552, 544
In the text
NASA ADS
-
Götz, M., McKeith, C. D., Downes, D., & Greve, A. 1990, A&A, 240, 52
In the text
NASA ADS
-
Greve, A., Wills, K. A., Neininger, N., & Pedlar, A. 2002, A&A, 383, 56
In the text
NASA ADS
-
Hartquist, T. W., Dyson, J. E., & Williams, R. J. R. 1997, ApJ, 482, 182
In the text
NASA ADS
-
Heckathorn, H. M. 1972, ApJ, 173, 501
In the text
NASA ADS
-
Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 74, 833 (HAM-90)
In the text
NASA ADS
-
Ichikawa, T., van Driel, W., Aoki, T., et al. 1994, ApJ, 433, 645
In the text
NASA ADS
-
Kronberg, P. P., & Sramek, R. A. 1985, Science, 277, 28
In the text
-
Larkin, J. E., Graham, J. R., Matthews, K., et al. 1994, ApJ, 420, 159
In the text
NASA ADS
-
Lehnert, M. D., Heckman, T. M., & Weaver, K. A. 1999, ApJ, 523, 575
In the text
NASA ADS
-
Loiseau, N., Nakai, N., Sofue, Y., Wielebinski, R., & Klein, U. 1990, A&A, 228,
331
In the text
NASA ADS
-
Lynds, C. R., & Sandage, A. R. 1963, ApJ, 137, 1005
In the text
NASA ADS
-
Mao, R. Q., Henkel, C., Schulz, A., et al. 2000, A&A, 358, 433
In the text
NASA ADS
-
McKeith, C. D., Castles, J., Greve, A., & Downes, D. 1993, A&A, 272, 98
In the text
NASA ADS
-
McKeith, C. D., Greve, A., Downes, D., & Prada, F. 1995, A&A, 293, 703 (M-95)
In the text
NASA ADS
-
Muxlow, T. W. B., Pedlar, A., Wilkinson, P. W., et al. 1994, MNRAS, 266, 455
In the text
NASA ADS
-
Nakai, N., Hayashi, M., Handa, T., Sofue, Y., & Hasegawa, T. 1987, PASJ, 39, 685
In the text
NASA ADS
-
Neininger, N., Guelin, M., Klein, U., Garcia-Burillo, S., & Wielebinski, R. 1998,
A&A, 339, 737
In the text
NASA ADS
-
O'Connell, R. W., Gallagher, J. S. III, Hunter, D. A., & Colley, W. N. 1995, ApJ, 446,
L 10
-
Ohyama, Y., Taniguchi, Y., Iye, M., et al. 2002, PASJ, 54, 891
In the text
NASA ADS
-
Sakai, S., & Madore, B. F. 1999, ApJ, 526, 599
In the text
NASA ADS
-
Scarrott, S. M, Eaton, W., & Axon, D. J. 1991, MNRAS, 252, 12
In the text
-
Schulz, H., & Wegner, G. 1992, A&A, 266, 167
In the text
NASA ADS
-
Seaquist, E. R., & Clark, J. 2001, ApJ, 552, 133 (SC-01)
In the text
NASA ADS
-
Shen, J., & Lo, K. Y. 1995, ApJ, 445, L 99
In the text
NASA ADS
-
Shopbell, P. L., & Bland-Hawthorn, J. 1998, ApJ, 493, 129 (SBH-98)
In the text
NASA ADS
-
Sofue, Y., Reuter, H.-P., Krause, M., Wielebinski, R., & Nakai, N. 1992,
ApJ, 395, 126
In the text
NASA ADS
-
Suchkov, A. A., Balsara, D. S., Heckman, T. M., & Leitherer, C. 1994, ApJ, 430, 511
In the text
NASA ADS
-
Suchkov, A. A., Berman, V. G., Heckman, T. M., & Balsara, D. S. 1996, ApJ, 463, 528
In the text
NASA ADS
-
Strickland, D. K., Ponman, T. J., & Stevens, I. R. 1997, A&A, 320, 378
In the text
NASA ADS
-
Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511
In the text
NASA ADS
-
Telesco, C. M., Campins, H., Joy, M., Dietz, K., & Decher, R. 1991, ApJ, 369, 135
In the text
NASA ADS
-
Tenorio-Tagle, G., & Muñoz-Tuñon, C. 1997, ApJ, 478, 137
In the text
-
Thuma, G., Neininger, N., Klein, U., & Wielebinski, R. 2000, A&A, 358, 65
In the text
NASA ADS
-
Tomisaka, K., & Ikeuchi, S. 1988, ApJ, 330, 695
In the text
NASA ADS
-
Tomisaka, K., & Bregman, J. N. 1993, PASJ, 45, 513
In the text
NASA ADS
-
Umemura, S., Iki, K., Shibata, K., & Sofue, Y. 1988, PASJ, 40, 25
In the text
NASA ADS
-
Walter, F., Weiß, A., & Scoville, N. 2002, ApJ, 580, L 21 (WWS-02)
In the text
NASA ADS
-
Weiß, A., Neininger, N., Hüttemeister, S., & Klein, U. 2001, A&A, 365, 571
In the text
NASA ADS
-
Wills, K. A., Das, M., Pedlar, A., Muxlow, T. W. B., & Robinson, T. G. 2000, MNRAS, 316,
33
In the text
NASA ADS
-
Yokoo, T., Fukue, J., & Taniguchi, Y. 1993, PASJ, 45, 687
In the text
NASA ADS
-
Yun, M. S., Ho, P. T. P., & Lo, K. Y. 1994, Nature, 372, 530
In the text
NASA ADS
Copyright ESO 2004




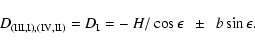
![\begin{displaymath}{\sin}[{\varphi}({\it z})] = \sqrt{{R(}{\it z})^{2} - {\it r}...
...{\it z)},\ \ {\cos}[{\varphi}({\it z})] = {\it r}/{R(}{\it z)}
\end{displaymath}](/articles/aa/full/2004/10/aa3753/img117.gif)