A&A 416, 79-110 (2004)
DOI: 10.1051/0004-6361:20034273
M. Dessauges-Zavadsky 1 - F. Calura 2 - J. X. Prochaska 3 - S. D'Odorico 4 - F. Matteucci2,5
1 - Observatoire de Genève, 51 Ch. des Maillettes, 1290 Sauverny, Switzerland
2 -
Dipartimento di Astronomia-Universitá di Trieste, via G. B. Tiepolo 11, 34131 Trieste, Italy
3 -
UCO/Lick Observatory, University of California at Santa Cruz, Santa Cruz, CA 95064, USA
4 -
European Southern Observatory, Karl-Schwarzschildstr. 2, 85748 Garching bei München, Germany
5 -
INAF, Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11, 34131 Trieste, Italy
Received 3 September 2003 / Accepted 26 November 2003
Abstract
By combining our UVES-VLT spectra of a sample of four damped Ly![]() systems (DLAs) toward the
quasars Q0100+13, Q1331+17, Q2231-00 and Q2343+12 with the existing HIRES-Keck spectra, we
covered the total optical spectral range from 3150 to 10 000 Å for the four quasars. This large
wavelength coverage and the high quality of the spectra allowed us to measure the column densities
of up to 21 ions, namely of 15 elements - N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Ni,
Zn. This comprehensive set of ionic column densities and elemental abundances severely contrasts
with the majority of DLAs for which only a handful of ions and elements is typically observed. Such
a large amount of information is necessary to constrain the photoionization and dust depletion
effects, two important steps in order to derive the intrinsic chemical abundance patterns of DLAs.
We evaluated the photoionization effects with the help of the Al+/Al++,
Fe+/Fe++, N0/N+ and Ar/Si, S ratios, and computed dust corrections. Our analysis
revealed that the DLA toward Q2343+12 requires important ionization corrections. This makes the
abundance determinations in this object uncertain. The access to the complete series of relatively
robust intrinsic elemental abundances in the other three DLAs allowed us to constrain their star
formation history, their age and their star formation rate by a detailed comparison with a grid of
chemical evolution models for spiral and dwarf irregular galaxies. Our results show that the
galaxies associated with these three DLAs in the redshift interval
systems (DLAs) toward the
quasars Q0100+13, Q1331+17, Q2231-00 and Q2343+12 with the existing HIRES-Keck spectra, we
covered the total optical spectral range from 3150 to 10 000 Å for the four quasars. This large
wavelength coverage and the high quality of the spectra allowed us to measure the column densities
of up to 21 ions, namely of 15 elements - N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Ni,
Zn. This comprehensive set of ionic column densities and elemental abundances severely contrasts
with the majority of DLAs for which only a handful of ions and elements is typically observed. Such
a large amount of information is necessary to constrain the photoionization and dust depletion
effects, two important steps in order to derive the intrinsic chemical abundance patterns of DLAs.
We evaluated the photoionization effects with the help of the Al+/Al++,
Fe+/Fe++, N0/N+ and Ar/Si, S ratios, and computed dust corrections. Our analysis
revealed that the DLA toward Q2343+12 requires important ionization corrections. This makes the
abundance determinations in this object uncertain. The access to the complete series of relatively
robust intrinsic elemental abundances in the other three DLAs allowed us to constrain their star
formation history, their age and their star formation rate by a detailed comparison with a grid of
chemical evolution models for spiral and dwarf irregular galaxies. Our results show that the
galaxies associated with these three DLAs in the redshift interval
![]() -2.5 are
either outer regions of spiral disks (radius
-2.5 are
either outer regions of spiral disks (radius ![]() kpc) or dwarf irregular galaxies (showing a
bursting or continuous star formation history) with ages varying from some 50 Myr only to
kpc) or dwarf irregular galaxies (showing a
bursting or continuous star formation history) with ages varying from some 50 Myr only to ![]() 3.5 Gyr and with moderate star formation rates per unit area of
3.5 Gyr and with moderate star formation rates per unit area of
![]()
![]() yr-1 kpc-2.
yr-1 kpc-2.
Key words: cosmology: observations - galaxies: abundances - galaxies: evolution - galaxies: quasars: absorption lines
The study of high redshift galaxies and the access to their physical properties can be done using either emission or absorption line spectroscopy. Absorption line spectroscopy is a very powerful technique, and it presents several advantages compared to the information which can be derived from emission. First, it allows one to detect objects up to very high redshift. Indeed, the quasars (QSOs) detected up to redshifts of 6.2 (Fan et al. 2001) can be used as background searchlights for useful probes of the intervening Universe up to lookback times of 95% of the age of the Universe. Second, through the analysis of QSO absorption lines we can study the spatial distribution, motion, chemical enrichment and ionization histories of gaseous structures on a variety of scales, ranging from the intergalactic medium to high column density absorption systems associated with galaxies. Third, since the detection of material intercepting a line of sight to a given QSO is dependent only on the column density of the gas and the luminosity of the QSO, this is a unique technique for probing the chemical composition and physical conditions in the interstellar medium of various types of galaxies over a large range of lookback times, detected independently of their distance, luminosity, star formation history and morphology.
While the major part of the baryon content of the present-day galaxies is concentrated in stars, an epoch must have existed at which the essential of the mass of galaxies still lay in the gas. The
damped Ly![]() systems (DLAs) observed in QSO spectra are characterized by large column densities
of neutral hydrogen, >
systems (DLAs) observed in QSO spectra are characterized by large column densities
of neutral hydrogen, >
![]() cm-2, and dominate the cosmic mass density of neutral
hydrogen gas (e.g. Storrie-Lombardi & Wolfe 2000; Storrie-Lombardi et al. 1996). The general view is that the DLA systems probably
represent some early stages in the evolution of the galaxies we see around us today, perhaps at a
time shortly after they had condensed out of the intergalactic medium, but before they had time to
form many stars, so that most of their mass still resided in the interstellar medium. These objects
thus are by far our best laboratory for studying the galaxies at high redshift, in their early
stages of evolution, and for tracking the galactic chemical evolution through the cosmic ages.
cm-2, and dominate the cosmic mass density of neutral
hydrogen gas (e.g. Storrie-Lombardi & Wolfe 2000; Storrie-Lombardi et al. 1996). The general view is that the DLA systems probably
represent some early stages in the evolution of the galaxies we see around us today, perhaps at a
time shortly after they had condensed out of the intergalactic medium, but before they had time to
form many stars, so that most of their mass still resided in the interstellar medium. These objects
thus are by far our best laboratory for studying the galaxies at high redshift, in their early
stages of evolution, and for tracking the galactic chemical evolution through the cosmic ages.
However, the reconstruction of the star formation histories of DLAs from the abundance pattern
measurements is not straightforward and led to contradictory results
(Molaro et al. 2000; Vladilo 2002a; Prochaska & Wolfe 1999; Centurión et al. 2000; Lu et al. 1996). The access to abundance ratios involving
two elements formed on different timescales, in particular the ![]() /Fe ratios, examined
together with [Fe/H], or any other metallicity tracer such as [Zn/H], is crucial, since the star
formation history of a galaxy is completely determined by the [
/Fe ratios, examined
together with [Fe/H], or any other metallicity tracer such as [Zn/H], is crucial, since the star
formation history of a galaxy is completely determined by the [![]() /Fe] versus [Fe/H]
distributions (e.g. Matteucci 2001). The principal difficulty, however, is to disentangle the
nucleosynthetic contributions from dust depletion effects. Because we are studying gas-phase
elemental abundances in DLAs, the observed abundances may not represent the intrinsic composition
of the system if part of the elements is removed from the gas to the solid phase (Savage & Sembach 1996).
Several pieces of evidence show that some dust is indeed present in DLAs
(e.g. Pei et al. 1991; Prochaska & Wolfe 2002). Another effect which has to be carefully examined, although
usually assumed negligible is the photoionization effect (e.g. Vladilo et al. 2001; Viegas 1995), since
in gas-phase studies a fraction of the gas may also be ionized.
/Fe] versus [Fe/H]
distributions (e.g. Matteucci 2001). The principal difficulty, however, is to disentangle the
nucleosynthetic contributions from dust depletion effects. Because we are studying gas-phase
elemental abundances in DLAs, the observed abundances may not represent the intrinsic composition
of the system if part of the elements is removed from the gas to the solid phase (Savage & Sembach 1996).
Several pieces of evidence show that some dust is indeed present in DLAs
(e.g. Pei et al. 1991; Prochaska & Wolfe 2002). Another effect which has to be carefully examined, although
usually assumed negligible is the photoionization effect (e.g. Vladilo et al. 2001; Viegas 1995), since
in gas-phase studies a fraction of the gas may also be ionized.
The difficulty to correctly evaluate the photoionization effects and the degeneracy between dust
depletion and nucleosynthesis in DLAs is accentuated by the limited number of ions and elements
typically detected in these galaxies. To determine the "intrinsic'' chemical abundance patterns,
free from ionization and dust depletion effects and to be then able to study the DLA galaxies individually, we need to examine several column density ratios of adjacent ions of the same
element and the relative abundances of as many elements as possible. We thus aimed at obtaining for
a few damped Ly![]() systems the column density measurements of many ions of different
ionization levels and the abundance measurements of the complete series of accessible elements in
DLAs. Until now the DLA galaxy population has been analyzed as a whole and chemical evolution models
were constructed in order to interpret the abundance patterns observed in DLAs as an ensemble,
considering them as an evolutionary sequence (e.g. Jimenez et al. 1999; Hou et al. 2001; Mathlin et al. 2001; Matteucci et al. 1997),
while several pieces of evidence - the low redshift deep imaging revealing a variety of
morphological types belonging to the DLA population (e.g. Nestor et al. 2002; Le Brun et al. 1997), the large
scatter in the
systems the column density measurements of many ions of different
ionization levels and the abundance measurements of the complete series of accessible elements in
DLAs. Until now the DLA galaxy population has been analyzed as a whole and chemical evolution models
were constructed in order to interpret the abundance patterns observed in DLAs as an ensemble,
considering them as an evolutionary sequence (e.g. Jimenez et al. 1999; Hou et al. 2001; Mathlin et al. 2001; Matteucci et al. 1997),
while several pieces of evidence - the low redshift deep imaging revealing a variety of
morphological types belonging to the DLA population (e.g. Nestor et al. 2002; Le Brun et al. 1997), the large
scatter in the ![]() over Fe-peak element abundance ratios at a given metallicity and the large
scatter observed in the metallicities - show that the DLAs trace galaxies with different
evolutionary histories. Some may have formed stars on timescales similar to that of the early Milky
Way, while others apparently did so more slowly or intermittently, so that the Fe-peak elements
could catch up with the
over Fe-peak element abundance ratios at a given metallicity and the large
scatter observed in the metallicities - show that the DLAs trace galaxies with different
evolutionary histories. Some may have formed stars on timescales similar to that of the early Milky
Way, while others apparently did so more slowly or intermittently, so that the Fe-peak elements
could catch up with the ![]() -elements. The DLA systems thus likely sample a wide range of
galaxy types, and consequently a variety of star formation histories. It is very important to
determine the star formation history of each of these high redshift galaxies individually to better
understand the galaxy formation and evolution.
-elements. The DLA systems thus likely sample a wide range of
galaxy types, and consequently a variety of star formation histories. It is very important to
determine the star formation history of each of these high redshift galaxies individually to better
understand the galaxy formation and evolution.
We thus attempted a new approach for studying the DLA galaxy population, focusing on individual
systems. By combining our UVES-VLT spectra with the existing HIRES-Keck spectra we
obtained the column density measurements of some 21 ions, namely of 15 elements - N, O, Mg, Al,
Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Ni, Zn -, in four DLA systems in the redshift interval
![]() .
The complete analysis of the four DLA systems is described in
Sects. 2 and 3. In Sect. 4, we address the question
of photoionization effects, and in Sect. 5 we analyze the dust content and discuss
for each system individually the intrinsic chemical abundances. Finally, the relative abundances as
a function of the metallicity and the redshift are systematically compared with a grid of chemical
evolution models for spiral and dwarf irregular galaxies in Sect. 6.
.
The complete analysis of the four DLA systems is described in
Sects. 2 and 3. In Sect. 4, we address the question
of photoionization effects, and in Sect. 5 we analyze the dust content and discuss
for each system individually the intrinsic chemical abundances. Finally, the relative abundances as
a function of the metallicity and the redshift are systematically compared with a grid of chemical
evolution models for spiral and dwarf irregular galaxies in Sect. 6.
Table 1: Journal of observations.
The selected quasars Q0100+13, Q1331+17, Q2231-00 and Q2343+12 with four intervening DLAs in the
redshift interval
![]() -2.5 are relatively bright with V=16.5-17.5 and already known
from the literature. Indeed, the DLAs toward Q0100+13, Q1331+17 and Q2231-00 were carefully and
accurately analyzed by Prochaska & Wolfe (1999) and Prochaska et al. (2001) thanks to high-resolution spectra
obtained with the HIRES echelle spectrograph on the Keck I telescope at Mauna Kea, in Hawaii, and
some results also obtained from HIRES-Keck spectra on the DLA toward Q2343+12 were presented by e.g.
Lu et al. (1998).
-2.5 are relatively bright with V=16.5-17.5 and already known
from the literature. Indeed, the DLAs toward Q0100+13, Q1331+17 and Q2231-00 were carefully and
accurately analyzed by Prochaska & Wolfe (1999) and Prochaska et al. (2001) thanks to high-resolution spectra
obtained with the HIRES echelle spectrograph on the Keck I telescope at Mauna Kea, in Hawaii, and
some results also obtained from HIRES-Keck spectra on the DLA toward Q2343+12 were presented by e.g.
Lu et al. (1998).
To complete the wavelength coverage of the HIRES-Keck spectra of these quasars, we used the unique
capability of the Ultraviolet-Visual Echelle Spectrograph UVES (D'Odorico et al. 2000) on the VLT
8.2 m Kueyen ESO telescope at Paranal, Chile, and we obtained high resolution, high signal-to-noise
ratio spectra for each quasar in the blue
![]() -4500 Å and in the far-red
-4500 Å and in the far-red
![]() -10 000 Å. The observations were performed in visitor mode in September 2000 for one object
and in service mode in summer 2001 for the three other objects under good seeing conditions
(between 0.5
-10 000 Å. The observations were performed in visitor mode in September 2000 for one object
and in service mode in summer 2001 for the three other objects under good seeing conditions
(between 0.5
![]() and 1.0
and 1.0
![]() ). For each observation, slit widths of 1
). For each observation, slit widths of 1
![]() in the blue and of 0.9
in the blue and of 0.9
![]() in the
red were chosen with a CCD binning of
in the
red were chosen with a CCD binning of ![]() resulting in a resolution of FWHM
resulting in a resolution of FWHM
![]() km s-1 and 6.4 km s-1, respectively. Relevant details of the observations are collected
in Table 1. The total exposure times of each quasar were split in multiple exposures
of 3600 or 4500 s.
km s-1 and 6.4 km s-1, respectively. Relevant details of the observations are collected
in Table 1. The total exposure times of each quasar were split in multiple exposures
of 3600 or 4500 s.
The spectra were reduced using the ESO data reduction package MIDAS and the UVES pipeline in
an interactive mode available as a MIDAS context. A detailed description of the pipeline can
be found in Ballester et al. (2000). To make sure of the best result, we made a systematic check of
each step of the pipeline reduction. The wavelengths of the reduced one-dimensional spectra were
converted to a vacuum-heliocentric scale, and the individual spectra of each object were co-added
using their signal-to-noise ratio as weights in order to get the maximum signal-to-noise ratios.
The final step was the normalization of the resulting spectra obtained by dividing them by a spline
function fitted to smoothly connect the regions free from absorption features. The continuum in the
Ly![]() forest was fitted by using small regions deemed to be free of absorptions and by
interpolating between these regions with a spline. An average signal-to-noise ratio per pixel of
forest was fitted by using small regions deemed to be free of absorptions and by
interpolating between these regions with a spline. An average signal-to-noise ratio per pixel of
![]() 30, 55 and 45 was achieved in the final spectra at
30, 55 and 45 was achieved in the final spectra at
![]() Å, 7500 Å and
9000 Å, respectively.
Å, 7500 Å and
9000 Å, respectively.
By combining our UVES-VLT spectra with the existing HIRES-Keck spectra obtained by Prochaska & Wolfe (1999) we cover the total spectral range from 3150 to 10 000 Å for the four observed quasars, and hence have access for the first time to up to 21 ions and 15 elements for each of their intervening DLAs.
The column densities of the metal species were derived with the Voigt profile fitting technique.
This technique consists in fitting theoretical Voigt profiles to the observed DLA absorption metal
lines well described as a complex of components, each defined by a redshift z, a Doppler
parameter b, a column density N and the corresponding errors. The fits were performed using a
![]() minimization routine fitlyman in MIDAS (Fontana & Ballester 1995). We assumed that
metal species with similar ionization potentials can be fitted using identical component
fitting parameters, i.e. the same b (which means that macroturbulent motions dominate over
thermal broadening) and the same z in the same component, and allowing for variations from metal
species to metal species in N only. We distinguish three categories of metal species with similar
ionization potentials: the low-ion transitions (i.e. the neutral and singly ionized species), the
intermediate-ion transitions (e.g. Fe III, Al III), and the high-ion transitions
(e.g. C IV, Si IV). We used relatively strong (but not saturated) lines to fix the
component fitting parameters (b and z), and excellent profile fits could then be achieved for
weak metal lines and for metal lines located in the Ly
minimization routine fitlyman in MIDAS (Fontana & Ballester 1995). We assumed that
metal species with similar ionization potentials can be fitted using identical component
fitting parameters, i.e. the same b (which means that macroturbulent motions dominate over
thermal broadening) and the same z in the same component, and allowing for variations from metal
species to metal species in N only. We distinguish three categories of metal species with similar
ionization potentials: the low-ion transitions (i.e. the neutral and singly ionized species), the
intermediate-ion transitions (e.g. Fe III, Al III), and the high-ion transitions
(e.g. C IV, Si IV). We used relatively strong (but not saturated) lines to fix the
component fitting parameters (b and z), and excellent profile fits could then be achieved for
weak metal lines and for metal lines located in the Ly![]() forest where the probability of
blending is high by allowing only the column density to vary. We had a sufficient number of
relatively strong metal-line profiles to well constrain the fitting parameters in the four studied
DLAs exhibiting multicomponent velocity structures.
forest where the probability of
blending is high by allowing only the column density to vary. We had a sufficient number of
relatively strong metal-line profiles to well constrain the fitting parameters in the four studied
DLAs exhibiting multicomponent velocity structures.
Table 2: Atomic data.
Throughout the analysis we adopted the list of atomic data - laboratory wavelengths and
oscillator strengths - presented in Table 2. The most recent measurements of
![]() and f-values of the metal-ions that impact the abundances of DLA systems and their
references are reported there. Information on the atomic data of additional useful metal-ions can
be found in Prochaska et al. (2001) and on the web site of "The HIRES Damped Ly
and f-values of the metal-ions that impact the abundances of DLA systems and their
references are reported there. Information on the atomic data of additional useful metal-ions can
be found in Prochaska et al. (2001) and on the web site of "The HIRES Damped Ly![]() Abundance
Database''
Abundance
Database''![]() maintained by Prochaska and
collaborators. Finally, we adopt the solar meteoritic abundances from Grevesse & Sauval (1998).
maintained by Prochaska and
collaborators. Finally, we adopt the solar meteoritic abundances from Grevesse & Sauval (1998).
The measured component per component ionic column densities obtained from the fitting model
solutions of the low- and intermediate-ion transitions are summarized in
Tables 3-7. The reported errors are the 1![]() errors on
the fits computed by fitlyman. They possibly underestimate the real error on the measure,
since they do not take into account the uncertainty on the continuum level determination. For the
components where the line profile is saturated, the column densities are listed as lower limits.
The values reported as upper limits are cases with significant line blending with H I clouds
of the Ly
errors on
the fits computed by fitlyman. They possibly underestimate the real error on the measure,
since they do not take into account the uncertainty on the continuum level determination. For the
components where the line profile is saturated, the column densities are listed as lower limits.
The values reported as upper limits are cases with significant line blending with H I clouds
of the Ly![]() forest or with telluric lines. The fitting solutions of the low- and
intermediate-ion transitions are shown in Figs. 2, 4,
6 and 8 for the four DLA. In these velocity plots, v=0
corresponds to an arbitrary component, and all the identified components are marked by small
vertical bars. The thin solid line represent the best-fitting solution. The telluric lines have
been identified thanks to the spectra of a hot, fast rotating star taken in the same nights as the
scientific exposures.
forest or with telluric lines. The fitting solutions of the low- and
intermediate-ion transitions are shown in Figs. 2, 4,
6 and 8 for the four DLA. In these velocity plots, v=0
corresponds to an arbitrary component, and all the identified components are marked by small
vertical bars. The thin solid line represent the best-fitting solution. The telluric lines have
been identified thanks to the spectra of a hot, fast rotating star taken in the same nights as the
scientific exposures.
The neutral hydrogen column densities were estimated from the fits of the Ly![]() damping line
profiles. The b-values were fixed at 20 km s-1, and the redshift z were left as a free
parameter or fixed to the redshift of the strongest component of the metal-line profiles according
to the system (see comments in the following sub-Sections). When other lines of the Lyman series
were accessible in our spectra, we used them to check the H I column densities derived from
the Ly
damping line
profiles. The b-values were fixed at 20 km s-1, and the redshift z were left as a free
parameter or fixed to the redshift of the strongest component of the metal-line profiles according
to the system (see comments in the following sub-Sections). When other lines of the Lyman series
were accessible in our spectra, we used them to check the H I column densities derived from
the Ly![]() lines. Figures 1, 3, 5 and
7 show the results of the H I fitting solutions for the four DLA systems. The
small vertical bar corresponds to the redshift obtained in the best-fitting solution and the thin
solid line represents the best fit.
lines. Figures 1, 3, 5 and
7 show the results of the H I fitting solutions for the four DLA systems. The
small vertical bar corresponds to the redshift obtained in the best-fitting solution and the thin
solid line represents the best fit.
Table 3:
Component structure of the
![]() DLA system toward Q0100+13.
DLA system toward Q0100+13.
We now briefly describe the fitting results for the four individual DLA systems. Their Mn II
![]() 2576, 2594, 2606, Ti II
2576, 2594, 2606, Ti II
![]() and Mg II
and Mg II
![]() 1239,1240 fits and column density measurements have already been discussed in details in
Dessauges-Zavadsky et al. (2002a, hereafter Paper I). Let's just remind that the Mg II
1239,1240 fits and column density measurements have already been discussed in details in
Dessauges-Zavadsky et al. (2002a, hereafter Paper I). Let's just remind that the Mg II
![]() 1239,1240 lines are detected in the DLA Ly
1239,1240 lines are detected in the DLA Ly![]() damping line red wing and that they
have been fitted after a local renormalization of the spectrum around the Mg II lines with
the fit of the Ly
damping line red wing and that they
have been fitted after a local renormalization of the spectrum around the Mg II lines with
the fit of the Ly![]() damping wing profile. The errors on the measured Mg+ column densities
have been estimated by varying the continuum level by 5%.
damping wing profile. The errors on the measured Mg+ column densities
have been estimated by varying the continuum level by 5%.
This system was carefully studied by Wolfe et al. (1994), and subsequently by Prochaska & Wolfe (1999) and
Prochaska et al. (2001). Thanks to the UVES spectra we confirm some of their column density
measurements, namely N(Zn+), N(Cr+) and N(Fe+) obtained from the Fe II
![]() 2249, 2260, 2344, 2374 lines not present in the HIRES spectra, and we obtain new column
density measurements of S II, Ar I, P II, N I and Mg II (see
Fig. 2). We also get upper limits on the column densities of two intermediate-ions,
N II and Fe III located in the Ly
2249, 2260, 2344, 2374 lines not present in the HIRES spectra, and we obtain new column
density measurements of S II, Ar I, P II, N I and Mg II (see
Fig. 2). We also get upper limits on the column densities of two intermediate-ions,
N II and Fe III located in the Ly![]() forest, by using the profile shapes of the
intermediate-ion lines Al III
forest, by using the profile shapes of the
intermediate-ion lines Al III ![]() 1854, 1862 observed in the HIRES spectra to constrain
the fitting parameters (see Fig. 2).
1854, 1862 observed in the HIRES spectra to constrain
the fitting parameters (see Fig. 2).
The low-ion absorption line profiles of this system are characterized by 4 components. Their
redshifts, b-values and column densities are presented in Table 3. Two of the 4
components, the components 3 and 4, are too weak to be accurately identified in the weak metal-lines
and in the metal-lines located in the Ly![]() forest. Thus, we prefer to avoid measuring them
in most of the observed transitions. Being weak and since we are interested in the relative
elemental abundances, this has no impact on the final conclusions on this DLA system. The
intermediate-ion lines show very similar profiles to the low-ion profiles suggesting they are
coming from the same absorption regions. Their fitting solutions are given in Table 3.
forest. Thus, we prefer to avoid measuring them
in most of the observed transitions. Being weak and since we are interested in the relative
elemental abundances, this has no impact on the final conclusions on this DLA system. The
intermediate-ion lines show very similar profiles to the low-ion profiles suggesting they are
coming from the same absorption regions. Their fitting solutions are given in Table 3.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0273F1.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg58.gif) |
Figure 1:
Normalized UVES spectra of Q0100+13 showing the DLA Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.6cm,clip]{0273F2.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg59.gif) |
Figure 2:
Velocity plots of the metal line transitions (normalized intensities shown by dots
with |
| Open with DEXTER | |
Table 4:
Component structure of the
![]() DLA system toward Q1331+17.
DLA system toward Q1331+17.
Figure 1 shows the fitting solutions of two Lyman lines of this DLA, Ly![]() and
Ly
and
Ly![]() ,
observed in the UVES spectra. The fits were obtained by fixing the b-value at 20
km s-1 and the redshift at
z = 2.309027, i.e. at the redshift of the strongest metal-line
component (the component 1). The measured H I column density,
,
observed in the UVES spectra. The fits were obtained by fixing the b-value at 20
km s-1 and the redshift at
z = 2.309027, i.e. at the redshift of the strongest metal-line
component (the component 1). The measured H I column density, ![]() (H I)
(H I)
![]() ,
is very similar to the one derived by Pettini et al. (1990) from low-resolution spectra.
Giving the high H0 column density, the red wing of the Ly
,
is very similar to the one derived by Pettini et al. (1990) from low-resolution spectra.
Giving the high H0 column density, the red wing of the Ly![]() damping profile extends over
the S II
damping profile extends over
the S II ![]() 1250, 1253, 1259 lines. Similarly to the Mg II
1250, 1253, 1259 lines. Similarly to the Mg II ![]() 1240 line
(the Mg II
1240 line
(the Mg II ![]() 1239 line being heavily blended), we had first to locally renormalize
the spectrum with the fit of the Ly
1239 line being heavily blended), we had first to locally renormalize
the spectrum with the fit of the Ly![]() damping wing profile before measuring the S+ column
density.
damping wing profile before measuring the S+ column
density.
This famous DLA system has been studied by a large number of authors. We mention here only the work
of Prochaska & Wolfe (1999) and Prochaska et al. (2001) who obtained the highest quality data and made the
most accurate analysis. By extending their wavelength coverage with our UVES data, we obtained
additional column density measurements of S II, P II, N I, Mg II,
Mn II and Cl I. We confirm the Prochaska & Wolfe (1999) and Prochaska et al. (2001) column
density measurements of Si II, Fe II, C I, Mg I and Al III (see
Fig. 4). But, their N(Ni+) and N(Cr+) measurements differ from ours by
almost 0.1 dex. We also confirm the revised value of N(Zn+) of Prochaska et al. (2001) obtained by
correcting the contamination of Zn II ![]() 2026 by the Mg I
2026 by the Mg I ![]() 2026 profile.
The detection of the relatively strong Mg I
2026 profile.
The detection of the relatively strong Mg I ![]() 2852 line in the UVES spectra has
allowed us to measure even more reliably this contamination. Finally, we obtain a more constraining
upper limit for N(Ti+) from the Ti II
2852 line in the UVES spectra has
allowed us to measure even more reliably this contamination. Finally, we obtain a more constraining
upper limit for N(Ti+) from the Ti II ![]() 3384 line than the higher value deduced
by Prochaska et al. (2001) from the Ti II
3384 line than the higher value deduced
by Prochaska et al. (2001) from the Ti II ![]() 1910 lines having a 3 times lower oscillator
strength.
1910 lines having a 3 times lower oscillator
strength.
The fitting solutions of the detected components in the low-ion metal-lines are presented in
Table 4. A surprising particularity of this system known as a system exhibiting the
largest dust depletion level of any DLA is that the fits of the refractory element lines require 6 components (2 components at ![]() km s-1, see Fig. 4), while the
non-refractory and mildly refractory element lines are well fitted with 5 components only (1 component at v = 0 km s-1, see Fig. 4). The refractory elements showing
weak absorption lines, like the Mg II
km s-1, see Fig. 4), while the
non-refractory and mildly refractory element lines are well fitted with 5 components only (1 component at v = 0 km s-1, see Fig. 4). The refractory elements showing
weak absorption lines, like the Mg II ![]() 1239, 1240 and Cr II
1239, 1240 and Cr II ![]() 2056, 2062
lines, are borderline cases, in the sense that the component 1 is detected but only marginally.
Concerning the component 6, it is only observed in the strongest metal-line transitions.
2056, 2062
lines, are borderline cases, in the sense that the component 1 is detected but only marginally.
Concerning the component 6, it is only observed in the strongest metal-line transitions.
| |
Figure 3:
Same as Fig. 1 but for Q1331+17. The vertical bars correspond to the wavelength centroids of the components used for the best fit,
z = 1.776724 and
z = 1.786345, referring to the DLA system and an additional absorber, respectively. The measured H I column densities are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{0273F4.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg65.gif) |
Figure 4: Same as Fig. 2 for the DLA toward Q1331+17. The zero velocity is fixed at z = 1.776370. |
| Open with DEXTER | |
The detection of the Cl I ![]() 1347 line is exceptional. Cl0 has previously been
observed only by Ledoux et al. (2002) and Prochaska et al. (2003) in the DLA toward Q0551-366 and in the
DLA toward FJ081240.6+320808, respectively. In the DLA system studied in this paper, we detect only
the components 2 and 3 of the Cl I
1347 line is exceptional. Cl0 has previously been
observed only by Ledoux et al. (2002) and Prochaska et al. (2003) in the DLA toward Q0551-366 and in the
DLA toward FJ081240.6+320808, respectively. In the DLA system studied in this paper, we detect only
the components 2 and 3 of the Cl I ![]() 1347 line, the other components 4, 5 and 6 are
blended with Ly
1347 line, the other components 4, 5 and 6 are
blended with Ly![]() forest absorptions. However, since the line profiles of S II
forest absorptions. However, since the line profiles of S II
![]() 1250, Si II
1250, Si II ![]() 1808 and C I
1808 and C I ![]() 1656 show very little absorption
at v > 25 km s-1 (only
1656 show very little absorption
at v > 25 km s-1 (only ![]() 20% of the total column density for S II and
Si II), we consider the Cl I column density derived from the components 2 and 3 as a
value. We adopt an error on N(Cl I) of 0.10 dex to account for the possible contribution
from the blended components 4, 5 and 6. Nevertheless, the Cl0 column density measurement provides
only a strict lower limit on the Cl absolute abundance of [Cl/H] > -1.37, since the dominant state
of Cl should be Cl II in DLAs (the ionization potential of Cl0 is 13.01 eV which is lower
than that of hydrogen). The Cl II column density cannot unfortunately be determined in this
DLA system due to the low rest-wavelengths of the Cl II lines.
20% of the total column density for S II and
Si II), we consider the Cl I column density derived from the components 2 and 3 as a
value. We adopt an error on N(Cl I) of 0.10 dex to account for the possible contribution
from the blended components 4, 5 and 6. Nevertheless, the Cl0 column density measurement provides
only a strict lower limit on the Cl absolute abundance of [Cl/H] > -1.37, since the dominant state
of Cl should be Cl II in DLAs (the ionization potential of Cl0 is 13.01 eV which is lower
than that of hydrogen). The Cl II column density cannot unfortunately be determined in this
DLA system due to the low rest-wavelengths of the Cl II lines.
The N I column density is not easy to derive in this DLA. First, given the high H I
column density of this DLA system, the N I triplet at
![]() Å is
blended with the blue damping wing of the DLA Ly
Å is
blended with the blue damping wing of the DLA Ly![]() absorption line. We thus have to
renormalize the spectral region covering the N I
absorption line. We thus have to
renormalize the spectral region covering the N I ![]() 1200 triplet with the fit of the
Ly
1200 triplet with the fit of the
Ly![]() damping wing profile, before fitting the N I lines. Second, it is difficult to
determine whether the derived N I column density is a lower or an upper limit. Indeed, the
component 2 of all the detected N I lines is saturated, even in the weakest N I
transition at
damping wing profile, before fitting the N I lines. Second, it is difficult to
determine whether the derived N I column density is a lower or an upper limit. Indeed, the
component 2 of all the detected N I lines is saturated, even in the weakest N I
transition at
![]() Å. Thus, we are inclined to assume that the derived
column density is a lower limit. But, when looking carefully at the N I line profiles, they
all show a stronger component 4 than the component 5, on the opposite to what is observed in other
low-ionization transition profiles. This suggests that the N I lines are likely blended with
Ly
Å. Thus, we are inclined to assume that the derived
column density is a lower limit. But, when looking carefully at the N I line profiles, they
all show a stronger component 4 than the component 5, on the opposite to what is observed in other
low-ionization transition profiles. This suggests that the N I lines are likely blended with
Ly![]() forest absorptions. Therefore, we finally assume that the derived N I column
density is an upper limit.
forest absorptions. Therefore, we finally assume that the derived N I column
density is an upper limit.
While fitting the Ly![]() damping line, we found it necessary to include, besides the
contribution of the DLA at
z = 1.776724 corresponding to the redshift of the metal-line component
4, a second absorber shifted by about 1079 km s-1 redwards of the DLA system (see
Fig. 3). The redshift of this second absorber,
damping line, we found it necessary to include, besides the
contribution of the DLA at
z = 1.776724 corresponding to the redshift of the metal-line component
4, a second absorber shifted by about 1079 km s-1 redwards of the DLA system (see
Fig. 3). The redshift of this second absorber,
![]() ,
is accurately
determined thanks to the detections of several associated metal-lines (see also Lopez & Ellison 2003).
The derived H I column densities of the DLA and the second absorber are
,
is accurately
determined thanks to the detections of several associated metal-lines (see also Lopez & Ellison 2003).
The derived H I column densities of the DLA and the second absorber are ![]() (H I
(H I
![]() and
and
![]() ,
respectively. They confirm the previous
measurements made by Pettini et al. (1994).
,
respectively. They confirm the previous
measurements made by Pettini et al. (1994).
| |
Figure 5:
Same as Fig. 1 but for Q2231-00. The vertical bar corresponds to the
wavelength centroid of the component used for the best fit left as a free parameter,
z = 2.065774.
The measured H I column density is |
| Open with DEXTER | |
Table 5:
Component structure of the
![]() DLA system toward Q2231-00.
DLA system toward Q2231-00.
![\begin{figure}
\par\includegraphics[width=16.6cm,clip]{0273F6.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg71.gif) |
Figure 6: Same as Fig. 2 for the DLA toward Q2231-00. The zero velocity is fixed at z = 2.066161. |
| Open with DEXTER | |
This DLA system was previously observed and analyzed by Lu et al. (1996) and Prochaska & Wolfe (1999), and
recently completed by Prochaska et al. (2001). Throughout their analysis they adopted the H I
column density measured by Lu & Wolfe (1994). We obtain here a new value for the ![]() (H I)
of
(H I)
of
![]() from the Ly
from the Ly![]() damping line observed in the UVES spectra (see
Fig. 5). The fit was performed by fixing the b-value at 20 km s-1 and by
leaving the redshift as a free parameter.
damping line observed in the UVES spectra (see
Fig. 5). The fit was performed by fixing the b-value at 20 km s-1 and by
leaving the redshift as a free parameter.
The UVES spectra provide column density measurements of the S+, P+, N0, Mn+ and Mg0
ions (see Fig. 6), and confirm the N(Si+), N(Zn+), N(Cr+) and
N(Ni+) measurements of Prochaska & Wolfe (1999). The fit of the Mg I ![]() 2852 line
clearly shows that the contamination of Zn II
2852 line
clearly shows that the contamination of Zn II ![]() 2026 by the Mg I
2026 by the Mg I ![]() 2026
profile is negligible. We note that we had to fit the Mg I profile with slightly different
fitting parameters in comparison to the ones we have used for other low-ion metal lines (see
Table 5). By combining the Fe II
2026
profile is negligible. We note that we had to fit the Mg I profile with slightly different
fitting parameters in comparison to the ones we have used for other low-ion metal lines (see
Table 5). By combining the Fe II ![]() 1608, 1611 lines detected in the HIRES
spectra and the Fe II
1608, 1611 lines detected in the HIRES
spectra and the Fe II ![]() 2260, 2344, 2374 lines observed in the UVES spectra, we deduce a more accurate measurement of N(Fe+). Finally, we obtain a revised value for N(Ti II) of
2260, 2344, 2374 lines observed in the UVES spectra, we deduce a more accurate measurement of N(Fe+). Finally, we obtain a revised value for N(Ti II) of
![]() from the Ti II
from the Ti II ![]() 3067, 3073 lines. We succeed in deriving an upper
limit on the column density of the intermediate-ion, Fe III, located in the Ly
3067, 3073 lines. We succeed in deriving an upper
limit on the column density of the intermediate-ion, Fe III, located in the Ly![]() forest, by using the Al III lines observed in the HIRES spectra to constrain the fitting
parameters (see Fig. 6 and Table 5). The intermediate-ion lines show
very similar profiles to the low-ion line profiles.
forest, by using the Al III lines observed in the HIRES spectra to constrain the fitting
parameters (see Fig. 6 and Table 5). The intermediate-ion lines show
very similar profiles to the low-ion line profiles.
The low-ion line profiles are characterized by a relatively complex velocity structure composed of 11 components presented in Table 5 and spread over 180 km s-1 in velocity space. But, only the 5 strongest components, the components 4, 5, 9, 10 and 11, are detected in the weak metal-lines. They contain only about 75% of the total column density obtained by summing the contributions of the 11 components. This shows that when computing the abundance ratios [X/Y], it is necessary to consider only the column densities of the velocity components detected in both the X and Y profiles to avoid under/overestimations of the relative abundances.
An additional difficulty which appears in absorption systems with complex metal-line profiles is
that the probability of blending in the Ly![]() forest is higher over a larger velocity interval.
For this reason it is more sensible to consider the measured P+ and N0 column densities as
upper limits, the P II and N I lines being located in a region of the Ly
forest is higher over a larger velocity interval.
For this reason it is more sensible to consider the measured P+ and N0 column densities as
upper limits, the P II and N I lines being located in a region of the Ly![]() forest with numerous absorption lines (see Fig. 6). The S+ column density is a
borderline case, and unfortunately only the S II
forest with numerous absorption lines (see Fig. 6). The S+ column density is a
borderline case, and unfortunately only the S II ![]() 1253 line from the S+ triplet
can be used to determine N(S+), the two other lines are heavily blended with Ly
1253 line from the S+ triplet
can be used to determine N(S+), the two other lines are heavily blended with Ly![]() clouds.
We consider the measured N(S+) as a value, assuming that the adopted error on N(S+)
covers the possible H I blendings.
clouds.
We consider the measured N(S+) as a value, assuming that the adopted error on N(S+)
covers the possible H I blendings.
This DLA system has first been studied by Sargent et al. (1988). The chemical abundance measurements obtained from HIRES spectra were mainly used in statistical samples (e.g. Prochaska & Wolfe 1998; Vladilo et al. 2003; Lu et al. 1998). Recently, D'Odorico et al. (2002) and Vladilo et al. (2003) reported some additional abundance measurements from UVES spectra. We present here the first complete set of elemental abundances of this DLA.
From our UVES spectra, we measured the column densities of O I, Ar I, N I,
Fe II, Zn II, Cr II and Mn II, and obtained an upper limit on the
column density of P II contaminated by the Ly![]() clouds. The metal absorption profiles
are characterized by an extremely complex velocity structure extended over 350 km s-1 in
velocity space and composed of 23 components (see Fig. 8 and Table 6).
The dominant feature is the group of 5 components around
clouds. The metal absorption profiles
are characterized by an extremely complex velocity structure extended over 350 km s-1 in
velocity space and composed of 23 components (see Fig. 8 and Table 6).
The dominant feature is the group of 5 components around
![]() km s-1, with the
components 18-20 being the strongest ones. These components are heavily saturated in strong
metal-lines, but are the only components detected in weak metal-lines. They contain about 62% of
the total column density.
km s-1, with the
components 18-20 being the strongest ones. These components are heavily saturated in strong
metal-lines, but are the only components detected in weak metal-lines. They contain about 62% of
the total column density.
The Ly![]() line is outside our UVES wavelength coverage, therefore we adopt the H I
column density measurement (
line is outside our UVES wavelength coverage, therefore we adopt the H I
column density measurement (![]() (H I)
(H I)
![]() )
obtained by D'Odorico et al. (2002).
Figure 7 shows the fit of the Ly
)
obtained by D'Odorico et al. (2002).
Figure 7 shows the fit of the Ly![]() line which confirms this N(H0)
measurement. This relatively low H0 column density and the presence of a strong N II
line which confirms this N(H0)
measurement. This relatively low H0 column density and the presence of a strong N II
![]() 1083 line as well as of other intermediate-ion lines - Al III
1083 line as well as of other intermediate-ion lines - Al III ![]() 1854,
Fe III
1854,
Fe III ![]() 1122 and S III
1122 and S III ![]() 1012 - with very similar profiles to the
low-ion metal line profiles (see Fig. 8 and Table 7) suggest that
some photoionization corrections may be required in this DLA system. A discussion on the
photoionization corrections is presented in Sect. 4.
1012 - with very similar profiles to the
low-ion metal line profiles (see Fig. 8 and Table 7) suggest that
some photoionization corrections may be required in this DLA system. A discussion on the
photoionization corrections is presented in Sect. 4.
The photoionization effects have to be carefully examined in absorption metal-line systems, when the main goal is to provide a complete and unbiased interpretation of the chemical abundance patterns. Indeed, as we are studying gas-phase abundances, a fraction of the gas may be ionized and we need to determine this fraction to be sure that we are measuring the intrinsic abundances. The dust depletion effects also affect the gas-phase abundance measurements. The manner we tackle this issue is described in the next section.
| |
Figure 7:
Same as Fig. 1 but for Q2343+12. The Voigt fit was performed with the H I column density measured by D'Odorico et al. (2002, Sect. 3.2) from the Ly |
| Open with DEXTER | |
Table 6:
Component structure of the
![]() DLA system toward Q2343+12.
DLA system toward Q2343+12.
Table 7:
Component structure of the
![]() DLA system toward Q2343+12 - continued.
DLA system toward Q2343+12 - continued.
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{0273F8.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg77.gif) |
Figure 8: Same as Fig. 2 for the DLA toward Q2343+12. The zero velocity is fixed at z = 2.429942. |
| Open with DEXTER | |
It is generally assumed that in the DLA systems the ionization fraction is low, so that the
dominant ionization state in H I regions is the neutral one for elements with the first
ionization potential >13.6 eV (e.g. O0, N0) and the singly ionized one for elements with
the first ionization potential <13.6 eV and the second >13.6 eV (e.g. Fe+, Si+). The
reason for this is that the bulk of the H0 gas is self-shielded from
![]() eV photons,
but transparent to
eV photons,
but transparent to
![]() eV photons. Under this assumption, the correction factors for
ionization are small, and thus the column densities of low-ions are equal to the column densities
of elements, e.g. N(Si+)
eV photons. Under this assumption, the correction factors for
ionization are small, and thus the column densities of low-ions are equal to the column densities
of elements, e.g. N(Si+) ![]() N(Si). However, the detection of intermediate-ionization
transitions, like Al++, in the DLA systems provided doubts on the ionization levels in DLAs.
The ionization potential of Al+ is 18.8 eV, i.e. greater than that of hydrogen, therefore
Al++ is likely present in ionized and not in neutral gas, since photons with
N(Si). However, the detection of intermediate-ionization
transitions, like Al++, in the DLA systems provided doubts on the ionization levels in DLAs.
The ionization potential of Al+ is 18.8 eV, i.e. greater than that of hydrogen, therefore
Al++ is likely present in ionized and not in neutral gas, since photons with
![]() eV cannot so easily penetrate gas clouds with large H I column densities. In addition,
the observations show a good correlation between the velocity structures of Al III and
singly ionized and neutral species (e.g. Prochaska & Wolfe 1999; Wolfe & Prochaska 2000; Lu et al. 1996). To explain the
similarity between the Al III and low-ionization species line profiles, Howk & Sembach (1999) and
Izotov & Thuan (1999) proposed that these lines originate in the same ionized region or in a mix of
neutral and ionized clouds, and stressed the importance of abundance corrections for ionization
effects. Furthermore, indirect arguments to consider ionized gas in DLAs came from studies of the
warm ionized medium in the Milky Way and other nearby galaxies (Sembach et al. 2000; Howk et al. 1999; Jenkins et al. 2000).
eV cannot so easily penetrate gas clouds with large H I column densities. In addition,
the observations show a good correlation between the velocity structures of Al III and
singly ionized and neutral species (e.g. Prochaska & Wolfe 1999; Wolfe & Prochaska 2000; Lu et al. 1996). To explain the
similarity between the Al III and low-ionization species line profiles, Howk & Sembach (1999) and
Izotov & Thuan (1999) proposed that these lines originate in the same ionized region or in a mix of
neutral and ionized clouds, and stressed the importance of abundance corrections for ionization
effects. Furthermore, indirect arguments to consider ionized gas in DLAs came from studies of the
warm ionized medium in the Milky Way and other nearby galaxies (Sembach et al. 2000; Howk et al. 1999; Jenkins et al. 2000).
Several authors have investigated the ionization effects in the DLA systems (Vladilo et al. 2001; Howk & Sembach 1999; Izotov et al. 2001; Viegas 1995). Although the different approaches used to deal with the problem of photoionization in DLAs have led to slightly different conclusions, it was generally found that ionization corrections in DLAs are negligible, being below the measurement errors, except for some particular systems like the DLA toward GB 1759+7539 studied by Prochaska et al. (2002b). While the authors stress that this particular DLA system has several characteristics which separate it from the majority of DLAs, its properties highlight the importance of assessing the ionization state of each DLA system. The photoionization model computations are generally performed using the CLOUDY photoionization equilibrium software package (e.g. Ferland et al. 1998). To avoid computing heavy photoionization models, Prochaska et al. (2002b) defined a number of photoionization diagnostics which provides a qualitative "first-look'' analysis of the ionization state in a DLA system and of the level of required ionization corrections. In the following sub-sections, we apply these photoionization diagnostics to each of the four DLAs studied and qualitatively evaluate the importance of ionization corrections.
According to the anti-correlation between ![]() (H0) and
(H0) and ![]() (Al++)/N(Al+) found
by Vladilo et al. (2001), where the Al++/Al+ column density ratio is assumed to be at a first
approximation an indicator of the ionization level in the gas, the high H I column density,
(Al++)/N(Al+) found
by Vladilo et al. (2001), where the Al++/Al+ column density ratio is assumed to be at a first
approximation an indicator of the ionization level in the gas, the high H I column density,
![]() (H I
(H I
![]() ,
of this DLA system suggests that the ionization corrections
are low. The following three additional and more reliable ionization indicators are at our disposal
in this DLA system.
,
of this DLA system suggests that the ionization corrections
are low. The following three additional and more reliable ionization indicators are at our disposal
in this DLA system.
Thanks to the high efficiency of UVES in the blue, we have the spectral coverage for this DLA
system of the rarely detected intermediate-ion transitions, Fe III and N II at
![]() and 1083 Å, respectively. The column density ratios
Fe++/Fe+ and N+/N0 are the most reliable ionization indicators, since the
recombination coefficient of Al+ is rather uncertain, being likely overestimated
(Nussbaumer & Storey 1986). The observed Fe III and N II lines show the same profiles as
the low-ion profiles and are well fitted with the fitting parameters deduced for the low-ion lines.
Located in the Ly
and 1083 Å, respectively. The column density ratios
Fe++/Fe+ and N+/N0 are the most reliable ionization indicators, since the
recombination coefficient of Al+ is rather uncertain, being likely overestimated
(Nussbaumer & Storey 1986). The observed Fe III and N II lines show the same profiles as
the low-ion profiles and are well fitted with the fitting parameters deduced for the low-ion lines.
Located in the Ly![]() forest, one of the 2 components is clearly blended in both
intermediate-ion lines (see Fig. 2), therefore we derived only upper limits on
their column densities. These limits lead to
forest, one of the 2 components is clearly blended in both
intermediate-ion lines (see Fig. 2), therefore we derived only upper limits on
their column densities. These limits lead to ![]() (Fe++)/N(Fe
+)< -1.54 and
(Fe++)/N(Fe
+)< -1.54 and
![]() (N+)/N(N
0) < -1.24. According to the photoionization diagnostics established by
Prochaska et al. (2002b), in a system where Fe++/Fe+< -1.60 dex and N+/N0< -1.00 dex, the ionization fraction, x, defined as the ratio of H+ over (H
(N+)/N(N
0) < -1.24. According to the photoionization diagnostics established by
Prochaska et al. (2002b), in a system where Fe++/Fe+< -1.60 dex and N+/N0< -1.00 dex, the ionization fraction, x, defined as the ratio of H+ over (H
![]() ), is
expected to be lower than 10%. Thus, the measured Fe++ and N+ column densities are in
agreement with the expectations for a DLA with a H I column density higher than 1021
cm-2.
), is
expected to be lower than 10%. Thus, the measured Fe++ and N+ column densities are in
agreement with the expectations for a DLA with a H I column density higher than 1021
cm-2.
Another ionization indicator that we can consider in this system is argon. Indeed, Ar has a very
high photoionization cross-section for photons with energy higher than 13.6 eV which is about ten
times higher than the one of H I, and thus Ar is very sensitive to ionization effects
(Sofia & Jenkins 1998). The comparison of the Ar abundance with the abundance of another ![]() -element
- O, S, or Si - provides indication on the ionization level in the gas. In this system, we
measure [Ar/S
-element
- O, S, or Si - provides indication on the ionization level in the gas. In this system, we
measure [Ar/S
![]() ,
and according to Prochaska et al. (2002b), an observed value of
[Ar0/S
+] >-0.20 dex indicates x < 10%.
,
and according to Prochaska et al. (2002b), an observed value of
[Ar0/S
+] >-0.20 dex indicates x < 10%.
In summary, the high H I column density, the Al++/Al+, Fe++/Fe+ and N+/N0 column density ratios, and the Ar0/S+ abundance ratio, all point to a low ionization fraction in this DLA system, and thus to low ionization corrections. The ionization corrections should indeed be lower than 0.1 dex for all the elements, except probably for Ar.
This is another very high H I column density system with ![]() (H I
(H I
![]() .
The high H I column density suggests that the ionization level is low in this DLA
(Vladilo et al. 2001). However, we do not detect any very reliable ionization indicator in this system
to confirm this statement. Only the Al++/Al+ column density ratio is available for which we
derive an upper limit of <-0.76 dex from the HIRES spectra. This limit indicates that the
ionization corrections should be low in this system.
.
The high H I column density suggests that the ionization level is low in this DLA
(Vladilo et al. 2001). However, we do not detect any very reliable ionization indicator in this system
to confirm this statement. Only the Al++/Al+ column density ratio is available for which we
derive an upper limit of <-0.76 dex from the HIRES spectra. This limit indicates that the
ionization corrections should be low in this system.
Two ionization indicators are accessible in this DLA with a H I column density of ![]() (H I
(H I
![]() .
The first one is the Al++/Al+ column density ratio
obtained from the HIRES spectra, and the second one is the upper limit on the Fe++/Fe+
column density ratio obtained from the UVES spectra. However, the Al II line is so heavily
saturated that no reliable N(Al+) lower limit can be deduced. We thus derive an estimation of
the Al++/Al+ column density ratio by using Si+ as a proxy of Al+ assuming the
.
The first one is the Al++/Al+ column density ratio
obtained from the HIRES spectra, and the second one is the upper limit on the Fe++/Fe+
column density ratio obtained from the UVES spectra. However, the Al II line is so heavily
saturated that no reliable N(Al+) lower limit can be deduced. We thus derive an estimation of
the Al++/Al+ column density ratio by using Si+ as a proxy of Al+ assuming the ![]() (Si+) versus
(Si+) versus ![]() (Al+) correlation found by Vladilo et al. (2001). We obtain
(Al+) correlation found by Vladilo et al. (2001). We obtain
![]() (Al++)/N(Al
(Al++)/N(Al
![]() .
With regard to the second ionization indicator,
the Fe III
.
With regard to the second ionization indicator,
the Fe III ![]() 1122 line is located in the Ly
1122 line is located in the Ly![]() forest and is strongly blended
with H I clouds. Consequently, the deduced Fe++ column density upper limit is not
stringent. We get
forest and is strongly blended
with H I clouds. Consequently, the deduced Fe++ column density upper limit is not
stringent. We get ![]() (Fe++)/N(Fe+)
(Fe++)/N(Fe+) ![]() .
.
Unfortunately the Ar I lines as well as the N II line are beyond the quasar flux cut-off, no other ionization indicator is hence accessible in this DLA system. If we trust the derived Al++/Al+ column density ratio measurement, the ionization corrections should not be significant.
The low H I column density of ![]() (H I)
(H I)
![]() suggests that the
ionization corrections might be relevant in this system. Several strong intermediate-ion lines with
very similar profiles to the low-ion line profiles are observed in this system, namely
Al III, Fe III, N II and S III (see Fig. 8). This is
indeed a first indication that photoionization is playing an important role here. The second
straightforward indication is provided by the Ar/O and Ar/Si abundance ratio measurements. They are
very low in this system. We find [Ar/O
suggests that the
ionization corrections might be relevant in this system. Several strong intermediate-ion lines with
very similar profiles to the low-ion line profiles are observed in this system, namely
Al III, Fe III, N II and S III (see Fig. 8). This is
indeed a first indication that photoionization is playing an important role here. The second
straightforward indication is provided by the Ar/O and Ar/Si abundance ratio measurements. They are
very low in this system. We find [Ar/O
![]() and [Ar/Si
and [Ar/Si
![]() ,
in
agreement with the measurements by Vladilo et al. (2003). The Ar/Si abundance ratio in this DLA system
is even lower than the [Ar/Si] abundance ratio of
,
in
agreement with the measurements by Vladilo et al. (2003). The Ar/Si abundance ratio in this DLA system
is even lower than the [Ar/Si] abundance ratio of
![]() measured in the DLA system toward
GB 1759+7539 by Prochaska et al. (2002b) whose analysis showed important ionization corrections.
measured in the DLA system toward
GB 1759+7539 by Prochaska et al. (2002b) whose analysis showed important ionization corrections.
The measured ![]() (Al++)/N(Al
(Al++)/N(Al
![]() obtained by taking Si+ as a
proxy of Al+ according to the correlation identified by Vladilo et al. (2001),
obtained by taking Si+ as a
proxy of Al+ according to the correlation identified by Vladilo et al. (2001),
![]() (Fe++)/N(Fe+)< 0.37 derived from the Fe III
(Fe++)/N(Fe+)< 0.37 derived from the Fe III ![]() 1122 line which
is only partially blended with Ly
1122 line which
is only partially blended with Ly![]() clouds (in the components 4 and 5), and
clouds (in the components 4 and 5), and
![]() (N+)/N(N
0)> -0.10 confirm that the ionization corrections are important in this
DLA system. Indeed, a system with Fe++/Fe+> -1 dex and N+/N0> -0.2 dex is
expected to have an ionization fraction, x, higher than 50% (Prochaska et al. 2002b). We suspect
that the ionization corrections in this DLA system are of similar magnitude as the ones of the DLA
toward GB 1759+7539, namely between 0.1 to >0.5 dex depending on the ion. Such high ionization
corrections prevent us from deriving reliable chemical abundances in this DLA system. Therefore, we
do not include this DLA in the following Sections where we discuss the chemical abundances of
individual systems and make a detailed comparison with chemical evolution models.
(N+)/N(N
0)> -0.10 confirm that the ionization corrections are important in this
DLA system. Indeed, a system with Fe++/Fe+> -1 dex and N+/N0> -0.2 dex is
expected to have an ionization fraction, x, higher than 50% (Prochaska et al. 2002b). We suspect
that the ionization corrections in this DLA system are of similar magnitude as the ones of the DLA
toward GB 1759+7539, namely between 0.1 to >0.5 dex depending on the ion. Such high ionization
corrections prevent us from deriving reliable chemical abundances in this DLA system. Therefore, we
do not include this DLA in the following Sections where we discuss the chemical abundances of
individual systems and make a detailed comparison with chemical evolution models.
The small sample of DLAs studied in this paper is unique, because by combining the UVES-VLT data with the HIRES-Keck data we could measure the abundances of up to 15 elements - N, O, Mg, Al, Si, P, S, Cl, Ar, Ti, Cr, Mn, Fe, Ni, Zn. This contrasts with the majority of DLAs for which only a handful of elements (Si, Fe, occasionally Cr, Zn, Ni) is usually detected (e.g. Prochaska et al. 2001; Prochaska & Wolfe 1999; Lu et al. 1996). This low amount of information on individual systems has until now severely limited the interpretation of the DLA abundance patterns.
The interpretation of the elemental abundance patterns in DLAs is by far not straightforward, the principal difficulty is to disentangle the nucleosynthetic contributions from the dust depletion effects. Several pieces of evidence show that dust is indeed present in DLAs (e.g. Pei et al. 1991; Pettini et al. 1994; Prochaska & Wolfe 2002; Hou et al. 2001). Therefore, as we are measuring gas-phase elemental abundances in DLAs, in presence of dust the observed abundances may not represent the intrinsic chemical composition of the system if part of the elements is removed from the gas to the solid phase, as it happens in the interstellar medium of our Galaxy (Savage & Sembach 1996). Consequently, the refractory elements (e.g. Si, Fe, Cr, Ni) preferentially incorporated into dust grains are not the best diagnostic elements and their relative ratios have to be cautiously interpreted, since their differential depletion can mimic the expected nucleosynthetic abundance patterns.
In Sect. 4 we have seen that at least the ionization effects are playing a negligible role in three out of the four DLAs studied in this paper. To constrain now the dust depletion effects, the access to a large number of elements is crucial, since elements with the same nucleosynthetic origin provide information on the dust depletion level in DLAs.
Fe-peak elements and Zn. When comparing the absolute abundances of different
iron-peak elements, Cr, Fe, Ni, and of Zn measured in the DLAs toward Q0100+13, Q1331+17 and
Q2231-00, we notice variations, while in the Galactic stars, Cr, Fe, Ni and Zn track each other
and have solar values relative to Fe
(apart from Zn which seems to be enhanced by at maximum 0.1-0.2 dex relative to Fe, see Prochaska et al. 2000; Mishenina et al. 2002). These absolute abundance variations are in line with the variations
observed in the Galactic ISM due to the differential depletion (e.g. Savage & Sembach 1996), and are
thus suggestive as being the result of a differential depletion present in the DLA systems. Hence,
the measured [Zn/Fe, Cr, Ni] ratios, when assumed as being the result of the different degree of
incorporation into dust grains of Zn, a volatile element (almost undepleted), and of Fe, Cr and Ni,
refractory elements, clearly show that dust depletion has to be seriously taken into account in
the DLA systems toward Q1331+17 and Q2231-00, for which we find [Zn/Fe
![]() and
and
![]() ,
respectively. The DLA toward Q1331+17, in particular, exhibits one of the largest
dust depletion level of any DLA. On the contrary, the DLA toward Q0100+13 shows a low [Zn/Fe] ratio
of
,
respectively. The DLA toward Q1331+17, in particular, exhibits one of the largest
dust depletion level of any DLA. On the contrary, the DLA toward Q0100+13 shows a low [Zn/Fe] ratio
of
![]() ,
and thus requires negligible dust corrections.
,
and thus requires negligible dust corrections.
Alpha-elements. Another similar way to highlight the presence of dust in the DLA
systems is the comparison of the absolute abundances of different ![]() -elements. In the Galactic
stars the
-elements. In the Galactic
stars the ![]() -elements track more or less each other (within
-elements track more or less each other (within ![]() dex). Thus, by
comparing
dex). Thus, by
comparing ![]() -elements of different dust depletion levels, their relative ratios when
differing from the solar value are indicative of the presence of dust. In the DLA toward Q0100+13
we measure [S/Mg
-elements of different dust depletion levels, their relative ratios when
differing from the solar value are indicative of the presence of dust. In the DLA toward Q0100+13
we measure [S/Mg
![]() ,
where Mg is relatively strongly depleted in the Galactic ISM
and S is a non-refractory element (Savage & Sembach 1996). This ratio is in agreement with the measured
[Zn/Fe] ratio, both of them suggest a small amount of dust in this DLA system. In the DLA toward
Q1331+17 we measure [S/Si
,
where Mg is relatively strongly depleted in the Galactic ISM
and S is a non-refractory element (Savage & Sembach 1996). This ratio is in agreement with the measured
[Zn/Fe] ratio, both of them suggest a small amount of dust in this DLA system. In the DLA toward
Q1331+17 we measure [S/Si
![]() .
Since Si is only a mildly refractory element
(Savage & Sembach 1996), the observed S overabundance relative to Si indicates important amount of dust.
We also have the measurement of [S/Mg]
.
Since Si is only a mildly refractory element
(Savage & Sembach 1996), the observed S overabundance relative to Si indicates important amount of dust.
We also have the measurement of [S/Mg]
![]() in this DLA system. This abundance
ratio rather indicates no presence of dust, but we ascribe this result to the weak accuracy of the
Mg II column density measurement, which may be slightly overestimated due to some blends in
the Ly
in this DLA system. This abundance
ratio rather indicates no presence of dust, but we ascribe this result to the weak accuracy of the
Mg II column density measurement, which may be slightly overestimated due to some blends in
the Ly![]() forest (see Paper I and Sect. 3.2). Finally, in the DLA toward Q2231-00
we measure [S/Si
forest (see Paper I and Sect. 3.2). Finally, in the DLA toward Q2231-00
we measure [S/Si
![]() and [Si/Ti
and [Si/Ti
![]() .
The [S/Si] ratio is in agreement
with the conclusions derived from the [Zn/Fe] ratio, which highlights the presence of dust in this
DLA system. On the other hand, the measured undersolar [Si/Ti] ratio, while Ti is a strongly
refractory element, does not confirm these findings. At a first glance, the undersolar [Si/Ti]
ratio can only be the result of an overestimation of the Ti II column density.
.
The [S/Si] ratio is in agreement
with the conclusions derived from the [Zn/Fe] ratio, which highlights the presence of dust in this
DLA system. On the other hand, the measured undersolar [Si/Ti] ratio, while Ti is a strongly
refractory element, does not confirm these findings. At a first glance, the undersolar [Si/Ti]
ratio can only be the result of an overestimation of the Ti II column density.
Table 8: Summary of the absolute abundances in the three DLA systems studied.
Table 9: Summary of the relative abundances in the three DLA systems studied.
Three main approaches can be used to circumvent the problem of dust depletion in the studies of
DLA abundance patterns. The first one consists in considering only the DLA systems with no
or low dust depletion, [Zn/Cr
![]() (Pettini et al. 2000; Molaro et al. 2000; Lopez et al. 2002). Indeed, if
the amount of dust is small, the dust depletion levels are negligible. This is valid for the DLA
toward Q0100+13, which has a low [Zn/Cr
(Pettini et al. 2000; Molaro et al. 2000; Lopez et al. 2002). Indeed, if
the amount of dust is small, the dust depletion levels are negligible. This is valid for the DLA
toward Q0100+13, which has a low [Zn/Cr
![]() ratio. However, for the two other DLAs,
other solutions have to be found. The second approach consists in trying to quantify the dust
depletion effects and provide dust corrections to the measured abundances. Several authors have
considered different methods to compute the dust depletion corrections
(e.g. Vladilo 1998; Savaglio et al. 2000). Recently, Vladilo (2002a,b) elaborated a new and
more complete method for correcting for dust depletion. Finally, the third approach consists in
focusing on non-refractory and mildly refractory elements, such as N, O, S, Ar, and Zn. In this way
one has directly access to the intrinsic abundances of DLAs
(Molaro et al. 2000; Centurión et al. 2000; Dessauges-Zavadsky et al. 2002b). This approach to tackle the problem of dust depletion is
by far the most accurate one. It is applicable to all DLAs whatever their amount of dust, and
is independent of any assumption on the properties of dust in DLAs and of errors that may be
introduced by a complex dust correction procedure.
ratio. However, for the two other DLAs,
other solutions have to be found. The second approach consists in trying to quantify the dust
depletion effects and provide dust corrections to the measured abundances. Several authors have
considered different methods to compute the dust depletion corrections
(e.g. Vladilo 1998; Savaglio et al. 2000). Recently, Vladilo (2002a,b) elaborated a new and
more complete method for correcting for dust depletion. Finally, the third approach consists in
focusing on non-refractory and mildly refractory elements, such as N, O, S, Ar, and Zn. In this way
one has directly access to the intrinsic abundances of DLAs
(Molaro et al. 2000; Centurión et al. 2000; Dessauges-Zavadsky et al. 2002b). This approach to tackle the problem of dust depletion is
by far the most accurate one. It is applicable to all DLAs whatever their amount of dust, and
is independent of any assumption on the properties of dust in DLAs and of errors that may be
introduced by a complex dust correction procedure.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0273F9.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg108.gif) |
Figure 9:
The nucleosynthetic abundance pattern of the DLA at
|
| Open with DEXTER | |
In our study we considered the second and the third approach to circumvent the problem of dust depletion. In Table 8 we summarize all the absolute abundances, and in Table 9 we summarize the relative abundances which are further used in the paper. Both the observed and dust-corrected values are reported. The dust corrections were performed using the method developed by Vladilo (2002a,b). This method groups together several dust correction models based on different assumptions. They are labeled E00, E11 when one assumes that the intrinsic [Zn/Fe] ratio is equal to +0.10 dex and S00, S11 when the intrinsic [Zn/Fe] ratio is equal to +0.00 dex (see more details in Vladilo 2002a). The absolute abundances, [X/H], were obtained by summing the contributions of all the components reported in Tables 3-6. The relative abundances, [X/Y], were computed by considering only the column densities of the components detected both in the X and Y profiles. In this way one avoids an overestimation of abundances derived from strong metal-line profiles relative to the abundances derived from weaker metal-line profiles in which generally only the strongest components are detected. In the case of very weak lines, like the Ti II lines for instance, one can indeed underestimate the [X/Fe] ratios by up to 0.3-0.4 dex by considering the total Fe abundance generally derived from strong Fe II lines. In the three DLAs studied this effect is particularly important in the DLA toward Q2231-00 which show complex metal-line profiles, with a large number of components. The same approach has already been used in Paper I.
In this section we describe the derived intrinsic abundance patterns of the DLAs toward
Q0100+13, Q1331+17 and Q2231-00. Their interpretation will be presented in Sect. 6. To
present the abundance patterns we use the same type of diagrams as the ones used by
Prochaska et al. (2003). The dust-corrected elemental abundances are plotted on a logarithmic
scale, where hydrogen is defined to have
![]() and, in a general way, for any
element X,
and, in a general way, for any
element X,
![]() ,
and are compared with the solar abundance
pattern from Grevesse & Sauval (1998) (shown by the solid line) scaled to match the observed sulfur
metallicity of each DLA system. This way of showing the elemental abundances as a function of the
atomic number, Z, has the advantage that we see in the same plot all the measured abundances in a
system, and this allows us to directly identify possible deviations from solar values.
,
and are compared with the solar abundance
pattern from Grevesse & Sauval (1998) (shown by the solid line) scaled to match the observed sulfur
metallicity of each DLA system. This way of showing the elemental abundances as a function of the
atomic number, Z, has the advantage that we see in the same plot all the measured abundances in a
system, and this allows us to directly identify possible deviations from solar values.
Figures 9-11 show the nucleosynthetic patterns of the DLAs toward Q0100+13, Q1331+17 and Q2231-00, respectively. At a first glance, the abundance patterns of these high redshift galaxies resemble that of the solar neighborhood indicating that their nucleosynthetic enrichment histories are not too dissimilar from our Galaxy. However, at closer inspection, one notes several important differences.
The DLA toward Q0100+13 (Fig. 9) shows a slight enhancement of the
![]() -elements S and Mg abundances relative to the Zn and Fe-peak element abundances, namely
[S/Zn
-elements S and Mg abundances relative to the Zn and Fe-peak element abundances, namely
[S/Zn
![]() and [Mg/Fe]
and [Mg/Fe]
![]() .
This
.
This ![]() /Fe-peak enhancement
is suggestive of an enrichment by massive stars. Indeed, the
/Fe-peak enhancement
is suggestive of an enrichment by massive stars. Indeed, the ![]() -elements are produced in less
than
-elements are produced in less
than
![]() yrs by type II supernovae (SNe) resulting from massive stars and the Fe-peak
elements are mainly produced by type Ia SNe on longer timescales, between 108-109 yrs.
yrs by type II supernovae (SNe) resulting from massive stars and the Fe-peak
elements are mainly produced by type Ia SNe on longer timescales, between 108-109 yrs.
The dust-corrected ratio of the two ![]() -elements Mg and S, [Mg/S]
-elements Mg and S, [Mg/S]
![]() ,
shows that these two elements closely track each other in the DLA. On the other hand, the
,
shows that these two elements closely track each other in the DLA. On the other hand, the
![]() -element Ar is slightly underabundant relative to S, as noted in Sect. 4.
The Fe-peak elements Fe, Ni and Cr show solar values one relative to the other, as observed in the
Galactic stars with similar metallicities (see Table 8).
-element Ar is slightly underabundant relative to S, as noted in Sect. 4.
The Fe-peak elements Fe, Ni and Cr show solar values one relative to the other, as observed in the
Galactic stars with similar metallicities (see Table 8).
In this system, one also observes the odd-even effect, which corresponds to an underabundance of
odd-Z elements relative to the even-Z elements of the same nucleosynthetic origin. Indeed, we
obtained [P/S
![]() at [P/H]
at [P/H]
![]() ,
which even shows evidence for an
enhanced odd-even effect. This value is similar to the [P/Si] =-0.21 at [P/H] =-1.16, [P/Si]
=-0.40 at [P/H] =-2.30 and [P/Si] =-0.30 at [P/H] =-1.20 values measured toward other DLAs
by Levshakov et al. (2002), Molaro et al. (2001) and Outram et al. (1999), respectively, and is indicative of
massive supernovae. Phosphorus abundance measurements in DLAs are very important to understand
the nucleosynthesis of this element, because no P abundance measurement exists in the Galactic
stars. The observed odd-even effect in the P/S ratio is in agreement with the findings of
Goswami & Prantzos (2000).
,
which even shows evidence for an
enhanced odd-even effect. This value is similar to the [P/Si] =-0.21 at [P/H] =-1.16, [P/Si]
=-0.40 at [P/H] =-2.30 and [P/Si] =-0.30 at [P/H] =-1.20 values measured toward other DLAs
by Levshakov et al. (2002), Molaro et al. (2001) and Outram et al. (1999), respectively, and is indicative of
massive supernovae. Phosphorus abundance measurements in DLAs are very important to understand
the nucleosynthesis of this element, because no P abundance measurement exists in the Galactic
stars. The observed odd-even effect in the P/S ratio is in agreement with the findings of
Goswami & Prantzos (2000).
Finally, the DLA shows an undersolar [N/S] ratio of
![]() at [S/H
at [S/H
![]() .
N is
an element of particular interest, since it has a complex nucleosynthetic origin. Synthesized in
the CNO cycle of stars, N is either a secondary element in the sense that it is produced in
proportion to C and O originally present in the star, or a primary element in the sense that it can
be produced starting from C and O manufactured by the star "in situ''. In the N/
.
N is
an element of particular interest, since it has a complex nucleosynthetic origin. Synthesized in
the CNO cycle of stars, N is either a secondary element in the sense that it is produced in
proportion to C and O originally present in the star, or a primary element in the sense that it can
be produced starting from C and O manufactured by the star "in situ''. In the N/![]() versus
versus
![]() /H diagram, the secondary N over
/H diagram, the secondary N over ![]() -element ratio is expected to increase steeply
with the increasing metallicity, while the primary N over
-element ratio is expected to increase steeply
with the increasing metallicity, while the primary N over ![]() -element ratio remains constant
when the metallicity increases (Talbot & Arnett 1974). The progenitors of primary N have not been fully
constrained yet. The most recent stellar models of Meynet & Maeder (2002) including the stellar rotation
indicate that the intermediate-mass stars are the main producers of N. The [N/S] ratio reached in
the DLA toward Q0100+13 is a "high'' value, in the sense that it is close to the primary N
"plateau'' at [N/S
-element ratio remains constant
when the metallicity increases (Talbot & Arnett 1974). The progenitors of primary N have not been fully
constrained yet. The most recent stellar models of Meynet & Maeder (2002) including the stellar rotation
indicate that the intermediate-mass stars are the main producers of N. The [N/S] ratio reached in
the DLA toward Q0100+13 is a "high'' value, in the sense that it is close to the primary N
"plateau'' at [N/S
![]() .
It is at the upper end of the range of N/S values measured in
DLAs and in good agreement with the typical values observed in H II regions at similar
metallicities (e.g. Pilyugin et al. 2002; Izotov & Thuan 1999).
.
It is at the upper end of the range of N/S values measured in
DLAs and in good agreement with the typical values observed in H II regions at similar
metallicities (e.g. Pilyugin et al. 2002; Izotov & Thuan 1999).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{0273F10.ps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg118.gif) |
Figure 10:
The nucleosynthetic abundance pattern of the DLA at
|
| Open with DEXTER | |
The DLA toward Q1331+17 (Fig. 10) has almost a solar abundance pattern. Very few
differences are observed. Indeed, the Fe-peak elements Fe, Ni and Cr closely track each other, the
two ![]() -elements S and Si also (see Table 8), and the
-elements S and Si also (see Table 8), and the ![]() -element over
Fe-peak element ratios - Si/Fe, S/Zn and S/Fe - are all solar. Only the Mg/Fe ratio is slightly
oversolar (see Table 9). We would like to note that the S00 and S11 dust
correction models of Vladilo (2002a) which assume a solar ratio of Zn/Fe, lead to
[S/Fe]
-element over
Fe-peak element ratios - Si/Fe, S/Zn and S/Fe - are all solar. Only the Mg/Fe ratio is slightly
oversolar (see Table 9). We would like to note that the S00 and S11 dust
correction models of Vladilo (2002a) which assume a solar ratio of Zn/Fe, lead to
[S/Fe]
![]() (see Table 9). Such an undersolar
(see Table 9). Such an undersolar
![]() -element over Fe-peak element ratio is neither observed in Galactic stars nor predicted by
chemical evolution models. Thus, this provides evidence that [Zn/Fe] > 0 (intrinsically) in this
DLA system. Ti exhibits a large underabundance relative to the Fe-peak elements and this, although
Ti is an
-element over Fe-peak element ratio is neither observed in Galactic stars nor predicted by
chemical evolution models. Thus, this provides evidence that [Zn/Fe] > 0 (intrinsically) in this
DLA system. Ti exhibits a large underabundance relative to the Fe-peak elements and this, although
Ti is an ![]() -element, and even after having applied the dust corrections. At a first glance,
the only way to explain this observation is that we have underestimated the Ti upper limit.
-element, and even after having applied the dust corrections. At a first glance,
the only way to explain this observation is that we have underestimated the Ti upper limit.
We measure the abundances of P and Mn, two odd-Z elements. The odd-even effect is less marked in
this system than in the DLA toward Q0100+13. We get [P/Si]
![]() when the E00
dust correction is applied and [P/Si]
when the E00
dust correction is applied and [P/Si]
![]() when the E11 dust correction is
applied at [P/H
when the E11 dust correction is
applied at [P/H
![]() ,
and [Mn/Fe
,
and [Mn/Fe
![]() (without dust corrections, and
(without dust corrections, and
![]() ,
,
![]() when the E00, E11 dust corrections are applied, respectively) at
[Fe/H]
when the E00, E11 dust corrections are applied, respectively) at
[Fe/H]
![]() .
.
We have detected the Cl I ![]() 1347 line in this DLA system, which allows us to
measure the Cl0 column density and to provide a lower limit on the total Cl absolute abundance.
Cl is also an odd-Z element. This is the third Cl abundance upper limit derived in a DLA system,
the other two were obtained by Ledoux et al. (2002) and Prochaska et al. (2003). Cl abundance measurements
in DLAs are very important to constrain the Cl nucleosynthesis in the low metallicity regime, in
particular because no Cl abundance measurement exists in Galactic stars. Cl measurements are
available in planetary nebulae of the Galactic disk (PNe; e.g. Costa et al. 1996; Kwitter et al. 2003)
and in the Galactic disk ISM (e.g. Welty et al. 1999). Oversolar [Cl/S] ratios between +0.09 and
+0.5 dex are observed in type II PNe, and undersolar [Cl/S] ratios of -0.6 and -0.2 dex are
measured in the cold and warm Galactic disk ISM, respetively, suggesting that Cl is dust depleted. In
the DLA studied here we derive a lower limit on the [Cl/S] ratio of >-0.11 at [Cl/H] > -1.37,
and in the DLA studied by Ledoux et al. (2002) and Prochaska et al. (2003) [Cl/S] > -0.33 and >-0.68,
respectively. These three lower limits measured in DLAs suggest that the Cl/S ratios likely are
solar to oversolar similarly to what is observed in PNe, thus leaving very little space for an
odd-even effect for Cl. The chemical evolution models of Goswami & Prantzos (2000) computed with the
Woosley & Weaver (1995) yields predict a solar Cl/S ratio, and hence a negligible odd-even effect for Cl.
1347 line in this DLA system, which allows us to
measure the Cl0 column density and to provide a lower limit on the total Cl absolute abundance.
Cl is also an odd-Z element. This is the third Cl abundance upper limit derived in a DLA system,
the other two were obtained by Ledoux et al. (2002) and Prochaska et al. (2003). Cl abundance measurements
in DLAs are very important to constrain the Cl nucleosynthesis in the low metallicity regime, in
particular because no Cl abundance measurement exists in Galactic stars. Cl measurements are
available in planetary nebulae of the Galactic disk (PNe; e.g. Costa et al. 1996; Kwitter et al. 2003)
and in the Galactic disk ISM (e.g. Welty et al. 1999). Oversolar [Cl/S] ratios between +0.09 and
+0.5 dex are observed in type II PNe, and undersolar [Cl/S] ratios of -0.6 and -0.2 dex are
measured in the cold and warm Galactic disk ISM, respetively, suggesting that Cl is dust depleted. In
the DLA studied here we derive a lower limit on the [Cl/S] ratio of >-0.11 at [Cl/H] > -1.37,
and in the DLA studied by Ledoux et al. (2002) and Prochaska et al. (2003) [Cl/S] > -0.33 and >-0.68,
respectively. These three lower limits measured in DLAs suggest that the Cl/S ratios likely are
solar to oversolar similarly to what is observed in PNe, thus leaving very little space for an
odd-even effect for Cl. The chemical evolution models of Goswami & Prantzos (2000) computed with the
Woosley & Weaver (1995) yields predict a solar Cl/S ratio, and hence a negligible odd-even effect for Cl.
Prochaska & Wolfe (1999) also reported the detection of C II* in the DLA toward Q1331+17. The
presence of both strong C II* and Cl I absorptions suggests that the gas resides
in a cold neutral medium, characteristic of highly depleted gas in the Milky Way. This DLA precisely
shows an important dust depletion level, with [Zn/Fe
![]() .
Furthermore, the observation
of significant Cl I requires at least a modest molecular hydrogen fraction. Indeed, in
regions where H2 is optically thick, Cl II reacts rapidly with H2 to form HCl+,
which in turn leads to Cl I and H I. Because the conversion of Cl II to
Cl I is faster than the photoionization of Cl I, Cl is primarily neutral in regions
where H2 is abundant but otherwise is primarily ionized (Jura & York 1978).
.
Furthermore, the observation
of significant Cl I requires at least a modest molecular hydrogen fraction. Indeed, in
regions where H2 is optically thick, Cl II reacts rapidly with H2 to form HCl+,
which in turn leads to Cl I and H I. Because the conversion of Cl II to
Cl I is faster than the photoionization of Cl I, Cl is primarily neutral in regions
where H2 is abundant but otherwise is primarily ionized (Jura & York 1978).
Finally, the derived upper limits on [N/S] and [N/Si] are at the upper end of the range of
N/![]() values measured in DLAs (see Table 9). They are close to the primary N
"plateau''.
values measured in DLAs (see Table 9). They are close to the primary N
"plateau''.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0273F11.ps}\end{figure}](/articles/aa/full/2004/10/aa0273/Timg127.gif) |
Figure 11:
The nucleosynthetic abundance pattern of the DLA at
|
| Open with DEXTER | |
The DLA toward Q2231-00 (Fig. 11) shows a solar [Si/Fe] ratio, but enhanced
[S/Zn, Fe] and [Ti/Zn, Fe] ratios (see Table 9). The S abundance was derived from a
single S II line located in the Ly![]() forest (see Sect. 3.3), and we believe
that it may be partly blended with H I clouds. The comparison of the dust-corrected absolute
abundances of Si and S, two
forest (see Sect. 3.3), and we believe
that it may be partly blended with H I clouds. The comparison of the dust-corrected absolute
abundances of Si and S, two ![]() -elements, shows further evidence for a slight overestimation
of the abundance of S, since [S/Si]
-elements, shows further evidence for a slight overestimation
of the abundance of S, since [S/Si]
![]() when the E00 dust correction is
applied. Although the adopted large error on the S abundance measurement takes into account
this slight overestimation, in Fig. 11 we scale the solar values to match the dust
corrected silicon metallicity, instead of the observed sulfur metallicity as done in
Figs. 9 and 10. The Ti abundance is also very difficult to
measure, thus it is very likely that it is overestimated, as already suspected in Sect. 5.1.
when the E00 dust correction is
applied. Although the adopted large error on the S abundance measurement takes into account
this slight overestimation, in Fig. 11 we scale the solar values to match the dust
corrected silicon metallicity, instead of the observed sulfur metallicity as done in
Figs. 9 and 10. The Ti abundance is also very difficult to
measure, thus it is very likely that it is overestimated, as already suspected in Sect. 5.1.
The Fe-peak elements, Fe, Ni and Cr, track very well each other, as observed in the Galactic stars
with similar metallicities (see Table 8). With the abundance measurement of the
Fe-peak element Mn, we highlight a rather pronounced odd-even effect in this DLA system, [Mn/Fe
![]() at [Fe/H]
at [Fe/H]
![]() .
Another odd-Z element detected in this
system is P. Only an upper limit on the [P/Si] abundance ratio is derived, [P/Si]
.
Another odd-Z element detected in this
system is P. Only an upper limit on the [P/Si] abundance ratio is derived, [P/Si]
![]() ,
which is potentially in line with an odd-even effect for P.
,
which is potentially in line with an odd-even effect for P.
The obtained [N/Si, S] upper limits (see Table 9) are again "high'', close to the
primary N "plateau''. We do not believe that the observed N I lines are heavily blended
with Ly![]() forest lines.
forest lines.
Until now the DLA galaxy population has been analyzed as a whole. Several chemical evolution models
were constructed in order to interpret the abundance patterns observed in DLAs as an ensemble,
considering them as an evolutionary sequence, i.e. objects caught in a different phase of their
evolution (e.g. Jimenez et al. 1999; Hou et al. 2001; Mathlin et al. 2001; Matteucci et al. 1997). However, several pieces of evidence
- like the low redshift deep imaging revealing a variety of morphological types belonging to the
DLA population (e.g. Nestor et al. 2002; Le Brun et al. 1997), the large scatter in the ![]() over Fe-peak
element abundance ratios at a given metallicity and the large scatter observed in the
metallicities - indicate that the DLAs trace galaxies with different star formation histories.
Some may have formed stars on timescales similar to that of the early Milky Way, while others
apparently did so more slowly or intermittently, so that the Fe-peak elements could catch up with
the
over Fe-peak
element abundance ratios at a given metallicity and the large scatter observed in the
metallicities - indicate that the DLAs trace galaxies with different star formation histories.
Some may have formed stars on timescales similar to that of the early Milky Way, while others
apparently did so more slowly or intermittently, so that the Fe-peak elements could catch up with
the ![]() -elements.
-elements.
Thanks to the large number of elements detected in the DLA systems studied in this paper, we are for the first time in a very appropriate situation to analyze these high redshift galaxies individually. The different elemental abundances at disposal allow us, in particular, to constrain the star formation history (hereafter SFH, and SF for the star formation) and the age of the associated galaxies by means of a direct comparison with a grid of chemical evolution models for spiral and dwarf irregular galaxies (see Calura et al. 2003) rather than just by means of a comparison with the solar abundance pattern as presented in Sect. 5.3. We present below the approach which has been applied. The derived results for the DLAs toward Q0100+13, Q1331+17 and Q2231-00 are summarized in Table 10.
Table 10: Nature of the galaxies associated with the DLA systems studied.
A chemical evolution model allows one to follow in detail the evolution of abundances of several chemical species, starting from the matter reprocessed by the stars and restored into the ISM through stellar winds and supernova explosions. Here we briefly summarize the major ingredients of the chemical evolutions models used in this work which we identify as "spiral'' and "dwarf irregular'' models according to the type of galaxies they do match best. These models are the same as the models used by Calura et al. (2003) in their study of the DLA nature. A detailed description of the "spiral'' model can be found in Chiappini et al. (2001,1997) and of the "dwarf irregular'' model in Bradamante et al. (1998) and Recchi et al. (2002,2001). In both models no instantaneous recycling approximation is adopted, namely the stellar lifetimes are properly taken into account.
The spiral galaxies are assumed to form as a result of two main infall episodes (Chiappini et al. 1997).
During the first episode the halo forms and the gas shed by the halo rapidly gathers in the center
leading to the formation of the bulge. During the second episode, a slower infall of external gas
gives rise to the disk with the gas accumulating faster in the inner than in the outer region
("inside-out'' scenario, Matteucci & François 1989). The process of disk formation is much longer than
the halo and bulge formation, with timescales varying from ![]() 2 Gyr in the inner disk to
2 Gyr in the inner disk to ![]() 7 Gyr in the solar region and up to 13 Gyr in the outer disk. In particular, a timescale of 7
Gyr in the solar neighborhood is required to fit the G-dwarf metallicity distribution
(Chiappini et al. 1997; Boissier & Prantzos 1999). The adopted SFR expression is:
7 Gyr in the solar region and up to 13 Gyr in the outer disk. In particular, a timescale of 7
Gyr in the solar neighborhood is required to fit the G-dwarf metallicity distribution
(Chiappini et al. 1997; Boissier & Prantzos 1999). The adopted SFR expression is:
![\begin{displaymath}\psi(R,t) = \nu [\frac{\sigma(R,t)}{\sigma(R_{\odot},t)}]^{2(...
...(R,t_{\rm Gal})}{\sigma(R,t)}]^{k-1} \sigma^{k}_{\rm gas}(R,t)
\end{displaymath}](/articles/aa/full/2004/10/aa0273/img139.gif) |
(1) |
Due to the "inside-out'' scenario and the threshold density adopted in the "spiral'' model, the SFH is different at different galactocentric radii. Indeed, in the inner regions of the disk
where the rate of accretion of matter onto the disk is fast, a high gas surface density, well above
the critical threshold, is reached and maintained during a long period, and hence the SF is
almost continuous through the galaxy lifetime. On the other hand, in the outer regions of the disk
(radius
![]() kpc) where the rate of accretion of matter onto the disk is slow, the SFH
proceeds in a gasping way, due to the fact that in these regions the gas is always close to the
critical threshold. As a consequence, the external regions of the disk look like the Magellanic
irregulars where this kind of SF seems to take place (Tosi et al. 1991). These different star formation
histories at different galactocentric radii are associated with different abundance patterns which
can be compared with observations.
kpc) where the rate of accretion of matter onto the disk is slow, the SFH
proceeds in a gasping way, due to the fact that in these regions the gas is always close to the
critical threshold. As a consequence, the external regions of the disk look like the Magellanic
irregulars where this kind of SF seems to take place (Tosi et al. 1991). These different star formation
histories at different galactocentric radii are associated with different abundance patterns which
can be compared with observations.
When comparing the "spiral'' model with our observations of DLA systems, we run a set of models
each of them corresponding to a different galactocentric radius R. This radius represents the
position at which the QSO line of sight crosses the disk of the observed DLA galaxy. Finally, we
need to constrain the formation redshift, ![]() ,
of the "spiral'' model, which is the single
free parameter.
,
of the "spiral'' model, which is the single
free parameter.
We adopt a model based on the work of Bradamante et al. (1998), in which the dwarf irregular galaxies
form owing to a continuous infall of pristine gas with an infall timescale of 0.5 Gyr, until a mass
of ![]() 109
109 ![]() is accumulated. The evolution of dwarf irregular galaxies is assumed to
be characterized by a bursting star formation history. This particular model was built to
reproduce the chemical properties of the local blue compact galaxies (BCGs). The parameters which
need to be defined in this model are the number of bursts of SF that the galaxy has undergone, and
for each burst, the star formation efficiency,
is accumulated. The evolution of dwarf irregular galaxies is assumed to
be characterized by a bursting star formation history. This particular model was built to
reproduce the chemical properties of the local blue compact galaxies (BCGs). The parameters which
need to be defined in this model are the number of bursts of SF that the galaxy has undergone, and
for each burst, the star formation efficiency, ![]() ,
(same definition as in the "spiral'' model),
the burst duration,
,
(same definition as in the "spiral'' model),
the burst duration, ![]() ,
and the time of occurrence of the burst,
,
and the time of occurrence of the burst, ![]() ,
i.e. the time
necessary for the infall of pristine gas before the SF starts. Hence, the star formation rate in
the "dwarf irregular'' model can proceed either in short bursts of a duration from 10 to 200 Myr
separated by long quiescent periods, or at a low regime but continuously, namely in one or two long
episodes of inefficient SF lasting between 3 and 13 Gyr. In this model, the adopted SFR is:
,
i.e. the time
necessary for the infall of pristine gas before the SF starts. Hence, the star formation rate in
the "dwarf irregular'' model can proceed either in short bursts of a duration from 10 to 200 Myr
separated by long quiescent periods, or at a low regime but continuously, namely in one or two long
episodes of inefficient SF lasting between 3 and 13 Gyr. In this model, the adopted SFR is:
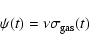 |
(2) |
The dwarf irregular galaxies are particularly sensitive to outflows resulting from the energy
injection from the SN explosions. Indeed, galactic winds develop when the thermal energy of the gas
equals its binding energy (Matteucci & Tornambé 1987). In the "dwarf irregular'' model used in this paper,
the rate of gas loss via galactic winds is assumed to be proportional to the SF, and the recent
chemodynamical results of Recchi et al. (2001), suggesting that the wind is differential, are adopted.
This implies that the ejecta of type Ia SNe and intermediate-mass stars are lost from the parent
galaxy more easily than type II SN ejecta, so that the Fe and N ejection efficiencies are larger
than the ejection efficiencies of ![]() -elements (e.g. O, Mg). This is due to the fact that
the type Ia SNe can transfer into the ISM more energy than the type II SNe, since they explode in
an already rarefied and hot medium. The IMF is taken from Salpeter (1955).
-elements (e.g. O, Mg). This is due to the fact that
the type Ia SNe can transfer into the ISM more energy than the type II SNe, since they explode in
an already rarefied and hot medium. The IMF is taken from Salpeter (1955).
For the comparison of the "dwarf irregular'' model with our observations of DLA systems, we assume
that these high redshift galaxies have undergone a single burst of SF. This can be justified
by the fact that the DLA galaxies are probably young galaxies. We thus need to essentially constrain
three free parameters, the burst star formation efficiency, ![]() ,
the burst duration,
,
the burst duration,
![]() ,
and the time of occurrence of the burst,
,
and the time of occurrence of the burst, ![]() .
.
We describe here the nucleosynthesis prescriptions adopted in both the "spiral'' and "dwarf
irregular'' models. They include the yields of Nomoto et al. (1997a) for massive stars (
![]() ), the yields of van den Hoeck & Groenwegen (1997) for low- and intermediate-mass stars (
), the yields of van den Hoeck & Groenwegen (1997) for low- and intermediate-mass stars (
![]() )
and the yields of Nomoto et al. (1997b) for type Ia SNe (model W7). For Zn and
Ni we consider the following specific prescriptions.
)
and the yields of Nomoto et al. (1997b) for type Ia SNe (model W7). For Zn and
Ni we consider the following specific prescriptions.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{0273F12.eps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg150.gif) |
Figure 12:
Observed and predicted [Ni/Fe] versus [Fe/H] distributions in the solar neighborhood for
two different nucleosynthetic prescriptions for the production of Ni. The dashed line
corresponds to the model with
|
| Open with DEXTER | |
The nucleosynthesis of Zn is a debated issue, since what process is making Zn is rather uncertain. According to stellar models, the production of Zn can ensue via s-processes in low- and high-mass stars during He-core burning as well as during explosive nucleosynthesis events occurring in type Ia and II SNe (Matteucci et al. 1993, and references therein). This uncertainty in the Zn production has repercussions on the reliability of Zn yields. In this paper we use the Zn yields adopted by Calura et al. (2003), which were estimated by extrapolating the Galactic star abundance observations in the solar neighborhood to the high redshift Universe, assuming Fe and Zn track each other as observed in the metallicity range where the DLAs lie (Prochaska et al. 2000; Mishenina et al. 2002).
The Ni yields have also some difficulties to reproduce the Galactic star abundance observations.
Therefore, similarly to Zn, we assumed for the Ni production the results of Matteucci et al. (1993), in
which a good fit to the solar abundance of Ni is found if the bulk of its production is ascribed to
type Ia SNe. However, since a non-negligible fraction of Fe also comes from type II SNe
(Nomoto et al. 1997a) and since the abundance of Fe seems to vary in lockstep with that of Ni in the
solar vicinity, the type II SNe should also produce some Ni. In our models the amount of Ni
produced through explosive nucleosynthesis in massive stars scales with the Fe yields, according to
![]() ,
where
,
where ![]() represents a multiplicative factor. We
have run a chemical evolution model for the solar vicinity varying
represents a multiplicative factor. We
have run a chemical evolution model for the solar vicinity varying ![]() in order to reproduce
the [Ni/Fe] versus [Fe/H] distribution observed in Galactic stars of different metallicities.
Figure 12 shows this [Ni/Fe] versus [Fe/H] distribution compared with the predictions
for the solar neighborhood model, when two values of
in order to reproduce
the [Ni/Fe] versus [Fe/H] distribution observed in Galactic stars of different metallicities.
Figure 12 shows this [Ni/Fe] versus [Fe/H] distribution compared with the predictions
for the solar neighborhood model, when two values of ![]() are adopted (dashed line:
are adopted (dashed line:
![]() ;
solid line:
;
solid line:
![]() ). The choice of
). The choice of
![]() gives a satisfactory agreement
between the predictions and the observations, in particular in the metallicity range occupied by
the DLAs ([Fe/H
gives a satisfactory agreement
between the predictions and the observations, in particular in the metallicity range occupied by
the DLAs ([Fe/H![]() ). For Ni produced in type Ia SNe, we assume a constant value
). For Ni produced in type Ia SNe, we assume a constant value
![]()
![]() .
.
To be able to constrain the star formation history of DLAs from the comparison of their abundance
patterns with chemical evolution models, we first need to understand how the abundance patterns can
provide information on the star formation history of galaxies. In few words, the absolute
abundances depend on the model assumptions (i.e. the SFH), whereas the relative abundances depend
only on the nucleosynthesis, the stellar lifetimes and the IMF. Relative abundances can therefore
be used as cosmic clocks if they involve two elements formed on different timescales, like it is the
case of the ![]() -element over Fe-peak element ratios and the N over
-element over Fe-peak element ratios and the N over ![]() -element ratios. As
a consequence, these abundance ratios when examined together with the absolute abundances [Fe/H],
or any other metallicity tracer such as [Zn/H], and [
-element ratios. As
a consequence, these abundance ratios when examined together with the absolute abundances [Fe/H],
or any other metallicity tracer such as [Zn/H], and [![]() /H], respectively, completely determine
the star formation history of a galaxy. On the other hand, when these abundance ratios are
examined as a function of the redshift, they provide constraints on the age of a galaxy,
defined as the epoch at which the galaxy has started to form stars (Matteucci 2001).
/H], respectively, completely determine
the star formation history of a galaxy. On the other hand, when these abundance ratios are
examined as a function of the redshift, they provide constraints on the age of a galaxy,
defined as the epoch at which the galaxy has started to form stars (Matteucci 2001).
The relative abundances that we have at disposal in the DLA systems studied here are [Si/Fe],
[S/Zn], [S/Fe], [Mg/Fe], [Ni/Fe], [N/Si] and [N/S]. For each DLA individually, we consider all of
them at once to first constrain the SFH and then the age of the associated galaxy by means of a
detailed comparison with a grid of chemical evolution models. This grid includes the "spiral''
model computed at different galactocentric radii from R = 2 to 18 kpc and the "dwarf irregular''
model computed for a single burst of SF with different characteristics defined by varying the three
free parameters ![]() ,
,
![]() and
and ![]() .
The adopted cosmology is
H0 = 65
km s-1 Mpc-1 (and hence h=0.65),
.
The adopted cosmology is
H0 = 65
km s-1 Mpc-1 (and hence h=0.65),
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=15.2cm,clip]{0273F13.eps}\end{figure}](/articles/aa/full/2004/10/aa0273/Timg156.gif) |
Figure 13:
Observed and predicted abundance ratios versus metallicity for the DLA at
|
| Open with DEXTER | |
To determine the best chemical evolution model reproducing the abundance patterns observed in each
DLA system by taking into account all the different informations available on the system, we use a
statistical test when the best solution cannot be clearly identified by eye. This test consists
first in determining the minimal distance between the data point and the curve of a given chemical
model in each abundance diagram at disposal. For this purpose, we consider the 1 ![]() error
on the data point (or more precisely the covariance matrix of the 1
error
on the data point (or more precisely the covariance matrix of the 1 ![]() measurement error),
and we derive this minimal distance by computing the distances di from the data point to the
points defining the considered model curve and by looking for the di for which the
di/
measurement error),
and we derive this minimal distance by computing the distances di from the data point to the
points defining the considered model curve and by looking for the di for which the
di/![]() ratio is minimal. Second, once the minimal distances for all the abundance
diagrams considered in each system and for a given model are derived, we compute their weighted
mean. Finally, the comparison of the weighted means obtained for different chemical models
determines the best chemical evolution model which represents the data points and thus the DLA
galaxy. The upper and lower limits are not taken into account in this test.
ratio is minimal. Second, once the minimal distances for all the abundance
diagrams considered in each system and for a given model are derived, we compute their weighted
mean. Finally, the comparison of the weighted means obtained for different chemical models
determines the best chemical evolution model which represents the data points and thus the DLA
galaxy. The upper and lower limits are not taken into account in this test.
To determine the nature of this DLA galaxy, we have five different abundance ratios at disposal.
We can thus try to constrain the best chemical evolution model which reproduces this DLA galaxy by
taking into account the information provided by the following five diagrams: [S/Zn] versus [Zn/H],
[S/Fe] versus [Fe/H], [Mg/Fe] versus [Fe/H], [Ni/Fe] versus [Fe/H] and [N/S] versus [S/H]. For the
absolute and relative abundances of refractory elements we consider the dust-corrected values as
derived with the dust correction method of
Vladilo (2002a,b). In
this DLA system, however, the dust corrections are small, since the [Zn/Fe] ratio is close to solar
(
![]() ).
).
![\begin{figure}
\par\includegraphics[width=15.2cm,clip]{0273F14.eps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg159.gif) |
Figure 14:
Observed and predicted abundance ratios versus redshift for the DLA at
|
| Open with DEXTER | |
We considered the "spiral'' model at the galactocentric radii
R = 6, 8, 12, and 18 kpc. The
"spiral'' model at R = 8 kpc best reproduces the five abundance ratios measured in this high
redshift galaxy (see the thick dashed-dotted curves in Fig. 13). We might be
satisfied with this solution, since the model curves are in agreement with the data points within
less than 1 ![]() in four out of the five diagrams. In the case of the Ni/Fe ratio, the model is
in agreement only within 2-3
in four out of the five diagrams. In the case of the Ni/Fe ratio, the model is
in agreement only within 2-3 ![]() .
But, to have a complete picture and to check the uniqueness
of the derived solution, we investigated whether a "dwarf irregular'' model can also correctly
reproduce the data points. We considered a "dwarf irregular'' model with a single burst of SF and
explored the following values for the three parameters characterizing the burst:
.
But, to have a complete picture and to check the uniqueness
of the derived solution, we investigated whether a "dwarf irregular'' model can also correctly
reproduce the data points. We considered a "dwarf irregular'' model with a single burst of SF and
explored the following values for the three parameters characterizing the burst:
![]() Gyr-1,
Gyr-1,
![]() Gyr and
Gyr and
![]() Gyr. The "dwarf irregular'' model which best reproduces the data points has one
burst with a star formation efficiency
Gyr. The "dwarf irregular'' model which best reproduces the data points has one
burst with a star formation efficiency ![]() Gyr-1 and a short duration
Gyr-1 and a short duration
![]() Gyr (see the thin solid curves in Fig. 13). The burst occurs after
Gyr (see the thin solid curves in Fig. 13). The burst occurs after
![]() Gyr
of continuous infall of pristine gas. These "dwarf irregular'' model characteristics very
well match the starburst parameters determined for the BCGs (e.g. Lanfranchi & Matteucci 2003). In
summary, two chemical evolution models yet tracing different star formation histories correctly
reproduce the abundance ratio versus metallicity distributions observed in the DLA toward Q0100+13.
The "spiral'' model at R = 8 kpc has a continuous SFH, whereas the "dwarf irregular'' model
constrained by the observations has a bursting SFH (see Sect. 6.1). The identification of
the best model among these two is very difficult, because at this intermediate metallicity both
models yield very similar chemical abundance patterns. The distinction is more pronounced at [Fe/H] < -2 or at [Fe/H] > -1.
Gyr
of continuous infall of pristine gas. These "dwarf irregular'' model characteristics very
well match the starburst parameters determined for the BCGs (e.g. Lanfranchi & Matteucci 2003). In
summary, two chemical evolution models yet tracing different star formation histories correctly
reproduce the abundance ratio versus metallicity distributions observed in the DLA toward Q0100+13.
The "spiral'' model at R = 8 kpc has a continuous SFH, whereas the "dwarf irregular'' model
constrained by the observations has a bursting SFH (see Sect. 6.1). The identification of
the best model among these two is very difficult, because at this intermediate metallicity both
models yield very similar chemical abundance patterns. The distinction is more pronounced at [Fe/H] < -2 or at [Fe/H] > -1.
![\begin{figure}
\par\includegraphics[width=15.2cm,clip]{0273F15.eps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg163.gif) |
Figure 15:
Observed and predicted abundance ratios versus metallicity for the DLA at
|
| Open with DEXTER | |
We carried out the investigation of the age of the system, namely the most likely redshift of
formation, ![]() ,
of the system, for the two models. For the "spiral'' model at R = 8 kpc, we
analyzed the [Zn/H], [Ni/Fe], [Mg/Fe], [S/Zn], [S/Fe] and [N/S] versus redshift diagrams. The
estimated redshift of formation is between
,
of the system, for the two models. For the "spiral'' model at R = 8 kpc, we
analyzed the [Zn/H], [Ni/Fe], [Mg/Fe], [S/Zn], [S/Fe] and [N/S] versus redshift diagrams. The
estimated redshift of formation is between
![]() -3 with the best solution being at
-3 with the best solution being at
![]() which is in excellent agreement with all the data points (see the thick dashed-dotted curves
in Fig. 14). The DLA system is observed at
which is in excellent agreement with all the data points (see the thick dashed-dotted curves
in Fig. 14). The DLA system is observed at
![]() ,
hence
,
hence
![]() corresponds to an age of the DLA galaxy of
corresponds to an age of the DLA galaxy of
![]() Gyr. In the case of the
"dwarf irregular'' model, the determination of the age is more complex, because this model has
several free parameters. The parameter having the lowest impact is the time of occurrence of the
burst,
Gyr. In the case of the
"dwarf irregular'' model, the determination of the age is more complex, because this model has
several free parameters. The parameter having the lowest impact is the time of occurrence of the
burst, ![]() ,
according to the adopted definition of the age (see Sect. 6.2). In
addition,
,
according to the adopted definition of the age (see Sect. 6.2). In
addition, ![]() is difficult to determine, whereas the star formation efficiency,
is difficult to determine, whereas the star formation efficiency, ![]() ,
and the
burst duration,
,
and the
burst duration, ![]() ,
can be robustly constrained by the observations. It is the burst
duration which has the largest weight in the determination of the age of the system. We
satisfactorily reproduce the data points (within 1
,
can be robustly constrained by the observations. It is the burst
duration which has the largest weight in the determination of the age of the system. We
satisfactorily reproduce the data points (within 1 ![]() )
for
)
for ![]() values between 0.05 and
0.20 Gyr. Hence, we feel confident in concluding that the possible age of the system is between
0.05-0.20 Gyr. Given the assumption that the galaxy has undergone a single burst of SF, the
corresponding redshift of formation is between 2.35-2.47.
values between 0.05 and
0.20 Gyr. Hence, we feel confident in concluding that the possible age of the system is between
0.05-0.20 Gyr. Given the assumption that the galaxy has undergone a single burst of SF, the
corresponding redshift of formation is between 2.35-2.47.
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{0273F16.eps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg166.gif) |
Figure 16:
Observed and predicted abundance ratios versus redshift for the DLA at
|
| Open with DEXTER | |
Both models point to a young age for the DLA galaxy, lower than 250 Myr. This age is consistent
with the ![]() -element over Fe-peak element enhancement observed in this DLA system (see
Sect. 5.3), which indicates that the enrichment of this system is dominated
by massive star products and requires a minimal contribution from type Ia SNe. In addition, we saw
in Sect. 5.3 that the N/S ratio in this DLA system is relatively high, very
close to the primary N "plateau'', [N/S
-element over Fe-peak element enhancement observed in this DLA system (see
Sect. 5.3), which indicates that the enrichment of this system is dominated
by massive star products and requires a minimal contribution from type Ia SNe. In addition, we saw
in Sect. 5.3 that the N/S ratio in this DLA system is relatively high, very
close to the primary N "plateau'', [N/S
![]() .
This N/S ratio and the estimated
age for the DLA galaxy provide important constraints on the N stellar progenitors. Indeed, such a
high N/S value can be reached within less than 250 Myr, only if N is produced by intermediate-mass
stars with masses between 5-8
.
This N/S ratio and the estimated
age for the DLA galaxy provide important constraints on the N stellar progenitors. Indeed, such a
high N/S value can be reached within less than 250 Myr, only if N is produced by intermediate-mass
stars with masses between 5-8 ![]() ,
which have lifetimes between 30 and 70 Myr, and by
massive stars. Chiappini et al. (2003) recently showed that the same chemical evolution models as those
used in this paper, but computed with the recent published stellar yields of Meynet & Maeder (2002) which
take into account the effects of rotation in the stellar evolution, still reproduce such high N/S
values within a timescale lower than 250 Myr.
,
which have lifetimes between 30 and 70 Myr, and by
massive stars. Chiappini et al. (2003) recently showed that the same chemical evolution models as those
used in this paper, but computed with the recent published stellar yields of Meynet & Maeder (2002) which
take into account the effects of rotation in the stellar evolution, still reproduce such high N/S
values within a timescale lower than 250 Myr.
We have collected a lot of information on this DLA system. The observed abundance ratios at our
disposal are [S/Zn], [S/Fe], [Si/Fe], [Mg/Fe], [Ni/Fe] and the upper limits on [N/S] and [N/Si].
This DLA system has a very high [Zn/Fe
![]() ratio and exhibits one of the largest dust
depletion level of any DLA. In Fig. 15 we can see the high differences between
the observed and dust-corrected values.
ratio and exhibits one of the largest dust
depletion level of any DLA. In Fig. 15 we can see the high differences between
the observed and dust-corrected values.
First, we examined the "spiral'' model at the galactocentric radii
R = 8, 12, 16 and 18 kpc.
The best model reproducing the data points in the [S/Zn] versus [Zn/H], [S/Fe] versus [Fe/H],
[Si/Fe] versus [Fe/H], [Mg/Fe] versus [Fe/H] and [Ni/Fe] versus [Fe/H] diagrams is the "spiral''
model of outer regions of the disk, at R = 16 kpc (see the thick dashed-dotted curves in
Fig. 15). The model curves are in excellent agreement with the data points within
less than 1 ![]() in the five diagrams. Secondly, we investigated the "dwarf irregular'' model
to check the uniqueness of the solution. We considered the "dwarf irregular'' model with a single
burst of SF and explored a large range of values for the three parameters characterizing the burst.
We found out that the "dwarf irregular'' model with a bursting SFH cannot reproduce the
observations, which show solar
in the five diagrams. Secondly, we investigated the "dwarf irregular'' model
to check the uniqueness of the solution. We considered the "dwarf irregular'' model with a single
burst of SF and explored a large range of values for the three parameters characterizing the burst.
We found out that the "dwarf irregular'' model with a bursting SFH cannot reproduce the
observations, which show solar ![]() -element over Fe-peak element ratios, because the bursting
SFH predicts
-element over Fe-peak element ratios, because the bursting
SFH predicts ![]() -enhanced patterns. On the other hand, the "dwarf irregular'' model with a
continuous SFH characterized by a single burst of SF with a star formation efficiency in the range
-enhanced patterns. On the other hand, the "dwarf irregular'' model with a
continuous SFH characterized by a single burst of SF with a star formation efficiency in the range
![]() -0.09 Gyr-1, with the best value being
-0.09 Gyr-1, with the best value being
![]() Gyr-1, and a duration
over the whole Hubble time satisfactorily reproduces the observations (see the thin solid curves in
Fig. 15).
Gyr-1, and a duration
over the whole Hubble time satisfactorily reproduces the observations (see the thin solid curves in
Fig. 15).
![\begin{figure}
\par\includegraphics[width=15.2cm,clip]{0273F17.eps}
\end{figure}](/articles/aa/full/2004/10/aa0273/Timg170.gif) |
Figure 17:
Observed and predicted abundance ratios versus metallicity for the DLA at
|
| Open with DEXTER | |
Again none of these two models having a different star formation history - the "spiral'' model of outer regions of the disk has a bursting SFH (see Sect. 6.1.1), while the "dwarf irregular'' model constrained by the observations has an inefficient continuous SFH - can be easily discarded, because they yield similar chemical abundance patterns due to the fact that they both are characterized by a weak SF. The Mg/Fe ratio could be used as a discriminant between the two models (see Fig. 15), but there are substantial uncertainties in the Mg yields (e.g. Chiappini et al. 1999).
We investigated the age of the DLA galaxy for the two models. For this purpose, we considered the
[Zn/H], [S/Zn], [S/Fe], [Si/Fe], [Mg/Fe] and [Ni/Fe] versus redshift diagrams. The range of
redshifts of formation determined for the "spiral'' model at R = 16 kpc is
![]() -3, with
the best solution being at
-3, with
the best solution being at
![]() (see the thick dashed-dotted curves in
Fig. 16). For the "dwarf irregular'' model with an inefficient continuous SF
rate, the estimated redshift of formation is large, roughly around
(see the thick dashed-dotted curves in
Fig. 16). For the "dwarf irregular'' model with an inefficient continuous SF
rate, the estimated redshift of formation is large, roughly around
![]() (see the thin
solid curves in Fig. 16). The DLA system is observed at
(see the thin
solid curves in Fig. 16). The DLA system is observed at
![]() ,
hence
,
hence
![]() and
and
![]() correspond to an age of the DLA galaxy of
correspond to an age of the DLA galaxy of
![]() Gyr and
Gyr and ![]() 3.5 Gyr, respectively.
3.5 Gyr, respectively.
According to the recent WMAP results, the reionization seems to have occurred at a redshift
considerably higher than what was thought previously, namely at
![]() (Bennett et al. 2003). Therefore, if the intergalactic medium has been reionized by the first stars
formed in very young galaxies, a redshift of the order of 10 could be reasonable for the appearance
of the first galactic structures in the Universe. The derived solution that the associated galaxy
with the DLA system at
(Bennett et al. 2003). Therefore, if the intergalactic medium has been reionized by the first stars
formed in very young galaxies, a redshift of the order of 10 could be reasonable for the appearance
of the first galactic structures in the Universe. The derived solution that the associated galaxy
with the DLA system at
![]() toward Q1331+17 may be a dwarf irregular galaxy with a
continuous SFH formed at
toward Q1331+17 may be a dwarf irregular galaxy with a
continuous SFH formed at
![]() thus is possible. The solution that the associated galaxy is
a spiral galaxy with the QSO line of sight crossing the outer regions of its disk at R=16 kpc and
an age of 1.5 Gyr is also plausible. Both models point to a large age for this DLA galaxy. This
reflects the long timescale necessary to accrete the gas as well as to reach the observed solar
thus is possible. The solution that the associated galaxy is
a spiral galaxy with the QSO line of sight crossing the outer regions of its disk at R=16 kpc and
an age of 1.5 Gyr is also plausible. Both models point to a large age for this DLA galaxy. This
reflects the long timescale necessary to accrete the gas as well as to reach the observed solar
![]() -element over Fe-peak element ratios (see Sect. 5.3) which require a
substantial contribution from type Ia SNe, releasing the Fe-peak elements only after 108-109
yrs. But, both models fail in reproducing the measured [N/S] and [N/Si] upper limits, since they
predict almost solar [N/S, Si] ratios at [S, Si/H]
-element over Fe-peak element ratios (see Sect. 5.3) which require a
substantial contribution from type Ia SNe, releasing the Fe-peak elements only after 108-109
yrs. But, both models fail in reproducing the measured [N/S] and [N/Si] upper limits, since they
predict almost solar [N/S, Si] ratios at [S, Si/H]
![]() .
Such high N/
.
Such high N/![]() values at
these low metallicities have never been observed in any DLA and H II region. This suggests
that the yields of van den Hoeck & Groenwegen (1997) may lead to an overestimation of the N production by
intermediate-mass stars at the lower end of masses and by low-mass stars, which had time to release
N in this DLA galaxy, given the inferred long age. In the case of the N production by massive
intermediate-mass stars, the yields of van den Hoeck & Groenwegen (1997) are more reliable.
values at
these low metallicities have never been observed in any DLA and H II region. This suggests
that the yields of van den Hoeck & Groenwegen (1997) may lead to an overestimation of the N production by
intermediate-mass stars at the lower end of masses and by low-mass stars, which had time to release
N in this DLA galaxy, given the inferred long age. In the case of the N production by massive
intermediate-mass stars, the yields of van den Hoeck & Groenwegen (1997) are more reliable.
In this system, the measured abundance ratios at disposal are [S/Zn], [S/Fe], [Si/Fe], [Ni/Fe], and
the upper limits on [N/Si] and [N/S]. We consider the dust-corrected values, since non-negligible
dust corrections are required in this system with [Zn/Fe]
![]() .
We first investigated
the "spiral'' model to reproduce the [S/Zn] versus [Zn/H], [S/Fe] versus [Fe/H], [Si/Fe] versus
[Fe/H] and [Ni/Fe] versus [Fe/H] diagrams. The favored "spiral'' model turned out to be the one
representing the inner regions of the galactic disk, i.e. at galactocentric radii R<8 kpc. In
the inner regions of the disk compared to the outer regions, the infall of external gas is faster
and leads to higher gas densities, and hence to a more efficient SF (see Sect. 6.1.1). The
.
We first investigated
the "spiral'' model to reproduce the [S/Zn] versus [Zn/H], [S/Fe] versus [Fe/H], [Si/Fe] versus
[Fe/H] and [Ni/Fe] versus [Fe/H] diagrams. The favored "spiral'' model turned out to be the one
representing the inner regions of the galactic disk, i.e. at galactocentric radii R<8 kpc. In
the inner regions of the disk compared to the outer regions, the infall of external gas is faster
and leads to higher gas densities, and hence to a more efficient SF (see Sect. 6.1.1). The
![]() -elements thus are more enhanced relative to the Fe-peak elements at metallicities [Fe/H]
< -1.5 dex in the inner regions of the disk than in the outer regions. Despite this, the
"spiral'' model of inner regions of the disk does not succeed in reproducing all the measured data
points (see the thick dashed-dotted curves in Fig. 17). It mainly fails in
correctly reproducing the [S/Zn] versus [Zn/H] and [S/Fe] versus [Fe/H] data points, and the [N/Si]
versus [Si/H] and [N/S] versus [S/H] upper limits.
-elements thus are more enhanced relative to the Fe-peak elements at metallicities [Fe/H]
< -1.5 dex in the inner regions of the disk than in the outer regions. Despite this, the
"spiral'' model of inner regions of the disk does not succeed in reproducing all the measured data
points (see the thick dashed-dotted curves in Fig. 17). It mainly fails in
correctly reproducing the [S/Zn] versus [Zn/H] and [S/Fe] versus [Fe/H] data points, and the [N/Si]
versus [Si/H] and [N/S] versus [S/H] upper limits.
We then considered the "dwarf irregular'' model. We assumed a single burst of SF and explored the
following values for the three free parameters characterizing the burst: ![]() -5.0 Gyr-1,
-5.0 Gyr-1,
![]() Gyr and
Gyr and
![]() Gyr. The "dwarf irregular'' model
which best reproduces the data points has one burst with a very high star formation efficiency
Gyr. The "dwarf irregular'' model
which best reproduces the data points has one burst with a very high star formation efficiency ![]() Gyr-1 and a duration
Gyr-1 and a duration
![]() Gyr (see the thin solid curves in
Fig. 17). The burst occurs after
Gyr (see the thin solid curves in
Fig. 17). The burst occurs after
![]() Gyr of continuous infall of pristine
gas. This model is the favored one in comparison with the "spiral'' model of inner regions of the
disk. It reproduces at 1
Gyr of continuous infall of pristine
gas. This model is the favored one in comparison with the "spiral'' model of inner regions of the
disk. It reproduces at 1 ![]() all the abundance ratios. Only the [N/S] upper limit is at odds.
all the abundance ratios. Only the [N/S] upper limit is at odds.
We investigated the age of the DLA galaxy assuming the constrained "dwarf irregular'' model. As in
the case of the DLA toward Q0100+13, the parameter having the highest impact in the age
determination is the duration of the burst. We feel confident in assuming an age between
0.05-0.15 Gyr, corresponding to the range of values explored for ![]() .
This yields a
redshift of formation between 2.10-2.16 given the assumption that the galaxy has undergone a
single burst of SF.
.
This yields a
redshift of formation between 2.10-2.16 given the assumption that the galaxy has undergone a
single burst of SF.
The star formation is a key parameter in the formation and evolution of galaxies. Therefore, the
knowledge of the star formation rate (SFR) of galaxies is very important. Kennicutt (1983)
provided the first precise diagnostics for the measure of the SFR, such as emission-line fluxes and
UV continuum luminosities. Later Madau et al. (1996) reconstructed the cosmic star formation history
by measuring the comoving luminosity density of star-forming galaxies as a function of redshift.
While the original work of Madau et al. (1996) showed a peak in the cosmic star formation at
![]() -2, recent results, based on larger samples of galaxies and corrections for dust extinction of
the emitted starlight, do not show such a peak. The SFR per unit comoving volume increases by a
factor of
-2, recent results, based on larger samples of galaxies and corrections for dust extinction of
the emitted starlight, do not show such a peak. The SFR per unit comoving volume increases by a
factor of ![]() 10 in the redshift interval z = [0,1], and then either remains constant at z>1
up to z=6 (Steidel et al. 1999) or keeps increasing to even higher redshifts
(Lanzetta et al. 2002; Calura & Matteucci 2003). However, the galaxies from which these results are derived are
unlikely to be representative of the bulk of the galaxy population in the Universe. Indeed, whereas
the SFR per unit area for the Milky Way is
10 in the redshift interval z = [0,1], and then either remains constant at z>1
up to z=6 (Steidel et al. 1999) or keeps increasing to even higher redshifts
(Lanzetta et al. 2002; Calura & Matteucci 2003). However, the galaxies from which these results are derived are
unlikely to be representative of the bulk of the galaxy population in the Universe. Indeed, whereas
the SFR per unit area for the Milky Way is
![]()
![]() yr-1 kpc-2 (Kennicutt 1998), the comoving SFR at
yr-1 kpc-2 (Kennicutt 1998), the comoving SFR at ![]() 3 is inferred from Lyman-break galaxies,
a highly luminous population of star-forming objects in which
3 is inferred from Lyman-break galaxies,
a highly luminous population of star-forming objects in which
![]()
![]() yr-1
kpc-2 (Pettini et al. 2001). As a result, the existing measurements of the cosmic star
formation history take into account the contribution of only highly luminous and star-forming
galaxies. The access to the star formation rates in other types of galaxies thus is crucial.
yr-1
kpc-2 (Pettini et al. 2001). As a result, the existing measurements of the cosmic star
formation history take into account the contribution of only highly luminous and star-forming
galaxies. The access to the star formation rates in other types of galaxies thus is crucial.
The DLA galaxy population is ideal for this purpose. Indeed, these objects sample various types of galaxies over a large range of lookback times (see Sects. 6.2.1-6.2.3), since they are detected independently of their distance, luminosity and SFH. In addition, because the DLAs are not drawn from a flux limited sample of galaxies, we are able to derive the SFR values below those determined from radiation emitted by star-forming galaxies. Recently, Wolfe et al. (2003b,a) provided the first estimations of SFRs per unit area in DLAs. Their technique to infer the SFRs consists in determining the rate at which the neutral gas in DLAs is heated.
In this work, we also have access to the SFRs of DLAs. Indeed, in the case of the "spiral'' model
the SFR per unit area is a direct output of the model, and in the case of the "dwarf irregular''
model the different physical quantities correspond to the absolute values, thus to derive the SFR
per unit area we assume a spherical symmetry and a galactic radius of 5 kpc. The derived star
formation rates per unit area for the DLAs studied are given in Table 11, and are between
![]()
![]() yr-1 kpc-2. They were obtained for the models
constrained in the previous sections (Sects. 6.2.1-6.2.3). They correspond in
the case of the "spiral'' model to the SFR that the DLA galaxy has at the time of its observations
and in the case of the "dwarf irregular'' model to the average SFR integrated over the time of the
burst of SF, i.e. over the period when the SF is active. The errors on the derived SFRs are very
difficult to estimate. Our SFR measurements are in agreement with the interval of SFR values
obtained by Wolfe et al. (2003b,a)
yr-1 kpc-2. They were obtained for the models
constrained in the previous sections (Sects. 6.2.1-6.2.3). They correspond in
the case of the "spiral'' model to the SFR that the DLA galaxy has at the time of its observations
and in the case of the "dwarf irregular'' model to the average SFR integrated over the time of the
burst of SF, i.e. over the period when the SF is active. The errors on the derived SFRs are very
difficult to estimate. Our SFR measurements are in agreement with the interval of SFR values
obtained by Wolfe et al. (2003b,a)![]() in DLAs using
a completely different technique. We thus confirm that the SFRs per unit area in DLAs are moderate
and similar to that measured in the Milky Way disk.
in DLAs using
a completely different technique. We thus confirm that the SFRs per unit area in DLAs are moderate
and similar to that measured in the Milky Way disk.
Table 11: Determination of the star formation rates.
The damped Ly![]() systems are our best laboratory to study the high redshift galaxies. Indeed,
accurate chemical abundances of these systems can be obtained over a large interval of cosmic time,
and they thus offer the best opportunity to track the chemical evolution of galaxies in the
Universe. The DLA galaxy population has until now been analyzed as a whole and chemical evolution
models were constructed in order to interpret the abundance patterns of these objects as an
ensemble, considering them as an evolutionary sequence. However, several pieces of evidence show
that the DLAs likely trace galaxies of different types and with different evolutionary histories.
At this stage of knowledge, one would like to define more precisely the star formation histories
and the chemical evolution stages sampled by these objects. Therefore, we aimed at constructing a
sample of DLAs for which one would be able to constrain the star formation history, the age and the
star formation rate of each system individually. For this purpose, it is first imperative to obtain
comprehensive sets of elemental abundances.
systems are our best laboratory to study the high redshift galaxies. Indeed,
accurate chemical abundances of these systems can be obtained over a large interval of cosmic time,
and they thus offer the best opportunity to track the chemical evolution of galaxies in the
Universe. The DLA galaxy population has until now been analyzed as a whole and chemical evolution
models were constructed in order to interpret the abundance patterns of these objects as an
ensemble, considering them as an evolutionary sequence. However, several pieces of evidence show
that the DLAs likely trace galaxies of different types and with different evolutionary histories.
At this stage of knowledge, one would like to define more precisely the star formation histories
and the chemical evolution stages sampled by these objects. Therefore, we aimed at constructing a
sample of DLAs for which one would be able to constrain the star formation history, the age and the
star formation rate of each system individually. For this purpose, it is first imperative to obtain
comprehensive sets of elemental abundances.
By combining our UVES-VLT spectra of a sample of four DLAs in the redshift interval
![]() toward the quasars Q0100+13, Q1331+17, Q2231-00 and Q2343+12 with the existing HIRES-Keck
spectra, we covered the total optical spectral range from 3150 to 10 000 Å for the four quasars.
Thanks to this large wavelength coverage and the high quality of the spectra, we succeeded in
measuring the column densities of up to 21 ions, namely of 15 elements - N, O, Mg, Al, Si, P, S,
Cl, Ar, Ti, Cr, Mn, Fe, Ni, Zn. With the detections of adjacent ions of the same element, such
as Al+/Al++, Fe+/Fe++ and N0/N+, and of the Ar/Si, S ratios, we
constrained the photoionization effects, which may affect the DLA gas-phase abundances. Our analysis
revealed that the DLA toward Q2343+12 requires important ionization corrections, while in the three
other DLAs the ionization corrections are negligible. With the detection of both refractory and
mildly/non-refractory elements of the same nucleosynthetic origin, we evaluated the dust depletion
effects and computed the dust corrections using the method of Vladilo (2002a,b). The
dust corrections are particularly important in the DLA toward Q1331+17. This system with [Zn/Fe
toward the quasars Q0100+13, Q1331+17, Q2231-00 and Q2343+12 with the existing HIRES-Keck
spectra, we covered the total optical spectral range from 3150 to 10 000 Å for the four quasars.
Thanks to this large wavelength coverage and the high quality of the spectra, we succeeded in
measuring the column densities of up to 21 ions, namely of 15 elements - N, O, Mg, Al, Si, P, S,
Cl, Ar, Ti, Cr, Mn, Fe, Ni, Zn. With the detections of adjacent ions of the same element, such
as Al+/Al++, Fe+/Fe++ and N0/N+, and of the Ar/Si, S ratios, we
constrained the photoionization effects, which may affect the DLA gas-phase abundances. Our analysis
revealed that the DLA toward Q2343+12 requires important ionization corrections, while in the three
other DLAs the ionization corrections are negligible. With the detection of both refractory and
mildly/non-refractory elements of the same nucleosynthetic origin, we evaluated the dust depletion
effects and computed the dust corrections using the method of Vladilo (2002a,b). The
dust corrections are particularly important in the DLA toward Q1331+17. This system with [Zn/Fe
![]() exhibits one of the largest dust depletion level of any DLA. The constraint of
both the photoionization and dust depletion effects allowed us to determine relatively robust intrinsic chemical abundance patterns of three out of the four DLAs studied.
exhibits one of the largest dust depletion level of any DLA. The constraint of
both the photoionization and dust depletion effects allowed us to determine relatively robust intrinsic chemical abundance patterns of three out of the four DLAs studied.
The intrinsic chemical abundance patterns are the signature of the star formation history of
galaxies, which one needs to correctly interpret. For this purpose, we called on the chemical
evolution models for spiral and dwarf irregular galaxies (see Calura et al. 2003). By comparing
these models with the distributions of the abundance ratios of two elements produced on different
timescales as a function of the metallicity we can constrain the star formation history of a DLA
galaxy, and with the distributions of the same abundance ratios considered as a function of the
redshift we can constrain the age of a galaxy. The access to several abundance ratios, [S/Zn],
[S/Fe], [Si/Fe], [O/Zn], [Mg/Fe], [Ni/Fe], [N/S], [N/Si] and [N/O], in the same DLA allowed us for
the first time to determine the star formation history and the age of three DLA systems. We were
also able to estimate the star formation rates per unit area of the DLAs, since the SFR is a direct
output of the chemical evolution models, once they are constrained. Our results show that the galaxy
associated with the DLA toward Q0100+13 is either a spiral galaxy showing similar characteristics
as those observed in the solar neighborhood (![]() kpc) or a dwarf irregular galaxy with a
single burst of SF with properties similar to the ones observed in the BCGs. It is a young galaxy
with an age of
kpc) or a dwarf irregular galaxy with a
single burst of SF with properties similar to the ones observed in the BCGs. It is a young galaxy
with an age of
![]() Myr or between 50-200 Myr, respectively. The galaxy associated with
the DLA toward Q1331+17 is very likely a spiral galaxy observed in the outer regions of its disk
(
Myr or between 50-200 Myr, respectively. The galaxy associated with
the DLA toward Q1331+17 is very likely a spiral galaxy observed in the outer regions of its disk
(![]() kpc) and
kpc) and
![]() Gyr old. But, it can also well be a dwarf irregular galaxy with
an inefficient continuous SFH and an age
Gyr old. But, it can also well be a dwarf irregular galaxy with
an inefficient continuous SFH and an age ![]() 3.5 Gyr. Finally, the galaxy associated with the
DLA toward Q2231-00 is a dwarf irregular galaxy with a single intense burst of SF and an age
between 50-150 Myr. The estimated star formation rates per unit area of these three objects are
between
3.5 Gyr. Finally, the galaxy associated with the
DLA toward Q2231-00 is a dwarf irregular galaxy with a single intense burst of SF and an age
between 50-150 Myr. The estimated star formation rates per unit area of these three objects are
between
![]()
![]() yr-1 kpc-2. They are in agreement with the
values obtained by Wolfe et al. (2003b,a) in DLAs using a different technique, and similar to
the SFR per unit area measured in the Milky Way disk.
yr-1 kpc-2. They are in agreement with the
values obtained by Wolfe et al. (2003b,a) in DLAs using a different technique, and similar to
the SFR per unit area measured in the Milky Way disk.
This work shows that the DLAs studied may either be associated with the outer regions of disks of
spiral galaxies (![]() kpc) or with dwarf irregular galaxies with bursting or continuous star
formation histories. Observed at redshifts
kpc) or with dwarf irregular galaxies with bursting or continuous star
formation histories. Observed at redshifts
![]() -2.5, they may be very young galaxies
with ages between 50-250 Myr, but also galaxies with ages larger than >1.5 Gyr. Although
this work needs to be extended to a larger sample of DLA systems to be representative of the overall
population of DLAs at high redshift, we can already derive a number of conclusions. Our limited
sample is centered at
-2.5, they may be very young galaxies
with ages between 50-250 Myr, but also galaxies with ages larger than >1.5 Gyr. Although
this work needs to be extended to a larger sample of DLA systems to be representative of the overall
population of DLAs at high redshift, we can already derive a number of conclusions. Our limited
sample is centered at ![]() ,
a redshift region where spectroscopic data on light-emitting
galaxies just start to become available. We do not find any association of DLAs with episodes of
massive star formation, the derived star formation rates per unit area are moderate. Clearly this
is not the standard scenario, and we cannot exclude this possibility for all objects in the DLA
sample. Actually there is an indication of a recent massive burst of star formation in at least the
DLA at
,
a redshift region where spectroscopic data on light-emitting
galaxies just start to become available. We do not find any association of DLAs with episodes of
massive star formation, the derived star formation rates per unit area are moderate. Clearly this
is not the standard scenario, and we cannot exclude this possibility for all objects in the DLA
sample. Actually there is an indication of a recent massive burst of star formation in at least the
DLA at
![]() toward Q0347-3819 (Levshakov et al. 2002; Dessauges-Zavadsky et al. 2002b). The DLAs at
toward Q0347-3819 (Levshakov et al. 2002; Dessauges-Zavadsky et al. 2002b). The DLAs at
![]() do not appear to be associated with a homogeneous population of galaxies, neither in
terms of star formation history (morphological type) and age. This result is in agreement with the
studies of DLAs at low redshifts (z<1) where different types of galaxies have been shown to be
the optical counterparts (e.g. Nestor et al. 2002; Le Brun et al. 1997). Our results confirm once again that
simple plots of DLA abundances versus redshift cannot be used to estimate the overall metal
evolution of the Universe, because the local parameters (as determined by the star formation history
of the associated galaxy) would dominate the scatter in the measurements. We plan to extend our
comparison of the DLA abundance patterns with chemical evolution models in 2004 to additional 5 objects for which the data have already been acquired.
do not appear to be associated with a homogeneous population of galaxies, neither in
terms of star formation history (morphological type) and age. This result is in agreement with the
studies of DLAs at low redshifts (z<1) where different types of galaxies have been shown to be
the optical counterparts (e.g. Nestor et al. 2002; Le Brun et al. 1997). Our results confirm once again that
simple plots of DLA abundances versus redshift cannot be used to estimate the overall metal
evolution of the Universe, because the local parameters (as determined by the star formation history
of the associated galaxy) would dominate the scatter in the measurements. We plan to extend our
comparison of the DLA abundance patterns with chemical evolution models in 2004 to additional 5 objects for which the data have already been acquired.
Acknowledgements
The authors wish to extend special thanks to all people working at ESO/Paranal for the high quality of the UVES spectra obtained in service mode. We are grateful to G. Meynet for useful discussions and to A. M. Wolfe for interesting comments. We particularly thank C. Chiappini for many interesting advises and for her help to clarify important points. M.D.-Z. is supported by the Swiss National Funds. This work has partly been done during M.D.-Z. ESO studentship and has benefited of the support from the European Commission Research and Training Network "The Physics of the Intergalactic Medium''.