A&A 415, 1-7 (2004)
DOI: 10.1051/0004-6361:20034587
F. De Paolis 1 - A. Geralico 1,2 - G. Ingrosso 1 - A. A. Nucita 1 - A. Qadir3,4
1 -
Dipartimento di Fisica, Università di Lecce, and INFN,
Sezione di Lecce, via Arnesano, CP 193, 73100 Lecce, Italy
2 -
International Center for Relativistic Astrophysics - ICRA,
University of Rome "La Sapienza'', 00185 Roma, Italy
3 -
Department of Mathematics, Quaid-i-Azam University, Islamabad,
Pakistan
4 - Department of Mathematical Sciences, King Fahd
university of Petroleum and Minerals, Dhahran 31261, Saudi Arabia
Received 14 May 2003 / Accepted 17 October 2003
Abstract
Gravitational lensing is a well known phenomenon
predicted by the General Theory of Relativity. It is now a
well-developed observational technique in astronomy and is
considered to be a fundamental tool for acquiring information
about the nature and distribution of dark matter. In particular,
gravitational lensing experiments may be used to search for black
holes. It has been proposed that a Schwarzschild black hole may
act as a retro-lens (Holz & Wheeler 2002) which, if
illuminated by a powerful light source (e.g. the Sun), deflects
light ray paths to large bending angles so that the light may
reach the observer. Here, by considering the strong field limit
in the deflection angle and confining our analysis to the black
hole equatorial plane, we extend the Holz-Wheeler results to
slowly spinning Kerr black holes. By considering the Holz-Wheeler
geometrical configuration for the lens, source and observer we
find that the inclusion of rotation does not substantially change
the brightness of the retro-lensing images with respect to the
Schwarzschild case. We also discuss the possibility that the next
generation space-based telescopes may detect such retro-images and
eventually put limits on the rotational parameter of the black
hole.
Key words: gravitation - gravitational lensing
Gravitational lensing of electromagnetic waves is a well-understood phenomenon (see e.g. Schneider et al. 1992 for a comprehensive treatment) predicted by the theory of General Relativity. In the last years, gravitational lensing has been also used as an observational tool to investigate the mass distribution both in galaxy clusters (using distant QSOs as sources, Canizares 1982) and in galactic halos. In the latter case, the phenomenon, which is called gravitational microlensing, led to the discovery of Massive Astrophysical Compact Halo Objects (MACHOs) in the halo of our Galaxy (Alcock et al. 1993; Aubourg et al. 1993).
As a dark object moves across the source-observer line of sight it
acts as a gravitational lens leading to the formation of two
unresolved images of the source and to an overall source light
magnification. Despite the low probability of observing such
events, Paczynsky (1986) showed that the continuous
observation of at least ![]() 106 stars implies a
non-negligible chance of detecting a microlensing event towards
the LMC.
106 stars implies a
non-negligible chance of detecting a microlensing event towards
the LMC.
Since the early 1990s several collaborations (MACHO (see e.g.
Alcock et al. 1993), EROS (Aubourg et al.
1993) and OGLE (Stanek et al. 1995)) have
been monitoring millions of stars towards the LMC, the SMC, as
well as towards the galactic center detecting hundreds of
microlensing events due to MACHOs along the line of sight.
Unfortunately, the physical nature of MACHOs is still unknown,
since the observed light curves of a microlensing event can be
reproduced by models depending on a number of free parameters
(mass, distance and transverse velocity of the lens). So,
different populations of objects such as brown dwarfs, white
dwarfs, main sequence stars and black holes may be consistent with
microlensing observations. In particular, it is generally accepted
that a population of black holes may exist in the Galaxy and it
has been claimed that these compact objects have already been
detected in microlensing surveys (Quinn et al. 1999;
Bennett et al. 2002; Agol et al. 2002). At least
6 extremely long events detected by the MACHO, GMAN and MPS
collaborations towards the galactic bulge (Bennett et al.
2002) exhibit very strong microlensing parallax signals
which lead to mass estimates up to ![]()
![]() .
Since
the estimated upper limits on the absolute lens brightness are
always less than
.
Since
the estimated upper limits on the absolute lens brightness are
always less than ![]()
![]() ,
this favors the stellar
black hole hypothesis (Mao et al. 2002) and suggests that a
substantial fraction of the galactic lenses may be massive stellar
remnants.
,
this favors the stellar
black hole hypothesis (Mao et al. 2002) and suggests that a
substantial fraction of the galactic lenses may be massive stellar
remnants.
Despite some experimental uncertainties, the theory of
gravitational lensing, which was originally developed in the weak
field approximation, has successfully explained all gravitational
lensing observations from the giant blue luminous arcs in the rich
cluster of galaxies (Lynds & Petrosian 1989; Soucail et al.
1987) to the first Einstein ring MG 1131+0456 at redshift
![]() (Hewitt et al. 1988) to microlensing
events detected towards the SMC, LMC, the galactic bulge and the
M 31 galaxy (see e.g. Alcock et al. 2000).
(Hewitt et al. 1988) to microlensing
events detected towards the SMC, LMC, the galactic bulge and the
M 31 galaxy (see e.g. Alcock et al. 2000).
Moreover, by using the next generation of high resolution imaging telescopes, it would be possible to test the theory of gravitational lensing in the presence of strong gravitational fields since the inspection of the images formed will allow us to investigate regions very close to the surface of compact massive objects such as neutron stars and black holes.
In a very interesting paper Holz & Wheeler (2002) proposed
that a Schwarzschild black hole may act as retro-lens or
retro-MACHO. This means that if the black hole is illuminated by a
powerful light source, photons, due to its strong gravitational
field, can be deflected by large bending angles. In the case of
perfect alignment of source, black hole and Earth (with the Earth
in the middle), the bending angles are odd multiples of ![]() leading to a series of circular rings.
leading to a series of circular rings.
However, black holes would be characterized by a non-zero intrinsic angular momentum, which breaks the Schwarzschild spherical symmetry and affects the gravitational field around the compact object. Thus, we expect a modification in the phenomenology of the gravitational lensing. Here, we investigate the retro-lensing phenomenon for slowly rotating Kerr black holes considering photon trajectories close to the black hole equatorial plane. Our treatment follows the second order expansion (given by Bozza 2003) of the large deflection angles of light rays winding around the retro-MACHO in the impact parameter b.
This paper is structured as follows. In Sect. 2 we briefly review the Schwarzschild retro-MACHO lensing results obtained by Holz & Wheeler (2002). In Sect. 3 we extend the Holz & Wheeler (2002) results to Kerr black holes. In Sect. 4 we investigate different geometries among the lens, the source and the observer and discuss the possibility that the next generation high resolution telescopes may have the capabilities necessary to detect such lensing events.
In gravitational microlensing, photons from a distant source
suffer a very small angular deflection and the weak field
approximation always works satisfactorily. However, strong field
effects may be extremely important if the lens is a collapsed
compact object. In fact, very close to a neutron star or a black
hole, GR plays an important role and the study of the relativistic
images which form (as a consequence of light deflection) allows us
to investigate the regions close to the event horizon. The light
bending angle in the presence of a static black hole is not
limited to small angles but may reach large values (![]() and odd
multiples of
and odd
multiples of ![]() if source, observer and retro-MACHO are
perfectly aligned, see Holz & Wheeler 2002) so that photons
emerge in the direction of the source itself. Therefore, a
Schwarzschild black hole, if illuminated by a powerful light
source, shines back with a series of micro-arcsecond rings.
if source, observer and retro-MACHO are
perfectly aligned, see Holz & Wheeler 2002) so that photons
emerge in the direction of the source itself. Therefore, a
Schwarzschild black hole, if illuminated by a powerful light
source, shines back with a series of micro-arcsecond rings.
In the case of perfect alignment between the source, the observer and the lens the image of the source, in the plane orthogonal to the line of sight and containing the source, is an annulus with outer and inner radii corresponding to the appropriate impact parameters for photons coming from the top and bottom parts of the source.
However, in the general case the source, the observer and the
black hole are not aligned. We consider a reference frame centered
at the source S and with axes X and Y on the Earth orbital
plane (see Fig. 1). We choose Y to contain the lens
in the Z-Y plane and define the misalignment angle ![]() as
the angle between the observer-lens direction
(
as
the angle between the observer-lens direction
(
![]() )
and the Y axis. Note that the case with
)
and the Y axis. Note that the case with
![]() and Earth in the orbit position O corresponds to
perfect alignment.
and Earth in the orbit position O corresponds to
perfect alignment.
As the Earth moves on its orbit, the image rings deform into arcs
whose angular extent is
![]() ,
where
,
where
![]() is the
angle between the source-observer and observer-lens
(
is the
angle between the source-observer and observer-lens
(
![]() and
and
![]() )
directions, respectively.
)
directions, respectively.
The total area of each image is thus given by (Holz & Wheeler
2002)
The amplification of each image is given by the ratio between the
area of the image given by Eq. (1) to that of the
source
![]() ,
i.e.
,
i.e.
At this stage, we only need to evaluate the photon impact
parameter values ![]() and
and ![]() so that light rays coming from
the source are deflected toward the observer.
so that light rays coming from
the source are deflected toward the observer.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{figgeometria.ps}
\end{figure}](/articles/aa/full/2004/07/aa3977/Timg41.gif) |
Figure 1:
The geometry of a
retro-lensing event is shown in the case of a general
configuration for the lens, source and observer positions. Photons
emitted by the Sun S, in the center of the reference frame, move
towards the retro-MACHO L (a Schwarzschild or a Kerr black hole)
which, for simplicity, is placed on the Z-Y plane. Light rays,
which interact with the black hole strong gravitational field, may
suffer a path deflection to bending angle multiples of |
| Open with DEXTER | |
The expected light curves (i.e. magnitudes m corresponding to a
certain amplification ![]() as a function of time) for a
retro-lensing event due to a Schwarzschild black hole are shown in
Fig. 2 for different misalignment angles
as a function of time) for a
retro-lensing event due to a Schwarzschild black hole are shown in
Fig. 2 for different misalignment angles ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,height=5.5cm,clip]{plot0rot.ps}
\end{figure}](/articles/aa/full/2004/07/aa3977/Timg49.gif) |
Figure 2:
The expected visual magnitude mof the arcs forming close to a
|
| Open with DEXTER | |
The results by Holz & Wheeler (2002) on retro-lensing events hold in the case of Schwarzschild black holes. However, in general, a black hole is characterized by a non-zero intrinsic angular momentum which breaks the spherical symmetry and affects the gravitational field around the compact object.
Indeed, black holes are the ultimate stage of stellar evolution and may form by SNII explosions. Since stars rotate, angular momentum conservation implies that black holes also rotate. Black hole rotation is also confirmed by recent X-ray observations of Fe line width (Zakharov et al. 2002). Moreover, super massive black holes at the center of QSOs, AGNs and galaxies show beamed jet emission implying that they have non zero angular momentum.
Thus, due to black hole angular momentum J, we expect a
modification in the phenomenology of both the usual gravitational
lensing and the retro-MACHO microlensing. Such modifications are
evaluated by a second order expansion of the photon deflection
angles in the spin parameter
![]() .
Here,
.
Here,
![]() is the black hole Schwarzschild radius
is the black hole Schwarzschild radius![]() . We consider light trajectories
on the black hole equatorial plane and a more general treatment
will be addressed elsewhere (Zakharov et al. 2003).
However, we expect that the maximal effect due to the black hole
spin occurs for photons lying in the equatorial plane while for
partially inclined orientations the effect becomes closer to the
Schwarzschild case (that is recovered for
. We consider light trajectories
on the black hole equatorial plane and a more general treatment
will be addressed elsewhere (Zakharov et al. 2003).
However, we expect that the maximal effect due to the black hole
spin occurs for photons lying in the equatorial plane while for
partially inclined orientations the effect becomes closer to the
Schwarzschild case (that is recovered for ![]() ).
).
A simple and reliable method to investigate the subject has been recently proposed by Bozza (2003) (for an exhaustive review of the topics see also Bozza 2002a) who revisited the Schwarzschild and Kerr black hole lensing in a strong gravitational field.
Considering light rays on the black hole equatorial plane
(
![]() ), the Kerr line element in Boyer-Lindquist
coordinates (t, x,
), the Kerr line element in Boyer-Lindquist
coordinates (t, x, ![]() ,
,
![]() )
is given by
)
is given by
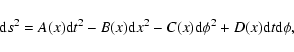 |
(8) |
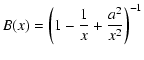 |
|||
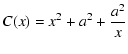 |
|||
| (9) |
Following Bozza (2003) the impact parameter b of light
rays approaching the black hole is
After a straightforward calculation, the whole deflection angle
(i.e. the bending angle for a photon with impact parameter b) is
given by
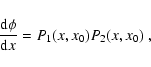 |
(12) |
| R(z,x0) | = | ||
| f(z,x0) | = | P2(x,x0) . | (15) |
![\begin{figure}
\par\includegraphics[width=7.8cm,height=5.7cm,clip]{photonsphere.ps}
\end{figure}](/articles/aa/full/2004/07/aa3977/Timg72.gif) |
Figure 3:
The radius of the
photosphere as a function of the black hole spin parameter a is
shown. As expected, for positive values of a (i.e. for light
rays co-rotating with the black hole) photons are allowed to get
closer to the black hole. For
|
| Open with DEXTER | |
Once the photosphere radius xm (for a given value of a) is
known, one can evaluate the deflection angle ![]() from Eq. (14). Thus, retaining only terms up to
O(x0-xm), one obtains
from Eq. (14). Thus, retaining only terms up to
O(x0-xm), one obtains
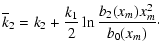 |
(21) |
![\begin{figure}
\par$\begin{array}{c} \includegraphics[width=7cm,height=5.7cm,cli...
...ncludegraphics[width=7.4cm,height=5.7cm,clip]{bbarra.ps}\end{array}$\end{figure}](/articles/aa/full/2004/07/aa3977/Timg84.gif) |
Figure 4:
The coefficients
|
| Open with DEXTER | |
Therefore, by solving Eq. (20) with respect to the
impact parameter b, one finally obtains the generalization
of the Chandrasekhar relation for Schwarzschild black holes given
in Eq. (6) to Kerr black holes
We are now ready to apply this formalism to the retro-lensing
phenomenon. In Fig. 5, assuming
![]() ,
we
plot the impact parameter
,
we
plot the impact parameter ![]() as a function of the black hole
spin parameter a. As one can see, for co-rotating photons
(a>0) the impact parameters decreases with respect to the
Schwarzschild case (i.e. photons may get closer to the black
hole).
as a function of the black hole
spin parameter a. As one can see, for co-rotating photons
(a>0) the impact parameters decreases with respect to the
Schwarzschild case (i.e. photons may get closer to the black
hole).
![\begin{figure}
\par\includegraphics[width=7.7cm,height=5.7cm,clip]{parametroimpatto.ps}
\end{figure}](/articles/aa/full/2004/07/aa3977/Timg89.gif) |
Figure 5:
The impact parameter
b, evaluated for the deflection angle
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{graficototale01.ps}
\end{figure}](/articles/aa/full/2004/07/aa3977/Timg90.gif) |
Figure 6:
The expected
retro-lensing light curves for a Kerr black hole with mass
|
| Open with DEXTER | |
Let us now consider the Sun as the light source and a black hole
of mass
![]() at a distance of 0.01 pc. Since the solar
luminosity in the optical band is
at a distance of 0.01 pc. Since the solar
luminosity in the optical band is
![]() erg s-1, corresponding to an optical visual
magnitude
erg s-1, corresponding to an optical visual
magnitude
![]() ,
the expected magnitude m of the
retro-lensed image can be evaluated as
,
the expected magnitude m of the
retro-lensed image can be evaluated as
| (24) |
In the case of a Kerr black hole we can evaluate the Sun image
amplification by using Eqs. (3)-(5),
in the most favorable case of perfect alignment (![]() ). For
this purpose we only need to evaluate, through Eq.
(22), the impact parameters corresponding
to the bending angles for which light rays emitted by the Sun may
reach the observer after deflection of the angles
). For
this purpose we only need to evaluate, through Eq.
(22), the impact parameters corresponding
to the bending angles for which light rays emitted by the Sun may
reach the observer after deflection of the angles
![]() and
and
![]() defined in Sect. 2. For a
defined in Sect. 2. For a
![]() Kerr
black hole with spin parameter a=0.1 at a distance of 0.01 pc
and misalignment angle
Kerr
black hole with spin parameter a=0.1 at a distance of 0.01 pc
and misalignment angle ![]() ,
the expected retro-lensing
light curve is given in Fig. 6 (red solid line). In
the same figure we also give the light curve (dashed red line)
corresponding to counter-rotating photons. As expected, for a Kerr
black hole with spin parameter a, only a modification up to the
second order in the retro-MACHO amplification appears, as is
evident by inspecting Fig. 6 where the lightcurves for
the Kerr black hole case are reported (dashed and solid red lines)
together with the corresponding one for a Schwarzschild black hole
with the same mass and
,
the expected retro-lensing
light curve is given in Fig. 6 (red solid line). In
the same figure we also give the light curve (dashed red line)
corresponding to counter-rotating photons. As expected, for a Kerr
black hole with spin parameter a, only a modification up to the
second order in the retro-MACHO amplification appears, as is
evident by inspecting Fig. 6 where the lightcurves for
the Kerr black hole case are reported (dashed and solid red lines)
together with the corresponding one for a Schwarzschild black hole
with the same mass and ![]() (central black solid line)
(central black solid line)![]() . We also notice that we have neglected multiple rotations
of the photons around the black hole. As emphasized by Holz &
Wheeler (2002), photons may form a series of deformed rings
corresponding to deflection angles that differ by
. We also notice that we have neglected multiple rotations
of the photons around the black hole. As emphasized by Holz &
Wheeler (2002), photons may form a series of deformed rings
corresponding to deflection angles that differ by ![]() (with
n as integer number). However, it is clear that the brightest
image is that corresponding to the outermost ring (obtained for
(with
n as integer number). However, it is clear that the brightest
image is that corresponding to the outermost ring (obtained for
![]() )
so that neglecting the other images does not
change substantially the retro-lensing image brightness.
)
so that neglecting the other images does not
change substantially the retro-lensing image brightness.
It has been shown by Holz & Wheeler (2002) that the limiting
distance ![]() at which the rings around a black hole of mass Milluminated by our Sun can be observed is given by
at which the rings around a black hole of mass Milluminated by our Sun can be observed is given by
![\begin{displaymath}\bar{m}\geq m_{\lambda} -2.5\log
\left[1.04\left(\frac{M}{M_{...
...}}\right)
\frac{D_{\rm OS}^2}{D_{\rm LS}D_{\rm OL}^2}\right]~,
\end{displaymath}](/articles/aa/full/2004/07/aa3977/img107.gif) |
(27) |
As is clear from Fig. 6, the spin effect on the image brightness is a minor effect and so it cannot increase substantially the image amplification with respect to the Schwarzschild black hole case. Moreover, as already stated, our analysis is confined to photons lying in the black hole equatorial plane and the retro-lensing image magnitude is calculated by using Eq. (4). This equation is rigorously valid only in the Schwarzschild case since it assumes that each part of the image is isoluminous (and this is not true for Kerr black holes). However, if we limit the estimate to only the total magnitude of the retro-lensing images, we do not expect a substantial change with respect to the Schwarzschild case since the increase in the luminosity of the corotating edge should approximately compensate the luminosity decrease of the counter-rotating edge.
We emphasize again that our treatment is valid only for slowly rotating black holes but it is clear that increasing the rotation parameter a, the brightness of the retro-lensing images also increases. A complete (purely numerical) treatment of this issue - valid for arbitrarily fast rotating black holes - will be published elsewhere (De Paolis et al. 2003b).
Since in the slow rotation limit the light curves are almost indistinguishable from the Schwarzschild case, the most important effect of the black hole spin is that of deforming the ring shape with respect to the Schwarzschild case (Peter 1976; Bray 1986). A detailed analysis of this effect will be presented elsewhere (Zakharov et al. 2003). Detecting the shape of the ring images might give a unique possibility of investigating the black hole parameters (spin a, mass M and relative position of observer-lens-black hole) in an active way.
To really observe the ring shape, the detecting instrument must
have a high enough angular resolution in the range 1-10 ![]() arcsec for most cases of interest. Future space-based
instruments like the Space Interferometry Mission (SIM) (see Shao
1998 for technical details), GAIA Satellite (see e.g.
Belokurov & Evans 2002), FAME (Johnston et al.
2000) and MAXIM (2003) would have the angular
resolution capabilities to resolve such images and therefore will
be able to observe retro-MACHOs if the instrumental limiting
magnitude satisfies Eq. (26).
arcsec for most cases of interest. Future space-based
instruments like the Space Interferometry Mission (SIM) (see Shao
1998 for technical details), GAIA Satellite (see e.g.
Belokurov & Evans 2002), FAME (Johnston et al.
2000) and MAXIM (2003) would have the angular
resolution capabilities to resolve such images and therefore will
be able to observe retro-MACHOs if the instrumental limiting
magnitude satisfies Eq. (26).