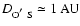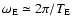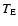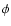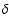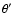Of course, since the observer moves around the Sun on a circular orbit of radius $D_{\rm O\hbox{$^\prime$ }S}\simeq 1~{\rm AU}$ with angular velocity $\omega _{\rm E}\simeq 2\pi/T_{\rm E}$ (being $T_{\rm E}$ the orbital period), the Earth position angle $\phi$ and the angles $\delta$ and $\theta \hbox{$^\prime$ }$ (see Fig. 1) are time dependent.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Note that the definition we use for the rotation parameter acorresponds to half of the value in the usual notation 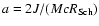$a=2J/(McR_{\rm Sch})$ . Indeed, following Bozza (2003) we measure distances in units of the Schwarzschild radius and not in units of the gravitational radius as is usually done (see e.g. Shapiro & Teukolsky 1983).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... line)

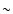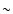Co-rotating and counter-rotating photons should produce an image scintillation due to their relative time delay. However, the time scale for such scintillations goes from $\sim$ 10^-5 s to $\sim$ 10 s for black holes with mass in the range 1 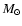$M_{\odot}$ -10⁶ M 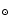$_{\odot}$ . Due to the short scintillation time scale with respect to the integration time required by observation, the net result is simply that of seeing the average, which coincides with the light curve for the Schwarzschild black hole.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Earth

It has been shown that the best chance of observing retro-lensing images in the future is by looking towards the galactic center black hole in Sgr A^* around which a very bright star (named S2) with a mass of about 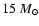$15~M_{\odot}$ is orbiting. The resulting magnitude of the retro-lensing images in the Schwarzschild case are in the range 33.3-36.8 (depending on the star distance from the black hole) in the K-band, close to the limiting magnitude of the next generation of space-based telescopes (De Paolis et al. 2003a).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.