A&A 415, 63-76 (2004)
DOI: 10.1051/0004-6361:20034122

Disk-bulge decompositions of spiral galaxies in UBVRI

C. Möllenhoff

Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany

Received 28 July 2003 / Accepted 20 October 2003

Abstract
A sample of 26 bright spiral galaxies ( ${B_{\rm tot}} < 12.7$) with low to medium inclination and without a bar was observed with UBVRI filters. The CAFOS focal reducer camera at the Calar Alto 2.2 m telescope was used. The surface-brightness distributions were fitted using a 2-dimensional algorithm with corresponding functions for the disk- and bulge-structure. For the disks an exponential function was used, for the bulges a Sérsic $R^{\beta}$ law, was applied with the concentration parameter $\beta = 1/n$ as another fit variable. Correlations of the resulting structural parameters of disks and bulges in UBVRI are investigated, giving clues to the formation history of the bulges.

We confirm that the large and bright bulges of early-type spirals are similar to elliptical galaxies. They were probably formed prior to the disks in a monolithic collapse or via early mergers. Late-type spirals have tiny and faint bulges with disk-like profiles. These bulges were probably formed after the disk in secular evolution processes, e.g. from a disk instability. The comparison of the color indices of corresponding spirals and bulges with population synthesis computations support above formation scenarios.

Key words: galaxies: spiral - galaxies: structure - galaxies: photometry - galaxies: fundamental parameters - galaxies: statistics - galaxies: formation

   
1 Introduction

   
1.1 Disk-bulge decompositions

The study of the the surface-brightness (SB) distribution is an important tool for a better understanding of spiral galaxies. The resulting structural parameters like disk scale-length, bulge effective radius, bulge/disk-ratio, color indices, etc. allow conclusions about the evolution of disks and bulges (for comprehensive reviews see e.g. Okamura 1988; Andredakis & Sanders 1994; Baggett et al. 1998; MacArthur et al. 2003). The morphological description of galaxies depends on the filter during observation, thus the intrinsic structural parameters will also vary with wavelength due to the color-dependent stellar populations and dust extinction effects. Thus, multi-wavelength information is required for a thorough description of the structural parameters. In this study the visual bands U, B, V, R, and I are used.

Table 1: The observed 26 spiral galaxies with some basic parameters. The Hubble types were taken from the Carnegie Atlas of Galaxies (Sandage & Bedke 1994). The column $B_{{\rm tot_o}}$ gives the extinction-corrected B magnitudes taken from RC3. The inclination $= {\rm arc cos}(b/a)$ stems from the V-fit in this paper (cf. $Q_{\rm d} = b/a$ in Table 2). The galactic extinction $A_{\rm g}(B)$, the internal extinction $A_{\rm i}(B)$, and the radial velocities $v_{\rm 3k}$ with respect to the 3K background were also taken from RC3. The determination of the distances and their references are explained in the text. The exposure times for the UBVRI images are given in seconds. NGC 1232 and 1288 were observed with the ESO VLT1 Antu (see text).

   
1.2 Sérsic profiles for the bulges

The radial surface-brightness (SB) profiles of the disks are usually described by an exponential function (e.g. Freeman 1970; Grosbøl 1985; Courteau 1996). The structure of the bulges is not so clear (Carollo et al. 1999). In former times the bulges were considered to be similar to elliptical galaxies and their SB profiles were described by a de Vaucouleurs R^1/4 function. In more recent work (Andredakis et al. 1995; Graham et al. 1996; Graham 2001; Möllenhoff & Heidt 2001, Paper I; MacArthur et al. 2003) it was found that the bulges are better described by a more general profile in a form proposed by Sérsic (1968): $F_{\rm bulge}(R) = I_{\rm s} \: \exp( -(R/R_{\rm s})^{\beta})$. Here $I_{\rm s}$ is the central flux density, $R_{\rm s}$ is a radial scale length, and the real number exponent $\beta$ (many authors use $1/n = \beta$ instead) determines the slope of the projected bulge SB distribution.

Andredakis et al. (1995) realized from K-band observations that the light profiles of bulges change systematically with the morphological types. The exponent $\beta$ varies from $\approx$0.25 for early-type spirals to $\approx$1 for late-type spirals, i.e. from a de Vaucouleurs to an exponential profile. This result has been confirmed by a number of authors in visual and near infrared (NIR) filters. (de Jong 1996a; Moriondo et al. 1998; Graham 2001, Paper I; MacArthur et al. 2003; Knapen et al. 2003).

   
1.3 Contents of this paper

In this study we intend to confirm and extend the structural relations between bulges and disks of spiral galaxies in 5 visual bands. Images in UBVRI of a sample of 26 spiral galaxies of different Hubble type with low or medium inclination were exposed. A focal reducer was used to get well-determined sky backgrounds. Two-dimensional model functions were fitted to the whole surface-brightness distribution. To get reliable photometric parameters, the fit procedure for each galaxy was accompanied by extensive different tests. The resulting structural parameters of the different galaxies were correlated, leading to general relations concerning the structure and evolution, especially of the bulges.

The paper is organized as follows. Section 2 describes the sample of the observed spiral galaxies and the determination of the distances. Sections 3 and 4 describe the observations, the data reduction, and the photometric calibrations. In Sect. 5 we present the two-dimensional method for a simultaneous fit of the whole surface-brightness (SB) distribution with a disk and a bulge. Section 6 describes the results and comparisons with other authors. Section 7 describes the results in dependence on color UBVRI. In Sect. 8 we show correlations and statistics of the structural parameters of disks and bulges. Sections 9 and 10 describe the photometric results. Section 11 compares the observed color indices with population synthesis calculations. In Sect. 12 we discuss the results and draw some conclusions.

   
2 The sample of spiral galaxies

   
2.1 Selection of the sample of galaxies

The observed sample of galaxies comprises 26 spirals with ${B_{\rm tot}} < 12.7$, of Hubble type Sa...Sc, and without strong bar, selected from the Revised Shapley-Ames Catalog (Sandage & Tammann 1981). Table 1 lists the observed galaxies, some basic parameters, and the exposure times for the five filters. The Hubble types were taken from Sandage & Bedke (1994) and transformed into the T-classes according to RC3 (de Vaucouleurs et al. 1991). $B_{\rm tot}$ and $v_{3\rm K}$ (radial velocity with respect to the 3K background) were taken from RC3. The distance determinations are described in the following subsection. Figure 1 shows the number and luminosity distribution of the sample galaxies over over Hubble types. The late-type spirals are slightly predominant due to our selection criterion ${B_{\rm tot}} < 12.7$, which prefers blue (late type) galaxies.

   
2.2 Distance determinations

The determination of the distances is crucial to obtain reliable scale lengths in kpc from the fit results in arcsec. We used different approaches for distance determinations, they are marked by a corresponding abbreviation in the column "Dist.Ref.'' of Table 1.

The most reliable distances exist for the calibrator galaxies with Cepheid distances from the HST key project (Freedman et al. 2001; Macri et al. 2001) Our galaxies with such distance determinations are marked with hst in Table 1. The revised distance to the Virgo cluster was determined in this way to 15.30 Mpc ($\it vir$).

For all other galaxies we used different sources from the literature and reduced them all to a common Hubble constant $H_{0} = 72 \pm 8$ km s^-1 Mpc^-1which is the optimum value from the HST key project (Freedman et al. 2001). In a first step the galaxy distances were calculated from the radial velocities by Tully (1988) or Tully et al. (1992), who considered the group kinematics of the galaxies (tul). These values were compared with the distances which Bottinelli et al. (1984, 1985, 1986, 1988) obtained from 21-cm line-widths via a revised B-band Tully-Fisher relation (bot). Tully and Bottinelli et al. have many galaxies in common. The distances from both authors are remarkably similar, so we used their mean values for those galaxies ($b\&t$). Finally, the SIMBAD databank was searched for dedicated papers on distances (sim). Sharina et al. (1996) determined the distance of NGC 628.

   
3 Observations

The observations were performed during March 2-7, 2000 at the 2.2 m telescope at the Calar Alto Observatory, Spain. The CAFOS focal reducer was used changing the focal ratio of the telescope from f/8 to f/4.4. The CCD camera was equipped with a SITE $2048 \times 2048$ pixel chip. The pixel size was 24$\mu$, corresponding to 0.53 arcsec. The circular field-of-use had a diameter of 16 arcmin. Standard Johnson U, B, V and Cousins R, I Filters were used. The exposure times in UBVRI are listed in Table 1.

	Figure 1: Distribution of the number of sample galaxies and their $B_{{\rm tot_o}}$ luminosities over Hubble types.
Open with DEXTER

Sky flats were exposed in every dawn and dusk phase. Furthermore, exposures of two empty fields in the night sky were obtained in all filters using the same exposure times as for the galaxies.

Photometric calibrations were performed every night, using stars in the open cluster NGC 2264 and the globular cluster NGC 2419 (Christian et al 1985; Racine & Harris 1975). The photometric quality of 3 nights was good or very good. One night was not photometric due to cirrus clouds. The non-photometric exposures of some galaxies through cirrus clouds make no problems for the geometrical parameters like scale-lengths, etc. In order to obtain reliable photometric data for those galaxies, additional, shortly exposed calibration images were obtained during a photometric night.

The observations of NGC 1232 and NGC 1288 were done in 1998 during the commissioning phase of the FORS focal reducer at the ESO VLT1 (Antu). For details see Möllenhoff et al. (1999).

   
4 Data reduction

The MIDAS program system was used for the data reduction. From comparison and evaluation of all bias exposures an optimal working bias image was constructed. Similarly, from comparison and evaluation of all flat-field exposures optimal working flat-field images were constructed for each color. Bias subtraction and flat-field division were performed in the usual manner. Then the images were flux-calibrated using the standard stars and were extinction-corrected. Values for the galactic-foreground extinction $A_{\rm g}(B)$ were taken from RC3 (as described in Burstein & Heiles 1984). The internal extinction in each galaxy $A_{\rm i}(B)$ is statistically dependent on the inclination and on the Hubble type. A corresponding interpolation formula was also taken from the RC3 (de Vaucouleurs et al. 1991). The extinction corrections for the other filters were computed by the coefficients given in Cardelli et al. (1989) (their Table 3). Since the K-corrections are very small they were not considered,

The flatness of the sky was checked in each image and corrected interactively, if necessary. The flatness of the sky down to less than 0.5% is an important condition for a reliable model of the surface-brightness distribution.

   
5 Two-dimensional fits to the SB distribution

   
5.1 Equations for the flux distribution

Instead of studying one-dimensional profiles it is advantageous to perform a two-dimensional fit to the whole two-dimensional surface-brightness distribution (Byun & Freeman 1995; de Jong 1996a; Moriondo et al. 1998; Wadadekar et al. 1999; Möllenhoff & Heidt 2001, Paper I; MacArthur et al. 2003). Two-dimensional surface-brightness functions for disk and bulge were fitted simultaneously to the observed flux distribution. For the radial flux distribution of the inclined disk we assumed the exponential law

$$F_{\rm disk}(R) = I_{\rm d} \: \exp( -R/R_{\rm d})$$ (1)

where $I_{\rm d}$ is the central flux density and $R_{\rm d}$ the radial scale-length. The disk was assumed to be thin and axisymmetric. This corresponds to the projected elliptical geometry

$$(x \cos({\rm PA_{d}}) + y \sin({\rm PA_{d}}))^2 / {Q_{\rm d}}^2 + (y \cos({\rm PA_{d}}) - x \sin({\rm PA_{d}}))^2$$ (2)

where $\rm PA_d$ is the position angle of the major axis measured counterclockwise from North, $Q_{\rm d} = b/a$ is the axis ratio, and $i = {\rm arccos}(b/a)$ is the inclination of the disk. Thus we have 4 free parameters for the disk: $I_{\rm d}, \: R_{\rm d}, \: {\rm PA_d}, \: Q_{\rm d}$.

For the flux distribution of the bulge we assumed the generalized exponential radial density law of Sérsic (1968) written in the form (Caon et al. 1993):

$$F_{\rm bulge}(R) = I_{\rm eff} \: \exp\left( -b_{\rm e} [(R/R_{\rm eff})^{\beta} - 1] \right),$$

$$b_{\rm e} = 1.9986/{\beta} - 0.327 \: \approx \: 2n - 0.33.$$ (3)

Here $R_{\rm eff}$ is the half-light or effective radius and $I_{\rm eff}$ is the flux density at $R_{\rm eff}$, the effective surface-brightness. The three-dimensional shape of the bulge was assumed to be spheroidal or triaxial, thus the projected shape in the sky is elliptical. Using a similar expression as Eq. (2) for the radius R we obtain the position angle ${\rm PA}_b$ and the ellipticity Q_b as further parameters for the bulge. Thus we have 5 free parameters for the bulge: $I_{\rm eff}, \: R_{\rm eff}, \: \beta, \: {\rm PA}_b, \: Q_{b}$.

   
5.2 Technical procedure of the fit

Fitting the total flux $F_{\rm tot} = F_{\rm disk} + F_{\rm bulge}$ simultaneously to the observed two-dimensional SB distribution results in a nonlinear system of equations for the 4 + 5 = 9 free parameters. A Levenberg-Marquardt algorithm was used for the solution of this system (e.g. Bevington & Robinson 1992). No inner or outer truncation radii for disk or bulge were adopted (for a discussion cf. MacArthur et al. 2003).

Several technical steps were necessary as prerequisites for the fit: Most images were cut to $1000 \times 1000$ pixels. For the larger objects like NGC 3031 we used the whole image of $2048 \times 2048$ pixels with a mask adapted to the circular field of view. The images were centered to the same world coordinates. The stars were marked interactively in the V image and were removed in all 5 colors. The center of the galaxy was measured in each image and the functions of Sect. 5.1 were fitted to the whole image. An ellipse fit to the isophotes in R yielded a rough guess for the start values of the parameters in the Levenberq-Marquardt iteration. Normally the fits was started in the I image, then using the results as start value for the R fit, etc., for V, B, and U. In order to ensure that the optimal model was found, the fit procedures were repeated starting from totally different start values, with slightly modified sky values, etc.

   
5.3 PSF and seeing

The atmospheric turbulence (seeing) distorts the SB profile of the galaxies, especially in the central region where the slope is steep. Therefore the seeing has a big influence especially on the bulge profile. The two-dimensional point spread function (PSF) was determined from several stars in each image and was approximated by an (elliptical) two-dimensional Gauss function. This PSF function was convolved with the SB model-function in each iteration step. The convolved SB fit model was then compared with the observed SB distribution and the control parameter $\chi^2$ was computed.

   
5.4 Error estimates

The fit procedures and their stability were tested extensively with artificial galaxies, including photon noise and seeing convolution. The statistical errors from the $\chi^2$-minimization can be computed from the curvature matrix in the Levenberg-Marquardt algorithm and are very small. The relevant errors here are systematic errors: e.g. non-correct sky-subtraction, non-uniformness of the sky, errors in the determination of the seeing point-spread-function. To estimate the error contributions of these effects, artificial galaxy images with typical sky levels, shot noise and seeing convolution were fitted with our 2-dim models. The sky level and the PSF were artificially set to different, slightly wrong values and the effect to the photometric parameters was studied.

An upper limit for the accuracy of the sky determination is $\approx$2%. This leads to errors for $R_{\rm d}$ and $R_{\rm eff}$ of $\approx$4%, for $I_{\rm d}$, $I_{\rm eff}$ and $\beta$ of $\approx$2%, and for the bulge/disk-ratio of $\approx$10%. A pessimistic estimate of the accuracy for the PSF determination of $\approx$10% leads to errors in above parameters of half the size. Thus we conclude that the errors due to inaccurate sky levels or PSF determinations are about $\approx$5% for the basic photometric parameters and $\approx$12% for the bulge/disk-ratios. Larger errors may result from irregular perturbations of the light distribution in the galaxies like asymmetric arms, bright star formation knots, etc. The size of such errors is dependent on the morphological perturbations in each individual galaxy.

We did not consider any external truncation radius of the galaxies (cf. Pohlen et al. 2000; Florido et al. 2001). An estimate of the corresponding errors was obtained by the fit of truncated artificial galaxies with our non-truncating algorithm. For a truncation radius of $R_{\rm trunc}/R_{\rm d} = 3, 4, 5$ we obtained for $I_{\rm d}$ and $I_{\rm eff}$ errors of $\approx$20, 6, 0.5%, and for $R_{\rm d}$ and $R_{\rm eff}$ errors of $\approx$13, 3, 0.3%, respectively.

   
6 Results of the fits to the galaxy images

   
6.1 Examples of galaxy images, fit models and residuum images

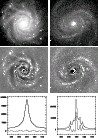Figure 2: Examples of fits of different qualities to Sc galaxies. Top row: V-images of NGC 3938 and NGC 4321. The size is 500 pix or 265 arcsec. Center row: corresponding two-dimensional residuum-images. The residuum of NGC 4321 shows bright star-formation knots in the bulge region. Bottom row: horizontal cuts through galaxy- (solid line), model- (dotted line), and residuum-image (bottom solid line).

Open with DEXTER

The left column of Fig. 2 demonstrates results of a good two-dimensional fit-procedure using the Sc-galaxy NGC 3938 as an example. The top image shows the central section of the V image. The stars are still included, they were removed before the fit. The center image shows the corresponding two-dimensional residuum, i.e. the difference (galaxy-model). While the arms produce positive (white) residua, the inter-arm regions produce negative (black) residua. The sky is around zero (grey). This example for a good fit produces a generally smooth and symmetric residuum image. For the important quantitative view the bottom diagram shows a horizontal cut through galaxy NGC 3938 V (solid line), model (dotted line), and residuum (bottom solid line). For a better visibility only the central 100 pixels are shown. The bottom residual line is near to an ideal line at zero level.

The right column of Fig. 2 demonstrates the results of the two-dimensional fit-procedure of the Sc-galaxy NGC 4321. This was one of the most problematic cases. It is already visible in the V image (top) that this galaxy has an especially bright central region (bulge). In the central residuum image very conspicuous bright knots appear in the bulge region. They are due to a number of bright star formation (SF) regions, arranged in a ring. These bright knots are of course also clearly visible in the one-dimensional cuts (bottom image). The two-dimensional fit searches an optimal smooth flux distribution for the bulge region, without considering these fluctuations on small spatial scales. The residual line shows the corresponding humps. Nevertheless, the perturbations to the overall flux distribution of the bulge are still small enough that we can trust in the resulting photometric parameters. This can be seen fromthe monotonic behaviour of all parameters of NGC 4321 in the Tables 2-4 (tables only available in electronic form). Only the slope parameter $\beta$ reaches unreasonable high values in U and B.

  

Table 2: Structural parameters of the disks. $SB_{\rm c}$ is the seeing-deconvolved and inclination-corrected central surface brightness in mag/square-arcsec. $R_{\rm d}$ is the radial scale-length of the exponential disk, given in arcsec and in kpc. $\rm PA_d$ is the position angle of the major axis (line of nodes). $Q_{\rm d} = b/a$ is the axis ratio of the model fit to the disk. Each value is given for the corresponding filters UBVRI. This table is only available in electronic form at the CDS (see footnote to title).

  

Table 3: Structural parameters of the bulges. $SB_{\rm eff}$ is the effective surface brightness in mag/square-arcsec. $R_{\rm eff}$ is the effective or half-light radius in kpc. The exponent $\beta = 1/n$ is the slope parameter of the bulge. ${\rm PA}_b$ is the position angle of the major axis (line of nodes). Q_b = b/a is the axis ratio of the model fit to the bulge. Each value is given for the corresponding filters UBVRI. This table is only available in electronic form at the CDS (see footnote to title).

  

Table 4: Absolute luminosities of the total galaxies, of the disks, and of the bulges. The last 5 columns are the bulge/disk-ratios. Each value is given for the corresponding filters UBVRI. This table is only available in electronic form at the CDS (see footnote to title).

   
6.2 Structure parameters in UBVRI

After a number of tests for each galaxy and detailed considerations about the reliability of the parameters we ended up with a set $I_{\rm d}, \: R_{\rm d}, \: {\rm PA}_{\rm d}, \: Q_{\rm d}, \: I_{\rm eff}, \: R_{\rm eff}, \: \beta, \: {\rm PA}_b, \: Q_{b}$ for each galaxy in each filter U, B, V, R, and I. Table 2 (only available in electronic form) lists the structural parameters for the disks of our galaxy sample. The central surface-brightness values  $SB_{\rm c}$ (in mag/square-arcsec) were obtained from the (seeing-deconvolved) central flux densities $I_{\rm d}$ of the disks using the photometric calibrations and corrections for galactic and internal extinction (Sect. 3). Note that these are the values if the galaxies were seen face on, i.e. the $I_{\rm d}$ values are inclination-corrected, $\cos(i) = Q_{\rm d} = b/a$. The scale-lengths $R_{\rm d}$ are given in arcsec and in kpc, using the distances from Table 1. The last columns give the position angles ${\rm PA}_{\rm d}$ and the axis ratios $Q_{\rm d} = b/a$ in all five colors.

Table 3 (only available in electronic form) lists the corresponding structural parameters for the bulges for UBVRI. The  $SB_{\rm eff}$ numbers were calculated from the $I_{\rm eff}$ as above. Since the bulges are spheroids with unknown true axis ratios no inclination corrections were applied. The effective radii $R_{\rm eff}$ are given in kpc. The following columns give the bulge exponents $\beta = 1/n$ for all five colors, the position angles ${\rm PA}_b$, and the axis ratios Q_b = b/a.

Using the disk-parameter values $I_{\rm d},\: R_{\rm d}$ (Table 2) it is easy to calculate the flux for the disks by integration from the center to infinity: $L_{\rm disk} = 2\pi I_{\rm d} R_{\rm d}^2$. In a similar manner the bulge flux was integrated: $L_{\rm bulge} = K_n I_{\rm eff} R_{\rm eff}^2$, where $n = 1/\beta$ and $\log(K_n) = 0.030 \log(n)^2 + 0.441 \log(n) + 1.079$ (Caon et al. 1993). The total flux is simply the sum of the fluxes of disk and bulge, the bulge/disk-ratio is the corresponding quotient. The absolute magnitudes were calculated using the distances from Table 1. Table 4 (only available in electronic form) lists the absolute magnitudes from the disk-bulge fits in UBVRI.

   
6.3 Comparison with other authors

Figure 3: Left: comparison between disk scale-lengths from other authors and our values. $R_{ \rm d2}/R_{\rm d1}$ is the corresponding ratio. The galaxy numbers refer to the corresponding numbers in Table 1. Right: direct comparison of the disk scale-lengths of NGC 4321 in UBVRI from different authors. The filled symbols are from this paper, the other symbols correspond to other authors and are explained in the text.

Open with DEXTER

Although there exists quite a number of papers with disk-bulge decompositions of galaxy images in visual bands, there are only few with common galaxies to our sample. Most of them present disk scale-lengths in only one filter. Since the disk scale-lengths are color-dependent, the comparison should be done for identical filters. In the following we compare our disk scale-lengths with the corresponding numbers from 4 authors in the literature. The left diagram in Fig. 3 shows the quotient  $R_{ \rm d2}/R_{\rm d1}$, i.e. the disk scale-lengths obtained by those authors divided by our corresponding values. The different symbols refer to:
1. Open circles: Baggett et al. (1998), 17 common galaxies in B. Mean value $<R_{\rm d2}/R_{\rm d1}>\ = 0.83 \pm 0.26$.
2. Triangles: Grosbøl (1985), 20 common galaxies in R. Mean value $<R_{\rm d2}/R_{\rm d1}>\ = 1.04 \pm 0.36$.
3. Squares: Simien & de Vaucouleurs (1986), 8 common galaxies in B. Mean value $<R_{\rm d2}/R_{\rm d1}>\ = 1.06 \pm 0.22$.
4. Crosses: Elmegreen & Elmegreen (1984), 8 common galaxies in B (+ crosses) and I ($\times$ crosses). Mean value $<R_{\rm d2}/R_{\rm d1}>~ = 0.93 \pm 0.74$ for Band $<R_{\rm d2}/R_{\rm d1}>\ = 1.19 \pm 0.30$ for I.
Very few extreme values (ratio >3) have been omitted. The mean value of all quotients and the standard deviations are $<R_{\rm d2}/R_{\rm d1}>\ = 0.99 \pm 0.30$and are drawn in Fig. 3 (full and dotted lines). Although there are some differences from author to author, the overall result is satisfying.

Bulge date were available only in Baggett et al. (1998) and in Simien & de Vaucouleurs (1986). Probably because of the different fit methods (they used R^1/4 profiles) their results are so different from our values that a comparison is not meaningful.

NGC 4321 is the galaxy from our sample with the most measurements in the literature. The right diagram in Fig. 3 shows the different values obtained for the disk scale-length $R_{\rm d}$. The filled circles correspond to the values from this paper. The open circles are the UBVRI values of del Rio & Cepa (2003). The squares are the BVRI values of Beckman et al. (1996). The triangles are the BVRI values of Pompei & Natali (1997). Two numbers for B and I stem each from Knapen & Beckman (1996, lozenges) and Elmegreen & Elmegreen (1984, asterisks). The + cross is the B value from de Jong (1996a). The numbers from Baggett et al. (1998, B), Grosbøl (1985, R), and Koopmann et al. (2001, R) are all represented with $\times$ crosses. Although the results show quite a scatter, the tendency of decreasing $R_{\rm d}$ towards the red colors is slightly detectable. As above, the bulge data in these papers stem from different assumptions about the bulge profiles and do not allow reasonable comparisons.

   
7 General trends in dependence of color UBVRI

   
7.1 Disk scale-lengths and bulge effective radii

	Figure 4: Disk scale-lengths $R_{\rm d}$ and bulge effective radii $R_{\rm eff}$, normalized to their I-value and plotted over colors. Each line connects the values from U, B, V, R, to I (=1). The normalized disk scale-lengths decrease, most normalized bulge effective radii increase from blue towards red colors.
Open with DEXTER

The inspection of the parameters in Tables 2 and 3 shows that there exist general trends in the behaviour of $R_{\rm d}$ and $R_{\rm eff}$ with color. In order to make these size correlations better visible we neutralize the variations from galaxy to galaxy by normalizing $R_{\rm d}$ and $R_{\rm eff}$ to their I-values of each galaxy. Figure 4 shows the behaviour of the normalized radii with color. The values for each galaxy are represented by a continuous line connecting the normalized values from U, B, V, R, to I (=1). We see the following clear trends:

1. The disk scale-lengths $R_{\rm d}$ decrease monotonically from U to I, i.e. in blue light the disks are more extended. There are some exceptions with nearly color-independent $R_{\rm d}$ and only two cases with increasing scale-lengths (NGC 278 and 4736, left diagram in Fig. 4). The growth of the disks towards the blue is probably the consequence of an increasing influence of star formation in the outer zones and/or a higher concentration of old stars in the central regions (cf. MacArthur et al. 2003).

2. Vice versa, the bulge effective radii $R_{\rm eff}$ increase from U to I, with a scatter larger than that of the disks. (right diagram in Fig. 4). Again there are some exceptions with nearly color independent $R_{\rm eff}$, and two cases with strongly decreasing effective radius (NGC 3031 and NGC 3521). The two galaxies which have their maximal $R_{\rm eff}$ in the V filter are NGC 4274 and NGC 5055. A further division of this diagram according to different Hubble types did not show clearer results; the number statistics is too small.

For 12 galaxies of our sample there exist similar photometric parameters from the near infrared (NIR), (Paper I). In general the trends of $R_{\rm d}$ and $R_{\rm eff}$ in the visual filters continue in the NIR. However, the scatter was larger there, due to the smaller signal-to-noise ratio and the smaller field of view ( $3 \times 3$ arcmin).

   
7.2 Bulge/disk-ratios and and bulge slope-exponent $\beta$

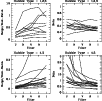Figure 5: Bulge/disk-ratios (left column) and $\beta$ (right column) plotted over colors. Each line connects the corresponding galaxy parameter values from U, B, V, R, to I. All bulge/disk-ratios show an increase from blue to red colors, for early to medium spirals (top) on a higher level, and and for late spirals (bottom) on a lower level. The behaviour of the exponent $\beta$ is just vice versa. Notice the different y-axis scales.

Open with DEXTER

Figure 5 shows the behaviour of bulge/disk-ratios and $\beta$ plotted over colors. Generally the bulge/disk-ratios increase monotonically from U to I, i.e. the bulges are more dominant in red colors. However, there is a distinction between the early- and late-type spirals: for early and medium types ($\rm HT=1$, 2, 3), the bulge/disk-ratios have large values and show a fairly strong increase from U to I (upper left diagram in Fig. 5). For late-type spirals ( $\rm HT=4,~ 5$) the bulge/disk-ratios have small values and show a weak increase from U to I, with less scatter (bottom left diagram in Fig. 5; the discordant line is from NGC 4254).

The bulge slope parameter $\beta$ decreases monotonically from U to I. For early and medium types, it varies between 0.6 and 0.2. (top right diagram in Fig. 5). For late type spirals $\beta$ varies more, from >1 in the blue to $\approx$0.3 in the red filters (bottom right diagram in Fig. 5). The trends of the bulge/disk-ratios and of $\beta$ in the visual colors are similarly continued in the NIR (Paper I).

Note that all considerations in this section are distance-independent. In the following section it will be shown that above characteristics are also reflected in the correlations with the Hubble types.

   
8 Correlations of structure parameters

   
8.1 Bulge structure-parameters over Hubble types

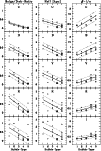Figure 6: Left column: the bulge/disk-ratios decrease from early to late Hubble types (NGC 2460 omitted). Center column: the bulge effective radii decrease to late Hubble types for all colors UBVRI. Right column: for early-type spirals the bulge slope-exponent $\beta$ is around 1/4, it increases towards $\beta \approx 1$ for the late-type spirals. The continuous lines are the linear regressions through the corresponding data points, the dotted lines represent the $1\sigma$-deviations.

Open with DEXTER

The left column of Fig. 6 shows the variation of the bulge/disk-ratios and the exponent $\beta$ with Hubble types. The bulge/disk-ratios (B/D) decrease in all colors towards the late type spirals. This is not surprising, since this is just part of the definition of the Hubble types. The slope of this correlation as well as the scatter are least in U: ( ${\rm B/D}(T=1) - {\rm B/D}(T=5) = 0.30$, $\sigma=0.04$). Both numbers increase towards the red colors (V: $\rm B/D(1) - B/D(5) = 0.60$, $\sigma=0.18$), (I: $\rm B/D(1) - B/D(5) = 0.66$, $\sigma=0.26$). In other words, the differences in bulge/disk-ratios between early- and late-type spirals are small in U, but with high significance (7.5$\sigma$). The corresponding differences are largest in I, but with lower significance (3$\sigma$). This finding was unexpected.

The center column of Fig. 6 shows that the effective radii  $R_{\rm eff}$ also decrease with Hubble types, early-type spirals have larger bulges. Here again the scatter is smallest for the blue colors.

The right column of Fig. 6 shows the correlation of the slope exponent $\beta$ over Hubble types for the different colors UBVRI. The exponent $\beta$ behaves just contrary to the bulge/disk-ratios: $\beta$ increases in all colors towards the late type spirals. This extends the K-band results of Andredakis et al. (1995) who found that $\beta = 1/n$ varies systematically with the Hubble types. The slope as well as the scatter are largest in U: ( $\beta(1) - \beta(5) = -1.12$, $\sigma=0.45$). Both numbers decrease towards the red colors (V: $\beta(1) - \beta(5) = -0.62$, $\sigma=0.27$), (I: $\beta(1) - \beta(5) = -0.32$, $\sigma=0.17$). The $\beta$-differences between early and late spirals are similarly significant in all colors ($\approx$$3\sigma$ The corresponding gradients in $\beta$ are largest in U. This finding was unexpected as well.

The plots of $R_{\rm eff}$ over Hubble types (center column of Fig 6) show the contrary behaviour of the corresponding variations and scatters of $\beta$, i.e. a shallow gradient with smaller scatter in U and a steep gradient with large scatter in I. It is an empirical finding that during the fit procedure $\beta$ and $R_{\rm eff}$ behave complementary: an increase of one of these parameters during the numerical iterations is accompanied by a decrease of the other one. Trujillo et al. (2001) have shown, that this behaviour is not a mathematical artefact but is founded on the physical structure of bulge-like components.

	Figure 7: The bulge absolute luminosities and the bulge effective radii  $R_{\rm eff}$ increase in all colors with the (inverse) slope exponent $n = 1/\beta$. The bright and large bulges are of de Vaucouleurs type (large n), the small and faint bulges have smaller exponents n (larger $\beta$).
Open with DEXTER

   
8.2 Correlations between bulge structure-parameters

The left column of Fig. 7 shows how for each color UBVRI the bulge luminosities depend on the (inverse) slope exponent $n = 1/\beta$. The bulges with large n (small $\beta$, i.e. similar to de Vaucouleurs profile) are brighter, as well absolutely as relative to the disks. This result is complementary to Fig. 5, which shows the correlations over colors and early- or late-type spirals: early-type spirals have brighter bulges and smaller $\beta$ values (i.e. larger n) than the late-type spirals. (see Paper I for similar results in NIR, or MacArthur et al. 2003).

The right column of Fig. 7 shows how for each color UBVRI the bulge effective radii $R_{\rm eff}$ depend on the (inverse) slope exponent $n = 1/\beta$. The bulges with large n (small $\beta$) are more extended.

Thus we can extend the corresponding conclusions from Sect. 7 as well to the linear sizes of bulges: the bulges of the early-type spirals are large, bright and are similar to elliptical galaxies, the bulges of the late types are tiny, faint and are similar to disks, especially in the blue colors.

   
8.3 Bulge-to-disk size-ratio

	Figure 8: The size ratio $R_{\rm eff}/R_{\rm d}$ correlates with Hubble types and with colors. The different colors were plotted in different symbols with an artificial offset to the corresponding HT: $\Delta {I} = -0.3$ (squares), $\Delta {R} = -0.15$ (triangles), V no offset (asterisks), $\Delta {B} = 0.15$ (lozenges), $\Delta {U} = 0.3)$ (circles), (NGC 2460 and 4254 were omitted).
Open with DEXTER

Late-type spirals have bulges with nearly exponential profiles. Courteau et al. (1996) fitted an exponential disk plus an exponential bulge to a large sample of late-type spiral galaxies. They found that the ratio of the corresponding scale-lengths was approximately constant: $R_{b}/R_{\rm d} = 0.09 \pm 0.05$ (r-band). Graham (2001) and MacArthur et al. (2003) performed similar studies (using Sérsic bulges) for galaxies of different Hubble types and found slightly different results (see Sect. 12).

Figure 8 shows the variation of our $R_{\rm eff}/R_{\rm d}$ values with Hubble types for the different colors UBVRI. We observe a clear trend of increasing $R_{\rm eff}/R_{\rm d}$ from late- to early-type spirals. Furthermore, for each morphology class ( $\rm HT = 1...5$) we separate the colors UBVRI by an artificial offset in HT: $\Delta {I} = -0.3$, $\Delta {R} = -0.15$, V no offset, $\Delta {B} = 0.15$, $\Delta {U} = 0.3)$. This separation shows a corresponding increasing trend from blue (U) to red (I) colors. The lines in each HT class give the linear regressions and the 1$\sigma$-deviations. Because of their extreme $R_{\rm eff}$ values NGC 2460 and 4254 (Table 3) have been omitted here. Table 5 shows the corresponding numbers from the linear regressions. Our results support the idea of a close connection between disk- and bulge-structure for late-type spirals. We obtain a steeper dependence with Hubble types than that found by MacArthur et al., even if we consider the small numbers of galaxies in the Hubble classes T=1 and T=2.

Table 5: $R_{\rm eff}/R_{\rm d}$ in UBVRI for the different Hubble types. This quotient decreases systematically from early to late spirals and decreases systematically from red to blue colors.

   
9 Photometric results of spiral galaxies

From the decomposition of each galaxy into disk and bulge we obtain the luminosities in each color and the corresponding color indices as well. Since NGC 2742 was exposed during non-photometric conditions and no later calibrations were possible, this galaxy is omitted in all following photometric diagrams.

   
9.1 Comparison with RC3

As a photometric check we compare the total B luminosities as well as $(B - V)_{\rm o}$ with the corresponding values from the RC3 (de Vaucouleurs et al. 1991). Here always the extinction-corrected values are used. The left diagram in Fig. 9 shows the comparison of the total luminosities. The scatter looks satisfying ( $1\sigma = 0.19$ mag). The object with the largest offset in $B_{\rm tot}$ is NGC 2855. The right diagram in Fig. 9 shows the comparison of the $(B - V)_{\rm o}$ values. Here the scatter is only $1\sigma = 0.076$ (note the different y-scales of the diagrams). The object with largest offset in $(B - V)_{\rm o}$ is NGC 628. There is no systematic error in our color indices: The mean value of the differences between RC3 and our $(B - V)_{\rm o}$ values is very small: -0.003 mag.

	Figure 9: Comparison between total B luminosities and $(B - V)_{\rm o}$ with the corresponding data of RC3.
Open with DEXTER

   
9.2 Absolute UBVRI luminosities

Figure 10 shows for each color UBVRI the variation of total-, of the disk-, and of the bulge-luminosities with Hubble types. The total-luminosities represent just the distribution of the selected sample. Apart from U the mean values of the total-luminosities show no variations with Hubble types. The disk-luminosities increase slightly with Hubble types, especially for the blue filters. In contrast to that the bulge-luminosities decrease with Hubble types for all colors. Late spirals have brighter disks and fainter bulges than the early types. This has the consequence that the bulge/disk-ratios decrease with Hubble types (Fig. 6). The increasing disk luminosities and the decreasing bulge luminosities act together here. Since the disk-luminosities are less variable towards the red colors, the decreasing bulge/disk-ratio in I is mainly a consequence of the bulge behaviour alone. This is consistent with the results of Trujillo et al. (2002) who found that for corresponding K observations the variations of the bulges are predominantly responsible for variations of the bulge/disk-ratios.

It is remarkable that the patterns of the scatter around the regression lines in Fig. 10 are very similar for total-, disk-, and bulge-luminosities as well. This scatter just reflects the individual luminosity variations from galaxy to galaxy.

The corrections for galactic and internal extinction have only a minor influence to above results. If we would plot in Fig. 10 the luminosities without these corrections they would look very similar, however slightly shifted. The shift due to the extinction correction in U was the largest: the regression line has moved to 0.47 mag brighter values. This shift was 0.30 mag in V and only 0.14 mag in I. The scatter remains the same, i.e. the variations are intrinsic.

   
10 Color indices

   
10.1 Dependency of color indices on Hubble types

	Figure 10: Absolute UBVRI-luminosities of the total galaxies, of the disks, and of the bulges over the Hubble types. While the disk-luminosities slightly increase to the late spirals, the bulge-luminosities decrease.
Open with DEXTER

	Figure 11: Blue color indices U-B and B-V (in mag) for the total galaxies, the disks, and the bulges. The enhanced star formation rate in late-type spirals causes the bluer color indices of disks and total galaxies.
Open with DEXTER

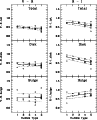	Figure 12: The red color indices V-R and R-I (in mag) for the total galaxies, the disks, and the bulges. For comparison reasons Figs. 11 and 12 have the same scale.
Open with DEXTER

The color indices were simply computed as the differences between the luminosities in the corresponding filters. In contrast to the absolute luminosities, color indices are independent on the distances. They are also much less sensitive to extinction corrections than the absolute luminosities.

Figure 11 shows the variations of the blue color indices U-B and B-V over the Hubble types, for the total galaxies, the disks, and the bulges, respectively. U-B total is $\approx$0.6 mag smaller for late-type spirals than for early types. (these numbers are always the mean values from the linear regression), i.e. the late types are bluer due to their stronger star formation. The results are similar for the disks. Concerning the bulges, the weak decrease of U-B with Hubble types is probably not significant since the scatter is fairly large here. The mean values of the bulges are about 0.3 (Hubble type T=1) to 0.7 mag (T=5) redder than those of the disks (for details see Sect. 10.2). B-V (Fig. 11, right column) shows a similar trend as U-B for the total galaxies and the disks, however with a weaker gradient and with slightly less scatter. Concerning the bulges, there is a tendency for redder color indices towards the late types, again with a fairly big scatter, probably not significant as well.

Figure 12 shows the corresponding variations of the red color indices V-R and R-I over the Hubble types. V-R total shows only a small gradient: the late spirals are slightly bluer (0.2 mag). For the disks the gradient is similar but is disappearing for the bulges. Compared to the blue color indices the scatter is smaller here (bulge mean value $V-R = 0.58 \pm 0.21$ mag). R-I shows a somewhat steeper gradient, $\approx$0.3 mag between early and late types for the total galaxies. Regarding the total luminosities, the late types are bluer in all color indices, even in the red ones.

The bulges show such large scatters in all color indices, that no significant statement about the existence of gradients is possible. We see no significant differences in the stellar populations of the bulges between early- or late-type spirals. This behaviour is different to that of the shape parameters (e.g. the slope $\beta$).

   
10.2 Color differences between bulges and disks

	Figure 13: Differences between the color indices of the bulges and those of the disks, plotted over the Hubble types. The disks are practically always bluer than the bulges.
Open with DEXTER

Figure 13 shows the differences of color indices between bulges and disks. Generally, the bulges are always redder than the disks. This is valid for the blue differences U-B, B-V and even for the red differences V-R, R-I. This tendency increases from early- towards late-type spirals. The offset point in the B-V diagram stems from NGC 3031. In the case of R-I the line of linear regression indicates slightly bluer bulges for early-type spirals. However, this is not significant because of the small number of Sa galaxies and the large scatter there. R-I seems to vanish for early spirals.

Peletier & Balcells (1996) compared optical and NIR colors for a sample of early-type spirals. They found that color differences (bulges at 0.5 $R_{\rm eff}$minus disks at 2$R_{\rm d}$) are very small: $\Delta(U-R) = 0.126 \pm 0.165$. From the results displayed in Fig. 13 we can not confirm these results; we find $\Delta(U-R) = 0.91~ \pm~ 0.50$ for early- (Sa) and $\Delta(U-R) = 1.55 \pm 0.50$ for late-type spirals (Sc). In contrast to Peletier & Balcells we used the whole bulge and whole disk to calculate the differences. The local gradients of these components are not large enough to explain these different results. Our statements above were made for the mean differences of the color indices between bulges and disks (using the linear regressions). Figure 13 shows that for the blue color indices (U-B and B-V) the bulges are redder than the disks for each single galaxy. This is especially true for U-R, where the mean difference increases from 0.9 for Sa- to 1.5 for Sc-galaxies. The minimum of the B-R difference is 0.5 mag. This is obviously the consequence of an increased star formation and/or a younger population in the disks of all Hubble types. Concerning the red color indices (V-R and R-I), here a few galaxies exist with a bluer bulge than the disk, however not the majority (Fig. 13).

   
11 Comparison with evolutionary synthesis models

11.1 Color indices of the total galaxies

In the following we compare the color indices of the total galaxies for different Hubble types with some recent evolutionary synthesis results. Figure 14 shows in the center of each sub-diagram our observational values U-B, B-V, V-R, and R-I from Sect. 10.1 for Sa-, Sb-, and Sc-spirals, respectively. The filled circles correspond to the total galaxies, together with their statistical $1\sigma$ error bars. For comparison reasons the color indices of the corresponding disks (open circles) and bulges (open triangles) are also drawn. The data values for these points are the corresponding values for Sa-, Sb-, Sc-galaxies from the linear regression through all points in Figs. 11 and 12.

Bicker et al. (2003) computed chemically consistent models for Sa-, Sb-, Sc-galaxies from their formation until to the age of 15 Gyr. The luminosities of the total galaxies in the filters U, B, V (Johnson) and R, I (Cousins) were calculated as well as the corresponding color indices.

Figure 14: Comparison of the observed color indices U-B, B-V (upper row) and V-R, R-I (lower row) for spiral galaxies with evolutionary synthesis models of Bicker et al. (2003) and Westera et al. (2002). The observational values for the total galaxies (filled circles) are drawn in the center, together with their error bars. The color indices of the corresponding disks (open circles) and bulges (open triangles) are also shown.

Open with DEXTER

On the left-hand sides in the diagrams of Fig. 14 the short solid lines give the results at 15 Gyr from the calculations of Bicker et al. The coincidence between observations and models is different for the different color indices: U-B: the models do not explain the redder observational values, especially for the Sa spirals ( $\rm offset = 0.25$ mag, i.e. >$1\sigma$). The Sb galaxies fit satisfying. The bluer observational values of the Sc-galaxies would fit with a younger age (3.7 Gyr). B-V and V-R: here we have a fairly good coincidence between observations and theory. The differences are smaller than the error bars. R-I: the Sa models are 0.13 mag bluer than the observations (>$1\sigma$). For Sb and Sc the models fit at 15 Gyr good or very good.

The general trend is that the evolutionary synthesis models of Bicker et al. (2003) show a smaller spread between Sa-, Sb-, and Sc-galaxies than our observations. Their Sa-galaxy models seem to be too blue in all color indices, especially in U-B and R-I. The differences can not be explained by systematic photometric errors in the observations (see Sect. 9.1).

   
11.2 Chemodynamical models

Westera et al. (2002b) calculated the color evolution of disk galaxy models from z=4 to z=0. They combined the 3-dimensional chemodynamical galaxy models of Samland & Gerhard (2003) with the latest SED library of Westera et al. (2002a) and a new galaxy evolutionary code. They obtained images in all filters U to M for two typical models: a collapse model with a burst-like star-formation phase and a slowly growing accretion model with a long lasting star-formation on a low level.

On the right-hand sides in the diagrams of Fig. 14 the short solid lines give the z=0 results for the galaxies from the calculations of Westera et al. The coincidence between observations and models is good: U-B: the collapse model has a similar color index as the Sb-galaxies, the accretion model is similar to the Sc observations. This is reasonable according to the different star formation scenarios. B-V: and V-R: this is a really good coincidence between observation and theory: collapse model for Sa- to Sb-, and accretion model for Sc-galaxies. The color indices are similar to those of Bicker et al. R-I: here the collapse- and accretion models are bluer than the corresponding models of Bicker et al. and have color indices of the Sc observations. The Sa observations are about 0.2 mag redder than the collapse models, the difference is larger than $1\sigma$. For Sb- and Sc-galaxies the corresponding models would still fit fairly good to the observations.

The chemodynamical synthesis models of Westera et al. (2002b) fit generally well to the observations: their collapse model to Sa-, or Sb-galaxies, their accretion model to Sc-galaxies. Only their R-I of the collapse model seems to be too blue.

   
11.3 Bulge color indices

Vazdekis et al. (1996) calculated evolutionary synthesis models for a sequence of early type (elliptical) galaxies. The short dotted lines on the right hand sides in Fig. 14 are the predicted color indices (age = 17 Gyr, high star formation rate $\nu = 10$). The open triangles in Fig. 14 are the observed color indices of the bulges. The scatter here is much large than for the total galaxies (cf. Figs. 11 and 12). The observed values tend to be slightly bluer than the models. However, due to the large scatter no separation between color indices of bulges from early- or late-type spirals is possible.

   
12 Discussions and conclusions

The correlations between the photometric parameters shown in the preceding sections support different formation mechanisms for bulges in early- or late-type spirals.

   
12.1 Evolution of the disks

It was shown in Sect. 7.1 that the disk scale-lengths $R_{\rm d}$ decrease monotonically from U to I, i.e. in blue light the disks are more extended. Different hints for such a color dependence of the disk scale-lengths were already found by several authors. The physical interpretation for this trend is still in discussion. Some authors came to the conclusion that this trend is due to the presence of dust in the inner zone (e.g. Beckman et al. 1996; Pompei & Natali 1997). Other authors stated, that the color gradients in face-on spiral galaxies are best explained by age- and metalicity-gradients in the stellar populations and that dust reddening plays a minor role (e.g. de Jong 1996b). This would mean that the disks have younger populations at large radii, i.e. the disks were be formed inside-out. A final decision is not yet possible at this stage of observations and dust models.

   
12.2 Structure of the bulges

1. Bulge effective radii: In contrast to the disks, the bulge effective radii $R_{\rm eff}$ increase from U to I, with a scatter larger than that of the disks. (right diagram in Fig. 4). Evans (1994) calculated the variations on the profiles of disks and bulges in dependence of the wavelength for different dust distributions. He found subtle differences in the disk scale-lengths of similar amount as observed. The disk-bulge models of Evans showed steeper inner profiles due to increasing dust extinction.

The dust models point to the same direction as the observations. However, it is not clear if the bulge behaviour in Fig. 4 may be explained by dust extinction alone. The size of the bulges is also correlated with the Hubble types: $R_{\rm eff}$ decreases to late spirals in all filters UBVRI. Since the slope $\beta$ is anticorrelated to $R_{\rm eff}$ (Fig. 6), it seems hard to explain how dust extinction alone could produce these parameter correlations.

2. Bulge radial profiles: The bulge slopes $\beta$ increase from early- to late-type spirals (right column of Fig. 6). As a corollary to the correlation over Hubble types we obtain also a relation between $R_{\rm eff}$ and $n = 1/\beta$ (Fig. 7). Together: bulges of early-type spirals are large and have similar profiles as ellipticals, while the bulges of late-type spirals are tiny have similar profiles as disks.

3. Bulge-to-disk size-ratios: In several studies nearly constant ratios of the characteristic radii of the disks and bulges were found. Courteau et al. (1996) stated that late types (Sb, Sc) are best fitted by an exponential disk plus an exponential bulge (fixed $\beta = 1$). The ratio of the corresponding scale lengths was approximately constant: $R_{b}/R_{\rm d} = 0.09 \pm 0.05$ (r-band).

Graham (2001) performed two-dimensional fits, using an exponential disk plus a Sérsic bulge. Studying different correlations of parameters with Hubble types he found that the mean $R_{\rm eff}/R_{\rm d}$ values are larger for early-type spirals than for the late-type spirals. However, the difference was not particularly significant. MacArthur et al. (2003) found $R_{\rm eff}/R_{\rm d} = 0.22 \pm 0.09$ in the I filter with a mild trend with Hubble types ( $R_{\rm eff}/R_{\rm d} = 0.20, 0.24$ for T=5, 1 respectively).

We found the ratio $R_{\rm eff}/R_{\rm d}$ to be small (0.06 to 0.15 from U to I) on a nearly constant level for Sc-, Sbc-, and Sb- spirals, however increasing significantly towards Sba-, and Sa-spirals (0.4 to 0.7 from U to I), (Fig. 8 and Table 5). This is another hint for a coupling of bulge- and disc-structure in late-type spirals, in contrast to early-type spirals.  

4. Bulge luminosities: In Fig. 6 we saw that the bulge/disk-ratios decrease to late spirals in all colors. Correspondingly, Fig. 10 shows that the bulge absolute luminosities decrease to late spirals in all colors, while the total luminosities of the sample galaxies are nearly constant over the Hubble types. Independently on any Hubble classification, one can state that bright and large bulges are of de Vaucouleurs type, while small and faint bulges are of exponential type.

Concerning the structure of the bulges, we observe a systematic change between early- and late-type spirals: a decrease in effective radius and luminosity and an increase of the exponent $\beta$. This is not just an effect of dust extinction. The bulges of early- and late-type spirals are different in their intrinsic structure.

   
12.3 Color indices

The decomposition of the spiral galaxies into disks and bulges allowed to calculate the luminosities and color indices of these components.

1. Bulge colors: In contrast to the disks, the color indices of the bulges (Figs. 11 and 12) show no significant gradient over the Hubble types, with a fairly high scatter. However, the bulges are always redder than the disks, for all Hubble types (Fig. 13). Their color indices correspond fairly well to the population synthesis models for ellipticals of Vazdekis et al. (1996), cf. Sect. 11.3. A color separation between bulges of early- and late-type spirals is not possible with our data.

2. Color indices and evolutionary synthesis: In Sect. 11 we compared the observed colors of the total galaxies with different evolutionary-synthesis models. Westera et al. (2002b) calculated the color evolution of disk galaxies for a collapse model and an accretion model, corresponding roughly to an early or secular bulge formation, respectively. The models fit generally well to the observations: their collapse model to Sa-, or Sb-galaxies, their accretion model to Sc-galaxies. This is another support for the existence of at least two different bulge formation mechanisms.

   
12.4 Formation of bulges

Concluded, early-type spirals have large and bright bulges with profiles similar to elliptical galaxies. These bulges were probably formed prior to the disks in a monolithic collapse or via early mergers. On the other hand, late-type spirals have tiny and faint bulges with strongly color dependent profiles, more similar to disks, especially in the blue colors. They are also correlated in size to the disks. The bulges in these galaxies were probably formed simultaneously or after the disks during a secular evolution process, e.g. from a disk instability (bar). Such a dynamical interaction between disk and bulge occurs on time scales shorter than a Hubble time.

The good consistency between observed color indices and evolutionary synthesis model calculations also supports the two different scenarios: 1. An early collapse of the bulge with a short burst of star formation for early-type spirals. 2. A less vigorous formation of the bulge for late-type spirals with a long-lasting star formation, either by accretion of matter (dwarf companions) or a secular formation of the bulge out of disk material.

These formation scenarios are only typical for early- or late-type spirals, respectively. Obviously we do not observe two distinct classes in the structure parameters, but a continuum. Therefore both mechanisms may work at different epochs in the same galaxies and leave the corresponding traces in the structure (cf. Trager et al. 1999).

The bulge stars are obviously old, but a bulge could have been formed recently, e.g. from a bar instability. An age determination of the bulges of the different spiral galaxies is not possible from out data. Detailed spectral information and line strength measurements would be necessary.

We observe a continuum in nearly all structural parameters over Hubble types (luminosity, size, shape). The Hubble type is mainly determined by the bulge/disk-ratio. Is it possible, that bulges grow such that galaxies evolve along the Hubble sequence? Aguerri et al. (2001) showed by collionless N-body simulations that an exponential bulge can grow due to satellite accretion and transforms its profile towards smaller $\beta$, i.e. towards early-type bulges. However, such an accretion would lead also to a thickening of the disk, thus the bulge growth must have been occurred before the last formation of a thin disk in the corresponding galaxy.

Acknowledgements

This project was supported by the Sonderforschungsbereich 439 of the Deutsche Forschungsgemeinschft (DFG). We are grateful to the Calar Alto team for the effective support during the observations. We acknowledge the use of the SIMBAD database (CNRS data centre, Strasbourg).

References

 
• Aguerri, J. A. L., Balcells, M., & Peletier, R. F. 2001, A&A, 367, 428 In the text NASA ADS  
• Andredakis, Y. C., Peletier, R. F., & Balcells, M. 1995, MNRAS, 275, 874 In the text NASA ADS  
• Andredakis, Y. C., & Sanders, R. H. 1994, MNRAS, 267, 283 In the text NASA ADS  
• Beckman, J. E., Peletier, R. F., Knapen, J. H., Corradi, R. L. M., & Gentet, L. J. 1996, ApJ, 467, 175 In the text NASA ADS  
• Baggett, W. E., Baggett, S. M., & Anderson, K. S. J. 1998, AJ, 116, 1626 In the text NASA ADS  
• Bevington, P. R., & Robinson, K. D. 1992, Data Reduction And Error Analysis For The Physical Sciences, 2nd Edition (Boston: McGraw-Hill) In the text  
• Bicker, et al. 2003, A&A, in preparation In the text  
• Bottinelli, L., Gouguenheim, L., Paturel, G., & de Vaucouleurs, G. 1984, A&AS, 56, 381 In the text NASA ADS  
• Bottinelli, L., Gouguenheim, L., Paturel, G., & de Vaucouleurs, G. 1985, A&AS, 59, 43 In the text NASA ADS  
• Bottinelli, G., Gougenheim, L., Paturel, G., & Teerikorpi, P. 1986, A&A, 156, 157 In the text NASA ADS  
• Bottinelli, G., Gougenheim, L., & Teerikorpi, P. 1988, A&A, 196, 17 In the text NASA ADS  
• Burstein, D., & Heiles, C. 1984, ApJS, 54, 33 In the text NASA ADS  
• Byun, Y. I., & Freeman, K. 1995, ApJ, 448, 563 In the text NASA ADS  
• Caon, N., Capaccioli, M., & D'Onofrio, M. 1993, MNRAS, 265, 1013 In the text NASA ADS  
• Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 In the text NASA ADS  
• Carollo, C. M., Ferguson, H. C., & Wyse, R. F. G. 1999, The Formation of Galactic Bulges (Cambridge Univ. Press) In the text  
• Christian, C. A., Adams, M., Barnes, J. V., et al. 1985, PASP, 97, 363 In the text NASA ADS  
• Courteau, S. 1996, ApJS, 103, 363 In the text NASA ADS  
• Courteau, S., de Jong, R. S., & Broeils, A. H. 1996, ApJ, 457, L73 In the text NASA ADS  
• de Jong, R. S. 1996a, A&AS, 118, 557 In the text NASA ADS  
• de Jong, R. S. 1996b, A&A, 313, 377 In the text NASA ADS  
• del Rio, M. S., & Cepa, J. 2003, A&A, 400, 421 In the text NASA ADS  
• de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (RC3) (New York, Heidelberg: Springer) In the text  
• Elmegreen, D. M., & Elmegreen, B. G. 1984, ApJS, 54, 127 In the text NASA ADS  
• Evans, R. 1994, MNRAS, 266, 511 In the text NASA ADS  
• Florido, E., Battaner, E., Guijarro, A., Garzón, F., & Jiménez-Vicente, J. 2001, A&A, 378, 82 In the text NASA ADS  
• Freeman, K. C., 1970, ApJ, 160, 811 In the text NASA ADS  
• Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 In the text NASA ADS  
• Graham, A. W. 2001, AJ, 121, 820 In the text NASA ADS  
• Graham, A., Lauer T. R., Colless, M., & Postman, M. 1996, ApJ, 465, 534 In the text NASA ADS  
• Grosbøl, P. J. 1985, A&AS, 60, 261 In the text NASA ADS  
• Knapen, J. H., & Beckman, J. E. 1996, MNRAS, 283, 251 In the text NASA ADS  
• Knapen, J. H., de Jong, R. S., Stedman, S., & Bramich, D. M. 2003, MNRAS, 344, 527 In the text NASA ADS  
• Koopmann, R. A., Kenney, J. D. P., & Young, J. 2001, ApJS, 135, 125 In the text NASA ADS  
• MacArthur, L. A., Courteau, S., & Holtzman, J. A. 2003, ApJ, 582, 689 In the text NASA ADS  
• Macri, L. M., Stetson, P. B., Bothun, G. D., et al. 2001, ApJ, 559, 243 In the text NASA ADS  
• Möllenhoff, C., Appenzeller, I., Gässler, W., et al. 1999, A&A, 352, L5 In the text NASA ADS  
• Möllenhoff, C., & Heidt, J. 2001, A&A, 368, 16 (Paper I) In the text NASA ADS  
• Moriondo, G., Giavonardi, C., & Hunt, L. K. 1998, A&AS, 130, 81 In the text NASA ADS  
• Okamura, S. 1988, PASP, 100, 524 In the text NASA ADS  
• Peletier, R. F., & Balcells, M. 1996, AJ, 111, 2238 In the text NASA ADS  
• Pohlen, M., Dettmar, R. J., & Lütticke, R. 2000, A&A, 357, L1 In the text NASA ADS  
• Pompei, E., & Natali, G. 1997, A&AS, 124, 129 In the text NASA ADS  
• Racine, R., & Harris, W. E. 1975, ApJ, 196, 413 In the text NASA ADS  
• Samland, M., & Gerhard, O. E. 2003, A&A, 399, 961 In the text NASA ADS  
• Sandage, A., & Bedke, J. 1994, The Carnegie Atlas of Galaxies, Carnegie Inst., Washington In the text  
• Sandage, A., & Tammann, G. A. 1981, A revised Shapley-Amescatalog of bright galaxies, Carnegie Institution, Washington In the text  
• Sérsic, J. L. 1968, Atlas de galaxias australes, Observatorio Astronómico de Córdoba In the text  
• Sharina, M. E., Karachentsev, I. D., & Tikhonov, N. A. 1996, A&AS, 119, 499 In the text NASA ADS  
• Simien, F., & de Vaucouleurs, G. 1986, ApJ, 302, 564 In the text NASA ADS  
• Trager, S. C., Dalcanton, J. J, & Weiner, B. J. 1999, in The formation of galactic bulges, ed. C. M. Carollo, H. C. Ferguson, R. F. G. Wyse (Cambridge University Press), 42 In the text  
• Trujillo, I., Graham, A. W., & Caon, N. 2001, MNRAS, 326, 869 In the text NASA ADS  
• Trujillo, I., Asensio Ramos, A., & Rubiño-Martín, J. A., et al. 2002, MNRAS, 333, 510 In the text NASA ADS  
• Tully, B. R. 1988, Nearby Galaxies Catalog (Cambridge) In the text  
• Tully, B. R., Shaya, E. J., & Pierce, M. J. 1992, ApJS, 80, 479 In the text NASA ADS  
• Vazdekis, A., Caruso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 In the text NASA ADS  
• Wadadekar, Y., Robbason, B., & Kembhavi, A. 1999, AJ, 117, 1219 In the text NASA ADS  
• Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, A. G. 2002a, A&A 381, 524 In the text NASA ADS  
• Westera, P., Samland, M., Buser, R., & Gerhard, O. E. 2002b, A&A, 389, 761 In the text NASA ADS