A&A 414, 429-443 (2004)
DOI: 10.1051/0004-6361:20031662
H. Bourdin1 - J.-L. Sauvageot2 - E. Slezak1 - A. Bijaoui1 - R. Teyssier2,3
1 - Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
2 - CEA/DSM/DAPNIA, Service d'Astrophysique, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
3 - NIC Consortium (Numerical Investigations in Cosmology, CEA Saclay)
Received 16 April 2003 / Accepted 19 September 2003
Abstract
Recent numerical simulations have
shown that the variations of the gas temperature in clusters of
galaxies are indicative of the dynamical state of these
clusters. Maps of the temperature variation show complex structures
with different shapes at different spatial scales, such as hot
compression regions, filaments, cooling flows, or large-scale
temperature profiles. A new multiscale spectro-imagery algorithm
for restoring the spatial temperature variations within clusters of
galaxies is presented here. It has been especially developed to work
with the EPIC MOS1, MOS2 and PN spectro-imagers on board the
XMM-Newton satellite. The temperature values are fitted to an emission
model that includes the source, the cosmic X-ray background and
cosmic-ray induced particle background. The spatial temperature
variations are coded at different scales in the wavelet space using
the Haar wavelet and denoised by thresholding the wavelet
coefficients. Our local temperature estimator behaves asymptotically
like an optimal mininum variance bound estimator. But it is highly
sensitive to the instrumental and astrophysical backgrounds, so that a
good knowledge of each component of the emission model is required.
Our algorithm has been applied to a simulated 60 ks observation of a
merging cluster at z =0.1. The cluster at different stages of
merging has been provided by 3-D hydrodynamical simulations of
structure formation (AMR). The multiscale approach has enabled us to
restore the faint structures within the core of the merging subgroups
where the gas emissivity is high, but also the temperature decrease at
large scale in their external regions.
Key words: galaxies: clusters: general - galaxies: interactions
Within the context of the so-called ![]() -Cold Dark Matter
scenario for hierarchical formation of structures, clusters of
galaxies are the largest structures and consequently the last ones
to have been formed. They are supposed to have undergone recently the transition between linear and non-linear
regimes. Actually, clusters of galaxies are formed by aggregation of groups
and subclusters of different masses along filamentary over-densities,
as shown by numerical simulations (Katz & White 1993; Colberg et al. 2000; Evrard 1990; Evrard et al. 2002).
-Cold Dark Matter
scenario for hierarchical formation of structures, clusters of
galaxies are the largest structures and consequently the last ones
to have been formed. They are supposed to have undergone recently the transition between linear and non-linear
regimes. Actually, clusters of galaxies are formed by aggregation of groups
and subclusters of different masses along filamentary over-densities,
as shown by numerical simulations (Katz & White 1993; Colberg et al. 2000; Evrard 1990; Evrard et al. 2002).
Most of the mass of clusters of galaxies is split into a dark matter component - around 70% of the total mass - and a gas halo component. The gas component is an optically thin plasma heated up to 108 K and confined within the gravitational potential at thermal equilibrium, which entails a thermal bremsstrahlung emission detectable in X-rays. Since the cluster accretion process is mainly driven by gravitation, observing the X-ray emission of this gas provides a significant piece of information about the dynamical state of the cluster as a whole. Besides, such studies are only limited by photon statistics since the intra-cluster gas is an extended source, whereas optical studies using galaxy counts are limited by the galaxy distribution. Recent hydrodynamic simulations (Ritchie & Thomas 2001; Ricker & Sarazin 2001; Roettiger et al. 1996; Teyssier 2002) have shown the sensibility of the gas surface brightness and temperature variations to events related to post and on-going mergers such as gas compressions, cooling flows and cold fronts. But our understanding of the details of the merger scenario, especially the physical processes occurring in the dissipative phase, must strongly be improved by benefitting from new observational data on nearby clusters. The new generation of X-ray telescopes (Chandra; XMM-Newton) now provides data with enough spatial and spectral resolution to try to detect such variations. However, the X-ray photon statistics with its typical emission of a few photons per second in a field of view (FOV) of 30 arcmin in diameter leads to a much lower signal-to-noise ratio than obtained with usual optical observations. Consequently any analysis of X-ray spectroscopic data must involve a spatial binning to increase the photon statistics. To do so, while preserving the best spatial resolution, multiscale algorithms can be applied. We introduce here such a multiscale spectro-imagery algorithm dedicated to the optimal mapping of temperature variations in the observed intra-cluster plasma.
This algorithm has been especially designed to process data from the XMM-EPIC spectro-imagers, MOS1, MOS2 and PN cameras. Thanks to a maximum likelihood algorithm the temperature of the gas inside each element of a grid covering the field of view is computed with its signal-to-noise ratio. Several computations are done for grids with different spatial resolution following a dyadic scheme, in order to obtain the final temperature map from significant temperature variations at different scales. To do so a wavelet formalism is applied: a selection of significant wavelet coefficients at different scales enables us to reconstruct the optimal temperature map. The spectral analysis is introduced in the first section while the multiscale algorithm is described in the second one. Results from simulations of EPIC-XMM data on merging clusters are discussed in the third section. The last section is devoted to our conclusions.
The EPIC spectro-imagers work in photon count mode. So, the data to be processed are a set of photon events, composed of the photon energy and its location on the detector surface. Given the events within an area of the detector we get the observed emission spectrum of the related region of the sky. By modeling this emission into its different astrophysical and instrumental components, the proper cluster emission can be inferred from this spectrum and the temperature and emissivity of the gas can be derived using an optically thin plasma emissivity model.
The observed emission spectrum has been modelled as a combination of three different emission components. The first of these components is the proper cluster emission, the second one is the cosmic X-ray background (CXB) and the last one is a "particle background'' which has been introduced to model the EPIC detector response to induced particles from interactions of cosmic particles with the satellite platform.
The first two components correspond to astrophysical sources. In that case the photons have to follow the telescope optical path before reaching the detector and the emission spectra of these sources must be convolved with the spectral instrumental response. The EPIC XMM-Newton photon counts suffer from a vignetting effect which depends both on coordinates on the detector and on the photon energy. Considering this energy dependence, the vignetting function of each EPIC camera is more or less flat at low energy (0.5-5 keV), but it decreases at high energy (>5 keV), so that the net statistics are poorer at high energy. The spatial vignetting function decreases the photons counts in the focal plane as a function of the distance to the detector optical axis. This vignetting effect has to be taken into account when considering the spectral instrumental response. The convolution of the CXB and cluster emissivity component can be done for each camera using the associated vignetting function provided that the mean spatial location of the analyzed events on the detector surface is known.
The cluster X-ray emission model is modelled as an optically thin
plasma emission (Mewe 1985, 1986). The plasma is considered to be a
hot (
![]() )
and low-density one (
)
and low-density one (
![]() cm-3) at the coronal limit (Sarazin 1986). Assuming the
plasma to be at the ionization equilibrium this emission model is
composed of two components. The first component is a continuum of
free-free and free-bound radiation emitted during the Coulomb
scattering of the electrons by the plasma ions. The second one
is a line radiation due to recombination of electrons after the
collision process of the different elements of the plasma. Under these
assumptions the shape of the emission spectra for the galaxy cluster
only depends on the plasma equilibrium temperature T and elements
abundances. But the optical path from the source to the detector
entails three distortions of this spectral shape when observed: the
redshift, the X-ray absorption due to ionization of galactic hydrogen
and the EPIC-XMM instrumental response. So, given the element
abundances of the plasma, the redshift of the source, the hydrogen
column density between the observer and the source and the EPIC-XMM
instrumental response, a table of normalized emission spectra
cm-3) at the coronal limit (Sarazin 1986). Assuming the
plasma to be at the ionization equilibrium this emission model is
composed of two components. The first component is a continuum of
free-free and free-bound radiation emitted during the Coulomb
scattering of the electrons by the plasma ions. The second one
is a line radiation due to recombination of electrons after the
collision process of the different elements of the plasma. Under these
assumptions the shape of the emission spectra for the galaxy cluster
only depends on the plasma equilibrium temperature T and elements
abundances. But the optical path from the source to the detector
entails three distortions of this spectral shape when observed: the
redshift, the X-ray absorption due to ionization of galactic hydrogen
and the EPIC-XMM instrumental response. So, given the element
abundances of the plasma, the redshift of the source, the hydrogen
column density between the observer and the source and the EPIC-XMM
instrumental response, a table of normalized emission spectra
![]() can be computed with temperature T and energy e. Such a table is
plotted in Fig. 1, where the emission spectra have
been convolved with the EPIC-XMM MOS1 focus instrumental response,
where no vignetting occurs.
can be computed with temperature T and energy e. Such a table is
plotted in Fig. 1, where the emission spectra have
been convolved with the EPIC-XMM MOS1 focus instrumental response,
where no vignetting occurs.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{f1.3867.eps}}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg24.gif) |
Figure 1:
Normalized emissivity
|
| Open with DEXTER | |
The cosmic X-ray background (CXB) is composed of three components. The
first two components correspond to the "soft X-ray background'' due
to the hot local bubble which can be modelled as an optically thin
plasma emission at 0.204 and 0.074 keV respectively. The third
component is modelled using a power-law emission with index
![]() and corresponds to the hard X-ray background (Lumb et al. 2002). As
for the cluster component, the CXB component have to be convolved with
the XMM-EPIC instrumental response. Figure 2 shows the three
X-ray background spectra convolved with the EPIC-XMM focus
instrumental response.
and corresponds to the hard X-ray background (Lumb et al. 2002). As
for the cluster component, the CXB component have to be convolved with
the XMM-EPIC instrumental response. Figure 2 shows the three
X-ray background spectra convolved with the EPIC-XMM focus
instrumental response.
For each camera, the "particle background'' can be modelled as a flat energy response plus some fluorescence lines of the detector in the 1.4-2 keV band (Al, Si). Contrary to the CXB the particles background does not correspond to photons following the telescope optical path but to particles impacting the CCD without interacting with the telescope mirrors. Consequently the particle background is supposed to be uniform on the detector surface and needs not be convolved with the instrumental response.
Let us call
![]() and
and
![]() the normalized particles and
astrophysical background components, respectively. We get an emission
spectrum with three components, where the relative contribution of each
component, i.e.
the normalized particles and
astrophysical background components, respectively. We get an emission
spectrum with three components, where the relative contribution of each
component, i.e.
![]() for the cluster,
for the cluster,
![]() for the CXB and
for the CXB and
![]() for the particles, can be taken into account by means of three
normalization terms,
for the particles, can be taken into account by means of three
normalization terms, ![]() ,
,
![]() and
and
![]() ,
respectively. Let us call
,
respectively. Let us call
![]() the normalized emission model and
the normalized emission model and ![]() its normalization
term, we get:
its normalization
term, we get:
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{f2.3867.eps}}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg38.gif) |
Figure 2:
Three component X-ray background
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{f3.3867.eps}}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg39.gif) |
Figure 3: EPIC-XMM MOS1 total focus emissivity in the line of sight of an isothermal cluster at 5 keV, taking into account the cluster component, but also CXB and particle background. |
| Open with DEXTER | |
Let us now consider a set of N events of known location on the
detector surface corresponding to a simulated or real galaxy cluster
observation. Providing that the mean background emissivities
![]() and
and
![]() are known, the temperature T and emissivity NS of the
cluster are the unknown parameters to be fitted to the global emission
model F(T,e).
are known, the temperature T and emissivity NS of the
cluster are the unknown parameters to be fitted to the global emission
model F(T,e).
The mean background emissivities
![]() and
and
![]() are supposed to be
known and uniform over the detector surface. Indeed, considering that
events in the 10-12 keV energy band are particles events exclusively,
the value of
are supposed to be
known and uniform over the detector surface. Indeed, considering that
events in the 10-12 keV energy band are particles events exclusively,
the value of
![]() can be computed by adding all the events within the
10-12 keV range and extrapolating the bolometric particle emissivity
from the particle emission model. The value of
can be computed by adding all the events within the
10-12 keV range and extrapolating the bolometric particle emissivity
from the particle emission model. The value of
![]() can be estimated
empirically from the emissivity of external regions of the FOV where
the CXB emissivity overcomes the cluster emissivity. Introducing the
emissivity parameter
can be estimated
empirically from the emissivity of external regions of the FOV where
the CXB emissivity overcomes the cluster emissivity. Introducing the
emissivity parameter
![]() to get a bounded parameter space,
Eqs. (1) and (2) can be rewritten as:
to get a bounded parameter space,
Eqs. (1) and (2) can be rewritten as:
| |
= | ||
| = | ![$\displaystyle {\rm N} \left[\frac{1}{r} - \frac{1}{{\rm N}} \big({\rm N}_{\rm B}+ {\rm N}_{\rm P}\big)
\right].$](/articles/aa/full/2004/05/aa3867/img48.gif) |
(4) |
![\begin{displaymath}{\rm V}= - \left[{\rm F}_{\rm M}\right]^{-1},\quad \textrm{wi...
...{ll}
F_{\rm 1}& \rho \\
\rho & F_{\rm 2}
\end{array}\right],
\end{displaymath}](/articles/aa/full/2004/05/aa3867/img68.gif)
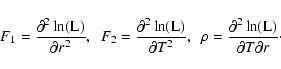
Let us spatially sample the EPIC-XMM FOV along both axes k and l.
Given an event-list associated with the pixel k, l, but also an
emission model
![]() taking into account the local
instrumental response, the maximum likelihood method described in the
previous section enables us to define a local estimator
taking into account the local
instrumental response, the maximum likelihood method described in the
previous section enables us to define a local estimator
![]() of the
parameter T(k,l).
of the
parameter T(k,l).
To compute the
![]() value with a high enough signal-to-noise ratio
the statistics may have to be enhanced by means of a spatial binning,
but this decreases the spatial resolution. Consequently, given the
requested signal-to-noise value, an optimal local bin size has to be
computed to define
value with a high enough signal-to-noise ratio
the statistics may have to be enhanced by means of a spatial binning,
but this decreases the spatial resolution. Consequently, given the
requested signal-to-noise value, an optimal local bin size has to be
computed to define
![]() ,
which entails a multiscale exploration
of the
,
which entails a multiscale exploration
of the
![]() signal. A natural multiscale exploration of a given
signal
signal. A natural multiscale exploration of a given
signal
![]() is provided by the wavelet transform
is provided by the wavelet transform
![]() (cf. Appendix B), where the signal
(cf. Appendix B), where the signal
![]() is unfolded in the
space-scale domain, with a as the scale parameter. Let us define
is unfolded in the
space-scale domain, with a as the scale parameter. Let us define
![]() the wavelet transform of
the wavelet transform of
![]() .
The aim of our
algorithm is to show the significant
.
The aim of our
algorithm is to show the significant
![]() variations at
different scales thanks to a thresholding of the wavelet space.
variations at
different scales thanks to a thresholding of the wavelet space.
The chosen wavelet transform is based on the Haar wavelet as will
be discussed in Sect. 3.2. As a first step,
successive binnings of the EPIC-XMM data set at each scale and fitting
of the emission model
![]() of Eq. (2)
with the maximum likelihood algorithm enable to define successive
approximations,
of Eq. (2)
with the maximum likelihood algorithm enable to define successive
approximations,
![]() ,
of the
,
of the
![]() distribution. Then
the "first guess'' set of wavelet coefficients
distribution. Then
the "first guess'' set of wavelet coefficients
![]() is computed by applying the high-pass
analysis filters corresponding to the Haar wavelet to
is computed by applying the high-pass
analysis filters corresponding to the Haar wavelet to
![]() .
Notice that this set of coefficients does not
constitute a real wavelet transform since the coefficients are
computed by means of different emission models from scale to
scale. Nevertheless, it may be considered as an approximation of the
real wavelet transform
.
Notice that this set of coefficients does not
constitute a real wavelet transform since the coefficients are
computed by means of different emission models from scale to
scale. Nevertheless, it may be considered as an approximation of the
real wavelet transform
![]() that we are looking for.
Within the wavelet space the respective noise and signal contribution
to the signal can be easily separated at each scale. This will be
described for the chosen transform in Sect. 3.3.
The last step, developed in Sect. 3.4,
consists of removing iteratively the noise contribution
to
that we are looking for.
Within the wavelet space the respective noise and signal contribution
to the signal can be easily separated at each scale. This will be
described for the chosen transform in Sect. 3.3.
The last step, developed in Sect. 3.4,
consists of removing iteratively the noise contribution
to
![]() ,
which leads to a new set of denoised wavelet
coefficients
,
which leads to a new set of denoised wavelet
coefficients
![]() .
The final set of coefficients will
consist of the expected
.
The final set of coefficients will
consist of the expected
![]() wavelet transform. This
process is performed from the lowest to the highest resolution
allowing us to construct in the direct space better and better
approximations of
wavelet transform. This
process is performed from the lowest to the highest resolution
allowing us to construct in the direct space better and better
approximations of
![]() and to obtain the optimal temperature map
and to obtain the optimal temperature map
![]() .
.
So as to compute the set of coefficients
![]() a
wavelet function has to be chosen. The 2-D Haar wavelet (Haar 1910) which matches
the square spatial sampling is the most suitable since a square
binning has been chosen. It is a compact support square kernel with
coefficients
a
wavelet function has to be chosen. The 2-D Haar wavelet (Haar 1910) which matches
the square spatial sampling is the most suitable since a square
binning has been chosen. It is a compact support square kernel with
coefficients
![]() and
and
![]() ,
following the amplitude normalization condition of the wavelet coefficients.
The Haar wavelet is anisotropic, so that the
wavelet transform results at each scale a = 2j with
,
following the amplitude normalization condition of the wavelet coefficients.
The Haar wavelet is anisotropic, so that the
wavelet transform results at each scale a = 2j with
![]() in a decomposition onto three detail spaces with wavelet
coefficients
in a decomposition onto three detail spaces with wavelet
coefficients
![]() where p=h,v,d indicates the
horizontal, vertical and diagonal details, respectively. Their value
can be computed from the convolution of the approximation at scale
where p=h,v,d indicates the
horizontal, vertical and diagonal details, respectively. Their value
can be computed from the convolution of the approximation at scale
![]() ,
,
![]() ,
using the high-pass analysis
filter
,
using the high-pass analysis
filter
![]() (cf. Appendix B).
(cf. Appendix B).
Let us associate with each pixel k, l of the FOV the set of events
found within a square bin of size
![]() .
The fitting of this
set of events to the model
.
The fitting of this
set of events to the model
![]()
![]() will enable us to compute the set of
coefficients
will enable us to compute the set of
coefficients
![]()
![]() . To do so, the approximations
. To do so, the approximations
![]() with their rms values
with their rms values
![]() are first computed thanks
to the maximum likelihood fitting of the model
are first computed thanks
to the maximum likelihood fitting of the model
![]() to the data corresponding to pixel k,l with
scale
to the data corresponding to pixel k,l with
scale
![]() .
Then the wavelet coefficients
.
Then the wavelet coefficients
![]() are computed by applying the high-pass
analysis filters
are computed by applying the high-pass
analysis filters
![]() (cf. Fig. B.2). The variances
(cf. Fig. B.2). The variances
![]() of the wavelet coefficients
of the wavelet coefficients
![]() are computed by applying the
low-pass analysis filter
are computed by applying the
low-pass analysis filter
![]() to the variances of the
smoothed plane
to the variances of the
smoothed plane
![]() .
.
The binning of the data has been chosen such that the smoothed
planes
![]() have the same number of pixels
whatever the scale is, yielding a redundant wavelet transform.
As it will be explained in the following section the redundancy has
been chosen in order to balance the usual poor statistics of the data.
have the same number of pixels
whatever the scale is, yielding a redundant wavelet transform.
As it will be explained in the following section the redundancy has
been chosen in order to balance the usual poor statistics of the data.
We get a set of coefficients
![]() with zero mean
value and variances
with zero mean
value and variances
![]() .
Given the
signal-to-noise ratio R, the coefficients
.
Given the
signal-to-noise ratio R, the coefficients
![]() with value overcoming R times the local variance will be considered as
significant whereas the other ones
with value overcoming R times the local variance will be considered as
significant whereas the other ones
![]() will
be considered as non-significant:
will
be considered as non-significant:
Notice that due to the redundancy of the algorithm, the wavelet
coefficients
![]() are computed from dependent
data. A crude estimation of dependency of the coefficients of a
wavelet plane is that they are linked to each other, providing that
they are included within a region of area a2. This information has
been used to remove some false detections of significant regions. The
connected significant regions of
are computed from dependent
data. A crude estimation of dependency of the coefficients of a
wavelet plane is that they are linked to each other, providing that
they are included within a region of area a2. This information has
been used to remove some false detections of significant regions. The
connected significant regions of
![]() are kept providing that
their area overcomes a2, but are considered non-significant otherwise.
are kept providing that
their area overcomes a2, but are considered non-significant otherwise.
This splitting of the wavelet space enables us to construct a true
wavelet transform
![]() from
from
![]() .
Since all the available information about
the variations of parameter
.
Since all the available information about
the variations of parameter
![]() is considered as being contained
within the significant domain of the wavelet space, the wavelet
transform
is considered as being contained
within the significant domain of the wavelet space, the wavelet
transform
![]() can be constructed by keeping the
coefficient values of the significant domain of
can be constructed by keeping the
coefficient values of the significant domain of
![]() .
Conversely the coefficient values of the
non-significant domain, where information about the variations of
.
Conversely the coefficient values of the
non-significant domain, where information about the variations of
![]() is considered as lost, will be
iteratively modified. Since no variation of
is considered as lost, will be
iteratively modified. Since no variation of
![]() has been
detected within this domain, a priori information will be added in
place of the lack of information: it will be supposed that the
has been
detected within this domain, a priori information will be added in
place of the lack of information: it will be supposed that the
![]() variations are minimal. This condition leads to the Tikhonov
smoothness constraint or regularization, where the gradient of the
smoothed planes defined as
variations are minimal. This condition leads to the Tikhonov
smoothness constraint or regularization, where the gradient of the
smoothed planes defined as
![]() have to be minimized, which
implies the following condition (cf. Bobichon & Bijaoui 1997):
have to be minimized, which
implies the following condition (cf. Bobichon & Bijaoui 1997):
Let us call
![]() and
and
![]() the wavelet coefficients computed by applying the high pass analysis filters
the wavelet coefficients computed by applying the high pass analysis filters
![]() to the respective appproximations,
to the respective appproximations,
![]() and
and
![]() ,
Eq. (7) is solved thanks to an iterative Van-Cittert algorithm on the wavelet coefficients constructed by
successive filtering and reconstruction of the smoothed planes
,
Eq. (7) is solved thanks to an iterative Van-Cittert algorithm on the wavelet coefficients constructed by
successive filtering and reconstruction of the smoothed planes
![]() at scale
at scale
![]() :
:
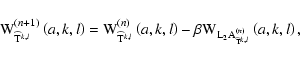 |
(9) |
We describe the coarse method we adopted to estimate
the final error on the temperature map
![]() .
The temperature
map
.
The temperature
map
![]() can be considered in the direct space as a linear
combination of the different wavelet coefficients
can be considered in the direct space as a linear
combination of the different wavelet coefficients
![]() .
For each pixel k, l, the
.
For each pixel k, l, the
![]() standard deviation is mainly due to the wavelet plane
standard deviation is mainly due to the wavelet plane
![]() standard deviation, where the
scale a corresponds to the highest resolution where
standard deviation, where the
scale a corresponds to the highest resolution where
![]() is found significant. Consequently, we
decided to estimate the error-bar
is found significant. Consequently, we
decided to estimate the error-bar
![]() from the
from the
![]() standard deviation. Since
standard deviation. Since
![]() is included within the significant
domain, the
is included within the significant
domain, the
![]() standard deviation is
close to the
standard deviation is
close to the
![]() standard deviation
value,
standard deviation
value,
![]() .
We get at pixel k, l,
.
We get at pixel k, l,
![$\sigma_{\widehat{{\rm T}}^{k,l}}(k,l) =
\sqrt {\sum\limits_{p}{\left[\sigma_{{\rm W}^{(0)}_{p,{\widehat{{\rm T}}^{k,l}}}}(a,k,l)\right]^2}}$](/articles/aa/full/2004/05/aa3867/img122.gif) ,
where a is the
highest resolution of structure detection.
,
where a is the
highest resolution of structure detection.
The performance and limits of the algorithm have been tested by means
of a set of simulated observations with different values of source
temperatures and emissivities, as well as background emissivities. The
spectral fitting performance will be introduced in a first section
with uniform source temperatures and emissivities. Then the multiscale
algorithm will be tested in a second section on model EPIC-XMM
observations with non-uniform temperatures and emissivities but with
only one gas emission component
![]() .
.
The spectral fitting performance of our algorithm has been tested
against different values of the parameters of the emission model -
cf. Eq. (3) -, taking or not taking into account
instrumental components. To do so, a cube
![]() is constructed
for different values of T(k,l) and
is constructed
for different values of T(k,l) and
![]() ,
the temperature and
emissivity of the source, respectively, as well as for
,
the temperature and
emissivity of the source, respectively, as well as for
![]() and
and
![]() ,
the background emissivities. The chosen simulated camera is the
EPIC-XMM MOS1. An observation can be simulated by drawing randomly
within the Poisson distribution of parameter
,
the background emissivities. The chosen simulated camera is the
EPIC-XMM MOS1. An observation can be simulated by drawing randomly
within the Poisson distribution of parameter
![]() a value for
the number of photons at position k,l,e. The models used
hereafter are
a value for
the number of photons at position k,l,e. The models used
hereafter are
![]() square images where the source
temperature and emissivity are considered uniform, and fixed at 3 keV
and 100 photons per pixel, respectively. The fitting is first tested
without any background emissivity and then with different particles
and CXB background emissivities values. In each case the vignetting
influence was also tested by constructing emission models with or
without vignetting. Just like for the first step of our multiscale
algorithm, the fitting of
square images where the source
temperature and emissivity are considered uniform, and fixed at 3 keV
and 100 photons per pixel, respectively. The fitting is first tested
without any background emissivity and then with different particles
and CXB background emissivities values. In each case the vignetting
influence was also tested by constructing emission models with or
without vignetting. Just like for the first step of our multiscale
algorithm, the fitting of
![]() is performed at different
resolutions a, leading to different maps
is performed at different
resolutions a, leading to different maps
![]() with a = 2j,
with a = 2j,
![]() .
Actually the
fitting has been performed on four successive resolutions with two
emission models at 100 and 200 photons per pixel respectively, leading
to eight maps with statistics increasing by a factor of two, from 200 to
25 600 cluster photons per pixel. The first spectral fitting test is
performed without any background. The mean, standard deviations and a
selection of six histograms of the different maps T(k,l,a)corresponding to this spectral fitting are plotted in
Fig. 4. An instrumental response with vignetting
factor was introduced for the first histogram, but without vignetting
for the second one. The histograms of Figs. 5 and 6
correspond to emission models with particles and
CXB background, respectively, where each background emissivity values
have been set to 0.5 and 2 times the value of the cluster emissivity.
.
Actually the
fitting has been performed on four successive resolutions with two
emission models at 100 and 200 photons per pixel respectively, leading
to eight maps with statistics increasing by a factor of two, from 200 to
25 600 cluster photons per pixel. The first spectral fitting test is
performed without any background. The mean, standard deviations and a
selection of six histograms of the different maps T(k,l,a)corresponding to this spectral fitting are plotted in
Fig. 4. An instrumental response with vignetting
factor was introduced for the first histogram, but without vignetting
for the second one. The histograms of Figs. 5 and 6
correspond to emission models with particles and
CXB background, respectively, where each background emissivity values
have been set to 0.5 and 2 times the value of the cluster emissivity.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{f4a.3867.eps}\includegraphics[width=8cm,clip]{f4b.3867.eps}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg129.gif) |
Figure 4:
Distribution of the results of the temperature fits for a
simulated EPIC-XMM MOS1 observation of an isothermal extended
source. The source emissivity is uniform. No backgound emission is
included. The histograms with increasing darkness correspond to three
fixed source emissivity |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{f5a.3867.eps}\includegraphics[width=8cm,clip]{f5b.3867.eps}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg130.gif) |
Figure 5: Same as Fig. 4 with real instrumental response and particles background emission simulated. Left: background emissivity value of 0.5 times the cluster emissivity value. Right: Background emissivity value of two times the cluster emissivity value. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{f6a.3867.eps}\includegraphics[width=8cm,clip]{f6b.3867.eps}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg131.gif) |
Figure 6: Same as Fig. 4 with real instrumental response and cosmic X-ray background emission simulated. Left: background emissivity of 0.5 times the cluster emissivity value. Right: Background emissivity value of two times the cluster emissivity value. |
| Open with DEXTER | |
Let us first consider the fitting of the isothermal emission model
![]() at 3 keV with a null background emissivity
(cf. Fig. 4). The temperature distributions obtained
from fittings with more than 1600 cluster photons per pixel are symmetric
around a peak value at 3 keV.
at 3 keV with a null background emissivity
(cf. Fig. 4). The temperature distributions obtained
from fittings with more than 1600 cluster photons per pixel are symmetric
around a peak value at 3 keV.
The maximum likelihood method used for the model fitting should
provide a consistent estimator whose variance is close to the
Rao-Cramer limit (Kendall & Stuart 1973) of the Minimum Variance
Bound (MVB) estimators. We have checked that the variances of the
temperature histograms are close to the mean of the MVB variances
values computed from the Fisher matrix after each spectral
fitting. They follow the statistics with N counts, so that
![]() .
The variances of distributions obtained
from fittings with more than 400 cluster photons per pixel are in agreement
with the MVB variance, but the variance of the distribution obtained with
200 cluster photons per pixel is not.
.
The variances of distributions obtained
from fittings with more than 400 cluster photons per pixel are in agreement
with the MVB variance, but the variance of the distribution obtained with
200 cluster photons per pixel is not.
The dispersion obtained with 200 cluster photons is asymmetric and does
not peak at the 3 keV value, so that a bias is evidenced. This "low
temperature bias'' is due to the emissivity of the high-energy part of
the source emission spectra, with a variation of several orders of
magnitude between the high and low temperature emission models
(cf. Fig. 1), and a high relative chance
fluctuation of the high-energy photons number. It has been reduced by
an histogram equalization of the energy distribution of the
photons. It is not worth fully removing this bias since it is only
important in the case of very poor statistics when the temperature
dispersion is high anyway. Instead of removing it, two conditions
have been added to the spectral fitting. The result of the temperature
fit of the different resolution elements is only taken into account
providing that on the one hand, the ![]() error bars values are lower
than 1 keV and on the other hand, more than about 500 photons are
available so that the statistics is considered high enough.
error bars values are lower
than 1 keV and on the other hand, more than about 500 photons are
available so that the statistics is considered high enough.
Now let us recall that due to the spatial variations of the detector response the different temperatures values are not computed following the same process which is questionable. To get rid of this drawback, but also to test the vignetting influence on the spectral fitting, a model with the same source component as the previous one but without vignetting has been built (cf. Fig. 4). The detector response is now uniform and similar to the focus response all over the detector surface. We get a close to MVB estimator at each resolution with lower temperature dispersions than the dispersions obtained when the vignetting effect occurs. Indeed, the removal of the vignetting effect results in providing much higher energy photons, which enhances the statistics and reduces the "low temperature bias''.
The particles background influence on the spectral fitting is tested thanks to a model series with vignetting and the same source temperature and emissivities as in Sect. 4.1.1 but with particles background emissivities of 0.5 and 2 times the cluster emissivity (cf. Fig. 5). The temperature variance is larger than in the case of null background emissivity and all the larger since the background emissivity increases. The fitted source temperatures are found to be still distributed around the T = 3 keV value in the case of a cluster emissivity higher than 3200 photons per pixels, but biased in the case of lower statistics. The "low-temperature bias'' is enhanced here since the source high-energy photons are much less numerous than the high-energy particles. Yet despite the bias, the temperature estimator follows the MVB variance in the case of a cluster emissivity value higher than 400 photons per pixel.
Let us now discuss the CXB influence on the spectral fitting thanks to a model series with vignetting and CXB emissivities of 0.5 and 2 times the cluster emissivity (cf. Fig. 6). Whatever the CXB emissivity is, the fitted temperatures peak at 3 keV in the case of a cluster emissivity value higher than 1600 photons per pixel, with lower dispersion and temperature bias than for the toy-model series with particles background. Also, the temperature estimator behaves like an MVB estimator. The vignetted CXB provides many fewer high-energy photons than the particles background. Consequently, on the one hand the global background emission is lowered which reduces the temperature dispersion and on the other hand the lack of background low-energy photons reduces the low-temperature bias.
Our temperature estimator is based on the maximum
likelihood function computed from the emission model
![]() ,
which provides a close to MVB estimator. Actually the Rao-Cramer limit of MVB estimators cannot be
reached, due to the dependency between both parameters r and T in the case of an emission model with background.
The variance and bias of the estimator cannot be
estimated analytically since the emission model is a numerical model,
but tests like those performed enable us to evaluate them for different
emission models. The temperature estimator behaves like an MVB
estimator in the case of good statistics - more than about 500 photons per
pixel - and low background - less than half of the cluster emissivity
in our case. Its use in cases of low statistics or high background level is more
critical and results must be analyzed carefully.
,
which provides a close to MVB estimator. Actually the Rao-Cramer limit of MVB estimators cannot be
reached, due to the dependency between both parameters r and T in the case of an emission model with background.
The variance and bias of the estimator cannot be
estimated analytically since the emission model is a numerical model,
but tests like those performed enable us to evaluate them for different
emission models. The temperature estimator behaves like an MVB
estimator in the case of good statistics - more than about 500 photons per
pixel - and low background - less than half of the cluster emissivity
in our case. Its use in cases of low statistics or high background level is more
critical and results must be analyzed carefully.
Let us now test the second step of our algorithm, i.e. the multiscale
analysis, on non-isothermal temperature maps built from a model.
The simulated source is an EPIC-XMM MOS1 2D model observation with
emission model
![]() .
Both particles and CXB background
emissivities,
.
Both particles and CXB background
emissivities, ![]() and
and ![]() ,
have been set to five photons per
pixel. The source is now composed of four isothermal emitting regions:
an external ring at 3 keV, two elliptical regions at 4 and 6 keV
respectively and the remaining central region at 5 keV. Three
emissivity models following a 2-D Gaussian distribution with total
flux of 105, 106 and 107 photons are tested. The
corresponding emissivity per pixel range from 10 photons at the edge
of the images to 100, 1000 and 10 000 photons, respectively, at the
centre of the image.
,
have been set to five photons per
pixel. The source is now composed of four isothermal emitting regions:
an external ring at 3 keV, two elliptical regions at 4 and 6 keV
respectively and the remaining central region at 5 keV. Three
emissivity models following a 2-D Gaussian distribution with total
flux of 105, 106 and 107 photons are tested. The
corresponding emissivity per pixel range from 10 photons at the edge
of the images to 100, 1000 and 10 000 photons, respectively, at the
centre of the image.
The images size is
![]() and the wavelet analysis was
performed on six scales in order to prevent large scale edge effects,
so that details with typical width
from 1 to 32 pixels are analysed. The source temperature distribution
and reconstructed temperature maps are shown in
Fig. 7. The temperature maps have been cut in the middle
of each picture so as to show the temperature variations with
error-bars in Fig. 8. As expected, the better the statistics
is the better the model is reproduced.
Due to the shape of the emissivity map of the
source (cf. top-left plot in Fig. 8), the temperature
variations can only be seen in the central regions with high
statistics whereas the external regions with low statistics have been
strongly smoothed. The temperature variations of the central regions
have been shown at the first scale for the model with 107 photons,
but have been smoothed due to the lower statistics for both
other models. In the external regions, a large-scale mean temperature
is computed whatever the global emissivity is due to the low statistics as
well as the isothermality of the model.
and the wavelet analysis was
performed on six scales in order to prevent large scale edge effects,
so that details with typical width
from 1 to 32 pixels are analysed. The source temperature distribution
and reconstructed temperature maps are shown in
Fig. 7. The temperature maps have been cut in the middle
of each picture so as to show the temperature variations with
error-bars in Fig. 8. As expected, the better the statistics
is the better the model is reproduced.
Due to the shape of the emissivity map of the
source (cf. top-left plot in Fig. 8), the temperature
variations can only be seen in the central regions with high
statistics whereas the external regions with low statistics have been
strongly smoothed. The temperature variations of the central regions
have been shown at the first scale for the model with 107 photons,
but have been smoothed due to the lower statistics for both
other models. In the external regions, a large-scale mean temperature
is computed whatever the global emissivity is due to the low statistics as
well as the isothermality of the model.
![\begin{figure}
\par\resizebox{12cm}{!}{
\begin{tabular}{cccc}
\resizebox{5cm}{!}...
...s[clip]{f7d.3867.eps}} \\
\end{tabular}}\hfill
\parbox[h]{55mm}
{}
\end{figure}](/articles/aa/full/2004/05/aa3867/Timg137.gif) |
Figure 7: Temperature maps of simulated EPIC-XMM MOS1 observations, - temperatures coded in keV -. Top-left: temperature model. Top-right: reconstructed temperature map for a global lemissivity of 105photons. Bottom left and right: reconstructed temperature map for a global emissivity of 106 and 107 photons, respectively. The dashed line on the reconstructed maps corresponds to profiles displayed in Fig. 8. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{18cm}{!}{
\begin{tabular}{cc}
\resizebox{5cm}{!}{\...
...cm}{!}{\includegraphics[clip]{f8c.3867.eps}} \\
\par \end{tabular}}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg138.gif) |
Figure 8:
Temperature profiles across the central region of simulated
EPIC-XMM MOS1 observations, - temperatures coded in keV -. Top-left:
emissivity profiles of the three emission models corresponding to
global emissivities of 105, 106 and 107 photons. Top-right:
temperature profile with error-bars for a global emissivity value of
105 photons. Bottom left and right: temperature profiles with
error-bars for respective global emissivity values of 106 and
107 photons. Bold line: temperature cuts, with grey shaded |
| Open with DEXTER | |
The quality of the result can been checked by comparing the temperature profiles along the dashed lines of Fig. 7 with the model temperature values (cf. Fig. 8). Notice that such a comparison is not straightforward due to the spatial rebinning of the restored temperature maps. That is why the temperature profile of each restored map needs to be compared with the profile of a "rebinned" model map. The rebinned model maps are computed by applying the wavelet algorithm to the model temperature map with same thresholding of the coefficients as applied for each restored map. To do so, the temperature values are averaged within grids at different scales instead of fitting the data. Two rebinned model map are compared with each restored map. The first one is obtained by computing the arithmetical mean of the temperatures of the model map within the different bins. The second one is obtained by computing a temperature mean which has been weighted by the cluster emissivity. The temperature profile of both rebinned model maps are superimposed to each restored map by means of dotted and dashed lines, respectively. Both cuts are closer to the cuts of the restored temperature maps than the cut of the non-rebinned temperature model. The cut computed from weighted means of the temperature model is in agreement with the restored temperature maps, since it is included within the corresponding error-bars.
To conclude about these simulated observations, the multiscale algorithm has enabled us to adapt the spatial resolution to the local available statistics. The significance of the result has been checked thanks to a multiscale unfolding of the model temperature map. The agreement between the rebinned model map and restored map shows that the spectral fitting is satisfactory whatever the scale or position where it is performed, despite the spatial variation of the likelihood function.
![\begin{figure}
\par\resizebox{18cm}{!}{
\begin{tabular}{cccc}
\resizebox{5cm}{!}...
...box{!}{5cm}{\includegraphics[clip]{f9h.3867.eps}} \\
\end{tabular}}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg140.gif) |
Figure 9:
Simulated merging cluster at
|
| Open with DEXTER | |
In order to test the ability of our algorithm to detect the
temperature variations expected within merging clusters, the
observation of a cluster at different stages of merging have been
simulated. This cluster has been obtained from adaptive mesh
refinement 3-D hydrodynamical simulations of structures formation (for
a complete description of the numerical simulation code, see Teyssier
2002). In order to simulate a merging cluster in a realistic
cosmological environment, a low resolution (
![]() )
large scale (
)
large scale (
![]() Mpc)
Mpc) ![]() -CDM simulation was
first performed. More than 100 large clusters of galaxies formed in
this run. One cluster undergoing a violent merger was selected.
Then, the exact same universe was re-simulated, adding many more
particles and mesh points in the region surrounding the cluster. The
same original box (400 h-1 Mpc aside) is now described with
400 000 particles and 4 times more mesh points within the cluster virial
radius. The mesh spacing in the cluster core has gone down to 6
-CDM simulation was
first performed. More than 100 large clusters of galaxies formed in
this run. One cluster undergoing a violent merger was selected.
Then, the exact same universe was re-simulated, adding many more
particles and mesh points in the region surrounding the cluster. The
same original box (400 h-1 Mpc aside) is now described with
400 000 particles and 4 times more mesh points within the cluster virial
radius. The mesh spacing in the cluster core has gone down to 6
![]() kpc,
corresponding to a formal resolution of
655363. This "zoom'' simulation lasted more than 100 CPU h
on the Fujitsu VPP 5000 at CEA Grenoble. For this work, the cluster is
always at the same comoving distance of z=0.1. Just the time has
increased from
kpc,
corresponding to a formal resolution of
655363. This "zoom'' simulation lasted more than 100 CPU h
on the Fujitsu VPP 5000 at CEA Grenoble. For this work, the cluster is
always at the same comoving distance of z=0.1. Just the time has
increased from
![]() ,
,
![]() ,
up to
,
up to
![]() .
This allows us to keep the same scale for all the images which is a
square of 26.5 arcmin aside, i.e. a full EPIC-XMM Newton field of
view. The projected gas emissivity and temperature of the merging
cluster at each time are shown in Fig 9.
.
This allows us to keep the same scale for all the images which is a
square of 26.5 arcmin aside, i.e. a full EPIC-XMM Newton field of
view. The projected gas emissivity and temperature of the merging
cluster at each time are shown in Fig 9.
The map of averaged gas temperatures corresponding to the early stage
of merging (
![]() )
shows hot filaments and substructures
(
)
shows hot filaments and substructures
(
![]() keV) superimposed on a temperature background at 0.5 keV.
The processes of gas heating and shocking are balanced by gas
relaxation within each subgroup at
keV) superimposed on a temperature background at 0.5 keV.
The processes of gas heating and shocking are balanced by gas
relaxation within each subgroup at
![]() ,
leading to two
isothermal subgroups at respective temperature of 2 and 4 keV, where
the hottest subgroup is the most massive. Eventually both subgroups
have merged leading to a hot single one at z=0. This merging
cluster begins to reach its equilibrium temperature of 4 keV, with hot
shocked regions superimposed from 5 to 6 keV. The temperature
discontinuity between the central regions of the cluster and the
background has increased during the merging process, since the central
regions of the cluster have been heated whereas the background
temperature remained constant.
,
leading to two
isothermal subgroups at respective temperature of 2 and 4 keV, where
the hottest subgroup is the most massive. Eventually both subgroups
have merged leading to a hot single one at z=0. This merging
cluster begins to reach its equilibrium temperature of 4 keV, with hot
shocked regions superimposed from 5 to 6 keV. The temperature
discontinuity between the central regions of the cluster and the
background has increased during the merging process, since the central
regions of the cluster have been heated whereas the background
temperature remained constant.
The 3-D temperature T(k,l,m) at pixel k, l, m, and emissivity
![]() distributions of the intra-cluster plasma being known, an
EPIC-XMM MOS1 observation can be simulated. To do so, the emitted
photons are randomly drawn among different temperatures from the
emission model of Poisson parameter T(k,l,m) and have to follow the
optical path from the source to the EPIC-XMM MOS1 focal plane. The
different distortions of the signal that would occur for a real
cluster at z=0.1 are taken into account: redshift, galactic
absorption and instrumental response including the PSF, vignetting and
energy response of the CCD detectors. The cluster and particle
background emissivities correspond to standard emissivities for a real
5 keV cluster at z = 0.1 observed during 60 ks, yielding a
background emissivity of
distributions of the intra-cluster plasma being known, an
EPIC-XMM MOS1 observation can be simulated. To do so, the emitted
photons are randomly drawn among different temperatures from the
emission model of Poisson parameter T(k,l,m) and have to follow the
optical path from the source to the EPIC-XMM MOS1 focal plane. The
different distortions of the signal that would occur for a real
cluster at z=0.1 are taken into account: redshift, galactic
absorption and instrumental response including the PSF, vignetting and
energy response of the CCD detectors. The cluster and particle
background emissivities correspond to standard emissivities for a real
5 keV cluster at z = 0.1 observed during 60 ks, yielding a
background emissivity of
![]() .
The CXB has not been taken into
account. The simulated EPIC-XMM count maps with restored temperature
maps are shown in Fig. 10.
.
The CXB has not been taken into
account. The simulated EPIC-XMM count maps with restored temperature
maps are shown in Fig. 10.
![\begin{figure}
\par\begin{tabular}{lll}%
\resizebox{5.6cm}{!}{\includegraphics[c...
...ebox{5cm}{!}{\includegraphics[clip]{f10f.3867.eps}}\\
\end{tabular}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg147.gif) |
Figure 10:
Simulated merging cluster at
|
| Open with DEXTER | |
The temperature maps of Fig. 10 have been restored with a
1![]() significant threshold. This simulated observation is closer
to the observation of a real cluster than the models of
the previous section. Indeed the instrumental components are supposed
to be similar, but the source emission is no longer a single component
model due to projection effects. We consequently must bear in mind
that the spectral fitting of each resolution element is not as accurate as described in Sect. 4.1. Let
us nevertheless compare the restored temperature maps of
Fig. 10 with the maps of averaged gas temperatures of
Fig. 9.
significant threshold. This simulated observation is closer
to the observation of a real cluster than the models of
the previous section. Indeed the instrumental components are supposed
to be similar, but the source emission is no longer a single component
model due to projection effects. We consequently must bear in mind
that the spectral fitting of each resolution element is not as accurate as described in Sect. 4.1. Let
us nevertheless compare the restored temperature maps of
Fig. 10 with the maps of averaged gas temperatures of
Fig. 9.
The counts vary by several orders of magnitude between high and low density regions (cf. count maps of Fig. 10). As expected from a multiscale algorithm, the resolution of the temperature maps is better in regions with high emissivity and statistics, than in regions with poor statistics. For instance, the closer to the core of the subgroups, the better resolved are the details of the hot substructures of the early stage of merger (
![]() ). Likewise the hot shocked regions in the central region of the cluster at z = 0 are well restored despite the light smoothing applied, whereas both subgroups at
). Likewise the hot shocked regions in the central region of the cluster at z = 0 are well restored despite the light smoothing applied, whereas both subgroups at
![]() and the single cluster at z = 0 have been detected at large scale as isothermal structures because of low statistics in the external regions.
and the single cluster at z = 0 have been detected at large scale as isothermal structures because of low statistics in the external regions.
These results on a simulated merging cluster at z = 0.1 allow us to conclude that our multiscale algorithm applied to real EPIC-XMM Newton observation of merging clusters should enable us to detect the expected temperature variations if they exist. Nevertheless the main building blocks of our algorithm, i.e. the spectral fitting and the multiscale temperature restoration, may still be improved. The spectral fitting uses a single component temperature model and a spectral modelling of projection effects with a multicomponent emission model might improve the detection of temperature variations. Also, the multiscale algorithm relies on a Haar wavelet which matches the square sampling of the data but leads to square patterns on the restored image, despite the regularization. Future improvements of the algorithm will include the use of other wavelets in order to better match the shape of the sources.
To take advantage of the spatial resolution of the new X-ray spectro-imagers, a new spectro-imagery algorithm has been introduced. This algorithm has been especially designed for the EPIC-XMM Newton cameras in order to restore the gas temperature variations within clusters of galaxies. The algorithm consists of two parts. First, an emission model of the source is fitted around each pixel of the detector surface, using regions of different areas, leading to a set of temperatures with error-bars at different scales. Then, the temperature variations are coded and thresholded in the wavelet space according to a significance criterion, and the wavelet transform of the optimal temperature map is obtained by regularizing the non-significant wavelet coefficients.
For the spectral fitting step, an emission model is fitted using a maximum likelihood method. The source emission spectrum, the astrophysical and instrumental backgrounds, but also the instrumental response and especially the vignetting factor are taken into account within the emission model. As far as the vignetting is concerned, this approach is different from the usual solution, where the vignetting is taken into account by modifying the data instead of the emission model, e.g. the "weight method'' described in Arnaud et al. (2001). The spectral fitting with full instrumental response modelling is more accurate in regions with very poor statistics and enables us therefore to reduce significantly the error bars in external regions of the FOV where the vignetting factor is important. However a temperature bias has been revealed in cases of poor statistics. This bias is enhanced in the case of high emissivity of the background with regard to the source emissivity, due to degeneracy effects in the shape of the emission spectra of each component. This result has to be kept in mind for sources like compact groups with low emissivities with regard to the background emissivity in the central region of the focal plane.
Our multiscale algorithm enables us to adapt the spatial resolution to the local statistics. In our test on a numerical simulation of a merging cluster at z = 0.1, the multiscale algorithm has enabled us to reveal not only faint temperature variations in the core of the merging subgroups, but also a large-scale temperature decrease in their external regions. The multiscale approach provides much more information than other methods using square or ring kernels. Nevertheless the results have still to be interpreted carefully. The final map has indeed been computed from a linear combination of spatially rebinned informations, and the knowledge of the area used for spectral fitting is not straightforward. Also, the chosen Haar wavelet transform is well suited to match the square spatial sampling but is not the best one since it implies block effects. Other wavelets that better match the temperature structures shape should be investigated.
Due to the spatial variation of the instrumental response, the different temperatures within different spatial bins are first computed from spectral fittings using different emission models. Thus, the wavelet transform of the expected temperature map is not computed linearly from the data. But a real wavelet transform is a linear process. This wavelet transform of the searched temperature map is obtained iteratively by regularizing the non-significant wavelet coefficients, which is questionable due to the non-linearity of the process. Yet this process has been tested on simulations and seems to perform well. The good behavior of the algorithm is due to the low spatial variations of the emission model, and especially to the low relative spatial variations of temperatures within the intra-cluster plasma. Consequently such an algorithm is well suited for restoring spatial variations of temperature within extended sources like clusters of galaxies but would not work for sources with high local variations of the emission model such as supernovae remnants.
The current spectro-imagery algorithm will be applied to a sample of merging clusters at different phases. Future developments are considered. The spectral fitting process could include spatial variations of the emission model in order to take into account projection effects. Moreover variations of other parameters such as the gas metalicity could be measured.
The model fitting algorithm is based on the pursuit of the maximum of
the likelihood function
![]() - cf. Eq. (5) - over the 2-D space with parameters r and T.
To do so, a 2-D minimization algorithm is required. The conjugate
gradient method was chosen for its fast convergence, but adapted to a
bounded parameter space with possibility of multiple maxima of the
likelihood function.
- cf. Eq. (5) - over the 2-D space with parameters r and T.
To do so, a 2-D minimization algorithm is required. The conjugate
gradient method was chosen for its fast convergence, but adapted to a
bounded parameter space with possibility of multiple maxima of the
likelihood function.
Let us recall the general method of minimization
algorithms. Considering a n-D function
![]() .
The function
.
The function
![]() and its gradient can be developed over the initial position
and its gradient can be developed over the initial position
![]() :
:
| (A.1) |
The minimization is obtained for
![]() .
Since
.
Since
![]() is usually non-linear S has to be developed iteratively over
successive positions
is usually non-linear S has to be developed iteratively over
successive positions
![]() .
Minimization are usually performed over
1-D cuts of
.
Minimization are usually performed over
1-D cuts of
![]() .
The successive directions of the cuts
depending on the algorithms. In case of the conjugate gradient
algorithm, a given position
.
The successive directions of the cuts
depending on the algorithms. In case of the conjugate gradient
algorithm, a given position
![]() corresponds to a minima in
direction
corresponds to a minima in
direction
![]() .
Then the next direction
.
Then the next direction
![]() is chosen to be a
conjugate direction from
is chosen to be a
conjugate direction from
![]() .
Contrary to the simple
gradient algorithm where
.
Contrary to the simple
gradient algorithm where
![]() is normal to
is normal to
![]() ,
here
,
here
![]() is chosen so that
is chosen so that
![]() stays as far as possible
normal to direction
stays as far as possible
normal to direction
![]() ,
i.e.
,
i.e.
![]() .
This condition prevents successive
explorations in the same direction. By differentiation of Eq. (A.2)
and by taking into account that
.
This condition prevents successive
explorations in the same direction. By differentiation of Eq. (A.2)
and by taking into account that
![]() at this
iteration, we get:
at this
iteration, we get:
| (A.3) | |||
| (A.4) |
In any case, both bounds
![]() ,
,
![]() must be included within the
bounded parameter space, so that the exploration support
must be included within the
bounded parameter space, so that the exploration support
![]() must be included within the
must be included within the
![]() interval where
interval where
![]() and
and
![]() are the parameter space bounds along the
direction
are the parameter space bounds along the
direction
![]() (cf. Fig. A.1). In case of good
statistics the likelihood function
(cf. Fig. A.1). In case of good
statistics the likelihood function
![]() has only one maximum
within the parameter space and the conditions
has only one maximum
within the parameter space and the conditions
![]() ,
,
![]() are enough. But in the case of bad statistics, some
multiple maxima events can appear, so that a choice has to be made
among the possible solutions. We observed in simulations of
observations that the good one is generally the closest to the center
of the parameter space. Indeed two kinds of false maxima can appear on
the T-axis. The first ones concern the low temperatures (T < 1 keV)
in case of degenerescence due to the similar shape of
the emission-lines complex and CXB emission in the soft band . The
second ones concern the high temperatures (T > 10 keV) in
case of degenerescence between the bremsstrahlung part of the cluster
emission and CXB emission in the hard band. Consequently, the closest solution
to the center of the parameter space,- where the
algorithm starts its pursuit-, is chosen in the case of multiple maxima.
To do so, a new constraint is added to
the exploration support
are enough. But in the case of bad statistics, some
multiple maxima events can appear, so that a choice has to be made
among the possible solutions. We observed in simulations of
observations that the good one is generally the closest to the center
of the parameter space. Indeed two kinds of false maxima can appear on
the T-axis. The first ones concern the low temperatures (T < 1 keV)
in case of degenerescence due to the similar shape of
the emission-lines complex and CXB emission in the soft band . The
second ones concern the high temperatures (T > 10 keV) in
case of degenerescence between the bremsstrahlung part of the cluster
emission and CXB emission in the hard band. Consequently, the closest solution
to the center of the parameter space,- where the
algorithm starts its pursuit-, is chosen in the case of multiple maxima.
To do so, a new constraint is added to
the exploration support
![]() at iteration i: the right
solution must be the closest to the starting point x=0, so that
at iteration i: the right
solution must be the closest to the starting point x=0, so that
![]() and
and
![]() are randomly drawn in the respective
are randomly drawn in the respective
![]() ,
and
,
and
![]() intervals up to get values where
intervals up to get values where
![]() and
and
![]() .
In case of bad statistics where no support
.
In case of bad statistics where no support
![]() can
match the previous condition, the undefined value is returned for both
parameters.
can
match the previous condition, the undefined value is returned for both
parameters.
This local pursuit of function
![]() is performed at each
iteration of the standard conjugate gradient algorithm. In case of
good statistics where a maximum is found, the convergence criterion
is performed at each
iteration of the standard conjugate gradient algorithm. In case of
good statistics where a maximum is found, the convergence criterion
![]() is obtained in a few iterations with
is obtained in a few iterations with
![]() .
.
![\begin{figure}
\resizebox{8.8cm}{!}{\includegraphics[clip]{f11.3867.eps}}\par
\end{figure}](/articles/aa/full/2004/05/aa3867/Timg184.gif) |
Figure A.1:
The bounded parameter space. At iteration i the minimum is obtained from
|
The wavelet transform of a 2-D signal
![]() is based on a
wavelet function which can be dilated and translated. The 2-D wavelet
leads to functions with compact support depending on three
parameters: the "scale'' or dilation factor a and both space
coordinates k,l. In our case, for geometrical and computational
reasons, the chosen wavelet is the Haar wavelet
(cf. Fig. B.1).
is based on a
wavelet function which can be dilated and translated. The 2-D wavelet
leads to functions with compact support depending on three
parameters: the "scale'' or dilation factor a and both space
coordinates k,l. In our case, for geometrical and computational
reasons, the chosen wavelet is the Haar wavelet
(cf. Fig. B.1).
Since the
![]() distribution is sampled in the direct space a
discrete wavelet transform
distribution is sampled in the direct space a
discrete wavelet transform
![]() can be associated to
can be associated to
![]() while preserving all the signal information. To do so the scale axis
can be sampled within a dyadic scheme so that a = 2j with
while preserving all the signal information. To do so the scale axis
can be sampled within a dyadic scheme so that a = 2j with
![]() .
The wavelet transform can be redundant within the space
axes, such as in the so called "a trous'' algorithm
(Holschneider 1989), or non-redundant , such as in the Mallat multi-resolution algorithm (Mallat 1989).
.
The wavelet transform can be redundant within the space
axes, such as in the so called "a trous'' algorithm
(Holschneider 1989), or non-redundant , such as in the Mallat multi-resolution algorithm (Mallat 1989).
On the one hand, the computation of the wavelet transform
![]() can be performed from the 2-D signal
can be performed from the 2-D signal
![]() .
Given a scale a,
"smoothed planes''
.
Given a scale a,
"smoothed planes''
![]() and wavelet coefficients
and wavelet coefficients
![]() can be defined, both being computed from the smoothed plane
can be defined, both being computed from the smoothed plane
![]() by applying low-pass
by applying low-pass
![]() and
high-pass
and
high-pass
![]() analysis filters, respectively.
The smoothed plane
analysis filters, respectively.
The smoothed plane
![]() corresponds to the smoothing of
corresponds to the smoothing of
![]() with a kernel of width a,
whereas the wavelet coefficients
with a kernel of width a,
whereas the wavelet coefficients
![]() corresponds to the
information lost between
corresponds to the
information lost between
![]() and
and
![]() .
Starting at scale
a=1, the first smoothed plane
.
Starting at scale
a=1, the first smoothed plane
![]() can be
defined, and the coefficients
can be
defined, and the coefficients
![]() and planes
and planes
![]() can
be computed iteratively from scale to scale.
can
be computed iteratively from scale to scale.
The wavelet transform using the anisotropic 2-D Haar wavelet is composed of three kinds of coefficients, the horizontal, vertical and diagonal coefficents,
![]() ,
,
![]() ,
,
![]() ,
respectively. According to the redundant shift invariant wavelet transform (Coifman & Donoho 1995), they are computed by applying the corresponding, horizontal, vertical and diagonal analysis filters, of Fig. B.2, following the analysis equations:
,
respectively. According to the redundant shift invariant wavelet transform (Coifman & Donoho 1995), they are computed by applying the corresponding, horizontal, vertical and diagonal analysis filters, of Fig. B.2, following the analysis equations:
| (B.1) | |||
| (B.2) | |||
| (B.3) | |||
| (B.4) |
In the case of the 2-D Haar wavelet transform, the smoothed plane
![]() at scale
at scale
![]() ,
is computed from a linear combination of the smoothed plane
,
is computed from a linear combination of the smoothed plane
![]() and the wavelet coefficients
and the wavelet coefficients
![]() ,
following the synthesis equation:
,
following the synthesis equation:
| (B.5) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{fig1a.eps}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg201.gif) |
Figure B.2:
The two dimensional analysis filters at scale 2j. The low-pass
|
![\begin{figure}
\par\includegraphics[width=7cm,clip]{fig1b.eps}\end{figure}](/articles/aa/full/2004/05/aa3867/Timg204.gif) |
Figure B.3:
The two dimensional synthesis filters at scale 2j. The low-pass
|