- ...
![[*]](/icons/foot_motif.gif)
- Considering an emission model with
a given emissivity
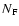 ,
the number of observed counts N is
expected to fluctuate like the standard deviation of the Poisson
parameter
,
the number of observed counts N is
expected to fluctuate like the standard deviation of the Poisson
parameter 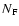 :
:
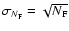 ,
so that the
,
so that the
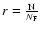 values are expected to fluctuate like
values are expected to fluctuate like
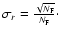 Consequently the expected rvalues can be bounded within the
Consequently the expected rvalues can be bounded within the
![$[-\Delta_r, +\Delta_r]$](/articles/aa/full/2004/05/aa3867/img59.gif) interval,
provided that
interval,
provided that
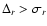 .
The
.
The 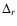 value of 1, corresponding to
value of 1, corresponding to
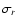 for one photon per pixel was chosen. Indeed,
for one photon per pixel was chosen. Indeed,
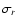 decreases with increasing statistics, - for
instance
decreases with increasing statistics, - for
instance
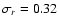 for
for
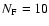 -, so that we always get
-, so that we always get
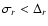 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
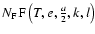
![[*]](/icons/foot_motif.gif)
- The scale parameter a has now been added because
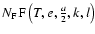 is in fact the weighted mean of
emission models corresponding to each event found within the square
bin of edge a.
is in fact the weighted mean of
emission models corresponding to each event found within the square
bin of edge a.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
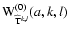
![[*]](/icons/foot_motif.gif)
- The p index is
hereafter omitted because the following processes do not depend on the
orientation of the coefficients.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.