A&A 414, 425-428 (2004)
DOI: 10.1051/0004-6361:20034184

Time-delay quasars: Scales and orders of magnitudes

P. Saha

Astronomy Unit, Queen Mary and Westfield College, University of London, London E1 4NS, UK
Observatoire astronomique, 11 rue de l'Université, 67000 Strasbourg, France

Received 12 August 2003 / Accepted 18 September 2003

Abstract
We can think of a lensed quasar as taking the Hubble time, shrinking it by $\sim$10-11, and then presenting the result to us as a time delay; the shrinking factor is of the order of fractional sky-area that the lens occupies. This cute fact is a straightforward consequence of lensing theory, and enables a simple rescaling of time delays. Observed time delays have a 40-fold range, but after rescaling the range reduces to 5-fold. The latter range depends on details of the lens and lensing configuration - for example, quads have systematically shorter rescaled time delays than doubles - and is as expected from a simple model. The hypothesis that observed time-delay lenses all come from a generalized-isothermal family can be ruled out. But there is no indication of drastically different populations either.

Key words: Gravitational lensing - galaxies: quasars: general

1 Introduction

Most of the observables in gravitational lensing (image positions and magnifications) are intrinsically dimensionless. The exception is the time delay between images, which takes its dimensionality straight from the universe[*]: $\Delta t \propto H_0^{-1}$. This remarkable fact is the essential reason for much research effort going into measuring time delays. The observations have been increasingly successful - in 1995 there was but one controversial time delay, currently there are nine non-controversial ones. These are summarized in Table 1 below.

But curiously, even as the image and time delay data have improved, the error bars on the inferred H0 have not. As an example, consider 0957+561. Between Kundic et al. (1997) and Oscoz et al. (2001) the time-delay value changed by only 2%. But meanwhile, whereas Kundic et al. (1997) quote $H_0=64\pm13$ (95% confidence) in the usual units of  $\rm km~s^{-1}~Mpc^{-1}$, Bernstein & Fischer (1999) with more imaging and more modelling conclude that the data imply only 77+29-24, while Keeton et al. (2000) assert that further data on the lensed host galaxy invalidates all previously published models, and they decline to give an H0 estimate at all. Basically, the problem is that simple lens models are unable to fit the images to the mas-level demanded by current data, while more complicated models can fit the data but are non-unique and can produce identical observables from very different values of H0.

Modellers have responded to this dilemma with two strategies. One is to try to identify simple models that both have enough parameters to fit or nearly fit the data and can be justified on galactic-structure grounds; Kochanek (2003) is typical of these. The other strategy is to try to explore the space of all plausible models allowed by the data; Raychaudhury et al. (2003) is a recent example. For a review by authors representing different points of view see Courbin et al. (2003).

In the current context of good data and active modelling but no consensus on models, it is interesting to step back and pose some questions that tend to get obscured in the details of modelling. First, we can think of the purpose of modelling time-delay lenses as being to discover one dimensionless number, the factor relating $\Delta t$ and H0-1. What contributions to this number are well-constrained and what are poorly constrained? What range of values do the data imply for the poorly-constrained part? Is that range systematically different for doubles and quads, and/or for isolated lensing galaxies versus interacting galaxies? And is that range consistent with what we expect from popular models? Nine systems is a small sample, but it is enough to provide preliminary answers to these questions, and to do so is the aim of this paper.

2 A scaling relation for time delays

In lensing theory the arrival time can be written as

\begin{displaymath}t({\setbox 0\hbox to 0pt{\hss$\scriptstyle\rightarrow$ } \the... ...htarrow$ } \theta\kern.6ex\raise 1.6ex\box0\kern-.2ex})\right] \end{displaymath} (1)

where the symbols have their usual meanings. For convenience, let us abbreviate this expression. First, we write $\tau({\setbox 0\hbox to 0pt{\hss$\scriptstyle\rightarrow$ } \theta\kern.6ex\raise 1.6ex\box0\kern-.2ex})$ for the expression inside square brackets. The factor outside square brackets equals H0-1 times a dimensionless distance factor D (say) that depends on redshifts and (weakly) on cosmology, but not on H0; for small $z_{\rm L}$ and large $z_{\rm S}$, $D\simeq z_{\rm L}(1+z_{\rm L})$. We note further that only differences in arrival-time between images are observable. Hence observable time delays have the form

 \begin{displaymath}\Delta t = H_0^{-1} ~ D ~ \Delta\tau. \end{displaymath} (2)

We expect that $\Delta\tau$ will be of the same order as $\vert{\setbox 0\hbox to 0pt{\hss$\scriptstyle\rightarrow$ } \theta\kern.6ex\rai... ...ss$\scriptstyle\rightarrow$ } \beta\kern.6ex\raise 1.6ex\box0\kern-.2ex}\vert^2$ but a few times smaller, the precise value depending on details of lens and lens configuration. For an observed lens we might predict

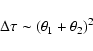\begin{displaymath}\Delta\tau \sim (\theta_1+\theta_2)^2 \end{displaymath} (3)

where $\theta_1,\theta_2$ are the $\theta$ values of the first and last images to arrive. To focus attention on the proportionality factor, I propose to consider the dimensionless quantity

 \begin{displaymath}\varphi \equiv {\Delta\tau \over \hbox{$1\over16$ }(\theta_1+\theta_2)^2} \cdot \end{displaymath} (4)

We can calculate $\varphi $ from a lens model, but not directly from observations. We can, however, measure a related quantity, a scaled time delay

 \begin{displaymath}\Delta T \equiv {\Delta t \over \hbox{$1\over16$ }(\theta_1+\theta_2)^2 ~ D} \end{displaymath} (5)

directly from observations, and substituting Eqs. (2) and (4) we see that

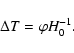\begin{displaymath}\Delta T = \varphi H_0^{-1} . \end{displaymath} (6)

The factor $\hbox{$1\over16$ }$ is ad hoc, but it allows the following interpretation. Recall that the image separation in a galaxy lens is about twice the Einstein radius:

 \begin{displaymath}\theta_1+\theta_2 \simeq 2\theta_{\rm E}. \end{displaymath} (7)

For an isothermal, the relation (7) is exact. But even for non-circular lenses, where $\theta_{\rm E}$ is not strictly defined, the image configuration can be used to define an effective $\theta_{\rm E}$. Using (7) the denominator in (4) is $\pi\theta_{\rm E}^2/(4\pi)$, i.e., the area of the Einstein ring as a fraction of the sky. In other words, if we scale the observed time delay by the lens's covering factor on the sky we get H0-1 times a "fudge factor'' of the order of unity.

For isothermal lenses, $\varphi $ ranges from 0 to 8, averaging $\hbox{$16\over3$ }$. To see this, recall that for isothermals, $\Delta\tau=2\theta_{\rm E}\beta$ and note that $\beta$ could be anywhere in the Einstein ring. Hence $\langle\beta\rangle=\hbox{$2\over3$ }\theta_{\rm E}$ and using (7) gives

 \begin{displaymath}\langle\Delta\tau\rangle_{\rm iso} = \hbox{$1\over3$ }(\theta_1+\theta_2)^2 . \end{displaymath} (8)

Equation (8) is interesting for comparison with non-isothermals, but for isothermals themselves, we can do better. Combining $\Delta\tau=2\theta_{\rm E}\beta$ with $\theta_1-\theta_2=2\beta$, which isothermals also satisfy, allows us to define

 \begin{displaymath}\Delta T_{\rm iso}\equiv {\Delta t \over \frac12(\theta_1^2-\theta_2^2) ~ D} \end{displaymath} (9)

which equals H0-1.

Witt et al. (2000, hereafter WMK) show that $\Delta T_{\rm iso}=H_0^{-1}$ is not restricted to isothermals but is valid for a large family of generalized-isothermal lenses, and argue that it will be generally applicable in nature. If so, $\varphi $ could be eliminated altogether. We can readily test if this is the case.

3 Scaling the data

We now present the obvious comparison of the scaled time delays $\Delta T = \varphi H_0^{-1}$ with current data.

Table 1 lists the relevant quantities for the various time-delay systems. The time delays references are given in the table, and the other data are taken from the CASTLES survey and compilation by Kochanek et al. (1998). For quads, only the first and last images (that is, the longest time delay) are considered, to enable a simple comparison with doubles. There are some caveats to the values of $\theta_1$ and $\theta_2$: for 1830 and 0218 the lens-centre is very uncertain and hence $\theta_1,\theta_2$ are especially uncertain, for 1608 the lens is apparently an interacting pair of galaxies, and 0957 and 0911 are in clusters and hence have large lensing contributions from other galaxies.

Table 1: Summary of time-delay data.

Figure 1 shows $\Delta T$ against $\Delta t$ for the currently known time-delay systems. Since error bars on time delays are typically a few percent they are not shown here. We notice three things:

The various caveats above do not appear to affect these points.


  \begin{figure} \includegraphics[width=8cm,clip]{saha_fig1.eps} \end{figure} Figure 1: Plot of the scaled time delay $\Delta T$ defined in Eq. (5) against the observed time delay. The various lenses are labelled by their short names: quads are labelled below, doubles above.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{saha_fig2.eps} \end{figure} Figure 2: As in Fig. 1, but omitting the D factor in the scaled time delay.
Open with DEXTER

We can also compare $\Delta T_{\rm iso}=H_0^{-1}$ against the data to test whether the lenses belong to the generalized isothermal family studied by WMK. Figure 3 shows $\Delta T_{\rm iso}$ against $\Delta t$ for the same systems. We notice the following

Again we must keep in mind the caveats above, and also that the large external shear in 1115, 0957 and 0911 means that for these lenses $\Delta T_{\rm iso}$ properly speaking requires a modification given in WMK but disregarded here. On the other hand, it seems unlikely that these caveats will solve the serious discrepancies we see. It appears more likely that most real lenses do not belong to the generalized isothermal family.

Whereas $\Delta T_{\rm iso}$ is rejected, are other scalings possible that improve upon $\Delta T$? L.L.R. Williams (personal communication) points out that the definition (Eq. 5) of $\Delta T$considers the size of the lens but not its asymmetry, and that if we multiply $(\theta _1+\theta _2)^2$ in the definition by a further factor of $\sqrt{(\theta_1-\theta_2)/(\theta_1+\theta_2)}$ as a measure of asymmetry, then the scaled time delays would range over a factor of only 2.5, with no significant trend. But the meaning of such an asymmetry correction in terms of lensing theory is not known.


  \begin{figure} \par\includegraphics[width=8cm,clip]{saha_fig3.eps} \end{figure} Figure 3: $T_{\rm iso}$ as defined in Eq. (9) against the observed time delay. The non-physical trend is significant (see text), and hence the generalized isothermal models are rejected.
Open with DEXTER

4 Modelling the range of $\varphi $

From the above, it appears that the scatter in $\varphi $ reflects a range of mass profiles and source positions, and that its value must be inferred for each lens by detailed modelling. But without going into detailed models for nine lenses, we can at least check whether the observed range of $\varphi $ is plausible.

Figure 4 shows such a check. The main plot is of $\varphi $against the area $(\theta _1+\theta _2)^2$ for an example model (an elliptical isothermal potential plus external shear.) The value of $\varphi $ is shown for different source positions, the two loops corresponding to source positions along the two caustics (actually just inside the caustics, to avoid computational problems). Quads are below the lower loop, with $\varphi\mathrel{\rlap{\lower3pt\hbox{$\mathchar''218$ }}\raise2pt\hbox{$\mathchar''13C$ }}2$. Doubles are between the two loops, with $2\mathrel{\rlap{\lower3pt\hbox{$\mathchar''218$ }}\raise2pt\hbox{$\mathchar''13... ...rel{\rlap{\lower3pt\hbox{$\mathchar''218$ }}\raise2pt\hbox{$\mathchar''13C$ }}6$[*]. The values are model-dependent - for example, a steeper model will have both loops somewhat higher. Also, the value of $(\theta _1+\theta _2)^2$depends on the source position: smaller for sources along the long axis of the potential, larger for sources perpendicular to that axis. But with these qualifications, Figure 4 shows that the general ranges of $\varphi $, including the separation of quads and doubles, is just as it is in the data, and there is no evidence that the observed systems come from drastically different populations of lenses.


  \begin{figure} \par\includegraphics[width=3.6cm,clip]{saha_fig4a.eps}\hspace*{2m... ...\includegraphics[width=7.2cm,clip]{saha_fig4c.eps}\hspace*{0.5mm}}\end{figure} Figure 4: Computation of $\varphi $ values from a simple model of 1115+080, taken from Saha & Williams (2003). The top two panels show an image morphology similar to 1115+080, and the corresponding source position. The lower panel shows $\varphi $ against $(\theta _1+\theta _2)^2$ for source positions along the two caustics. (The horizontal axis is not labelled because $(\theta _1+\theta _2)^2$ has arbitrary units: arcsec2, steradians, etc.) The lower loop corresponds to the diamond caustic and the upper loop corresponds to the outer caustic. Hence quads are below the lower loop and doubles are between the two loops.
Open with DEXTER

5 Summary

We see in this paper a new interpretation of lensing time delays: $\Delta t$ is H0-1 shrunk by the lens's covering factor on the sky, times a number of the order of unity. On separating off a redshift dependent-term (also of order unity) we are left with a number $\varphi $ (say) that summarizes the dependence on details of the lens and lens configuration.

Using these ideas, we can rescale the observed time delays for the nine currently-measured systems. The observed time delays range over a factor of 40, but the rescaled delays range over a factor of 5. The latter is the inferred range of $\varphi $, and moreover it appears that $\varphi\mathrel{\rlap{\lower3pt\hbox{$\mathchar''218$ }}\raise2pt\hbox{$\mathchar''13C$ }}2$ for quads and $2\mathrel{\rlap{\lower3pt\hbox{$\mathchar''218$ }}\raise2pt\hbox{$\mathchar''13... ...rel{\rlap{\lower3pt\hbox{$\mathchar''218$ }}\raise2pt\hbox{$\mathchar''13C$ }}6$. Reassuringly, the same spread in $\varphi $ is reproduced by a simple model.

Using rescaled time-delays we can also test the hypothesis that the observed lenses all belong to a generalized-isothermal family. This hypothesis is ruled out: it over-predicts time delaysfor large lenses. On the other hand, there is no indication that the known time-delay systems come from drastically different types of lenses.

Appendix A: Significance of trends

In Figs. 1 to 3 we have some points (xi,yi) and we want to know whether there is any trend in the scatter. There are many statistical tests relating to the significance of trends in data, but none of the standard ones address quite this question. However, it is not difficult to design a suitable statistical test. Let us pose the question: what is the probability of improving the fit to $y=\rm constant$ by shuffling the yi? If nearly all shufflings reduce the $\vert\rm slope\vert$ we would conclude that the data have a trend.

In the familiar straight-line fit, the slope is monotonic in  $\sum_ix_iy_i$. Hence as a statistic, $\sum_ix_iy_i$ is equivalent to the slope.

In the main text, I use the phrase "significant at the 95% level'' to mean that 5% of shufflings increase the $\vert\rm slope\vert$. Statisticians might use a phrase like "p-value of 95%''.

Acknowledgements
I am grateful to Rodrigo Ibata and Liliya Williams, who contributed some fruitful suggestions.

References


Copyright ESO 2004