A&A 413, 403-414 (2004)
DOI: 10.1051/0004-6361:20034008

Accretion disc dynamos opened up by external magnetic fields

D. Moss1 - A. Shukurov2


1 - Department of Mathematics, University of Manchester, Manchester M13 9PL, UK
2 - School of of Mathematics and Statistics, University of Newcastle, Newcastle upon Tyne NE1 7RU, UK

Received 26 June 2003 / Accepted 3 October 2003

Abstract
We show that a relatively weak poloidal external magnetic field, imposed in the outer parts of a Keplerian accretion disc, can open magnetic lines of a much stronger magnetic field generated by the dynamo in the inner disc. The resulting magnetic configuration can be favourable for launching a centrifugally driven wind. Even for a relatively weak external magnetic field (with energy density in excess of about only 10% of the thermal energy density at the outer disc radius) the geometry of the poloidal field in the disc neigbourhood is almost independent of the dynamo action, and is determined by the external field. The radial profile of the poloidal magnetic field on the disc surface is similar to that in the self-similar solution of Blandford & Payne (1982). We conclude that poloidal fields resulting from dynamo action can be important for launching a magneto-centrifugally driven outflow in accretion discs that occur in weakly magnetized environments, i.e. where an external field is too weak to be important. However, even a relatively weak external field can be wound up by the differential rotation to give a much stronger azimuthal field, and so modify dynamo action in the disc.

Key words: accretion, accretion disks - magnetic fields - magnetohydrodynamics (MHD) - turbulence

   
1 Introduction

Accretion discs and the associated winds and jets are expected to form and to evolve in a magnetic environment. As reviewed, e.g., by Königl & Ruden (1993) and Königl & Pudritz (2000), magnetic fields are essential for the accretion to occur, both as they directly brake the rotation via the Maxwell stresses and by driving an outflow (Bisnovatyi-Kogan & Ruzmaikin 1976; see, e.g., Pelletier & Pudritz 1992; Ferreira & Pelletier 1995; Casse & Ferreira 2000, and references therein), and as they generate turbulence in the disc (Balbus & Hawley 1998) to maintain viscous transport of angular momentum.

Accretion discs are believed to be a site of vigorous dynamo action (Pudritz 1981a,1981b; Stepinski & Levy 1991; Brandenburg et al. 1995), but virtually all models of magnetized accretion discs and associated outflows rely on externally supported magnetic fields, mainly because dynamos produce magnetic fields that close within the immediate vicinity of the disc, so the closed magnetic configuration cannot support an outflow extending to the observed very large distances (Pelletier & Pudritz 1992; Sect. V.B in Königl & Pudritz 2000). However, the numerical simulations of von Rekowski et al. (2003) show that a dynamo-generated magnetic field can support a vigorous outflow, provided the field can be opened up by, say, a thermally driven wind. Campbell (1999, 2000, 2001) and Campbell & Caunt (1999) discuss accretion disc models and outflows based on dynamo-generated magnetic fields using a simple, analytically solvable, one-dimensional dynamo model where the disc field matches a potential field in the disc corona; however, these authors do not discuss the global geometry of the magnetic field and how it can be opened at large distances from the disc.

It has been suggested by Reyes-Ruiz & Stepinski (1997) and Reyes-Ruiz (2000) that an external magnetic field can open magnetic lines of a dynamo-generated field to make the magnetic configuration suitable for the magneto-centrifugal wind launching (see also Moss & Shukurov 2001). We reconsider this idea here, with a fully nonlinear treatment of the dynamo action in the presence of an external magnetic field and estimate the external field required to produce the desired magnetic configuration.

A mean-field dynamo model for an accretion disc embedded into an external field is presented in Sect. 2, and we show in Sect. 3 that a rather weak external magnetic field can open up most or all the magnetic lines produced by the dynamo. We show in Sect. 3 that our results are insensitive to the details of the mean-field parameterization of the dynamo action and to the detailed distribution of the (turbulent) magnetic diffusivity in the disc and its environment. Our results are put into physical context in Sect. 4 where, in particular, we argue that external magnetic field strength required to open the dynamo field in the disc of a young stellar object is close to that of a field that can be trapped within a few tens of AU in the core of a molecular cloud.

   
2 The model

Our interest here is with magnetic fields that can be involved in launching large-scale outflows from an accretion disc, and so their scale must be comparable to the disc size and, in particular, be much larger than the disc's turbulent scale. Therefore, a mean-field description of the accretion disc is appropriate where space-averaged quantities are involved - e.g. the standard model of Shakura & Sunyaev (1973). However, the averaged induction equation contains not only terms responsible for turbulent magnetic diffusion and induction by differential rotation, but also a term related to the vectorial nature of magnetic field, known as the $\alpha$-term (not to be confused with the "alpha-coefficient'' of the Shakura & Sunyaev theory which we denote as $\alpha_{\rm SS}$ here). As similarly argued by Blackman (2001), a consistent mean-field description of thin accretion discs must also include the hydromagnetic $\alpha$-effect that quantifies the mean-field dynamo action.

2.1 The dynamo equations

We study a dynamo active disc embedded in a passive, conducting corona (halo), and solve the standard $\alpha^2\omega$ dynamo equation in the disc (e.g., Moffatt 1978; Zeldovich et al. 1983)

 \begin{displaymath}\frac{\partial \vec{B}}{\partial t} =\nabla\times(\vec{v}\ti... ...vec{B}+\alpha\vec{B}) -\nabla\times(\eta\nabla\times\vec{B}), \end{displaymath} (1)

where $\vec{B}$ is the mean magnetic field, $\vec{v}$ is the velocity field, and $\alpha$ and $\eta $, functions of position, are the turbulent transport coefficients, responsible for the dynamo action and turbulent magnetic diffusion, respectively. We introduce an inwardly directed axisymmetric radial accretion flow resulting from the standard model of a viscous accretion disc (Shakura & Sunyaev 1973; Frank et al. 1985) and impose an axisymmetric vertical magnetic flux at distant boundaries. We introduce cylindrical polar coordinates $(r,\phi,z)$with the z-axis parallel to the angular velocity and z=0 at the disc midplane, and study axisymmetric solutions of Eq. (1).

The coefficient $\alpha$ in Eq. (1) must be an odd function of z because it arises from the interaction of the Coriolis force with turbulence in stratified medium, $\alpha\propto\vec{\Omega}\cdot\nabla\rho$(Parker 1979) or with magnetic buoyancy (Brandenburg 1997). As discussed by e.g. Ruzmaikin et al. (1988), solutions of Eq. (1) only weakly depend on the particular choice of the functional dependence of $\alpha$ on z. Solutions with $\alpha$independent of the magnetic field grow exponentially in time provided the magnetic Reynolds numbers based on $\alpha$ and $\Omega$, as defined in Eqs. (7) and (8) below, are large enough. The growth will saturate as soon as the Lorentz force becomes significant; the saturation is often modelled with an algebraic dependence of $\alpha$ on magnetic field strength such that $\alpha$ decreases as B grows. Thus we adopt an $\alpha$-effect described by

 
$\displaystyle \alpha= \left\{\begin{array}{ll} \displaystyle\frac{\alpha_0\sin(... ...(kB_{\rm eq}^2)}, &\vert z\vert\leq h,\\ 0,&\vert z\vert>h, \end{array}\right.$     (2)

where h(r) is the semi-thickness of the dynamo active disc, identified with the gas scale height, $\alpha_0(r)$ is the background (unquenched) magnitude of the $\alpha$-effect, $B_{\rm eq}=(4\pi\rho v_{\rm t}^2)^{1/2}$ is the magnetic field strength at equipartition with turbulent kinetic energy, with the gas density denoted as $\rho$ (a function of r) and the turbulent velocity, as $v_{\rm t}$. We have thus introduced a conventional $\alpha$-quenching nonlinearity that leads to the saturation of magnetic field growth at $B\simeq k^{1/2}B_{\rm eq}$. We have introduced a constant k of order unity to reflect some of the uncertainty in our ideas about the reaction of the large scale magnetic field on to the turbulent motions (but ignoring ongoing controversies about the nature and effectiveness of the feedback of the dynamo generated fields on the $\alpha$-effect - see, e.g., Vainshtein & Cattaneo 1992; Blackman & Field 2000; Kleeorin et al. 2000, 2002; Brandenburg & Subramanian 2000). Brandenburg (1997,2000) has argued that Eq. (1) provides a reasonable approximation to accretion disc dynamos where turbulence is driven by the magneto-rotational instability, provided $\alpha_0<0$ in Eq. (2), which leads to the dominance of magnetic fields with dipolar symmetry, $B_{r,\phi }(r,z)=-B_{r,\phi }(r,-z),\ B_{z}(r,z)=B_{z}(r,-z)$.

We consider only axisymmetric solutions, and so write

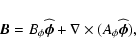\begin{displaymath}\vec{B}=B_\phi\widehat{\vec{\phi}} +\nabla\times(A_\phi\widehat{\vec{\phi}}), \end{displaymath} (3)

where $B_\phi $ and $A_\phi$ are the azimuthal components of the magnetic field and vector potential, respectively (with $\widehat{\vec{\phi}}$ the unit vector). The velocity field is split into

 \begin{displaymath}\vec{v}=u(r)\widehat{\vec{r}}+r\Omega(r)\widehat{\vec{\phi}} +\vec{u}_{\rm dia}, \end{displaymath} (4)

where $\vec{u}_{\rm dia}=-\frac{1}{2}\nabla\eta$ allows for the turbulent diamagnetism (a transport of the mean magnetic field to regions with lower turbulent intensity - Zeldovich 1956; Roberts & Soward 1975), u is the prescribed radial inflow, and $\Omega$ is the angular velocity taken here to be independent of z. (This choice is perhaps rather arbitrary: however we did verify that our solutions changed only slightly, and that our conclusions were unaltered, when we took $\Omega\propto r_{\rm sph}^{-3/2}$, where $r_{\rm sph}=(r^2+z^2)^{1/2}$). The disc semi-thickness h increases with radius, and for convenience of reference we define the local disc aspect ratio,

\begin{displaymath}\lambda(r)=h(r)/r. \end{displaymath}

Regarding the turbulent magnetic diffusivity $\eta $, we consider a disc corona where $\eta $ can be larger or smaller than that in the disc itself, and so we set

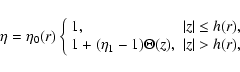
\begin{displaymath}\eta=\eta_0(r) \left\{\begin{array}{ll}1,&\vert z\vert\leq h(... ... 1+(\eta_1-1)\Theta(z),&\vert z\vert>h(r), \end{array}\right. \end{displaymath}

where $\eta_0(r)$ is the diffusivity in the disc - see Sect. 2.2,

\begin{displaymath}\Theta(z)=1 -\exp\left[-\frac{(\vert z\vert-h)^2}{l_\eta^2}\right] \end{displaymath}

is a smoothed step function and, rather arbitrarily, $l_\eta=\frac{1}{2}[Z-h(r)]$, with z the vertical size of the computational domain, see Sect. 2.3. Thus, $\eta $ smoothly varies in z over a range $l_\eta$ if $\eta_1\neq 1$, from $\eta=\eta_0$ in the disc to $\eta\approx\eta_0\eta_1$ in the corona. Because the physical conditions around accretion discs are rather uncertain, we consider models with the turbulent magnetic diffusivity in the corona both significantly larger and smaller than in the disc (i.e., $\eta _1>1$ and $\eta _1<1$, respectively), as well as with no vertical dependence of $\eta $ (i.e., $\eta _1=1$). A large turbulent diffusivity may be more appropriate to an accretion disc corona supported by turbulent pressure (Ouyed & Pudritz 1997; von Rekowski et al. 2003). Clearly, the larger is the magnetic diffusivity outside the disc, the easier will be the dragging of the external vertical magnetic field by the radial flow, which is confined to the disc.

   
2.2 The physical model

We take the physical state of the disc to be that of a conventional viscous accretion disc ("$\alpha$-disc'', e.g., Frank et al. 1985), and for convenience we reproduce the solution here, in standard notation, for the disc scale height

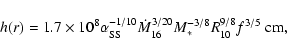
\begin{displaymath}h(r)=1.7\times 10^8 \alpha_{\rm SS}^{-1/10} \dot M_{16}^{3/20}M_*^{-3/8}R^{9/8}_{10}f^{3/5}\ {\rm cm}, \end{displaymath}

gas density

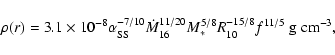
\begin{displaymath}\rho(r)=3.1\times 10^{-8} \alpha_{\rm SS}^{-7/10} \dot M_{16}^{11/20}M_*^{5/8}R^{-15/8}_{10}f^{11/5}\ {\rm g~ cm}^{-3}, \end{displaymath}

kinematic turbulent viscosity

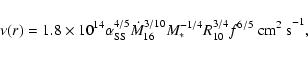
\begin{displaymath}\nu(r)=1.8\times 10^{14} \alpha_{\rm SS}^{4/5} \dot M_{16}^{3/10}M_*^{-1/4}R^{3/4}_{10}f^{6/5}\ {\rm cm^2~ s}^{-1}, \end{displaymath}

radial velocity

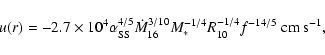
\begin{displaymath}u(r)=-2.7\times 10^4 \alpha_{\rm SS}^{4/5} \dot M_{16}^{3/10}M_*^{-1/4}R^{-1/4}_{10}f^{-14/5}\ {\rm cm ~s}^{-1}, \end{displaymath}

and equipartition magnetic field strength

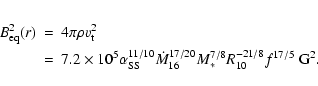
\begin{eqnarray*}B_{\rm eq}^2(r)&=&4\pi\rho v_{\rm t}^2\\ &=&7.2\times 10^5 \al... ...} \dot M_{16}^{17/20}M_*^{7/8}R^{-21/8}_{10}f^{17/5}\ {\rm G}^2. \end{eqnarray*}


Here $\alpha_{\rm SS}$ is the Shakura-Sunyaev viscosity parameter (we repeat, not to be confused with the $\alpha$-coefficient of the mean field dynamo theory), $\dot M_{16}$ is the mass accretion rate in units of 1016 g s-1, M* is the mass of the central object in solar masses and R10 is the radius in units of 1010 cm; f(r)=[1-(R*/r)1/2]1/4, where R* is the radius of the central object, varies with r insignificantly for the values we considered, so we put f=1. We have used the relation $v_{\rm t}=\alpha_{\rm SS}c_{\rm s}$ to estimate $B_{\rm eq}$, with

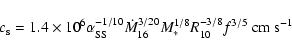
\begin{displaymath}c_{\rm s}=1.4\times 10^6 \alpha_{\rm SS}^{-1/10} \dot M_{16}^{3/20}M_*^{1/8}R^{-3/8}_{10}f^{3/5}\ {\rm cm ~s}^{-1} \end{displaymath}

the speed of sound, estimated the dynamo coefficient as

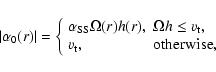
\begin{displaymath}\vert\alpha_0(r)\vert= \left\{\begin{array}{ll}\alpha_{\rm SS... ... v_{\rm t},\\ v_{\rm t},&\mbox{otherwise,} \end{array}\right. \end{displaymath}

and also introduced the turbulent magnetic Prandtl number ${\cal P}$, so that the magnetic diffusivity in the disc is given by

 \begin{displaymath}\eta_0(r)={\cal P}\nu(r). \end{displaymath} (5)

The rotation law is of softened Keplerian form,

 \begin{displaymath}\Omega(r)=\left[\frac{GM_*}{(r+r_{\rm min})^3}\right]^{1/2}, \end{displaymath} (6)

with $r_{\rm min}=10^{-4}R$ the inner disc radius. We take for our standard case a relatively large value of R= 1016 cm, so that $r_{\rm min}=10^{12}$ cm.

   
2.3 Boundary conditions and the external field

We wish to impose a uniform vertical field at large distances above and below the disc plane, and so there apply the boundary conditions

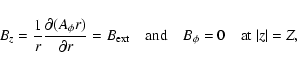
\begin{displaymath}B_z=\frac{1}{r}\frac{\partial(A_\phi r)}{\partial r}=B_{\rm ext} \quad\mbox{and}\quad B_\phi=0 \quad\mbox{at}\ \vert z\vert=Z, \end{displaymath}

where $B_{\rm ext}$ is the strength of the external magnetic field. We also explore solutions with non-uniform Bz at |z|=Z, allowing for a concentration of external field towards the disc axis. The salient features of the solutions appear to be quite independent of this detail, with the total magnetic flux through the disc midplane being the most important single characteristic of the external field.

We consider solutions with fixed parity with respect to the plane z=0(in fact, we only consider dipole-like fields, see Sect. 2.5), and so calculations are performed in the region $0\le z \le Z$ only, with suitable symmetry conditions on z=0.

The choice of the inner and outer radii of the disc is important. We need to choose the outer radius R large enough that the important features of the system are captured. On the other hand, angular velocity gradients, and so dynamo generation, are strongest in the inner regions. But it is computationally difficult to handle a disc in which the ratio $r_{\rm min}/R$ is too small. After some experimentation, we chose

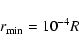
\begin{displaymath}r_{\rm min}=10^{-4} R \end{displaymath}

for the bulk of our computations. In order to reduce the effects of the outer radial boundary of the computational domain, we extended the computational domain to r=f, with fR>1, but we put $\alpha=0$ and u=0 in r>R. Thus the physical disc is embedded both radially and vertically in a passive envelope. Equally, the ratio Z/R has to be large enough that the poloidal field tends to the imposed external field $B_{\rm ext}\widehat{\vec z}$ in an unforced manner as $\vert z\vert\rightarrow Z$. Essentially, we require that solutions should not change quantitatively if Z/R is further increased. Numerical experimentation showed that with

\begin{displaymath}f_R=4 \quad\mbox{and}\quad z_{\rm max} = Z/R=3, \end{displaymath}

solutions were insensitive to further increase in these numbers, and we used these values in all the simulations discussed below - see Sect. 2.5.

The radial boundary conditions are

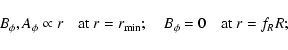
\begin{displaymath}B_\phi, A_\phi \propto r \quad\mbox{at}\ r=r_{\rm min}; \quad B_\phi=0 \quad\mbox{at}\ r=f_RR; \end{displaymath}

$A_\phi\propto r$ implies $B_z\to\mbox{const}$. We avoided imposing a boundary condition on the poloidal field at r=R, as it is difficult to formulate satisfactorily in a system where an imposed external magnetic field coexists with a dynamo field. Our formulation of the problem allows us to use

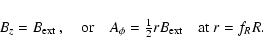
\begin{displaymath}B_z=B_{\rm ext}~,\quad\mbox{or}\quad A_\phi={\textstyle{\frac{1}{2}}} r B_{\rm ext} \quad\mbox{at}\ r=f_RR. \end{displaymath}

This gave satisfactory behaviour in general (in that solutions are independent of fR if fR is large enough), and is consistent with the pure dynamo solutions found when $B_{\rm ext}=0$.

   
2.4 Nondimensionalization

Equation (1) is nondimensionalized in terms of the length R and time $h(R)^2/\eta(R)$. Thus in dimensionless units, $\vert z\vert\le z_{\rm max}=Z/R$, $r\le f_R$. Angular velocity, radial velocity and $\alpha$ are measured in units of their values $\Omega_0$, u0 and $\alpha_0$ at r=R, and $\vec{B}$ is measured in units of $B_0=k^{1/2}B_{\rm eq}$ at r=R; the corresponding unit of $A_\phi$ is RB0. Taking k=1 and $\alpha _{\rm SS}=0.01$ for definiteness, this corresponds to $B_0=1.7\times 10^{-5}~{\rm G}$ in models with $R=10^{16}~{\rm cm}$, but $B_0=7.1\times 10^{-3}~{\rm G}$ in Sect. 3.4 where $R=10^{14}~{\rm cm}$. We assume $\rho$ to be independent of z in $\vert z\vert\le h(r)$; its value in |z|> h(r) is irrelevant, as $\alpha=0$there and $\rho$ only enters via the alpha-quenching term in Eq. (2). We take as standard values

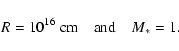
\begin{displaymath}R=10^{16}~{\rm cm}\quad\mbox{and}\quad M_*=1. \end{displaymath}

The dimensionless governing parameters that quantify the hydromagnetic $\alpha$-effect, magnetic field twisting by differential rotation and the radial dragging of magnetic field are, respectively,
   
                            $\displaystyle R_\alpha$ = $\displaystyle \frac{\alpha_0h(R)}{\eta(R)}=-1.85{\cal P},$ (7)
$\displaystyle R_\omega$ = $\displaystyle \frac{\Omega(R)h^2(R)}{\eta(R)}=1.85 {\cal P}\alpha_{\rm SS}^{-1},$ (8)
Ru = $\displaystyle \frac{\vert u(R)\vert h(R)}{\eta(R)} =0.143{\cal P}\alpha_{\rm SS}^{-1/10}\dot M_{16}^{3/20};$ (9)

in addition, the global disc aspect ratio is given by

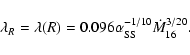
\begin{displaymath}\lambda_R=\lambda(R)= 0.096\alpha_{\rm SS}^{-1/10}\dot M_{16}^{3/20}. \end{displaymath}

From now onwards we refer always to dimensionless quantities, unless otherwise stated.

   
2.5 The code

For our initial exploratory investigations (where we took $r_{\rm min}=0.01$, fR=1) we used the axisymmetric dynamo code written in cylindrical polar coordinates $(r,\phi,z)$ described in Moss & Shukurov (2001). For computations with $r_{\rm min}=10^{-4}$, fR>1 we modified this code to use $\ln r$ as the radial variable. Having verified that odd parity solutions were strongly preferred for $\alpha_0<0$, we sought solutions in the half-space $z\ge 0$, and also changed to using $\ln z$ as the independent variable rather than z, solving in $z_{\rm min}\le z\le Z$, with $z_{\rm min}=10^{-4}$ usually. Thus the boundary conditions to select the odd parity solutions are applied at $z=z_{\rm min}$ rather than at z=0; comparison with the version of the code using z as variable and $z_{\rm min}=0$showed that this inaccuracy was unimportant for our investigation.

For the revised version of the code we used a semi-implicit Dufort-Frankel scheme for the time stepping, rather than the Runge-Kutta integrator used previously, as the restrictions on the time step were then less stringent. Our standard computational grid had 101 points uniformly distributed in $\ln r$ and 201 points in $\ln z$.

Table 1: of results with magnetic diffusivity $\eta $ independent of z(i.e., $\eta _1=1$), $R_\alpha =-1.85$, $R_\omega =185$, Ru=0.64, $\alpha _{\rm SS}=0.01$, ${\cal P}=1$, and $\lambda =0.43$. $E_{\rm t}$ and $E_{\rm d}$ are the field energies in the whole computational domain and near the disc respectively (see text), s=EP/ETis the ratio of energies in the poloidal and toroidal magnetic field in the whole domain, and F0 is the signed flux through the disc plane in $r\le 1$. The final entry (asterisked) has $R_\alpha =0$, and refers to a purely advective calculation, with no dynamo action.

   
3 Results

   
3.1 Models with magnetic diffusivity independent of z

We describe firstly a "standard'' set of computations, with $\alpha _{\rm SS}=0.01$, ${\cal P}=1$, $\dot M_{16}=10^3$, giving $R_\alpha =-1.85$, $R_\omega =185$, Ru=0.64, $\lambda_R=0.43$. The magnetic diffusivity is taken to be independent of z, i.e. the form (5) holds at all z ($\eta _1=1$), and $B_{\rm ext}$ increases from zero to "saturation'' values. A summary of these results is presented in Table 1. There $E_{\rm t}$ is the total magnetic energy in the computational domain, $E_{\rm d}$ is the magnetic energy within the disc, $0\le z \le \lambda_R$, $F_0=2\pi \int_0^1 B_zr~{\rm d}r$is the signed flux of (vertical) magnetic field through the disc mid-plane ($r\le 1$), and s is the ratio of poloidal to azimuthal field energies. Note that s is always small, and that the energy is predominantly in the toroidal part of the magnetic field, even though it is the poloidal field geometry that shows the most obvious changes as $B_{\rm ext}$ increases. (Of course, generation of toroidal field from poloidal by the winding action of the differential rotation is independent of the source of the poloidal field.)


  \begin{figure} \par\includegraphics[width=8.6cm]{aa0008f1.eps}\end{figure} Figure 1: The dependence of the near-disc energy $E_{\rm d}$ (solid) and poloidal flux through the disc plane F0 (dashed) on $B_{\rm ext}$ for the dynamo solutions with $\eta $ independent of z(see also Table 1). The dotted lines show the same quantities for the purely advective solutions.
Open with DEXTER

In Fig. 1 we plot F0 and $E_{\rm d}$ as a function of the external field strength $B_{\rm ext}$. This shows a smooth transition between pure dynamo solutions in the limit $B_{\rm ext}\rightarrow 0$, where the disc magnetic field is independent of $B_{\rm ext}$, and purely advective solutions for large $B_{\rm ext}$, where the dynamo action is suppressed by the contribution of the external field to $\alpha$-quenching as described by Eq. (2). For example, the magnetic energy and total flux are always equal to or in excess of the greater of the values for the pure dynamo and pure advection fields. For $B_{\rm ext} \ga 3$, the solutions are essentially purely advective, and scale with the asterisked entry in Table 1 as $E_{\rm t}, E_{\rm d}\propto B_{\rm ext}^2$, $F_0\propto B_{\rm ext}$.

The geometry of the solutions is of interest. We first display, in Fig. 2, an intermediate case with $B_{\rm ext}=0.01$. There is a region where field lines close within the disc, and the field generally resembles a typical disc dynamo field. Further from the axis ($r\ga 2$) the imposed field is relatively unaffected by the dynamo action in the disc. Solutions for several other values of $B_{\rm ext}$ are illustrated in Fig. 3. For the pure dynamo solution, the poloidal field lines close within, or not far outside of, the disc region $r\le R$. Essentially no field lines get as far as the upper boundary $z=z_{\rm max}=3$(Fig. 3a). For $B_{\rm ext}\ga 0.01$, a substantial proportion of the field lines passing through z=0 reverse their curvature above the disc and continue to large values of z, see Figs. 2 and 3b. Comparison between the purely advective solution, shown in Fig. 3d, and Fig. 3c shows that the dynamo is essentially irrelevant for the poloidal field for $B_{\rm ext}\ga 0.1$, as the poloidal field is then dominated by the imposed (poloidal) external field. However, the azimuthal field is essentially that of the pure dynamo, unless $B_{\rm ext}\ga1$.

We further verified that in the absence of advection (Ru=0), for larger values of $B_{\rm ext}$ there is no accumulation of poloidal field lines towards the inner parts of the disc, and the poloidal field is near to vertical everywhere. In other words, the bunching together of poloidal field lines when $B_{\rm ext}\ga1$ is a purely advective effect rather than a result of any dynamo action (which is suppressed for such a strong external field).


  \begin{figure} \par\includegraphics[clip,width=8.8cm]{run232.epsi}\end{figure} Figure 2: Poloidal field lines for the solution with $B_{\rm ext}=0.01$, $R_\alpha =-1.85$, $R_\omega =185$, Ru=0.64, $\lambda =0.43$, $\eta $ independent of z, as represented in Table 1 Here and in other similar figures below, the solution at z<0 is obtained from that shown by the symmetry, $B_{r,\phi }(r,z)=-B_{r,\phi }(r,-z),\ B_{z}(r,z)=B_{z}(r,-z)$. Labels on the curves refer to the magnitude of the poloidal flux function $rA_\phi $, and are equally spaced at intervals of 0.01 from 0.01 to 0.07.
Open with DEXTER

We then sought to increase the effects of advection by taking ${\cal P}=10$ (i.e. reducing $\eta(r)$ while keeping $\nu(r)$ unchanged); then Ru=6.4. But dynamo action is then also enhanced, with $R_\alpha =-18.5$, $R_\omega =1850$. This was computationally more demanding, and we only calculated a few examples. For numerical reasons we here put $r_{\rm min}=z_{\rm min}=3\times 10^{-4}$. The essential features of the solutions are unaltered. We show in Fig. 4 the poloidal field lines with $B_{\rm ext}=0.01, 0.1$and 10. The only significant change from the models with ${\cal P}=1$ is that the transition from dynamo dominated to external field dominated solutions appears to occur at rather larger values of $B_{\rm ext}$(by a factor estimated as between 3 and 10), consistent with the stronger dynamo action.

We also made some exploratory calculations with a nonuniform magnetic field imposed at the boundary z=Z, corresponding to a concentration of the external magnetic flux towards the axis having been produced during collapse. We took two forms of this boundary condition:

 \begin{displaymath} A_\phi\vert _{z=Z} = {\textstyle{\frac{1}{2}}} B_{\rm ext}r(1-f_{\rm I}r^2), \end{displaymath} (10)

corresponding to

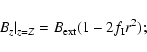
\begin{displaymath}B_z\vert _{z=Z} = B_{\rm ext}(1-2f_{\rm I}r^2); \end{displaymath}

and

 \begin{displaymath} A_\phi\vert _{z=Z} ={\textstyle{\frac{1}{2}}}B_{\rm ext}r(1-f_{\rm II}\tanh{r}), \end{displaymath} (11)

with

\begin{displaymath}B_z\vert _{z=Z} =B_{\rm ext}\left[1-f_{\rm II}\left(\tanh{r}-{\textstyle{\frac{1}{2}}}\cosh^{-2}{r}\right)\right]. \end{displaymath}

The choices $f_{\rm I}=0.028$ and $f_{\rm II}=0.9$ give an imposed field Bz at r=4 that is approximately 10% of that on the axis r=0. With these values the boundary condition (10) gives an imposed field at z=Z that is relatively uniform within r<1, but falls off more rapidly in r>1, whereas with (11) the region of stronger field is confined to the vicinity of the axis r=0, and Bz(r,Z) is almost uniform in r>1. Taking our standard parameters used earlier in this section with these values of $f_{\rm I}$ and $f_{\rm II}$, we found that the field topology near the disc plane (say in $\vert z\vert\la 1$) was qualitatively little altered from those in the standard case (Figs. 2 and 3) as $B_{\rm ext}$ changed. In particular, with boundary condition (10) we found that the near-disc field structure shown in Fig. 2 (where $B_{\rm ext}=0.01$) was quite closely reproduced with $B_{\rm ext}=0.018$. Using boundary condition (11), the field structure shown in Fig. 2 was approximately reproduced near the disc with $B_{\rm ext}=0.03$. The overall trends with increasing $B_{\rm ext}$ were similar in the standard case (uniform boundary condition), and when using boundary conditions (10) and (11). We can note that the values of $B_{\rm ext}$ identified above in cases (10) and (11) give approximately the same flux of $\vec{B}$ through the plane z=Z within r=4 as in the standard case with $B_{\rm ext}=0.01$.


  \begin{figure} \begin{tabular}{ll} (a)\includegraphics[clip,width=7.8cm]{run230.... ...i} &(d)\includegraphics[clip,width=7.8cm]{run239.epsi}\end{tabular} \end{figure} Figure 3: As in Fig. 2, but for several values of the external magnetic field: a) $B_{\rm ext}=0$ - pure dynamo solution; b) $B_{\rm ext}=0.03$; c) $B_{\rm ext}=0.1$. Panel d) shows the purely advective solution, $R_\alpha =0$. Contours are equally spaced as a function of poloidal flux $rA_\phi $, between levels 0.007 and 0.064 in a) and between 0.01 and 0.023 in b); and are logarithmically spaced (factor of 2), between levels 0.01 and 0.64 in c) and between 0.12 and 61.4 in d).
Open with DEXTER

   
3.2 Models with magnetic diffusivity either enhanced or reduced in the corona

The models discussed above have a magnetic diffusivity that is independent of height. The value of the diffusivity above an accretion disc is quite uncertain. Thus we also studied solutions with the coronal magnetic diffusivity both enhanced, by a factor $\eta _1=3$, and reduced, $\eta _1=0.3$. A summary is presented in Table 2, for the same dynamo parameters as used in Table 1. Again, dynamo action can be seen to influence solutions whilst $B_{\rm ext}\la 1$. For larger values of $B_{\rm ext}$, the solutions approach the appropriate purely advective solutions (asterisked entries in Table 2, suitably scaled). Typical poloidal field configurations, with $B_{\rm ext}=0.01$and 10, are shown in Fig. 5. Overall, the results are very similar to those discussed above with no z-dependence of $\eta $, although the poloidal field lines are somewhat more strongly bent in a more highly conducting halo ($\eta _1<1$) - as naively might be expected.

As can be seen in Table 2, the results for magnetic diffusivity independent of height ($\eta _1=1$, Table 1) and enhanced coronal diffusivity ($\eta _1=3$) are similar even quantitatively. However, a disc surrounded by a better conducting corona ( $\eta _1=0.3$) maintains a larger vertical magnetic flux and azimuthal field strength, presumably because of the dependence of the dynamo on boundary effects at the disc-corona interface.


  \begin{figure} \par\begin{tabular}{lll} (a)\includegraphics[clip,width=4.9cm]{ru... ...i} &(c)\includegraphics[clip,width=4.9cm]{run266.epsi}\end{tabular} \end{figure} Figure 4: Poloidal field lines for models with increased magnetic Prandtl number, ${\cal P}=10$ and a range of external magnetic field strengths: a) $B_{\rm ext}=0.01$; b) $B_{\rm ext}=0.10$; c) $B_{\rm ext}=10.0$. The other parameters are $R_\omega =1850$, $R_\alpha =-18.5$, Ru=6.4, $\lambda =0.43$and $\eta _1=0.1$. Contours are equally spaced as a function of poloidal flux $rA_\phi $.
Open with DEXTER

   
3.3 Solutions with excluded external field

We also found for standard choices of parameters, solutions for which the external field is excluded from the inner part of the disc, that is the external field is in the opposite sense to the dynamo dominated field close to the axis; of course, such configurations occur only when the external field and the seed field for the dynamo are independent. In this case magnetic fields generated by the dynamo cannot merge with the external field and the vicinity of the disc is magnetically isolated from the surroundings. The external field bends to "flow around'' the disc region so that the disc is surrounded by a closed current sheet. The net signed magnetic flux of Bz within radius r in the disc plane changes sign at some radius $r_{\rm f}$, i.e. $r_{\rm f}$ is the smallest radius at which the external field passes through the plane z=0. In other words, $r_{\rm f}$ is the radius in the plane z=0 of the magnetic cocoon surrounding the disc. Figure 6 shows the poloidal field geometry for solutions of this type for several values of $B_{\rm ext}$. As $\vert B_{\rm ext}\vert$ increases, $r_{\rm f}$ decreases (e.g. $r_{\rm f}=2.1, 0.9$ for $B_{\rm ext}= -0.01, -0.10$respectively), and for $\vert B_{\rm ext}\vert\ga 1$ the solutions are almost indistinguishable (apart from sign of the field) from the corresponding solutions of Table 1. (There remains a small reduction in the value of $E_{\rm d}$.)

Clearly, neither in configurations with a closed magnetosphere (as Fig. 6a), nor in those with an externally dominated field, that bends away from the z-axis in the vicinity of the disc plane (Fig. 6b), will wind launching occur.

In the limit of large external field, the field configuration is identical with that in the "standard'' case, being now independent of the relative directions of the dynamo and external fields, cf. Figs. 3d and 6c. We note that the influence of the external field dominates over that of the dynamo generated field at approximately the same strength as in the previous set of simulations where it is directed in the same sense as the dynamo field.


  \begin{figure} \begin{tabular}{ll} (a)\includegraphics[clip,width=7.8cm]{run252.... ...i} &(d)\includegraphics[clip,width=7.8cm]{run246.epsi}\end{tabular} \end{figure} Figure 5: Poloidal field lines for models with magnetic diffusivity either increased ($\eta _1>1$) or reduced ($\eta _1<1$) in the corona, for various values of $B_{\rm ext}$: a) $\eta _1=3$, $B_{\rm ext}=0.01$; b) $\eta _1=3$, $B_{\rm ext}=10.0$; c) $\eta _1=0.3$, $B_{\rm ext}=0.01$; and d) $\eta _1=0.3$, $B_{\rm ext}=10.0$. The other parameters are $R_\alpha =-1.85$, $R_\omega =18.5$, Ru=0.64 and $\lambda =0.43$. Contours are equally spaced as a function of poloidal flux $rA_\phi $.
Open with DEXTER

Table 2: Table 1, but with enhanced and reduced coronal diffusivities ($\eta _1=3$ and 0.3). The asterisked entries have $R_\alpha =0$, and refer to purely advective calculations, with no dynamo action.

   
3.4 Solutions for a smaller disc

We recognize the possibility that the disc at large radii may be sufficiently dense and cool that ionization even by cosmic rays would be insufficient to justify treating it as a conducting medium. We can expect that this would affect the nature of the dynamo solutions, since the local dynamo number

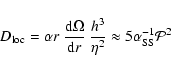
\begin{displaymath}D_{\rm loc}=\alpha r~\frac{{\rm d}\Omega}{{\rm d}r}~\frac{h^3}{\eta^2} \approx5\alpha_{\rm SS}^{-1}{\cal P}^{2} \end{displaymath}

is independent of radius for the scalings of Sect. 2.2. Thus, to determine how this would affect our conclusions, we performed a set of calculations with an outer disc radius R=1014 cm, again embedding the disc in a box $r_{\rm min}\le r\le 4R$, $z_{\rm min}\le z \le 3R$, with $r_{\rm min}=z_{\rm min}=10^{-4}R$. Here we took $\eta $ independent of z, and ${\cal P}=1$. Thus, this corresponds in some ways to a truncated version of the model of Sect. 3.1 The results are presented in Table 3 for a range of values of the external field parameter $B_{\rm ext}$; we have denoted this by $B_{\rm ext}^{(14)}$, to emphasize that with our standard scaling procedure the magnetic field is scaled with the equipartition field at 1014 cm rather than that at 1016 cm, as used in the earlier solutions. Note that $B_{\rm eq}\vert _{r=10^{14}~{\rm cm}}/B_{\rm eq}\vert _{r=10^{16}~{\rm cm}} \approx 420$ (see Sect. 2.2), and that energies are, correspondingly, in units of this larger $B_{\rm eq}$. To confirm this result, we repeated two of these computations with the disc of radius $10^{14}~{\rm cm}$ embedded in the same sized computational domain as in the standard set of simulations discussed in Sects. 3.1 and 3.2, i.e., we now took fR=400 and fZ=300. The results from these computations, which required many more mesh points, were remarkably similar to those described immediately above.

When presented in dimensionless form, quantitative results obtained for the smaller disc, as shown in Table 3, are not dissimilar to those found with the standard larger disc, as given in Table 1. More qualitatively, the shapes of the magnetic field lines are very similar for the same dimensionless $B_{\rm ext}$, so we do not show them for the smaller disc. In terms of dimensional quantities, this means that a stronger external field is required to open up the dynamo-generated field in a smaller disc. The difference is a factor of 420 if the disc radii differ by a factor of 100. As we argue in Sect. 4, this feature is related to the global nature of the dynamo solutions.

  
4 Discussion

A peculiar feature of the standard accretion disc model is that the dynamo number does not vary much with radius because a decrease in the rotational shear is compensated by the disc flaring (e.g. Pudritz 1981b). As discussed in Sects. 2.2 and 2.4, the dynamo number is estimated as $D=R_{\alpha}R_{\omega}\approx5\alpha_{\rm SS}^{-1}{\cal P}^{2}$. The dynamo action can maintain a non-decaying dipolar magnetic field in a disc surrounded by vacuum if $D> D_{\rm cr}=30$-70 (Parker 1979; Soward 2003), i.e., for $\alpha_{\rm SS}<0.1$for ${\cal P}=1$. Therefore, the growth rate of the magnetic field remains positive at all radii if $\alpha_{\rm SS}$ is small enough. In this sense, the dynamo region in an accretion disc has no natural outer radius. An effective outer radius can be identified with that at which the steady-state magnetic field becomes negligible or comparable with an external magnetic field. Thus, the effective radius of the dynamo region may depend on the external magnetic field - a rather unusual situation.


  \begin{figure} \par\begin{tabular}{lll} (a)\includegraphics[clip,width=4.9cm]{ru... ... &(c)\includegraphics[clip,width=4.9cm]{run236rr.epsi}\end{tabular} \end{figure} Figure 6: Poloidal field lines for models with excluded external field, with various values of the latter: a) $B_{\rm ext}=-0.01$; b) $B_{\rm ext}=-0.10$; c) $B_{\rm ext}=-10.0$. Solid contours indicate field lines which originate in the dynamo-dominated part of the disc ($A_\phi >0$), and do not connect with the external field, broken contours show field lines that connect with the external field ($A_\phi <0$). The other parameters are $R_\omega =185$, $R_\alpha =-1.85$, Ru=0.64, $\lambda =0.43$and $\eta _1=1.0$. Contours are equally spaced as a function of poloidal flux $rA_\phi $.
Open with DEXTER

Table 3: of results with a smaller disc ( $R=10^{14}~{\rm cm}$), else as for Table 1. F0 is the signed flux through the disc plane in $r\le 1$ (corresponding to 1014 cm) and $B_{\rm ext}^{(14)}$ is the dimensionless strength of the external field, but now measured in the units of $k^{1/2}B_{\rm eq}$at that radius.

As discussed in Sect. 3.4, a stronger external magnetic field is required to open up poloidal magnetic lines produced by the dynamo in a disc of smaller radius. This can be understood as follows. Large-scale magnetic fields generated by the dynamo have a global nature: since most of magnetic lines are closed within the disc, a change in the size of the dynamo system leads to a change in the magnetic field throughout the whole region. The dynamo action is most efficient near the axis, but magnetic lines that pass through that region cross the disc midplane again near the outer boundary of the disc. This explains why a relatively weak external magnetic field can open up the strong field in the inner parts of the disc: magnetic lines that reconnect with the external field at large radii are anchored near the disc axis; automatically the lever arm of such open field lines will be large. This feature makes dynamo solutions slightly modified by an external field especially favourable for wind launching. We show in Fig. 7 the opening angle of magnetic lines at the disc surface, $\theta=\arctan{B_z/B_r}$for the model presented in Figs. 2 and 3. For a cold flow, the magneto-centrifugal wind can be launched if $\theta<60^\circ$(Blandford & Payne 1982); pressure effects (Pelletier & Pudritz 1992) and finite disc thickness (Campbell 1999) result in slightly larger critical values of the launching angle.


  \begin{figure} \par\includegraphics[clip,width=8.7cm]{aa0008f7.eps}\end{figure} Figure 7: The opening angle of magnetic lines, $\theta=\arctan{B_z/B_r}$ at the disc surface z=h(r)(the "launch angle'') for the model presented in Figs. 2 and 3, with a range of external field strengths, $B_{\rm ext}=0.01$ (solid), 0.1 (dashed) and 1.0 (dotted). The values favourable for launching a magneto-centrifugal wind are in the range $\theta \protect\la 60^\circ$.
Open with DEXTER


  \begin{figure} \par\includegraphics[clip,width=8.6cm]{aa0008f8.eps}\end{figure} Figure 8: The variation of the function F(r) (the flux passing through the disc plane within radius r) with radius for the model presented in Figs. 2 and 3, with external field strengths $B_{\rm ext}=0.0$ (solid), 0.1 (long-dashed), 1.0 (short-dashed) and 10.0 (no dynamo action, dotted). The approximately linear parts of these plots through the bulk of the disc region correspond approximately to power laws  r0.66, r0.73, r0.92, r1.0, respectively.
Open with DEXTER

Apart from having an appropriate opening angle, the magnetic field of the disc must satisfy several other requirements in order to support a magnetically driven outflow. For example, the vertical current $I_z\propto rB_\phi$ must not diverge at $r\to0,\infty$ in order to avoid instabilities that would disrupt the outflow (Pelletier & Pudritz 1992). The radial variation of the azimuthal magnetic field far from the axis can be expected to (and, in our model, does) follow closely that of the equipartition field - this expectation arises from the form of the nonlinearity adopted, Eq. (2). This implies that $I_z\propto r^{-5/16}$ away from the axis, and so there is a physically reasonable reduction of the vertical current at large r. The axisymmetric dynamo solutions discussed here of course have $B_\phi\to0$ for $r\to0$, keeping the current finite at the axis.

A constraint on the radial distribution of poloidal magnetic flux in a steady-state accretion disc, with angular momentum transport by the outflow, is discussed in detail by Pelletier & Pudritz (1992) whose solutions have $F(r)=2\pi\int_0^r B_z r'~{\rm d}r'=2\pi rA_\phi(r)\propto r^{3/(2\xi)}$(with $B_z\simeq B_\phi\propto r^{-1}{\rm d}F/{\rm d}r$) where $\xi$ is a constant and all quantities are taken at z=0. Depending on the value of $\xi$, the flow at large z collimates to a cylindrical shell if $\xi>2$or diverges if $\xi<2$; the case $\xi=2$ corresponds to the self-similar solution of Blandford & Payne (1982). From the requirement that the terminal outflow speed decreases with radius, Pelletier & Pudritz (1992) obtain $\xi\geq{\textstyle{\frac{3}{2}}}$; these authors favour the value $\xi=3$ because it produces $B_\phi\propto r^{-1}$ and a vertical current that remains independent of radius.


  \begin{figure} \par\includegraphics{aa0008f9.eps}\end{figure} Figure 9: The variation of the toroidal magnetic field $B_\phi $along open poloidal magnetic field lines as a function of height z. a) The model with $B_{\rm ext}=0.01$ along field lines with values of the flux function $rA_\phi = 0.01$ (solid), 0.02 (broken) and 0.04 (dotted) - see Fig. 2 where magnetic field lines are labelled with the values of $rA_\phi $; these field lines intercept the disc plane z=0 at radii r = 0.0059, 0.13, 0.25 respectively. b) The model with $B_{\rm ext}=0.1$, see Fig. 3c, along the field lines with $rA_\phi = 0.02$ (solid), 0.04 (broken) and 0.10 (dotted), which meet the plane z = 0 at r = 0.049, 0.13, 0.43respectively. In each case the position at which the field line meets the disc surface is indicated by a square.
Open with DEXTER

Kinematic (linear) dynamo solutions of dipolar parity in a thin disc with aspect ratio $\lambda$ have the asymptotic scaling $A_\phi\propto hB_0\lambda_R^{-2/3}a(r)$ for $\lambda_R\ll1$ (Soward 1978, 1992, 2003), where a(r) is a certain slowly varying function of radius. Assuming that this scaling applies to the (nonlinear) steady-state solutions as well, and that all the variables can be replaced by their values at the local radius r(in particular, with $\lambda_R$ replaced by $\lambda(r)=h(r)/r$), we obtain $A_\phi\propto r^{-13/48}a(r)$ for the scalings adopted in Sect. 2.2, which gives $F(r)\propto r^{0.73}a(r)$. We show in Fig. 8 the radial distribution of the the flux function F(r) for models illustrated in Figs. 2 and 3. The solutions where the external field is not dominant, i.e. $B_{\rm ext}\la 0.1$, are in excellent agreement with the asymptotic results, given that a(r)varies insignificantly with r away from the boundaries. The corresponding value of $\xi$, in the radial range where the power-law approximation is meaningful, is $\xi\approx2$, a value remarkably similar to that in the model of Blandford & Payne (1982). The agreement is especially close for external fields of moderate strength, $B_{\rm ext}\simeq 0.01$-0.1. Figure 10 displays the dependence on radius of the field components Br, Bz and $B_\phi $ at the disc surface z=h(r).

A notable difference of the dynamo solutions with a conducting corona around the disc from the magnetic configurations employed in modelling disc outflows is that $\vert B_\phi\vert\gg\vert B_z\vert,\vert B_r\vert$ not only within the dynamo active disc but also in its immediate vicinity (see Fig. 10, and below in this section). We show in Fig. 9 the variation of the toroidal magnetic field along selected open poloidal field lines. A strong gradient of magnetic pressure that can contribute to driving an outflow is evident in these solutions. If efficient, such magnetic pressure driving can relax the limitation on the launch angle $\theta$ discussed above. We note, however, that pressure-driven winds require that the total pressure gradient is maintained by effects whose time scale is shorter than the sound crossing time across the disc, $\tau_{\rm s}=h/c_{\rm s}$. But the dynamo regeneration time $\tau$ can hardly be shorter than $\tau_{\rm s}$. Indeed, $\tau$ must be longer than both the rotation period and the turbulent eddy turnover time, $\tau\ga l/v_{\rm t}$, where $l\simeq h$ is the turbulent scale and $v_{\rm t}\simeq \alpha_{\rm SS}c_{\rm s}<c_{\rm s}$. Therefore, the total pressure will remain equilibrated in spite of the growth of the magnetic field due to dynamo action.

According to our numerical solutions, the external field affects the disc dynamo significantly if

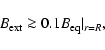
\begin{displaymath}B_{\rm ext}\ga 0.1 B_{\rm eq}\vert _{r=R}, \end{displaymath}

where R is the outer disc radius. With our chosen disc parameters, $B_{\rm eq}=1.7\times 10^{-5}$ G at r=1016 cm, so an external field of order $1~\mu{\rm G}$, can open up the entire poloidal field inside a radius of about $2\times 10^{15}$ cm. The poloidal field strength is about $1~\mu{\rm G}$ at this radius, and maybe 1000 times larger at the inner edge of the disc. This creates a field geometry appropriate for wind launching. Because of the global nature of the dynamo-generated magnetic field, mentioned above, a stronger external field is required to open up magnetic lines in a smaller disc. For example, $B_{\rm eq}\simeq7\times10^{-3}$ G at r=1014 cm, and so an external field stronger than 10-4 G is required to affect the dynamo in a disc of that radius.

The strength of the external magnetic field around an accretion disc is not well known from either theory or observations. An extrapolation of magnetic field strengths observed in molecular clouds (Crutcher 1999) to a number density of $10^8~{\rm cm}^{-3}$ yields a field of about 10-2 G which would be sufficient to affect the dynamo in a disc of radius about $5\times 10^{12}~$cm or larger. However, only an uncertain fraction of this field will be retained in the collapsing gas that eventually forms an accretion disc (e.g. Desch & Mouschouvias 2001; Nakano et al. 2002). Most discussions of wind launching from accretion discs use external magnetic fields of strength equal to $B_{\rm eq}$ without any detailed justification.

A useful estimate of the strength of the dipolar poloidal magnetic field within a dynamo active disc and in its vicinity can be obtained from asymptotic dynamo solutions of Soward (1978, 1992, 2003) for a disc surrounded by vacuum. From the requirement that the production rate of the poloidal magnetic field by the $\alpha$-effect balances turbulent diffusion, we obtain $\alpha B_\phi\simeq \eta \partial^2 A_\phi/\partial z^2$, which yields an order of magnitude estimate $\alpha B_\phi\simeq \eta\lambda^{2/3} A_\phi/h^2$, where the factor $\lambda^{2/3}$ arises because the lowest-order term in the expansion of $A_\phi$ in $\lambda$ is independent of z for solutions of dipolar symmetry (see Soward 2003 for a review). With $B_z=r^{-1}\partial rA_\phi/\partial r\simeq A/L$, where Lis the radial scale of the eigenmode, we obtain (Soward, private communication)

 \begin{displaymath} B_z\simeq R_\alpha \frac{h}{\lambda^{2/3}L} B_\phi, \end{displaymath} (12)

and $B_r\simeq B_z$, with $R_\alpha$ defined in Eq. (7). For a linear solution, $L\simeq \lambda^{-2/3}h$ and this yields $B_z\simeq B_r\simeq R_\alpha B_\phi$.

To obtain a tentative estimate for a steady-state, nonlinear solution, it is often assumed that nonlinear magnetic effects reduce the dynamo number to its critical value to saturate the dynamo action, but the structure of the solution remains similar to that of the marginally stable eigenmode. Then one can use $R_{\alpha}=D_{\rm cr}/R_\omega$ in the steady state, assuming that magnetic field is still too weak to affect the differential rotation, and so $R_\omega$ remains unchanged. With $B_\phi\simeq B_{\rm eq}$, we obtain

 \begin{displaymath} B_{\rm p}\simeq\frac{D_{\rm cr}}{R_\omega}B_{\rm eq} \simeq25\alpha_{\rm SS}{\cal P}^{-1}B_{\rm eq}, \end{displaymath} (13)

where we have adopted $D_{\rm cr}=50$. Thus, the dynamo can maintain a dipolar poloidal magnetic field of a strength comparable with the equipartition magnetic field in the disc, $B_{\rm p}\simeq B_\phi\simeq B_{\rm eq}$.


  \begin{figure} \par\includegraphics[clip,width=8.6cm]{aa0008f10.eps}\end{figure} Figure 10: The variation as a function of radius of the unsigned field components Br (dotted), Bz (solid) and $B (=B_\phi $, dashed) at the disc boundary, for the model with $B_{\rm ext}=0.01$, compare Fig. 2. In this solution, Br, Bz>0, $B_\phi <0$. The broken straight line illustrates the dependence r-5/4, corresponding to that of the fields in the Blandford & Payne (1982) model - see discussion in the text.
Open with DEXTER

The estimates Eqs (12) and (13) have certain limitations, and Fig. 10 shows that $B_{\rm p}\ll B_\phi$ at the disc surface in our solutions. Firstly, Eqs. (12) and (13) are valid for a disc surrounded by vacuum. Our numerical solutions with a conducting corona indicate that the critical value of the dynamo number is significantly (by a factor of about 3) smaller than for a disc surrounded by vacuum. Correspondingly, the ratio $B_{\rm p}/B_\phi$ is smaller by the same factor. Secondly, and perhaps more importantly, nonlinear effects can affect the solution more strongly than is assumed in Eq. (13). It can reasonably be expected that the radial scale of the nonlinear solution is comparable to the disc radius, i.e. $L\simeq\lambda^{-1}h$, which would yield, instead of Eq. (13),

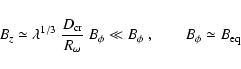
\begin{displaymath}B_z\simeq\lambda^{1/3}~\frac{D_{\rm cr}}{R_\omega}~ B_\phi\ll B_\phi\;, \qquad B_\phi\simeq B_{\rm eq} \end{displaymath}

in a thin disc, $\lambda\ll 1$. We note in this connection that if disc parameters were such that the dynamo number were only slightly larger than $D_{\rm cr}$, then our solutions would be compatible with Eq. (13).

Altogether, it appears that magnetic field generated by the mean-field dynamo in accretions discs have properties favourable for launching MHD outflows. However, our dynamo solutions are based on an accretion disc structure in which angular momentum is carried away by viscous stress. Magnetic braking is plausibly a stronger mechanism of angular momentum transfer (e.g. Pelletier & Pudritz 1992). Therefore, the radial velocity can be larger than that used here; moreover, it can be a function of magnetic field. As discussed by Moss et al. (2000), stronger inflow inhibits the dynamo action and enhances the dragging of the external magnetic field. However, this effect should be rather weak under realistic conditions where the turbulent magnetic Reynolds number based on the inflow speed is less than or of order unity. Furthermore, we hope that the qualitative features of the magnetic field are sufficiently robust - mean-field dynamos are in general remarkably insensitive to the details of the model.

If the magnetic field in the disc is produced by the dynamo without being significantly affected by the external field, wind launching becomes problematic. However, pressure-driven winds can open the magnetic lines produced by the dynamo and thus help to launch a magneto-centrifugal wind (cf. von Rekowski et al. 2003). On the other hand, a weak external magnetic field opens up the magnetic configuration produced by the dynamo to create conditions favourable for magneto-centrifugal wind launching. An even stronger external magnetic field, capable of supporting strong enough accretion by contributing to angular momentum transfer, may not need any help from the dynamo action if it is bent strongly enough by the inflow.

5 Conclusions

We have shown that a relatively weak external poloidal magnetic field $\vec{B}_{\rm ext}$ can open up magnetic lines generated by the mean-field dynamo in a standard accretion disc. The resulting geometry of poloidal magnetic lines is favourable for magneto-centrifugally driven outflows, with magnetic lines starting near the axis opened first (i.e., for smaller $B_{\rm ext}$). The structure of the poloidal field lines is very sensitive to the external magnetic field strength $B_{\rm ext}$, and becomes practically independent of the dynamo if $B_{\rm ext}$ exceeds about 10% of the value corresponding to equipartition with thermal energy at the outer disc radius, denoted B0. Even a relatively weak external poloidal magnetic field can be wound up by the differential rotation in the disc to give a strong azimuthal field, which in turn can dominate the dynamo generated field. There is a small range of $B_{\rm ext}$, $0.01\la B_{\rm ext}/B_0 \la 0.1$ (somewhat depending on the parameters chosen - see Sect. 3) where the field is a true hybrid of the dynamo and advected fields; these fields have both suitable launching angles and field lines extending to large z. The radial scaling of the magnetic field for $B_{\rm ext}/B_0\la 0.1$is very close to that of Blandford & Payne's (1982) self-similar solution. However, the range of values of $B_{\rm ext}$ in physical units where these hybrid solutions can be found depends crucially on the effective radius of the accretion disc, which is not a priori a well known quantity. Nevertheless, for plausible values of the disc radius, these fields are not exceptionally strong in the context of current models of the star formation process.

Acknowledgements
We are grateful to M. Camenzind, R. Pudritz and A. M. Soward for useful discussions and to an anonymous referee for careful reading of the manuscript and very helpful suggestions. We acknowledge support from PPARC (Grant PPA/G/S/2000/00528) and NATO (Grant PST.CLG 974737).

References


Copyright ESO 2003