Table 1:
of results with
magnetic diffusivity 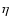 independent of z(i.e.,
independent of z(i.e., 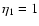 ),
),
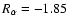 ,
,
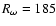 ,
Ru=0.64,
,
Ru=0.64,
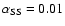 ,
,
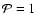 ,
and
,
and
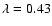 .
.
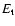 and
and 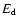 are the field energies in the
whole computational domain and near the
disc respectively (see text), s=EP/ETis the ratio of energies in the poloidal and toroidal magnetic field
in the whole domain, and F0 is the signed flux through
the disc plane in
are the field energies in the
whole computational domain and near the
disc respectively (see text), s=EP/ETis the ratio of energies in the poloidal and toroidal magnetic field
in the whole domain, and F0 is the signed flux through
the disc plane in 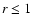 .
The final entry (asterisked) has
.
The final entry (asterisked) has
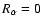 ,
and refers to a purely
advective calculation, with no dynamo action.
,
and refers to a purely
advective calculation, with no dynamo action.
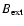 |
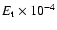 |
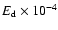 |
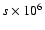 |
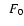 |
| 0.0 |
5.1 |
4.8 |
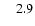 |
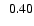 |
|
0.01 |
5.1 |
4.8 |
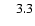 |
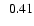 |
|
0.03 |
5.3 |
4.9 |
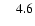 |
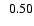 |
|
0.10 |
6.0 |
5.5 |
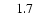 |
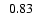 |
|
1.0 |
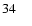 |
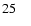 |
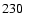 |
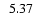 |
|
10.0 |
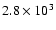 |
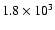 |
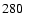 |
54.7 |
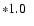 |
 |
 |
 |
 |
Source LaTeX |
All tables |
In the text