A&A 412, 603-613 (2003)
DOI: 10.1051/0004-6361:20031457

Dynamics of thick discs around Schwarzschild-de Sitter black holes

L. Rezzolla1,2 - O. Zanotti1,3 - J. A. Font3


1 - SISSA, International School for Advanced Studies, via Beirut, 2-4 34014 Trieste, Italy
2 - INFN, Sezione di Trieste, via A. Valerio, 2 34127 Trieste, Italy
3 - Departamento de Astronomía y Astrofísica, Universidad de Valencia, Dr. Moliner 50, 46100 Burjassot, Spain

Received 30 July 2003 / Accepted 12 September 2003

Abstract
We consider the effects of a cosmological constant on the dynamics of constant angular momentum discs orbiting Schwarzschild-de Sitter black holes. The motivation behind this study is to investigate whether the presence of a radial force contrasting the black hole's gravitational attraction can influence the occurrence of the runaway instability, a robust feature of the dynamics of constant angular momentum tori in Schwarzschild and Kerr spacetimes. In addition to the inner cusp near the black hole horizon through which matter can accrete onto the black hole, in fact, a positive cosmological constant introduces also an outer cusp through which matter can leave the torus without accreting onto the black hole. To assess the impact of this outflow on the development of the instability we have performed time-dependent and axisymmetric hydrodynamical simulations of equilibrium initial configurations in a sequence of background spacetimes of Schwarzschild-de Sitter black holes with increasing masses. The simulations have been performed with an unrealistic value for the cosmological constant which, however, yields sufficiently small discs to be resolved accurately on numerical grids and thus provides a first qualitative picture of the dynamics. The calculations, carried out for a wide range of initial conditions, show that the mass-loss from the outer cusp can have a considerable impact on the instability, with the latter being rapidly suppressed if the outflow is large enough.

Key words: accretion: accretion discs - black holes - relativity - hydrodynamics - cosmological constant

   
1 Introduction

Relativistic accretion tori orbiting around stellar-mass black holes have been the subject of renewed interest over the last few years in connection with the different astrophysical scenarios where these objects are expected to form, such as the core collapse of a massive star leading to a "failed" supernova explosion (a collapsar), or in the catastrophic merger of two (unequal mass) neutron stars in a close binary system. However, thick accretion discs are probably present at much larger scales as well, surrounding quasars and other active galactic nuclei, and feeding their central supermassive black holes. One of the major issues about such systems concerns their dynamical stability. This has important implications on the most favoured current models for the central engines of $\gamma$-ray bursts, either collapsars or binary neutron star mergers, for long and short bursts, respectively (see, e.g. Meszaros 2002 for a recent review).

Discs around black holes may suffer from a number of instabilities produced either by axisymmetric or by non-axisymmetric perturbations and further triggered by the presence of magnetic fields. A type of instability that has been studied in a number of works and that could take place when the discs are geometrically thick and axisymmetric is the so-called runaway instability (see Font & Daigne 2002a; Zanotti et al. 2003 and references therein). To appreciate the mechanism leading to the development of this instability, consider an inviscid fluid torus with a vertical structure and internal pressure gradients orbiting around a black hole (either Schwarzschild or Kerr). If the fluid is non self-gravitating, it will be contained within isopotential surfaces which generically possess a cusp on the equatorial plane (Fishbone & Moncrief 1976; Kozlowski et al. 1978; Abramowicz et al. 1978). As a result, material from the disc can accrete onto the black hole through the cusp as the result of small deviations from hydrostatic equilibrium.

Any amount of matter lost by the disc and captured by the black hole will increase its mass (and angular momentum), resulting in a modification of the equipotential surfaces which may cause the cusp to move deeper inside the torus more rapidly than the inner edge of the torus. When this happens, additional disc material will be allowed to fall into the black hole in an increasingly accelerated manner leading to the runaway instability.

Although this instability was first studied in the 80's (Abramowicz et al. 1983; Wilson 1984), time-dependent hydrodynamical simulations have been performed only recently, either with SPH techniques and pseudo-Newtonian potentials (Masuda & Eriguchi 1997; Masuda et al. 1998), or with high-resolution shock-capturing (HRSC hereafter) techniques in general relativity (Font & Daigne 2002a; Zanotti et al. 2003). These investigations have shown that, under the (idealised) assumption of constant specific angular momentum distributions, relativistic tori around Schwarzschild and Kerr black holes are generically unstable to the runaway instability, if non self-gravitating. The inclusion of more generic initial conditions, however, can disfavour the occurrence of the instability. Recently, Font & Daigne (2002b) (see also Daigne & Font 2003) have shown through numerical simulations that the runaway instability is suppressed when a non-constant distribution of the angular momentum is assumed for the torus (increasing as a power-law of the radius), a result which is in agreement with studies based on a recent perturbative analysis (Rezzolla et al. 2003a,b). While a similar stabilizing effect has been shown to be provided by the black hole if this is rotating (Wilson 1984; Abramowicz et al. 1998), Masuda & Eriguchi (1997) were able to show that the inclusion of the self-gravity of the torus effectively favours the instability. Clearly, a final conclusion on the occurrence of this instability has not been reached yet and will have to wait for fully general relativistic simulations. However, the increasingly realistic investigations performed recently have addressed several important aspects and the prospects are that we may be close to reaching a detailed description of the dynamics of the instability.

A further physical process acting against the instability and which has not been investigated so far, is provided by the existence of a repulsive force pointing in the direction opposite to the black hole's gravitational attraction. Such a force could disturb and even balance the standard outflow of mass through the inner cusp, thus potentially suppressing the runaway instability. As suggested recently by Stuchlík et al. (2000), such conditions could arise naturally in a black hole spacetime with a positive cosmological constant, i.e. in a Schwarzschild-de Sitter spacetime. In such a spacetime, in fact, a second cusp appears in the outer parts of the equilibrium tori, near the so-called "static radius''. Assuming a value for the relict cosmological constant $\Lambda \sim 10^{-56}$ cm-2 as deduced from recent cosmological observations of the vacuum energy density (Krauss 1998) and compatible with a sample of observational estimates provided by the analysis of a large number of high redshift supernovae (Perlmutter et al. 1999; Riess et al. 1998), Stuchlík et al. (2000) find that the location of this outer cusp for the largest stationary discs which can be built in a Schwarzschild-de Sitter spacetime is at about 50-100 kpc for supermassive black holes with masses in the range ${\sim} 10^8~ M_{\odot}{-}10^9~ M_{\odot}$. As for the inner one, a slight violation of the hydrostatic equilibrium at the outer cusp would induce a mass outflow from the disc and away from the black hole, which could affect the overall dynamics of the torus.

However, this is not the only way in which a cosmological constant could modify the dynamics of a disc orbiting around a Schwarzschild-de Sitter black hole. As argued by Stuchlík et al. (2000), in fact, a cosmological constant could produce a sensible modification in the accretion processes onto primordial black holes during the very early stages of expansion of the Universe, when phase transitions could take place, and the effective cosmological constant can have values in many orders exceeding its present value (Kolb & Turner 1990). Furthermore, a positive cosmological constant could also result into strong collimation effects on jets escaping along the rotation axis of the central black hole (Stuchlík et al. 2000).

The aim of this paper is to investigate one of these intriguing possibilities through numerical simulations. More precisely, we present a comprehensive study of the nonlinear hydrodynamics of constant angular momentum relativistic tori evolving in a sequence of background Schwarzschild-de Sitter spacetimes with increasing black holes masses. Our study clarifies the dynamical impact of a mass outflow on the occurrence of the runaway instability in such relativistic tori.

We note that our setup will not be an astrophysically realistic one. There are two important reasons for this. Firstly, given the present estimates for the value of the cosmological constant and for the masses of the supermassive black holes believed to exist in the centre of galaxies and active galactic nuclei, we are still lacking sufficient observational evidence that stationary thick accretion discs exist on scales of about 100 kpc. Secondly, even assuming that such objects are present within large galaxies, numerical calculations would have to face the present computational limitations which make it extremely hard to simulate accurately accretion discs with very low rest-mass densities and over such length scales. As a result, we will adopt a value for the cosmological constant that is unrealistically high. This yields discs with radial extents that are sufficiently small to be evolved numerically with satisfactory accuracy and provides a first qualitative description of the role that a cosmological constant could play on the dynamics of relativistic tori. In addition to this, the calculations reported here also offer a way of assessing how the self-gravity of the torus, which is basically contrasting the gravitational attraction of the black hole, could modify the overall inertial balance. This will provide a useful insight when fully relativistic calculations solving for the Einstein equations coupled to a self-gravitating matter source will be performed.

The organization of the paper is as follows. In Sect. 2 we briefly review the main properties of relativistic tori in a Schwarzschild-de Sitter spacetime. Next, in Sect. 3 we present the hydrodynamics equations and the numerical methods implemented in our axisymmetric evolution code. The material presented in this section is rather limited, since the details have previously been reported in a number of papers. The last part of this section is devoted to a discussion of the initial data we use for the simulations. The numerical results are then described in Sect. 4 and, finally, Sect. 5 contains our conclusions. Throughout the paper we use a space-like signature (-,+,+,+) and a system of geometrized units in which c = G = 1. The unit of length is chosen to be the gravitational radius of the black hole, $r_{\rm g} \equiv G M/c^2$, where M is the mass of the black hole. Greek indices run from 0 to 3 and Latin indices from 1 to 3.

   
2 Stationary configurations in a Schwarzschild-de Sitter spacetime

Building on a wide literature discussing equilibrium configurations of perfect fluid relativistic tori orbiting around Schwarzschild or Kerr black holes, Stuchlík et al. (2000) have recently extended these results to the case of a Schwarzschild-de Sitter black hole. In spherical coordinates (t, r, $\theta,\phi)$ the line element of this spacetime reads

 \begin{displaymath}{\rm d}s^2=-\left(1-\frac{2M}{r}-y\frac{r^2}{M^2}\right){\rm ... ...+ r^2\left({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2\right) , \end{displaymath} (1)

where M is the mass of the black hole and the cosmological constant $\Lambda$ is incorporated in the dimensionless parameter y defined as

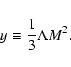\begin{displaymath}y \equiv\frac{1}{3}\Lambda M^2 . \end{displaymath} (2)

This parameter has to be smaller than a critical value y < $y_{\rm c} \equiv 1/27$ in order to produce static regions of the spacetime where equilibrium configurations can be found. We note that a negative cosmological constant, corresponding to a Schwarzschild-anti de Sitter black hole, does not introduce new qualitative features in the development of the runaway instability when compared to a Schwarzschild spacetime and will not be considered here. In what follows we briefly recall the main features of stationary configurations in a Schwarzschild-de Sitter spacetime, referring the reader to the work of Stuchlík et al. (2000) for an exhaustive discussion.

The perfect fluid with four-velocity $u^{\mu}$ is described by the usual stress-energy tensor

 \begin{displaymath} T^{\mu\nu}\equiv (e+p)u^\mu u^\nu+p g^{\mu\nu} = \rho h u^\mu u^\nu+p g^{\mu\nu} , \end{displaymath} (3)

where $g^{\mu\nu}$ are the coefficients of the metric (1) in which, however, the black hole mass M could be a function of time to account for the mass accreted onto the black hole (cf. the discussion of Eq. (23) below). The fluid variables e, p, $\rho$, and $h = (e+p)/\rho$ are the proper energy density, the isotropic pressure, the rest mass density, and the specific enthalpy, respectively. An equation of state (EOS) of polytropic type, $p = \kappa \rho^\gamma = \rho\epsilon(\gamma-1)$, completes the thermodynamical description of the fluid. Here, $\kappa $ is the polytropic constant, $\gamma$ is the adiabatic index and $\epsilon=e/\rho - 1$ is the specific internal energy. As shown by Kozlowski et al. (1978) (see also Fishbone & Moncrief 1976), the pressure gradients can balance the gravitational and centrifugal forces, allowing for the existence of stationary configurations of matter in non-geodesic circular motion and contained within closed "constant pressure'' equipotential surfaces. Under the conditions of hydrostatic equilibrium and of axisymmetry (i.e. $\partial_t = \partial_{\phi} = 0$) the relativistic Euler equations for a fluid with four-velocity $u^{\alpha} = (u^t, 0, 0, u^{\phi})$ take the simple Bernouilli-type form

 \begin{displaymath} \frac{\nabla_i p}{e+p} = - \nabla_i W + \frac{\Omega \nabla_i \ell}{1- \Omega \ell} , \hspace*{2cm} i=r,\theta, \end{displaymath} (4)

where $W = W(r,\theta) \equiv \ln(u_t)$ is the effective potential, $\ell\equiv -u_\phi/u_t$ is the specific angular momentum, and $\Omega\equiv u^\phi/u^t$ is the coordinate angular velocity as measured by an observer near the static radius, where the spacetime geometry is very close to a flat one (Stuchlík et al. 2000). Note that an explicit relation exists between the angular velocity and the specific angular momentum, which is given by $\Omega=-\ell (g_{tt}/g_{\phi\phi})$.

Once M and $\Lambda$ have been prescribed, the explicit expression for the potential $W(r,\theta)$ in the Schwarzschild-de Sitter spacetime is simply given by (Stuchlík et al. 2000)

 \begin{displaymath} W (r, \theta) = \frac{1}{2}\ln \left[ \frac{ \left(1 - 2 {M... ... \big(1 - 2 {M}/{r} - y {r^2}/{M^2}\big) \ell^2} \right]\cdot \end{displaymath} (5)

It is apparent from Eq. (4) that the simplest and indeed best studied configurations are obtained when the distribution of specific angular momentum $\ell $ is prescribed to be constant. In this case, which is also the one considered here, $W(r,\theta)$ shows three local extrema in the equatorial plane, one more than in the case of a Schwarzschild spacetime (cf. Fig. 1).
  \begin{figure} \par\includegraphics[width=8.25cm,clip]{fig0a.ps}\hspace*{1cm} \includegraphics[width=8.25cm,clip]{fig0b.ps}\end{figure} Figure 1: Schematic diagram for the Keplerian specific angular momentum $\ell _{_{\rm K}}$ in a Schwarzschild-de Sitter spacetime ( left panel) and the corresponding effective potential W ( right panel) once a constant value for $\ell $ has been chosen (cf. Fig. 2). The figure reports the different radial locations that are relevant for our discussion: the inner and outer cusp points $r_{\rm ci}, r_{\rm co}$, the inner and outer radii for the torus $r_{\rm in}, r_{\rm out}$, the inner and outer marginally stable orbits $r_{\rm ms,i}, r_{\rm ms,o}$, and the location of the maximum pressure in the torus $r_{\rm max}$ (see text for details). Note that $r_{\rm ci}, r_{\rm co}$ and  $r_{\rm max}$ are determined once a value for the constant specific angular momentum has been chosen (this is shown with the long-dashed line in the left panel) and that the inner and outer radii need not coincide with the corresponding locations of the cusps but are set by the value chosen for the potential $W_{\rm {in}}$ (this is shown with the long-dashed line in the right panel). Reported for comparison with a short-dashed line are $\ell _{_{\rm K}}$ and W in a Schwarzschild spacetime; the radial coordinate is shown on a logarithmic scale.
Open with DEXTER

Ordering these points with increasing values of r, the first extremum corresponds to the position of the inner cusp, $r_{\rm ci}$, where the equipotential surface has a self-crossing point in the $(r,\theta)$ plane. The second extremum corresponds to the position of the "centre'' of the torus, $r_{\max}$, where the internal pressure of the torus has its maximum. The third extremum, finally, marks the position of the outer cusp, $r_{\rm co}$, which is not present in the Schwarzschild spacetime and represents the distinctive contribution of the non-zero cosmological constant (see Fig. 1 for a schematic diagram). Note that for a configuration with constant $\ell $, a local extremum of W is also a point of vanishing pressure gradients (cf. Eq. (4)). As a result, the fluid motion on a circular orbit of radius $r_{\rm ci}$, $r_{\rm max}$ or $r_{\rm co}$ is a purely geodetic one, with the specific angular momentum being given by the Keplerian one $\ell _{_{\rm K}}$for a point-like particle at that radius. In a Schwarzschild-de Sitter spacetime this is given by

 \begin{displaymath} \ell^2_{_{\rm K}}(r,y) \equiv \frac{r^3M\left(1-y {r^3}/{M^3}\right)}{\big(r - 2M - y {r^3}/{M^2}\big)^2} \cdot \end{displaymath} (6)

If the black hole is a Schwarzschild one, then y=0 and the admittable values for a constant distribution of specific angular momentum that will lead to a torus of finite size are

 \begin{displaymath} \ell_{\rm ms} < \ell < \ell_{\rm mb} , \end{displaymath} (7)

where $\ell_{\rm ms} = 3\sqrt{6}/2$ and $\ell_{\rm mb} = 4$ represent the Keplerian specific angular momentum at the marginally stable and at the marginally bound orbits, respectively. In the case of a Schwarzschild-de Sitter black hole, however, the allowed parameter space is more complex since in this case one needs to take into account also the admittable values for y. While a detailed discussion of this issue is provided by Stuchlík et al. (2000), we here remind that for $y\ne 0$, a toroidal configuration of finite size is obtained for values of the specific angular momentum that satisfy

 \begin{displaymath} \ell_{\rm ms,i} < \ell < \ell_{\rm ms,o} , \end{displaymath} (8)

where now $\ell_{\rm ms,i}$ and $\ell_{\rm ms,o}$ represent the values of the specific angular momentum at the inner and outer marginally stable radii, respectively, and correspond to the local minimum and maximum of the Keplerian specific angular momentum given by Eq. (6) (cf. Fig. 1). Hence, $\ell_{\rm ms,i}$ and $\ell_{\rm ms,o}$provide the minimum and maximum values of $\ell(r,y)$ for which stable Keplerian circular orbits exist. Note that the very existence of these stable circular orbits depends on the values of y and, in particular, these can be found only if $y < y_{\rm ms} =12/15^4 \sim 2.37\times 10^{-4} < y_{\rm c}$.

In other words, given a value for the dimensionless parameter ${\bar y} < y_{\rm ms}$, circular orbits can exist for $\ell_{\rm ms,i}({\bar y}) < \ell < \ell_{\rm ms,o}({\bar y})$. Clearly, these orbits will be at radii smaller than the static radius $r_{\rm s}\equiv {\bar y}^{-1/3}$, at which the angular momentum (6) is zero and where the gravitational attraction of the black hole is exactly balanced by the cosmological repulsion[*].

Finally, it is worth reminding that for point-like particles, the decreasing part of $\ell^2_{_{\rm K}}$ (i.e. for $r<r_{\rm {ms,i}}; \; r >r_{\rm {ms,o}}$) corresponds to unstable circular geodesics, while the increasing part (i.e. for $r_{\rm {ms,i}} < r <r_{\rm {ms,o}}$) corresponds to stable circular geodesics. For a perfect fluid, however, internal pressure gradients allow the torus to occupy a region which would be geodesically unstable for point-like particles. A schematic diagram showing the behaviour of the Keplerian specific angular momentum $\ell _{_{\rm K}}$ and the corresponding effective potential W in a Schwarzschild-de Sitter spacetime, as well as the locations of the different radii that have been discussed so far is presented in Fig. 1. The Schwarzshild case is also displayed for comparison with a dashed line.

Once a value for the cosmological parameter and for the angular momentum have been fixed, Eq. (4), supplemented by the polytropic EOS, can be integrated analytically for any $r \leq r_{\rm s}$, to yield the rest-mass density distribution inside the torus

 \begin{displaymath} \rho(r,\theta) = \left\{\frac{\gamma-1}{\kappa \gamma} \left[\exp({W_{\rm in}-W})-1\right]\right\}^{1/(\gamma-1)} , \end{displaymath} (9)

where $W_{\rm in} \equiv W(r_{\rm in},\pi/2)$ and $r_{\rm {in}}$ is the inner edge of the torus. The latter is assumed to be a free parameter and is effectively controlled by the potential gap $\Delta W_{\rm i} \equiv W(r_{\rm in},\pi/2) - W(r_{\rm ci},\pi/2)$.

Hereafter, we will focus on tori built in a parameter space that is smaller than the one discussed so far. In particular, we will consider tori with constant specific angular momentum in the range $\ell_{\rm {ms,i}} \leq \ell\leq\ell_{\rm {ph}} < \ell_{\rm ms,o}$, where $\ell^2_{\rm {ph}} \equiv r^3/(r - 2M - y r^3/M^2)$ is the angular momentum of the unstable photon circular geodesic (Stuchlík et al. 2000). Furthermore, the hydrodynamical evolution of these tori will be followed in Schwarzschild-de Sitter spacetimes with dimensionless cosmological constant $0 \leq y \leq y_{\rm e} = 1/118~125 \sim 8.46\times 10^{-6}$, where $y_{\rm e}$ corresponds to the value of y for which the minimum of  $\ell_{\rm {ph}}$ is equal to the Keplerian angular momentum of the outer marginally stable orbit (Stuchlík et al. 2000).

   
3 Hydrodynamic equations and numerical approach

3.1 Basic equations

Suitable initial data for the torus (see Sect. 3.3 for specific details) are evolved forward in time using a two-dimensional (2D) general relativistic hydrodynamics code. The equations for a perfect fluid are implemented using the formulation developed by Banyuls et al. (1997) in which, adopting a 3+1 decomposed spacetime, the covariant conservation laws of the density current and of the stress-energy tensor are recast into a first-order, flux-conservative system of the type

  
$\displaystyle \frac{\partial {\vec U}}{\partial t} + \frac{\partial [\alpha {\v... ...\frac{\partial [\alpha {\vec F}^{\theta}]}{\partial \theta} = {\vec {\cal S}} ,$     (10)

where $\alpha\equiv\sqrt{-g_{00}}$ is the lapse function of the Schwarzschild-de Sitter metric and ${\vec U} \equiv (D, S_r, S_{\theta}, S_{\phi})$ is the state-vector of "conserved'' variables. These represent the relativistic rest-mass density and the relativistic momenta in the three coordinate directions, respectively. The conserved variables are expressed in terms of the "primitive'' variables $\rho, v_{i},$ and $\epsilon$ through the relations $D \equiv \rho \Gamma$ and $S_j \equiv \rho h \Gamma^2 v_j$, where the covariant components of the three-velocity vi can be obtained from the contravariant components $v^i\equiv u^i/\alpha u^t$ through the coefficients of the spatial 3-metric $\gamma_{ij}$, i.e. $v_i=\gamma_{ij}v^j$. The Lorentz factor $\Gamma$ is assumed to be measured by a local static observer and is given by $\Gamma\equiv\alpha u^t = (1-v^2)^{-1/2}$, with $v^2 \equiv \gamma_{ij}v^i v^j$. Finally, the vectors ${\vec F}^{i}$ and ${\vec {\cal S}}$ appearing in Eq. (10) represent the fluxes and sources of the evolved quantities, respectively, the latter being due entirely to the spacetime curvature. The explicit expressions of these terms can be easily generalized from the Schwarzschild case and are

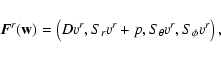\begin{displaymath}{\vec F}^{r}({\bf w}) = \left(D v^{r}, S_r v^{r} + p, S_{\theta} v^{r}, S_{\phi} v^{r} \right) , \end{displaymath} (11)


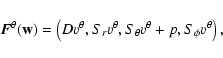\begin{displaymath}{\vec F}^{\theta}({\bf w}) = \left(D v^{\theta} , S_{r} v^{\... ...a} , S_{\theta} v^{\theta} + p , S_{\phi} v^{\theta}\right) , \end{displaymath} (12)


\begin{displaymath}{\vec {\cal S}}({\bf w}) = \left({\cal S}_1,{\cal S}_2,{\cal S}_3,{\cal S}_4\right) , \end{displaymath} (13)

where
                                          $\displaystyle {\cal S}_1$ $\textstyle \equiv$ $\displaystyle D\left({\cal A} v^r - {\cal B} v^\theta\right) ,$ (14)
       
$\displaystyle {\cal S}_2$ $\textstyle \equiv$ $\displaystyle -\left(\frac{M}{\alpha r^2}- \frac{r y}{\alpha M^2}\right)(\tau +... ... + \frac{\alpha}{r}\left(S_\theta v^\theta + S_\phi v^\phi - 2 S_r v^r\right) ,$ (15)
       
$\displaystyle {\cal S}_3$ $\textstyle \equiv$ $\displaystyle S_\theta \left({\cal A} v^r - {\cal B} v^\theta\right) + \alpha r^2 S^\phi v^\phi\sin\theta \cos\theta ,$ (16)
       
$\displaystyle {\cal S}_4$ $\textstyle \equiv$ $\displaystyle S_\phi\left({\cal A}v^r - {\cal B}v^\theta\right) ,$ (17)

and where
$\displaystyle {\cal A} \equiv \frac{M}{\alpha r^2} - \frac{2\alpha}{r} - \frac{r y}{\alpha M^2} ,$     (18)
       
$\displaystyle {\cal B} \equiv \alpha \cot\theta .$     (19)

It should be noted that since the dynamical evolution is assumed to be adiabatic, no evolution equation for the relativistic total energy density $\tau\equiv \rho h \Gamma^2 - p -D$ is solved here.

3.2 Numerical approach

The numerical code we use is the same employed by Zanotti et al. (2003) to study the dynamics of constant angular momentum relativistic discs around a Schwarzschild black hole. For the present investigation the code has been extended to account for the modifications introduced by the Schwarzschild-de Sitter geometry. The general relativistic hydrodynamics equations are solved by means of a HRSC scheme based on Marquina's flux formula (see e.g. Font 2000 for a review of these methods in numerical general relativistic hydrodynamics).

In order to cover optimally the large spatial extent of the equilibrium configurations and yet reach a satisfactory spatial resolution in the regions closer to the two cusps where the fluid motion needs to be calculated most accurately, we have introduced an important technical modification in the handling of the radial-coordinate grid. More precisely, we use a non-uniform radial grid with a logarithmic spacing, which is double-varied in the vicinities of the inner and outer cusps. The coordinate mapping used for this purpose is reminiscent of a tortoise coordinate mapping but it has been extended to a Schwarzschild-de Sitter metric as

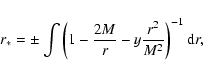\begin{displaymath}r_{\ast}= \pm \int \left(1-\frac{2M}{r}-y \frac{r^2}{M^2}\right)^{-1}{\rm d}r , \end{displaymath} (20)

where the $\pm$ sign distinguishes whether the mapping is made for increasing or decreasing values of the coordinate r, respectively.

As a result of this mapping, a radial grid of Nr=300 zones allows to cover a spatial domain going from $r_{_{\rm {MIN}}}= 2.1$ to $r_{_{\rm {MAX}}} = 100$ with a minimum radial spacing of the innermost part of the grid $\Delta r =10^{-4}$ and, correspondingly, a minimum radial spacing $\Delta r=10^{-3}$ for the outermost part of the radial grid. The two grids join smoothly at r=48.6, where the resolution is $\Delta r=2.72$. The angular grid, on the other hand, is more straightforward to build and consists of $N_{\theta}=70$ equally spaced zones extending from 0 to $\pi$ (cf. Zanotti et al. 2003)

As in Zanotti et al. (2003), a low density "atmosphere" is introduced in those parts of the numerical domain outside the torus. The initial atmosphere model chosen corresponds to the spherically symmetric accretion solution of non-interacting test fluid particles. The maximum density of the atmosphere is typically 5 to 6 orders of magnitude smaller than the density at the centre of the torus. In all of the validating tests performed, the hydrodynamical evolution of the torus was found to be unaffected by the presence of this atmosphere, which is evolved as the bulk of the fluid.

Finally, the mass outflows at the innermost and outermost radial points are computed respectively as

 \begin{displaymath} \dot{m}_{\rm i}(r_{_{\rm MIN}})\equiv - 2\pi\int_0^{\pi} \sqrt{-g} D v^r {\rm d}\theta \Big\vert_{r_{_{\rm MIN}}} , \end{displaymath} (21)

and

 \begin{displaymath} \dot{m}_{\rm o}(r_{_{\rm MAX}})\equiv 2\pi\int_0^{\pi} \sqrt{-g} D v^r {\rm d}\theta \Big\vert_{r_{_{\rm MAX}}} , \end{displaymath} (22)

where g is the determinant of the metric and $\sqrt{-g}=r^2\sin\theta$.

Table 1: Main properties of the tori considered in the numerical calculations. From left to right the columns report: the name of the model, the specific angular momentum $\ell $ (normalized to M), the polytropic constant $\kappa $, the inner and outer cusps of the torus, $r_{\rm ci}$ and $r_{\rm co}$, the radial position of the pressure maximum $r_{\rm max}$ (all radii are in units of the gravitational radius $r_{\rm g}$), the potential gaps $\Delta W_{\rm {i}}\equiv W_{\rm {in}}-W_{\rm {ci}}$ and $\Delta W_{\rm {o}}\equiv W_{\rm {in}}-W_{\rm {co}}$, where $W_{\rm {in}}$ is the potential at the inner edge of the disc. The last column reports the orbital period at the centre of the torus, $t_{\rm orb}$, expressed in milliseconds. All of the models share the same value of the cosmological parameter y=10-6, the same mass for the black hole, $M=10~M_{\odot}$, the same adiabatic index $\gamma =4/3$, and the same torus-to-hole mass ratio $M_{\rm t}/M=0.2$.

Note that the mass outflow given by Eq. (21) corresponds effectively to the mass accretion rate onto the black hole and is used to account for the instantaneous increase of the black hole mass at every time step. This, in turn, provides information about the changes in the background spacetime, fundamental for the appearance of the runaway instability (Font & Daigne 2002a; Zanotti et al. 2003). As mentioned in the Introduction, since we neglect the self-gravity of the torus, the hydrodynamics equations are solved in a sequence of background Schwarzschild-de Sitter spacetimes with increasing black hole masses. In practice, the spacetime evolution is achieved through a remapping of the metric functions at each time level of the type

 \begin{displaymath} g_{\mu \nu}\left(r,M^{n},y\right) \longrightarrow {\tilde g}_{\mu \nu}\left(r,M^{n+1},y\right) , \end{displaymath} (23)

where $M^{n+1}=M^n + \Delta t \ \dot m_{\rm i}^n(r_{_{\rm MIN}})$ is the mass of the black hole at the new timelevel tn+1. A detailed discussion on the validity of this approximation can be found in Font & Daigne (2002a) and in Zanotti et al. (2003). The prescription (23) is justified and can be regarded as a very good approximation when the variation of the black hole mass per unit time, $\dot m_{\rm i}^n$, is very small. This is certainly the case for the small disc-to-hole mass ratios  $M_{\rm t}/M$ considered here (cf. Table 1).


  \begin{figure} \mbox{ \includegraphics[height=6.3cm,width=6.1cm,clip]{fig1.ps}\i... ...{fig2.ps}\includegraphics[height=6.3cm,width=6.2cm,clip]{fig3.ps} } \end{figure} Figure 2: Radial profiles of the potential at the equatorial plane for models labelled A ( left), B ( centre) and C ( right), respectively. The local maxima in each plot indicate the location of the cusps. The horizontal lines fix the potential of the fluid element at the edges of the torus for each of the models considered. Models A, B and C differ among each other by the value of the angular momentum $\ell $which is reported in the lower right corners of the different panels.
Open with DEXTER

   
3.3 Initial data

As shown by Font & Daigne (2002a) and Zanotti et al. (2003), the runaway instability is a robust feature of constant angular momentum relativistic tori in Schwarzschild and Kerr spacetimes, if these are non self-gravitating. This result does not depend on the way the instability is triggered, i.e. by either artificially expanding the torus over the potential barrier at the inner cusp (Font & Daigne 2002a), or by introducing perturbations in an otherwise stable torus (Zanotti et al. 2003). As discussed above, however, the presence of an outer cusp in a Schwarzschild-de Sitter spacetime is likely to affect the robustness of this conclusion. In order to investigate to what extent an outflow of mass can interfere with the development of the runaway instability we have studied the behaviour of three different classes of models, which we refer to as A, B and C. These models are distinguished on whether the effective potential at the inner cusp, $W_{\rm {ci}}$, is less than, equal to, or larger than the effective potential $W_{\rm {co}}$ at the outer cusp, respectively. Furthermore, for each of these classes of models we have considered three different initial configurations, as shown in Fig. 2, with the potential at the inner edge of the torus, $W_{\rm {in}}$, being different from the potential barrier, $W_{\rm {ci}}$, by the adjustable amount  $\Delta W_{\rm i}$.

Note that for all of the models of the class A, the hydrostatic equilibrium is always violated at the inner cusp, i.e. $W_{\rm {in}} > W_{\rm {ci}}$, and a mass outflow will necessarily take place at the inner edge of the disc once the initial data is evolved. Furthermore, a mass loss will take place also at the outer cusp for models A2 and A3, which have $W_{\rm {in}} > W_{\rm {co}} > W_{\rm {ci}}$. For all of the models of the class B, on the other hand, the hydrostatic equilibrium is violated at both cusps and by the same amount, i.e. $W_{\rm {in}} > W_{\rm {ci}} = W_{\rm {co}}$ and, again, the mass outflows are regulated by the potential jump  $\Delta W_{\rm i}$. Finally, for all of the models of the class C, the hydrostatic equilibrium is always violated at the outer cusp, i.e. $W_{\rm {in}} > W_{\rm {co}}$, and also at the inner cusp for models C2 and C3, for which $W_{\rm {in}} > W_{\rm {ci}} > W_{\rm {co}}$. All of these different initial conditions are illustrated in Fig. 2, whose different panels show the effective potential curves and the values of $W_{\rm {in}}$ for the three classes of models.

Summarized in Table 1 are the potential jumps $\Delta W_{\rm i}$ and  $\Delta W_{\rm o}$, as well as the most relevant parameters of the various initial models considered here. Note that we have used a polytropic index $\gamma =4/3$ and adjusted the polytropic constant so as to have a small torus-to-hole mass ratio $M_{\rm t}/M=0.2$, thus minimizing the error introduced by neglecting the self-gravity of the torus.

A final comment will be made on the value adopted for the dimensionless cosmological constant y. As mentioned in the Introduction, the primary goal of our investigation is to provide a first qualitative analysis of the dynamics of thick discs in spacetimes with a positive cosmological constant. Because of this, and in order to avoid shortcomings with observations or computational resources, we have performed numerical simulations with y=10-6 for a black hole of mass $M=10~M_{\odot}$. These parameters, although unrealistic, allow us to construct sufficiently compact discs and perform numerical simulations with a satisfactory spatial resolution. We expect that all of the qualitative conclusions we draw from our simulations will continue to hold when considering more realistic values for both the cosmological constant and the black hole masses.

   
4 Results

As mentioned above, the development of the runaway instability appears to be a robust feature of the dynamics of non self-gravitating tori orbiting around Schwarzschild or Kerr black holes with constant distributions of specific angular momentum. This conclusion has been reached after numerous simulations have been performed for a large range of torus-to-hole mass ratios $M_{\rm t}/M$ and under a number of different initial conditions (Font & Daigne 2002a; Zanotti et al. 2003). In all of these simulations, the onset and full development of the instability was observed when the spacetime geometry was suitably modified to account for the black hole's mass-increase due to accretion. As a result of the instability, the torus is very rapidly accreted onto the black hole and this is most clearly signalled by the exponential growth in time of the rest-mass accretion rate at the innermost radial grid point. The growth-time for the instability is inversely proportional to the ratio $M_{\rm t}/M$ and is comparable with the dynamical (i.e. orbital) timescale when $M_{\rm t}/M \sim 1$.


  \begin{figure} \par\includegraphics[width=8cm,clip]{fig4.ps}\hspace*{0.5cm} \includegraphics[width=8cm,clip]{fig5.ps}\end{figure} Figure 3: Time evolution of the inner ( left panel) and of the outer ( right panel) mass outflows for the models of class A. The data is shown in units of solar masses per second, while the time is expressed in units of the orbital period. Note that only models A1 (solid line) and A2(dotted line) are runaway unstable. The solid circles in the two panels indicate the time at which $\dot{m}_{\rm i} > \dot{m}_{\rm o}$ for model A2.
Open with DEXTER


  \begin{figure} \par\includegraphics{figure4.EPS}\end{figure} Figure 4: Velocity field and equally spaced isocontours of the logarithm of the rest-mass density for model A2 at an early time ( left panel) and at a later time ( right panel); the times reported are in units of the orbital period. Initially the outer mass flux dominates the dynamics of the torus. However, the gravitational attraction of the black hole eventually overcomes the effect of the cosmological constant and the runaway instability takes place. This leads to the large inward-directed fluxes and to the disappearance of the torus inside the black hole in a few orbital periods.
Open with DEXTER

In the case of a Schwarzschild-de Sitter black hole, however, the rest-mass of the torus can change not only because of losses through the inner cusp leading to accretion onto the black hole, but also because of outflows from the outer cusp and away from the black hole. While both allowed, the impact that these two mass outflows could have on the dynamics of the torus is very different. The first one, in fact, induces changes in the black hole mass and could therefore lead to the runaway instability. The second one, on the other hand, does not produce changes of the background spacetime and cannot therefore produce an instability. Nevertheless, it can affect the hydrodynamical evolution in a number of different ways: firstly, by reducing the amount of rest-mass in the torus available for accretion and, secondly, by producing significant alterations of the velocity field, especially in the outer regions of the torus.

We have followed the hydrodynamical evolution of the models described in Table 1 over a number of orbital periods sufficiently large to reveal the impact of a positive cosmological constant on the occurrence of the runaway instability. In Figs. 3, 5 and 7 we show the two mass outflows $\dot{m}_{\rm i}$ and $\dot{m}_{\rm o}$ as a function of the orbital period $t_{\rm orb}=2\pi/ \Omega_{\rm max}$ at the centre of the torus, and for the three classes of models listed in Table 1. The three small insets shown in the panels for $\dot{m}_{\rm i}$ offer a view of the evolution of the rest-mass of the torus after this has been normalized to its initial value. The description of the dynamics of the tori is also completed with Figs. 4 and 6, which show equally spaced isocontours of the logarithm of the rest-mass density and, superimposed, the velocity field for models A2 and B2, respectively, at two different times during the evolution.

As it is apparent from a rapid look at these figures, the runaway instability is no longer the only possible evolution of the system, whose dynamics is instead the result of the interplay between the inner and the outer mass outflows. The occurrence of the runaway instability is clearly visible in the left panel of Fig. 3 for model A1 (solid line). Model A1, in fact, has initial conditions that resemble those encountered for a Schwarzschild black hole, with the outer radius of the torus located far from the outer cusp (cf. Figs. 1 and 2). As a result, the right panel of Fig. 3, shows that the outer mass outflow is in this case very small (indeed slightly negative as a result of accretion onto the torus of the infalling atmosphere), while the mass accretion rate onto the black hole (left panel) grows exponentially and undisturbed until the full development of the runaway instability at $t\sim 24.2\; t_{\rm orb}$. The dynamical evolution is different for models A2 (dotted line) and A3 (dashed line), where the competition between the two outflows at the inner and outer edges of the disc is closer to a balance and the initial outer mass-loss is non-negligible. For model A2, in particular, this is clearly visible in the left panel of Fig. 4, which shows that at early times ( $t\sim 1.2\; t_{\rm orb}$) the largest fluid velocities ( $v\sim 4\times 10^{-3}$) are reached in the outer regions of the torus and are outwardly directed. However, the outer mass-loss eventually becomes insufficient to prevent the development of the runaway instability, which takes place after $t\sim 33\; t_{\rm orb}$. The corresponding velocity field (with all vectors pointing towards the black hole) and the isocontours of the logarithm of the rest-mass density displayed in the right panel of Fig. 4 (at time $t\sim 30.0\; t_{\rm orb}$) show the important reduction in size undergone by the torus, which is about to disappear entirely inside the black hole after a few more orbital periods. This type of evolution does not take place for model A3, whose dynamics is completely dominated by the mass outflow through the outer cusp and for which the runaway instability does not develop (cf. Fig. 3).


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{fig6.ps}\hspace*{0.5cm} \includegraphics[width=8.2cm,clip]{fig7.ps}\end{figure} Figure 5: Same as Fig. 3 but for the models of class B.
Open with DEXTER


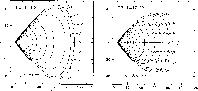  \begin{figure} \par\includegraphics{figure6.EPS}\end{figure} Figure 6: Same as Fig. 4 but for model B2. The intense mass ouflow across the outer edge of the disc removes a large fraction of its mass, and suppresses the runaway instability. The final disc reaches a quasi-steady state.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.45cm,clip]{fig8.ps}\hspace*{0.5cm} \includegraphics[width=8.45cm,clip]{fig9.ps}\end{figure} Figure 7: Same as Fig. 3 but for the models of class C.
Open with DEXTER

To better interpret the dynamics behind these simulations it is useful to compare the amount of rest-mass in the torus after the first 10 orbital periods of the evolution for the three models of class A (see inset in the left panel of Fig. 3). The residual rest-mass of the torus is 99%, 90%, and 55% of the initial one for the models A1, A2, and A3, respectively. This may appear somewhat surprising given the fact that the mass outflow from the inner cusp is smaller in the case of model A3 than it is for model A2, despite A3 having a larger initial potential jump  $\Delta W_{\rm i}$. The explanation for this comes from looking at the right panel of Fig. 3 which shows that the mass outflow from the outer cusp is however larger for model A3 than it is for model A2. As a result, the torus is emptied more efficiently, and this happens mostly through the outer cusp.

It is also very instructive to compare the mass outflows at the inner and outer edges of the disc for the three models of class A. Doing so leads to the important result that $\dot{m}_{\rm i} > \dot{m}_{\rm o}$ at all times for model A1 and that $\dot{m}_{\rm i} < \dot{m}_{\rm o}$ at all times for model A3. In other words, the unstable and the stable models seem to differ from each other on whether the mass outflow from the inner edge is larger or smaller than the corresponding mass-loss from the outer edge. In the case of model A2, on the other hand, the two mass outflows are closer to a balance and $\dot{m}_{\rm i} > \dot{m}_{\rm o}$ only for $t \gtrsim 18 \; t_{\rm orb}$, after which the runaway instability clearly develops; the time when this happens is shown with the filled circles in the two panels of Fig. 3. It appears, therefore, that an increasing potential gap at the outer edge of the torus favours the outflow of mass from the outer cusp but it also disfavours (and to a larger extent) the mass outflow from the inner cusp, with the corresponding accretion onto the black hole being severely suppressed. As a result, the feed-back of the black hole spacetime onto the overall dynamics of the system is considerably reduced and the runaway instability suppressed. Stated differently, the development of the runaway instability appears to be related to the efficiency of the mass-loss through the edges of the disc and, in particular, the instability is effectively "extinguished'' whenever the mass outflow from the outer edge of the disc and away from the black hole is larger than the mass outflow from the inner edge of the disc and onto the black hole. The condition $\dot{m}_{\rm i} < \dot{m}_{\rm o}$ can thus be used as a simple sufficient condition for the suppression of the runaway instability in a thick disc orbiting around a Schwarzschild-de Sitter black hole.

The role played by a positive cosmological constant on the dynamics of the discs and described so far for the models of class A is present also for the models of class B and C, although with some slight differences. As discussed in Sect. 3.3 and illustrated in Fig. 2, the models of class B are built with the outer and inner edges having the same effective potential. One would therefore expect that this would yield to very similar mass outflows at the two boundaries of the disc. However, the two panels of Fig. 5 show that the mass fluxes through the outer edges of the discs to infinity are always larger than the ones towards the black hole (i.e. $\dot{m}_{\rm i} < \dot{m}_{\rm o}$). As a result, the models of class B are all stable to the runaway instability. This is particularly apparent in models B2and B3, for which the outer mass outflows are at least a couple of orders of magnitude larger than the corresponding mass outflows onto the black hole, and which become negligibly small (i.e. ${\dot m}_{\rm i} < 10^{-8}~ M_{\odot}/{\rm s}$) well before 10 orbital periods. As a result, a large amount of the matter in those discs is not accreted onto the black hole, but escapes to infinity. This is illustrated in the small inset of the left panel of Fig. 5 which shows that after about 20 orbital periods more than 60% of the torus rest-mass is lost for model B2 and more than 90% for model B3.

Once the outflows die-off in the tori of class B, the remaining matter reaches a quasi-stable equilibrium, accreting onto the black hole on a timescale which is essentially controlled by the rate of mass-loss through the inner cusp. The importance of the mass outflow at the outer edges of the discs of class B is also apparent from Fig. 6, which shows the velocity field and isocontours of the logarithm of the rest-mass density of model B2 at an early and a later stage of the evolution. Note how the left panels of Figs. 4 and 6 have velocity fields that differ mostly in modulus but are equally oriented, while the right panels are substantially different with velocity fields that have opposite orientations leading to the disappearence of the torus into the black hole and to infinity, respectively. We also note that while the difference between the inner and outer mass outflows remains large also in the case of model B1, the dynamics is in this case much closer to an equilibrium, with the torus being still progressively emptied to infinity, but on a much larger timescale. No runaway instability was observed for this model over the time for which the calculations were carried out ( $t\sim 33\; t_{\rm orb}$).

Finally, for models C (see Fig. 7), the dynamics of the discs is particularly simple and the final result is rather clear to interpret. In this case, in fact, all the discs are built with an effective potential which is larger at the outer edge (cf. Fig. 2) and represent, therefore, initial conditions that are conceptually the opposite of those in models A. Because of the high potential barrier at the inner edge of the disc, the inner mass outflow is always rather minute and several orders of magnitude smaller than the corresponding mass outflow from the outer edge. As a result, the mass in the torus is lost very rapidly to infinity and very little is accreted onto the black hole. In particular, in the most dramatic case of model C3, the residual rest-mass in the torus is less than 20% after only 6 orbital periods.

   
5 Conclusions

We have investigated the effect of a positive cosmological constant on the dynamics of non self-gravitating thick accretion discs orbiting Schwarzschild-de Sitter black holes with constant distributions of specific angular momentum. The motivation behind this investigation has been that of assessing the role played by an effective repulsive force in the onset and development of the runaway instability, which represents a robust feature in the dynamics of constant angular momentum tori. In addition to the inner cusp near the black hole horizon, through which matter can accrete onto the black hole when small deviations from the hydrostatic equilibrium are present, thick discs in a Schwarzschild de-Sitter spacetime also possess an outer cusp through which matter can leave the torus without accreting onto the black hole. As a result of this mass-loss to infinity, the changes in the background metric (which are responsible for the development of the runaway instability) may be altered considerably and the instability thus suppressed.

As a simple way to evaluate this effect we have considered a sequence of Schwarzschild-de Sitter spacetimes differing only in their total mass and have performed time-dependent general relativistic hydrodynamical simulations in these background metrics of thick discs which are initially slightly out of hydrostatic equilibrium. In doing this we have adopted an unrealistically high value for the cosmological constant which however yields sufficiently small discs (extending up to about a few hundred gravitational radii) to be accurately resolved with fine enough axisymmetric numerical grids.

We have performed a number of simulations involving initial configurations of constant specific angular momentum discs differing both for the relative amplitude of the peaks in the effective potential and for the potential jump at the inner and outer cusps. The results obtained indicate that the runaway instability is no longer the only possible evolution of these systems but that their dynamics is rather the end-result of the interplay between the inner and the outer mass outflows. On the one hand, in fact, we have evolved initial models for which the cosmological constant has a weak influence; these models have negligible mass outflows to infinity while maintaining large mass outflows onto the black hole, which then lead to the development of the runaway instability. On the other hand, we have evolved initial models which are significantly influenced by the cosmological constant; these models develop mass outflows through the outer cusp which are much larger than those appearing at the inner cusp and, hence, do not develop the runaway instability. Placed somewhere between these two classes of initial configurations there exist initial models for which the mass outflows from the inner and outer cusps are more closely balanced. In these cases the runaway instability may or may not develop and we have noticed that a simple comparison between the mass outflows can be used to deduce the fate of the accreting disc. More specifically, we have found that the condition $\dot{m}_{\rm i} < \dot{m}_{\rm o}$ provides a simple sufficient condition for the suppression of the runaway instability in a thick disc orbiting around a Schwarzschild-de Sitter black hole.

In spite of the idealized setup used, the simulations performed here provide a first qualitative description of the complex nonlinear dynamics of thick discs in Schwarzschild-de Sitter spacetimes and we expect that most of the results obtained will continue to hold also when more realistic values for the cosmological constant are used. Aa a final comment we note that besides providing a qualitative description of the role that a cosmological constant could play on the dynamics of relativistic tori, these calculations also offer a way of assessing, at least qualitatively, the inertial role that the self-gravity of the torus plays in the development of the runaway instability. This will be very useful when studying the dynamics of relativistic tori with numerical codes solving also the full Einstein equations.

Acknowledgements

It a pleasure to thank Z. Stuchlík for useful comments. Financial support for this research has been provided by the Italian MIUR, by the Spanish Ministerio de Ciencia y Tecnología (grant AYA 2001-3490-C02-01) and and by the EU Network Programme (Research Training Network Contract HPRN-CT-2000-00137). L.R. also acknowledges the kind hospitality at the KITP in Santa Barbara, where part of this research was carried out (NSF grant PHY99-07949). The computations were performed on the Beowulf Cluster for numerical relativity "Albert100'', at the University of Parma.

References


Copyright ESO 2003