Table 1:
Main properties of the tori considered in the numerical
calculations. From left to right the columns report: the name of the
model, the specific angular momentum 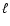 (normalized to M), the
polytropic constant
(normalized to M), the
polytropic constant 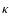 ,
the inner and outer cusps of the torus,
,
the inner and outer cusps of the torus,
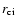 and
and
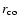 ,
the radial position of the pressure
maximum
,
the radial position of the pressure
maximum
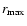 (all radii are in units of the gravitational
radius
(all radii are in units of the gravitational
radius 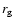 ), the potential gaps
), the potential gaps
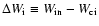 and
and
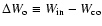 ,
where
,
where
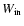 is the potential at the
inner edge of the disc. The last column reports the orbital period at the
centre of the torus,
is the potential at the
inner edge of the disc. The last column reports the orbital period at the
centre of the torus,
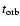 ,
expressed in milliseconds. All of
the models share the same value of the cosmological parameter
y=10-6, the same mass for the black hole,
,
expressed in milliseconds. All of
the models share the same value of the cosmological parameter
y=10-6, the same mass for the black hole,
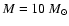 ,
the same
adiabatic index
,
the same
adiabatic index
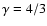 ,
and the same torus-to-hole mass ratio
,
and the same torus-to-hole mass ratio
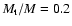 .
.
| Model |
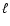 |
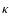 (cgs)
(cgs) |
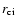 |
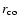 |
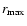 |
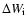 |
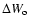 |
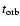 (ms)
(ms) |
| A1 |
3.84 |
8.970
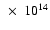 |
4.419 |
94.866 |
8.822 |
0.010 |
-0.010 |
8.11 |
| A2 |
3.84 |
2.568
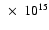 |
4.419 |
94.866 |
8.822 |
0.025 |
0.005 |
8.11 |
| A3 |
3.84 |
4.372
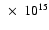 |
4.419 |
94.866 |
8.822 |
0.032 |
0.012 |
8.11 |
| B1 |
3.94 |
2.295
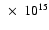 |
4.133 |
94.564 |
9.876 |
0.004 |
0.004 |
9.61 |
| B2 |
3.94 |
3.775
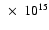 |
4.133 |
94.564 |
9.876 |
0.010 |
0.010 |
9.61 |
| B2 |
3.94 |
6.740
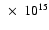 |
4.133 |
94.564 |
9.876 |
0.020 |
0.020 |
9.61 |
| C1 |
4.00 |
3.025
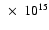 |
4.000 |
94.373 |
10.489 |
-0.007 |
0.007 |
10.51 |
| C2 |
4.00 |
7.120
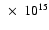 |
4.000 |
94.373 |
10.489 |
0.007 |
0.021 |
10.51 |
| C2 |
4.00 |
1.125
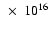 |
4.000 |
94.373 |
10.489 |
0.020 |
0.034 |
10.51 |
Source LaTeX |
All tables |
In the text