A&A 412, 879-891 (2003)
DOI: 10.1051/0004-6361:20031496
Activity on the surface of the nucleus of comet 46P/Wirtanen
O. Groussin - P. Lamy
Laboratoire d'Astrophysique de Marseille,
BP 8, 13376 Marseille Cedex 12, France
Received 4 March 2003 / Accepted 6 May 2003
Abstract
We present a thermal model of the nucleus of comet 46P/Wirtanen, constrained by the temporal variations of the water production rate, in order to understand the activity on its surface. We consider a spherical nucleus with a macroscopic mosaic of small and numerous active and inactive regions. At heliocentric distances 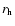 > 1.5 AU, the active regions represent 5-15% of the surface. At
> 1.5 AU, the active regions represent 5-15% of the surface. At  1.5 AU, a rapid increase takes place and the active fraction reaches 70 to 100
1.5 AU, a rapid increase takes place and the active fraction reaches 70 to 100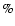 in about 10 days, and then remains approximately constant up to perihelion where
in about 10 days, and then remains approximately constant up to perihelion where
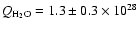 molecule s-1. Post-perihelion, this fraction returns to
molecule s-1. Post-perihelion, this fraction returns to  10
10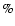 .
The model is consistent with a geometric albedo
.
The model is consistent with a geometric albedo 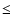 0.06. A refractory crust likely forms post-perihelion and can explain the variations of the activity over an orbit. Finally, we derived an erosion of
0.06. A refractory crust likely forms post-perihelion and can explain the variations of the activity over an orbit. Finally, we derived an erosion of  0.5 m per revolution and a remaining lifetime for the nucleus of several hundred revolutions.
0.5 m per revolution and a remaining lifetime for the nucleus of several hundred revolutions.
Key words: comets: individual: 46P/Wirtanen
For comet 46P/Wirtanen, the potential target of the ROSETTA mission![[*]](/icons/foot_motif.gif) , and more generally for all comets, an outstanding question is to understand, describe and quantify the activity on the surface of the nucleus. A standard, coarse approach consists in calculating the active fraction from the observations of
, and more generally for all comets, an outstanding question is to understand, describe and quantify the activity on the surface of the nucleus. A standard, coarse approach consists in calculating the active fraction from the observations of
 (A'Hearn et al. 1995). In the case of 46P/Wirtanen, Lamy et al. (1998) determined a radius of 0.6 km and derived an active fraction higher than 60% on the basis of a water production rate
(A'Hearn et al. 1995). In the case of 46P/Wirtanen, Lamy et al. (1998) determined a radius of 0.6 km and derived an active fraction higher than 60% on the basis of a water production rate
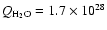 molecule s-1 measured by Stern et al. (1998). This implies that large amounts of water-releasing materials are present over the bulk of its surface or just under it.
molecule s-1 measured by Stern et al. (1998). This implies that large amounts of water-releasing materials are present over the bulk of its surface or just under it.
A major improvement in describing the activity of a cometary nucleus was proposed by Julian et al. (1999) who developed a model for comet 1P/Halley with five localized active regions. This model separately considers the thermal behaviour of the active and inactive regions and includes heat conduction into the nucleus. The variations in strength of the five active regions with the rotation of the nucleus and its heliocentric distance are both taken into account, leading to a variation of the water production rate in agreement with the observations. However, this model of localized active regions does not appear appropriate to 46P/Wirtanen where widespread activity is highly probable based on the above estimate of the active fraction and also, on the conspicuous absence of any structure in the coma (Fink et al. 1997).
Table 1:
Water production rate measurements of 46P/Wirtanen.
Several thermal models were developed in order to describe the activity of 46P/Wirtanen but they all have problems and limitations in the calculation of the water production rate. The models of Capria et al. (1996) and de Sanctis et al. (1999) give a water production rate too low compared with the observations, althougth they assumed a 100% active surface. The models of Möhlmann (1999) and Benkhoff (1999) both made approximations when they calculate
 :
Möhlmann (1999) assumed an arbitrary active fraction of 50% of the illuminated hemisphere while Benkhoff (1999) calculated the water production rate at the sub-solar point, without taking into account the lower insolation at higher latitude and longitude. Moreover, none of these models fit the observed variations of the water production rates with the heliocentric distance. The only two attempts to do so were performed by Crifo & Rodionov (1997) and Enzian et al. (1999). In their study of the coma of 46P/Wirtanen, the former authors developed different models of the nucleus to obtain "input conditions'', and they adjusted what they call the "active surface icy area fraction'' as a function of heliocentric distance, to be in agreement with the estimated
:
Möhlmann (1999) assumed an arbitrary active fraction of 50% of the illuminated hemisphere while Benkhoff (1999) calculated the water production rate at the sub-solar point, without taking into account the lower insolation at higher latitude and longitude. Moreover, none of these models fit the observed variations of the water production rates with the heliocentric distance. The only two attempts to do so were performed by Crifo & Rodionov (1997) and Enzian et al. (1999). In their study of the coma of 46P/Wirtanen, the former authors developed different models of the nucleus to obtain "input conditions'', and they adjusted what they call the "active surface icy area fraction'' as a function of heliocentric distance, to be in agreement with the estimated
 .
Enzian et al. (1999) used a quasi-3D
model including heat and gas diffusion inside a rotating spherical nucleus made of a porous dust-ice matrix. However, according to these authors, the calculated
.
Enzian et al. (1999) used a quasi-3D
model including heat and gas diffusion inside a rotating spherical nucleus made of a porous dust-ice matrix. However, according to these authors, the calculated
 does not fit well the observations beyond 1.5 AU.
does not fit well the observations beyond 1.5 AU.
In this article, we attempt to describe the pattern of activity on the nucleus of 46P/Wirtanen, coherent with the most recent determination of its physical properties (size, rotation period) and with the measured water production rate at different heliocentric distances, for the 1997 apparition, which has witnessed a major effort in preparation of the ROSETTA mission. The required thermal model takes into account all first-order physical processes, insolation, reradiation, water ice sublimation and heat conduction. We summarize and discuss in the following section the determinations of the water and dust production rates derived from the observations performed during the 1997 apparition of 46P/Wirtanen. In Sect. 3, we present the properties of the surface of the nucleus derived from the measured
 .
In Sect. 4, we present the dynamical evolution of the surface and the role of a refractory crust. Conclusions are given in Sect. 5.
.
In Sect. 4, we present the dynamical evolution of the surface and the role of a refractory crust. Conclusions are given in Sect. 5.
For the present study, we compiled the results of Bertaux et al. (1999), Fink et al. (1998), Farnham & Schleicher (1998) and Stern et al. (1998), as summarized in Table 1.
As illustrated in Fig. 1, the bulk of the measurements were obtained inside 1.5 AU, with two exceptions, one determination at 2.47 AU and one upper limit at 2.72 AU by Stern et al. (1998), both pre-perihelion. They suggest a very slow increase of
 up to
up to  1.5 AU where a sudden jump of a factor
1.5 AU where a sudden jump of a factor  30 took place in about 10 days.
The reality of this jump can hardly be questioned since the data have been obtained with the same spatial instrument (SOHO-SWAN) and analyzed with the same method (Haser's model) in a self-consistent way. The uncertainty of 25% affecting the results appears reliable as it takes into account many factors, including the calibration, the variability of the solar flux and the model. Even a larger uncertainty of 40% would still imply a jump of
30 took place in about 10 days.
The reality of this jump can hardly be questioned since the data have been obtained with the same spatial instrument (SOHO-SWAN) and analyzed with the same method (Haser's model) in a self-consistent way. The uncertainty of 25% affecting the results appears reliable as it takes into account many factors, including the calibration, the variability of the solar flux and the model. Even a larger uncertainty of 40% would still imply a jump of
 at
at  1.5 AU.
Then
1.5 AU.
Then
 regularly increases up to perihelion. We note that the observations of Fink et al. (1998) yield higher water production rates than the others (roughly a factor 2.5), perhaps a consequence of their method which uses the OI1D band at 6300 Å and which could be contaminated by the NH2 band at 6334 Å, although the authors paid attention to this difficulty. Post-perihelion,
regularly increases up to perihelion. We note that the observations of Fink et al. (1998) yield higher water production rates than the others (roughly a factor 2.5), perhaps a consequence of their method which uses the OI1D band at 6300 Å and which could be contaminated by the NH2 band at 6334 Å, although the authors paid attention to this difficulty. Post-perihelion,
 regularly decreases, even if the data are quite scattered. There is an asymmetry between the pre and post-perihelion behaviours in the range 1.4-1.064 AU as the gradient
regularly decreases, even if the data are quite scattered. There is an asymmetry between the pre and post-perihelion behaviours in the range 1.4-1.064 AU as the gradient
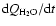 is steeper post than pre-perihelion. The lack of data at heliocentric distances beyond 1.5 AU post-perihelion do not allow us to confirm this trend.
is steeper post than pre-perihelion. The lack of data at heliocentric distances beyond 1.5 AU post-perihelion do not allow us to confirm this trend.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3685_f1.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg19.gif) |
Figure 1:
Measured water production rates [molecule s-1] of 46P/Wirtanen as function of heliocentric distance [AU] for the 1997 apparition. |
| Open with DEXTER |
We note that
 can also be derived from the heliocentric magnitudes
can also be derived from the heliocentric magnitudes 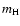 ,
using the empirical law
,
using the empirical law
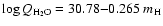 derived from the analysis of 15 comets by Jorda (1995), but we are not confident in this method for 46P/Wirtanen. The heliocentric magnitudes for the 1997 apparition of 46P/Wirtanen indicates an erratic behaviour (see Fig. 1 of Rickman and Jorda 1998) and we find no evidence for a temporal correlation of
derived from the analysis of 15 comets by Jorda (1995), but we are not confident in this method for 46P/Wirtanen. The heliocentric magnitudes for the 1997 apparition of 46P/Wirtanen indicates an erratic behaviour (see Fig. 1 of Rickman and Jorda 1998) and we find no evidence for a temporal correlation of 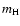 with
with
 ,
especially during the strong jump at 1.5 AU pre-perihelion. Moreover, most of the magnitudes were measured by amateurs astronomers with inherent large uncertainties, and are subject to difficulties of interpretation.
,
especially during the strong jump at 1.5 AU pre-perihelion. Moreover, most of the magnitudes were measured by amateurs astronomers with inherent large uncertainties, and are subject to difficulties of interpretation.
Table 2:
Af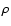 measurements of 46P/Wirtanen.
measurements of 46P/Wirtanen.
The quantity 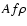 is a robust parameter to compare the dust emission of a comet at different times as it is observation-independent. However, the mean albedo A of the dust grains (not to be confused with the Bond albedo of the nucleus in Sect. 3.1) is a function of wavelength and phase angle, a situation which complicates the comparison of various measurements. We compiled in Table 2 the
is a robust parameter to compare the dust emission of a comet at different times as it is observation-independent. However, the mean albedo A of the dust grains (not to be confused with the Bond albedo of the nucleus in Sect. 3.1) is a function of wavelength and phase angle, a situation which complicates the comparison of various measurements. We compiled in Table 2 the 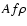 measurements of Farnham & Schleicher (1998), Fink et al. (1998), Jockers et al. (1998), Lamy et al. (1998), Schulz et al. (1998) and Stern et al. (1998), all obtained during the 1997 apparition of comet 46P/Wirtanen. Errors bars, when given by the authors, are quite large.
measurements of Farnham & Schleicher (1998), Fink et al. (1998), Jockers et al. (1998), Lamy et al. (1998), Schulz et al. (1998) and Stern et al. (1998), all obtained during the 1997 apparition of comet 46P/Wirtanen. Errors bars, when given by the authors, are quite large.
As illustrated in Fig. 2, the general trend is an increase of 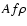 when the comet approaches perihelion and a decrease thereafter. There is a slow, irregular increase between 2.8 and 1.8 AU pre-perihelion, from
when the comet approaches perihelion and a decrease thereafter. There is a slow, irregular increase between 2.8 and 1.8 AU pre-perihelion, from 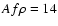 to 20 cm. At 1.6 AU,
to 20 cm. At 1.6 AU, 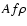 has increased by a factor
has increased by a factor  4 to reach 76 cm, according to the observations of Schulz et al. (1998). This may well be related to the aforementioned increase of
4 to reach 76 cm, according to the observations of Schulz et al. (1998). This may well be related to the aforementioned increase of
 at
at  1.5 AU. The low value of 15 cm at 1.31 AU reported by Stern et al. (1998) in the ultraviolet (2950 Å) may well be artificially biased by a change in the properties of the dust grains. At this distance, we expect the coma to contain a significant fraction of large particles which are not efficient scatters in the UV. A scaling by a factor
1.5 AU. The low value of 15 cm at 1.31 AU reported by Stern et al. (1998) in the ultraviolet (2950 Å) may well be artificially biased by a change in the properties of the dust grains. At this distance, we expect the coma to contain a significant fraction of large particles which are not efficient scatters in the UV. A scaling by a factor  3 between the UV and visible domains is plausible and would bring the measurements of Stern et al. (1998) in rough agreement with the others. Inside
3 between the UV and visible domains is plausible and would bring the measurements of Stern et al. (1998) in rough agreement with the others. Inside  1.2 AU,
1.2 AU, 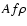 appears to undergo erratic variations to finally reach its maximum at perihelion, 157 cm according to Jockers et al. (1998). Post-perihelion,
appears to undergo erratic variations to finally reach its maximum at perihelion, 157 cm according to Jockers et al. (1998). Post-perihelion, 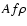 regularly decreases to reach 30 cm at 1.5 AU. We note that the last value of Farnham & Schleicher (1998) at 1.7 AU has a huge error bar. The lack of data do not allow to give more precise conclusions on the behaviour of
regularly decreases to reach 30 cm at 1.5 AU. We note that the last value of Farnham & Schleicher (1998) at 1.7 AU has a huge error bar. The lack of data do not allow to give more precise conclusions on the behaviour of 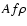 .
.
It is difficult to estimate the dust production rate
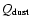 from
from 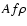 ,
as this requires a model and several parameters characterizing the gas and dust outflows (Newburn & Spinrad 1985; Singh et al. 1992). For 46P/Wirtanen, only two estimates of
,
as this requires a model and several parameters characterizing the gas and dust outflows (Newburn & Spinrad 1985; Singh et al. 1992). For 46P/Wirtanen, only two estimates of
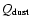 have been published: 4 kg s-1 at 2.5 AU (Lamy et al. 1998) and 140 kg s-1 near perihelion (Farnham et al. 1998). Using water production rates of
have been published: 4 kg s-1 at 2.5 AU (Lamy et al. 1998) and 140 kg s-1 near perihelion (Farnham et al. 1998). Using water production rates of  8 kg s-1 at 2.5 AU (Stern et al. 1998) and
8 kg s-1 at 2.5 AU (Stern et al. 1998) and  480 kg s-1 near perihelion (Bertaux et al. 1999), we obtain a dust-to-gas ratio in the range 0.3-0.5. From their ISOCAM observations at 9.62 and 15.0
480 kg s-1 near perihelion (Bertaux et al. 1999), we obtain a dust-to-gas ratio in the range 0.3-0.5. From their ISOCAM observations at 9.62 and 15.0 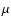 m, Colangeli et al. (1998) derived a dust-to-gas ratio of
m, Colangeli et al. (1998) derived a dust-to-gas ratio of  1 in the heliocentric distance range 2.0-2.5 AU, pre-perihelion. This slightly higher value could be due to a higher sensitivity of the ISOCAM observations to the larger grains, if they dominate the
coma at
1 in the heliocentric distance range 2.0-2.5 AU, pre-perihelion. This slightly higher value could be due to a higher sensitivity of the ISOCAM observations to the larger grains, if they dominate the
coma at  2 AU. All these estimates must be taken with caution because of inherent large uncertainties.
2 AU. All these estimates must be taken with caution because of inherent large uncertainties.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3685_f2.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg26.gif) |
Figure 2:
Measured 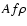 [cm] of 46P/Wirtanen as function of heliocentric distance [AU] for the 1997 apparition.
[cm] of 46P/Wirtanen as function of heliocentric distance [AU] for the 1997 apparition. |
| Open with DEXTER |
We now present a thermal model in order to calculate the water production rate of 46P/Wirtanen as a function of heliocentric distance, in order to interpret the observations of Fig. 1. We consider the first-order physical processes, insolation, reradiation, water ice sublimation and heat conduction. The water production rate is calculated at each point of the surface, taking into account the variations of insolation with latitude and longitude and the diurnal cycle (thermal inertia). The nucleus is assumed to be spherical with a radius of 0.6 km and a rotation period of 6 h (Lamy et al. 1998). The direction of the spin-axis is unknown and we assume that it is perpendicular to the orbital plane. In this configuration, we note that a null thermal inertia also represents a pole-on or a non-rotating nucleus. Next, we present the results on the fit of the variations of the water production rate of comet 46P/Wirtanen with the heliocentric distance by our thermal model. The aim is to constrain the surface properties of the nucleus by the measured water production rate. We study the pre- and post-perihelion cases and discuss the case of a non-spherical nucleus.
The model is a combination of the Standard Thermal Model (Lebofsky & Spencer 1989) and of the Mixed Model (Lamy et al. 2002), both upgraded by introducing the heat conduction as implemented by Groussin et al. (2003) for Centaurs Chiron and Chariklo. A fraction 1-x (
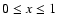 )
of the surface is composed only of refractory material (hereafter region A), represented by a standard thermal model with heat conduction, while a fraction x is composed of a "dirty ice'' (hereafter region B), represented by a mixed model with heat conduction. The "dirty ice'' is a microscopic mixture of water ice and refractory grains, whose differential size distribution function of the grains has a power index of
)
of the surface is composed only of refractory material (hereafter region A), represented by a standard thermal model with heat conduction, while a fraction x is composed of a "dirty ice'' (hereafter region B), represented by a mixed model with heat conduction. The "dirty ice'' is a microscopic mixture of water ice and refractory grains, whose differential size distribution function of the grains has a power index of 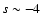 ,
as measured on 46P/Wirtanen (Colangeli et al. 1998) and on 1P/Halley (Lamy et al. 1987). Consequently, regions A are inactive and regions B are active. Inactive regions A could be in fact active regions covered by a crust which inhibits the activity. Active regions B are small, numerous, and located all over the nucleus.
We assume that there is no thermal coupling between regions A and B, which means that each region has its own surface temperature. This hypothesis is motivated by the very low conductivity of cometary nuclei, as explained in Sect. 3.1.2 (thermal inertia).
The surface energy balance for regions A is given by:
,
as measured on 46P/Wirtanen (Colangeli et al. 1998) and on 1P/Halley (Lamy et al. 1987). Consequently, regions A are inactive and regions B are active. Inactive regions A could be in fact active regions covered by a crust which inhibits the activity. Active regions B are small, numerous, and located all over the nucleus.
We assume that there is no thermal coupling between regions A and B, which means that each region has its own surface temperature. This hypothesis is motivated by the very low conductivity of cometary nuclei, as explained in Sect. 3.1.2 (thermal inertia).
The surface energy balance for regions A is given by:
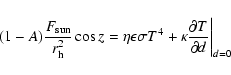 |
(1) |
and for regions B by:
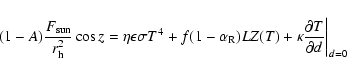 |
(2) |
where
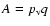 is the product of the geometric albedo
is the product of the geometric albedo 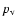 by the phase integral q,
by the phase integral q,
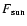 [Wm-2] is the solar constant,
[Wm-2] is the solar constant, 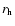 [AU] is the heliocentric
distance, z is the zenithal angle,
[AU] is the heliocentric
distance, z is the zenithal angle, 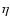 is the beaming factor introduced by
Lebofsky et al. (1986),
is the beaming factor introduced by
Lebofsky et al. (1986), 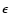 is the infrared emissivity,
is the infrared emissivity,
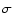 [J K-4 m-2 s-1] is the Stefan Boltmann's
constant, T [K] is the surface temperature, f is the fraction of
water ice in the microscopic mixture of refractory material and water ice of
region B (
[J K-4 m-2 s-1] is the Stefan Boltmann's
constant, T [K] is the surface temperature, f is the fraction of
water ice in the microscopic mixture of refractory material and water ice of
region B (
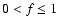 and f=1 for pure water ice),
and f=1 for pure water ice),
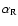 accounts for the recondensation of water ice on
the surface (Crifo 1987), L [J kg-1] is the
latent heat of sublimation of water ice, Z(T) [kg s-1 m-2] is the
accounts for the recondensation of water ice on
the surface (Crifo 1987), L [J kg-1] is the
latent heat of sublimation of water ice, Z(T) [kg s-1 m-2] is the
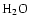 production rate,
production rate,
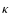 [Wm-1 K-1] is the thermal conductivity and d measures the depth.
[Wm-1 K-1] is the thermal conductivity and d measures the depth.
For the latent heat of sublimation of water ice L, we took a standard value:
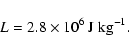 |
(3) |
The H2O production rate Z(T) is given by:
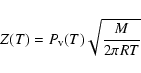 |
(4) |
where M= 18 g mol-1 is the H2O molecular weight and R= 8.314 J K -1mol-1 is the gas constant. The vapor pressure
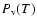 [Pa] is given by (Fanale & Salvail 1984; Skorov 1999):
[Pa] is given by (Fanale & Salvail 1984; Skorov 1999):
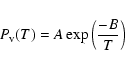 |
(5) |
where A= 3.56  1012 Pa and B= 6162 K. The numerical values of the other parameters will be discussed in Sect. 3.1.2.
1012 Pa and B= 6162 K. The numerical values of the other parameters will be discussed in Sect. 3.1.2.
We consider the one-dimensional (y) time-dependent (t) equation for the heat conduction:
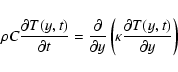 |
(6) |
where 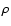 [kg m-3] is the mass density and C [J kg-1 K-1] is the specific heat capacity of the nucleus. We solve this equation as in Groussin et al. (2003), using a method described in detail by Spencer et al. (1989). The boundary conditions at the surface are given by Eq. (1) for inactive regions A and by Eq. (2) for active regions B. The method assumes that the temperature remains constant below a (thick enough) layer of thickness d, which gives the boundary condition at the base of the integrated thickness. We choose
[kg m-3] is the mass density and C [J kg-1 K-1] is the specific heat capacity of the nucleus. We solve this equation as in Groussin et al. (2003), using a method described in detail by Spencer et al. (1989). The boundary conditions at the surface are given by Eq. (1) for inactive regions A and by Eq. (2) for active regions B. The method assumes that the temperature remains constant below a (thick enough) layer of thickness d, which gives the boundary condition at the base of the integrated thickness. We choose 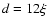 ,
where
,
where 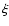 [m] is the characteristic length of the heat wave defined as
[m] is the characteristic length of the heat wave defined as
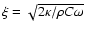 with
with 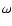 the rotational frequency;
the rotational frequency; 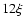 is sufficient to reach the convergence for the surface temperature. The thermal behaviour of the nucleus is described by its thermal inertia
is sufficient to reach the convergence for the surface temperature. The thermal behaviour of the nucleus is described by its thermal inertia
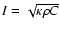 [MKS where 1 MKS = 1 J K-1 m-2 s-1/2]. We obtain the spatial distribution of the temperature at the surface of the nucleus,
[MKS where 1 MKS = 1 J K-1 m-2 s-1/2]. We obtain the spatial distribution of the temperature at the surface of the nucleus,
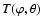 ,
where
,
where 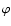 and
and 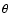 are the longitude and latitude respectively. From this temperature distribution, we derive the total water production rate by integrating the local water production rate at each point over the surface via:
are the longitude and latitude respectively. From this temperature distribution, we derive the total water production rate by integrating the local water production rate at each point over the surface via:
The results are presented in Sect. 3.2.
The various parameters involved in our thermal model are not known for cometary nuclei. We discuss below how we selected their respective values, as summarized in Table 3.
The infrared emissivity 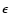 is taken equal to 0.95, the middle point of the interval 0.9-1.0 always quoted in the literature. As the interval is very small and the value near 1.0, this uncertainty has a negligible influence on the calculated surface temperature and consequently, on the water production rate.
is taken equal to 0.95, the middle point of the interval 0.9-1.0 always quoted in the literature. As the interval is very small and the value near 1.0, this uncertainty has a negligible influence on the calculated surface temperature and consequently, on the water production rate.
The beaming factor 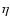 reflects the influence of surface roughness which produces an anisotropic thermal emission. The values of
reflects the influence of surface roughness which produces an anisotropic thermal emission. The values of 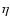 determined for a few asteroids and satellites vary from 0.7 to 1.2 (Spencer et al. 1989; Harris 1998). The value of
determined for a few asteroids and satellites vary from 0.7 to 1.2 (Spencer et al. 1989; Harris 1998). The value of 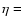 0.756, derived from observations of 1 Ceres and 2 Pallas by Lebofsky et al. (1986) has often been considered a standard and used for other solar system objects (e.g., Centaur 1997 CU26, Jewitt & Kalas 1998). However, for low albedo objects such as cometary nuclei, Lagerros (1998) pointed out that a rather high surface roughness is required in order to achieve this value. His recommendation led us to select the more appropriate value
0.756, derived from observations of 1 Ceres and 2 Pallas by Lebofsky et al. (1986) has often been considered a standard and used for other solar system objects (e.g., Centaur 1997 CU26, Jewitt & Kalas 1998). However, for low albedo objects such as cometary nuclei, Lagerros (1998) pointed out that a rather high surface roughness is required in order to achieve this value. His recommendation led us to select the more appropriate value 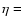 0.85. As the temperature varies as
0.85. As the temperature varies as
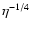 ,
the beaming factor has an important effect on the water production rate, especially at large heliocentric distances:
,
the beaming factor has an important effect on the water production rate, especially at large heliocentric distances: 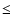 10% for
10% for
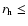 2 AU, but
2 AU, but 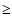 60% for
60% for
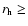 4 AU.
4 AU.
The Bond albedo
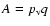 requires a knowledge of the geometric albedo
requires a knowledge of the geometric albedo 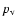 and of the phase integral q which measures the angular dependence of the scattered radiation. We choosed
and of the phase integral q which measures the angular dependence of the scattered radiation. We choosed
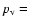 0.04, which is a canonical value used for cometary nuclei, and q= 0.28, the value found for 253 Mathilde (Clark et al. 1999) since the surface properties of this asteroid (
0.04, which is a canonical value used for cometary nuclei, and q= 0.28, the value found for 253 Mathilde (Clark et al. 1999) since the surface properties of this asteroid (
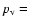 0.047 and
0.047 and
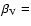 0.04 mag deg-1) are typical of cometary nuclei.
0.04 mag deg-1) are typical of cometary nuclei.
The recondensation of water ice on the surface is discussed in details in Crifo (1987). We adopted his recommended value
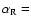 0.25.
0.25.
The thermal inertia I [MKS] is the only parameter which is required to solve the heat Eq. (6) and obtain the spatial distribution temperature at the surface of the nucleus. The thermal inertia of cometary nuclei is expected to be low, much lower than that of the Moon (50 MKS, Winter & Saari 1969) and that of Mars (24 MKS to 800 MKS, Mellon et al. 2002). It has been estimated for a few small bodies in the Solar System: I< 15 MKS for main-belt asteroids (Spencer et al. 1989), 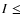 10.5 MKS for Asbolus (Fernandez et al. 2002), and I= 3 MKS and
10.5 MKS for Asbolus (Fernandez et al. 2002), and I= 3 MKS and 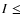 2 MKS for Chiron and Chariklo respectively (Groussin et al. 2003). In view of the situation, we considered a large range of values for the thermal inertia of 46P/Wirtanen, namely 0-20 MKS.
2 MKS for Chiron and Chariklo respectively (Groussin et al. 2003). In view of the situation, we considered a large range of values for the thermal inertia of 46P/Wirtanen, namely 0-20 MKS.
At this stage, all parameters except x and f are estimated using plausible assumptions and our model is therefore left with only these two free parameters (x, f).
Table 3:
The model parameters.
Our model has two free parameters, the fraction of active regions on the surface x, and the fraction of water ice in the ice-refractory material mixture f. We consider a range of values in order to test their influence on
 :
:
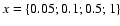 and
and
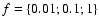 .
These ranges are very large to reflect broad possibilities. Figure 3
displays the variation of
.
These ranges are very large to reflect broad possibilities. Figure 3
displays the variation of
 as a function of heliocentric distance for the above values of the parameters x and f. As illustrated by the hatched region, the thermal inertia I, in the range 0-20 MKS, has no influence on
as a function of heliocentric distance for the above values of the parameters x and f. As illustrated by the hatched region, the thermal inertia I, in the range 0-20 MKS, has no influence on
 for
for
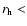 1.5 AU. The influence increases beyond to reach
1.5 AU. The influence increases beyond to reach  10% at 3 AU, a negligible effect in view of the influence of the other parameters x and f (see below).
10% at 3 AU, a negligible effect in view of the influence of the other parameters x and f (see below).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f3.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg73.gif) |
Figure 3:
Pre-perihelion, water production rates [molecule s-1] as
a function of heliocentric distance [AU] for a
thermal inertia of 10 J K-1 m-2 s-1/2 and for different
values of x and f. The hatched region corresponds to the range
0<I<20 MKS, restricted to the case x=1 and f=1 for clarity. |
| Open with DEXTER |
The influence of the parameter f is easy to understand: the higher f, the higher
 ,
as there is more water ice on the surface in the microscopic mixture of the active regions. When f varies from 0.01 to 1,
,
as there is more water ice on the surface in the microscopic mixture of the active regions. When f varies from 0.01 to 1,
 increases by a factor
increases by a factor  1.3 for
1.3 for
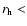 1.5 AU and a factor
1.5 AU and a factor  3 at 3 AU.
The parameter x has the strongest effect. The higher x, the higher
3 at 3 AU.
The parameter x has the strongest effect. The higher x, the higher
 ,
as there are more active regions. The variation of
,
as there are more active regions. The variation of
 with x is a geometric effect and is thus directly proportional to x. To summarize, for
with x is a geometric effect and is thus directly proportional to x. To summarize, for
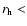 1.5 AU, the behaviour of the model is dominated by the parameter x while f plays a second order role; for
1.5 AU, the behaviour of the model is dominated by the parameter x while f plays a second order role; for
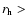 1.5 AU, x and f play equally important roles which are difficult to separate.
1.5 AU, x and f play equally important roles which are difficult to separate.
It is not possible to find a unique combination of f and x which fits all the observations. As we do not have any a-priori knowledge of f, except that f>0 for obvious reasons (
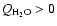 molecule s-1), we choose values between 0.01 and 1. Following this consideration, it is now possible to discriminate between different values of x to determine its range. We can distinguish three different phases. During the first one, when
molecule s-1), we choose values between 0.01 and 1. Following this consideration, it is now possible to discriminate between different values of x to determine its range. We can distinguish three different phases. During the first one, when
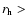 1.5 AU, x lies between 0.05 and 0.15, based on the very sparce data in this region and on the error bars. Around 1.5 AU, x increases strongly to reach values higher than
0.7 in about 10 days. Thereafter and up to perihelion, x remains between 0.7 and 1,
in view of the observational error bars. Consequently, there is a rapid transition from a low to a high level of activity, during which the surface of the nucleus is completely modified. A blow-off of a crust could explain such a phenomenon and this will be discussed in Sect. 4.
1.5 AU, x lies between 0.05 and 0.15, based on the very sparce data in this region and on the error bars. Around 1.5 AU, x increases strongly to reach values higher than
0.7 in about 10 days. Thereafter and up to perihelion, x remains between 0.7 and 1,
in view of the observational error bars. Consequently, there is a rapid transition from a low to a high level of activity, during which the surface of the nucleus is completely modified. A blow-off of a crust could explain such a phenomenon and this will be discussed in Sect. 4.
The visible geometric albedo of the nucleus depends on x and f, which gives another constraint on these parameters. The geometric albedo of comet 46P/Wirtanen is unknown but, according to the results obtained on several short-period comets, we are confident that
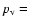 0.02-0.06
(Lamy et al. 2004). According to Clark et al. (1984), the reflectance of water ice is reduced by a factor 5 if mixed with 10% of charcoal.
To estimate the impact of x and f on the geometric albedo, we calculate the geometric albedo of a spherical nucleus composed of a mixture of water ice and refractory material, using a numerical code written by Roush (1994), in the framework of the Hapke theory. We choose 3 differents refractory materials: a silicate known as "astronomical silicate'' in the literature (Draine & Lee 1984), glassy carbon and kerogen. Taking into account large ranges for the numerous parameters involved in this calculation (e.g., optical constants, grain size, Hapke's h parameter), and in order to be consistent with a geometric albedo in the range 0.02 to 0.06, we find that f remains unconstrained as long as
0.02-0.06
(Lamy et al. 2004). According to Clark et al. (1984), the reflectance of water ice is reduced by a factor 5 if mixed with 10% of charcoal.
To estimate the impact of x and f on the geometric albedo, we calculate the geometric albedo of a spherical nucleus composed of a mixture of water ice and refractory material, using a numerical code written by Roush (1994), in the framework of the Hapke theory. We choose 3 differents refractory materials: a silicate known as "astronomical silicate'' in the literature (Draine & Lee 1984), glassy carbon and kerogen. Taking into account large ranges for the numerous parameters involved in this calculation (e.g., optical constants, grain size, Hapke's h parameter), and in order to be consistent with a geometric albedo in the range 0.02 to 0.06, we find that f remains unconstrained as long as 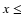 0.15. As the surface fraction x increases, the fraction of ice f is bound to progressively lower values. For instance, for
0.15. As the surface fraction x increases, the fraction of ice f is bound to progressively lower values. For instance, for 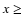 0.7, f cannot exceed
0.7, f cannot exceed  0.5. Combining the constraint imposed by the geometric albedo and that imposed
by the variation of the observed water production rate with heliocentric distance, we found that x and f must satisfy the following conditions:
0.5. Combining the constraint imposed by the geometric albedo and that imposed
by the variation of the observed water production rate with heliocentric distance, we found that x and f must satisfy the following conditions:
-
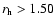 AU,
AU,
![$x \in [0.05,0.15]$](/articles/aa/full/2003/49/aa3685/img79.gif) and
and
![$f \in [0.01,1]$](/articles/aa/full/2003/49/aa3685/img80.gif) ;
;
-
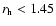 AU,
AU,
![$x \in [0.7,1]$](/articles/aa/full/2003/49/aa3685/img82.gif) and
and
![$f \in [0.01,0.5]$](/articles/aa/full/2003/49/aa3685/img83.gif) .
.
The abrupt transition at 1.45-1.50 AU obviously results from the jump of
 .
We further verify that
.
We further verify that
 varies by less than 1% when the geometric albedo remains in the range 0.02-0.06. Figure 4 displays the water production rate of our model for these acceptable ranges of the parameters. As the observations of Fink et al. (1998) seems too high, as explained in Sect. 2.1, we rescaled them (
varies by less than 1% when the geometric albedo remains in the range 0.02-0.06. Figure 4 displays the water production rate of our model for these acceptable ranges of the parameters. As the observations of Fink et al. (1998) seems too high, as explained in Sect. 2.1, we rescaled them (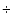 2.5) to agree with the observations of Bertaux et al. (1999), Farnham & Schleicher (1998) and Stern et al. (1998). The hatched region then covers all the observations within
2.5) to agree with the observations of Bertaux et al. (1999), Farnham & Schleicher (1998) and Stern et al. (1998). The hatched region then covers all the observations within 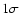 .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f4.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg86.gif) |
Figure 4:
Pre-perihelion, water production rates [molecule s-1] as a function of heliocentric distance [AU] for the best ranges of the parameters f and x. |
| Open with DEXTER |
It is a satisfactory result in view of the difficulties to interpret the water production rates with a consistent thermal model. Moreover, it is in agreement with the results of Crifo & Rodionov (1997). For their study of the coma of 46P/Wirtanen, they developed two different models of the nucleus, an homogeneous and an inhomogeneous sphere of dusty ice, with a radius of 1.4 km. The homogeneous model assumes that the entire surface of the nucleus is covered by active regions, while the inhomogeneous model considers that active regions are 45 sectors in longitude, spaced at 45
sectors in longitude, spaced at 45 intervals. Their constraint comes from the visual magnitudes of the coma for several apparitions between 1947 and 1991, converted to water production rates using an empirical formula derived from many cometary observations by Rickman & Jorda (1998). For the homogeneous model, Crifo & Rodionov (1997) found that what they call the "active surface icy area fraction'' must vary with heliocentric distance, from 0.14 at 1 AU to 0.032 at 2 AU and 0.0025 at 3 AU. Using our definition of the active fraction x, and a radius of 0.6 km, this roughly corresponds to x= 0.76 at 1 AU, x= 0.17 at 2 AU and x= 0.013 at 3 AU, which is quite compatible with our results, at least at 1 and 2 AU. As their inhomogeneous model is so different from ours, a comparison of the results is irrelevant.
intervals. Their constraint comes from the visual magnitudes of the coma for several apparitions between 1947 and 1991, converted to water production rates using an empirical formula derived from many cometary observations by Rickman & Jorda (1998). For the homogeneous model, Crifo & Rodionov (1997) found that what they call the "active surface icy area fraction'' must vary with heliocentric distance, from 0.14 at 1 AU to 0.032 at 2 AU and 0.0025 at 3 AU. Using our definition of the active fraction x, and a radius of 0.6 km, this roughly corresponds to x= 0.76 at 1 AU, x= 0.17 at 2 AU and x= 0.013 at 3 AU, which is quite compatible with our results, at least at 1 and 2 AU. As their inhomogeneous model is so different from ours, a comparison of the results is irrelevant.
We derive the following power exponents for the water production rate: n=-2.4 for
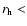 1.5 AU and n=-3.0 for
1.5 AU and n=-3.0 for
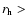 1.5 AU. These values are lower than those of Jorda et al. (1995) and Stern et al. (1998) who obtained n=-4.75 and n=-4.9 respectively as our model contains 2 differents levels of activity separated by a transition region at 1.5 AU.
1.5 AU. These values are lower than those of Jorda et al. (1995) and Stern et al. (1998) who obtained n=-4.75 and n=-4.9 respectively as our model contains 2 differents levels of activity separated by a transition region at 1.5 AU.
Our model has several advantages:
- 1.
- It is based on first order processes, thus excluding complicated assumptions (e.g., porosity, pore and grain size,...) resulting in a small number of unknown parameters.
- 2.
- It uses the nucleus size of 0.6 km and the rotation period of 6 h determined by Lamy et al. (1998) from Hubble Space Telescope observations.
- 3.
- It does not require a halo around the nucleus (e.g., Benkhoff & Boice 1996) to artificially increase the water production rate as there is enough water coming from the nucleus itself.
- 4.
- It is in agreement with a pattern of widespread activity over the nucleus, consistent with the absence of structure (jets) in the coma.
- 5.
- It gives a water production rate at perihelion of
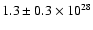 molecule s-1, depending on the fraction of active regions x, in agreement with the results of Bertaux et al. (1999) who derived
molecule s-1, depending on the fraction of active regions x, in agreement with the results of Bertaux et al. (1999) who derived
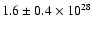 molecule s-1.
molecule s-1.
Figure 5 displays the water production rate as a function of heliocentric distance, including the observations of Bertaux et al. (1999), the observations of Fink et al. (1998) divided by a factor 2.5 (see Sect. 2.1) and our model with a thermal inertia of 10 MKS and the different values of x and f defined above. The scattered data show a decrease of activity with heliocentric distance with however considerable fluctuations. If correct, the
last observation of Bertaux et al. (1999) at 1.35 AU would indicate a sudden decline of
 by a factor
by a factor  3, implying that the active fraction dropped to
3, implying that the active fraction dropped to 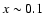 .
The last observation of Fink et al. (1998) at 1.47 AU is in agreement with this trend, although the formal value is slightly larger than that of Bertaux et al. (1999). However, the corresponding spectra has a low signal-to-noise ratio so that the real error bar for that particular value is certainly much larger than the standard error of 20% quoted by Fink et al. (1998).
.
The last observation of Fink et al. (1998) at 1.47 AU is in agreement with this trend, although the formal value is slightly larger than that of Bertaux et al. (1999). However, the corresponding spectra has a low signal-to-noise ratio so that the real error bar for that particular value is certainly much larger than the standard error of 20% quoted by Fink et al. (1998).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f5.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg91.gif) |
Figure 5:
Post-perihelion, water production rates [molecule s-1] as a
function of heliocentric distance [AU] for a thermal inertia of
10 J K-1 m-2 s-1/2 and for different values of x and f. |
| Open with DEXTER |
As explained above, the roles of I and f are negligible near perihelion and we only have to play with the fraction of active regions on the surface, x. According to the observations of Bertaux et al. (1999), x decreased from 1 to 0.1 in less than 20 days between 1.24 and 1.35 AU. The rapid formation of a thin refractory crust could here again explain these variations and is the subject of Sect. 4.
The nucleus of 46P/Wirtanen is not spherical as Lamy et al. (1998) estimated a semi-axis ratio 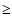 1.2. In order to assess the error resulting from the assumption of a spherical nucleus, we calculate the water production rate in the case of an ellipsoidal nucleus, defined by its 3 semi-axis a, b and c. We assume a>b=c and consider 4 different cases: a/b= 1.0, 1.2, 1.5 and 2.0. We calculate the value of a and b in order to have an mean cross-section
1.2. In order to assess the error resulting from the assumption of a spherical nucleus, we calculate the water production rate in the case of an ellipsoidal nucleus, defined by its 3 semi-axis a, b and c. We assume a>b=c and consider 4 different cases: a/b= 1.0, 1.2, 1.5 and 2.0. We calculate the value of a and b in order to have an mean cross-section
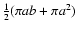 equals to that of the spherical case, i.e.
equals to that of the spherical case, i.e. 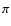 0.62 km2. In each case, we calculate the minimum and maximum water production rates, corresponding to a line-of-sight in the direction of a and b respectively (Table 4). The influence of a non-spherical nucleus is
0.62 km2. In each case, we calculate the minimum and maximum water production rates, corresponding to a line-of-sight in the direction of a and b respectively (Table 4). The influence of a non-spherical nucleus is  10% on
10% on
 for a/b= 1.2, but can reach
for a/b= 1.2, but can reach  40% for an extreme value of a/b= 2.0. In conclusion, this effect remains comparable to the uncertainties affecting
40% for an extreme value of a/b= 2.0. In conclusion, this effect remains comparable to the uncertainties affecting
 (
( 20-25%).
20-25%).
Table 4:
Water production rate for a non-spherical nucleus.
More generally, geometric effects such as large-scale concavities and topographical depressions, as seen on 19P/Borrelly, can also change the water production rate. However, the calculations of Colwell (1997) indicate that "the sublimation rate per unit area from surfaces within a crater is less than from a flat surface'' (for
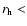 3 AU) because of shadow effects. Thus, the active fractions derived in our work, which assumes a flat surface, are thus lower limits. As this fraction already reaches 70-100% at perihelion, it cannot be much larger. Consequently, this effect cannot be important on the nucleus of 46P/Wirtanen.
3 AU) because of shadow effects. Thus, the active fractions derived in our work, which assumes a flat surface, are thus lower limits. As this fraction already reaches 70-100% at perihelion, it cannot be much larger. Consequently, this effect cannot be important on the nucleus of 46P/Wirtanen.
The above study allowed us to determine the main properties of the surface of the nucleus (i.e., the parameters x and f) at a given time, in a "static'' way. In order to complete our analysis of the surface of the nucleus of comet 46P/Wirtanen, we must understand the dynamical evolution of the surface and, in particular, explain the variations of x with heliocentric distance. The rapid increase of x at 1.5 AU is probably the consequence of an outburst, i.e., the blow-off of a crust covering the surface (Brin & Mendis 1979; Rickman et al. 1990; Crifo & Rodionov 1997). So, we first focus our attention on the formation of a refractory crust over the active regions B and then its influence on the water production rate. Next, we calculate the erosion of the nucleus of comet 46P/Wirtanen and finally, we propose a scenario for the dynamical evolution of its surface.
The formation of a refractory crust over an active region may result from two different processes: accumulation of rubbles and ballistic redeposition of refractory material (Whipple 1951; Brin & Mendis 1979; Podolak & Herman 1985; Rickman et al. 1990; Jewitt 2002). The rubble crust consists of debris that are too large to be ejected by drag forces from the surface of a sublimating body. The ballistic crust is formed by redeposition of refractory grains, ejected by drag forces, but too heavy to reach the escape velocity.
The key parameter to study the formation of a crust is the critical radius  [m], i.e., the maximum radius of a refractory grain which can lift off the nucleus by drag force. The classical calculation of
[m], i.e., the maximum radius of a refractory grain which can lift off the nucleus by drag force. The classical calculation of  was first implemented by Whipple (1951) and then used by many authors in various forms (e.g., Brin & Mendis 1979; Crifo & Rodionov 1997) but, always without taking into account the centrifugal force. As the rotational period of 46P/Wirtanen is only 6 h, the centrifugal force is not negligible and must be included in the calculation of
was first implemented by Whipple (1951) and then used by many authors in various forms (e.g., Brin & Mendis 1979; Crifo & Rodionov 1997) but, always without taking into account the centrifugal force. As the rotational period of 46P/Wirtanen is only 6 h, the centrifugal force is not negligible and must be included in the calculation of  ,
as implemented by Rickman et al. (1990) and Jorda (1995):
,
as implemented by Rickman et al. (1990) and Jorda (1995):
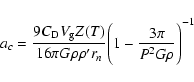 |
(8) |
where
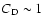 is the dimensionless drag cofficient depending on the shape of the grain,
is the dimensionless drag cofficient depending on the shape of the grain, 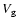 [m s-1] is the velocity of the escaping gas molecules, Z(T) [kg s-1m-2] is the water ice free sublimation rate (Eq. (4)) at temperature T [K] calculated at the sub-solar point, G is the gravitational constant,
[m s-1] is the velocity of the escaping gas molecules, Z(T) [kg s-1m-2] is the water ice free sublimation rate (Eq. (4)) at temperature T [K] calculated at the sub-solar point, G is the gravitational constant, 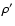 and
and 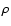 [kg m-3] are the density of the grain and the nucleus respectively, P= 6 h is the rotational period of the nucleus and
[kg m-3] are the density of the grain and the nucleus respectively, P= 6 h is the rotational period of the nucleus and
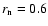 km is its radius. We make the standard assumption that the velocity of the escaping gas molecules
km is its radius. We make the standard assumption that the velocity of the escaping gas molecules 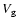 is equal to the thermal velocity of the gas
is equal to the thermal velocity of the gas
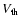 :
:
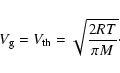 |
(9) |
The introduction of the centrifugal force increases  by a factor 1.4, compared to the classical calculation.
by a factor 1.4, compared to the classical calculation.
The above calculation of  assumes that the grain is already carried away by the gas as the very takeoff of the grain from the surface of the nucleus is not considered. The model therefore gives an upper limit for
assumes that the grain is already carried away by the gas as the very takeoff of the grain from the surface of the nucleus is not considered. The model therefore gives an upper limit for  which probably becomes grossly unrealistic for values in excess of a few centimeters. Figure 6 shows the maximum size of a grain which can escape the nucleus by drag and centrifugal forces as a function of heliocentric distance. We use I=0, 10 and 20 MKS and a density for the nucleus and the dust grains
which probably becomes grossly unrealistic for values in excess of a few centimeters. Figure 6 shows the maximum size of a grain which can escape the nucleus by drag and centrifugal forces as a function of heliocentric distance. We use I=0, 10 and 20 MKS and a density for the nucleus and the dust grains 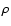 =
= 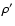 = 1000 kg m-3. The smaller the heliocentric distance, the larger the grains which can escape from the surface of the nucleus.
= 1000 kg m-3. The smaller the heliocentric distance, the larger the grains which can escape from the surface of the nucleus.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f6.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg103.gif) |
Figure 6:
Maximum radius of a grain which can escape the nucleus by drag forces as a function of heliocentric distance [AU] for different thermal inertia I
[J K-1 m-2 s-1/2] and a nucleus density 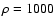 kg m-3. kg m-3. |
| Open with DEXTER |
The thermal inertia has a negligible influence on  for
for
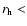 2.5 AU. Beyond, and considering the two extreme cases I= 0 and 20 MKS,
2.5 AU. Beyond, and considering the two extreme cases I= 0 and 20 MKS,  varies by a factor
varies by a factor  1.4 at 4 AU and by a factor
1.4 at 4 AU and by a factor  20 at 6 AU. The curve indicates that, near perihelion, blocks of
20 at 6 AU. The curve indicates that, near perihelion, blocks of  1 m, if they exist, can be lift off. We seriously question this result as the water ice located underneath such large boulders is never illuminated and thermally insulated from the surface (see Sect. 4.2); as a consequence, sublimation does not take place and the boulder cannot be ejected by drag forces. From other considerations, Keller (1990) suggested an upper limit of
1 m, if they exist, can be lift off. We seriously question this result as the water ice located underneath such large boulders is never illuminated and thermally insulated from the surface (see Sect. 4.2); as a consequence, sublimation does not take place and the boulder cannot be ejected by drag forces. From other considerations, Keller (1990) suggested an upper limit of  10 cm for the critical radius, so that
10 cm for the critical radius, so that  could be overestimated by a factor 10 when calculated from Eq. (8).
could be overestimated by a factor 10 when calculated from Eq. (8).
In conclusion, (i) the calculation of  used in the literature since the 50's is based on an oversimplified model and certainly does not apply for boulders larger than
used in the literature since the 50's is based on an oversimplified model and certainly does not apply for boulders larger than  10 cm, and (ii) the value of
10 cm, and (ii) the value of  given by Eq. (8) is anyway an upper limit as the energy required for the takeoff of the grain is not taken into account. This is an important point of cometary physics that the ROSETTA mission will hopefully clarify. For the moment, we shall keep in mind the above limitations in the study of the formation of a rubble crust on the surface of the nucleus presented below.
given by Eq. (8) is anyway an upper limit as the energy required for the takeoff of the grain is not taken into account. This is an important point of cometary physics that the ROSETTA mission will hopefully clarify. For the moment, we shall keep in mind the above limitations in the study of the formation of a rubble crust on the surface of the nucleus presented below.
The refractory grains which are too heavy to be ejected from the nucleus (radius
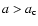 )
form a rubble crust. Using a differential size distribution function of the grains with a power index of s=-4 (Colangeli et al. 1998) and a maximium and minimum radius of the grain size distribution
)
form a rubble crust. Using a differential size distribution function of the grains with a power index of s=-4 (Colangeli et al. 1998) and a maximium and minimum radius of the grain size distribution
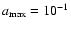 m and
m and
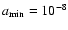 m respectively, we can derive their fraction
m respectively, we can derive their fraction  which is equal to (Jewitt 2002):
which is equal to (Jewitt 2002):
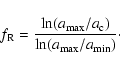 |
(10) |
The time to form a rubble crust is equal to (after correction for the missing factor 1-f in the equation of Jewitt 2002):
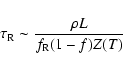 |
(11) |
where L (m) is the crust thickness necessary to inhibit the sublimation of water ice. We choose 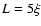 ,
where
,
where  (m) is the characteristic length of the heat wave (see Sect. 3.1.1). At this depth L, the diurnal temperature variations are less then 1% of those at the surface. Using standard values for
(m) is the characteristic length of the heat wave (see Sect. 3.1.1). At this depth L, the diurnal temperature variations are less then 1% of those at the surface. Using standard values for 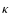 ,
,
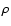 ,
C and P, and the definition of
,
C and P, and the definition of
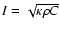 ,
we obtained
,
we obtained
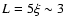 mm for I=10 MKS and
mm for I=10 MKS and 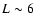 mm for I=20 MKS. The cases I=0 is rejected as it implies L=0 mm, and consequently
mm for I=20 MKS. The cases I=0 is rejected as it implies L=0 mm, and consequently
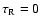 ,
which is not acceptable. To obtain a lower limit on
,
which is not acceptable. To obtain a lower limit on
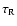 ,
we took the extreme case I= 1 MKS which imply
,
we took the extreme case I= 1 MKS which imply 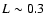 mm. The calculation of
mm. The calculation of 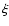 neglects the diffusion of the gas and L may be larger, as explained below in Sect. 4.2.
neglects the diffusion of the gas and L may be larger, as explained below in Sect. 4.2.
Using Eqs. (10) and (11), we estimate the time
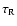 necessary to have a sufficient amount of refractory material on the surface to form a crust. Figure 7 shows the results for a density
necessary to have a sufficient amount of refractory material on the surface to form a crust. Figure 7 shows the results for a density
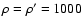 kg m-3, a fraction of water ice in the ice-refractory material mixture f= 0.5 and a thermal inertia between 1 and 20 MKS. The higher the thermal inertia, the longer
kg m-3, a fraction of water ice in the ice-refractory material mixture f= 0.5 and a thermal inertia between 1 and 20 MKS. The higher the thermal inertia, the longer
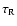 .
The formation of a crust must not exceed the orbital period of 46P/Wirtanen, that is 5.5 yr (
.
The formation of a crust must not exceed the orbital period of 46P/Wirtanen, that is 5.5 yr ( 2000 days).
Consequently, assuming the calculation of
2000 days).
Consequently, assuming the calculation of  given by Eq. (8) to be correct, the formation of a crust is not possible at heliocentric distances less than 2.6 AU as the required time is too long (Fig. 7).
But, as explained previously (see Sect. 4.1.1), the calculation of
given by Eq. (8) to be correct, the formation of a crust is not possible at heliocentric distances less than 2.6 AU as the required time is too long (Fig. 7).
But, as explained previously (see Sect. 4.1.1), the calculation of  is based on a oversimplified standard model. Since
is based on a oversimplified standard model. Since  could be overestimated by a factor 10, the formation of a rubble crust is in fact much easier, even near perihelion (Fig. 7). For example, at
could be overestimated by a factor 10, the formation of a rubble crust is in fact much easier, even near perihelion (Fig. 7). For example, at  1.5 AU, a crust can form in
1.5 AU, a crust can form in  0.5-9 days, depending on I in the range 1-20 MKS, which could explain the rapid decrease of the post-perihelion activity (see Sect. 4.2).
0.5-9 days, depending on I in the range 1-20 MKS, which could explain the rapid decrease of the post-perihelion activity (see Sect. 4.2).
If the thickness of the mantle L necessary to inhibit the sublimation of water ice is larger, the required time to form it will be longer. If a tenfold increase is required, i.e. L= 3-60 mm (depending on I), the time
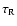 to form a crust is 10 times longer. For I in the range 1-20 MKS,
to form a crust is 10 times longer. For I in the range 1-20 MKS,
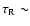 5-90 days at
5-90 days at  1.5 AU and the formation of a crust is still possible post-perihelion. For a thermal inertia of 3 MKS, as derived for Centaurs (Groussin et al. 2003), the required time is only 15 days.
1.5 AU and the formation of a crust is still possible post-perihelion. For a thermal inertia of 3 MKS, as derived for Centaurs (Groussin et al. 2003), the required time is only 15 days.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f7.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg118.gif) |
Figure 7:
Time to form a refractory crust as a function of heliocentric distance [AU] for a thermal inertia I= 1-20 MKS. The fraction of water ice in the active regions is f=0.5. The vertical hatched region represents the case where  is calculated by Eq. (8) and the diagonal hatched line where the value of
is calculated by Eq. (8) and the diagonal hatched line where the value of  is divided by a factor 10.
is divided by a factor 10. |
| Open with DEXTER |
Therefore, the formation of a rubble crust post-perihelion is highly probable, of whatever thickness in the range 0.3-60 mm, with I in the range 1-20 MKS. According to Fig. 6, this crust is composed of grains whose size is in the range 0.1-10 cm, if they exist. The refractory material cannot be dominated by grains larger than a few centimeters, otherwise they will accumulate rapidly on the surface, forming a thick crust which may definitely stop the activity forever (see Sect. 4.2). For this reason,
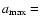 10 cm appears to be an upper limit for the maximum size of the grains, using a power index of the differential size distribution function s=-4. If
10 cm appears to be an upper limit for the maximum size of the grains, using a power index of the differential size distribution function s=-4. If
 is smaller, the time to form the crust is longer. For a power index s=-5, the size distribution function of the grains is dominated by sub-millimetric grains and
is smaller, the time to form the crust is longer. For a power index s=-5, the size distribution function of the grains is dominated by sub-millimetric grains and
 could be larger but then, the grains larger than 1 mm may not be numerous enough to form a crust. For a power index s=-3,
could be larger but then, the grains larger than 1 mm may not be numerous enough to form a crust. For a power index s=-3,  90% of the nucleus refractory material is composed of boulders larger than
90% of the nucleus refractory material is composed of boulders larger than
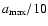 .
If
.
If
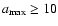 cm, too many large grains will accumulate on the surface and definitely stop the activity, as explained previously. Consequently, the power index of the size distribution function of the refractory material mixed with the ice is rather constrained at about s
cm, too many large grains will accumulate on the surface and definitely stop the activity, as explained previously. Consequently, the power index of the size distribution function of the refractory material mixed with the ice is rather constrained at about s 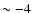 in order to allow the formation of a rubble crust of
in order to allow the formation of a rubble crust of  1 cm, thick enough to inhibit the production of water vapor (see Sect. 4.2), but not so thick as to prevent its blow-off at the next return (Brin & Mendis 1979). We feel that the value s=-4 determined by Colangeli et al. (1998) for 46P/Wirtanen is highly significant and consistent with the possibility of the build-up of a crust. The influence of
1 cm, thick enough to inhibit the production of water vapor (see Sect. 4.2), but not so thick as to prevent its blow-off at the next return (Brin & Mendis 1979). We feel that the value s=-4 determined by Colangeli et al. (1998) for 46P/Wirtanen is highly significant and consistent with the possibility of the build-up of a crust. The influence of
 in the range
10-6-10-8 m on the values of
in the range
10-6-10-8 m on the values of 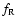 and
and
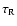 is
is  30%, which is negligible in view of the previous considerations on
30%, which is negligible in view of the previous considerations on
 and s.
and s.
In the above analysis, the temperature T was calculated at the sub-solar point. At higher zenithal angles, T and Z(T) decrease. On the contrary  increases with the zenithal angle as the critical radius
increases with the zenithal angle as the critical radius  decreases (Eqs. (8) and (10)). Finally, Z(T) decreases faster than
decreases (Eqs. (8) and (10)). Finally, Z(T) decreases faster than  increases and so the larger the zenithal angle, the longer the time to form a rubble crust. For example, at 1.5 AU with I= 3 MKS and using
increases and so the larger the zenithal angle, the longer the time to form a rubble crust. For example, at 1.5 AU with I= 3 MKS and using  divided by a factor 10, the time to form a crust is
divided by a factor 10, the time to form a crust is  16 days and
16 days and  18 days for latitudes of 45
18 days for latitudes of 45 and 60
and 60 respectively, while it is
respectively, while it is  15 days at the equator. These differences are not large.
15 days at the equator. These differences are not large.
Jewitt (2002) defined the escape radius 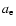 as the radius of a particule which can just reach the escape velocity
as the radius of a particule which can just reach the escape velocity 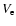 .
The refractory grains which can escape from the nucleus (
.
The refractory grains which can escape from the nucleus (
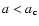 )
but which are too heavy to reach the escape velocity (
)
but which are too heavy to reach the escape velocity (
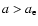 )
form the ballistic crust. Their fraction
)
form the ballistic crust. Their fraction 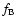 is equal to (Jewitt 2002):
is equal to (Jewitt 2002):
![\begin{displaymath}%
f_{\rm B}=\frac{\ln(a_{\rm c}/a_{\rm e})}{\ln \left(a_{{\rm...
...\rm th}}}\right]}{\ln\left(a_{{\rm max}}/a_{{\rm min}}\right)}
\end{displaymath}](/articles/aa/full/2003/49/aa3685/img130.gif) |
(12) |
where
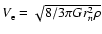 (m s-1) is equal to 0.45 m s-1 for 46P/Wirtanen using the parameters of Table 3. The time to form a ballistic crust is equal to (after correction for the missing factor 1-f in the equation of Jewitt 2002):
(m s-1) is equal to 0.45 m s-1 for 46P/Wirtanen using the parameters of Table 3. The time to form a ballistic crust is equal to (after correction for the missing factor 1-f in the equation of Jewitt 2002):
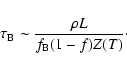 |
(13) |
Our calculations indicate that the fraction 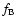 is almost constant and equals to
is almost constant and equals to  2
2 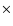 10-4, which implies very long times
10-4, which implies very long times
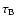 :
at perihelion
:
at perihelion
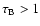 yr while the comet stays only a few weeks in this zone and at aphelion
yr while the comet stays only a few weeks in this zone and at aphelion
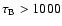 yr, much longer than the orbital period of 5.5 yr. Consequently, the formation of ballistic crust is impossible. This result is not surprising as the formation of a ballistic crust strongly depends upon gravity, which is very low for 46P/Wirtanen owing to its radius of only 0.6 km.
yr, much longer than the orbital period of 5.5 yr. Consequently, the formation of ballistic crust is impossible. This result is not surprising as the formation of a ballistic crust strongly depends upon gravity, which is very low for 46P/Wirtanen owing to its radius of only 0.6 km.
The thermal behaviour of the crust is described by Eq. (1). Heat conduction (i.e. thermal inertia) in the crust allows to transfer part of the incoming solar energy inside the nucleus to sublimate the underlying water ice. In a first approximation, the water ice is assumed to be pure and all the sublimated molecules reach the surface through the crust and escape from the nucleus. These assumptions yield an upper limit for the water production rate and for the thickness of the crust. Our model is adapted from the work of Julian et al. (1999) developed for the dust-mantled regions of 1P/Halley with the numerical solution of the equations as implemented by Groussin et al. (2003). We assume that the crust entirely covers the nucleus surface and consider a thermal inertia of 10 MKS.
The water production rate on the surface is plotted as a function of the thickness of the crust in Fig. 8. It rapidly decreases when the thickness increases, in agreement with the work of Julian et al. (1999) on comet 1P/Halley.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f8.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg136.gif) |
Figure 8:
Water production rate [molecule s-1] of the nucleus of 46P/Wirtanen as a function of the thickness of the crust (mm) assuming a thermal inertia I=10 MKS. The dashed line bridges the rate corresponding to a 0.5 mm thick crust to the rate at the surface of the nucleus (no crust). |
| Open with DEXTER |
This analysis does not take into account the advection of the gas in the crust which allows to transport more energy from the top of the crust to its bottom through the pores, inducing a higher temperature under the crust than the one we calculated and therefore a higher water production rate (Skorov et al. 1999). Consequently, the thickness of the crust required to inhibit the water production could be larger, and the time to form it longer. However, the above discussion shows that there exists an ample margin and the formation of a crust remains possible even if L is underestimated by a factor 10.
Altogether, the results of Sects. 4.1.2 and 4.2 show that the formation of a refractory crust over active areas is a process of paramount importance. It can form fast enough and then be efficient enough to rapidly choke the post-perihelion activity until the comet reaches a heliocentric distance of  1.5 AU at its next return.
1.5 AU at its next return.
In order to complete our analysis of the nucleus of 46P/Wirtanen, we calculate the erosion of the nucleus over several orbits in the framework of our model, presented in Sect. 3. The key parameter is here the dust-to-gas ratio
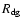 .
Depending on
.
Depending on
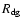 ,
which controls the ability of the gas to drag the dust, the surface will be eroded more or less rapidly. Assuming the same bulk density for water ice and the refractory material,
,
which controls the ability of the gas to drag the dust, the surface will be eroded more or less rapidly. Assuming the same bulk density for water ice and the refractory material,
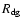 is defined as:
is defined as:
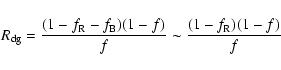 |
(14) |
since
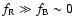 .
Between 2.0 and 2.5 AU, Colangeli et al. (1998) derived
.
Between 2.0 and 2.5 AU, Colangeli et al. (1998) derived
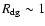 .
In this heliocentric distance range, according to Eq. (10) with
.
In this heliocentric distance range, according to Eq. (10) with  divided by 10 and I= 0-20 MKS, we find
divided by 10 and I= 0-20 MKS, we find
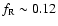 .
Using this result and Eq. (14), we derive
.
Using this result and Eq. (14), we derive 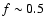 ,
which seems a plausible value for the fraction of water ice in the active regions. For the same reasons, we derive
,
which seems a plausible value for the fraction of water ice in the active regions. For the same reasons, we derive 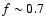 and
and 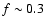 for
for
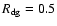 and 2 respectively.
and 2 respectively.
We now calculate the erosion of the active regions B of the nucleus over one revolution. According to our previous results, 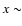 0.10 for
0.10 for
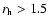 AU and
AU and 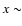 0.85 for
0.85 for
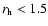 AU.
In order to accelerate the numerical process, we limit the calculation to the sub-solar point and to I= 0 MKS which results in an upper limit for the erosion (the higher the temperature, the higher
AU.
In order to accelerate the numerical process, we limit the calculation to the sub-solar point and to I= 0 MKS which results in an upper limit for the erosion (the higher the temperature, the higher
 ). We choose f= 0.3, 0.5 and 0.7, corresponding to
). We choose f= 0.3, 0.5 and 0.7, corresponding to
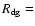 0.5, 1 and 2, respectively. We integrate the erosion over one revolution of 46P/Wirtanen with an initial radius of 0.6 km using Kepler equations with a variable time step. The first result is that 90% of the erosion is completed inside 1.5 AU, which is the direct consequence of the increase of x and of the sublimation rate. As the influence of I on
0.5, 1 and 2, respectively. We integrate the erosion over one revolution of 46P/Wirtanen with an initial radius of 0.6 km using Kepler equations with a variable time step. The first result is that 90% of the erosion is completed inside 1.5 AU, which is the direct consequence of the increase of x and of the sublimation rate. As the influence of I on
 for
for
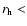 1.5 AU is negligible (see Fig. 3), its influence on the erosion is also negligible. Moreover, as the erosion takes place over most of the nucleus since
1.5 AU is negligible (see Fig. 3), its influence on the erosion is also negligible. Moreover, as the erosion takes place over most of the nucleus since
![$x \in [0.7,1]$](/articles/aa/full/2003/49/aa3685/img82.gif) ,
it can be considered (in a first approximation) homogeneous over the entire nucleus, leading to a general resurfacing. Pits are not expected to form contrary to the case of localized active regions. For f= 0.3, 0.5 and 0.7, we obtain erosions of
,
it can be considered (in a first approximation) homogeneous over the entire nucleus, leading to a general resurfacing. Pits are not expected to form contrary to the case of localized active regions. For f= 0.3, 0.5 and 0.7, we obtain erosions of  0.4,
0.4,  0.5 and
0.5 and  0.9 m respectively for one orbit. We derive a lifetime for the nucleus, defined as the time necessary to completely erode it, of 1700, 1200 and 700 orbital periods respectively. In summary, the nucleus of comet 46P/Wirtanen looses a layer of thickness
0.9 m respectively for one orbit. We derive a lifetime for the nucleus, defined as the time necessary to completely erode it, of 1700, 1200 and 700 orbital periods respectively. In summary, the nucleus of comet 46P/Wirtanen looses a layer of thickness  0.5 m per orbit and has a remaining lifetime of several thousands years assuming an homogeneous internal structure and no drastic orbital perturbations.
0.5 m per orbit and has a remaining lifetime of several thousands years assuming an homogeneous internal structure and no drastic orbital perturbations.
In view of all these results, we now attempt to present a possible, coherent scenario for the evolution of the surface of comet 46P/Wirtanen during its 1997 apparition and, in turn, over the forthcoming orbits. This non-unique scenario, summarized in Fig. 9, is characterized by the following steps.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{3685_f9.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg150.gif) |
Figure 9:
A possible scenario for the temporal evolution of the surface of comet 46P/Wirtanen. |
| Open with DEXTER |
-
- (i)
- Pre-perihelion, between
 4 and
4 and  1.5 AU, approximately 10% of the surface is active. The activity increases regularly with the temperature as the comet approaches the Sun. The active regions (i.e.
1.5 AU, approximately 10% of the surface is active. The activity increases regularly with the temperature as the comet approaches the Sun. The active regions (i.e.  10% of the surface) loose a thickness of
10% of the surface) loose a thickness of  20 cm. The comet spends 20% of its time in this region.
20 cm. The comet spends 20% of its time in this region.
- (ii)
- At
 1.5 AU, the crust blows off, in agreement with the results of Brin & Mendis (1979) and Rickman et al. (1990). This is a runaway process as less crust means more exposed ice, more free sublimation and more gas to drag the rest of the crust, which could explain the sudden increase of the water production rate at
1.5 AU, the crust blows off, in agreement with the results of Brin & Mendis (1979) and Rickman et al. (1990). This is a runaway process as less crust means more exposed ice, more free sublimation and more gas to drag the rest of the crust, which could explain the sudden increase of the water production rate at  1.5 AU. The activity becomes rapidly widespread, to reach 70 to 100% of the surface.
1.5 AU. The activity becomes rapidly widespread, to reach 70 to 100% of the surface.
- (iii)
- Up to perihelion, this global activity of the nucleus continues. A thickness of
 25 cm is globally eroded, implying a general resurfacing of the nucleus. The nucleus becomes "bald''.
25 cm is globally eroded, implying a general resurfacing of the nucleus. The nucleus becomes "bald''.
- (iv)
- At perihelion, the activity reaches its maximum.
- (v)
- Post-perihelion, the erosion actively continues until choked by the build-up of a crust. This process takes place as the temperature and the sublimation rate decrease, thus offering an appropriate environment. The water production measurements suggest that it is completed at about 1.5 AU. In the mean-time, a thickness of <25 cm has been removed from the surface. As no activity is possible over the regions covered by a refractory crust, they remain inactive until the next perihelion
passage. Only
 10% of the surface remain active.
10% of the surface remain active.
- (vi)
- After the formation of the crust and up to 4 AU, the activity decreases regularly with the temperature as the comet recedes from the Sun. Active regions (i.e.
 10% of the surface) are eroded by
10% of the surface) are eroded by  20 cm.
20 cm.
- (vii)
- Beyond
 4 AU, where the comet spends half of its time, the activity reaches very low levels as suggested by the non-detection of a coma at 4.98 AU with the VLT (Boehnhardt et al. 2002). Our calculation shows that the active regions are eroded by only
4 AU, where the comet spends half of its time, the activity reaches very low levels as suggested by the non-detection of a coma at 4.98 AU with the VLT (Boehnhardt et al. 2002). Our calculation shows that the active regions are eroded by only  15 cm.
15 cm.
The dynamical process (i)
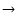 (vii) presented here is in agreement with the observed water production rates of the 1997
passage and can continue over several passages. Depending upon the thickness of the crust formed post-perihelion, its blow-off at the next perihelion passage could be shifted relative to 1.5 AU and be more or less violent. Although we performed extensive calculations in order to validate this scenario, we realize that it requires the ad-hoc assumption of the blow-off of the crust at 1.5 AU pre-perihelion.
(vii) presented here is in agreement with the observed water production rates of the 1997
passage and can continue over several passages. Depending upon the thickness of the crust formed post-perihelion, its blow-off at the next perihelion passage could be shifted relative to 1.5 AU and be more or less violent. Although we performed extensive calculations in order to validate this scenario, we realize that it requires the ad-hoc assumption of the blow-off of the crust at 1.5 AU pre-perihelion.
Strictly speaking, this scenario requires a low obliquity of the nucleus. However, because of its low thermal inertia (0<I< 20 MKS) and because of the uniform distribution of the active areas all over the nucleus, this scenario remains valid for a high obliquity. Indeed, the thermal behaviour of the nucleus on the day side where all the physical processes take place and especially the water ice sublimation, is identical for a thermal inertia of 0 and 20 MKS, whatever the orientation of the spin axis. Widespread activity over the nucleus as opposed to restricted localized areas likely leads to frequent changes in this orientation (Jorda, private communication). As a consequence, the erosion of the nucleus remains grossly uniform, preventing it from becoming extremely elongated.
One can argue that the variations of the water production rate could be explained by a seasonal effect due to a high obliquity of the nucleus and a localized active area, as proposed by Sekanina (1988) for comet 2P/Encke. But, for 46P/Wirtanen, this localized active area is very large as 70 to 100% of the nucleus becomes active near perihelion. Such a large active area would become progressively active as the sub-solar point transits over it when the comet approaches the Sun; this is totally inconsistent with the observed fast increase of the water production rate in  10 days at 1.5 AU. Seasonal effects have also been rejected for the same reasons by Lamy et al. (2003) to explain an outburst on comet 2P/Encke four days after its 2000 perihelion passage.
10 days at 1.5 AU. Seasonal effects have also been rejected for the same reasons by Lamy et al. (2003) to explain an outburst on comet 2P/Encke four days after its 2000 perihelion passage.
Finally, over the long term, planetary perturbations may alter the orbit of the comet, and our scenario could become inadequate.
We have presented a thermal model in order to explain the variations of the water production rate of the comet 46P/Wirtanen with heliocentric distance. The model takes into account the first order physical processes, insolation, reradiation, water ice sublimation and heat conduction, and the water production rate is calculated at each point of the surface. We have also analysed the formation and the influence of a refractory crust, and proposed a scenario for the temporal evolution of the surface. Our main results are summarized below.
- 1.
- Our model is a macroscopic mosaic of active and inactive regions. Active regions are composed of a microscopic mixture of refractory material and water ice. They are small, numerous and located all over the nucleus. Pre-perihelion, when
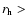 1.5 AU, active regions cover 5-15% of the surface of the nucleus. This fraction increases rapidly in
1.5 AU, active regions cover 5-15% of the surface of the nucleus. This fraction increases rapidly in  10 days at
10 days at  1.5 AU to reach 70-100% and remains constant up to perihelion. Post-perihelion, the activity decreases rapidly and the active fraction goes down again to
1.5 AU to reach 70-100% and remains constant up to perihelion. Post-perihelion, the activity decreases rapidly and the active fraction goes down again to  10%. The model is consistent with a geometric albedo lower than 0.06.
10%. The model is consistent with a geometric albedo lower than 0.06.
- 2.
- Assuming a thermal inertia in the range 0-20 MKS and a fraction of ice in the active regions in the range 1-100%, our model is in good agreement (at the 1
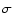 level) with the measured water production rate pre-perihelion. It yields a value at perihelion of
level) with the measured water production rate pre-perihelion. It yields a value at perihelion of
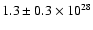 molecule s-1.
molecule s-1.
- 3.
- The post-perihelion formation of a refractory crust, efficiently inhibiting the water ice sublimation, is highly probable. At the subsequent return of the comet, this crust blows off, likely explaining the sudden increase of activity at
 1.5 AU observed during the 1997 apparition. This scenario could continue over several revolutions. At each return, the "outburst'' could be shifted relative to 1.5 AU and be more or less violent, depending on the thickness of crust previously formed, post-perihelion.
1.5 AU observed during the 1997 apparition. This scenario could continue over several revolutions. At each return, the "outburst'' could be shifted relative to 1.5 AU and be more or less violent, depending on the thickness of crust previously formed, post-perihelion.
- 4.
- Post-perihelion, the heliocentric distance at which the crust forms depends strongly upon the calculation of the critical radius
 which is based on an oversimplified model, so that
which is based on an oversimplified model, so that  could be overestimated. We expect the ROSETTA mission to clarify this point.
could be overestimated. We expect the ROSETTA mission to clarify this point.
- 5.
- Widespread activity over the nucleus likely leads to frequent changes in the direction of the spin axis resulting in a grossly uniform erosion of the nucleus. Assuming a dust-to-gas ratio between 0.5 and 2, we derived an erosion rate of
 0.5 m per revolution. This implies a complete resurfacing of the bulk of the surface of the nucleus after each perihelion passage. The remaining lifetime of the nucleus, assuming an homogeneous composition and no drastic planetary perturbation, amounts to several hundred orbital revolutions.
0.5 m per revolution. This implies a complete resurfacing of the bulk of the surface of the nucleus after each perihelion passage. The remaining lifetime of the nucleus, assuming an homogeneous composition and no drastic planetary perturbation, amounts to several hundred orbital revolutions.
- 6.
- A non-spherical nucleus with a semi-axis ratio a/b=1.2 would not change significally the above results.
We believe that our conclusions have important consequences for the ROSETTA mission, notably the planning of the operations and of the observations. An extension of the mission beyond perihelion passage to witness the possible formation of a crust looks highly desirable. More generally, we emphasize that our model makes detailed predictions amenable to a direct comparison with observational results expected from the orbiter and the lander.
Beyond comet 46P/Wirtanen, our conclusions have far reaching consequences for the population of small cometary nuclei uncovered by the Hubble Space Telescope observations. Likewise 46P/Wirtanen, the activity is probably widespread over their surface, consistent with the absence of structures (jets) in their coma. Contrary to the current view (e.g., A'Hearn 1995; Jewitt 2001), the pattern of activity restricted to a few active vents appears to be a property shared by only a few, probably large nuclei such as 1P/Halley, 19P/Borrelly, 109P/Swift-Tuttle and C/1995 O1 Hale-Bopp.
Acknowledgements
We thank the referee, Prof. M. A'Hearn, for his helpful comments.
-
A'Hearn, M. F., Millis, R. L., Schleicher, D. G., Osip, D. J., & Birch, P. V. 1995, Icarus, 118, 223
In the text
NASA ADS
-
Benkhoff, J., & Boice, D. C. 1996, Planet. Space Sci., 44, 665
In the text
NASA ADS
-
Benkhoff, J. 1999, Planet. Space Sci., 47, 735
In the text
NASA ADS
-
Bertaux, J. L., Costa, J., Makinen, T., et al. 1999, Planet. Space Sci., 47, 725
In the text
NASA ADS
-
Boehnhardt, H., Delahodde, C., Sekiguchi, T., et al. 2002, A&A, 387, 1107
In the text
NASA ADS
-
Brin, G. D., & Mendis, D. A. 1979, AJ, 229, 402
In the text
-
Capria, M. T., Capaccioni, F., Coraldini, A., et al. 1996, Planet. Space. Sci., 44, 987
In the text
NASA ADS
-
Clark, R. N., & Lucey, P. G. 1984, JGR., 89, 6341
In the text
NASA ADS
-
Clark, B. E., Veverka, J., Helfenstein, P., et al. 1999, Icarus, 140, 53
In the text
NASA ADS
-
Colangeli, L., Bussoletti, E., Pestellini, C. C., et al. 1998, Icarus, 134, 35
In the text
NASA ADS
-
Colwell, J. E. 1997, Icarus, 125, 406
In the text
NASA ADS
-
Crifo, J. F. 1987, A&A, 187, 438
In the text
NASA ADS
-
Crifo, J. F., & Rodionov, A. V. 1997, Icarus, 127, 319
In the text
NASA ADS
-
de Sanctis, M. C., Capaccioni, F., Capria, M. T., et al. 1999, Planet. Space Sci., 47, 855
In the text
NASA ADS
-
Delsemme, A. H., & Miller, D. C. 1971, Planet. Space. Sci., 19, 1229
NASA ADS
-
Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89
In the text
NASA ADS
-
Enzian, A., Klinger, J., Schwehm, G., & Weissman, P. R. 1999, Icarus, 138, 74
In the text
NASA ADS
-
Fanale, F. P., & Salvail, J. R. 1984, Icarus, 60, 476
In the text
NASA ADS
-
Farnham, T. L., & Schleicher, D. G. 1998, A&A, 335, L50
In the text
NASA ADS
-
Fernández, Y. R., Jewitt, D. C., & Sheppard, S. S. 2002, AJ, 123, 1050
In the text
NASA ADS
-
Festou, M. C. 1981, A&A, 95, 69
NASA ADS
-
Fink, U., Fevig, R. A., Tegler, S. C., & Romanishin, W. 1997, Planet. Space Sci., 45, 1383
In the text
NASA ADS
-
Fink, U., Hicks, M. D., Fevig, R. A., & Collins, J. 1998, A&A, 335, L37
In the text
NASA ADS
-
Groussin, O., Lamy, P., & Jorda, L. 2003, A&A, in press
In the text
-
Harris, A. W. 1998, Icarus, 131, 291
In the text
NASA ADS
-
Jewitt, D., & Fernandez, Y. 2001, Collisional processes in the solar system, ed. M. Ya. Marov, & H. Rickman, Astrophysics and space science library (Dordrecht: Kluwer Academic Publishers, ISBN 0-7923-6946-7), 261, 143
In the text
-
Jewitt, D., & Kalas, P. 1998, ApJ, 499, L103
In the text
NASA ADS
-
Jewitt, D. 2002, AJ, 123, 2, 1039
In the text
NASA ADS
-
Jockers, K., Credner, T., & Bonev, T. 1998, A&A, 335, L56
In the text
NASA ADS
-
Jorda, L. 1995, Ph.D. Thesis, Observatoire de Paris-Meudon, Université de Paris VII
In the text
-
Jorda, L., Lamy, P. L., Toth, I., et al. 2000, ESA-SP, 455, 61
-
Julian, W. H., Samarasinha, N. H., & Belton, M. J. S. 1999, Icarus, 144, 160
In the text
-
Keller, H. U. 1990, Physics and Chemistry of Comets, 48-50, ed. F. Huebner, A&A Library (Springer-Verlag), ISBN 3-540-51228-4
In the text
-
Lagerros, J. S. V. 1998, A&A, 332, 1123
In the text
NASA ADS
-
Lamy, P. L., Grün, E., & Perrin, J. M. 1987, A&A, 187, 767
In the text
NASA ADS
-
Lamy, P. L., Toth, I., Jorda, L., & Weaver, H. A. 1998, A&A, 335, L25
In the text
NASA ADS
-
Lamy, P., Toth, I., Jorda, L., et al. 2002, Icarus, 156, 442
In the text
NASA ADS
-
Lamy, P., Biesecker, D. A., & Groussin, O. 2003,
Icarus, 163, 142
In the text
NASA ADS
- Lamy, P. L., Toth, I., Fernandez, Y., & Weaver, H. A. 2004,
The sizes, shape, albedos and colors of cometary nuclei, Commet II,
ed. M. Festou, H. U. Keller, & H. A. Weaver (Tucson: the University of Arisona Press), in press
In the text
-
Lebofsky, L. A., Sykes, M. V., Tedesco, E. F., et al. 1986, Icarus, 68, 239
In the text
NASA ADS
-
Lebofsky, L. A., & Spencer, J. R. 1989, Asteroids II, 128
In the text
-
Mellon, M. T., Kretke, K. A., Smith, M. D., & Pelkey, S. M. 2002, LPI 33, 1416
In the text
-
Möhlmann, D. 1999, Planet Space Sci., 47, 971
In the text
NASA ADS
-
Newburn, R. L., & Spinrad, H. 1985, AJ, 90, 2591
In the text
NASA ADS
-
Podolak, M., & Herman, G. 1985, Icarus, 61, 267
In the text
NASA ADS
-
Rickman, H., Fernandez, J. A., & Gustafson, B. A. S. 1990, A&A, 237, 524
In the text
NASA ADS
-
Rickman, H., & Jorda, L. 1998, Adv. in Space Res., 21, 1491
In the text
NASA ADS
-
Roush, T. L. 1994, Icarus, 108, 243
In the text
NASA ADS
-
Schulz, R., Arpigny, C., Manfroid, J., et al. 1998, A&A, 335, L46
In the text
NASA ADS
-
Sekanina, Z. 1988, AJ, 95, 911
In the text
NASA ADS
-
Singh, P. D., de Almeida, A. A., & Huebner, W. F. 1992, AJ, 104, 848
In the text
NASA ADS
-
Skorov, Yu. V., Kömle, N. I., Markiewicz, W. J., & Keller, H. U. 1999, Icarus, 140, 173
In the text
NASA ADS
-
Spencer, J. R., Lebofsky, L. A., & Sykes, M. V. 1989, Icarus, 78, 337
In the text
NASA ADS
-
Stern, S. A., Parker, J. W., Festou, M. C., et al. 1998, A&A, 335, L30
In the text
NASA ADS
-
Whipple, F. L. 1951, ApJ, 113, 464
In the text
NASA ADS
-
Winter, D., & Saari, J. 1969, ApJ, 156, 1135
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3685_f1.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3685_f2.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg26.gif)
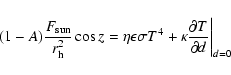
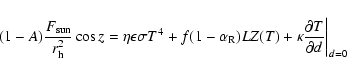
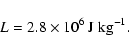
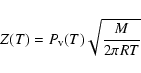
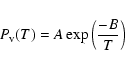
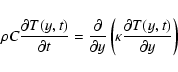
![$\displaystyle r_{\rm n}^2 \int_{-\pi}^{\pi} \int_{-\pi/2}^{\pi/2} x f (1-\alpha_{\rm R})Z[T(\varphi,\theta)] \cos \theta {\rm d}\theta {\rm d}\varphi.$](/articles/aa/full/2003/49/aa3685/img58.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f3.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f4.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f5.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg91.gif)
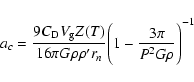
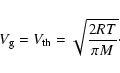
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f6.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg103.gif)
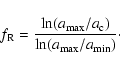
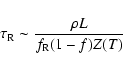
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f7.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg118.gif)
![\begin{displaymath}%
f_{\rm B}=\frac{\ln(a_{\rm c}/a_{\rm e})}{\ln \left(a_{{\rm...
...\rm th}}}\right]}{\ln\left(a_{{\rm max}}/a_{{\rm min}}\right)}
\end{displaymath}](/articles/aa/full/2003/49/aa3685/img130.gif)
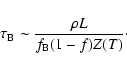
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3685_f8.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg136.gif)
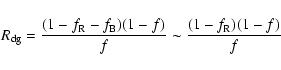
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{3685_f9.ps}\end{figure}](/articles/aa/full/2003/49/aa3685/Timg150.gif)