A&A 410, 1011-1022 (2003)
DOI: 10.1051/0004-6361:20031250

Solar type IV burst spectral fine structures[*]

II. Source model

E. Ya. Zlotnik1 - V. V. Zaitsev1 - H. Aurass2 - G. Mann2 - A. Hofmann2


1 - Institute of Applied Physics RAS, 603600 Nizhny Novgorod, Russia
2 - Astrophysical Institute Potsdam, 14482 Potsdam, Germany

Received 2 June 2003 / Accepted 28 July 2003

Abstract
We discuss a source model for the origin of solar type IV burst fine structures (FS) using the data of an event in AR 7792 on 25 October 1994. After giving a comprehensive observational treatment of FS (Paper I), here we repeat the main observed facts to construct a simplified radio source model. It consists of two interacting loops (named LS1 and EL) with one spatial order of magnitude scale difference (turning heights 70 and 7 Mm). We consider the implications of this model for physical mechanisms of broad band pulsations (BBP) and zebra patterns (ZP). Our analysis leads to the conclusion that meter wave BBP and ZP originate from a common magnetic source structure - a large asymmetric coronal loop. It is shown that the BBP result from periodically repeated injections of fast electrons into the asymmetric magnetic trap. The excitation of plasma waves is due to the stream instability when these electrons are propagating along the loop. We demonstrate that a two percent quasi-periodic modulation of a magnetic field component in EL is sufficient for it to act as a periodic electron accelerator. The ZP is due to a plasma wave instability at the levels of double plasma resonance (DPR) in an inhomogeneous source distributed along the loop axis of LS1. The DPR frequencies appear at those height levels where the upper hybrid frequency is equal to a harmonic of the gyrofrequency. Two Appendices review theoretical details needed to understand the given ZP interpretation. The gyrofrequency as a function of height was derived from a force-free extrapolated field line that passes the coronal radio source. After knowing the loop turning height and the magnetic field strength we identified for a fixed observing time the harmonic number of each zebra stripe. The comparison of the calculated DPR levels with the observed zebra stripe peak frequencies yields a density law for the ZP source volume. It turns out that this is a barometric law with a temperature near 106 K. We demonstrate that the drift of the whole ZP to higher frequencies can be explained as a signature of magnetic field decrease and/or plasma cooling in the ZP source. The time delay between BBP and ZP was found to be due to the higher fast particle threshold of the DPR versus the beam instability. The present analysis confirms the double plasma resonance model for the ZP fine structure, and underlines the significance of force-free extrapolated photospheric fields for coronal magnetic field modelling.

Key words: Sun: flares - Sun: corona - Sun: radio radiation - Sun: magnetic fields

1 Introduction


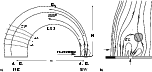  \begin{figure} \par\hbox to \hsize{\hfill a)\epsfig{file=MS4049f1a.eps,scale=0.3... ...mm}b)\raisebox{5mm}{\epsfig{file=MS4049f1b.eps,scale=0.3} }\hfill}\end{figure} Figure 1: Source model from optical, X-ray and radio measurements (see Paper I). a) The loop LS1 is the main source of BBP and ZP: fast electron streams exciting BBP are injected at the SW footpoint. ZP stripes arise at the DPR levels (stippled) in the NE part of LS1. b) Enlargement of the encircled SW range: the leading spot in conflict with the emerging parasitic polarity loop (EL). The wavy circle is a site of reconnection and electron acceleration.
Open with DEXTER

In Paper I, we gave an extended introduction to the problem of solar radio burst continuum fine structures (FS) with special regard to broad band pulsations (BBP) and zebra patterns (ZP). There, the reader can find detailed reference to earlier work in the field. Paper I presents the FS observations for the event of October 25, 1994 in active region NOAA 7792 and explains (together with Aurass et al. 1999) the relation between the radio data and the magnetic field measurements in the photosphere, its extrapolation to the corona, and to the Yohkoh soft X-ray and the H$\alpha$ imaging data. Here we briefly summarize the data directly related to the occurrence of radio pulsations and zebra patterns and which can elucidate the most probable reasons of their origin.

a)
Broadband pulsations (BBP): we recall Figs. 3, 5, 6, and 9 of Paper I. The duration of BBP emission was about 3.5 min (10:$05\div10$:08:30 UT). The period of BBP in the frequency band $150\div 400$ MHz was, on average, 1.33 s. The lower frequency boundary of BBP appeared rather sharp in the beginning of the event but slowly drifted from about 150 MHz to 130 MHz in the final stage. In the dynamic spectrum, BBP (the single pulses) sometimes have a weakly pronounced form of type J bursts (Suzuki & Dulk 1985 for this term). Also, the pulses reveal a rather high negative frequency drift ( ${\rm d}f/{\rm d}t \simeq 250$ MHz s-1). At a given heliographic observing frequency, source motion was observed in the course of a single pulse. The speed was $1.1 \times 10^5$ km s-1. The main BBP source was about -40% (right handed) circularly polarized. In the following we assume fundamental mode emission for the BBP source.

b)
Zebra pattern (ZP): we recall Figs. 3, 7, 8, and 11 of Paper I. The ZP became strongest during the final stage of the BBP (within 1 min from 10:$08\div10$:09 UT) between $130\div 220$ MHz. More than 20 stripes can be discriminated. Mostly, stripes drift from lower to higher frequencies. The drift velocity was of the order of 2 MHz s-1. The frequency interval between adjacent stripes at a fixed moment tended to increase with frequency from 2 MHz at 150 MHz to 5 MHz at 220 MHz. This interval also increases with time towards the end of the event. Heliographic observations showed that the radio emission in ZP sources was circularly polarized (-26%, right handed). Again, we assume fundamental mode emission of the FS source. The sources were located in the NE of the active region. There the magnetic field was weaker than in the center of AR 7792. The ZP source moved perpendicularly to the former observed BBP source. The instantaneous stripe frequency drift rate was linearly related to the speed of the projected source motion. It is important that some time delay exists between the occurrence of BBP and the appearance of intense ZP on the dynamic spectrum.

c)
Magnetic field: in Aurass et al. (1999) and Paper I we investigated in detail the force-free extrapolation of the Kitt Peak magnetographic measurements in a certain area (assuming plane geometry) around the sigmoidal flaring active region before and after our event of interest. We tried to obtain the best possible representation of the loop structures visible in radio, H$\alpha$, and soft X-ray images. As mentioned, the FS sources were both situated in and nearby the north-eastern branch of the sigmoidally formed loop pattern. We named this part of the coronal magnetic field loop system "LS1''. Here, in searching for representative parameters to apply theories of FS formation, we use for the unknown coronal magnetic field LS1 the extrapolated field values obtained for LS1 as shown in Fig. 2 of Paper I. As we will see, for simplicity the use of one representative field line of LS1 is sufficient in the present work. For completeness we recall that in a certain time of FS evolution the source of BBP at high frequencies was split into two subsources. In this time, the second large loop system (LS2) came into play. We will use the term "LS2'' also in the following, but it plays no quantitative role in FS modelling.

2 A source model

Using the observational data and bearing in mind our interpretation of BBP and ZP in the event of interest, we plotted in Fig. 1 a simplified outline of a source model thereby sketching the origin of the observed FS. The main source of BBP and ZP is located in a highly asymmetric loop forming a magnetic trap. Magnetic field strengths at the loop footpoints were $B_1\approx 200\div 300$ G and $B_2\approx 20\div 30$ G. The diameters of footpoint regions were taken as $d_1\approx 14.7$ Mm and $d_2\approx 57.3$ Mm, correspondingly. The distance between footpoints was $w\approx 132.8$ Mm. The loop extended up to $H\approx 75$ Mm above the photosphere, and the average magnetic field at the top of the trap was $B_{\rm top} \approx 2$ G. The source of fast electrons was concentrated near the footpoint d1with strong magnetic field B1. We know that the interaction of a small-scale loop system saturating emerging parasitic flux with the loop systems LS1 and LS2 (Fig. 2 of Paper I, and Aurass et al. 1999) is driven during the flare. The accelerated electrons were moving along the trap axis from its footpoint to the top. We suggest that the fast electrons arise either due to the interaction of the asymmetric loop LS1 with emerging flux EL, or due to processes inside the compact loop EL with following injection into the big trap LS1.

According to radio imaging data (see Paper I), the ZP source was localized in the region of a weak magnetic field in the trap LS1 (d2), while the BBP source was closer to the footpoint with a strong magnetic field (d1). We will argue that the BBP in the considered event are associated with fast electron beams, periodically injected into the trap LS1 from the accelerator. A part of such electrons is trapped in LS1. Multiple injections result in an increase of the number of trapped electrons. At some stage, the threshold for instability at the levels of double plasma resonance is overcome, and enhanced radiation of plasma waves occurs as zebra pattern in corresponding regions (marked by dotted lines in Fig. 1). The simultaneous change of the different ZP stripes which are generated in spatially distributed sources within LS1 gives strong evidence for collective processes in the loop and for ongoing changes of the physical conditions in the trap volume.

3 Pulsations

In this section we consider two possible reasons for radio pulsations that are widely discussed in the literature:

1.
the modulation of radio emission flux density by MHD-oscillations of coronal magnetic loops, and
2.
the pulsed acceleration of electrons in the radiation source volume.
A variety of the second mechanism is the periodic injection of fast electrons after having been accelerated outside the radio source[*].

When MHD oscillations develop, the magnitude of the magnetic field strength and the mirror ratio in the trap are modulated. That changes both the energy spectrum and the number of trapped particles. Therefore for any generation mechanism the radio emission flux density will be modulated with the period of MHD oscillations in a wide frequency band. MHD oscillations may be excited as a result of a pulsed disturbance inside a loop (Roberts et al. 1984), chromosphere evaporation (Zaitsev & Stepanov 1989), or due to bounce-resonance, when a period of bounce-oscillations of energetic particles in the trap coincides with one of the periods of MHD oscillations of the trap (Meerson et al. 1978).

A periodic regime of acceleration is possible under the oscillation dynamics of current sheets (Tajima et al. 1982; Tajima et al. 1987; Sakai & Oshava 1987), as well as in large scale electric fields of the coronal magnetic loops when MHD oscillations or current oscillations are excited (Zaitsev et al. 1998).

3.1 Magneto-hydrodynamic loop oscillations

Eigen modes of coronal magnetic tubes have been investigated by numerous authors (see, for example, the review by Aschwanden 1987). These investigations showed that a slow sound mode and a fast kink-mode are not capable of explaining oscillations with periods of the order of 1 s. The best fit for such events is given by the fast sausage mode and the magnetosonic wave MHD mode. The fast kink mode exists only in rather thin tubes, when $a/L \lesssim 10^{-2}$, where a is a radius of the tube, L is its length. Also, the kink-mode implies that the plasma density ${\varrho}$inside the tube exceeds markedly the density ${\varrho_0}$outside it: ${\varrho}\gg{\varrho_0}$. In our case at least the first condition is not valid because the greatest diameter of the magnetic loop is of the order of its length (see Fig. 1). Propagating MHD waves have the basic frequency $\omega = k_{\perp}V_{\rm A}$, where $k_{\perp}=j_{01}a^{-1}(1-\varrho/\varrho_0)^{-1/2}$, j01=2.4is the first zero of the Bessel function J0, $V_{\rm A}= B~/\sqrt{4\pi\varrho}$ is the Alfvén velocity inside the cylinder. At ${\varrho_0}/{\varrho}\ll 1$ the oscillation period $\tau_{\rm p}=2\pi/\omega$ is equal to:

 \begin{displaymath}\tau_{\rm p}=\frac{2\pi a}{j_{01}V_{\rm A}}\approx 2.6\frac{a}{V_{\rm A}}\cdot \end{displaymath} (1)

The relation (1) is obtained for a homogeneous magnetic cylinder. In our case the magnetic trap is essentially non-homogeneous one. Its radius a and Alfvén velocity $V_{\rm A}$ change with height. We can calculate the dependence of the Alfvén velocity inside the trap on the height using the extrapolation of the magnetic field into the corona. Also we can use the dynamic spectrum of the radio event taking into account that the apex of the trap (where magnetic field is $B\approx 2$ G at the height $h \approx 65$ Mm) corresponds to a plasma frequency of $f_{\rm p}=(e^2N/\pi m)^{1/2} \approx 130$ MHz and a plasma density of $N\approx 2\times 10^8$ cm-3 (e and mare charge and mass of electron), respectively. Assuming a barometric height distribution of electron density in the loop with the temperature $T=2\times 10^6$ K, we obtain that the Alfvén velocity in the loop sharply increases from top towards footpoints ( $V_{\rm A} =3\times 10^7$ cm s-1 for plasma level $f_{\rm p}=130$ MHz and $V_{\rm A} =4\times 10^8$ cm s-1 for plasma level $f_{\rm p}=220$ MHz. The loop radius decreases from apex towards footpoints as approximately $a/a_{\rm top}\approx (B_{\rm top}/B)^{1/2}$, where $a_{\rm top}$ and $B_{\rm top}$ are loop radius and magnetic field in the trap apex. It follows from Eq. (1) that the oscillation period will markedly depend on the height. For example, for $f_{\rm p}=130$ MHz (apex of the loop) the period is $\tau_{\rm p}=50$ s, while for $f_{\rm p}=220$ MHz it is equal to $\tau_{\rm p}=0.7$ s. Thus, the considered MHD waves are not capable to provide synchronous pulsations in a wide frequency interval and are no appropriate cause for the observed radio pulsations.

3.2 Pulsed acceleration of electrons

Another source of pulsations can be the periodic acceleration of electrons and/or their periodic injection into a coronal magnetic loop. The question arises to identify the driving force of such a periodic and long-lasting effect. The answer was given by Aurass et al. (1999): from inside the loop system LS1 (Fig. 1) the approaching western flare ribbon of the erupting arcade might act as a permanent driver of the activity in our model configuration (see also Vrsnak et al. 2000). The following facts support that at least in our event of interest the pulsations were due to periodic injection of electron beams into the loop:

1.
The source of acceleration was localized at the leading footpoint of the trap (SW in Fig. 1, see Aurass et al. 1999).
2.
The pulses revealed a negative frequency drift like type III and sometimes also J bursts. If the negative frequency drift is associated with electron beams propagating from dense to rarefied plasma in the solar corona, the J shape confirms the presence of a trap-like source (see Fig. 6 in Paper I).
3.
The radio images showed that the sources of separate pulses tend to move along the trap axis from high to low frequencies with a velocity of the order of (1/3)c, c is the speed of light.
We consider now several possibilities of a periodically acting acceleration mechanism.

3.2.1 Current sheet oscillations (periodic reconnection)

According to our model (Fig. 1) we assume that a big coronal loop (the source of pulsations) interacts with a compact emerging loop (EL). In the region of possible magnetic reconnection (shown by a wavy circle in Fig. 1b) fast particles might occur and penetrate into LS1. The possibility of the pulsed regime of magnetic reconnection was noted in Smith (1977), but the period of oscillations was not calculated. Tajima et al. (1987) considered explosive reconnection of two current-carrying loops and found the possibility of periodic energy release by analytic calculations and computer simulations. The attraction of two loops carrying the current $\vec{j}$ is due to Ampere's force $(1/c)[\vec{j}\times\vec{B}]$. The lowest period of pulsations

 \begin{displaymath}\tau_{\min}=2\pi \beta^{3/2}(d/V_{\rm A}) \end{displaymath} (2)

is determined by a typical sheet width d, Alfvén velocity $V_{\rm A}$ and the ratio of kinetic to magnetic pressure $\beta= 8\pi N T \kappa /B^2$. Here B is the magnetic field outside the current sheet, T is plasma temperature, $\kappa$ is the Boltzmann constant. The period of pulsations increases together with the amplitude resulting in a transit time $a/V_{\rm A}$ for the tube of radius a. At $V_{\rm A}\approx 10^3$ km s-1 and $a\sim 10^3$ km this mechanism gives periods close to the observed ones. Acceleration of particles is caused by electrostatic and induction fields resulting from the coalescence of two coronal loops.

In our case the additional circumstance initiating reconnection may be associated with the flare ribbon shown in Fig. 1. It can compress the footpoints of the loop LS1 and play the role of a driver for fast reconnection. However the pulsation quality Q in the current loop coalescence model is rather low. Computer simulations by Tajima et al. (1987) show that the energy of electrostatic and inductive fields decreases by an order of magnitude after just the first few (3-4) oscillations. In contrast, for our event the quality of pulsations was extremely high ( $Q\sim 10^2$).

3.2.2 RLC-Oscillations of emerging magnetic loop (EL)

A further cause for BBP may be the resonance oscillations of a current-carrying magnetic loop. This becomes clear in treating it as an equivalent electric circuit. The electric circuit approach has been applied to the different problems of solar and stellar physics including flares (e.g., Alfvén & Carlqvist 1967; Spicer 1976; Kan et al. 1983; Melrose & McClymont 1987; Melrose 1991; Zaitsev & Stepanov 1992; Zaitsev et al. 1998), filaments (e.g., Kuperus & Raadu 1974; van Tend & Kuperus 1978; Martens 1978; Scheurwater & Kuperus 1988), loop transients (Anzer 1978), heating of flux tubes (Ionson 1982), as well as the electrodynamics of hot stars (Conti & Underhill 1988) and disk-accreting magnetic neutron stars (Miller et al. 1994). In our case an appropriate loop (a source of accelerated particles) may be the compact emerging magnetic flux EL shown in Fig. 1b. An electric current flows along the loop between the footpoints and is closed through the photosphere at heights corresponding to the level[*] $\tau_{5000}=1$. The electric circuit is closed along the shortest path between the footpoints. The electro-motive force resulting in the electric current and large-scale electric field accelerating the particles is concentrated in the loop footpoints and is associated with the coupling of convective plasma flows and the loop magnetic field. Similar to reconnection, in this case the flare ribbon interacting with the loop LS1 can play an active part, being an accelerator of the photospheric convection as well as an amplifier of electric fields and currents in the loop EL.

Let us represent the total current through the loop crossection as $I=I_0+I_{\sim}$, where I0 is a quasi-stationary current along the loop and $I_{\sim}$ is a small oscillating fraction. Then the equation for the oscillating fraction has the following form:

 \begin{displaymath}\frac{{\rm d}^2 I_{\sim}}{{\rm d}t^2} + \frac{c^2R(I_0)}{L} \frac{DI_{\sim}}{{\rm d}t} +\frac{c^2 I_{\sim}}{LC(I_0)} =0, \end{displaymath} (3)

where R(I0), L and C(I0) are equivalent resistance, inductance and capacity of the loop, respectively. The equivalent resistance and capacity depend on the magnetic field inside the loop which is determined by currents in a self-consistent model.

For the case $B_z^2\gg B_{\varphi}^2$ (weakly twisted magnetic loop) the period of current oscillations is given by relation (Zaitsev et al. 1998):

 \begin{displaymath}\tau_{RLC}=\frac{2\pi}{c}\sqrt{LC(I_0)}=2\pi\frac{a}{V_{\rm A... ... \frac{7}{4}\right)^{1/2} ~\left(\frac{a}{l}\right)^{1/2}\cdot \end{displaymath} (4)

Assuming for the loop EL in Fig. 1b the magnetic field $B\approx 80$ G (the magnitude of emerging magnetic field), plasma density $N= 2\times 10^9$ cm-3 (the highest frequency of pulsations, 400 MHz), the sizes $a\approx 1$ Mm and $l\approx \pi b \approx 10$ Mm, we obtain the period $\tau_{RLC}\approx 1.4$ s, close to the observed pulsation period 1.33 s. Note that the Q-factor for current oscillations in the current-carrying magnetic loop, determined by the relation Q=(L/C(I0))1/2(cR(I0))-1, is rather high and can get values $Q=10^3\div 10^4$ for typical parameters of flaring magnetic loops (Zaitsev et al. 1998).

Let us consider DC-electric field acceleration in a current-carrying loop more in detail.

The current-carrying loop can produce fast electrons due to the direct acceleration in a large scale electric field. Such a field is formed in footpoints of the small emerging current-carrying coronal loop (EL), where converging flows of photospheric plasma exist[*]. In this case the positive charge prevails near the magnetic tube axis, and negative one is located mainly at its outskirts. A charge separation results from the fact that the ions are magnetized less than electrons, so the ions are more easily transported by convective flows. The projection of the electric field on the magnetic field which causes particle acceleration is determined by the relation (Zaitsev et al. 2000):

 \begin{displaymath}E_{\parallel}=\frac{\vec{E}\vec{B}}{B}\approx \frac{1-F}{2-F}... ...gma v_{\rm c}B^2}{eNc^2(1+\alpha B^2)}~~~ \frac{B_{\rm r}}{B}, \end{displaymath} (5)

where $B_{\rm r}$ is the radial component of the magnetic field in the region of electric field generation (assumed to be rather small: $B_{\rm r}\ll B$), $F=N_{\rm a}m_{\rm a}/(N_{\rm a}m_{\rm a} + Nm_{\rm i})$ is the relative density of the neutral plasma component with atom density $N_{\rm a}$ and atomic mass $m_{\rm a}$, $N=N_{\rm i}$ is the number density of electrons and ions, $\sigma =e^2N/m_{\rm e}(\nu_{\rm ei}+\nu_{\rm ea})$ is the conductivity due to electron-ion collisions (collision number $\nu_{\rm ei}$) and electron-atom collisions (collision number $\nu_{\rm ea}$), $v_{\rm c}$ is the velocity of convective flow, $\alpha=\sigma F^2/(2-F)c^2Nm_{\rm i}\nu_{\rm ia}$, $\nu_{\rm ia} = 6\times 10^{-11}N_{\rm a}\sqrt{T}$is an effective ion-atom collision number (Golant et al. 1977).

When the electric field is periodically modulated, the following scenario of pulsed acceleration arises. A modulation can occur due to periodic change of the radial component of magnetic field caused by either MHD-oscillations of coronal magnetic loop or oscillations of electric current flowing through cross-section of the loop (RLC-oscillations): $B_{\rm r}(t)=B_{\rm r0}+\delta B_{\rm r} \sin{\Omega t}$. In this case the modulation of a beam of accelerated runaway electrons may be rather deep even if the change $\delta E_{\parallel}=E_{\parallel} (\delta B_{\rm r})/B_{\rm r0}$ of the accelerating field is small, since (as shown below) the condition $E_{\rm D} /E_{\parallel}\gg 1$ is valid in the source of acceleration, where $E_{\rm D}=e\Lambda \omega_{\rm p}^2/v_{\rm T}$ is the Dreicer field, $\omega_{\rm p}^2=4\pi e^2 N/m$, $v_{\rm T}=(\kappa T/m)^{1/2}$, $\Lambda$ is the Coulomb logarithm. The productivity of the acceleration mechanism for runaway electrons is determined by (Knoefel & Strong 1979):

 \begin{displaymath}\dot N [{\mbox s}^{-1}]=0.35 N\nu_{\rm ei} V \left(\frac{E_{\... ...}} {E_{\parallel}}} - \frac{E_{\rm D}}{4E_{\parallel}}\right], \end{displaymath} (6)

where V is the volume of the acceleration region. We see that assuming $N_{\rm b}\approx 10^3$ cm-3 (see Sect. 4.3), $v_{\rm b}\approx 10^{10}$ cm s-1, and[*] $S\approx 7\times 10^{18}$ cm2, we obtain a minimum rate of electron acceleration $\dot N \simeq 7\times 10^{29}$ el s-1. This value is $5\div 7$ orders of magnitude less than the rate of electron acceleration in large flares (Miller et al. 1997). When electrons are accelerated by the electrostatic field of current-carrying loops, the region of acceleration is concentrated in the chromospheric footpoints of the loop. We take for the acceleration region T=105 K, N=1010 cm-3, $V\simeq (7\div 10)\times 10^{24}$ cm3. So, the necessary rate of acceleration will be provided under the condition $E_{\rm D}/E_{\parallel}=46$. The energy of electrons in pulsations $\epsilon \approx 30$ keV will be acquired at the acceleration length of 2.5 Mm. In the chromosphere the condition $\alpha B^2\gg 1$ is valid. Using relation (5) we find the ratio of the Dreicer field to the accelerating field: $E_{\rm D}/E_{\parallel}\approx 10 F \left(3\times 10^4/v_{\rm c}\right) \left(10^6/T\right)^{3/2} \cdot (B/B_{\rm r})$, with $v_{\rm c}$ in cm s-1, T in K. At T=105 K the main atmospheric neutral constituent is helium due to dielectron recombination (Burgess 1964). In this case F is about $7\times 10^{-4}$. If the convection is rather slow ( $v_{\rm c}=10^4$ cm s-1), the necessary value of the ratio $E_{\rm D}/E_{\parallel}=46$ will be reached if RLC-oscillations produce a radial magnetic field $B_{\rm r}/B \gtrsim 10^{-2}$. When the amplitude $B_{\rm r}$ becomes so large, the velocity and the density of fast electrons will be increased, too.

Under conditions of the corona and chromosphere the ratio of Dreicer's field to accelerating one is usually rather great. With an exponential dependence of parameter $\dot N$ on ${E_{\rm D}}/{E_{\parallel}}$the modulation appears to be deep at $(\delta B_{\rm r}/B_{\rm r})\gtrsim (E_{\parallel}/E_{\rm D}) \approx 2\times 10^{-2}$, i.e. at small oscillations of the radial component of the magnetic field.

Decimetric pulsations with lower periods ( $T\approx 0.54$ s, see Figs. 1 and 9 in Paper I) occurring at the final stage of the event can be associated with the modulation of radiation inside the emerging loop EL. It seems that in this case the magnetic connection between LS1 and EL becomes insignificant, and accelerated electrons remain in EL. Here they are accumulated and can give rise to a plasma wave instability. The decrease of the LRC pulsation period down to 0.54 s may be due to the growth of the non-potential $B_{\varphi}$ component when EL is emerging more and more. It causes a decrease of the equivalent capacity of the electric circuit (Eq. (4)) that results in a decrease of the pulsation period.

4 Zebra-pattern

Zebra patterns pose the intriguing problem for theorists to explain such a highly structured emission-absorption "surface'' in the frequency-time plane. ZP were discovered in the early days of solar radio burst spectral observations (see, for example, Elgaroy 1961; Slottje 1972a,b, 1981; Bernold 1980; Chernov et al. 1975). The picture is so specific that for a long time there were doubts about its solar origin. Chernov et al. (1998) compared IZMIRAN, AIP, and ARTEMIS observations to verify the solar origin of ZP. Already some theories of ZP formation were put forward.

ZP exists against the background of the type IV continuum. While short-time type III bursts and other fast drifting bursts are associated with electron streams propagating through the corona along magnetic field lines, the long-lasting type IV radio emission is understood as radiation provided by electrons having non-equilibrium distribution over the velocity perpendicular to the magnetic field (trapped electrons, so-called ring-type or loss-cone distributions). Similar mechanisms of instability are considered for ZP.

The most prominent feature of the event of interest are several (here about 20) parallel drifting emission and absorption stripes spaced by approximately equal frequency intervals from each other. The spacing is usually much less than the frequency of radiation. This, together with a high brightness temperature, implies a coherent generation mechanism of radio emission at harmonics of some characteristic frequency in the source volume.

The first question is what instability can provide the observed frequency spectrum. One possibility is the excitation of Bernstein modes at gyrofrequency harmonics in a quasi-homogeneous compact source (Rosenberg 1972; Zheleznyakov & Zlotnik 1975). Another opportunity is the enhanced generation of plasma waves at the upper hybrid frequency in an inhomogeneous flux tube. The emission will grow at the levels of so-called double-plasma resonance (DPR). The kinetic and hydrodynamic case were firstly considered by Zheleznyakov & Zlotnik (1975) and Kuijpers (1975a,b, 1980), respectively, later developed by Mollwo (1973, 1983), Winglee & Dulk (1986), and others.

Longitudinal plasma waves cannot escape from the solar corona. So, a conversion of plasma waves to electromagnetic radiation has to take place. As a mechanisms of nonlinear transformation of plasma into radio waves, there was suggested the coalescence of Bernstein modes with plasma waves (Rosenberg 1972; Chiuderi et al. 1973; Zlotnik 1976, 1977). Other approaches were the coalescence of two plasma waves at the upper hybrid frequency in weakly anisotropic plasma (Zlotnik 1976), and the coalescence of plasma waves with whistler waves (Chernov 1976, 1990).

As done with the BBP in the previous section, our aim is now to select a proper ZP mechanism based on our source model Fig. 1. Firstly, bearing in mind the rather great amount of recorded zebra stripes, we reject the generation of Bernstein modes in a homogeneous source. Their growth rate decreases sharply with harmonic number increase. According to Zheleznyakov & Zlotnik (1975) the Bernstein mode model cannot explain ZP with more than 4 or 5 stripes. We claim that the most probable cause of ZP is plasma wave generation in an inhomogeneous source. In the given magnetic flux tube (Fig. 1) there are height levels where the upper hybrid frequency[*] $f_{\rm uh}$= $\sqrt{f_{\rm p}^2 + f_B^2}$ coincides with the frequencies of harmonics of electron gyrofrequency $f_B=eB/2\pi mc$:

 \begin{displaymath}f_{\rm uh}\equiv \sqrt{f_{\rm p}^2 + f_B^2}\simeq s~f_B \end{displaymath} (7)

(s is the harmonic number).

These height levels in the loop system (corresponding with a sequence of plasma frequency levels) emit bright but narrow band radio radiation. To explain this more in detail some theoretical considerations are necessary. For easier reading we placed this in the Appendices: the main results of the theory of longitudinal waves propagating perpendicular to the magnetic field, including waves near $f_{\rm uh}$, are summarized in Appendix A, and some theory of the kinetic DPR instability can be found in Appendix B. The results are used in the following sections.

4.1 The generation mechanism


  \begin{figure} \par\hbox to \hsize{\hfill\hspace{5mm}\raisebox{-2ex}{a)}% \epsfi... ...}\raisebox{-2ex}{c)}% \epsfig{file=aa4049f2c.eps,scale=0.58}\hfill} \end{figure} Figure 2: The DPR source of ZP: a) gyroharmonics sfB and plasma frequency $f_{\rm p}$ via height h. Intersection points are DPR levels. b) Positive frequency drift due to magnetic field decrease. Solid sfB(t1) and dotted sfB(t2) are gyroharmonics at times t2>t1. The DPR level moves to higher frequencies. c) Frequency drift due to plasma cooling. Solid and dotted $f_{\rm p}$ are plasma frequency at t2 and t1. The decrease of the scale of $f_{\rm p}$ (and of electron density) results from plasma cooling ( T(t2)<T(t1)). Again, the DPR level moves to higher frequencies.
Open with DEXTER

The enhanced generation of electrostatic modes arises in the hybrid band $(s-1)~f_B < f_{\rm uh} < s~f_B$ if the instability occupies the wavelength interval with a normal dispersion law (see Zheleznyakov & Zlotnik 1975). The highest increments appear near the lower boundary of the hybrid band. The bandwidth of instability can be much less that the distance fB between the harmonics for a sufficiently high velocity of nonthermal electrons[*]. The peak increment doesn't markedly depend on the harmonic number. This is in accordance with the observations.

The consideration given in Appendices A and B refers to the instability in the homogeneous plasma with constant electron density and magnetic field. Now let us turn to a nonhomogeneous source as shown in Fig. 1a. We assume that LS1 is filled with equilibrium plasma (for the moment we do not invoke a possible influence of the approaching flare ribbon) and a minor amount of hot electrons with ring-type velocity distribution. If the gradients of magnetic field and electron density along the lines of force are not the same, the DPR condition (7) is realized at discrete layers. These are defined by the intersections of the curves $f_{\rm uh}$and sfB in Fig. 2[*]. At these layers the enhanced emission arises, and the dynamic spectrum will consist of alternating dark and light stripes. It is easy to see that in the framework of such a scheme the distance between the zebra stripes

 \begin{displaymath}\Delta f/f_B \approx \frac{L_B}{\vert L_N-L_B\vert} \end{displaymath} (8)

is determined both by the gyrofrequency, that is by the magnitude of the magnetic field B, and by the height scales of the magnetic field $L_B=B({\rm d}B/{\rm d}h)^{-1}$ and the electron density $L_N=2N({\rm d}N/{\rm d}h)^{-1}$.

The generation mechanism shown includes the nonlinear transformation of longitudinal electrostatic waves-excited at the upper hybrid frequency-into electromagnetic radiation freely escaping the corona. The frequency interval between the stripes is equal to (8) if the radiation is a result of the coalescence of high frequency plasma waves (i.e. at a frequency close to $f_{\rm p}$) and some low frequency waves (for example, whistlers or ion sound waves). Another transformation mechanism is the scattering of plasma waves by ions. If the radio emission is a result of the coalescence of two high frequency plasma waves, the right side of (8) must increase by 2. Both cases can be distinguished by polarization measurements. The radiation at twice the plasma frequency should be only weakly polarized in a relatively weak magnetic field. In our event the circular polarization degree of ZP was -26%. Thus, the ZP are most probably fundamental mode emission at the local plasma frequency. The distance between the stripes is equal to (8). In this paper we simply assume that the transformation took place without further considering this necessary step to obtain radio emission.

If for the characteristic length scales $L_N\ll L_B$, then the distance $\Delta f$ is equal to the electron gyrofrequency: this means $\Delta f\approx f_B$. In this case we immediately find the magnetic field in the source. But if we apply this approach to our data of interest, say at about 200 MHz with $\Delta f$ of about 2 MHz, we obtain $s\sim 100$. If electrons radiate at such high harmonics their energy must be rather great. Therefore the weakly relativistic approximation is not valid. No zebra stripes would appear.

Consequently, the inverse case must be more probable so that the magnetic field changes with height faster than the electron density. This is the case in Fig. 2. Here $\Delta f$ is LN/LB times less than the gyrofrequency:

 \begin{displaymath}L_N\gg L_B, ~~~~~~~~ \Delta f/f_B\approx {L_B}/{L_N}, \end{displaymath} (9)

Evidently, the ZP may appear only if the distance between the adjacent DPR layers is greater than the bandwidth of a single stripe at the given harmonic. Otherwise we would observe a continuum emission. As is shown in Appendix B, the bandwidth $\delta f$ of DPR radiation at a spatially fixed point of the source is negligibly small compared to fB. The true bandwidth is determined by the plasma inhomogeneity and the finite size of the source of a separate stripe. The frequency interval of enhanced emission $\delta f$ must be less than the distance between the stripes. That is, it must satisfy the inequality $\delta f/\Delta f < L_B/L_N$. Indeed, it can be shown (see also Appendix B) that the bandwidth $\delta f$ is rather small compared to fB.

The described qualititative model of the source can easily explain many features of ZP. It is seen from (9) and from Fig. 2a that the frequencies at the DPR levels are not fully equidistant. Moreover, in the framework of our source model (under condition $L_N\gg L_B$), this distance increases with frequency in accordance with observations. This can be nicely seen in Fig. 7 of Paper I.

Our source model can naturally explain the observed positive frequency drift of zebra-stripes towards higher frequencies when the burst decays. Such a drift is a common feature for many ZP (see, for example, Slottje 1981). The positive frequency drift can be caused by the decrease of the magnetic field in the source: in this case the set of curves sfB(h) in Fig. 2a is moving to lower frequencies relative to the curve $f_{\rm p}(h)$, and each point of intersection - defining the frequency of a fixed stripe - is moving up along the curve $f_{\rm p}(h)$ (Fig. 2b). The positive drift is also obtained by a change of the steepness of the curve $f_{\rm p}(h)$: if the scale LN decreases with time towards the end of event (that means cooling of plasma in the loop takes place), then the curve $f_{\rm p}(h)$ become steeper. The points of intersection with harmonics sfB(h) are again moving up providing the positive frequency drift of zebra stripes (Fig. 2c). An increase of the distance between stripes with time seen on the dynamic spectrum follows from the suggested scheme, too[*].

An essential feature of our source model is the spatial separation between sources of different stripes. From this point of view it might appear strange that the change of frequency of different stripes occurs synchronously. Actually, this is due to the fact that the collective processes prevail in the loop, and the magnetic trap changes as a whole. During the flare of interest, X-ray and radio data confirm a reformation of the field and density structure in the active region corona (Aurass et al. 1999).

4.2 Matching of theory and observations

From the previous discussion of the emission mechanism, the ZP gives information about magnetic fields in the corona. This is of some diagnostic importance because direct measurements in the corona by optical observations are impossible, and until now spatially resolved field estimates from radio data were tried only using the well-known theory of microwave emission (e.g. Gelfreikh 1998; Klein 1992). However for AR NOAA 7792 the force-free extrapolated coronal field was derived from photospheric field measurements (Paper I). In Fig. 3 we present a typical height over field strength plot along a selected field line of the FS loop system LS1 (compare Fig. 2 of Paper I).

  \begin{figure} \par\hbox to \hsize{\hfill \raisebox{-2ex}{a)}% \epsfig{file=aa40... ...aisebox{-2ex}{b)}% \epsfig{file=aa4049f3b.eps,scale=0.6} % \hfill}\end{figure} Figure 3: Magnetic field line selected from extrapolated LS1 (see Fig. 2 of Paper I): a) perspective view; b) height dependence of field strength.
Open with DEXTER

Thus, we can plot the dependence of gyrofrequency harmonics sfB(h) on the height and check for which density model the DPR effect appears. This must be compared with the zebra stripe frequencies (Fig. 4). Let us do this for certain selected times.


  \begin{figure} \par\hbox to \hsize{\hfill\epsfig{file=MS4049f4.eps,scale=0.3} % \hfill}\end{figure} Figure 4: The dynamic spectrum of ZP 10:08: $20 \div 10$:08:50. The white dotted line enhances the time evolution of a single zebra stripe (s=17 according to our counting). Dark dotted lines mark two instantaneous spectra used in Fig. 5.
Open with DEXTER

According to our scheme shown in Fig. 2a, the minimum magnetic field at the loop apex corresponds to the maximum harmonic number. The lowest frequency of ZP at 10:08:23 UT is 136.9 MHz (Fig. 4). The magnetic field along the chosen line has its minimum value $B_{\min}\approx 1,76$ G at a height of $h \approx 66750$ km. We conclude that the highest harmonic number at this moment is $s_{\max}\simeq 136.9$ MHz $/f_B(B_{\min})\simeq 27$. Being bound to the height, we can determine the numbers of harmonics of zebra stripes on the instantantaneous spectrum at the moment 10:08:23 and plot dependencies sfB(h) for harmonics $s = 11\div 27$ (Fig. 5a). Horizontal lines in this figure are the observed frequencies on zebra stripes at the selected moment. The points of intersection of two sets of curves (sfB (h) and the observed frequencies of ZP) marked by dots are the DPR levels. The line connecting these points is the expected distribution of plasma frequency $f_{\rm p}(h)$ (or electron density) over the height.


  \begin{figure} \par\hbox to \hsize{\hfill \raisebox{-2ex}{a)}% \epsfig{file=aa40... ...m}\raisebox{-2ex}{b)}% \epsfig{file=aa4049f5b.eps,scale=.9}\hfill}\end{figure} Figure 5: Observations versus theory: horizontal lines are peak frequencies of zebra stripes. A grid of gyroharmonics $s = 11\div 27$ is plotted using the field along the selected extrapolated field line (Fig. 3). Intersections are marked by dots and represent the DPR levels. Thick line is the barometric plasma frequency (electron density) law over height for a) the spectrum at 10:08:23 UT ( $T=1.18\times 10^6$ K); b) the spectrum at 10:08:33 UT ( $T=0.80\times 10^6$ K). The dotted line in b) is the thick line of a).
Open with DEXTER

To what extent does a distribution correspond to the true electron density in the loop? The electron density over height follows a barometric law because of hydrostatic equilibrium (Priest 1987), so the plasma frequency $f_{\rm p}=(e^2N/\pi m)^{1/2}$ decreases with the height in the following way:

 \begin{displaymath}f_{\rm p}=f_{{\rm p}0}\exp(-h/10^4 T). \end{displaymath} (10)

Do the DPR levels confirm the extrapolated magnetic field and a barometric electron density distribution with a reasonable temperature? Let us assume that at least two observed frequencies coincide with some harmonics and find the temperature T and $f_{{\rm p}0}$.

Looking for the best fit for matching two sets of frequencies (observed frequencies of zebra stripes and the values given by intersection of the curves $f_{\rm p}(h)$ and sfB(h)) we found for the frequency interval $130\div 160$ MHz for the moment 10:08:23 UT: $T=1.18\times 10^6$ K and $f_{{\rm p}0}= 234$ MHz ( $N_0= 6.8\times 10^8$ cm-3)[*]. The dependence $f_{\rm p}(h)$ is shown in Fig. 5a by a thick line. The remaining intersection points are also situated at the thick curve. This means that the frequencies of DPR levels given by the theory coincide surprisingly well with observed frequencies of zebra stripes.

It should be emphasized that we used two independent sets of data - the peak frequencies of zebra stripes and the extrapolated magnetic field along a field line - and obtained the electron density law. It was found to be a barometric distribution with a reasonable temperature. This fact is no coincidence. It undoubtedly confirms the DPR model of zebra stripe origin.

We will now use the same approach to calculate the observed stripes somewhat later. At 10:08:33 UT there was a maximum amount of harmonics at higher frequencies (Fig. 4). Let us assume that the magnetic field is the same as at 10:08:23 UT and try to understand what parameters are changed while the zebra stripes drifted to higher frequencies. Accepting the harmonic numbers for stripes at 10:08:23 UT we can follow the stripes and match the observed frequencies of stripes at 10:08:33 UT. For example, we followed the stripe s=17 (white dotted line on dynamic spectrum in Fig. 4).

This stripe corresponds to f=168 MHz on 10:08:33 UT. Thus, having found the numbers of harmonics, we can get the expected DPR points and plot Fig. 5b for the moment 10:08:33 UT. Here, we obtain a temperature of $T=0.80\times 10^6$ K (solid curve in Fig. 5b). For comparison, the curve $f_{\rm p}(h)$ for the moment 10:08:23 UT is shown in Fig. 5b by a dotted line.

The zebra stripe peak frequencies for both times reveal an increase of the exponent in the barometric electron density distribution and, consequently, a decrease of the plasma temperature within the 10 s interval between. Thus, if cooling of plasma in the trap happens in the way shown in Fig. 2c it can naturally explain the observed frequency drift of zebra stripes.

The relatively low temperature of the background plasma is not surprising. As it is shown in Appendices A and B, the higher the ratio $v_{\rm e}/v_{\rm T}$, the better the conditions for the generation of narrow band stripes at DPR levels (see Fig. A.1 with instability boundaries indicated). Calculations by Winglee & Dulk (1986) confirmed the easier appearance of zebra stripes at lower temperatures of the background plasma.

By matching of theoretical and observed frequencies of zebra stripes we found a plasma temperature decrease in the source volume with time. We considered in the same manner as before the frequency spectrum at 10:08:48 UT when many stripes were recorded. Again tracing a fixed harmonic from 10:08:23 UT we find the numbers of harmonics at the later time. The temperature given by fitting the barometric distribution is now $T=0.75\times 10^6$ K. So, the ZP time evolution gives convincing evidence of cooling of the plasma in the coronal loop towards the end of the event.

However, plasma cooling must not be the only reason for the observed positive drift of zebra stripes. Bearing in mind that a fixed stripe drifts to higher frequencies (the harmonic s=17 is marked in Fig. 4), we can find from the spectrum at 10:08:48 UT that the lowest frequency stripe corresponds to a harmonic number s=32. This number requires magnetic fields of $B\approx 1.5$ G in the trap apex which is less than the minimum magnetic field in our approximation derived from the selected field line. We conclude that the magnetic field decreases between 10:08:33 UT and 10:08:48 UT.

Note that the decrease of the magnetic field will result in an apparent motion of the zebra stripe source to regions with greater electron density. This effect was observed in the radio images as a motion of the source with a velocity proportional to the drift rate of zebra stripes (Fig. 11 of Paper I).

By comparing the evolution of the stripe frequencies over time both effects - the plasma cooling and the decrease of the magnetic field - act in the same manner on the radiation pattern. With plasma temperature and magnetic field strength decay the stripes drift to higher frequencies and, simultaneously, more stripes become visible at the low frequency edge of the FS pattern. The rise of the emission frequency of a given stripe with time possibly reveals the temperature decay. The appearance of new stripes at the low frequency edge more probably may be interpreted as a decay of the reference field strength of stripe interpretation.

Note that in Fig. 5 we used only the assumption that the lowest frequency of the ZP stripe at 10:08:23 UT corresponds to the harmonic number s=27. In its turn this assumption is based on the minimum magnetic field value $B_{\min}\approx 1.76$ G at the top of LS1 along the selected field line. If we admit that the ZP source extended not to the very top of the trap, and the interval of harmonic numbers is, say, $s=10\div 24$ or $12\div 26$, we can try to find the barometric distribution corresponding to the DPR levels, but the fitting is much worse than in Fig. 5a for $s=13\div 27$. For sets with lower harmonic numbers, the line connecting the DPR levels cannot be reconciled with any barometric distribution. Thus we claim that the height distributions of the magnetic field and electron density shown in Fig. 5 are quite reliable.

We have considered above only one selected force line of the extrapolated magnetic field in the radio source loop LS1. It has been chosen because it is just in the center of the bunch of force lines of the magnetic field forming the shape of the coronal loop. The same procedure of fitting the DPR conditions for other field lines results in approximately the same harmonic numbers (with a small dispersion of the maximum s) and the parameters of the barometric distribution of the background plasma.

4.3 Time delay between BBP and ZP

The strong ZP emission arises approximately 2.5 min after the BBP (see Paper I). Since the sources of BBP and ZP were located in the same coronal magnetic loop, this time delay implies that the ZP appearance was preceded by about 100 injections of fast particles into the magnetic trap. This is due to the fact that the instability threshold is markedly higher for plasma waves excited by the DPR effect than the threshold of beam instability which forms BBP.

Therefore, numerous injections of fast electron beams into the trap are necessary in order to "pump up'' a large number of energetic electrons and to "switch on'' the DPR instability. If injected beams are rather weak, then first the BBP appear, and after some time they can be accompanied by ZP.

When a fast electron beam is injected along the magnetic field of the trap the increment of beam instability is determined by the relation:

 \begin{displaymath}\gamma_{\rm b}=2\pi \frac{N_{\rm b}}{N}\left(\frac{v_{\rm b}}{\Delta v_{\parallel}}\right)^2 f_{\rm p}, \end{displaymath} (11)

where $N_{\rm b}$ is the number density of electrons in the beam, $v_{\rm b}$is a mean velocity of the beam, $\Delta v_{\parallel}$ is a dispersion of the electron velocities longitudinal to the magnetic field. The criterion of beam instability $\gamma_{\rm b} > \nu_{\rm ei}$ gives a threshold electron density for the beam $N_{\rm b}^{\min}$:

 \begin{displaymath}N_{\rm b}^{\min}=\frac{\nu_{\rm ei}}{2\pi f_{\rm p}}\left(\frac{\Delta v_{\parallel}}{v_{\rm b}} \right)^2 N. \end{displaymath} (12)

Assuming $N=2\times 10^8$ cm-3 ( $f_{\rm p}\simeq 130$ MHz), $T=2\times 10^6$ K, $\Delta v_{\parallel}\sim v_{\rm b}/3$, we obtain the threshold value $N_{\rm b}^{\min}\sim 12$ cm-3 or $N_{\rm b}^{\min}/N \sim 6\times 10^{-8}$.

Scattering of beam electrons on the excited plasma turbulence results in an increase of dispersion of fast electrons over the velocities perpendicular to the magnetic field. Due to the "loss cone'' in the trap, an anisotropic distribution function is formed and special conditions are created for plasma wave generation in DPR regions. The highest increment of DPR instability at plasma waves is given by the relation (Zheleznyakov & Zlotnik 1975a):

 \begin{displaymath}\gamma_{\rm uh} \simeq 2\pi \frac{N_{\rm uh}}{N} f_B. \end{displaymath} (13)

The excess of the increment $\gamma_{\rm uh}$ over effective number of electron- ion collisions $\nu_{\rm ei}$ determines the minimum number density of trapped electrons $N_{\rm uh}^{\min}$ for plasma wave growth:

 \begin{displaymath}N_{\rm uh}^{\min}=\frac{\nu_{\rm ei}}{2\pi f_B}N. \end{displaymath} (14)

It follows from (12) and (14) that the instability threshold for the DPR instability is much higher than for the beam instability:

 \begin{displaymath}\frac{N_{\rm uh}^{\min}}{N_{\rm b}^{\min}}\sim \left(\frac{v_{\rm b}}{\Delta v_{\parallel}} \right)^2 s. \end{displaymath} (15)

In (15) we have taken into account that under the DPR condition we can put $f_{\rm p} \approx sf_B$. Assuming $s\approx 10$, $v_{\rm b}/\Delta v_{\parallel}\approx 1/3$, we obtain $N_{\rm uh}^{\min}\approx 10^2 N_{\rm b}^{\min}$. It means that it is necessary to inject about 102 beams into the trap in order to provide the DPR instability. This fact may be considered as a cause of the time delay of ZP to BBP.

Numerous injections of electron beams into the coronal magnetic field result in a gradual increase of trapped energetic particles and "switching on'' of the DPR instability. Therefore, the ZP shows a tendency to appear at lower frequencies ( $130\div 220$ MHz) compared to pulsations ( $130\div 400$ MHz). We believe the reason is that the effective electron ion collision number restricting the DPR instability threshold is lower near the trap apex than at its footpoints. The amount of trapped particles tends to be concentrated at the trap apex. So, the conditions for ZP generation are better in the upper part of the coronal loop, this means at low observing frequencies.

5 Discussion and conclusions

This paper gives a discussion of different theoretical approaches for the physical understanding of some common solar radio type IV burst continuum fine structures (FS). The FS of interest are broad band decimetric and metric radio pulsations (BBP) with roughly persistent upper and lower frequency boundary in the period range of $0.5\div 5$ s and special quasi-harmonic structure of the spectrum known as a zebra pattern (ZP). In Paper I we presented an extended discussion of a classic example of BBP and ZP thereby discussing the single FS element (the pulse and the zebra stripe) in spectral and radio imaging data. Additionally we discussed a statistical analysis of the BBP period (for the selected single event), the cross relationship between spatially split sources of a single pulsation pulse, and a linear regression relation between the local drift rate of a zebra stripe and the projected speed of zebra stripe source motion in space. Based on Paper I we developed here (Paper II) a FS source model. This model consists of an asymmetric loop configuration with an electron accelerator at those footpoints where the magnetic flux is spatially more concentrated. It turns out that the BBP periodicity follows from periodic electron injections; it is an accelerator property. Further we understand that ZP are due to distributed radio emission sources at double plasma resonance levels near the wider footpoint of the source model configuration. We demonstrate that the observations of BBP and ZP can well be understood in the frame of our source model. It allows us to decide between competing BBP and ZP mechanisms if we specify those model parameters which we can obtain from the data set in Paper I.

We summarize and discuss in the following our results concerning the most probable BBP and ZP mechanisms.

5.1 The origin of pulsations

We considered the distributions of magnetic field and electron density along the pulsation source volume and came to the conclusion that the Alfvén velocity inside the loop sharply increases from the loop apex to its footpoints. Therefore, MHD oscillations are not capable of inducing synchronous radio pulsations in a broad frequency band and we can exclude them from the BBP mechanisms.

The BBP source was moving yielding a negative frequency drift typical of type III and J bursts. The direction of the motion coincided approximately with the projection of the trap axis on the photosphere. This fact, together with the wide source branching at the high frequency edge of the discussed BBP (Paper I) favours assuming that the BBP were driven by a periodic injection of fast electron beams into the coronal magnetic field. This generation mechanism is similar to that of type III bursts.

The source of fast electrons was located in one of the footpoints of the loop which was embedded in the strong magnetic field of a north polarity sunspot. Near this sunspot, emerging magnetic flux of opposite polarity was observed. We suppose that this emerging flux was connected with a current-carrying magnetic loop (EL in Fig. 1), which interacted with the large coronal magnetic loop LS1. We discussed two possible mechanisms of pulsating particle acceleration - pulsed dynamics of explosive magnetic reconnection when two magnetic loops LS1 and EL collide (Tajima et al. 1987), and acceleration by an electrostatic field in the compact current-carrying loop EL. If we consider the loop EL as an equivalent circuit, the modulation of acceleration occurs due to RLC oscillations (Zaitsev et al. 1998). The pulsed regime of explosive reconnection cannot explain BBP in the event of interest because this effect can provide only a few pulsation pulses (Tajima et al. 1987).

5.2 The origin of zebra pattern

The origin of ZP is enhanced generation of plasma waves in regions of inhomogeneous coronal magnetic traps where the condition of double plasma resonance $f_{\rm uh}=sf_B$ is fulfilled (DPR levels). We checked this by deriving the (unknown) coronal gyrofrequency from the force-free extrapolated magnetic field together with the radio source site information. The height dependence of the density was found to be well in accordance with a barometric density law assuming $T \sim 10^6$ K. We obtained a good coincidence between the stripe frequencies predicted by theory and the observed stripe pattern. The observed increase of intervals between stripes with frequency and time is also well confirmed by the theory.

The considered zebra stripes show a positive frequency drift of up to 2 MHz s-1. In the framework of the DPR mechanism this follows from plasma cooling in the trap (that results in the increase of the electron density gradient and a shift of the points of intersection of the curves sfB(h) and $f_{\rm uh}(h)$ towards higher frequencies) or/and by expansion of the loop LS1 (that results in a decrease of magnetic field). The same effects can explain the downward motion of the ZP source. The DPR instability has a much higher threshold value of fast electron density than the beam instability. This explains the time delay between BBP and ZP.

We have shown that the dynamic spectrum of ZP in the event of interest with relatively large numbers of radiation stripes cannot be understood by excited Bernstein modes. We can also exclude nonlinear scattering of plasma waves on whistlers (Chernov 1976, 1990): it is unlikely that solitary whistler waves are positioned in an inhomogeneous coronal magnetic loop just according to a definite law in order to provide the systematic increase of the interval between the stripes with frequency.

5.3 Conclusions

The main results of our case study of type IV radio burst fine structures - broad band pulsations (BBP) and zebra patterns (ZP) - can be summarized as:

In our work we obtained - based on all available observations about the event of interest - a comprehensive common physical model for broad band pulsations and zebra pattern radio burst fine structures. We gave a physical explanation of its frequent common and ordered appearance in the dynamic spectrum. We found that the quasi-periodicity of BBP must be an accelerator property, and proposed an accelerator model in which a minor magnetic field oscillation can stimulate periodic beam injections. The present analysis can be taken for a cross confirmation of the double plasma resonance model of the ZP fine structure, and also underlines by means of radio observations the significance of force-free extrapolated photospheric field measurements for coronal magnetic field modelling.

Acknowledgements
We are grateful to K.-L. Klein for his cooperation in Part I of this work. The present work was possible due to joint grants 02-02-04005 (RFBR-DFG) and 436RUS 113/675/2-1 R (DFG-RFBR). The authors are grateful to the Deutsche Forschungsgemeinschaft and the Russian Foundation for Basic Research. The work by E.Z. and V.Z. was also supported by RFBR grants 01-02-17252 and 02-02-16239. The authors are thankful to the referee, Dr. Jan Kuijpers, for useful comments.

References

  
Online Material

Appendix A. Electrostatic waves perpendicular to the magnetic field

We emphasize some aspects of the theory of longitudinal wave excitation by trapped electrons considering only the kinetic instability. The hydrodynamic instability requires much higher values of nonequilibrium electron densities. We assume that the density of nonequilibrium electrons is small compared to background plasma. The dispersion properties of the waves are determined by the equilibrium component and can be described by well-known equations (for example Bekefi 1971; Zheleznyakov 1977, 2000):

 \begin{displaymath}{\bf\epsilon_{\parallel}^{(0)}=1-\omega_p^2 \sum_{l=1}^{\inft... ...l(\lambda)}{(\omega^2-\vec{l}^2\omega_{\vec{B}}^2)\lambda}=0.} \end{displaymath} (A.1)

Here

 \begin{displaymath}\lambda=\frac{k_{\perp}^2v_{\rm T}^2}{\omega_B^2}; ~~~~~~~~~~ v_{\rm T}^2=\frac{\kappa T}{m}, \end{displaymath} (A.2)

$k_{\perp }$ is the transverse component of the wave vector $\vec k$to the magnetic field $\vec B$, $I_l(\lambda)$ is the modified l-order Bessel function, $\kappa$ is the Boltzmann constant. The dispersion Eq. (A.1) is valid for angles $\alpha$ between the magnetic field $\vec B$ and the wave vector $\vec k$ satisfying $\cos^2\alpha \ll 1$ (Zheleznyakov 2000 for details). If

 \begin{displaymath}\lambda =\frac{k_{\perp}^2v_{\rm T}^2}{\omega_B^2}\ll 1, \end{displaymath} (A.3)

(i.e. the wavelength is much greater than the gyroradius of thermal electrons), then (A.1) reduces to:
 
                             $\displaystyle \epsilon_{\parallel}^{(0)}$ = $\displaystyle 1 - \frac{\omega_{\rm p}^2}{\omega^2-\omega_B^2} -\frac{3\omega_{\rm p}^2\omega_B^2\lambda}{(\omega^2-4\omega_B^2)(\omega^2-\omega_B^2) }$  
    $\displaystyle -\frac{\omega_{\rm p}^2}{\omega^2-s^2\omega_B^2}\frac{s}{(s-1)}\left(\frac {\lambda}{2}\right)^{s-1}=0.$ (A.4)

Under condition (A.3) Eq. (A.1) has solutions at the frequencies close to the cyclotron harmonics $s\omega_B$ (the so-called Bernstein modes):

 \begin{displaymath}\omega^2-s^2\omega_B^2 = \frac{\omega_{\rm p}^2\omega_B^2}{[(... ...^2]} \frac{s(s+1)}{(s-2)!}\left(\frac{\lambda}{2}\right)^{s-1} \end{displaymath} (A.5)

and close to the upper hybrid resonance frequency $\omega_{\rm uh}$:

 \begin{displaymath}\omega^2=\omega_{\rm uh}^2+3\lambda \omega_B^2=\omega_{\rm uh}^2+3k_{\perp}^2v_{\rm T}^2. \end{displaymath} (A.6)

Because $\omega $ is close to one of the harmonics, or to the hybrid frequency, we may simplify (A.1) taking only the main terms in the infinite sum (l=1,2, and the resonance term with $l=s\approx \omega/\omega_B$, $s\geq 3$). The dispersion curves $\omega=\omega(\lambda)$ for the ratio $\omega_{\rm uh}/\omega_B =15$ at arbitrary $\lambda$ are shown in Fig. A.1.
  \begin{figure} \par\hbox to \hsize{\hfill\epsfig{file=aa4049f6.eps,scale=0.7}\hfill}\end{figure} Figure A.1: Plasma waves perpendicular to the magnetic field in the equilibrium plasma: qualititative dispersion curves for Bernstein modes and plasma waves at the frequency of upper hybrid resonance. Straight lines mark the instability boundaries for two different ratios $v_{\rm e}/v_{\rm T}$ at $s\simeq 15$.

It is seen that the Bernstein mode frequencies are close to the values $s\omega_B$ at small and great $\lambda$. For $\lambda\sim s^2$ the dispersion curves below  $\omega_{\rm uh}$ pass from one harmonic to the other and occupy the whole interval $(s-1)\omega_B<\omega<s\omega_B$. As for the plasma waves in the vicinity of the hybrid frequency, the dispersion curves do not much deviate from those of Bernstein modes at $\lambda>s$. But a qualititative difference is present at $\lambda<s$. Three curves inside the hybrid band correspond to different locations of $\omega_{\rm uh}$ within the given interval. It is clear from these curves the limits of validity of (A.6) are $\lambda\ll 1$, or

 \begin{displaymath}k_{\perp}^2 v_{\rm T}^2\ll \omega_B^2, \end{displaymath} (A.7)

but not $k_{\perp}^2 v_{\rm T}^2\ll \omega^2\approx s\omega_B^2$, that is $\lambda \ll s^2$ as for the case of inclined wave propagation far from $\alpha=\pi/2$. This difference is due to the resonance term in $\epsilon_{\parallel}^{(0)}$ in (A.4). The curves in Fig. A.1 show that (A.6) is valid only inside the hybrid band $(s-1)\omega_B<\omega<s\omega_B$determined by $s\simeq \omega_{\rm uh}/\omega_B$. It cannot be extended to the band $s\omega_B<\omega<(s+1)\omega_B$adjacent to the hybrid band from above, as done by Winglee & Dulk (1986). Hence, contrary to the results by Winglee & Dulk (1986), who concluded that the kinetic instability of plasma waves described by relation (A.6) may contain several harmonics, the relation (A.6) for longitudinal waves close to $\omega_{\rm uh}$ is valid only inside the interval $\Delta\omega\leq\omega_B$[*].

Note that the behaviour of the dispersion curves as shown in Fig. A.1 for longitudinal waves in the vicinity of the hybrid frequency remains only under the condition $\vert\omega - l\omega_B\vert\gg \sqrt{2}k_{\parallel}v_{\rm T}$. Its violation results in strong damping of electrostatic modes in the background plasma. If the angle between the wave vector $\vec k$ and the magnetic field $\vec B$ is far enough from $\pi/2$ ( $k_{\parallel}v_{\rm T} \gg \omega_B$) the solutions of the dispersion equation are close to the well known expressions for the isotropic plasma under the condition $\omega_{\rm p} \gg \omega_B$ (for example Ginzburg 1967; Zheleznyakov 2000; Melrose 1980).

Appendix B. Growth rates for the DPR instability

Following Zheleznyakov & Zlotnik (1975)[*] and Winglee & Dulk (1986), we will consider the distribution function of nonequilibrium electrons in the form

 \begin{displaymath}f(v_{\parallel}, v_{\perp}) = \frac{v_\perp^2 c^3}{4\pi \sqrt... ...t(-\frac{v_{\parallel}^2 + v_{\perp}^2}{2v_{\rm e}^2}\right)}, \end{displaymath} (B.1)

where $v_{\parallel}$ and $v_{\perp}$ are the longitudinal and transverse components of electron velocity $\vec v$ relative to the magnetic field. The distribution over transverse velocities is peaked at $v_{\rm e}$ and the dispersion is of the order of the same $v_{\rm e}$. Such a function known as DGH function (Dory et al. 1965) has the main features of the distribution of particles trapped by the magnetic field: particles with small velocities are missing and the mean velocity along the magnetic field is equal to zero. This distribution function can provide discrete radiation stripes, unlike the loss-cone distribution resulting in continua (Winglee & Dulk 1986). If we assume

 \begin{displaymath}v_{\rm T}^2\ll v_{\rm e}^2 \ll c^2 \end{displaymath} (B.2)

we can neglect the wave damping in the background plasma and find the growth rate as

 \begin{displaymath}\gamma={\mbox{Im}}\omega\approx -\frac{Im \epsilon_{\parallel... ...}/\partial\omega \right]}_{\epsilon_{\parallel}^{(0)}=0}}\cdot \end{displaymath} (B.3)

where
 
                                 $\displaystyle \epsilon_{\parallel}^{(1)}$ = $\displaystyle \frac{2\pi \omega_{\rm p}^2}{k^2} \sum_{l=-\infty}^{\infty} \int_{-\infty}^{\infty}{\rm d}v_{\parallel} \int_{-\infty}^{\infty}{\rm d}v_{\perp}$  
    $\displaystyle \times\frac{J_l^2\left( k_{\perp}v_{\perp}/\omega_B\right)\left(k... ... f/\partial v_{\perp}\right)} {\omega -l\omega_B - k_{\parallel}v_{\parallel}},$ (B.4)

$k_{\parallel }$ is the component of wave vector $\vec k$ parallel to magnetic field $\vec B$. The relation (B.4) is written neglecting relativistic effects[*]. The imaginary part of $\epsilon_{\parallel}^{(1)}$(B.4) is

 \begin{displaymath}\mbox{Im}\epsilon_{\parallel}^{(1)}=\sqrt{\frac{\pi}{2}} \fra... ...}\left[\delta_l\varphi_l +(\delta_l+1)\zeta\varphi'_l \right], \end{displaymath} (B.5)

where
 
                                        $\displaystyle z_l=\frac{\omega-l\omega_B}{\sqrt{2k_{\parallel}v_{\rm e}}}; ~~~~~~~ \delta_l=\frac{\omega-l\omega_B}{l\omega_B}; ~~~~~~~~$  
    $\displaystyle \zeta = \frac{k_{\perp}^2v_{\rm e}^2}{\omega_B^2}=\lambda \frac{v_{\rm e}^2} {v_{\rm T}^2};~~~~~~~ \varphi_l={\rm e}^{-\zeta}I_l(\zeta)$ (B.6)
    $\displaystyle \mbox{ ($I_l(\zeta)$\space is the modified $l$ -order Bessel function).}$  

When the frequency $\omega $ is close to the harmonic $s\omega_B$, so that $\vert\delta_s\vert\ll 1, ~~~z_{s\pm 1}^2 \ll 1$, one s-term retains in (B.5):

 \begin{displaymath}\mbox{Im}\epsilon_{\parallel}^{(1)}\approx \frac{\sqrt{\pi}\o... ...mega_B(\omega-s \omega_B)}\varphi'_s(\zeta)z_s \exp{(-z_s^2)}. \end{displaymath} (B.7)

In the equilibrium plasma
$\displaystyle \left[ {\partial\epsilon_{\parallel}^{(0)}}/{\partial\omega} \right]_{\epsilon_{\parallel}^{(0)}=0} >0,$      

the growth rate (B.3) will be positive if $Im\epsilon_{\parallel}^{(1)}$is negative. This implies that the considered system is unstable for $\varphi'_s(\zeta)<0$, that is for

 \begin{displaymath}\zeta\equiv \frac{k_{\perp}^2v_{\rm e}^2}{\omega_B^2}>\zeta_{\rm cr}\approx s^2 \end{displaymath} (B.8)

or

 \begin{displaymath}\lambda\equiv \frac{k_{\perp}^2v_{\rm T}^2}{\omega_B^2}> \lam... ...m cr}\approx \left( s\frac{v_{\rm T}}{v_{\rm e}}\right)^2\cdot \end{displaymath} (B.9)

The instability boundary is shown in Fig. A.1 by dotted lines for two ratios $v_{\rm e}/v_{\rm T}=20$ and $v_{\rm e}/v_{\rm T}=4$.

It is important that the $k_{\parallel }$-dependence of $\gamma $(B.3) is due to the function $z_s\exp{(-z_s^2)}$. Hence for a fixed frequency and the corresponding values $k_{\perp}=k_{\perp}(\omega)$ the increment is peaked at $z_s=1/\sqrt{2}$, that is at an optimal value:

 \begin{displaymath}k_{\parallel}^{\rm opt}=\frac{\vert\omega-s\omega_B\vert}{v_{\rm e}}\cdot \end{displaymath} (B.10)

The optimal values of $k_{\perp }$ defining the peak growth rate, according to (B.7), correspond to the minimum of the function $\varphi'_s(\zeta)$. It happens at $\zeta^{\rm opt}\approx 2s^2$ or
 
                          $\displaystyle k_{\perp}^{\rm opt}$ = $\displaystyle \frac{\omega_B}{v_{\rm e}}\sqrt{\zeta^{\rm opt}}\approx \sqrt{ 2}\frac{s \omega_B}{v_{\rm e}}; ~~~~~~$  
$\displaystyle \lambda^{\rm opt}$ = $\displaystyle \frac{v_T^2}{v_{\rm e}^2}\zeta^{\rm opt}\approx 2\left( s\frac{v_T}{v_{\rm e}}\right)^2$ (B.11)

(with the instability boundary (B.8)-(B.9)). Relations (B.10)-(B.11) define the angle between the line-of-sight and the magnetic field at which the peak growth rate is realized.

It should be noted that all formulas after (B.7) are valid only if $\vert\omega-s\omega_B\vert/\omega_B\ll 1$. They are given to show the qualititative behaviour of the growth rate and to outline the boundary parameters.


  \begin{figure} \par\hbox to \hsize{\hfill a)\epsfig{file=aa4049f7a.eps,scale=0.75} % \hspace*{5mm}b)\epsfig{file=aa4049f7b.eps,scale=0.75}\hfill}\end{figure} Figure B.1: The growth rate of the waves in the hybrid band $14<\omega _{\rm uh}/\omega _B<15$ for $v_{\rm e}/v_{\rm T}=20$: a) $k_{\perp }$-dependence of $\gamma $ for the optimal values of  $k_{\parallel }$; b) the dependence of maximum growth rate on the position of $\omega $ inside the hybrid band.

To investigate the frequency dependence of the growth rate within the whole interval $(s-1)\omega_B<\omega<s\omega_B$ we should refer to expressions (A.1), (B.3) and (B.5) with the terms l=s-1 and s. An example of the growth rate $\gamma(\lambda)$ for s=15 at $v_{\rm e}/v_{\rm T}=20$ is given in Fig. B.1. These curves show the dependence of $\gamma(\lambda, k_{\parallel})$ on $\lambda$ at the optimal $k_{\parallel}^{\rm opt}$providing the peak values of the growth rate for the given $\lambda$ (or $k_{\perp }$) (Fig. B.1a), and the dependence of the peak growth rate on the position of the upper hybrid frequency inside the band $14\omega_B<\omega<15\omega_B$ (Fig. B.1b).

Note that the hybrid band is not distinguished by values of $\mbox{Im}\epsilon_{\parallel}{(1)}$ against other harmonic bands: the numerator in the growth rate $\gamma $ (B.3) (including the position of instability boundaries) behaves similar for Bernstein modes and for waves in the hybrid band. The dispersion curves at $\lambda \equiv k_{\perp}^2 v_{\rm T}^2/\omega_B^2 <s$drastically distinguish the hybrid band from other harmonic intervals. Instead of anomalous dispersion typical for Bernstein modes at $s<\omega_{\rm uh}/\omega_B$, the normal dispersion described approximately by (A.6) takes place. A specific feature of such dispersion is that the derivative $\left[{\partial\epsilon_{\parallel}^{(0)}}/ {\partial \omega}\right]_{\epsilon_{\parallel}^{(0)}=0}$ is considerably less than that of Bernstein modes and for branches of dispersion curves with anomalous dispersion in the hybrid band at $\lambda>s$.

A strong instability is realized at sufficiently great velocities $v_{\rm e}$ of the nonequilibrium electrons ( $v_{\rm e}^2>sv_{\rm T}^2$) when the instability boundary $\lambda_{\rm cr}=(v_{\rm T}^2/v_{\rm e}^2)s^2$ is located in the region of the normal dispersion ( $\lambda_{\rm cr}< s$). Taking into account (B.11) and the fact that the dispersion in the hybrid band changes its sign at $\lambda \sim s$, we conclude that the enhanced radiation at $\omega_{\rm uh}$ (the DPR effect) can occur under the condition:

 \begin{displaymath}\lambda^{\rm opt}<s ~~~~~~~{\mbox{or}}~~~~~ \frac{v_{\rm e}^2}{v_{\rm T}^2}>2\frac{\omega_{\rm p}}{\omega_B}\cdot \end{displaymath} (B.12)

This is illustrated by instability boundaries shown by dotted lines in Fig. A.1. For a rather low mean perpendicular velocity of nonequilibrium electrons $v_{\rm e}/v_{\rm T}=4$ the DPR effect doesn't exist.

The peak increment weakly depends on the harmonic number s if the conditions (B.8)-(B.12) are valid. Actually it is mainly determined by the minimum of the function $\varphi'(k_{\perp}^2v_{\rm e}^2/v_{\rm T}^2)$ which doesn't change markedly with index s.

It should be also noted that at high harmonics the frequency intervals where the relativistic effects have to be taken into account can occupy a marked part of the hybrid band. In the frequency interval

 \begin{displaymath}\Delta\omega \sim s\omega_B\frac{v_{\rm e}^2}{v_{\rm c}^2}, \end{displaymath} (B.13)

adjacent to the harmonic $s\omega_B$ from below, the non-relativistic consideration given above is not valid. It leads to the fact that the values $k_{\parallel}^{\rm opt}$ determined by (B.10) are beyond the nonrelativistic approximation boundaries: $\vert k_{\parallel}\vert\gg {\omega v_{\rm e}}/{c^2}$. So, when plotting the graphs in Fig. B.1 at these frequencies (dotted lines), instead of $k_{\parallel}^{\rm opt}$ we took the value $k_{\parallel }$ at the boundary of validity limits of nonrelativistic formulas: $k_{\parallel}^{\rm opt} \sim (\omega v_{\rm e}/c^2)$.

We obtain the following peak growth rate for $v_{\rm e}/v_{\rm T}=20$ and the ratio $\omega_{\rm p}/\omega_B\approx s =15$.

 \begin{displaymath}\gamma_{\max}\sim \omega_B\frac{N_{\rm e}}{N_0}\cdot \end{displaymath} (B.14)

This value is one to two orders of magnitude greater than the growth rate of Bernstein modes.

In order to estimate the frequency interval in which the enhanced generation takes place, we refer to the relations (B.5), (B.6) and (A.6). A typical scale of change of the function $\varphi'(\zeta)$, determining the growth rate, is $\Delta\zeta \sim 1$, i.e.

 \begin{displaymath}\frac{\Delta k_{\perp}}{k_{\perp}}\sim \frac{\omega_B^2}{2k_{\perp}^2 v_{\rm e}^2}\cdot \end{displaymath} (B.15)

On the other hand, it follows from the dispersion relation (A.6) valid not quite close to harmonics, that at a given frequency  $\omega_{\rm uh}$ (at given electron density and magnetic field) the relative bandwidth is:

 \begin{displaymath}\frac{\delta \omega}{\omega_B}\sim \frac{3k_{\perp}^2 v_{\rm T}^2}{s\omega_B^2}\frac{\Delta k_{\perp}}{k_{\perp}}\cdot \end{displaymath} (B.16)

Combining (B.15) and (B.16) we have:

 \begin{displaymath}\frac{\delta\omega}{\omega_B}\sim \frac{3}{2s}~~~~\frac{v_{\rm T}^2}{v_{\rm e}^2}\cdot \end{displaymath} (B.17)

This means that the frequency interval of the plasma waves excited in a fixed point occupies a negligibly small part of the distance $\omega_B$ between the neighboring harmonics. The computation results shown in Fig. B.1 confirm the qualititative conclusion that the frequency interval of enhanced generation (greater growth rate) is much less than $\omega_B$. The bandwidth of the excited waves is determined by the inhomogeneity of the medium in the source.

The dependence of the maximum growth rate (over all $\lambda$) on the ratio $\omega_{\rm uh}/\omega_B$ (that is, on the position of the upper hybrid frequency inside the hybrid band) shown in Fig. B.1b is explained as follows. If $\omega_{\rm uh}$ is far from $s\omega_B$ and $(s-1)\omega_B$, in the region of the normal dispersion the derivative in the denominator in (B.3) varies only slightly with $\omega_{\rm uh}$ (at great s). When $\omega_{\rm uh}$ approaches the lower boundary of the hybrid band $(s-1)\omega_B$, the growth rate increases due to the multiplier $[\omega-(s-1)\omega_B]$ in $\mbox{Im}\epsilon_{\parallel}^{(1)}$, written similarly to (B.7) for the harmonic s-1.At the upper boundary of the hybrid band ( $\omega_{\rm uh}\sim s\omega_B$) the growth rate doesn't increase or increases only slightly since in the interval $(s-\omega/\omega_B)< s(v_{\rm e}^2/c^2)$the non-relativistic approximation for  $k_{\parallel}^{\rm opt}$ (B.10) breaks and the value zs in (B.7) markedly decreases. When $\omega_{\rm uh}$ is close to $s\omega_B$ or $(s-1)\omega_B$, the dispersion curves approach the harmonics. Then in the expression for  $\epsilon_{\parallel}^{(0)}$ (A.4) the resonance term involving the multiplier $(\omega^2-s^2\omega_B^2)^{-1}$ or $(\omega^2-(s-1)^2\omega_B^2)^{-1}$ dominates. As a result, the value $\partial\epsilon_{\parallel}^{(0)}/ \partial\omega$ increases sharply, leading to the decrease of the growth rate in a small region around points $\omega_{\rm uh}=s\omega_B$ and $\omega_{\rm uh}=(s-1)\omega_B$.


Copyright ESO 2003