- ... structures
![[*]](/icons/foot_motif.gif)
- Appendices A and B are only available in electronic form at http://www.edpsciences.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... source
![[*]](/icons/foot_motif.gif)
- A third way to explain BBP is the non-linear
pulsating stage of instability (Trakhtengertz 1968; Zaitsev 1970; Kuijpers
1978).
We don't consider this approach for our event of interest because we would
obtain BBP with too short periods (milliseconds, Zaitsev & Zlotnik 1986).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... level
![[*]](/icons/foot_motif.gif)
-
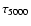 is an
optical depth in the line
is an
optical depth in the line
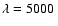 A. At the level
A. At the level
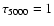 the conductivity is isotropic.
the conductivity is isotropic.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exist
![[*]](/icons/foot_motif.gif)
- Electron acceleration due
to magnetic field reconnection in several small regions within a flaring flux
tube was analyzed by Kuijpers (1981). Such a mechanism provides sporadic
acceleration of electrons.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... and
![[*]](/icons/foot_motif.gif)
- Cross section of the pulsation source
at the trap apex.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
frequency
![[*]](/icons/foot_motif.gif)
- Unlike the Appendices here and hereafter the term
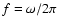 is used instead of
is used instead of 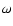 for convenient comparison with
observations.
for convenient comparison with
observations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... electrons
![[*]](/icons/foot_motif.gif)
- for example
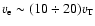 at harmonics
at harmonics
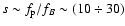 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- As it will be seen
later, in the source of ZP the inequality
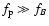 or
or 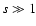 is
fulfilled. That is why the dependence
is
fulfilled. That is why the dependence
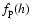 instead
of
instead
of
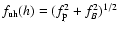 is plotted in this figure.
is plotted in this figure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... too
![[*]](/icons/foot_motif.gif)
- Correspondingly, the negative
and wave-like drift of zebra stripes given for example in Elgaroy (1961) can be
associated with the increase of the magnetic field or plasma heating in the
source volume.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)
![[*]](/icons/foot_motif.gif)
- The density
shouldn't be considered as an extrapolated value of
electron density at h=0 because, obviously, the temperature is
not constant along the loop, being much lower towards its foot; it is a local
parameter without large scale importance.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
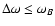
![[*]](/icons/foot_motif.gif)
- Winglee & Dulk (1986) considered
only the first order corrections over the small parameters
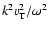 in the "thermal'' dielectric tensor. That
corresponds to neglecting the important resonance term in
(A.4).
in the "thermal'' dielectric tensor. That
corresponds to neglecting the important resonance term in
(A.4).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1975)
![[*]](/icons/foot_motif.gif)
- The basic reference is
Zheleznyakov & Zlotnik (1975). We will not refer to it repeatedly but it is
relevant for most details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
effects
![[*]](/icons/foot_motif.gif)
- It should be
emphasized that in the nonrelativistic
approach the instability
determined by the pole in the denominator
in (B.4) is due to grouping and re-distribution of
electrons over longitudinal velocities
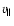 under
the action of a wave field, though the distribution
(B.1) over
under
the action of a wave field, though the distribution
(B.1) over
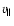 is an equilibrium function.
In this case the reversal of the sign of the right side of
(B.4) is due to
is an equilibrium function.
In this case the reversal of the sign of the right side of
(B.4) is due to
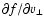 .
The
Doppler shift is a necessary detail of such an instability, and it
was this effect in the nonrelativistic approach that was supposed as the cause
of the instability responsible for the ZP. The statement that in this work the
Doppler shift was neglected (as made by Winglee & Dulk 1986)
is a misunderstanding.
.
The
Doppler shift is a necessary detail of such an instability, and it
was this effect in the nonrelativistic approach that was supposed as the cause
of the instability responsible for the ZP. The statement that in this work the
Doppler shift was neglected (as made by Winglee & Dulk 1986)
is a misunderstanding.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.