A&A 410, 337-341 (2003)
DOI: 10.1051/0004-6361:20030959

Astrometry from mutual events of Jovian satellites in 1997[*]

R. Vasundhara1 - J.-E. Arlot2 - V. Lainey2 - W. Thuillot2


1 - Indian Institute of Astrophysics, Bangalore, India
2 - Institut de mécanique céleste et de calcul des éphémérides - Observatoire de Paris, UMR 8028 CNRS, 77 avenue Denfert-Rochereau, 75014 Paris, France

Received 5 February 2003 / Accepted 16 April 2003

Abstract
Astrometric results of observations of the mutual events of the Galilean satellites of Jupiter of the PHEMU97 campaign by the Institut de Mécanique Céleste et de Calcul des Éphémérides are presented. These astrometric positions can be directly utilized in the construction of future ephemerides. We attempt here to compare the residuals of the relative astrometric positions of satellites with respect to the E3, G5, E5 and L1 ephemerides. The model to fit the observed light curves includes the intensity variations on the surface of satellites using the mosaics constructed by the teams at the US Geological Survey from Voyager and Galileo imagery.

Key words: occultations - eclipses - planets and satellites: general - astrometry - ephemerides

1 Introduction

The four major satellites of Jupiter occult and eclipse each other twice during the orbital period of Jupiter of about 11.6 yrs. The astrometric results of mutual events are capable of yielding accuracies of the order of $0\hbox{$.\!\!^{\prime\prime}$ }03$. This data set therefore has great potential in studies of secular variations in mean motion of the satellites. Of utmost importance is the evaluation of $\dot{n}_1/n_1$ (Aksnes & Franklin 2001; de Sitter 1928; Goldstein & Jacobs 1986; Goldstein & Jacobs 1995; Greenberg et al. 1986; Lieske 1998; Vasundhara et al. 1996). Addition of the mutual event data of the 1997 apparition to the earlier series of 1973, 1979, 1985 and 1991 apparitions will extend the existing time base of these data sets from 18 yrs (1973-1991) to 24 yrs. Such a data set will be helpful to re-investigate the secular variation of the mean motion of these satellites. We present here the astrometric positions derived by fitting the mutual event light curves collected during the observational campaign PHEMU97. These may be directly utilized for further upgrading the ephemerides.

2 Observations

The observations of the mutual events were made in 1997, taking opportunity of the transit of the Sun and the Earth through the equatorial plane of Jupiter. At that time, a large number of mutual occultations and eclipses occurred. These observations were carried out photometrically to obtain the light curves to determine the magnitude drop during the events. Each observation has been carefully referred to UTC, allowing astrometric use. Since the events occurred at specific dates, we organized a worldwide campaign of observations allowing to record 275 light curves for 148 events from 42 sites. All these data will be published in a catalogue and are available at the website of the Institut de Mécanique Céleste et de Calcul des Éphémérides[*]. In the past, we used these observations only to evaluate the shift of the dynamical model. However, a photometric analysis made for astrometric purposes will provide results of high interest.

3 Photometric astrometry

The light curves were fitted using the model presented in Vasundhara (1994). Hapke's photometric function with corrections for macroscopic roughness (Hapke 1984) was used to describe the limb darkening on the satellites for the occultation events. The values of the Hapke's parameters were adopted from McEwen et al. (1988) for Io and from Domingue & Verbiscer (1997) for the other satellites. For the eclipse events, the gradient of the penumbral intensity may play a more dominant role in determining the shape of the light curves than the variations in limb darkening due to surface roughness. These light curves were therefore modeled assuming a smooth photometric function (Hapke 1981) to evaluate the limb darkening. The intensity variations on the surface of the satellites were taken into account by using the mosaics of the satellites constructed using Voyager and Galileo imagery made by various groups. The mosaics of Io at 5 km/pixel through green and near infrared filters (NIR) were constructed by Geissler et al. (1999) using images obtained by Galileo's Solid State Imaging System (SSI) at lowest phase angles ranging from $0\hbox{$.\!\!^\circ$ }5$ to $13 \hbox{$.\!\!^\circ$ }9$. A simple Lunar-Lambert phase dependent photometric function from McEwen (1991) was used to account for limb darkening. The medium phase angle images ( $4 \hbox{$.\!\!^\circ$ }1{-}4 \hbox{$.\!\!^\circ$ }9$) were directly mosaicked while the low phase angle ( $0\hbox{$.\!\!^\circ$ }5$) and higher phase angle ( $13 \hbox{$.\!\!^\circ$ }9$) images were corrected to account for variation with phase angle by these authors. For Europa, the mosaic constructed by the United States Geological Survey (USGS) team using Voyager 1 & 2 and Galileo images was used. Their image processing included corrections for limb darkening using modified Hapke function and normalizing brightness variations due to differences in Sun angle and viewing geometry (Phillips et al. 1997). Considering the lower contrast of features on Europa, a lower resolution of 8 km/pixel was considered adequate. The mosaics of Ganymede (at 2 km/pixel) and Callisto (at 4 km/pixel) constructed by the USGS team were down loaded from the website of the United States Geological Survey, Astrogeology Program, Flagstaff, Arizona[*]. The construction of the mosaics as described by Becker et al. (1999) involved radiometric calibration, photometric normalization by applying the Lunar-Lambert values that were derived from empirical fits to Hapke's functions (McEwen 1991). All these mosaics are thus well calibrated and ideally suited for modeling low phase angle ground based observations as in the present case.

The impact parameter and the time difference between the observation and the prediction were derived as free parameters by fitting the observed light curves to the model using "Grid Search'' technique (Bevington 1969). In case of occultations and also for eclipse events close to opposition the two satellites are very close in the aperture for photometry using photoelectric photometry as well as aperture photometry of CCD data. Ideally, the contribution of the two satellites should be measured just before/after the event. This was not carried out in the majority of the cases. Hence the contribution "r'' of the eclipsing/occulting satellite to the total flux

r=IS1/(IS1+IS2) (1)

was determined as a third parameter, where IS1 and IS2 are the sky subtracted flux measurements of the eclipsing/occulting satellite and eclipsed/occulted satellites respectively. The fitted parameter "r'' (Eq. (1)) should in principle absorb the uncertainty in the sky measurements. The solutions converged within 6-8 iterations for the good quality light curves. The impact parameter "IP'' and "r'' both influence the depth of the light curve. The former also influences the duration of the light curve. As the relative velocity between the two satellites for occultations and the velocity of the eclipsed satellite relative to the shadow center for eclipses can be determined accurately from theory, "IP'' and hence "r'' are determined without ambiguity except in case of very noisy light curves. As the model takes into account the shift in the light center on the satellite from the geometric center due to intensity variations on the surface of the satellite due to phase effects (Aksnes et al. 1986), the fitted time shift is a direct measure of the delay/advance in longitude at the time of geometric conjunction as compared to predictions using the E3 (Lieske 1987). The time

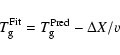\begin{displaymath}T_{\rm g}^{\rm Fit}$ $ =$ $ T_{\rm g}^{\rm Pred} - \Delta X/v \end{displaymath} (2)

gives the fitted time of close approach of the geometric centers of the two satellites for occultations and the time of close approach of the eclipsed satellite to the shadow center for eclipses, where v is the velocity of the occulted (eclipsed) satellite relative to the occulting (eclipsing) satellite. The fitted $\Delta X$ in the above equation represents the shift of the computed curve along the time axis required to fit the observations. The fitted astrometric results for different sets of events are given in Table 1. The date of the event is given in Col. 1. Following the normal practice of designating the events, the code 1E2 indicates that Io eclipses Europa. Similarly, 1O2 denotes the occultation of Europa by Io. The derived value of $T_{\rm g}^{\rm Fit}$, fitted impact parameter, IP and $\Delta X$ are given in Cols. 2-4 respectively. The (O-C) in the impact parameter is given in Col. 5. The differential sky plane coordinates $\Delta \alpha \cos {\delta} $ and $\Delta \delta $of J2000 epoch, in the sense (S2-S1) in arcsec are given in Cols. 6 and 7 respectively. The orbital longitudes $\phi 1$ and $\phi 2$ of the occulting/eclipsing and occulted/eclipsed satellites, geocentric for occultations and heliocentric for eclipses are given in Cols. 8 and 9 respectively. The site of observations are given in the last column.


  \begin{figure} \par\includegraphics[width=11cm,clip]{ranw.ps} \end{figure} Figure 1: O-C in $(\Delta $ RA $\cos(\delta))$ with respect to E3, G5, E5 and L1 respectively. Smaller points indicate eclipses and the larger ones occultations.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=10.2cm,clip]{decnw.ps} \end{figure} Figure 2: O-C in $\Delta \delta $ with respect to E3, G5, E5 and L1. Smaller points indicate eclipses and the larger ones occultations.
Open with DEXTER


  \begin{figure} \mbox{\includegraphics[width=6cm,clip]{geo1.ps}\hspace{4mm} \incl... ....ps}\hspace{25mm} \includegraphics[width=4cm,clip]{labelfig3.ps} }\end{figure} Figure 3: Satellite positions at the time of events involving different pairs of satellites during the mutual event series of 1997.
Open with DEXTER

4 Comparison with theory

The (O-C) in differential coordinates $\Delta \alpha \cos {\delta} $ and $\Delta \delta $of the pairs of satellites are plotted in Figs. 1 and 2 respectively with respect to E3, G5, E5 and L1 (see references below). The symbols used for the different events are as follows: 1E2: open triangles, 1O3/1E3: stars, 1E4: open stars. 2E1: filled triangles, 2O3: open circles, 3O1/3E1: crosses, 3O2/3E2: filled circles, 3O4/3E4: open hexagons, 4O1/4E1: filled hexagons, 4O2/4E2: open squares and 4O3/4E3: filled squares. Due to differences in the data sets that went into generation of these ephemerides, it is of interest to look for existence of general trends if any, in the residuals. For instance, Lieske progressively updated Sampson's (1921) theory starting from E1 (Lieske 1977) using the eclipse data of 1878-1903 to generate E2 (Lieske 1980) by adding visual eclipses between 1903 and 1972, photographic data between 1967 and 1978, and mutual events of 1973. The E3 (Lieske 1987) ephemerides was derived by further mutual event pairs from 1979, 183 pairs of data from Voyager optical navigation images and 15 711 classical eclipses from 1652-1983. Arlot (1982) used 8856 individual photographic observations between 1891 to 1978 to derive the G5 ephemeris. The E5 sets of constants were derived by Lieske by adding to the data set the mutual event astrometric positions of 1985 and 1991, recent photographic observations from Pascu (1994) covering 1980-1991 and Jovian eclipse timings. Lainey (2002) used all the observations used in the construction of G5, 200 photographic positions by Pascu (1994) made during the years 1986 to 1990, astrometric positions of the 1985 and 1991 mutual event series, and 200 CCD observations from Flagstaff (Stone & Harris 2000; Stone 2001) to construct the first version of the ephemerides L1. Thus, a comparison of E3 with E5 will help to investigate the influence of mutual events in the construction of new ephemerides and the ability of the dynamical model to fit all the data. The ephemeride G5 was generated using only photographic data, hence its comparison with E3 and G5 will be interesting to see how the eclipse timings and the mutual event data have influenced E3 and E5.

5 Interpretations and conclusions

Unlike the mutual events of the 1991 series which were predominant in the 2O1/2E1 events, the present series provided a good opportunity to record events between different pairs of satellites. The longitude of the satellites at the time of the events are shown in Fig. 3. The same symbols are used for different events as used in Figs. 1 and 2. The mean and rms of the residuals in the relative right ascensions and declinations are given in Table 2. The rms of the residuals with respect to the four ephemerides are very nearly the same for different pairs of satellites . The light curves were also fitted without considering the intensity variations due to surface features (model-WOIV). The rms residuals of the fits using this model are marginally larger compared to the corresponding values derived using the model-WIV by $ \sim$ $ 0 \hbox{$.\!\!^{\prime\prime}$ }01$ i.e. $ \sim$35 km. This is much lower than the rms of the residuals which are in the range $ 0 \hbox{$.\!\!^{\prime\prime}$ }05{-}0 \hbox{$.\!\!^{\prime\prime}$ }07$. It may be noted that the light curves were obtained by a diverse section of observers and instruments, errors in the observed depths of the light curves are transmitted in the determination of the impact parameters. Although as mentioned in Sect. 3, the parameter "r'' was derived as a free parameter to take into account these uncertainties, fits using the model-WIV will help in better constraining this parameter and the impact parameter compared to the fits using the model-WOIV because the former takes into advantage the subtle asymmetries in the light curves due to surface features. The full potential of this model can best be realized with high quality light curves, as the genuine asymmetries may otherwise be lost in noise.

Interesting trends in the residuals of the relative right ascensions between different pairs of satellites compared to the ephemerides E3, G5, E5 and L1 (Sect. 4) are noticed. The events involving J4 are delayed by $ 0\hbox{$.\!\!^{\prime\prime}$ }1048$ compared to E3. Lowest residuals are obtained with respect to G5 both in right ascension and declination. Thus J4 related events appear to be best represented by G5 and closely followed by L1.

As shown in Figs. 1 and 2, O-C in RA and Dec with respect to these four ephemerides for the occultation and eclipse events between Io and Ganymede (1O3/1E3 and 3O1/3E1) do not differ significantly. On the other hand, significant differences are noticed for the eclipse events between Io and Europa (1E2 and 2E1) These are more for the former type of events, which occurred when Io was closer to western elongation and hence the timings of the events are more susceptible to the constants of Europa (Fig. 3).

In any given mutual event series, as the inter-combination of events is limited, inclusion of data sets of several apparitions will help to simultaneously improve the constants of motions of these satellites. The astrometric positions presented in the present work will therefore substantially increase the mutual event data set. Improvements in the residuals by including the intensity variations on the surface of the satellites in the fit to the light curves has been demonstrated in the present investigation. A re-analysis of all the mutual event light curves of the previous series using this model will help in removing systematic shifts in the relative right ascensions of a given satellite pair, which otherwise might be misinterpreted as real longitude residuals.

Acknowledgements
This work has been made possible thanks to all the observatories where observations were made and has been supported by CNRS and PNP (Programme National de Planétologie).

References

  
Online Material

Table 1: Astrometric results of the 1997 events.

Table 2: Residuals.


Copyright ESO 2003