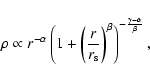 |
(1) |
A&A 408, 27-38 (2003)
DOI: 10.1051/0004-6361:20030922
M. Le Delliou1,2 - R. N. Henriksen1
1 - Queen's University, Kingston, Ontario, K7L 3N6, Canada
2 -
Observatoire de Lyon, 69000 Saint Genis-Laval, France
Received 31 March 2003 / Accepted 10 June 2003
Abstract
The self-similar infall model (SSIM) is normally discussed in the
context of radial orbits in spherical symmetry. However it is possible
to retain the spherical symmetry while permitting the particles to
move in Keplerian ellipses, each having the squared angular momentum
peculiar to their "shell''. The
spherical "shell'', defined for example by the particles turning at a given radius, then
moves according to the radial equation of motion of a "shell''
particle. The "shell'' itself has no physical existence except as an
ensemble of particles, but it is convenient to sometimes refer to the shells
since it is they that are followed by a shell code.
In this note we find the distribution of squared angular momentum as a
function of radius that yields the NFW density profile for the final
dark matter halo. It transpires that this distribution is amply
motivated dimensionally. An effective "lambda'' spin
parameter is roughly constant over the shells. We also study the effects
of angular momentum on the relaxation of a dark matter system using
a three dimensional representation of the relaxed phase space.
Key words: cosmology: theory - dark matter - large-scale structure of Universe - galaxies: halos - galaxies: formation - galaxies: evolution
The radial Self-Similar Secondary Infall model (SSIM:
FG84,Moutarde et al. 1995,HW99) predicts a "one-sided attractor'' final
density profile according to (but see (Hoffman & Shaham 1985) for a slightly
different dependence on the cosmological spectral index)
Recently Lokas & Hoffman (Lokas & Hoffman 2000) have studied the consequences of abandoning the self-similar aspect of the SSIM in favour of an adiabatic invariant calculation, and of introducing a more detailed form of the initial power spectrum. However the self-similarity has been found to arise naturally in most shell code simulations (i.e. it is not an assumption) and in any case the results of Lokas & Hoffman are very close to those cited above for the SSIM. The authors conclude by suggesting that it is prominently the presence of angular momentum that flattens the central cusp.
Indeed numerous authors have emphasized the effect of an isotropic velocity dispersion (thus of non-radial motion) in the core of collisionless haloes. Thus (Huss et al. 1999b)'s Fig. 17 shows an NFW-type density cusp flattening relative to the isothermal profile just where the velocity dispersion changes from predominantly radial to isotropic. This flattening doesn't appear, in (Huss et al. 1999a), for the case of pure radial force. A similar result was obtained by (Tormen et al. 1997), and (Teyssier et al. 1997) who also found that singular isothermal profiles arise during radial infall while isotropic velocity dispersions are associated with flatter profiles. Similarly, Moutarde et al. (Moutarde et al. 1995) correlate flat density profiles with higher dimensionality of the available phase space during infall and they confirm the natural development of self-similarity after turn-around. Thus we are motivated to consider a simple extension of the SSIM that includes the effects of angular momentum (i.e. of each orbiting particle producing in general a smooth velocity "anisotropy'' - the limits being purely radial or spherically symmetric in velocity space - at each point on a spherical "shell'').
Such a spherical model corresponds strictly neither to reality nor to the 3D N-body simulations of cosmological dark halo fields, which display marked non-sphericity (e.g. in Huss et al. 1999a; Huss et al. 1999b; Moutarde et al. 1995; Teyssier et al. 1997; Tormen et al. 1997). Some groups have even proposed a triaxial density profile to replace the spherical (NFW) fit (Jing & Suto 2002). We can regard the spherical model as the result of a kind of "coarse-graining'' or averaging in angle, but it remains unclear in principle whether the averaging before the evolution as done here is equivalent to the averaging after the evolution as done in the simulations (NFW). In practice we simply examine to what extent the respective profiles agree.
Various authors (Ryden & Gunn 1987; White & Zaritsky 1992; Ryden 1993; Subramanian et al. 1999a; Subramanian 1999b; Sikivie et al. 1997![]() )
have treated degrees of velocity anisotropy (orbital angular momentum) in the
SSIM and found hints of shallow inner density cusps, and in at least
one case
links between the NFW inner slope and isotropic velocities
(Ryden & Gunn 1987)
were found. However none of these semi-analytic treatments followed
the system through relaxation by phase mixing and instability
(HW99,Merrall 2003) to its final form. In Ryden (1993) the spherical
symmetry was broken and the final phase space was studied but the
particle orbits were confined to poloidal planes. Nevertheless slightly flatter
spherically averaged density profiles were found which may reflect
the correlation with higher dimensionality found above (Moutarde et al. 1995). We pursue
the possible effects of general velocity anisotropy here by the use of a
spherically-symmetric shell code, whose only constraint is that
the angular momentum should be zero averaged over shells.
)
have treated degrees of velocity anisotropy (orbital angular momentum) in the
SSIM and found hints of shallow inner density cusps, and in at least
one case
links between the NFW inner slope and isotropic velocities
(Ryden & Gunn 1987)
were found. However none of these semi-analytic treatments followed
the system through relaxation by phase mixing and instability
(HW99,Merrall 2003) to its final form. In Ryden (1993) the spherical
symmetry was broken and the final phase space was studied but the
particle orbits were confined to poloidal planes. Nevertheless slightly flatter
spherically averaged density profiles were found which may reflect
the correlation with higher dimensionality found above (Moutarde et al. 1995). We pursue
the possible effects of general velocity anisotropy here by the use of a
spherically-symmetric shell code, whose only constraint is that
the angular momentum should be zero averaged over shells.
In fact the system is made up of particles on elliptical orbits that lie in planes through the centre of the system and are isotropically distributed in angle at any point on a sphere. Thus the vector angular momentum on the sphere is zero. A spherical "shell'' may be defined as the set of particles at a given radius that are all at the same phase in their orbits. It might be the turn-around or apocentric phase for example. Subsequently the shell comoves with the same set of particles according to the radial equation of motion of a particle.
Because of the spherical symmetry, angular momentum has to be introduced to the particles ad hoc, after which it is conserved. This was done in (White & Zaritsky 1992) by introducing a heuristic source term that switches off at turnaround, or in another context simply by assigning an angular momentum distribution at turn-around time (Sikivie et al. 1997).
In this work, two forms of angular momentum are assigned at the turn-around of a given set of particles. It is convenient subsequently to speak of this angular momentum squared as being assigned to a shell, but the reality is as described above. In the next section, we will briefly explain our implementation of angular momentum in the SSIM. The effect on the density profile will be shown in Sect. 3. Section 4 will focus on other consequences for the SSIM's relaxation. A brief discussion regarding mass-angular momentum correlation will be presented in Sect. 5 before a concluding discussion (Sect. 6).
We seek a natural way of assigning the particle angular momentum on a shell "a priori'' so that our eventual agreement with the NFW density profile should not simply be an empirical fit. There are two possibilities which seem rather natural to us. The first one is to assign that distribution of angular momentum over the "shells'' which allows the generalized self-similarity described by Henriksen (Henriksen 1989) to hold until shell crossing. Unfortunately this self-similarity does not carry through into the virialized system by way of a constant logarithmic derivative of the turn-around time with respect to the turn-around radius as in (FG84) or in (HW99). In fact rather than yielding a prediction for the final density profile in terms of the assigned magnitude of angular momentum as might be anticipated, we find that the permitted magnitude is so small that no essential change is produced in the relaxed density profile. This distribution will be referred to as the self-similar angular momentum profile or SSAM.
The second distribution that we consider and the one that seems to produce the most satisfying results physically is simply that given by dimensional analysis in a spherically symmetric self-gravitating system. This is simply a power law distribution and will be referred to as the power law angular momentum profile or PLAM.
Following (Henriksen 1989) the radial equation of motion may be written in
the "Friedman'' form
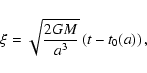
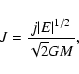 |
(6) |
The solution to Eq. (3) before shell crossing and
up to turn-around is
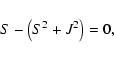 |
(8) |
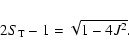 |
(9) |
The expression for the initial mass inside radius r for a constant density background
perturbed by a power law
![]() is
is
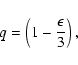
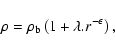
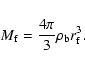
We calculate the initial specific energy of a shell in a de Sitter
cosmology after the addition of the angular momentum as
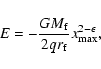 |
(15) |
The mass at this self-similar cut-off is
fortunately large compared to the fiducial mass as it becomes (11)
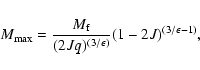 |
(16) |
In this section we consider the simplest initial distribution of angular
momentum (that is a correlation with the initial mass as above) that may be expected on dimensional grounds. This is the
Keplerian form (the specific rotational kinetic energy is a fixed
fraction J2 of the specific binding energy)
Once again the angular momentum distribution can not be maintained
beyond an outer scale ![]() where now
where now
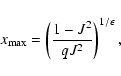 |
(19) |
In the numerical work below we present examples for
![]() ,
the "shallow'' case and for
,
the "shallow'' case and for
![]() ,
the "steep'' case. For the
SSAM J is essentially the specific spin parameter (
,
the "steep'' case. For the
SSAM J is essentially the specific spin parameter (
![]() )
and calculations
were carried out with
)
and calculations
were carried out with
![]() for the shallow
case and with
for the shallow
case and with
![]() for the steep case. These
values are rather small compared to the median value of
for the steep case. These
values are rather small compared to the median value of
![]() reported in (Peebles 1993). This shows clearly the limitations
imposed by this angular momentum distribution together with the
constraint of forming a core.
reported in (Peebles 1993). This shows clearly the limitations
imposed by this angular momentum distribution together with the
constraint of forming a core.
For the PLAM distribution, J2 is actually rather larger than the spin
parameter wherever x/a is small. The values used for J2 were
10-3 for the shallow case and
![]() in the steep case. These are much closer to the
values for the spin parameter found in cosmological simulations. If
J2 is taken much larger than these values the outermost shells
did not reach the center. In this latter event the core displayed
isolated phase mixing "islands'' (Sikivie et al. 1997).
in the steep case. These are much closer to the
values for the spin parameter found in cosmological simulations. If
J2 is taken much larger than these values the outermost shells
did not reach the center. In this latter event the core displayed
isolated phase mixing "islands'' (Sikivie et al. 1997).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{H4419F1.EPS}
\end{figure}](/articles/aa/full/2003/34/aah4419/Timg69.gif) |
Figure 1:
"Power law'' angular momentum (PLAM): density profiles
for critical values of the angular momentum near the end of the self-similar
quasi-equilibrium phase in the shallow (
|
| Open with DEXTER | |
We use a shell code with a semi-analytic treatment of the energy calculation (Le Delliou 2001) to follow the development of the dark matter halo through the shell crossing phase. This code has been well tested elsewhere (Le Delliou 2001) and is known to reproduce standard results (HW99).
As was indicated above the SSAM distribution did not produce density
profiles that were significantly different from those found in pure
radial infall. In particular the relations between the power law index
of the initial density perturbation ![]() and the final density
power law in the bound core were the same as those found for radial
infall (FG84,HW99). Thus we do not present these results
here.
and the final density
power law in the bound core were the same as those found for radial
infall (FG84,HW99). Thus we do not present these results
here.
The PLAM initial distribution with the parameters given above evolved to cores having the density profiles shown in (Fig. 1). The time indicated on the figures is that defined in (HW99) and refers to the logarithmic time near the end of the self-similar infall "equilibrium'' phase.
The figure shows that both in the steep and shallow case the profile is no longer well fit by a power law even in the intermediate regions. Rather there is a smoothly varying convexity in the logarithmic slope that is well fit by the indicated NFW profile except in the most central regions. There a flattening occurs that is more pronounced than is accounted for by the NFW profile. Flattening is anticipated relative to the self-similar slope on general thermodynamic grounds in the coarse-graining study of (Henriksen & Le Delliou 2002), and the presence of a central point mass (perhaps imitated here by numerically smoothed density cusps) can produce such flattened cusps (Nakano & Makino 1999). Unfortunately our numerical resolution is too poor in this core region to say that this flattening is a physically significant result.
We also show piecewise power law fits in
various regions of the figure in order to emphasize the inadequacy of a global power law
fit. One sees moreover that the apparent slope does tend toward
r-3 in the external regions. The theoretical power law slope for
undisturbed radial infall is 2.0 for the shallow case and
![]() for the steep case. Neither of these values fits
the whole density profile of these cores.
for the steep case. Neither of these values fits
the whole density profile of these cores.
We note that the force "smoothing'' length
![]() occurs near the
mid-point of the indicated spatial range. This does not affect the
validity of the density profile inside this radius however as was
established numerically and by coarse graining in (Henriksen & Le Delliou 2002)
for pure radial infall. Their interpretation of the results in terms
of "turn-round'' relaxation of the shells is unchanged by the present extention of phase
space dimensionality since, as seen in Sect. 4,
relaxation still takes place mostly outside of the "smoothing'' length
(Le Delliou 2001). However even if the relaxation argument still holds,
it cannot be made to predict the exact slope of the NFW profile. We shall
examine in detail the NFW profile dependence on resolution in Sect.
3.2.
occurs near the
mid-point of the indicated spatial range. This does not affect the
validity of the density profile inside this radius however as was
established numerically and by coarse graining in (Henriksen & Le Delliou 2002)
for pure radial infall. Their interpretation of the results in terms
of "turn-round'' relaxation of the shells is unchanged by the present extention of phase
space dimensionality since, as seen in Sect. 4,
relaxation still takes place mostly outside of the "smoothing'' length
(Le Delliou 2001). However even if the relaxation argument still holds,
it cannot be made to predict the exact slope of the NFW profile. We shall
examine in detail the NFW profile dependence on resolution in Sect.
3.2.
Our results ought to be compared to the results of the similar study of Hozumi et al. (Hozumi et al. 2000). These authors also investigate the effect of smoothly anisotropic velocity distributions (but with zero net angular momentum on shells, just as in our case) on the density profile. Instead of using a shell code however, they integrate the CBE directly starting from non-equilibrium power law density distributions. Moreover they initiate their calculation with an "ad hoc'' distribution function that is simply a Gaussian in each of the radial and azimuthal velocities, each Gaussian having different dispersions. In contrast we have started our simulations in this work from actual cosmological initial conditions radially, on which we have imposed rather natural distributions of angular momentum. The effect is that our collapse begins from a well-defined surface in phase space.
Despite the differences in the initial conditions, we observe that the
conclusions drawn in the two works are rather similar. Their parameter
![]() is essentially our parameter J-2 (our radial specific
kinetic energy is essentially GM/r) which we have taken in
the range
100-1000 for the favoured PLAM. Although the largest value used
in their paper is
is essentially our parameter J-2 (our radial specific
kinetic energy is essentially GM/r) which we have taken in
the range
100-1000 for the favoured PLAM. Although the largest value used
in their paper is
![]() ,
because our ratio of kinetic energy to
binding energy (
,
because our ratio of kinetic energy to
binding energy (
![]() )
is much closer to
unity than is theirs, the calculations are more comparable than it
might seem. Hozumi et al. have not fitted their profiles with a NFW
curve, but their
conclusions about the central flattening resemble ours. This suggests
that particle angular momentum is indeed playing a role in determining the
density profiles of dark matter halos, and hence of galaxies.
)
is much closer to
unity than is theirs, the calculations are more comparable than it
might seem. Hozumi et al. have not fitted their profiles with a NFW
curve, but their
conclusions about the central flattening resemble ours. This suggests
that particle angular momentum is indeed playing a role in determining the
density profiles of dark matter halos, and hence of galaxies.
We conclude then in this section that the PLAM of Eq. (20) does yield the NFW density profile over most of a dark matter halo. Moreover the required amplitude of the angular momentum does not need to exceed that likely to be provided by tidal interactions. The PLAM places the embryonic halo particles on a surface in phase space which may therefore reveal something of the tidal fields they experience near turn-around.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H4419F2.EPS}
\end{figure}](/articles/aa/full/2003/34/aah4419/Timg76.gif) |
Figure 2:
Smaller smoothing length
|
| Open with DEXTER | |
The motivation in (Moore et al. 1999) for proposing an alternate universal profile to the NFW profile is based on their observation of a resolution dependence of the inner slope. This resolution problem was also pointed out in the studies by (Jing & Suto 2000). (Moore et al. 1999) claim that their results show that the inner slope converges towards their proposed profile.
We have tested our results under changes in resolution using two different "smoothing'' lengths.
Similarly to the results of (Moore et al. 1999), an increase in resolution
in our model steepens the profile. This can be measured by the increase
of the concentration factor c ![]() when the "smoothing'' length is reduced, as seen in Fig. 2.
Nevertheless, contrary to (Moore et al. 1999), the NFW profile is still
the best fit, provided the appropriate change in concentration factor
has been performed.
when the "smoothing'' length is reduced, as seen in Fig. 2.
Nevertheless, contrary to (Moore et al. 1999), the NFW profile is still
the best fit, provided the appropriate change in concentration factor
has been performed.
We interpret these results in terms of the centrifugal
acceleration at a given radius between the two "smoothing'' lengths: thus
its regularised expression in the model reads
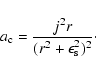
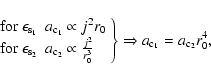
Therefore resolution appears to fix the magnitude of the NFW profile's concentration parameter c. Nevertheless, we have established that the addition of angular momentum to CDM haloes transforms the single power-law density profile into two slope NFW type profile.
We begin by considering the
![]() projection of phase space and the
corresponding virial ratios, for comparison with the well-known radial
results (HW99). These are shown in Figs. 3 and 4 for the SSAM and
the PLAM respectively. In each figure the "shallow'' and "steep''
initial profiles are displayed, although these in fact show little
difference in behaviour. In our simulations we used "equal mass
modeling'' of the "shells''.
projection of phase space and the
corresponding virial ratios, for comparison with the well-known radial
results (HW99). These are shown in Figs. 3 and 4 for the SSAM and
the PLAM respectively. In each figure the "shallow'' and "steep''
initial profiles are displayed, although these in fact show little
difference in behaviour. In our simulations we used "equal mass
modeling'' of the "shells''.
In (HW99), the shell modeling used smaller masses for inner shells than for outer shells in order to improve the dynamical mass resolution at the beginning of the infall. This allowed for the SSIM's quasi-equilibrium self similar state to be achieved almost as soon as the core forms, to the detriment of an accurate phase space description that is our objective here. The use of constant mass shells leads to a relatively coarser mass resolution in the central part of the halo, which part corresponds to the set of shells that first forms the core, and so the quasi-equilibrium state is not achieved as gracefully. In fact this choice results in a poor modeling of the constant self-similar mass flux needed to maintain self-similarity during the accretion of innermost shells into the core. Each new shell acts almost as an overdensity perturbation to the previously established core and disturbs it from self-similar equilibrium until it is "digested'' (Le Delliou 2001). Thus the equal mass modeling simulation requires an initial period of stabilization to reach the self-similar quasi-equilibrium. This period should be roughly the time to accrete the shell of the unequal mass modeling simulation that possesses the same mass as the constant mass used here. This conjecture was successfully tested.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4419F3.EPS}
\end{figure}](/articles/aa/full/2003/34/aah4419/Timg86.gif) |
Figure 3:
SSAM: virial ratios and phase space projections
in the radius/radial velocity plane near the end of the self-similar
quasi-equilibrium phase for critical values of the angular momentum
in the shallow (
|
| Open with DEXTER | |
The phase space projections (the lower panels of Figs. 3 and 4 display the phase space distribution of shells in the radius-radial velocity plane) reveal that there remains a stream of outer particles for which the angular momentum is so large that they will never fall into the core (their rotational kinetic energy makes them unbound). Indeed, since the initial angular momentum distribution for the particles is monotonically increasing with radius, and since the angular momentum is conserved exactly throughout the simulations including the initial radial ordering until shells reach the core; so near the end of the self-similar phase, the shells with increasingly large angular momentum are contributing to the mass flux. Given higher and higher angular momentum, there is a point at which angular momentum induces an inner turn around radius at the size of the self-similar core. Particles with smaller angular momentum will be able to enter the core but with a reduced radial velocity compared with the purely radial radial SSIM. This gradual extinction of the mass flux due to increasing particle angular momentum (velocity anisotropy) gradually shifts the system from its intermediate quasi-static phase to its final virialized phase.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4419F4.EPS}
\end{figure}](/articles/aa/full/2003/34/aah4419/Timg87.gif) |
Figure 4:
"Power law'' angular momentum (PLAM): virial
ratios and phase space projections in the radius/radial velocity plane
near the end of the self-similar quasi-equilibrium phase for critical
values of the angular momentum in the shallow (
|
| Open with DEXTER | |
Comparing the phase space projections of the SSAM and the PLAM in Figs. 3 and 4 respectively we note that the SSAM seems less homogeneous. The exploration of the 3D phase space in Sect. 4.3 will confirm the impression that the SSAM is less relaxed in phase space during the accretion phase.
Considering the way resolution affects the virial ratio and
![]() projection of phase space, the previous remarks on the system's relaxation
can be extended.
projection of phase space, the previous remarks on the system's relaxation
can be extended.
The previous stabilisation delay for equal mass "shell'' modeling is increased when using the reduced "smoothing'' length. Here this period encompasses almost all of the self-similar phase (Fig. 5's upper panels). Nevertheless, the right panel indicates that there still is an interval where the virial ratio is slowly decreasing from a higher value than 1.
We interpret this interval as due to the increase in the maximum acceleration felt by shells in the central parts of the halo: the scattering of shells is then much stronger, which makes it more difficult for the system to settle down. To minimise this inertial noise, the mass resolution should follow the "smoothing'' length reduction. We adopted an optimum balance between the mass, force and time resolutions found by trial and error.
It is remarkable that the noise in the virial ratio (Fig. 5) is diminished with the "smoothing'' length: if on one hand the equilibrium is achieved slower, it is on the other hand of a more stable final nature. Thus even if the mass flux resolution is not sufficient to account for the stabilisation delay, it still provides a good basis of understanding the relaxed system.
Adding to this picture, the phase space of the smaller
![]() simulation appears more relaxed than its larger
simulation appears more relaxed than its larger
![]() counterpart; the relaxation region at the edges of the system restricts
itself to the first outer stream and all traces of the phase space
mixing sheets washes out (Fig. 5's
lower right and left panels). Such relaxation explains why the smaller
counterpart; the relaxation region at the edges of the system restricts
itself to the first outer stream and all traces of the phase space
mixing sheets washes out (Fig. 5's
lower right and left panels). Such relaxation explains why the smaller
![]() simulation's phase space is slightly wider in
radial velocity and narrower in radius. This also shows in the more
concentrated smaller
simulation's phase space is slightly wider in
radial velocity and narrower in radius. This also shows in the more
concentrated smaller
![]() NFW fit (Fig. 2).
NFW fit (Fig. 2).
In the light of N-body studies such as that of Knebe et al. (Knebe et al. 2000),
inaccuracy in the dynamics from two body scattering excludes "smoothing''
lengths much smaller than that used in our regular simulations, at given
mass resolution. The mass resolution limitations on accuracy as well
as the smoothing-length-time-step relation shed light on the low smoothing
length cut off![]() .
.
The nature of relaxation in the SSIM leads to the density profile being trustworthy even below its "smoothing'' length, but only a few times above its mass resolution characteristic length. This is caused by the fact that relaxation in the SSIM essentially occurs in the few dynamical times that particles are freshly incorporated into the self-similar core, mainly around the secondary turnaround radii, i.e. near the radial boundary of the core.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4419F5.EPS}
\end{figure}](/articles/aa/full/2003/34/aah4419/Timg95.gif) |
Figure 5:
Smaller smoothing length
|
| Open with DEXTER | |
All of the phase space maps presented are measured at T=12 which corresponds to a clear end of the self-similar infall phase and beginning of the isolated system virialised phase.
This section explores the nature of the mass distribution in the radius-radial
velocity-angular momentum phase space for systems with a shallow (
![]() )
initial density profile. The SSAM and PLAM models are both presented here
for comparison purposes.
All of these phase space maps are measured at T=12 which corresponds
to a clear end of the self-similar infall phase and the beginning of the
isolated system virialized phase. To get a complete
sense of the topology of the winding and relaxation of the original
Liouville stream of Hubble flow shells, we use tilted projections of the
(
X,Y, j2) space. We recall that initially, with the power law
distribution of angular momentum and the Hubble radial velocity, the
particles lie on a curve in this phase space.
)
initial density profile. The SSAM and PLAM models are both presented here
for comparison purposes.
All of these phase space maps are measured at T=12 which corresponds
to a clear end of the self-similar infall phase and the beginning of the
isolated system virialized phase. To get a complete
sense of the topology of the winding and relaxation of the original
Liouville stream of Hubble flow shells, we use tilted projections of the
(
X,Y, j2) space. We recall that initially, with the power law
distribution of angular momentum and the Hubble radial velocity, the
particles lie on a curve in this phase space.
Figure 6, denoted from top left to bottom right (a), (b) and (c), allow for a finer analysis of the final state: (a) shows a clear relaxation. The core appears to be rather smoothly populated in this projection. Figure 6b displays more clearly the outer phase mixing streams. The most striking fact that is made clear in Fig. 6c is that the relaxed shells lie on a thin surface in phase space: this is a 2-dimensional sheet in the shape of a soaring bird, the neck and beak pointing toward large radius and angular momentum, while the high velocity wings spread progressively over higher and higher values of j2. The accumulation of shells at low radius forms a flat basin.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.4cm,clip]{H4419F6A.PS}\hsp...
...udegraphics[angle=-90,width=7.9cm,clip]{H4419F6C.PS}\hspace*{4cm}}\end{figure}](/articles/aa/full/2003/34/aah4419/Timg97.gif) |
Figure 6:
Phase space exploration using the "power
law'' form of angular momentum near the end of the self-similar quasi-equilibrium
phase (shallow initial density contrasts
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H4419F7A.PS}\hsp...
...cludegraphics[angle=-90,width=8cm,clip]{H4419F7C.PS}\hspace*{4cm}}\end{figure}](/articles/aa/full/2003/34/aah4419/Timg98.gif) |
Figure 7:
Phase space exploration using the self-similar
form of angular momentum near the end of the self-similar quasi-equilibrium
phase (shallow initial density contrasts
|
| Open with DEXTER | |
The existence of the phase space surface found in the previous section
implies correlations in the various projections. Recently one group has reported finding a universal
angular momentum profile in N-body simulations in terms of a halo's
cumulative mass (Bullock et al. 2001) according to
(Bullock et al. 2001) also find
a power law describing the correlation between angular momentum
and radially cumulative mass (
![]() where M=M(<r)and
where M=M(<r)and
![]() ). For this reason we consider these
correlations in the two systems of the previous section in order to
determine whether our choice of initial angular momentum is
compatible with these simulations.
). For this reason we consider these
correlations in the two systems of the previous section in order to
determine whether our choice of initial angular momentum is
compatible with these simulations.
Dimensional analysis and
the definition of the final density profile as
![]() leads one to approximate the self-similar model's relaxed state with power
laws for the angular momentum (
leads one to approximate the self-similar model's relaxed state with power
laws for the angular momentum (
![]() )
and
for the mass profiles (
)
and
for the mass profiles (
![]() ). Thus, s can be predicted to be
). Thus, s can be predicted to be
![]() .
In turn the
SSIM gives the index
.
In turn the
SSIM gives the index ![]() as a function of the initial index
as a function of the initial index ![]() as:
as:
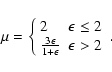
![\begin{figure}
\par\includegraphics[width=17.1cm,clip]{H4419F8.EPS}
\end{figure}](/articles/aa/full/2003/34/aah4419/Timg112.gif) |
Figure 8: Two angular momentum profiles and their correlations. |
| Open with DEXTER | |
Empirically, the previous section's phase space structure warns us
that a correlation
M - j2 may not be most readily
found from
a simple regression on all shells. Instead we might try to fit just the
correlation from the projected mean surface about which the shells are
distributed.
The projection of phase space into the
j2-X plane forms a caustic that appears to be a reasonable
measure to compare with the predicted angular momentum profile. Figure 8 illustrates the angular
momentum profile correlations: the thin continuous lines are mere
power law fits to all of the particles, and their values do
not reflect the self-similar calculations. By contrast, a
![]() fit to the phase space caustic verifies the predictions for the
shallow case. We have not investigated for this note the steep case but have
no reason to believe the results would be different. Moreover, the density
profiles show some steepening
on the outer edges of the halo (Fig. 1),
which translates into evidence for a flattening of the mass profile,
hence of the mass-angular momentum profile as in Eq. (21).
fit to the phase space caustic verifies the predictions for the
shallow case. We have not investigated for this note the steep case but have
no reason to believe the results would be different. Moreover, the density
profiles show some steepening
on the outer edges of the halo (Fig. 1),
which translates into evidence for a flattening of the mass profile,
hence of the mass-angular momentum profile as in Eq. (21).
These results are remarkable in that they rest on the idea that the
dimensional angular momentum distribution used initially (17)
also obtains in the ultimate halo. The same thing is true for the
SSAM. Consequently the final correlation
![]() merely reflects the
universality of the density profile in the intermediate ranges for the
initially "flat'' density perturbation.
merely reflects the
universality of the density profile in the intermediate ranges for the
initially "flat'' density perturbation.
In this note we have studied the effects of particle angular momentum on the density profile and phase space structure of the final halo in the Self-Similar Infall Model (SSIM) for the formation of dark matter halos. We have used a simple shell code since the angular momentum averaged over each sphere is zero. We find the NFW profile to be an excellent fit to the density profile produced when an initial angular momentum distribution provided by simple dimensional arguments (PLAM) is assigned. This fit holds until the very central regions where extra flattening is expected on thermodynamic grounds (this flattening probably proceeds to a Gaussian with sufficient resolution, Henriksen & Le Delliou 2002).
In addition we have shown that the initial line in phase space develops into a fairly well defined surface in phase space in the final halo. The "ridge'' or cusp of this surface when projected into angular momentum- position space is also predicted by the same dimensional argument. It seems then that some memory of the initial correlation between position and angular momentum is retained in the final object.
An alternate distribution of initial angular momentum (SSAM) that was designed to maintain strict self-similarity until shell crossing produces a less relaxed final phase space distribution (at the same dimensionless time) that is rather less precisely distributed on a 2D surface in the phase space. It is not able to reproduce the NFW density profile, perhaps because of the reduced relaxation (as displayed by the higher dimensionality in the final phase space).
The question as to whether the successful angular momentum
distribution (PLAM) is actually established by tidal effects remains
unanswered here. It essentially requires the rotational kinetic energy
acquired by each halo particle to be a fixed fraction of the local
halo gravitational potential. That the local gravitational potential
should be an upper limit is clear, but it is not obvious why there
should be a fixed fraction for all shells. One might assign J2 as a
random variable about some mean to see how sensitive the results are
to a fixed value in the manner of (Sikivie et al. 1997).
However a coarse graining over the shells would tend
to produce the same mean independent of r and so we would expect a
similar coarse-grained result to what we have found here.
In fact
Ryden & Gunn (Ryden & Gunn 1987) do give the expected rms angular
momentum distribution with mass for Gaussian random primordial
perturbations. Their Fig. 10 suggests a
linear relation in the range of masses that interests us here. This
agrees approximately with our Eq. (20) when ![]() is close
to 2 at moderate radii.
is close
to 2 at moderate radii.
However although the results of the n-body simulations are
usually given as spherical averages, it is not evident that this gives
the same result as the strictly spherically symmetric calculation
reported here. Nevertheless the agreement with the results of Bullock
et al. (Bullock et al. 2001) is encouraging in this sense, even though they may not contain all of the relevant physics (van den Bosch et al. 2002; Chen & Jing 2002)![]() .
.
Acknowledgements
RNH acknowledges the support of an operating grant from the canadian Natural Sciences and Research Council. M LeD wishes to acknowledge the financial support of Queen's University, Université Claude Bernard - Lyon 1 and Observatoire de Lyon, and to thank Stéphane Colombi for stimulating discussions.