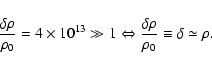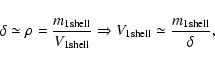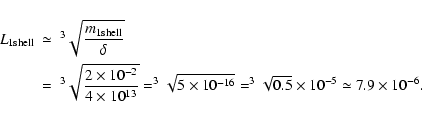- ...1997
![[*]](/icons/foot_motif.gif)
- The focus of (Sikivie et al. 1997) was on indentifying velocity streams from non spherically-symmetric
angular momentum distributions. Although the same geometry as used
here was employed, a (FG84, Bertschinger 1985)-type one particle
integration was used which assumes strict self-similar phase mixing
and so is insensitive to phase
space instability.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... SSIM
![[*]](/icons/foot_motif.gif)
- The approach from the force equation in (Sikivie et al. 1997) yields a slightly
different self-similar constraint for the angular momentum:
where
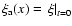 is obtained with
the combination of Eqs. (10), (13)
and S=x/a and we identify our conventions with
is obtained with
the combination of Eqs. (10), (13)
and S=x/a and we identify our conventions with

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- The NFW profile in terms of critical density, density and radial scales
reads
with
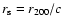 defining the concentration factor and
the two scales correlated through (see (NFW))
defining the concentration factor and
the two scales correlated through (see (NFW))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... off
![[*]](/icons/foot_motif.gif)
- An example calculation: the constant mass of one shell is given in
the simulation's unit as
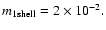 The maximum
density contrast in Fig. 2 can be taken as
The maximum
density contrast in Fig. 2 can be taken as
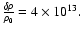 Because of its high
value, the density contrast, denoted
Because of its high
value, the density contrast, denoted 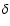 in this note, can
be identified with the density itself
in this note, can
be identified with the density itself
Thus, the volume of innermost shells can be evaluated as
so the characteristic length scale of a shell in the centre is given
by
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Chen & Jing 2002)
![[*]](/icons/foot_motif.gif)
- After we completed this work, the results from Hiotelis (2002) have come to our attention, that are similar to ours in the case of a same value for
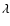 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
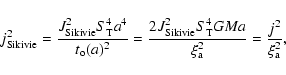
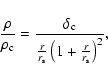
![\begin{displaymath}\delta _{\rm c}=\frac{c^{3}}{\left[ \ln (1+c)-\frac{c}{1+c}\right] }\cdot\end{displaymath}](/articles/aa/full/2003/34/aah4419/img79.gif)