A&A 408, 387-400 (2003)
DOI: 10.1051/0004-6361:20030911
On transformation between international celestial and terrestrial
reference systems
P. Bretagnon 1 - V. A. Brumberg2
1 - Institut de mécanique céleste et de calcul des
éphémérides, 75014 Paris, France
2 - Institute of Applied Astronomy, 191187 St. Petersburg, Russia
Received 19 February 2003 / Accepted 16 May 2003
Abstract
Based on the current IAU hierarchy of the relativistic reference systems,
practical formulae for the transformation between barycentric (BCRS) and geocentric (GCRS)
celestial reference systems are derived. BCRS is used to refer to ICRS, International
Celestial Reference System. This transformation is given in four versions, dependent on the
time arguments used for BCRS (TCB or TDB) and for GCRS (TCG or TT). All quantities
involved in these formulae have been tabulated with the use of the VSOP theories (IMCCE
theories of motion of the major planets)![[*]](/icons/foot_motif.gif) . In particular,
these formulae may be applied to account for the indirect
relativistic third-body perturbations in motion of Earth's
satellites and Earth's rotation problem. We propose to use the SMART theory (IMCCE theory of Earth's rotation) in constructing
the Newtonian three-dimensional spatial rotation transformation
between GCRS and ITRS, the International Terrestrial Reference
System. This transformation is compared with two other versions
involving extra angular variables currently used by IERS, the
International Earth Rotation Service. It is shown that the
comparison of these three forms of the same transformation may be
greatly simplified by using the proposed composite rotation
formula
. In particular,
these formulae may be applied to account for the indirect
relativistic third-body perturbations in motion of Earth's
satellites and Earth's rotation problem. We propose to use the SMART theory (IMCCE theory of Earth's rotation) in constructing
the Newtonian three-dimensional spatial rotation transformation
between GCRS and ITRS, the International Terrestrial Reference
System. This transformation is compared with two other versions
involving extra angular variables currently used by IERS, the
International Earth Rotation Service. It is shown that the
comparison of these three forms of the same transformation may be
greatly simplified by using the proposed composite rotation
formula![[*]](/icons/foot_motif.gif) .
.
Key words: relativity - reference systems - time
Recent IAU (2000) Resolution B1 (IAU 2001) on reference
systems and time scales involves much more profound use of general
relativity theory (GRT) in ephemeris astronomy compared to the IAU
(1991) Resolution A4 (see the explanatory supplement by Soffel et al. (2003) and the discussion on implementation of this
resolution in (IERS 2002). However, there still exists some
confusion in using the time scales TDB and TCB, TT and TCG, and in
GRT-consistent interpretation of ICRS and ITRS, the two main
reference systems (RSs). The aim of this paper is to present
explicitly the transformation ICRS
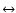 ITRS as
prescribed by the IAU Resolution B1(2000).
ITRS as
prescribed by the IAU Resolution B1(2000).
For astronomical practice it is sufficient to have only the reference systems ICRS and ITRS
with their physical realizations given by the reference frames ICRF and ITRF, respectively.
In the GRT framework, ICRS represents a four-dimensional Barycentric Celestial Reference System (BCRS) whereas ITRS represents a local four-dimensional geocentric system rotating with the
Earth. For the relationship between BCRS and ITRS it is necessary to introduce one more local
geocentric system with the same time scale, TCG, as used for ITRS and the same directions of
the spatial axes as for BCRS. Such a Geocentric Celestial Reference System (GCRS) is
introduced by the IAU Resolution B1.3 (2000). GCRS represents a system kinematically
non-rotating with respect to BCRS. This system rotates dynamically with respect to BCRS.
The angular velocity of this rotation has a relativistic order of smallness
and is caused by the motion of the geocentre around the solar system barycentre.
Indeed, the four-dimensional transformation from the barycentre to the geocentre can transform
any barycentric system BRS either into DGRS, a geocentric system dynamically non-rotating
with respect to BRS, or into KGRS, a geocentric system kinematically non-rotating with
respect to BRS. GCRS represents just such a KGRS suitable for astrometric purposes. The systems
of DGRS type are more preferable for celestial mechanics
enabling one to deal with the geocentric equations of motion without the terms caused by the
rotation of the system. One should note also that the classical concepts of ephemeris astronomy
and the system of astronomical constants are based on Newtonian mechanics with its absolute
time and absolute space. In Newtonian astronomy
such concepts are invariant under the transformation from the barycentre to the geocentre and
vice versa. Such invariance
does not take place in relativistic astronomy. To avoid possible confusion one has to go
beyond the framework of ICRS and ITRS systems.
One of the possibilities (not unique, of course) is to consider
several reference systems at the barycentric and geocentric levels
(Brumberg et al. 1996; Brumberg 1997).
At the barycentric level, along with ICRS (BCRS) one may
consider ecliptical BRSC and equatorial BRSQ systems. Their main
planes are chosen to coincide with planes of the ecliptic and
equator fixed for J2000.0. The coordinate time scale of all these
four-dimensional systems is 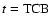 .
Their spatial coordinates
are designated in this paper by
.
Their spatial coordinates
are designated in this paper by
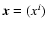 ,
,
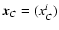 and
and
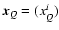 ,
respectively. At the geocentric level each
of these three system involves two geocentric systems, dynamically (D) or kinematically (K) non-rotating with respect to the
corresponding barycentric system. As a result one has at the
geocentric level six geocentric systems DGRS, KGRS, DGRSC, KGRSC,
DGRSQ and KGRSQ. They all have (within the post-Newtonian
approximation) the coordinate time scale u=TCG. Their spatial
coordinates are designated below by
,
respectively. At the geocentric level each
of these three system involves two geocentric systems, dynamically (D) or kinematically (K) non-rotating with respect to the
corresponding barycentric system. As a result one has at the
geocentric level six geocentric systems DGRS, KGRS, DGRSC, KGRSC,
DGRSQ and KGRSQ. They all have (within the post-Newtonian
approximation) the coordinate time scale u=TCG. Their spatial
coordinates are designated below by
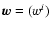 ,
,
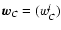 and
and
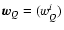 ,
respectively. If necessary,
the spatial coordinates for dynamically (D) or kinematically (K)
non-rotating systems may be distinguished explicitly by
indicating
,
respectively. If necessary,
the spatial coordinates for dynamically (D) or kinematically (K)
non-rotating systems may be distinguished explicitly by
indicating
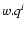 with q=1 for version D and q=0 for
version K. The GCRS system as defined by the IAU Resolution B1.3
(2000) corresponds in these notations to KGRS. VSOP theories of
planetary motion are constructed in BRSC (Bretagnon & Francou
1988). SMART theory of the Earth's rotation (Bretagnon
et al. 1997; 1998) is to be considered
in DGRSC. Since the ecliptic may be defined reasonably only at the
barycentric level, GRSC (in any version) should be regarded just
as another intermediate system between ICRS and ITRS. Quite
similarly, since the equator is defined reasonably only at the
geocentric level, BRSQ should be regarded as one more intermediary
between ICRS and ITRS.
with q=1 for version D and q=0 for
version K. The GCRS system as defined by the IAU Resolution B1.3
(2000) corresponds in these notations to KGRS. VSOP theories of
planetary motion are constructed in BRSC (Bretagnon & Francou
1988). SMART theory of the Earth's rotation (Bretagnon
et al. 1997; 1998) is to be considered
in DGRSC. Since the ecliptic may be defined reasonably only at the
barycentric level, GRSC (in any version) should be regarded just
as another intermediate system between ICRS and ITRS. Quite
similarly, since the equator is defined reasonably only at the
geocentric level, BRSQ should be regarded as one more intermediary
between ICRS and ITRS.
All expressions below are given in the post-Newtonian
approximation within c-2 accuracy.
This section deals with the transformation between the barycentric reference system BRS
(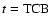 ,
,
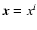 )
and geocentric reference system GRS (
)
and geocentric reference system GRS (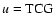 ,
,
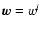 ).
The latter system is considered in both versions, KGRS (q=0) and DGRS (q=1) with explicit
designation, if necessary,
).
The latter system is considered in both versions, KGRS (q=0) and DGRS (q=1) with explicit
designation, if necessary,
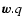 for the corresponding spatial coordinates.
Direct transformation of BRS coordinates xi for instant t to
GRS coordinates wi for instant u reads
for the corresponding spatial coordinates.
Direct transformation of BRS coordinates xi for instant t to
GRS coordinates wi for instant u reads
![\begin{displaymath}u=t-c^{-2}[A(t)+\vec v_E\vec r_E]+\ldots,
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img16.gif) |
(1) |
![\begin{displaymath}w^i=r^i_E+c^{-2}\left[{\textstyle{1\over 2}}\vec v_E\vec r_E
...
..._E r^i_E-{\textstyle{1\over 2}} \vec r_E^2 a^i_E\right]+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img17.gif) |
(2) |
with
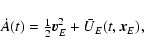 |
(3) |
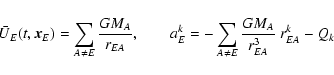 |
(4) |
and
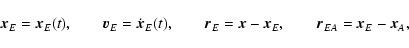 |
(5) |
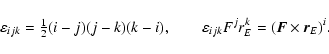 |
(6) |
Within c-2 accuracy
 represents
just the Newtonian potential (in the point-mass approximation) of
all solar system bodies (except the Earth) evaluated at the
geocentre (index A in (4) runs over the Sun, the Moon and
major planets). The Einstein summation rule (from 1 to 3) is
applied everywhere for any twice repeated Latin index unless
indicated otherwise. Functions Qk in the acceleration of the
Earth aEk represent small contributions caused by the
non-geodesic BRS motion of the Earth due to the interaction of
its quadrupole moments (IEmn) and the external masses
represents
just the Newtonian potential (in the point-mass approximation) of
all solar system bodies (except the Earth) evaluated at the
geocentre (index A in (4) runs over the Sun, the Moon and
major planets). The Einstein summation rule (from 1 to 3) is
applied everywhere for any twice repeated Latin index unless
indicated otherwise. Functions Qk in the acceleration of the
Earth aEk represent small contributions caused by the
non-geodesic BRS motion of the Earth due to the interaction of
its quadrupole moments (IEmn) and the external masses
with the comma designating here and below a partial derivative
with respect to the corresponding coordinate xi before the
substitution xi=xiE.
The inverse transformation to transform GRS coordinates wifor instant u to BRS coordinates xi for instant t reads
![\begin{displaymath}t=u+c^{-2}[A(u)+\vec v_E\vec w]+\ldots,
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img24.gif) |
(7) |
![\begin{displaymath}x^i=w^i+z^i_E(u)+c^{-2}\left[{\textstyle{1\over 2}}\vec v_E\v...
...\vec w w^i+{\textstyle{1\over 2}} \vec w^2 a^i_E\right]+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img25.gif) |
(8) |
with the relativistic time equation
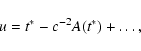 |
(9) |
and the TCG
representation of the motion of the Earth
For direct transformations (1) and (2) one should
know the function A=A(t) by integrating (3) numerically
or analytically. For the inverse transformation (7) and (8) to express the right-hand members in terms of u one
should get function
t*=t*(u) by inverting the equation (9) also in numerical or analytical form. Some analytical
expressions for it will be given below. The Eq. (9)
results from the transformation (7) applied in the
geocentre.
The geodesic rotation vector Fi including geodetic precession,
geodetic nutation and luni-solar-planetary terms (under the
non-rotating point-mass model) is computed by integrating the
expression
![\begin{displaymath}\dot F^i=\sum_{A\not=E}{GM_A \over r_{EA}^3} \left[\left(-{\t...
...\over 2}} \vec
v_E+2\vec v_A\right)\times\vec r_{EA}\right]^i.
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img27.gif) |
(11) |
Indeed, the complete expression for 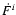 reads (e.g.,
Brumberg 1991)
reads (e.g.,
Brumberg 1991)
or else
where
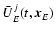 stands for the external
(with respect to the Earth) vector-potential evaluated at the
geocentre. In neglecting in
stands for the external
(with respect to the Earth) vector-potential evaluated at the
geocentre. In neglecting in
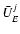 all contributions from
the non-point structure and proper rotations of the bodies one
has
all contributions from
the non-point structure and proper rotations of the bodies one
has
In combination with (4) it results in (11) if one
neglects also the terms with Qk. It presents no difficulties to
take into account the figure and spin dependent terms in the
vector-potential
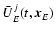 .
Some estimates show
(Vokrouhlický 1995) that solar spin terms may be
significant. However, due to possible uncertainty of such terms we
prefer to use in (11) the model of point masses. Explicit
expressions for
.
Some estimates show
(Vokrouhlický 1995) that solar spin terms may be
significant. However, due to possible uncertainty of such terms we
prefer to use in (11) the model of point masses. Explicit
expressions for
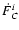 and FiC (geodesic rotation in BRSC) are given in Brumberg & Bretagnon (2001). For
BRSC (ecliptical BRS) and BRSQ (equatorial BRS) one has
and FiC (geodesic rotation in BRSC) are given in Brumberg & Bretagnon (2001). For
BRSC (ecliptical BRS) and BRSQ (equatorial BRS) one has
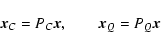 |
(12) |
and matrix relations
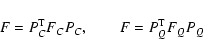 |
(13) |
with the relationships between matrix elements Fij and vector
components Fi as follows:
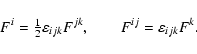 |
(14) |
By comparing IMCCE analytical VSOP theories constructed in BRSC
with JPL numerical ephemerides DE-405 constructed in ICRS one can
estimate the constant rotation matrices PC and PQ (Bretagnon
2002; Bretagnon et al. 2003)
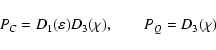 |
(15) |
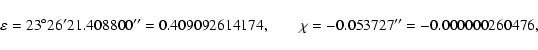 |
(16) |
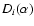 being elementary rotation matrices
being elementary rotation matrices
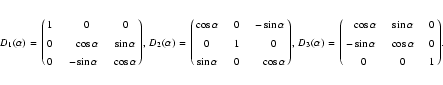 |
(17) |
Both the time-function A(t) and geodetic rotation vector Fi(t) are defined only by means of their time derivatives (3) and (11), respectively, involving additive
arbitrary constants to be determined from complementary
considerations. The necessity to introduce such a constant in A(t) was discussed in detail by Guinot (2000). Guinot
suggested to determine this constant so that t=u on January 1,
1977 0h 0m 0s TAI (
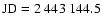 TAI) at the geocentre (1977
Origin) as prescribed by IAU Resolution A4 (1991). In what
follows, the function A(t) is always considered taking into
account this condition.
TAI) at the geocentre (1977
Origin) as prescribed by IAU Resolution A4 (1991). In what
follows, the function A(t) is always considered taking into
account this condition.
In the same manner, one may define a constant value in Fi. But
in this case it is reasonable to take J2000.0 as the fundamental
epoch recommended by IAU (1994) Resolution C7 (the epoch defined
at the geocentre at the date January 1.5, 2000 TT = JD 2451545.0 TT). Indeed, J2000.0 is the fundamental epoch for astronomical
reference systems and it is logically to demand Fi=0 at this
epoch. This value does not affect the relationship between BCRS and GCRS but it is of importance for the definition of DGRSs, i.e.
dynamically non-rotating geocentric systems. The geodetic
rotation vector Fi determines the mutual rotation of DGRS and
KGRS but under the proposed choice of the constant of integration,
these systems coincide at the epoch J2000.0 (the values of FiCin Brumberg & Bretagnon 2001 are given without such
a constant term).
The currently employed time scales satisfy the relations (see, for
example, BDL 1997):
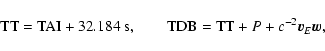 |
(18) |
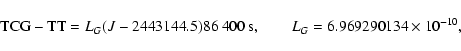 |
(19) |
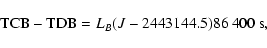 |
(20) |
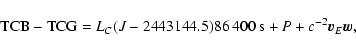 |
(21) |
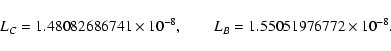 |
(22) |
 values are taken here from IAU
(2001). LG is now fixed by the IAU Resolution B1 (2000)
as a defining constant. By contrast, LC and hence
LB
(=LC+LG-LCLG) depend on specific planetary and lunar theories
employed in integrating (3) and are different for
different sets of planetary and lunar ephemerides. In the next
section we give data based on using VSOP ephemerides involving LC and LB values slightly different from (22). Pin (18) and (21) denotes the quasi-trigonometric
part of function A(t) vanishing at the 1977 Origin (A(t)without its linear secular trend c2LCt). As is well known, TAI
is the only time scale determined in practice from averaging the
readings of the clocks synchronized with respect to TT. In other
words, TAI represents the physical realization of TT.
values are taken here from IAU
(2001). LG is now fixed by the IAU Resolution B1 (2000)
as a defining constant. By contrast, LC and hence
LB
(=LC+LG-LCLG) depend on specific planetary and lunar theories
employed in integrating (3) and are different for
different sets of planetary and lunar ephemerides. In the next
section we give data based on using VSOP ephemerides involving LC and LB values slightly different from (22). Pin (18) and (21) denotes the quasi-trigonometric
part of function A(t) vanishing at the 1977 Origin (A(t)without its linear secular trend c2LCt). As is well known, TAI
is the only time scale determined in practice from averaging the
readings of the clocks synchronized with respect to TT. In other
words, TAI represents the physical realization of TT.
The function A(t) satisfying (3) is presented usually
(Fairhead & Bretagnon 1990; BDL 1997) as
with
|
LCt=LC(J-2443144.5)86400s
|
(24) |
and Ap(t)=P determined either numerically or in the analytical
form
![\begin{displaymath}A_p(t)=\sum_{\alpha}t^\alpha\left[
\sum_{k}A_k^\alpha\cos\left(\psi_k^\alpha+\nu_k^\alpha~t\right)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img49.gif) |
(25) |
It is to be noted that most existing solutions for
this function have been obtained so far in terms of TDB with no
additional constant discussed above (see Fukushima 1995;
Irwin & Fukushima 1999 and references therein).
The representation (23) enables one to transform (9) into
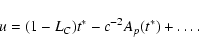 |
(26) |
Therefore, the inversion of (9) may be written either as
or else
|
t*=(1+LC)u+c-2Ap(u).
|
(28) |
These two expressions result in the function (10) in the
form
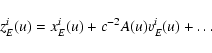 |
(29) |
or
![\begin{displaymath}z_E^i(u)=x^i_E\left[\left(1+L_C\right)u\right]+c^{-2}A_p(u)v^i_E(u)+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img52.gif) |
(30) |
(within the post-Newtonian accuracy one may neglect the
relativistic differences in the arguments of the relativistic
terms). Considering that the functions xiE(t) have in the
present analytical theories the form
![\begin{displaymath}x^i_E(t)=\sum_{\alpha}t^\alpha\left[
\sum_{k}X_{ik}^\alpha\cos\left(\psi_k^\alpha+\nu_k^\alpha~t\right)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img53.gif) |
(31) |
The presentation (30) is more advantageous retaining the LC factor within the arguments of the leading trigonometric
terms. Note again that the analytical ephemerides obtained in BRSC
should be first converted into BCRS in accordance with (15), i.e.
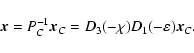 |
(32) |
Hence, returning to the standard designations for the time-scales
one has
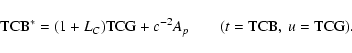 |
(33) |
Instead of TCB and TCG one often makes use of TDB and TT,
respectively, involving the scaling transformations (Brumberg &
Groten 2001a)
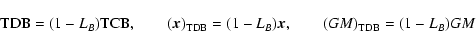 |
(34) |
and
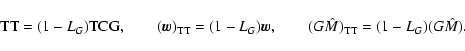 |
(35) |
Therefore, along with (33) one has three more expressions
depending on the employed arguments
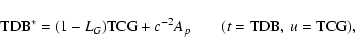 |
(36) |
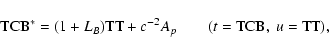 |
(37) |
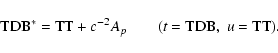 |
(38) |
The asterisk in (33), (36)-(38) has the
same meaning as in (9) relating the BRS event
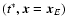 and the GRS event
and the GRS event
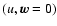 .
To summarize, one has for the BRS
.
To summarize, one has for the BRS
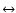 GRS
transformation four versions as follows:
GRS
transformation four versions as follows:
1. BRS with TCB, GRS with TCG:
Direct transformation:
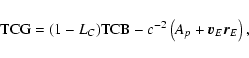 |
(39) |
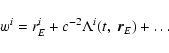 |
(40) |
with
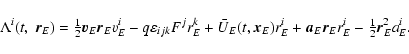 |
(41) |
Inverse transformation:
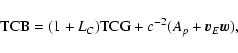 |
(42) |
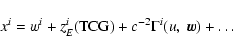 |
(43) |
with
![\begin{displaymath}z_E^i({\rm TCG})=x_E^i({\rm
TCB}^*)=x^i_E\left[\left(1+L_C\right){\rm TCG}\right]+c^{-2}A_pv^i_E+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img68.gif) |
(44) |
and
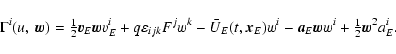 |
(45) |
Since
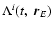 and
and
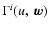 represent post-Newtonian corrections there is no need to
distinguish here between
represent post-Newtonian corrections there is no need to
distinguish here between
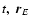 on the one hand and
on the one hand and
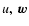 on the other hand. Evidently,
on the other hand. Evidently,
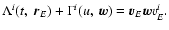
2. BRS with TDB, GRS with TCG:
Direct transformation:
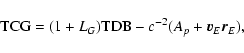 |
(46) |
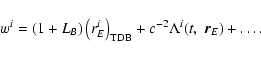 |
(47) |
Inverse transformation:
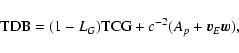 |
(48) |
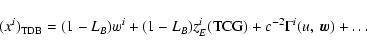 |
(49) |
with
![\begin{displaymath}(1-L_B)z_E^i({\rm TCG})=x_E^i({\rm
TDB}^*)=x^i_E\left[(1-L_G){\rm TCG}\right]+c^{-2}A_pv^i_E+\ldots .
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img79.gif) |
(50) |
3. BRS with TCB, GRS with TT:
Direct transformation:
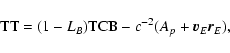 |
(51) |
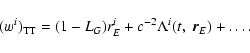 |
(52) |
Inverse transformation:
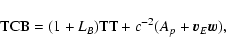 |
(53) |
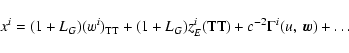 |
(54) |
with
![\begin{displaymath}(1+L_G)z_E^i({\rm TT})=x_E^i({\rm
TCB}^*)=x^i_E\left[(1+L_B){\rm TT}\right]+c^{-2}A_pv^i_E+\ldots .
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img84.gif) |
(55) |
4. BRS with TDB, GRS with TT:
Direct transformation:
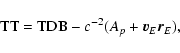 |
(56) |
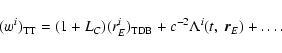 |
(57) |
Inverse transformation:
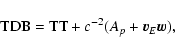 |
(58) |
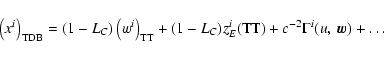 |
(59) |
with
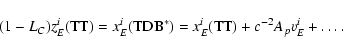 |
(60) |
In all these expressions
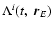 and
and
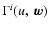 are determined by (41) and (45), respectively. Note that for
BCRS
are determined by (41) and (45), respectively. Note that for
BCRS
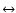 GCRS transformation one should always put
q=0.
It is to be noted that the function ziE(u) determined by one
of four options (44), (50), (55), (60) as well as the similar function
ziA(u)=xiA(t*)determined in the same manner for any body A are of importance
in computing indirect relativistic perturbations in the geocentric
motion of Earth's satellites, Earth's rotation problem
(precession-nutation theory), etc. In such problems, in
neglecting direct relativistic perturbations one has to deal with
Newtonian equations of motion in DGRS where the right-hand
members are functions of u and geocentric position vectors
GCRS transformation one should always put
q=0.
It is to be noted that the function ziE(u) determined by one
of four options (44), (50), (55), (60) as well as the similar function
ziA(u)=xiA(t*)determined in the same manner for any body A are of importance
in computing indirect relativistic perturbations in the geocentric
motion of Earth's satellites, Earth's rotation problem
(precession-nutation theory), etc. In such problems, in
neglecting direct relativistic perturbations one has to deal with
Newtonian equations of motion in DGRS where the right-hand
members are functions of u and geocentric position vectors
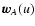 for perturbing bodies A. The coordinates of the
perturbing bodies are known in BRS in terms of time t. Denoting
for perturbing bodies A. The coordinates of the
perturbing bodies are known in BRS in terms of time t. Denoting
and using functions ziE(u),
ziA(u) one may express the geocentric position vectors of the
disturbing bodies as follows (Brumberg 1996):
![\begin{displaymath}w^i_A(u)=z^i_A(u)-z^i_E(u)+c^{-2}\bigl[\Lambda^i\left(t^*,~\vec
r_{AE}\right)+\vec v_E\vec r_{AE}v^i_{AE} \bigr],
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img92.gif) |
(61) |
where
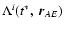 is determined
by (41) replacing
is determined
by (41) replacing 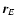 by
by
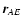 .
This
transformation enables one to take into account in DGRS the
indirect relativistic perturbations and to transform BRS arguments
into GRS arguments.
We have used the VSOP theories to compute the initial terms of the
series for
.
This
transformation enables one to take into account in DGRS the
indirect relativistic perturbations and to transform BRS arguments
into GRS arguments.
We have used the VSOP theories to compute the initial terms of the
series for 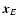 ,
,
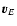 ,
,
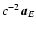 ,
,
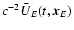 ,
c-2Ap,
,
c-2Ap,
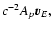 and
and
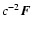 in function of
in function of 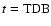 .
These series are to be used to
evaluate explicitly the coefficients in (56)-(60). For the sake of completeness we
computed also the series for
.
These series are to be used to
evaluate explicitly the coefficients in (56)-(60). For the sake of completeness we
computed also the series for
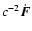 needed when
considering the equations of motion in GCRS. All values have been
computed using the astronomical unit as the unit of length and 1000 Julian years (365250 Julian days) as the unit of time. The
value of LC obtained with the VSOP solution reads
needed when
considering the equations of motion in GCRS. All values have been
computed using the astronomical unit as the unit of length and 1000 Julian years (365250 Julian days) as the unit of time. The
value of LC obtained with the VSOP solution reads
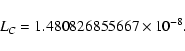 |
(62) |
In integrating the equations for 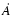 and
and
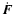 the additive constants were introduced to annul these
quantities for the 1977 Origin and J2000.0, respectively.
the additive constants were introduced to annul these
quantities for the 1977 Origin and J2000.0, respectively.
All series are presented in the form of (31) in Tables
1-20 containing the ordinal number of the term, components of the
trigonometric argument (mean longitudes of eight major planets
from Mercury to Neptune and arguments 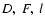 of the lunar
theory as described in (Bretagnon et al. 1988) given
to show the physical meaning of the term, coefficient X, the
phase angle
of the lunar
theory as described in (Bretagnon et al. 1988) given
to show the physical meaning of the term, coefficient X, the
phase angle 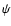 of the argument, the frequency
of the argument, the frequency 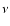 of the
argument and exposant
of the
argument and exposant 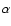 of power of t.
of power of t.
These series are available as Appendix B to the present paper.
If
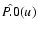 denotes the Earth's rotation matrix
relating ITRS and KGRSC (geocentric kinematically non-rotating
ecliptical reference system) and
denotes the Earth's rotation matrix
relating ITRS and KGRSC (geocentric kinematically non-rotating
ecliptical reference system) and 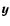 is the triplet of the
spatial coordinates of ITRS then ITRS
is the triplet of the
spatial coordinates of ITRS then ITRS
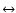 GCRS
transformation has the form (Brumberg & Groten
2001b)
GCRS
transformation has the form (Brumberg & Groten
2001b)
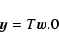 |
(63) |
with
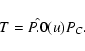 |
(64) |
The rotation matrix
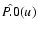 is defined by its three
Euler angles. This representation brings (64) to the form
is defined by its three
Euler angles. This representation brings (64) to the form
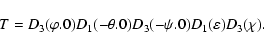 |
(65) |
It is to be noted that the SMART theory involves dynamical Euler
angles of matrix
 relating ITRS and DGRSC
(geocentric dynamically non-rotating ecliptical reference system)
but the transformation between dynamical and kinematical Euler
angles presents no difficulties (Brumberg 1997;
Bretagnon et al. 1997).
relating ITRS and DGRSC
(geocentric dynamically non-rotating ecliptical reference system)
but the transformation between dynamical and kinematical Euler
angles presents no difficulties (Brumberg 1997;
Bretagnon et al. 1997).
On the other hand, along with this "dynamical'' expression coming
from the dynamical treatment of the Earth's rotation problem there
is a "kinematical'' expression (e.g., Moritz & Mueller 1987
and different modifications in IERS documents)
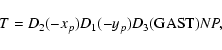 |
(66) |
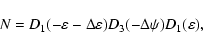 |
(67) |
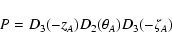 |
(68) |
used in astrometry and IERS programs. Here xp and yp are the
polar motion parameters, GAST stands for the Greenwich Apparent
Sidereal Time, 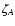 ,
zA and
,
zA and 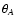 are the equatorial
precession parameters and
are the equatorial
precession parameters and
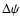 ,
,
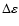 are
the astronomic nutation components in longitude and in obliquity,
respectively. Recently, IAU has recommended to use the
representation of rotation T based on the notion of
"non-rotating origin'' (Capitaine et al. 2000; IERS
2003)
are
the astronomic nutation components in longitude and in obliquity,
respectively. Recently, IAU has recommended to use the
representation of rotation T based on the notion of
"non-rotating origin'' (Capitaine et al. 2000; IERS
2003)
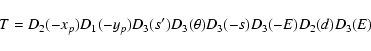 |
(69) |
under standard designations of the indicated papers.
The relationships between the representations (65),
(66) and (69) of the Earth's rotation may be
analysed by using the technique of Folkner et al.
(1994). This technique is based on the rotation formula
![\begin{displaymath}T=R(\vec A),\qquad R(\vec A)\vec x=\vec x-\sin a\left(\hat{\v...
...at {\vec A}\times \left(\hat{\vec A}\times\vec
x\right)\right]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img125.gif) |
(70) |
where
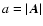 is the rotation angle,
is the rotation angle,
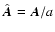 is
the unit vector along the rotation axis,
is
the unit vector along the rotation axis, 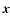 is an arbitrary
coordinate vector, and
is an arbitrary
coordinate vector, and
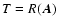 is the matrix of rotation
about the arbitrary axis
is the matrix of rotation
about the arbitrary axis
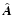 .
With this notation the
elementary rotations (17) will be
.
With this notation the
elementary rotations (17) will be
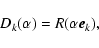 |
(71) |
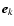 being a unit vector along xk axis. The technique of
Folkner et al. (1994) makes use of two relations
being a unit vector along xk axis. The technique of
Folkner et al. (1994) makes use of two relations
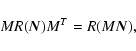 |
(72) |
valid for any rotation matrix M, and
![\begin{displaymath}R(\vec B)R(\vec A)\approx R\bigl[\vec A+\vec B+{\textstyle{1\over 2}}(\vec
A\times\vec B)\bigr],
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img134.gif) |
(73) |
valid for small rotation vectors 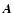 and
and 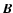 through
second order. Expressions (70)-(73) result from
the theory of rotations of analytical dynamics (e.g., Pars
1965) but to simplify discussion we give their
straightforward derivation in Appendix A. In addition to (73) we will need also the first-order composite rotation
formula
through
second order. Expressions (70)-(73) result from
the theory of rotations of analytical dynamics (e.g., Pars
1965) but to simplify discussion we give their
straightforward derivation in Appendix A. In addition to (73) we will need also the first-order composite rotation
formula
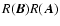 under the assumption that only one
of two vectors
under the assumption that only one
of two vectors 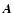 or
or 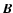 is small. Assuming that vector
is small. Assuming that vector 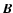 is small these composite first-order (with respect to
is small these composite first-order (with respect to 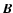 )
formulae read
)
formulae read
![\begin{displaymath}R(\vec B)R(\vec A) = R\Biggl[\vec A+{\displaystyle{a(1+\cos a...
...)\over 2\sin a}}\Biggr)\hat{\vec A}(\hat{\vec A}\vec B)\Biggr]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img138.gif) |
(74) |
and
![\begin{displaymath}R(\vec A)R(\vec B) = R\Biggl[\vec A+{\displaystyle{a(1+\cos a...
...\over 2\sin a}}\Biggr)\hat{\vec A}(\hat{\vec A}\vec B)\Biggr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img139.gif) |
(75) |
These formulae are derived in Appendix A. Combination of (74) and (75) results in the first-order
composition formula for small rotation vectors 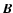 and
and 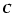
![\begin{displaymath}R(\vec C)R(\vec A)R(\vec B) =
R\Biggl[\vec A+{\displaystyle{a...
...r)\hat{\vec A}\bigl(
\hat{\vec A}(\vec B+\vec C)\bigr)\Biggr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img141.gif) |
(76) |
Let us note also that for small 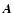 both formulae (74) and (75) result in the simple second-order
formula (73). In representation (65) the three
Euler angles
both formulae (74) and (75) result in the simple second-order
formula (73). In representation (65) the three
Euler angles
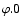 ,
,
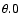 and
and
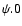 can be determined on the basis of the Earth's
rotation theory such as SMART97 (Bretagnon et al. 1997,
1998). Such theory involves the representation
can be determined on the basis of the Earth's
rotation theory such as SMART97 (Bretagnon et al. 1997,
1998). Such theory involves the representation
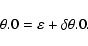 |
(77) |
From the defining expression for D1 we get the first-order
relation
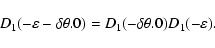 |
(78) |
On the other hand, by applying (72) one gets
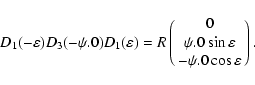 |
(79) |
Therefore, the
transformation matrix (65) can be represented as follows:
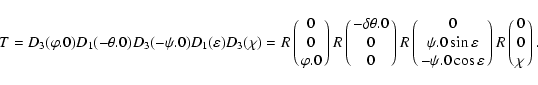 |
(80) |
Considering that the angles
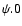 ,
,
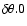 and
and 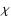 are small one gets with the aid of (73) the
first-order formula
are small one gets with the aid of (73) the
first-order formula
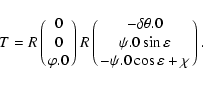 |
(81) |
It reduces to the composite rotation formula (75) with
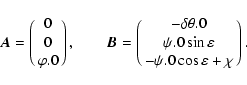 |
(82) |
Now let us return to the classical astrometric transformation,
i.e. (66)-(68). Using again (72) and (73) one may transform it to the product of four rotation
vectors, i.e.
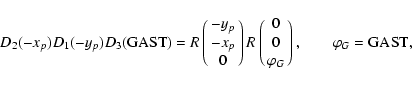 |
(83) |
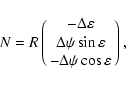 |
(84) |
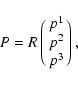 |
(85) |
pi being components of the vector of precession. Multiplication of
these vectors by using (72) results to the first-order
formula
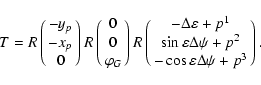 |
(86) |
It reduces to the composite rotation formula (76) with
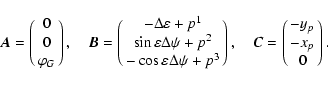 |
(87) |
In using the modern astrometric transformation (69) by
virtue of
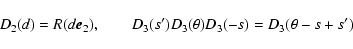 |
(88) |
and
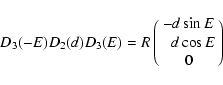 |
(89) |
one has
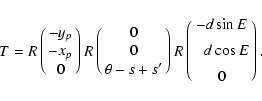 |
(90) |
It reduces to (76) with
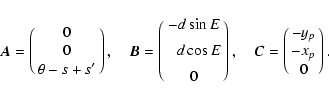 |
(91) |
Finally, for vector 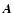 in representation (70) of
transformation (63) one has three first-order expressions
as follows:
in representation (70) of
transformation (63) one has three first-order expressions
as follows:
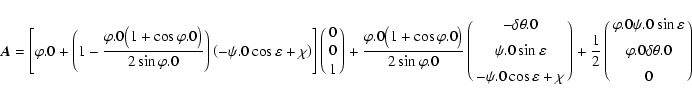 |
(92) |
in the case of (4.3),
in the case of (4.4), and
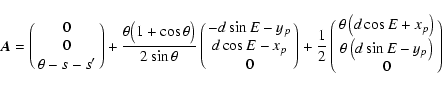 |
(94) |
in the case of (4.7). These three representations of the first
order with respect to the precession/nutation and polar motion
parameters may be useful to estimate different contributions (for
instance, the relativistic ones) in the rigorous general
transformations (65), (66) and (69).
Relations (39)-(60) enable one to get the direct
and inverse transformation between ICRS and GCRS for any of four
pairs of currently employed time arguments (TCG, TCB, TCG and TT).
In combination with relation (61) expressing geocentric
position vectors in terms of barycentric quantities they may be
used to take into account the relativistic third-body
perturbations in the geocentric equations of motion of Earth's
satellites and Earth's rotation equations. The direct and inverse
transformation between GCRS and ITRS is performed now by means of
Newtonian three-dimensional spatial rotations (63) under
equivalent forms (65), (66) or (69). If one
gets with the use of (61) the indirect relativistic
perturbations in the Euler angles relating DGRSC (dynamically
non-rotating geocentric RS)
and ITRS then this
transformation of the Newtonian form will become relativistic by its essence.
Acknowledgements
The participation of Dr. Jean-Louis Simon (IMCCE) in the final completing of this work and
preparing it for publication is greatly acknowledged. The second author is thankful to the
referee Dr. Nicole Capitaine for valuable comments that helped improve the manuscript (VAB).
In this Appendix we derive straightforwardly the relations (68)-(71) used in Sect. 4. The mutual Newtonian
three-dimensional rotation of the spatial axes of two reference
systems
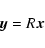 |
(A.1) |
is described by some
orthogonal rotation matrix R. The inverse transformation is
given by the transposed matrix
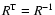 .
The elements of the
rotation matrix satisfy the relations
.
The elements of the
rotation matrix satisfy the relations
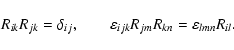 |
(A.2) |
Any rotation matrix may be represented in terms of a
skew-symmetric matrix T as follows (Pars 1965):
|
R=(E-T)-1(E+T)=(E+T)(E-T)-1.
|
(A.3) |
Matrix T is composed of the components of the rotation vector Ti
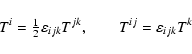 |
(A.4) |
(cf. matrix F and vector Fi of geodetic rotation
(14). The inversion of (A.3) results in
|
T=-(E-R)(E+R)-1=-(E+R)-1(E-R).
|
(A.5) |
The structure (A.4) of matrix T enables one to find easily
the elements of the inverse matrix
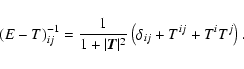 |
(A.6) |
Then from (A.3) one gets the representation of the elements of the
rotation matrix in terms of the corresponding rotation vector
![\begin{displaymath}R_{ij}= {\displaystyle{1\over 1+\vert\vec T\vert^2}}\left[\le...
...vert^2\right)\delta_{ij}+2T^iT^j+2\varepsilon_{ijk}T^k\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img172.gif) |
(A.7) |
The rotation vector admits the representation (Pars
1965)
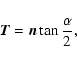 |
(A.8) |
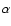 and
and 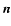 being the rotation angle and unit rotation
vector, respectively. Putting
being the rotation angle and unit rotation
vector, respectively. Putting
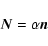 |
(A.9) |
one obtains from (A.7) the
representation of the rotation matrix
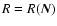 as follows:
as follows:
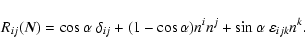 |
(A.10) |
By multiplying both sides by xj one
gets for any rotation vector 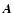
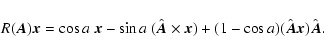 |
(A.11) |
By applying here the formula for the double cross
product one gets (70). For small vector 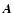 (small
(small
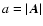 )
there results within the second-order accuracy
)
there results within the second-order accuracy
![\begin{displaymath}R(\vec A)\vec x\approx\vec x-(\vec A\times\vec x)+{\textstyle{1\over 2}} \left[\vec
A\times(\vec A\times\vec x)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img179.gif) |
(A.12) |
The second small rotation 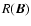 results in
results in
![\begin{displaymath}R(\vec B)R(\vec A)\vec x\approx R(\vec A)\vec x-(\vec B\times...
...ver 2}}\left[\vec B\times(\vec B\times R(\vec A)\vec
x)\right]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img181.gif) |
(A.13) |
or else
![\begin{displaymath}R(\vec B)R(\vec A)\vec x \approx\vec x-(\vec A\times\vec
x)-(...
...s\vec x)\right]+\left[\vec B\times(\vec
A\times\vec x)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img182.gif) |
(A.14) |
After easy vector algebra manipulation the latter relation is
transformed into
![\begin{displaymath}R(\vec B)R(\vec A)\vec x \approx\vec x-(\vec A\times\vec x)-(...
...left[(\vec A+\vec B)\times((\vec A+\vec B)\times\vec
x)\right]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img183.gif) |
(A.15) |
coinciding with the rotation formula
![\begin{displaymath}R(\vec A+\vec B+{\textstyle{1\over 2}} (\vec A\times\vec B))\...
...ft[(\vec A+\vec B)\times((\vec A+\vec B)\times\vec x)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img184.gif) |
(A.16) |
Coincidence of the right-hand members of (A.15) and (A.16) proves (73).
Returning now to the general formula (A.10) and
applying it for rotation about coordinate axes by putting
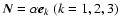 one gets
one gets
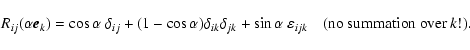 |
(A.17) |
Matrix elements (A.17) are just
elements of the rotation matrices (17) proving (71).
It remains to prove (72). Considering that for
any rotation matrix M, by virtue of (A.2)
one gets from (A.10)
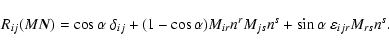 |
(A.18) |
Multiplying both sides by Mjk and using (A.2) one obtains
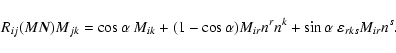 |
(A.19) |
Using (A.10) it is easy to see that the
right-hand member of (A.19) coincides with
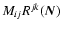 .
Hence,
.
Hence,
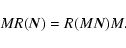 |
(A.20) |
This relation is equivalent to (72).
Let us derive now the composite rotation formulae (74) and (75). Combining the general rotation
formula (70) for any rotation vector 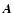 with the
first-order rotation formula for small vector
with the
first-order rotation formula for small vector 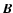
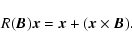 |
(A.21) |
one gets for the sequences of rotations:
If vector 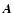 has variation
has variation
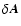 then the variation
of the rotation formula will be
then the variation
of the rotation formula will be
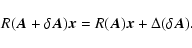 |
(A.24) |
Considering that
one gets from (70)
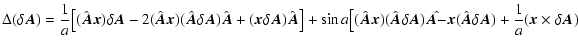 |
|
|
|
![$\displaystyle +{\displaystyle{1\over a}}(\hat{\vec A}\delta\vec A)(\hat{\vec A}...
...c A)\hat{\vec A}- a(\hat{\vec A}\delta\vec A)(\hat{\vec A}\times \vec x)\bigr].$](/articles/aa/full/2003/34/aa3628/img203.gif) |
|
|
(A.25) |
This formula enables one to find three elementary variations as
follows:
![\begin{displaymath}\Delta\bigl(\hat{\vec A}(\hat{\vec A}\vec B)\bigr)=\sin a
(\h...
...]+
\cos a (\hat{\vec A}\vec B)(\vec x\times\hat{\vec A}\bigr],
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img207.gif) |
(A.27) |
and
![\begin{displaymath}\Delta(\hat{\vec A}\times\vec B) = {\displaystyle{1-\cos a\ov...
...l[(\vec B\vec x)\hat{\vec A}-(\hat{\vec A}\vec
x)\vec B\bigr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img208.gif) |
(A.28) |
From these elementary variations it is easy to see that
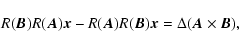 |
(A.29) |
and
![\begin{displaymath}\Delta(\vec B)-\Delta\bigl(\hat{\vec A}(\hat{\vec A}\vec
B)\b...
...\vec
B)+(\hat{\vec A}\vec B)(\hat{\vec A}\times \vec x)\bigr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img210.gif) |
(A.30) |
From (A.28) and (A.30) there results
![\begin{displaymath}\Delta(\vec A\times\vec B) +{\displaystyle{a(1+\cos a)\over \...
...c x-
\Delta\bigl(\hat{\vec A}(\hat{\vec A}\vec B)\bigr)\bigr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img211.gif) |
(A.31) |
Equations (A.31) and (A.29) result in the final composite
first-order (with respect to 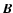 )
formulae (74) and (75).
This Appendix contains the initial terms of the series for
)
formulae (74) and (75).
This Appendix contains the initial terms of the series for 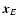 ,
,
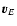 ,
,
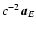 ,
,
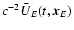 ,
c-2Ap,
,
c-2Ap,
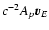 and
and
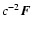 in function
of
in function
of 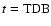 as computed with VSOP theories. These series are to be
used to evaluate explicitly the coefficients in (56)-(60). For the sake of completeness we give
also the series for
as computed with VSOP theories. These series are to be
used to evaluate explicitly the coefficients in (56)-(60). For the sake of completeness we give
also the series for
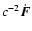 needed when considering
the equations of motion in GCRS. All values are given using the
astronomical unit as the unit of length and 1000 Julian years
(365250 Julian days) as the unit of time. The value of LCobtained with the VSOP solution reads
needed when considering
the equations of motion in GCRS. All values are given using the
astronomical unit as the unit of length and 1000 Julian years
(365250 Julian days) as the unit of time. The value of LCobtained with the VSOP solution reads
In integrating the equations for 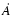 and
and
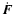 the
additive constants were introduced to annul these quantities for
the 1977 Origin and J2000.0, respectively.
the
additive constants were introduced to annul these quantities for
the 1977 Origin and J2000.0, respectively.
All series are presented in form of (31), i.e.
The data in the 6-column Tables 1-20 read:
ordinal number of the term, components of the trigonometric
argument (mean longitudes of eight major planets from Mercury to
Neptune and arguments 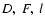 of the lunar theory) given to
show the physical meaning of the term, coefficient X, the phase
angle
of the lunar theory) given to
show the physical meaning of the term, coefficient X, the phase
angle 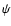 of the argument, the frequency
of the argument, the frequency 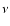 of the argument
and exposant
of the argument
and exposant 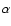 of power of t.
of power of t.
The truncation level is as follows:
0.5 E-03 au over 1000 yrs for 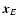 (Tables 1-3),
(Tables 1-3),
0.5 au/1000 yrs over 1000 yrs for 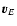 (Tables 4-6),
(Tables 4-6),
0.4 E-12 over 1000 yrs for
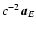 (Tables 7-9),
(Tables 7-9),
0.15 E-12 over 1000 yrs for
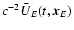 (Table 10),
(Table 10),
0.5 E-16 over 1000 yrs for c-2Ap (Table 11),
0.8 E-12 over 1000 yrs for
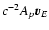 (Tables 12-14),
(Tables 12-14),
0.1 E-12 over 1000 yrs for
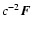 (Tables 15-17),
(Tables 15-17),
0.1 E-8 over 1000 yrs for
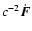 (Tables 18-20).
(Tables 18-20).
-
Bretagnon, P. 2002, Trans. Inst. Appl. Astron., 8, 33
In the text
-
Bretagnon, P., & Francou, G. 1988, A&A, 202, 309
In the text
NASA ADS
-
Bretagnon, P., Rocher, P., & Simon, J. L. 1997, A&A, 319, 305
In the text
NASA ADS
-
Bretagnon, P., Francou, G., Rocher, P., & Simon, J. L. 1998, A&A, 329, 329
In the text
NASA ADS
-
Bretagnon, P., Fienga, A., & Simon, J.-L. 2003, A&A, 400, 785
In the text
NASA ADS
-
Brumberg, V. A. 1991, Essential Relativistic Celestial Mechanics (Bristol: Hilger)
In the text
-
Brumberg, V. A. 1996, in Earth Rotation, Reference
Systems in Geodynamics and Solar System (Journées 1995), ed. N. Capitaine, B. Kolaczek, & S. Debarbat, Warsaw, 29
In the text
-
Brumberg, V. A. 1997, in Dynamics and Astrometry
of Natural and Artificial Celestial Bodies, ed. I. M. Wytrzyszczak, J. H. Lieske, & R. A. Feldman, IAU Coll. 165 (Poznan, 1996, Kluwer), 439
In the text
-
Brumberg, V. A., & Bretagnon, P. 2001, Trans. Inst. Appl. Astron. 6, 170 (in Russian)
In the text
-
Brumberg, V. A., & Groten, E. 2001a, A&A, 367, 1070
In the text
NASA ADS
-
Brumberg, V. A., & Groten, E. 2001b, J. Geodesy, 75, 673
In the text
-
Brumberg, V. A., Bretagnon, P., & Guinot, B. 1996, Celes. Mech. Dyn. Astron., 64, 231
In the text
NASA ADS
-
BDL 1997, Introduction aux
éphémérides astronomiques, Supplément explicatif à la Connaissance
des Temps, ed. J.-L. Simon, M. Chapront-Touzé, B. Morando, & W. Thuillot (Bureau des Longitudes)
In the text
-
Capitaine, N., Guinot, B., & McCarthy, D. D. 2000, A&A, 355, 398
In the text
NASA ADS
-
Fairhead, L., & Bretagnon, P. 1990, A&A, 229, 240
In the text
NASA ADS
-
Folkner, W. M., Charlot, P., Finger, M. H., et al. 1994, A&A, 287, 279
In the text
NASA ADS
-
Fukushima, T. 1995, A&A, 294, 895
In the text
NASA ADS
-
Guinot, B. 2000, in
J2000, A fundamental
epoch for origins of reference systems and astronomical models (Journées
2000), Obs. de Paris, ed. N. Capitaine, 209
In the text
-
IAU 2001, IAU Information Bull., 88,
28 (Errata: ibid., 89, 4, 2001)
In the text
-
IERS: 2002, Proc. of the IERS Workshop on the Implementation of the New IAU
Resolutions, IERS Techn. Note No. 29, ed. N. Capitaine, D. Gambis, D. D. McCarthy, et al.
In the text
-
IERS 2003, IERS Conventions 2000, In the text
http://maia.usno.navy.mil/conv2000.html, in press
-
Irwin, A. W., & Fukushima, T. 1999,
A&AS, 348, 642
In the text
NASA ADS
-
Moritz, H., & Mueller, I. I. 1987, Earth Rotation (New York: Ungar)
In the text
-
Pars, L. A. 1965, Analytical Dynamics, Chap. 7 (London: Heinemann)
In the text
-
Soffel, M., Klioner, S. A., Petit, G., et al. 2003, AJ, in press
In the text
-
Vokrouhlický, D. 1995, Phys. Rev. D,
52, 6894
In the text
NASA ADS
Copyright ESO 2003
![\begin{displaymath}u=t-c^{-2}[A(t)+\vec v_E\vec r_E]+\ldots,
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img16.gif)
![\begin{displaymath}w^i=r^i_E+c^{-2}\left[{\textstyle{1\over 2}}\vec v_E\vec r_E
...
..._E r^i_E-{\textstyle{1\over 2}} \vec r_E^2 a^i_E\right]+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img17.gif)
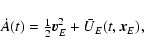
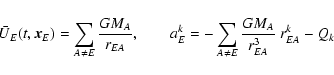
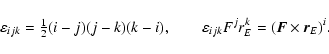
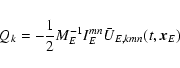
![\begin{displaymath}t=u+c^{-2}[A(u)+\vec v_E\vec w]+\ldots,
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img24.gif)
![\begin{displaymath}x^i=w^i+z^i_E(u)+c^{-2}\left[{\textstyle{1\over 2}}\vec v_E\v...
...\vec w w^i+{\textstyle{1\over 2}} \vec w^2 a^i_E\right]+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img25.gif)
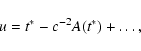
![\begin{displaymath}\dot F^i=\sum_{A\not=E}{GM_A \over r_{EA}^3} \left[\left(-{\t...
...\over 2}} \vec
v_E+2\vec v_A\right)\times\vec r_{EA}\right]^i.
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img27.gif)
![\begin{eqnarray*}\dot F^i=\varepsilon_{ijk}\Bigl[{\textstyle{3\over 2}} v^j_E a^k_E-2\bar
U^j_{E,k}(t,\vec x_E)+2v^j_EQ_k\Bigr]
\end{eqnarray*}](/articles/aa/full/2003/34/aa3628/img29.gif)
![\begin{eqnarray*}\dot F^i=\varepsilon_{ijk}\Bigl[{\textstyle{3\over 2}}v^j_E \ba...
...2\bar U^j_{E,k}(t,\vec x_E)+{\textstyle{1\over 2}}v^j_EQ_k\Bigr]
\end{eqnarray*}](/articles/aa/full/2003/34/aa3628/img30.gif)
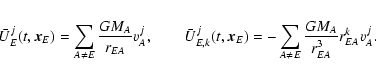
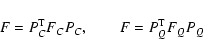
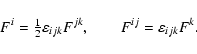
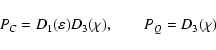
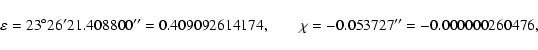
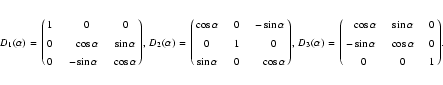
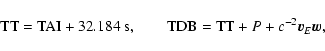
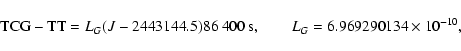
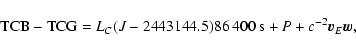
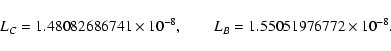
![\begin{displaymath}A_p(t)=\sum_{\alpha}t^\alpha\left[
\sum_{k}A_k^\alpha\cos\left(\psi_k^\alpha+\nu_k^\alpha~t\right)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img49.gif)
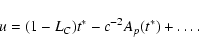
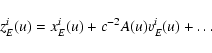
![\begin{displaymath}z_E^i(u)=x^i_E\left[\left(1+L_C\right)u\right]+c^{-2}A_p(u)v^i_E(u)+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img52.gif)
![\begin{displaymath}x^i_E(t)=\sum_{\alpha}t^\alpha\left[
\sum_{k}X_{ik}^\alpha\cos\left(\psi_k^\alpha+\nu_k^\alpha~t\right)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img53.gif)
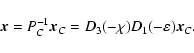
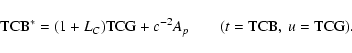
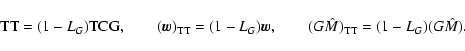
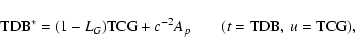
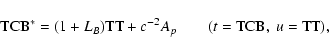
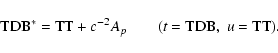
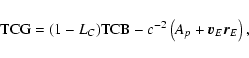
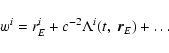
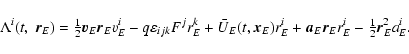
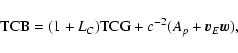
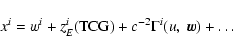
![\begin{displaymath}z_E^i({\rm TCG})=x_E^i({\rm
TCB}^*)=x^i_E\left[\left(1+L_C\right){\rm TCG}\right]+c^{-2}A_pv^i_E+\ldots
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img68.gif)
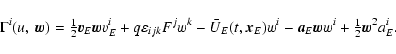
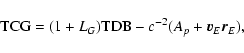
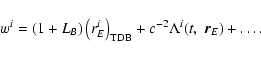
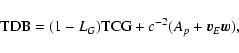
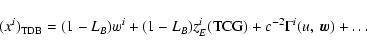
![\begin{displaymath}(1-L_B)z_E^i({\rm TCG})=x_E^i({\rm
TDB}^*)=x^i_E\left[(1-L_G){\rm TCG}\right]+c^{-2}A_pv^i_E+\ldots .
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img79.gif)
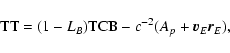
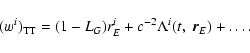
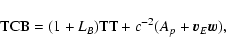
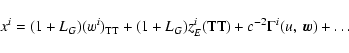
![\begin{displaymath}(1+L_G)z_E^i({\rm TT})=x_E^i({\rm
TCB}^*)=x^i_E\left[(1+L_B){\rm TT}\right]+c^{-2}A_pv^i_E+\ldots .
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img84.gif)
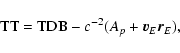
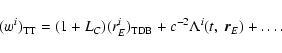
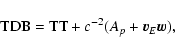
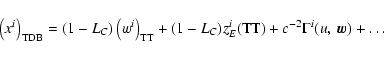
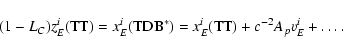
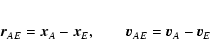
![\begin{displaymath}w^i_A(u)=z^i_A(u)-z^i_E(u)+c^{-2}\bigl[\Lambda^i\left(t^*,~\vec
r_{AE}\right)+\vec v_E\vec r_{AE}v^i_{AE} \bigr],
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img92.gif)
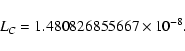
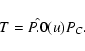
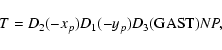
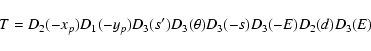
![\begin{displaymath}T=R(\vec A),\qquad R(\vec A)\vec x=\vec x-\sin a\left(\hat{\v...
...at {\vec A}\times \left(\hat{\vec A}\times\vec
x\right)\right]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img125.gif)
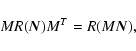
![\begin{displaymath}R(\vec B)R(\vec A)\approx R\bigl[\vec A+\vec B+{\textstyle{1\over 2}}(\vec
A\times\vec B)\bigr],
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img134.gif)
![\begin{displaymath}R(\vec B)R(\vec A) = R\Biggl[\vec A+{\displaystyle{a(1+\cos a...
...)\over 2\sin a}}\Biggr)\hat{\vec A}(\hat{\vec A}\vec B)\Biggr]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img138.gif)
![\begin{displaymath}R(\vec A)R(\vec B) = R\Biggl[\vec A+{\displaystyle{a(1+\cos a...
...\over 2\sin a}}\Biggr)\hat{\vec A}(\hat{\vec A}\vec B)\Biggr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img139.gif)
![\begin{displaymath}R(\vec C)R(\vec A)R(\vec B) =
R\Biggl[\vec A+{\displaystyle{a...
...r)\hat{\vec A}\bigl(
\hat{\vec A}(\vec B+\vec C)\bigr)\Biggr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img141.gif)
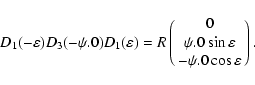
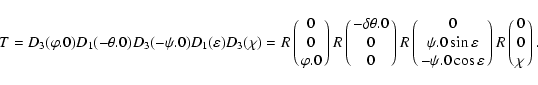
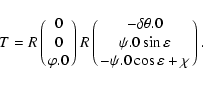
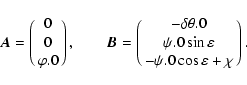
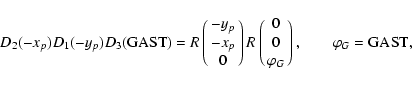
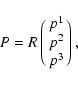
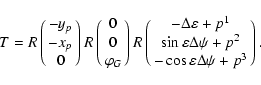
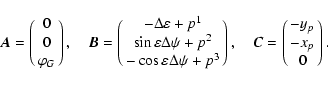
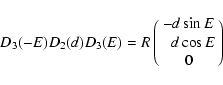
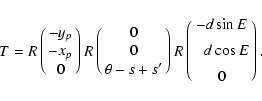
![$\displaystyle \left[\varphi_G+\left(1-{\displaystyle{\varphi_G \left(1+\cos
\va...
...t) \left(-\Delta \psi
\cos\varepsilon+p^3\right)\right]\pmatrix{0\cr 0\cr 1\cr}$](/articles/aa/full/2003/34/aa3628/img164.gif)
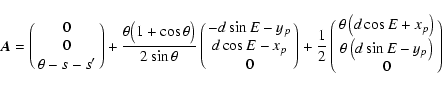
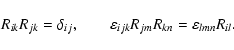
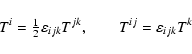
![\begin{displaymath}R_{ij}= {\displaystyle{1\over 1+\vert\vec T\vert^2}}\left[\le...
...vert^2\right)\delta_{ij}+2T^iT^j+2\varepsilon_{ijk}T^k\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img172.gif)
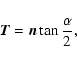
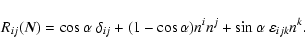
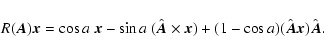
![\begin{displaymath}R(\vec A)\vec x\approx\vec x-(\vec A\times\vec x)+{\textstyle{1\over 2}} \left[\vec
A\times(\vec A\times\vec x)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img179.gif)
![\begin{displaymath}R(\vec B)R(\vec A)\vec x\approx R(\vec A)\vec x-(\vec B\times...
...ver 2}}\left[\vec B\times(\vec B\times R(\vec A)\vec
x)\right]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img181.gif)
![\begin{displaymath}R(\vec B)R(\vec A)\vec x \approx\vec x-(\vec A\times\vec
x)-(...
...s\vec x)\right]+\left[\vec B\times(\vec
A\times\vec x)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img182.gif)
![\begin{displaymath}R(\vec B)R(\vec A)\vec x \approx\vec x-(\vec A\times\vec x)-(...
...left[(\vec A+\vec B)\times((\vec A+\vec B)\times\vec
x)\right]
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img183.gif)
![\begin{displaymath}R(\vec A+\vec B+{\textstyle{1\over 2}} (\vec A\times\vec B))\...
...ft[(\vec A+\vec B)\times((\vec A+\vec B)\times\vec x)\right].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img184.gif)
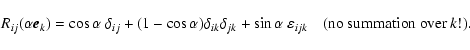
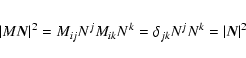
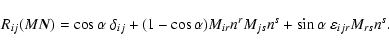
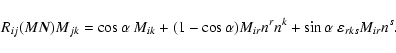
![\begin{eqnarray*}\delta a=\hat{\vec A}\delta\vec A, \qquad \delta\hat{\vec A}={\...
...\bigl[\delta\vec A- (\hat{\vec A}\delta\vec A)\hat{\vec A}\bigr]
\end{eqnarray*}](/articles/aa/full/2003/34/aa3628/img201.gif)
![\begin{displaymath}\Delta\bigl(\hat{\vec A}(\hat{\vec A}\vec B)\bigr)=\sin a
(\h...
...]+
\cos a (\hat{\vec A}\vec B)(\vec x\times\hat{\vec A}\bigr],
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img207.gif)
![\begin{displaymath}\Delta(\hat{\vec A}\times\vec B) = {\displaystyle{1-\cos a\ov...
...l[(\vec B\vec x)\hat{\vec A}-(\hat{\vec A}\vec
x)\vec B\bigr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img208.gif)
![\begin{displaymath}\Delta(\vec B)-\Delta\bigl(\hat{\vec A}(\hat{\vec A}\vec
B)\b...
...\vec
B)+(\hat{\vec A}\vec B)(\hat{\vec A}\times \vec x)\bigr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img210.gif)
![\begin{displaymath}\Delta(\vec A\times\vec B) +{\displaystyle{a(1+\cos a)\over \...
...c x-
\Delta\bigl(\hat{\vec A}(\hat{\vec A}\vec B)\bigr)\bigr].
\end{displaymath}](/articles/aa/full/2003/34/aa3628/img211.gif)
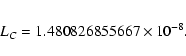
![\begin{eqnarray*}x^i_E(t)=\sum_{\alpha}t^\alpha\left[
\sum_{k}X_{ik}^\alpha\cos\left(\psi_k^\alpha+\nu_k^\alpha~t\right)\right].
\end{eqnarray*}](/articles/aa/full/2003/34/aa3628/img214.gif)