A&A 406, 1-5 (2003)
DOI: 10.1051/0004-6361:20030665
Numerical tests of dynamical friction in gravitational inhomogeneous systems
A. Del Popolo
Dipartimento di Matematica, Università Statale
di Bergamo,
via dei Caniana 2, 24129 Bergamo, Italy
Feza Gürsey Institute, PO Box 6 Çengelköy, Istanbul, Turkey
Bo
 çi University, Physics Department,
80815 Bebek, Istanbul, Turkey
çi University, Physics Department,
80815 Bebek, Istanbul, Turkey
Received 28 January 2003 / Accepted 10 April 2003
Abstract
In this paper, I test by numerical simulations the results of Del Popolo & Gambera (1998),
dealing with the extension of Chandrasekhar and Von Neumann's analysis of the
statistics of the gravitational field to systems in which particles
(e.g. stars, galaxies) are inhomogeneously distributed.
The paper is an extension of that of Ahmad & Cohen (1974), in which the authors
tested some results of the stochastic theory of dynamical friction developed by
Chandrasekhar & von Neumann (1943) in the case of homogeneous gravitational systems.
It is also a continuation of the work developed in
Del Popolo (1996a,b), which extended the results of Ahmad & Cohen (1973),
(dealing with the study of the probability distribution of the stochastic force in homogeneous gravitational
systems) to inhomogeneous gravitational systems.
Similarly to what was done by Ahmad & Cohen (1974) in the case of homogeneous systems,
I test, by means of the evolution of an inhomogeneous
system of particles,
that the theoretical rate of force fluctuation
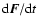 describes correctly
the experimental one.
I find that the stochastic force distribution obtained for
the evolved system is in good agreement with the Del Popolo & Gambera (1998) theory.
Moreover, in an inhomogeneous
background the friction force is actually enhanced relative to the
homogeneous case.
describes correctly
the experimental one.
I find that the stochastic force distribution obtained for
the evolved system is in good agreement with the Del Popolo & Gambera (1998) theory.
Moreover, in an inhomogeneous
background the friction force is actually enhanced relative to the
homogeneous case.
Key words: stars: statistics - celestial mechanics - methods: numerical
The study of the statistics of the fluctuating gravitational force in infinite
homogeneous systems was pioneered by Chandrasekhar & Von Neumann in two classical papers
(Chandrasekhar & Von Neumann 1942, 1943, hereafter CN43) and in several other papers by Chandrasekhar
(1941, 1943a-e, 1944a,b). The analysis of
the fluctuating gravitational field, developed by the authors, was
formulated by means of a statistical treatment. In their papers
Chandrasekhar & Von Neumann considered a system in which the
stars are distributed according to a uniform probability density,
no correlation among the positions of the stars is present and
where the number of stars constituting the system tends to infinity while
keeping the density constant.
Two distributions are fundamental for the description of the fluctuating
gravitational field:
1)
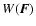 which gives the probability that a test star
is subject to a force
which gives the probability that a test star
is subject to a force 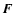 in the range
in the range 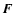 ,
,
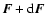 ;
;
2)
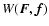 which gives the
joint probability that the star experiences a force F and a rate
of change f, where
which gives the
joint probability that the star experiences a force F and a rate
of change f, where
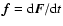 .
.
The first distribution, known as Holtsmark's law (Holtsmark 1919), in the
case of a homogeneous distribution of the stars, gives information only
on the number of stars experiencing a given force but it does not
describe some fundamental features of the fluctuations in
the gravitational field such as the speed of the fluctuations and
the dynamical friction. These features can be
described using the second distribution
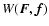 .
Hence, for the definition of the speed of fluctuations and of the
dynamical friction one must determine the distribution
.
Hence, for the definition of the speed of fluctuations and of the
dynamical friction one must determine the distribution
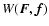 .
Information on dynamical friction can be obtained from the moments of this last distribution.
As stressed by Chandrasekhar & Von Neumann (1943), for a test star moving with velocity v in
a sea of field stars characterized by a random probability distribution
of the velocities,
.
Information on dynamical friction can be obtained from the moments of this last distribution.
As stressed by Chandrasekhar & Von Neumann (1943), for a test star moving with velocity v in
a sea of field stars characterized by a random probability distribution
of the velocities,
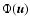 ,
we may write:
,
we may write:
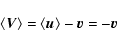 |
(1) |
where 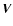 represents the velocity of a typical field star relative
to the one under consideration,
represents the velocity of a typical field star relative
to the one under consideration, 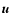 denotes the velocity of a
field star.
This asymmetry of the distribution of the relative velocities produces, as
shown by CN43, a
deceleration of the test star in the direction of motion.
This effect is known, from the Chandrasekhar papers, as "dynamical friction".
As quoted above, some information on dynamical friction can be obtained by means of the
first moment of f. As shown by CN43:
denotes the velocity of a
field star.
This asymmetry of the distribution of the relative velocities produces, as
shown by CN43, a
deceleration of the test star in the direction of motion.
This effect is known, from the Chandrasekhar papers, as "dynamical friction".
As quoted above, some information on dynamical friction can be obtained by means of the
first moment of f. As shown by CN43:
![\begin{displaymath}\left\langle \frac{{\rm d}{\vec F}}{{\rm d}t} \right\rangle_{...
...cdot {\vec v}}{ \vert {\vec F} \vert^2} \cdot {\vec F} \right]
\end{displaymath}](/articles/aa/full/2003/28/aa3532/img12.gif) |
(2) |
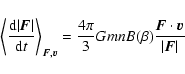 |
(3) |
where m is the mass of a field star, nl is the local density, and 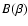 is definited
as:
is definited
as:
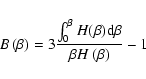 |
(4) |
where
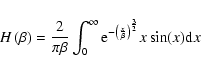 |
(5) |
and
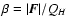 where
where
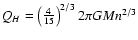 .
These equations show that the amount of acceleration in the direction
of
.
These equations show that the amount of acceleration in the direction
of
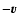 when
when
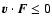 is greater than that
in the direction
is greater than that
in the direction
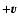 ,
when
,
when
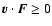 :
then
the star suffers a deceleration, the a priori probability that
:
then
the star suffers a deceleration, the a priori probability that
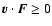 being equal to the probability that
being equal to the probability that
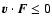 .
.
Several authors have stressed
the importance of stochastic forces and in particular dynamical friction
in determining the observed
properties of clusters of galaxies (White 1976; Kashlinsky 1986, 1987)
while others studied the role of dynamical friction in the orbital decay
of a satellite moving around a galaxy or in the merging
scenario (Bontekoe & van Albada 1987; Seguin & Dupraz 1996;
Dominguez-Tenreiro & Gomez-Flechoso 1998).
Chandrasekhar's theory (and in particular his
classical formula see Chandrasekhar 1943b)
is widely employed to quantify dynamical friction
in a variety of situations, even if
the theory developed is based on the
hypothesis that the stars are distributed uniformly and
it is well known that in stellar systems, the stars are not
uniformly distributed,
(Elson et al. 1987; Wybo & Dejonghe 1995; Zwart et al. 1997)
in galactic systems as well, the galaxies are not uniformly distributed
(Peebles 1980; Bahcall & Soneira 1982; Sarazin 1988;
Liddle & Lyth 1993;
White et al. 1993; Strauss & Willick 1995).
It is evident
that an analysis of dynamical friction taking account of the
inhomogeneity of astronomical systems can provide a more realistic
representation of the evolution of these systems.
Moreover from a pure theoretical standpoint we expect that inhomogeneity affects all the aspects of the fluctuating
gravitational field (Antonuccio & Colafrancesco 1994;
Del Popolo & Gambera 1996, 1997; Del Popolo et al. 1996; Gambera 1997).
Firstly, the Holtsmark distribution is no longer correct
for inhomogeneous systems. For these systems, as shown by Kandrup
(1980a,b, 1983), the Holtsmark distribution must be substituted
with a generalized form of the Holtsmark distribution
characterized by a shift of
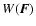 towards larger forces when inhomogeneity increases. This result
was already suggested by the numerical simulations of Ahmad & Cohen
(1973, 1974).
Hence when the inhomogeneity increases
the probability that a test particle experiences a
large force increases, secondly,
towards larger forces when inhomogeneity increases. This result
was already suggested by the numerical simulations of Ahmad & Cohen
(1973, 1974).
Hence when the inhomogeneity increases
the probability that a test particle experiences a
large force increases, secondly,
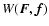 is changed by inhomogeneity.
Consequently, the values of the mean life of a state,
the first moment of
is changed by inhomogeneity.
Consequently, the values of the mean life of a state,
the first moment of 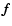 and the dynamical friction force
are changed by inhomogeneity with respect to those of homogeneous systems.
and the dynamical friction force
are changed by inhomogeneity with respect to those of homogeneous systems.
This paper must be intended as the continuation of
Del Popolo & Gambera (1998) paper, in
which
the
study of the effects of inhomogeneity on the distribution functions
of the stochastic forces and on dynamical friction was
performed.
As anticipated in Del Popolo & Gambera (1998), the next task to perform
was to test the result of the Del Popolo & Gambera (1998) paper
against N-body simulations, which is the object of the present paper.
The third step (to be developed in a future paper) should be that of
finding a formula that describes dynamical friction in homogeneous and
inhomogeneous systems only on the basis of
statistical theory.
Before continuing we want
to stress that when we speak of inhomogeneity we refer to inhomogeneity
in position distribution and not to that of velocity distribution. Our
work follows the spirit of Kandrup's (1980) in the sense that
we are interested in
the effect of a non-uniform distribution in the position of stars on the
distributions of the stochastic force.
The plan of the paper is the following: in Sect. 2 we review the
calculations and formulas needed to obtain
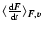 in the case of inhomogeneous systems.
In Sect. 3, I show how numerical experiments are performed and
they are compared with the theoretical results of Del Popolo & Gambera (1998).
Finally, in Sect. 4, I draw my conclusions.
in the case of inhomogeneous systems.
In Sect. 3, I show how numerical experiments are performed and
they are compared with the theoretical results of Del Popolo & Gambera (1998).
Finally, in Sect. 4, I draw my conclusions.
The introduction of the notion of dynamical friction is due to CN43. In the
stochastic formalism developed by CN43 the dynamical friction is discussed
in terms of 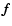 :
:
![\begin{displaymath}\overline {\vec f} = \frac{-2 \pi}{3} G m n B(\beta) \left[ {...
...cdot {\vec v}}{ \vert {\vec F} \vert^2} \cdot {\vec F} \right]
\end{displaymath}](/articles/aa/full/2003/28/aa3532/img25.gif) |
(6) |
where
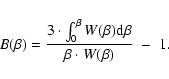 |
(7) |
As shown by CN43, the origin of dynamical friction is due to
the asymmetry in the distribution of relative velocities.
If a test star moves with velocity 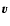 in a spherical
distribution of field stars, namely
in a spherical
distribution of field stars, namely
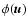 ,
then we have that:
,
then we have that:
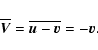 |
(8) |
The asymmetry in the distribution of relative velocities is conserved
in the final Eq. (6). In fact from Eq. (6)
we have:
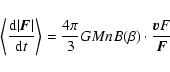 |
(9) |
(CN43). This means that when
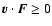 then
then
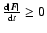 ,
while when
,
while when
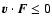 then
then
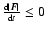 .
As a consequence, when
.
As a consequence, when 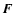 has a positive component in
the direction of
has a positive component in
the direction of 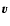 ,
,
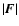 increases on average; while if
increases on average; while if 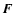 has
a negative component in the direction of
has
a negative component in the direction of 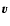 ,
,
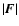 decreases on average.
Moreover, the star suffers a greater amount of acceleration in the
direction
decreases on average.
Moreover, the star suffers a greater amount of acceleration in the
direction
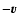 when
when
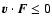 than in the direction
than in the direction
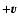 when
when
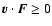 .
.
In other
words the test star suffers, statistically, an equal number of
accelerating and decelerating impulses. The modulus of
deceleration being larger than that of acceleration the star slows down.
Chandrasekhar & Von Neumann's analysis was extended to inhomogeneous systems
in Del Popolo & Gambera (1998), where
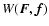 and its first momentum were calculated.
Supposing that the distribution function
and its first momentum were calculated.
Supposing that the distribution function 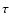 is given by:
is given by:
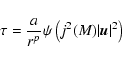 |
(10) |
where a is a constant
that can be obtained from the normalization condition for 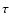 ,
j a
parameter (of dimensions of velocity-1),
,
j a
parameter (of dimensions of velocity-1), 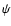 an arbitrary
function,
an arbitrary
function, 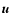 the velocity of a field star.
In other words we assumed, according to CN43 and Chandrasekhar
& von Newmann (1942), that the distribution of velocities is spherical,
i.e. the distribution function is
the velocity of a field star.
In other words we assumed, according to CN43 and Chandrasekhar
& von Newmann (1942), that the distribution of velocities is spherical,
i.e. the distribution function is
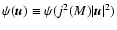 ,
but differently from the quoted papers we supposed that the positions
are not equally likely for stars, that is, the stars are
inhomogeneously distributed in space.
A lengthy calculation led us (see Del Popolo & Gambera 1998 for a derivation and the
meaning of symbols) to find that the first moment of
,
but differently from the quoted papers we supposed that the positions
are not equally likely for stars, that is, the stars are
inhomogeneously distributed in space.
A lengthy calculation led us (see Del Popolo & Gambera 1998 for a derivation and the
meaning of symbols) to find that the first moment of 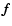 is given by:
is given by:
![\begin{displaymath}\overline {\vec f} = -\left( \frac{1}{2} \right)^{\frac{3}{3 ...
...t {\vec v}}{ \vert {
\vec F} \vert^2} \cdot {\vec F} \right]~~
\end{displaymath}](/articles/aa/full/2003/28/aa3532/img38.gif) |
(11) |
where:
![\begin{displaymath}A(p) = \int_{0}^{\infty} \left[ \frac{\sin{x}}{x^{(4 - p)/2}}...
...(8 - p)/2}} + \frac{3 \cos{x}}{x^{(6 - p)/2}} \right]{\rm d} x
\end{displaymath}](/articles/aa/full/2003/28/aa3532/img39.gif) |
(12) |
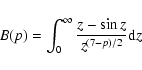 |
(13) |
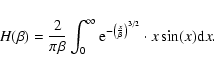 |
(15) |
The results obtained by us for an inhomogeneous system
are different (see Eq. (11)), as expected,
from those obtained by CN43 for
a homogeneous system (CN43 - Eq. (105) or Eq. (6)). At the same time
it is very interesting
to note that for p = 0 (homogeneous system) our result coincides,
as is obvious, with the
results obtained by CN43.
In inhomogeneous systems, Eq. (9) can be written, using
Eq. (11), as:
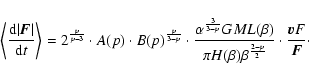 |
(16) |
In order to check the validity of the quoted relation (Eq. (16)), I have performed numerical experiments.
This was done similarly to Del Popolo (1996b) by evolving (now) 100 000 points (stars) acting under their mutual gravitational attraction. From the evolved positions and velocities of the stars,
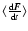 was computed as a function of velocity and force, similarly to Ahmad & Cohen (1974), and then compared with Eq. (16) as I shall describe in the following
was computed as a function of velocity and force, similarly to Ahmad & Cohen (1974), and then compared with Eq. (16) as I shall describe in the following![[*]](/icons/foot_motif.gif) .
.
To calculate the stochastic force in an inhomogeneous system,
I used an initial configuration in which particles were
distributed according
to a truncated power-law
density profile:
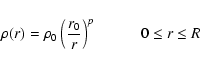 |
(17) |
(see Kandrup 1980; Del Popolo 1996a).
If the velocity distribution is everywhere isotropic then the equation relating the
configuration space density 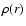 to the phase space density f(E) is:
to the phase space density f(E) is:
![\begin{displaymath}\rho(r)=4\pi \int_{U(r)}^{0} \sqrt{2\left[E-U(r)\right]} f(E) {\rm d}E
\end{displaymath}](/articles/aa/full/2003/28/aa3532/img54.gif) |
(18) |
where U(r) is the potential (normalized to zero at infinity). Equation (18)
may be converted into an Abel integral equation and inverted, giving
the phase space density:
 |
(19) |
(Eddington 1916; Binney & Tremaine 1987).
The initial conditions were generated
from the distribution function that can be obtained from
Eq. (19)
assuming a cut-off radius R=1, the mass of the system M=1,
r0 =0.15![[*]](/icons/foot_motif.gif) and G=1. All the particles had
equal mass.
To have a system whose total mass is contained in a unitary
sphere, Eq. (18)
was renormalized and
consequently also the potential of the system
which is obtained from Eq. (18)
through Poisson's equation.
and G=1. All the particles had
equal mass.
To have a system whose total mass is contained in a unitary
sphere, Eq. (18)
was renormalized and
consequently also the potential of the system
which is obtained from Eq. (18)
through Poisson's equation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.ps}
\end{figure}](/articles/aa/full/2003/28/aa3532/Timg56.gif) |
Figure 1:
The average value of the time rate of change of the magnitude of the force as the function of the velocity.
The solid line refers to the homogeneous case (Chandrasekhar & Von Neumann 1943). The dotted and dashed line refers to the cases p=2.5 and p=4, respectively (see Eq. (26)). Crosses represent the experimental points. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}
\end{figure}](/articles/aa/full/2003/28/aa3532/Timg57.gif) |
Figure 2:
The average value of the time rate of change of the magnitude of the force as the function of the force.
The solid line refers to the homogeneous case (Chandrasekhar & Von Neumann 1943). The dotted and dashed line refers to the cases p=2.5 and p=4, respectively (see Eq. (19)). Crosses represent the experimental points. |
| Open with DEXTER |
The system of 100 000 particles
was evolved over 150 dynamical times using a tree N-body code
(Hernquist 1987).
During the evolution of the system the essential quantities such as position, force, etc.,
for each test point of the system was sampled
every
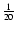 of a dynamical time (see Del Popolo 1996b; Ahmad & Cohen 1973 for details).
The average of the
of a dynamical time (see Del Popolo 1996b; Ahmad & Cohen 1973 for details).
The average of the
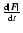 is a function of velocity, v, force, F,
and the angle between them. The test of Eq. (16) was performed in a similar way to that of
Ahmad & Cohen (1974), namely by integrating out two of the variables and examining
is a function of velocity, v, force, F,
and the angle between them. The test of Eq. (16) was performed in a similar way to that of
Ahmad & Cohen (1974), namely by integrating out two of the variables and examining
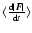 against the remaining one (see Ahmad & Cohen 1974).
As in Ahmad & Cohen (1974),
against the remaining one (see Ahmad & Cohen 1974).
As in Ahmad & Cohen (1974),
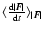 indicates
indicates
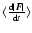 after integrating out the angle and velocity, while
after integrating out the angle and velocity, while
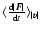 is
is
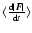 after integrating out the angle and force. In integrating out the angle,
one cannot average over the entire range 0 to
after integrating out the angle and force. In integrating out the angle,
one cannot average over the entire range 0 to 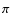 ,
since that would give zero.
Instead, the cosine was averaged from 0 to
,
since that would give zero.
Instead, the cosine was averaged from 0 to 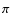 /2, and in the numerical experiments only those particles having a cosine in the quoted range were used. In order not to waste the statistics for half the particles the same trick of Ahmad & Cohen (1974) was used, namely when the cosine is in the range of
/2, and in the numerical experiments only those particles having a cosine in the quoted range were used. In order not to waste the statistics for half the particles the same trick of Ahmad & Cohen (1974) was used, namely when the cosine is in the range of 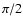 to
to 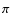 ,
the sign of
,
the sign of
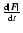 is changed and it is counted in the same statistics. This
corresponds to assume that the cosine between
is changed and it is counted in the same statistics. This
corresponds to assume that the cosine between 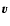 and
and 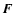 is uniformly distributed, which is what is found in numerical experiments. The average value of the cosine between 0 and
is uniformly distributed, which is what is found in numerical experiments. The average value of the cosine between 0 and 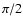 is 1/2.
is 1/2.
For a general distribution
 can be calculated as usual:
can be calculated as usual:
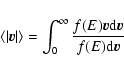 |
(20) |
and
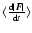 can be written, in units of
can be written, in units of
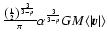 ,
as:
,
as:
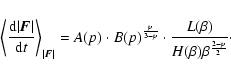 |
(21) |
In the particular case of
a Maxwellian distribution for velocities:
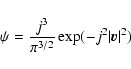 |
(22) |
where
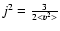 ,
so that:
,
so that:
 |
(23) |
we have that:
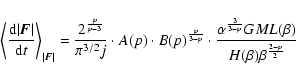 |
(24) |
that expressed in units of
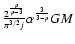 ,
then Eq. (24) becomes:
,
then Eq. (24) becomes:
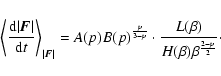 |
(25) |
Similarly to Ahamd & Cohen (1974),
since to integrate out the force from Eq. (16) one has a divergent result, I consider only particles up to a certain maximum value of the force,
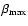 :
for example in the case p=0,
:
for example in the case p=0,
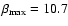 ,
that involves 97% of the particles. As observed by Ahmad & Cohen (1974), any cutoff of the force can be used as long as it is taken into account in both the experiment and the analytic evaluation of
,
that involves 97% of the particles. As observed by Ahmad & Cohen (1974), any cutoff of the force can be used as long as it is taken into account in both the experiment and the analytic evaluation of
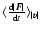 .
Defining:
.
Defining:
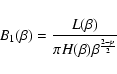 |
(26) |
and
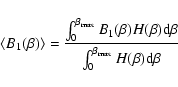 |
(27) |
we find, in units of
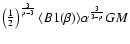 ,
that:
,
that:
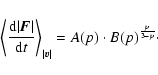 |
(28) |
The results of calculation and numerical experiments are plotted in Figs. 1 and 2.
In Fig. 1, I plot the average value of the time rate of change of
the magnitude of the force as a function of the velocity.
The solid line refers to the homogeneous case while the dotted and
dashed lines refer to the cases p=2.5 and p=4,
respectively. Crosses represent the experimental points. As shown, experimental points follow a linear relationship and there is a good agreement with the theoretical prediction
(Eq. (21)).
In Fig. 2, I plot the average value of the time rate of change of the magnitude of the force as the function of the force.
As in the previous figure, the solid line refers to the homogeneous case while the dotted and dashed line refers to the cases p=2.5 and p=4, respectively. In this case, the dependence is no longer linear: it behaves like 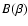 in the homogeneous case.
A comparison with numerical experiments shows that there is a good agreement with the theoretical prediction
(Eq. (28)).
The situation described in Ahmad & Cohen (1974),
that the experimental data were somewhere in between the theoretical curves for the one-particle and the infinite-particle case, is no longer present and the agreement is better, now. This is due to the larger number of particles used in the simulations. The plots show that Chandrasekhar & Von Neumann's theory of dynamical friction in gravitational systems gives a good description of experimental data (solid line and data), and so does the generalization of the quoted theory to inhomogeneous systems (dotted line, dashed line, and respective data). In inhomogeneous systems, Chandrasekhar's result
which relates the frictional force only to the local properties of the background at the position of the object, is no
longer true, and friction depends on the global structure of the system.
This point is in agreement with Maoz (1993), who showed that in inhomogeneous media the friction,
unlike Chandrasekhar's formula, depends on the global structure of the entire mass density field.
in the homogeneous case.
A comparison with numerical experiments shows that there is a good agreement with the theoretical prediction
(Eq. (28)).
The situation described in Ahmad & Cohen (1974),
that the experimental data were somewhere in between the theoretical curves for the one-particle and the infinite-particle case, is no longer present and the agreement is better, now. This is due to the larger number of particles used in the simulations. The plots show that Chandrasekhar & Von Neumann's theory of dynamical friction in gravitational systems gives a good description of experimental data (solid line and data), and so does the generalization of the quoted theory to inhomogeneous systems (dotted line, dashed line, and respective data). In inhomogeneous systems, Chandrasekhar's result
which relates the frictional force only to the local properties of the background at the position of the object, is no
longer true, and friction depends on the global structure of the system.
This point is in agreement with Maoz (1993), who showed that in inhomogeneous media the friction,
unlike Chandrasekhar's formula, depends on the global structure of the entire mass density field.
In this paper, I tested by numerical simulations the results of the Del Popolo & Gambera (1998) paper,
dealing with the average value of the time rate of change of the magnitude of the stochastic force in inhomogeneous gravitational systems. In agreement with Ahmad & Cohen (1974),
the stochastic theory of dynamical friction developed by
Chandrasekhar & Von Neumann (1943), in the case of homogeneous gravitational systems, gives a good description of the results of numerical experiments.
The stochastic force distribution obtained for
inhomogeneous systems, obtained by Del Popolo & Gambera (1998), is also
in good agreement with the results of numerical experiments.
Finally, in an inhomogeneous
background the friction force is actually enhanced relative to the
homogeneous case.
Acknowledgements
I am grateful to E. N. Ercan and G. Mamon for stimulating discussions during
the period in which this work was performed. I would
like to thank Bo
 çi University Research
Foundation for the financial support through the project code 01B304.
çi University Research
Foundation for the financial support through the project code 01B304.
- Ahmad, A., & Cohen, L. 1973, ApJ, 179, 885
In the text
NASA ADS
- Ahmad, A., & Cohen, L. 1974, ApJ, 188, 469
In the text
NASA ADS
- Antonuccio-Delogu, V., & Colafrancesco, S. 1994, ApJ, 427, 72
In the text
NASA ADS
- Bahcall, N. A., & Soneira, R. M. 1982, ApJ, 262, 419
In the text
NASA ADS
- Bontekoe, T. R., & van Albada, T. S. 1987, MNRAS, 224, 349
In the text
NASA ADS
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics, in Princeton Series in Astrophysics
(Princeton University Press)
In the text
- Chandrasekar, S. 1941, ApJ, 94, 511
In the text
NASA ADS
- Chandrasekar, S. 1943a, Rev. Mod. Phys., 15, 1
In the text
NASA ADS
- Chandrasekar, S. 1943b, ApJ, 97, 255
In the text
NASA ADS
- Chandrasekar, S. 1943c, ApJ, 97, 263
NASA ADS
- Chandrasekar, S. 1943d, ApJ, 98, 25
- Chandrasekar, S. 1943e, ApJ, 98, 47
- Chandrasekhar, S. 1944a, ApJ, 99, 47
In the text
NASA ADS
- Chandrasekhar, S. 1994b, ApJ, 99, 25
- Chandrasekhar, S., & Von Neumann, J. 1942, ApJ, 95, 489
In the text
NASA ADS
- Chandrasekhar, S., & Von Neumann, J. 1943, ApJ, 97, 1 (CN43)
In the text
NASA ADS
- Del Popolo, A. 1996a, A&A, 305, 999
In the text
NASA ADS
- Del Popolo, A. 1996b, A&A, 311, 715
In the text
NASA ADS
- Del Popolo, A., & Gambera, M. 1996, A&A, 308, 373
In the text
NASA ADS
- Del Popolo, A., & Gambera, M. 1997, A&A, 321, 691
In the text
NASA ADS
- Del Popolo, A., Gambera, M., & Antonuccio-Delogu, V. 1996, Mem. Soc. Astr. It., 67, 957
In the text
- Del Popolo, A., & Gambera, M. 1998, A&A, 342, 34
In the text
NASA ADS
- Dominguez-Tenreiro, R., & Gomez-Flechoso, M. A. 1998, MNRAS, 294, 465
In the text
NASA ADS
- Eddington, A. S. 1916, MNRAS, 76, 572
In the text
NASA ADS
- Elson, R., Hut, P., & Inagaki, S. 1987, ARA&A, 25, 565
In the text
NASA ADS
- Hernquist, L. 1987, ApJSS, 64, 715
In the text
- Holtsmark, P. J. 1919, Phys. Z., 20, 162
In the text
- Kandrup, H. E. 1980a, Phys. Rep., 63, 1
In the text
- Kandrup, H. E. 1980b, ApJ, 244, 1039
- Kandrup, H. E. 1983, Ap&SS, 97, 435
In the text
NASA ADS
- Kashlinsky, A. 1986, ApJ, 306, 374
In the text
NASA ADS
- Kashlinsky, A. 1987, ApJ, 312, 497
In the text
NASA ADS
- Liddle, A. R., & Lyth, D. H. 1993, Phys. Rep., 231, 2
In the text
- Maoz, E. 1993, MNRAS, 263, 75
In the text
NASA ADS
- Peebles, P. J. E. 1980, The large scale structure of the Universe (Princeton: Priceton University Press)
In the text
- Sarazin, C. 1988, X-ray emission from Clusters of Galaxies (Cambridge: Cambridge Univ. Press)
In the text
- Seguin, P., & Dupraz, C. 1996, A&A, 310, 757
In the text
NASA ADS
- Strauss, M. A., & Willick, J. A. 1995, Phys. Rep., 261, 271
In the text
NASA ADS
- White, S. D. M. 1976, MNRAS, 174, 19
In the text
NASA ADS
- White, S. D. M., Briel, U. G., & Henry, J. P. 1993, MNRAS, 261, L8
In the text
NASA ADS
- Wybo, M., & Dejonghe, H. 1995, A&A, 295, 347
In the text
NASA ADS
- Zwart, S. F. P., Tout, C. A., & Lee, H. M. 1997,
in Highlights of Astronomy, ed. J. Andersen (Kluwer Academic Publishers), 11
In the text
Copyright ESO 2003
![]() çi University, Physics Department,
80815 Bebek, Istanbul, Turkey
çi University, Physics Department,
80815 Bebek, Istanbul, Turkey![]() describes correctly
the experimental one.
I find that the stochastic force distribution obtained for
the evolved system is in good agreement with the Del Popolo & Gambera (1998) theory.
Moreover, in an inhomogeneous
background the friction force is actually enhanced relative to the
homogeneous case.
describes correctly
the experimental one.
I find that the stochastic force distribution obtained for
the evolved system is in good agreement with the Del Popolo & Gambera (1998) theory.
Moreover, in an inhomogeneous
background the friction force is actually enhanced relative to the
homogeneous case.
![]() which gives the probability that a test star
is subject to a force
which gives the probability that a test star
is subject to a force ![]() in the range
in the range ![]() ,
,
![]() ;
;![]() which gives the
joint probability that the star experiences a force F and a rate
of change f, where
which gives the
joint probability that the star experiences a force F and a rate
of change f, where
![]() .
.![]() .
Hence, for the definition of the speed of fluctuations and of the
dynamical friction one must determine the distribution
.
Hence, for the definition of the speed of fluctuations and of the
dynamical friction one must determine the distribution
![]() .
Information on dynamical friction can be obtained from the moments of this last distribution.
As stressed by Chandrasekhar & Von Neumann (1943), for a test star moving with velocity v in
a sea of field stars characterized by a random probability distribution
of the velocities,
.
Information on dynamical friction can be obtained from the moments of this last distribution.
As stressed by Chandrasekhar & Von Neumann (1943), for a test star moving with velocity v in
a sea of field stars characterized by a random probability distribution
of the velocities,
![]() ,
we may write:
,
we may write:
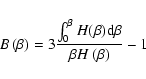
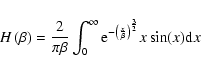
![]() towards larger forces when inhomogeneity increases. This result
was already suggested by the numerical simulations of Ahmad & Cohen
(1973, 1974).
Hence when the inhomogeneity increases
the probability that a test particle experiences a
large force increases, secondly,
towards larger forces when inhomogeneity increases. This result
was already suggested by the numerical simulations of Ahmad & Cohen
(1973, 1974).
Hence when the inhomogeneity increases
the probability that a test particle experiences a
large force increases, secondly,
![]() is changed by inhomogeneity.
Consequently, the values of the mean life of a state,
the first moment of
is changed by inhomogeneity.
Consequently, the values of the mean life of a state,
the first moment of ![]() and the dynamical friction force
are changed by inhomogeneity with respect to those of homogeneous systems.
and the dynamical friction force
are changed by inhomogeneity with respect to those of homogeneous systems.
![]() in the case of inhomogeneous systems.
In Sect. 3, I show how numerical experiments are performed and
they are compared with the theoretical results of Del Popolo & Gambera (1998).
Finally, in Sect. 4, I draw my conclusions.
in the case of inhomogeneous systems.
In Sect. 3, I show how numerical experiments are performed and
they are compared with the theoretical results of Del Popolo & Gambera (1998).
Finally, in Sect. 4, I draw my conclusions.
![]() :
:
![]() and its first momentum were calculated.
Supposing that the distribution function
and its first momentum were calculated.
Supposing that the distribution function ![]() is given by:
is given by:
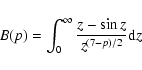
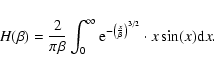
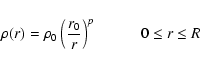
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.ps}
\end{figure}](/articles/aa/full/2003/28/aa3532/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}
\end{figure}](/articles/aa/full/2003/28/aa3532/Timg57.gif)
![]() can be calculated as usual:
can be calculated as usual:
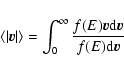
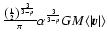 ,
as:
,
as:
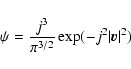

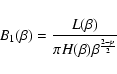
çi University Research Foundation for the financial support through the project code 01B304.