- ... following
![[*]](/icons/foot_motif.gif)
- In a inhomogeneous system, similarly
way to what happens in a homogeneous system,
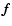 depends
on
depends
on 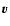 ,
,
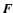 and
and 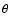 (the angle between
(the angle between 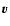 and
and 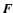 )
while unlike homogeneous systems,
)
while unlike homogeneous systems, 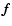 is a function of the inhomogeneity parameter p. The dependence of
is a function of the inhomogeneity parameter p. The dependence of 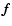 on p is not only due to the
functions A(p), B(p) and to the density parameter
on p is not only due to the
functions A(p), B(p) and to the density parameter 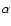 but
also to the parameter
but
also to the parameter
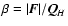 .
In fact in
inhomogeneous systems the normal field
.
In fact in
inhomogeneous systems the normal field
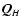 is given by
is given by
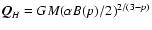 ,
clearly dependent on p.
,
clearly dependent on p.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... =0.15
![[*]](/icons/foot_motif.gif)
- This is the value I used, remember however that
the distribution is scale-free.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.