Table 4:
Model quantities averaged at the outer boundary for constant-opacity models (cf. Sect. 4.1). The models are named by adding a suffix to the respective model name in Table 2. The suffix is a combination of two model parameters, the piston velocity amplitude
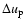 (Un, n in
(Un, n in
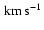 )
and the carbon/oxygen ratio
)
and the carbon/oxygen ratio
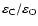 (Cnn, nn is
(Cnn, nn is
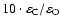 ). The last but two column,
). The last but two column,
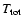 ,
gives the total time-interval of each model calculation. The numbers associated with models run for a shorter time-interval are less reliable than the others as the means are taken over short time intervals. The last but one column gives the type of wind: i, irregular wind; l p, periodic wind; l q, quasi-periodic wind; t, transition model; --, no wind. l (
,
gives the total time-interval of each model calculation. The numbers associated with models run for a shorter time-interval are less reliable than the others as the means are taken over short time intervals. The last but one column gives the type of wind: i, irregular wind; l p, periodic wind; l q, quasi-periodic wind; t, transition model; --, no wind. l (
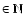 )
shows the (multi-)periodicity of dust shell formation in the unit of the piston period P. A tilde (e.g. "2q'') in the last but one column indicates a correspondence with the characterization only during a part of the calculated time-interval. The values shown in bold face for the PC models indicate that the value differs from the corresponding value given by HD97 (by
)
shows the (multi-)periodicity of dust shell formation in the unit of the piston period P. A tilde (e.g. "2q'') in the last but one column indicates a correspondence with the characterization only during a part of the calculated time-interval. The values shown in bold face for the PC models indicate that the value differs from the corresponding value given by HD97 (by 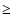
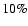 ). The symbols in the last column show whether the respective drift models show an increased/decreased (
). The symbols in the last column show whether the respective drift models show an increased/decreased (
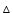 /
/
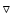 )
mass loss rate, or new wind (
)
mass loss rate, or new wind (
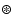 )
when compared to the corresponding PC model. For the PC models an "H'' indicates that the same model parameters were used in a model in HD97. The symbol printed in subscript in the last column indicates how the respective (differing) model is illustrated in Figs. 2, 3, 6 and 7.
)
when compared to the corresponding PC model. For the PC models an "H'' indicates that the same model parameters were used in a model in HD97. The symbol printed in subscript in the last column indicates how the respective (differing) model is illustrated in Figs. 2, 3, 6 and 7.
| Model |
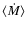 |
|
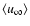 | |
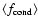 | |
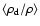 | |
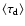 |
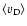 |
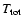 |
Type |
|
![\ensuremath{[10^{-6}\,{M}_{\odot}/\mbox{yr}]}](/articles/aa/full/2003/24/aah4181/img124.gif) |
|
![$[\ensuremath{\,\mbox{km}\,\mbox{s}^{-1}} ]$](/articles/aa/full/2003/24/aah4181/img113.gif) | |
![$[\%]$](/articles/aa/full/2003/24/aah4181/img125.gif) | |
[10-4] | |
[10-2] |
![$[\ensuremath{\,\mbox{km}\,\mbox{s}^{-1}} ]$](/articles/aa/full/2003/24/aah4181/img113.gif) |
[P] |
|
|
| |
| (
 ) ) |
|
| (
 ) ) |
|
| (
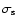 ) ) |
|
| (
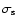 ) ) |
|
| (
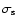 ) ) |
|
|
|
|
| POSITION COUPLED MODELS |
(illustrated with the symbol "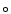 '') '') |
| |
|
| |
|
| R07FU2C18 |
0.53 | (0.27) |
|
5.3 | (0.88) |
|
36 | (0.16) |
|
16 | (0.87) |
|
38 | (2.6) |
|
240 |
i |
H |
| R07FU2C20 |
1.8 | (1.9) |
|
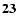 | (1.7) |
|
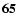 | (6.6) |
|
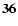 | (3.7) |
|
54 | (13) |
|
180 |
2q |
H |
| R07FU2C25 |
3.3 | (2.5) |
|
33 | (2.5) |
|
69 | (11) |
|
59 | (9.5) |
|
110 | (25) |
|
150 |
1q |
H |
| R07FU4C25 |
8.2 | (11) |
|
36 | (2.4) |
|
74 | (14) |
|
61 | (12) |
|
230 | (50) |
|
170 |
i |
H |
| R10FU2C15 |
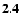 | (0.53) |
|
4.9 | (0.32) |
|
42 | (1.2) |
|
12 | (0.30) |
|
110 | (6.6) |
|
360 |
i |
H
 |
| R10FU2C16 |
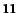 | (9.0) |
|
19 | (1.7) |
|
75 | (7.1) |
|
26 | (2.5) |
|
150 | (50) |
|
290 |
i |
H |
| R10FU2C18 |
15 | (12) |
|
25 | (1.6) |
|
74 | (11) |
|
33 | (4.9) |
|
210 | (59) |
|
250 |
2p |
H |
| R10FU2C20 |
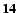 | (12) |
|
29 | (1.9) |
|
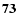 | (12) |
|
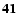 | (7.7) |
|
240 | (49) |
|
240 |
2q |
H |
| R13FU2C13 |
-- |
|
|
| |
|
| |
|
| |
|
| |
|
-- |
|
| R13FU2C14 |
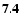 | (4.4) |
|
7.9 | (1.4) |
|
48 | (6.0) |
|
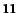 | (1.8) |
|
150 | (14) |
|
450 |
i |
H
 |
| R13FU4C14 |
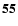 | (36) |
|
14 | (1.4) |
|
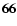 | (11) |
|
15 | (2.3) |
|
350 | (85) |
|
400 |
i |
|
| R13FU2C16 |
29 | (19) |
|
21 | (1.6) |
|
71 | (9.1) |
|
24 | (3.1) |
|
270 | (74) |
|
370 |
i |
H |
| DRIFT MODELS |
(illustrated with the symbol " '') '') |
| |
|
| |
|
| R07FU2C18 |
-- |
|
|
| |
|
| |
|
| |
|
| |
|
t |
|
| R07FU2C20 |
1.4 | (1.5) |
|
21 | (2.4) |
|
17 | (30) |
|
27 | (150) |
|
63 | (30) |
13 |
115 |
i |
 |
| R07FU2C25 |
1.9 | (2.5) |
|
34 | (2.9) |
|
31 | (29) |
|
57 | (280) |
|
98 | (33) |
11 |
87 |
i |
 |
| R07FU4C25 |
5.4 | (8.5) |
|
33 | (3.0) |
|
35 | (40) |
|
34 | (99) |
|
240 | (49) |
4.2 |
137 |
i |
 |
| R10FU2C15 |
4.4 | (5.5) |
|
13 | (2.7) |
|
40 | (34) |
|
16 | (54) |
|
57 | (36) |
9.7 |
120 |
i |
 |
| R10FU2C16 |
8.7 | (8.6) |
|
16 | (2.1) |
|
59 | (34) |
|
34 | (85) |
|
120 | (46) |
5.6 |
250 |
i |
 |
| R10FU2C18 |
9.5 | (11) |
|
22 | (2.2) |
|
47 | (37) |
|
22 | (52) |
|
150 | (54) |
4.0 |
65 |
i |
 |
| R10FU2C20 |
8.8 | (13) |
|
28 | (2.8) |
|
47 | (40) |
|
29 | (56) |
|
160 | (42) |
3.8 |
60 |
i |
 |
| R13FU2C13 |
15 | (9.7) |
|
10 | (0.88) |
|
47 | (30) |
|
7.8 | (12) |
|
98 | (33) |
2.8 |
160 |
3p |
 |
| R13FU2C14 |
18 | (15) |
|
13 | (1.1) |
|
66 | (26) |
|
12 | (15) |
|
160 | (45) |
2.5 |
440 |
i |
 |
| R13FU4C14 |
56 | (44) |
|
13 | (1.5) |
|
54 | (31) |
|
12 | (10) |
|
350 | (100) |
2.3 |
170 |
i |
|
| R13FU2C16 |
23 | (25) |
|
20 | (1.8) |
|
41 | (39) |
|
15 | (24) |
|
220 | (63) |
3.8 |
110 |
i |
 |
Source LaTeX |
All tables |
In the text