A&A 403, 329-337 (2003)
DOI: 10.1051/0004-6361:20030355
B. Tingley
Institut for Fysik og Astronomi (IFA), Aarhus Universitet, Ny Munkegade, Bygning 520, 8000 Aarhus C, Denmark
Received 27 August 2002 / Accepted 7 March 2003
Abstract
The idea of finding extrasolar planets (ESPs) through observations
of drops in stellar brightness due to transiting objects has been
around for decades. It has only been in the last ten years, however,
that any serious attempts to find ESPs became practical.
The discovery of a transiting planet around the star HD 209458 (Charbonneau
et al. 2000) has led to a veritable explosion of research,
because the photometric method is the only way to search a large number
of stars for ESPs simultaneously with current technology. To this point,
however, there has been limited research into the various techniques used
to extract the subtle transit signals from noise, mainly brief summaries
in various papers focused on publishing transit-like signatures in
observations. The scheduled launches over the next few years of satellites
whose primary or secondary science missions will be ESP discovery motivates
a review and a comparative study of the various algorithms used to perform
the transit identification, to determine rigorously and fairly which one
is the most sensitive under which circumstances, to maximize the results of
past, current, and future observational campaigns.
Key words: stars: planetary systems - occultations - methods: data analysis
Struve (1952) was the first to postulate that ESPs could be found in the event that they transited their parent stars, which would dim slightly as the ESP occulted some of the light. This possibility was further explored and developed first by Rosenblatt (1971) and later by Borucki & Summers (1984). Due to technological restraints, the first serious observational attempts were not performed until Doyle et al. (1996), who observed the main-sequence eclipsing binary CM Draconis for the tell-tale photometric dips that would indicate the presence of a planet. This system has several qualities that make it an excellent choice for a planet search, discussed in more detail in Schneider & Doyle (1995). First of all, both members are low-mass main sequence dwarfs, which means that they are physically smaller than a typical field star of comparable apparent magnitude. This leads, in turn, to deeper transits. Additionally, the orbital plane of a planet in a binary system is probably going to be very close to the orbital plane of the stars, increasing the chance that a planet would cause observable transits. (Barbieri et al. 2002). Other projects besides this single, on-going observational campaign began over the next few years, such as STARE (Brown & Charbonneau 2000) and VULCAN (Borucki et al. 2001), which used dedicated small telescopes with large fields of view to observe thousands of stars simultaneously. This area of research became much more active after the discovery of the planet around HD 209458 (Charbonneau et al. 2000) and many projects were initiated in the hopes of witnessing an ESP as it transited its parent star. Among these are several future satellite projects that list ESP searches as either primary or secondary goals (COROT, Eddington, Kepler, and MONS to name a few) and HST observations of 47 Tuc (Gilliland et al. 2000). These observations of 47 Tuc - like all of the recent and ongoing projects - observed a few transit-like events. All of these events, with one exception, proved to be grazing eclipses of binary stars after follow-up observations. This one exception was discovered by the OGLE group, who were ostensibly searching for optical gravitational lenses towards the LMC. They observed 59 transit-like signatures in foreground Milky Way stars, most of which repeated (Udalski et al. 2002). Of these 59, only one so far has proven in the end to be an ESP (Konacki et al. 2003).
Statistics gathered from high-precision spectroscopic searches for ESPs among F, G, K and M field stars suggest that approximately 1% of the observed objects have giant planets with a period of three to six days. If one considers that around 10% of all possible orbital orientations of short-period giant planets would produce observable transits, the expected frequency of detections becomes about one planet per 3000 stars (Borucki et al. 2001), provided the effects of daytime and the three transit requirement are included. If this is so, the paucity of detections from these various searches is slightly puzzling. It is understandable, perhaps, that ESPs in clusters could be influenced by the dense environment there, affecting planet formation and retention - but not all of the observing campaigns have been towards clusters. It is also possible that a statistical prediction of a small number of ESPs could results in no detections. However, the results from the OGLE survey, which has only one confirmed ESP out of 50 000 stars (Konacki et al. 2003), suggest that the expected frequency of detections determined by Borucki et al. is probably too optimistic.
There are, however, other factors that could affect planet detection. For example, a poorly conceived or implemented differential photometric reduction could increase S/N, hiding transits that would otherwise be detectable. Likewise, the algorithms used to pick the transits out of noise can also have a strong influence on the number of detections. In fact, the work of the OGLE group reveals the effect that improvements in detections algorithms can have. In their first report on the transit-like events from their observing campaign, they identified 46 events with an in-house algorithm described only as a "cross-correlation'' (Udalski et al. 2002). Soon afterwards, they published an update (Udalski et al. 2002) listing 59 events - the new ones identified with an improved algorithm, the BLS technique described by Kovács et al. (2002). There are many algorithms, called detectors in signal processing literature, which can extract signals from data. Therefore, it is possible that the seeming scarcity of photometric ESPs could be caused, at least in part, by the detectors used.
With this possibility raised, a review of the different techniques used for transit identification is overdue, as is a comparative analysis to test the various techniques and to determine which is best under which conditions. Considering the current and future projects that plan to search for ESPs using photometry, this is a rather important line of research, one which has not been adequately addressed in the literature to this point, despite a certain amount of debate on the topic. This study, and future studies along this line, could potentially have a large impact on photometric ESP searches, since pushing the high-confidence detection limit down even a fraction could potentially reveal transits that would otherwise remain unidentified, shrouded in noise.
Planet search campaigns using the photometric technique
are far more likely to discover short-period giant planets. Shortening the
period produces more transits in a given period of time, as well
as increasing the chance that a random orbital orientation will produce
an observable transit. This geometrical effect goes as the inverse of the
planetary orbital radius, or, using Kepler's third law, the period of the
orbit to the
![]() .
This means that, for
example, placing Earth in Mercury's orbit would increase the chance of
transit by a factor of 2.5, while moving it to an orbit with a period of 7
days would increase it by a factor of 14. To skew matters even more in the
favor of short-period planets, short-period giant planets will in theory
be inflated by incident radiation (Guillot et al. 1996).
This conclusion is supported by the derived
characteristics of both the planet around HD 209468 (Burrows et al.
2000) and OGLE-TR-56 (Konacki et al. 2003). This means
that a short-period planet should be larger than an equally-massed planet
further from the parent star and will therefore create deeper transits.
.
This means that, for
example, placing Earth in Mercury's orbit would increase the chance of
transit by a factor of 2.5, while moving it to an orbit with a period of 7
days would increase it by a factor of 14. To skew matters even more in the
favor of short-period planets, short-period giant planets will in theory
be inflated by incident radiation (Guillot et al. 1996).
This conclusion is supported by the derived
characteristics of both the planet around HD 209468 (Burrows et al.
2000) and OGLE-TR-56 (Konacki et al. 2003). This means
that a short-period planet should be larger than an equally-massed planet
further from the parent star and will therefore create deeper transits.
A transit identification algorithm is a mathematical tool that examines
light curves for the presence of transits. In general, this is done by
generating a test statistic (T) for each set of free parameters in some
fashion or another. If this test statistic exceeds a certain value determined
by the desired level of confidence that the event is not a chance occurrence
of noise (![]() ), then the algorithm decides that there is a transit-like
event in the light curve.
), then the algorithm decides that there is a transit-like
event in the light curve.
Detecting a signal in the presence noise is an old and well-studied problem, with a variety of fundamental techniques (or detectors) contained in the literature. However, the application of these various detectors in the special case of transit identification has not been thoroughly explored. While there have been many papers on planetary transit searches published in the past few years, these have primarily been focused on publishing results. The descriptions of the detectors used therein to isolate transit events have been condensed, neglecting a full description of the nuances that arise in this astronomical context. There are only a few exceptions. Kay (1998) states that a matched filter detector is the best in the case of Gaussian noise (white or colored, if pre-whitened), but this is not necessarily going to be the case in all circumstances, especially considering all of the processing that is required to prepare data for transit searches.
A literature search reveals a wide variety of detectors that can be used to identify transits in light curves. The first paper that attempts to deal with the topic of numerical methods for identifying transits is that of Jenkins et al. (1996). It discusses extensively the use of a matched filter detector in an attempt to identify transits in the particularly complicated case of the eclipsing binary CM Draconis. In their studies, Borucki et al. (2001) and Gilliland et al. (2000) used a slight variation on this same technique. In a further attempt to deal with the intricacies of CM Draconis, Doyle et al. (2000) developed a different detector. It is also labeled a matched filter approach, but it is fundamentally different from those used by other groups. To prevent confusion, this detector will hereafter be distinguished as Deeg's approach. Defaÿ et al. (2001) describes a detector based on Bayesian statistics that not only finds transits, but also determines the best-fit shape of the transit. Kovács et al. (2002) devises a box-fitting algorithm (BLS), which is based on direct least squares fits of step functions to the data. This is the only article that attempted to compare existing detectors. Among the detectors used in their comparison - which mostly included ones that were admittedly not designed for the identification of periodic events with short durations - was the Bayesian detector from Defaÿ et al. (2001), which did not fare favorably. Their article did not, however, include the matched filter approach in the analysis, nor were their comparisons completely rigorous, as they involved only a single simulated light curve.
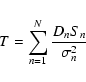 |
(1) |
Implementation of the matched filter approach for transit identification can be significantly more complex than the basic formulation of the matched filter. This becomes readily apparent in the case of CM Draconis. First of all, the binary nature of the system not only affects the light curve with its regular eclipses, but also severely complicates the pattern of transits of any planet which might be present (Jenkins et al. 1996). Secondly, the data are taken at several different telescopes, each with its own CCD camera - or even just two-star photometers in one case - meaning that the quality of the data will vary systematically (Deeg et al. 1998), further muddling time series. Thirdly, all of the good comparison stars in the field were significantly bluer than CM Draconis, which resulted in residual nightly extinction variations (Doyle et al. 2000). Clearly, a simple matched filter approach is not sufficient for this circumstance. Jenkins et al. (1996), cleaned the data to a high degree by subtracting model eclipses. However, this still left the problem with the residual nightly extinction variation, which led the same group to develop another detector.
Deeg's approach is also based on the idea of comparing the data with a series of test signals spanning parameter space. It was specifically designed for the complex circumstances found in a data set of several years of observations of CM Draconis. It differs fundamentally from the matched filter approach described above in that it includes a time-based weighting.
In order to generate their test statistic, Doyle et al. (2000)
generated a test signal with transits included (the with-planet test signal).
They subtracted this with-planet test signal from the light curve for each
individual night of observations and fit a parabola to what remained. Then
they fit a parabola to each individual night of observations, which is intended
to model the residual nightly extinction variation. These fits are then
compared to the original data and the residuals determined. From these
residuals, the test statistic is calculated:
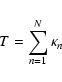 |
(2) |
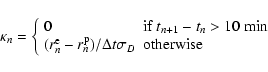
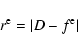
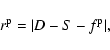
The Bayesian approach described by Defaÿ et al. (2001) is based on a different statistical philosophy than the previously mentioned techniques. In a nutshell, it estimates an unknown parameter through the maximization of a likelihood function, invoking as much prior information as possible in order to improve the estimation.
The primary parameter that Defaÿ et al. fit is the period of the signal
to be detected. They assume that the noise was WGN and then represented the
signal as an unknown Fourier series. By finding the most likely period of
the signal, the coefficients of the Fourier series can then be determined,
fitting the actual shape of the transit. The likelihood function that they
derive, to be maximized for frequency corresponding to the period of the
signal, is
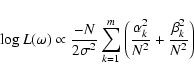 |
(3) |
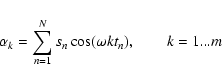 |
(4) |
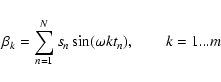 |
(5) |
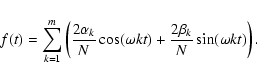 |
(6) |
The box-fitting method described by Kovács et al. (2002) is
essentially a ![]() fit of a square-well transit model to the
observations. Through minimization, they are able to remove the depth of the transit as a free parameter, reducing the computational load.
The expression to be minimized for a given n1 and n2 is
fit of a square-well transit model to the
observations. Through minimization, they are able to remove the depth of the transit as a free parameter, reducing the computational load.
The expression to be minimized for a given n1 and n2 is
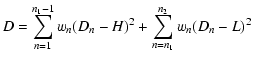 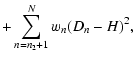 |
(7) |
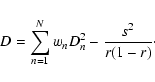 |
(8) |
![\begin{displaymath}T = {\rm max}\left\{\left[\frac{s^{2}({n_1},{n_2})}{r({n_1},{n_2})-[1-r({n_1},{n_2})]}\right]\right\}^{\frac{1}{2}}\cdot
\end{displaymath}](/articles/aa/full/2003/19/aa3043/img40.gif) |
(9) |
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{gausscomp.ps}
\end{figure}](/articles/aa/full/2003/19/aa3043/Timg41.gif) |
Figure 1: This figure shows the comparison between the distribution of the observations used to generate the virtual light curves (dashed line) and a Gaussian distribution (solid line). Notice the excess where the normalized distance from the center of the distribution is greater than 1.1. Despite the fact that it looks large, it is actually due to just 10 out of the 104 observations. |
| Open with DEXTER | |
The correlation is a very basic statistical tool used to measure how well
two samples resemble each other. It is not included here as a serious transit
identification method, but instead primarily as a point of reference.
Since it is not designed for transit identification,
it can be used as a benchmark to measure the effectiveness of the
statistical philosophies behind the various detectors. The textbook
definition of the coefficient of linear correlation is
![\begin{displaymath}T = \frac{\sum_{n=0}^{N-1}(D_{n}-\bar{D})(S_{n}-\bar{S})}
{[...
...{D})^{2}\sum_{n=0}^{N-1}
(S_{n}-\bar{S})^{2}]^{\frac{1}{2}}},
\end{displaymath}](/articles/aa/full/2003/19/aa3043/img42.gif) |
(10) |
Aigrain & Favata (2002) take the same Bayesian philosophies used by Defaÿ et al. (2001) and extend them to assume square well transits. Ultimately, the mathematical basis proves to be very similar to the matched filter, different primarily in the way that parameter space is explored - the matched filter makes cuts across parameter space, while the Bayesian ultimately integrates over parameter space. While this is interesting in and of itself, the limited number of parameters explored in the simulations performed in this analysis would not be sufficient to examine the effect of this difference. For this reason, no attempt to include this approach in this paper is made.
In order to compare the various transit identification techniques, virtual light curves should be generated in as realistic a manner as possible and the most influential parameters must be identified. In addition, a fair method to compare the results of the different techniques must be applied in order to form a definitive conclusion.
Several parameters are needed to characterize the signal caused by
a transiting ESP and more to characterize the observations of one. The
transit itself can be defined by a few physical parameters: depth, width,
time of the first observed transit and period. Including the observations
requires more: the S/N of the
observations, the rate of the observations and the time coverage of the
observations. This proves to be an unwieldy number of parameters to simulate,
so the period is fixed at 3 days and the width at 3 hours. Additionally,
the time of the first transit is also held constant, as it proved not to
make any difference. The depth of the
transit and the S/N are combined into one parameter, the normalized depth
(d). The period and the time coverage are also combined
into one parameter, the number of transits observed (
![]() ).
This leaves only the rate of observations (
).
This leaves only the rate of observations (
![]() ). By varying these
last three parameters, parameter space is covered to a sufficient extent for
an evaluation of detector performance.
). By varying these
last three parameters, parameter space is covered to a sufficient extent for
an evaluation of detector performance.
The standard technique to construct synthetic light curves is to use a random
number generator that produces WGN for the virtual observations. This
is an assumption that does not necessarily represent the properties of
the noise in real data. In order to avoid this, the virtual light curves are
created by drawing individual observations (as opposed to short sequences of
consecutive observations) randomly from a set of more than 104 real observations. This set is derived from observations of
NGC 6791 by Bruntt et al. (in preparation), consisting of data from 17 stars,
each non-variable, from a small region of the main sequence, and with variances
between
![]() and
and
![]() .
The light curve for
each star was
.
The light curve for
each star was ![]() -clipped, first to remove extreme outliers and
again to remove more intermediate outliers that ultimately reduced the
furthest outlier to slightly more than
-clipped, first to remove extreme outliers and
again to remove more intermediate outliers that ultimately reduced the
furthest outlier to slightly more than ![]() .
After this, each light
curve was individually normalized to create the combined set.
.
After this, each light
curve was individually normalized to create the combined set.
It is important to determine how closely this set of observations matches
WGN in order to understand how globally applicable the results from this
article can be. One way of doing this is to compare its right-tail
probabilities with that of the best-fit Gaussian. As the values in the
set are already normalized, a direct comparison to the complementary
cumulative distribution function (
![]() ,
where
,
where
![]() is the error
function) is sufficient. As can be seen in Fig. 1, there is an excess
far out in the wings of the distribution, which can be explained by
approximately 10 outlying observations. This is a very small percentage of
the total, meaning that the distribution strongly resembles the Gaussian
without being identical, which is typical of real observations.
is the error
function) is sufficient. As can be seen in Fig. 1, there is an excess
far out in the wings of the distribution, which can be explained by
approximately 10 outlying observations. This is a very small percentage of
the total, meaning that the distribution strongly resembles the Gaussian
without being identical, which is typical of real observations.
While the study of individual light curves might be instructive on a case by case basis, a Monte Carlo simulation is truly needed to compare the different detectors reliably. For each set of transit parameters, 104 light curves are generated. The temporal spacing of the simulated observations is allowed to vary up to 10% of the average spacing, with no large gaps representing daytime included - although in principle this would only affect the current implementation of the Bayesian approach.
Table 1:
Probabilities of detection for a false alarm rate of 1% for
various transit parameters and detectors.
![]() is the number of transit,
is the number of transit,
![]() is the rate of observations in observations per hour and
d is the depth of the transit in normalized magnitude - effectively
the S/N of the observations.
is the rate of observations in observations per hour and
d is the depth of the transit in normalized magnitude - effectively
the S/N of the observations.
There are two standard ways of comparing the performance of detectors. One is through an examination of Receiver Operating Curves (ROCs), which plot the chance of detection against the chance of false alarm. The better the detector is, the higher it lies in this type of diagram. The worst case scenario - simple guessing - is represented by a straight line with unity slope. These diagrams are easily made with a simple calculation from the with-transits and without-transit distributions for individual detectors and sets of transit parameters. Another way to compare detectors is to calculate the probability of detection at a given probability of false alarm. This is done simply by ranking the without-transit distributions, determining the detection thresholds corresponding to the desired false alarm probabilities (FAPs), and calculating the portions of the with-transit distributions that exceeds these values.
Table 2: This table contains the results from verification simulation, which used the input parameters (3,3,0.5). The first column lists the detectors. The second column lists the probabilities of detection from Table 1 for the same input parameters. The third column liststhe probability of detection based on 106 iterations with a FAP of 1%, while the accompanying errors are the standard deviation calculates from the 100 subsets of 104 iterations in the total sample. The last two columns show the probabilities of detection with false alarm probabilities of 10-3 and 10-4 respectively.
When using Monte Carlo simulations, more events always yield more reliable
results. Unfortunately, some of the algorithms - in particular the Bayesian -
are computationally intensive. Despite the use of a dedicated machine
with
![]() GHz Athlon processors working in parallel, the simulations
took several weeks to run in total, despite holding several of the
key parameters (period and duration) constant. The FAPs
that can be reliably estimated are restricted by the number of events used
in the Monte Carlo simulations. Reducing the FAP produces a broader
distribution in the results for a fixed number of events, which could blur the
distinction between the detectors.
To evaluate detector performance, it is necessary to use as low a FAP as
possible because the distributions are not identical, meaning that one
detector could be better than another at a relatively high FAP but worse
at a lower one.
A balance between these two needs is required. As 104 events were
used for the simulations, a FAP of 1% is suitable, providing a low enough
FAP for a good comparison while keeping the distributions narrow enough to
evaluate detector performance. In order to ascertain the results of this
analysis, a single set of parameters is simulated with 106 events,
allowing both for the widths of the distributions to be estimated and for
lower false alarm probabilities to be examined. This will help to verify
that the relative performance of the different detectors remains more or
less constant.
GHz Athlon processors working in parallel, the simulations
took several weeks to run in total, despite holding several of the
key parameters (period and duration) constant. The FAPs
that can be reliably estimated are restricted by the number of events used
in the Monte Carlo simulations. Reducing the FAP produces a broader
distribution in the results for a fixed number of events, which could blur the
distinction between the detectors.
To evaluate detector performance, it is necessary to use as low a FAP as
possible because the distributions are not identical, meaning that one
detector could be better than another at a relatively high FAP but worse
at a lower one.
A balance between these two needs is required. As 104 events were
used for the simulations, a FAP of 1% is suitable, providing a low enough
FAP for a good comparison while keeping the distributions narrow enough to
evaluate detector performance. In order to ascertain the results of this
analysis, a single set of parameters is simulated with 106 events,
allowing both for the widths of the distributions to be estimated and for
lower false alarm probabilities to be examined. This will help to verify
that the relative performance of the different detectors remains more or
less constant.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{rocs.ps}
\end{figure}](/articles/aa/full/2003/19/aa3043/Timg57.gif) |
Figure 2:
The plot on the left shows the Receiver Operating Curves
for all five detectors used in the simulations for the fixed set of parameters
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{Pdstraight.ps}
\end{figure}](/articles/aa/full/2003/19/aa3043/Timg59.gif) |
Figure 3:
A plot of
|
| Open with DEXTER | |
The simulations were performed and the results are shown in Table 1, which contains the input parameters (the number of transits, the rate of observations, and the depth of the transits) and the probabilities of detection for the different detectors described above. They demonstrate clearly that the matched filter is the superior detector. It is followed unexpectedly by the simple correlation and then Deeg's approach. The BLS and the Bayesian are significantly worse, despite the fact that these are the only two detectors that have had papers in the astronomical literature on them specifically. Table 2 demonstrates that the results in Table 1 are reliable, as the scatter of the distributions derived is less than the difference between the detectors and that the rank of the detectors does not change as the FAP is reduced. A pair of ROCs is given in Fig. 2. The left panel shows the response for different detectors to a single set of input parameters (3,5,0.5) and the right panel shows the response of a single detector (the matched filter approach) to different sets of input parameters.
The response of these different detectors to changes in parameters can also provide insight into their performance. From inspection, or just from a basic understanding of statistics, it seems likely that the significant parameters that govern the detectability of a transit are the number of observations of the planet during transit and the S/N of those observations. The number of observations during transit in these simulations is proportional to the rate of observations and the number of transits observed. The S/N is related to the depth of the transit in the simulations performed, as one can equate changing the depth of the transit to changing the S/N of the observations. These two fundamental parameters are also related in another way, as the S/N is inversely proportional to the square root of the exposure time.
In order to determine if there might be some definable relationship between
these fundamental parameters and the probability of detection, an
understanding of the latter must be obtained. If the with-transit
distribution is Gaussian, then the probability of detection will be equal
to the integral of this Gaussian from the point of the chosen false alarm
probability to infinity. This has no simple, analytical solution, but it
is
related to the exponential, which provides a starting point for the empirical
investigation. Figure 3 shows a plot of the number of observations during
transit times the square of the S/N (depth) versus
![]() ,
where
,
where
![]() is the probability of detection. While the fit is not
perfect, it does strongly suggest that the probability of detection can be
well-estimated from fundamental parameters. This is particularly true at
moderate to high probabilities, which is the region of interest. Hopefully this
will also mean that an estimation like this is possible for the false alarm
probability, although that analysis is beyond the scope of
the simulations performed here, as it would require several orders of magnitude
more iterations.
is the probability of detection. While the fit is not
perfect, it does strongly suggest that the probability of detection can be
well-estimated from fundamental parameters. This is particularly true at
moderate to high probabilities, which is the region of interest. Hopefully this
will also mean that an estimation like this is possible for the false alarm
probability, although that analysis is beyond the scope of
the simulations performed here, as it would require several orders of magnitude
more iterations.
A Monte Carlo simulation using randomly generated light curves drawn from a set of real data to compare the effectiveness of the different planetary transit identification algorithms has been performed. Of the methods tested, which included the matched filter approach, the linear correlation, the Bayesian of Defaÿ et al. (2001), the BLS of Kovács et al. (2002) and modified matched filter detector of Doyle et al. (2000), the matched filter demonstrated the best performance, while the BLS and the Bayesian both performed poorly by comparison.
An important thing to consider before dismissing the BLS and the Bayesian is that both of these detectors searched not only for the best phase but also for the best period, while the other detectors searched only for the best period in these simulations. This extra free parameter could certainly affect the results of the Monte Carlo simulations, even though the period search was strongly limited to a region close to the known period. Additionally, neither one of these techniques has the depth of the transit per se as a free parameter. However, the true advantage of this was not seen in the simulations in this paper, as only the known depth of the transit was searched for. This means that the approaches that had depth as a free parameter (the matched filter, the linear correlation, and Deeg's approach) were not entirely accurately represented, as they would otherwise have required more statistical tests, which would increase the overall level of the false alarms, reducing the detection probability at a FAP of 1%. Perhaps it is not surprising, then, that these three approaches ranked as the three best. As with Aigrain's approach, further analysis covering more parameters might be necessary for a completely accurate comparison.
The BLS, as stated in its description in Sect. 2.4, makes use of a ![]() fit. Interestingly, an expectation of the relative performance of a
fit. Interestingly, an expectation of the relative performance of a
![]() fit and the matched filter approach can inferred mathematically.
They are in fact closely related, the
fit and the matched filter approach can inferred mathematically.
They are in fact closely related, the ![]() fit being one type of purely
statistical test and the likelihood ratio from which the matched filter is
derived being another. It becomes evident when one expands the basic
formulation for the
fit being one type of purely
statistical test and the likelihood ratio from which the matched filter is
derived being another. It becomes evident when one expands the basic
formulation for the ![]()
| |
= | 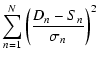 |
|
| = | ![$\displaystyle \sum_{n=1}^{N}\left[\left(\frac{D_{n}}{\sigma_{n}}\right)^{2}-2\l...
...}S_{n}}{\sigma_{n}}^{2}\right)+\left(\frac{S_{n}}{\sigma_{n}}\right)^{2}\right]$](/articles/aa/full/2003/19/aa3043/img62.gif) |
(11) |
The Bayesian approach exhibits several qualities that could affect its performance, related to the fact that it performs a Fourier fit to the shape of the transit. Defaÿ et al. (2001) state that this is an improvement over the matched filter approaches offered by Jenkins et al. (1996) and Doyle et al. (2000). However, according to Kay (1998), the use of known information to improve the chance of making the proper decision between hypotheses is one of the central ideas of the Bayesian philosophy. As the shape of any planetary transit can be represented very well by square wells of different depths and widths, it would seem that this information could be used to improve the chance of making an identification. Furthermore, this algorithm limits the number of frequencies used to make the fit to m=7, which the authors claim is sufficient. However, when using a multi-frequency Fourier fit, it is crucial to have enough frequencies to fit the ultimate transit shape accurately. Otherwise, signal energy will be lost, hurting the performance of the detector.
Lastly, in addition to the comparison of the detectors, there appears to be something of an empirical relation between the fundamental parameters (the number of observations during transit and the S/N of those observations) and the probability of detection at a fixed false alarm probability. The realization that transit signal energy is defined by the number of observations during transit times the square of the S/N of those observations is an important result itself, one that could be used to expand free parameter space later simulations without drastically increasing computational load.
Acknowledgements
Many thanks go to Jon Jenkins at SETI Institute for the great improvement he coaxed out of this paper with his patience and thorough refereeing. I would like to thank the Danish Natural Sciences Research Council for financial support. And finally I would like to thank Hans Kjeldsen and Jørgen Christiansen-Dalsgaard for all the support they have provided me over the past two years.