We present new single-dish (30-m) observations and an improved analysis of our earlier interferometric observations (Simon et al. 2002) of BP Tau
A&A 402, 1003-1011 (2003)
DOI: 10.1051/0004-6361:20030317
A. Dutrey 1 - S. Guilloteau 2 - M. Simon 3
1 - Laboratoire d'Astrophysique de l'Observatoire de
Grenoble, BP 53, 38041 Grenoble Cedex 9, France
2 -
Institut de
Radio Astronomie Millimétrique, 300 rue de la Piscine, 38406
Saint Martin d'Hères, France
3 -
Dept. of Physics and
Astronomy, State Univ. of New York, Stony Brook, NY 11794-3800,
USA
Received 9 August 2002 / Accepted 30 January 2003
Abstract
We present new single-dish (30-m) observations
and an improved analysis of our earlier
interferometric observations (Simon et al. 2002)
of BP Tau![]() . Our analysis yields
a detailed description of
the properties of the circumstellar disk.
The disk is small (outer radius 120 AU) and marginally optically thick in the
. Our analysis yields
a detailed description of
the properties of the circumstellar disk.
The disk is small (outer radius 120 AU) and marginally optically thick in the
![]()
![]() line. It is also relatively hot, about 50 K at 100 AU. The mm continuum emission is
consistent with a thermal emission from circumstellar dust with an emissivity index
line. It is also relatively hot, about 50 K at 100 AU. The mm continuum emission is
consistent with a thermal emission from circumstellar dust with an emissivity index
![]() ,
and a disk mass about
,
and a disk mass about
![]() .
The anomalously low
.
The anomalously low
![]() to dust
emission ratio implies that either CO is depleted by a factor of the order of 150 with
respect to H2, or has a very low gas to dust ratio, or highly anomalous dust properties.
The disk exhibits direct evidence of Keplerian rotation, but because of a combination of
insufficient resolution and optically thin CO emission, the mass derived for the star
remains inaccurate (between 0.6 and
to dust
emission ratio implies that either CO is depleted by a factor of the order of 150 with
respect to H2, or has a very low gas to dust ratio, or highly anomalous dust properties.
The disk exhibits direct evidence of Keplerian rotation, but because of a combination of
insufficient resolution and optically thin CO emission, the mass derived for the star
remains inaccurate (between 0.6 and
![]() for 140 pc). The unusual properties of the
circumstellar disk suggest that BP Tau may be a transient object in the process of clearing
its disk.
for 140 pc). The unusual properties of the
circumstellar disk suggest that BP Tau may be a transient object in the process of clearing
its disk.
Key words: stars: circumstellar matter - stars: pre-main sequence - radio lines: stars
CO line observations of low-mass Pre-Main-Sequence (PMS) stars in
Taurus-Auriga (![]() 140 pc, Kenyon et al. 1994) provide strong evidence that many of them
are surrounded by large (
140 pc, Kenyon et al. 1994) provide strong evidence that many of them
are surrounded by large (
![]() AU) Keplerian disks (GM Aur: Koerner
et al. 1993; GG Tau: Dutrey et al. 1994; MWC 480: Mannings et al. 1997). On the other
hand, recent submillimeter, NIR and optical observations of nearby young stars that have
already reached the Zero-Age-Main-Sequence (ZAMS) reveal that stars such as
AU) Keplerian disks (GM Aur: Koerner
et al. 1993; GG Tau: Dutrey et al. 1994; MWC 480: Mannings et al. 1997). On the other
hand, recent submillimeter, NIR and optical observations of nearby young stars that have
already reached the Zero-Age-Main-Sequence (ZAMS) reveal that stars such as ![]() Pic are
surrounded by optically thin dust disks (
Pic are
surrounded by optically thin dust disks (![]() Pic: Mouillet et al. 1997; Vega: Holland
et al. 1998, HR 4796: Schneider et al. 1999). These disks, unlike the ones surrounding T Tauri stars, do not contain a significant amount of gas (Lagrange et al. 1995) and dust
(Chini et al. 1991). They are thought to be second generation disks, associated with young
stars that have already dissipated the gas and dust surviving from the parent molecular
cloud, possibly to form planets. In these "debris disks'', the dust is believed to come
from the collision of larger bodies while most of the gas would be released from falling
and evaporating bodies (FEB) similar to comets, e.g.
Pic: Mouillet et al. 1997; Vega: Holland
et al. 1998, HR 4796: Schneider et al. 1999). These disks, unlike the ones surrounding T Tauri stars, do not contain a significant amount of gas (Lagrange et al. 1995) and dust
(Chini et al. 1991). They are thought to be second generation disks, associated with young
stars that have already dissipated the gas and dust surviving from the parent molecular
cloud, possibly to form planets. In these "debris disks'', the dust is believed to come
from the collision of larger bodies while most of the gas would be released from falling
and evaporating bodies (FEB) similar to comets, e.g. ![]() Pic (Vidal-Madjar et al. 1998). Astronomers have not been successful in identifying stars that
are dissipating their
primary gas and dust disks in transition between having
primary and secondary disks. T Tauri stars older than 107 years (usually Weak-line T Tauri stars and Naked T Tauri
stars) do not present mm emission in either CO or in the submillimeter continuum (Osterloh
& Beckwith 1995; Duvert et al. 2000).
Pic (Vidal-Madjar et al. 1998). Astronomers have not been successful in identifying stars that
are dissipating their
primary gas and dust disks in transition between having
primary and secondary disks. T Tauri stars older than 107 years (usually Weak-line T Tauri stars and Naked T Tauri
stars) do not present mm emission in either CO or in the submillimeter continuum (Osterloh
& Beckwith 1995; Duvert et al. 2000).
BP Tau is a prominent "classic'' T Tauri (CTT) star (e.g. Herbig
& Bell 1988). It
experiences high mass accretion
![]() from its
circumstellar disk, which produces its strong excess emission in the ultraviolet, visible,
and near infrared (Gullbring et al. 1998,
2000). It is very young; Gullbring et al.
(1998) estimate
from its
circumstellar disk, which produces its strong excess emission in the ultraviolet, visible,
and near infrared (Gullbring et al. 1998,
2000). It is very young; Gullbring et al.
(1998) estimate
![]() yr for its age. Yet,
despite these strong CTT characteristics, we found that its
yr for its age. Yet,
despite these strong CTT characteristics, we found that its
![]()
![]()
![]() line emission is unexpectedly weak,
apparently because it is optically thin (Simon et al. 2000, hereafter SDG). Realizing that
BP Tau could represent an object that is dissipating its disk at a very young age, we
undertook further analysis of our millimeter wave observations of this star. We obtained
new single-dish CO observations. Using improved phase calibration techniques, we carried
out a recalibration of our 1998-99 data and also were able to add data originally unusable.
Our new analysis enables us to derive properties of BP Tau's circumstellar disk. We report
our results here.
line emission is unexpectedly weak,
apparently because it is optically thin (Simon et al. 2000, hereafter SDG). Realizing that
BP Tau could represent an object that is dissipating its disk at a very young age, we
undertook further analysis of our millimeter wave observations of this star. We obtained
new single-dish CO observations. Using improved phase calibration techniques, we carried
out a recalibration of our 1998-99 data and also were able to add data originally unusable.
Our new analysis enables us to derive properties of BP Tau's circumstellar disk. We report
our results here.
![\begin{figure}
\par\includegraphics[angle=270,width=18cm,clip]{ms3001f1.eps}
\end{figure}](/articles/aa/full/2003/18/aa3001/Timg27.gif) |
Figure 1:
Channel maps of the BP Tau
|
| Open with DEXTER | |
The observations used 5 antennas and were carried out in winter 1998/1999 in D,
C2 and B1 configurations. Baselines up to 300 m provided
![]() resolution at PA
resolution at PA ![]() for the 1.3 mm continuum data.
The total on source
integration time is
for the 1.3 mm continuum data.
The total on source
integration time is ![]() 20 hours. We observed simultaneously at 89.2 GHz
(HCO+
20 hours. We observed simultaneously at 89.2 GHz
(HCO+
![]() )
and 230.5 GHz (
)
and 230.5 GHz (
![]()
![]() ). At 1.3 mm, the tuning was
double-side-band (DSB) while at 3.4 mm, the tuning was purely single-side band
(LSB). The backend was a correlator with one band of 10 MHz (spectral
resolution 0.23
). At 1.3 mm, the tuning was
double-side-band (DSB) while at 3.4 mm, the tuning was purely single-side band
(LSB). The backend was a correlator with one band of 10 MHz (spectral
resolution 0.23
![]() )
centered on the HCO+
)
centered on the HCO+
![]() line, one band of 20 MHz
(0.18
line, one band of 20 MHz
(0.18
![]() resolution) centered on the
resolution) centered on the
![]()
![]()
![]() line, and 2 bands of 160 MHz
for the 1.3 mm and 3.4 mm continuum, respectively. The phase and flux
calibrators were 0415+379 and 0528+134. The rms phase
noise was 8
line, and 2 bands of 160 MHz
for the 1.3 mm and 3.4 mm continuum, respectively. The phase and flux
calibrators were 0415+379 and 0528+134. The rms phase
noise was 8
![]() to 25
to 25
![]() and 15
and 15
![]() to 50
to 50
![]() at 3.4 mm and
1.3 mm, respectively, which
introduced position errors of <
at 3.4 mm and
1.3 mm, respectively, which
introduced position errors of <
![]() .
The estimated seeing is about 0.3''.
.
The estimated seeing is about 0.3''.
Between 1999 and 2000, we improved at IRAM the method to calibrate the 1.3 mm data (details can be found in the manuals given at http://iram.fr/PDBI/bure.html). The long baseline observations were re-calibrated accordingly, and some data originally unusable were added. Because the disk is so small, small phase calibration errors and/or seeing effects can results in systematic effects making the disk appear more face-on. Amplitude errors can also have a similar effect. These effects are partially removed by the new calibration process.
We used the GILDAS software package to reduce the data. Images were produced in natural weighting of the visibilities for both the continuum and line maps.
We detected the CO
![]() line emission
and 1.3 mm and 3.4 mm continuum emission in BP Tau. Figure 1 presents
channel maps of the CO
line emission
and 1.3 mm and 3.4 mm continuum emission in BP Tau. Figure 1 presents
channel maps of the CO
![]() ,
with the velocity gradient map. Compared to SDG, the figure
appears qualitatively similar. Figure 2 shows a comparison of the integrated
CO
,
with the velocity gradient map. Compared to SDG, the figure
appears qualitatively similar. Figure 2 shows a comparison of the integrated
CO
![]() map and the 1.3 mm map. Continuum emission was subtracted to produce the CO maps
presented in Figs. 1, 2 and the integrated flux given in Table 1. Flux density measurements and formal deconvolved Gaussian source sizes are
given in Table 1 for the dust and CO disks. The
map and the 1.3 mm map. Continuum emission was subtracted to produce the CO maps
presented in Figs. 1, 2 and the integrated flux given in Table 1. Flux density measurements and formal deconvolved Gaussian source sizes are
given in Table 1 for the dust and CO disks. The
![]() emission is resolved
while the 1.3 mm continuum appears only marginally resolved.
emission is resolved
while the 1.3 mm continuum appears only marginally resolved.
With a value of
![]() ,
the spectral index of the continuum is fully
consistent with thermal dust emission, mostly optically thin.
,
the spectral index of the continuum is fully
consistent with thermal dust emission, mostly optically thin.
Table 1: Apparent sizes derived from PdBI data.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{ms3001f2.eps}
\end{figure}](/articles/aa/full/2003/18/aa3001/Timg40.gif) |
Figure 2:
Integrated
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3001f3.eps}
\end{figure}](/articles/aa/full/2003/18/aa3001/Timg42.gif) |
Figure 3:
Spectra of
|
| Open with DEXTER | |
In order to estimate the
![]() column density inside the disk and to assess confusion from
molecular clouds, we observed the
column density inside the disk and to assess confusion from
molecular clouds, we observed the
![]()
![]() and
and
![]() lines, and the
lines, and the
![]()
![]() line with the
30-m telescope in August 1999. Two lines were observed simultaneously using the dual
frequency, dual polarization receivers of the 30-m telescope. Total integration times were 45 hours for the
line with the
30-m telescope in August 1999. Two lines were observed simultaneously using the dual
frequency, dual polarization receivers of the 30-m telescope. Total integration times were 45 hours for the
![]()
![]() line, 33 hours for the
line, 33 hours for the
![]()
![]() line and 13 hours for the
line and 13 hours for the
![]()
![]() line. The last transition was observed to check the ability to detect the BP Tau
disk despite the confusion with the molecular cloud along the line of sight.
line. The last transition was observed to check the ability to detect the BP Tau
disk despite the confusion with the molecular cloud along the line of sight.
We proceeded in two steps. We first took spectra in frequency switching mode to measure the
total intensities of the lines. We then proceeded with long integrations in wobbler
switching (with an offset of 30'') which removes the signal of most of the surrounding
material, because of the apparent rotation of the reference beam on the sky. Results are
presented in Fig. 3 and in Table 2. The 30-m
![]()
![]() spectrum
suffers from confusion in the velocity range 6-9 km s-1, but the line wings agree
very well with the spectrum obtained from the interferometric measurement (see
Fig. 3). For the
spectrum
suffers from confusion in the velocity range 6-9 km s-1, but the line wings agree
very well with the spectrum obtained from the interferometric measurement (see
Fig. 3). For the
![]()
![]() ,
where confusion is much more limited, there is
no detectable signal in the beam switch spectrum of the 30-m, except for two weak narrow
(0.5 km s-1) residual lines at the cloud velocities. In particular, in the blue wing
of the BP Tau disk emission, where no confusion occurs, we only get a
,
where confusion is much more limited, there is
no detectable signal in the beam switch spectrum of the 30-m, except for two weak narrow
(0.5 km s-1) residual lines at the cloud velocities. In particular, in the blue wing
of the BP Tau disk emission, where no confusion occurs, we only get a ![]() limit in
limit in
![]()
![]() of 0.12 Jy
of 0.12 Jy
![]() .
.
Comparison of the 30-m frequency switch and wobbler switch spectra (Figs. 3a,b) clearly shows that BP Tau is embedded in or lying in front of a molecular cloud. The
cloud actually has two velocity components, at 7.03 and 8.00
![]() respectively. The
measured antenna temperatures of the
respectively. The
measured antenna temperatures of the
![]()
![]() (2.35 K, not shown) and
(2.35 K, not shown) and
![]() (1.35 K, see
Fig. 3a) indicate a low density medium with sub-thermal excitation. The
[
(1.35 K, see
Fig. 3a) indicate a low density medium with sub-thermal excitation. The
[
![]() ]/[
]/[
![]() ]
line intensity ratios are 23 and 14 for both components, which,
considering possible enhancement of
]
line intensity ratios are 23 and 14 for both components, which,
considering possible enhancement of
![]() abundance by fractionation effects, indicates
essentially optically thin
abundance by fractionation effects, indicates
essentially optically thin
![]()
![]() emission (
emission (
![]() ). The
). The
![]()
![]() line appears
completely optically thin.
line appears
completely optically thin.
Table 2: 30-m data, line parameters.
From the LVG curves of Goldsmith et al. (1983), we derive an H2 density of ![]()
![]() cm-3, and an
cm-3, and an
![]() of order 10-6. Using the Taurus
abundance for CO relative to H2,
of order 10-6. Using the Taurus
abundance for CO relative to H2,
![]() (Cernicharo & Guélin 1987), and the
line width of
(Cernicharo & Guélin 1987), and the
line width of
![]() ,
we find an H2 column density of
,
we find an H2 column density of
![]() cm-2,
corresponding to
cm-2,
corresponding to
![]() .
However, at such low extinctions, CO is much less
abundant. Using
.
However, at such low extinctions, CO is much less
abundant. Using
![]() would give
would give
![]() ,
in agreement
with the extinction measured by Hartmann et al. (1998). The BP Tau disk could thus be
equally located behind one of the molecular clouds (or both), or in front of them if the
extinction is intrinsic to the disk.
,
in agreement
with the extinction measured by Hartmann et al. (1998). The BP Tau disk could thus be
equally located behind one of the molecular clouds (or both), or in front of them if the
extinction is intrinsic to the disk.
Given the small cloud opacity in the
![]()
![]() line, emission from the BP Tau disk, whose
systemic velocity is
line, emission from the BP Tau disk, whose
systemic velocity is
![]() ,
is free of any confusion at velocities outside
the
,
is free of any confusion at velocities outside
the
![]() range (see Fig. 3). Between 5.9 and 8.9
range (see Fig. 3). Between 5.9 and 8.9
![]() ,
the
appearance of the BP Tau disk in
,
the
appearance of the BP Tau disk in
![]() could be distorted by absorption by the molecular
cloud. We have checked that the apparent symmetry of the
could be distorted by absorption by the molecular
cloud. We have checked that the apparent symmetry of the
![]()
![]() profile (see
Fig. 3) and images (see Fig. 1) obtained with the
interferometer implies that absorption from any of the two velocity component of the
molecular cloud has an opacity less than 0.3, and contaminates the emission at a level at
most comparable to the noise. Parameters derived from the interferometer data are thus
essentially unbiased if the BP Tau disk is located behind the molecular cloud.
profile (see
Fig. 3) and images (see Fig. 1) obtained with the
interferometer implies that absorption from any of the two velocity component of the
molecular cloud has an opacity less than 0.3, and contaminates the emission at a level at
most comparable to the noise. Parameters derived from the interferometer data are thus
essentially unbiased if the BP Tau disk is located behind the molecular cloud.
Many of the parameters we derive from our analysis depend on the radial extent of the disk, and hence the actual distance to BP Tau. Table 3 provides the distance dependence of the measured disk parameters, and their value at the average distance of the Taurus cluster, 140 pc (Kenyon et al. 1994).
Table 3: Distance dependence of the parameters.
To estimate the properties of the BP Tau disk, we used a standard disk model (e.g. Pringle
1981) and the ![]() disk fitting procedures described in Guilloteau & Dutrey (1998).
The CO analysis is performed on the data containing the continuum.
disk fitting procedures described in Guilloteau & Dutrey (1998).
The CO analysis is performed on the data containing the continuum.
To model both the CO and the continuum data, we proceed as follows. We performed a ![]() minimization on the CO data and in a second step, we use the kinetic temperature derived
from the CO analysis to model the continuum data at 3.4 and 1.3 mm (both the CO and the
dust emissions are mostly optically thin and should trace the same region). In this way we
obtain an estimate of the H2 mass and the density. This value is also used to determine
the depletion factor
minimization on the CO data and in a second step, we use the kinetic temperature derived
from the CO analysis to model the continuum data at 3.4 and 1.3 mm (both the CO and the
dust emissions are mostly optically thin and should trace the same region). In this way we
obtain an estimate of the H2 mass and the density. This value is also used to determine
the depletion factor
![]()
![]() ]. We then iterate
the minimization with these new parameters for the CO data and the continuum. The results
are given in Table 4.
]. We then iterate
the minimization with these new parameters for the CO data and the continuum. The results
are given in Table 4.
Table 4:
Best parameters for the BP Tau disk (CO
![]() data and continuum).
data and continuum).
The ![]() fitting procedure indicates that the radial dependence of the velocity is
fitting procedure indicates that the radial dependence of the velocity is
![]() ,
so the rotation is Keplerian. The disk is found to be small, with an
outer radius of 120 AU. Although
,
so the rotation is Keplerian. The disk is found to be small, with an
outer radius of 120 AU. Although
![]() usually allows direct determination of the disk
kinematics, and hence of the stellar mass (Guilloteau & Dutrey 1998; Simon et al. 2000),
the analysis of the BP Tau disk is complicated by a combination of two facts.
usually allows direct determination of the disk
kinematics, and hence of the stellar mass (Guilloteau & Dutrey 1998; Simon et al. 2000),
the analysis of the BP Tau disk is complicated by a combination of two facts.
First, the
![]()
![]() line appears only moderately optically thick. For the best fit model,
the peak optical depth of the
line appears only moderately optically thick. For the best fit model,
the peak optical depth of the
![]()
![]() line is only 3, and in most of the disk (i.e. at
radii greater than about 50 AU) the line remains optically thin. Since in the optically
thin regime and high temperature limit, the line emission is proportional at first order to
line is only 3, and in most of the disk (i.e. at
radii greater than about 50 AU) the line remains optically thin. Since in the optically
thin regime and high temperature limit, the line emission is proportional at first order to
![]() (in the Rayleigh Jeans approximation, with constant
linewidth and X(r) being the molecular abundance with respect to H2, see Dartois
et al. 2003), the limited optical depth of
(in the Rayleigh Jeans approximation, with constant
linewidth and X(r) being the molecular abundance with respect to H2, see Dartois
et al. 2003), the limited optical depth of
![]()
![]() line leads to a relatively strong
coupling between the kinetic temperature distribution (Tk(r), q) and the CO molecular
density (
line leads to a relatively strong
coupling between the kinetic temperature distribution (Tk(r), q) and the CO molecular
density (
![]() ,
s).
,
s).
Second, the disk is small and only moderately resolved. In such a case, there is a
significant coupling between the brightness temperature distribution and the outer radius
![]() .
Steeper distributions can be compensated for by a larger radius; CO being
optically thin, the outer brightness distribution goes with p-q, so that a steeper
distribution means a lower value of q. A larger radius will require a higher disk
inclination to maintain the same total line flux, and thus modify the derived stellar mass
through the derivation of the
.
Steeper distributions can be compensated for by a larger radius; CO being
optically thin, the outer brightness distribution goes with p-q, so that a steeper
distribution means a lower value of q. A larger radius will require a higher disk
inclination to maintain the same total line flux, and thus modify the derived stellar mass
through the derivation of the
![]() parameters. Unfortunately, this degeneracy is
quite significant. Depending on the assumption on q, we found through minimizations that
the stellar mass could vary between 1.3 and 0.6
parameters. Unfortunately, this degeneracy is
quite significant. Depending on the assumption on q, we found through minimizations that
the stellar mass could vary between 1.3 and 0.6
![]() (for a distance D=140 pc) when q varied from 0.5 to -0.1, corresponding to inclinations varying between
28
(for a distance D=140 pc) when q varied from 0.5 to -0.1, corresponding to inclinations varying between
28![]() and 43
and 43![]() respectively. Assuming that the disk mid-plane and the star rotation axis are
perpendicular, the stellar period (Bouvier et al. 1986) and the
respectively. Assuming that the disk mid-plane and the star rotation axis are
perpendicular, the stellar period (Bouvier et al. 1986) and the ![]() of the star
(Hartman et al. 1986) can give an upper limit for the inclination angle,
of the star
(Hartman et al. 1986) can give an upper limit for the inclination angle,
![]() .
This limit is consistent with our data, but does not allow us to select between the two
extreme solutions.
.
This limit is consistent with our data, but does not allow us to select between the two
extreme solutions.
This degeneracy is a significant limitation of the current data. To avoid consequences of
this problem for the other disk parameters, we proceeded as follows. We fixed q = 0.3,
which was at all times the most positive value to be within 1 ![]() of the best fit in
the (
T100, q)
of the best fit in
the (
T100, q) ![]() plane.
plane.
Once q is fixed, the other couplings introduced by the partial optical thickness of CO
are illustrated in Fig. 4, which displays ![]() surfaces showing the
coupling between the CO depletion
surfaces showing the
coupling between the CO depletion
![]() and Tk, and between Tk
and
and Tk, and between Tk
and
![]() .
Since both couplings are relatively weak,
.
Since both couplings are relatively weak,
![]() is well
determined in all cases.
is well
determined in all cases.
Starting from this value of
![]() ,
we proceeded to perform 2-parameter
minimizations, with the density law exponent s fixed:
(T100,
,
we proceeded to perform 2-parameter
minimizations, with the density law exponent s fixed:
(T100,
![]() ), (
), (
![]() ,
,
![]() ,
and finally
,
and finally
![]() .
The whole process
was iterated several times to guarantee convergence.
At each step, (T100, q) was checked
to verify that q=0.3 was within
.
The whole process
was iterated several times to guarantee convergence.
At each step, (T100, q) was checked
to verify that q=0.3 was within ![]() .
.
The above process does not allow a separation of X(r) (or
![]() )
from
)
from ![]() .
We use the continuum emission from dust to provide an independent measurement
of
.
We use the continuum emission from dust to provide an independent measurement
of ![]() .
Dust emission being optically thin at such wavelengths, the continuum is
proportional to
.
Dust emission being optically thin at such wavelengths, the continuum is
proportional to
![]() .
Using
.
Using
![]() (see Beckwith et al. 1990), the measurements at 3.4 mm
and 1.3 mm allow us to constrain
(see Beckwith et al. 1990), the measurements at 3.4 mm
and 1.3 mm allow us to constrain ![]() ,
and thus
,
and thus
![]() .
Since Tk(r) has been
measured from the CO emission,
.
Since Tk(r) has been
measured from the CO emission, ![]() is determined. The dust emission also directly
constrainsp+q (see Pietu et al. 2003). We find
is determined. The dust emission also directly
constrainsp+q (see Pietu et al. 2003). We find
![]() .
Since the density
exponent is
s = p+1.5-q/2, this value is in agreement with (but more accurate than) that
derived from the measurement of s and q from
.
Since the density
exponent is
s = p+1.5-q/2, this value is in agreement with (but more accurate than) that
derived from the measurement of s and q from
![]() ,
which corresponds to
,
which corresponds to
![]() .
.
Since q is rather poorly constrained, p ranges from
![]() (for
(for
![]() as in DM Tau or GM Aur Guilloteau & Dutrey 1998; Dutrey et al. 1998), to
as in DM Tau or GM Aur Guilloteau & Dutrey 1998; Dutrey et al. 1998), to
![]() for our assumed value of q=0.3. The total mass derived from the nominal best model
is
for our assumed value of q=0.3. The total mass derived from the nominal best model
is
![]() ,
and the surface density at 100 AU 0.06 g cm-2 (of dust and
gas).
,
and the surface density at 100 AU 0.06 g cm-2 (of dust and
gas).
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms3001f4.eps}
\end{figure}](/articles/aa/full/2003/18/aa3001/Timg130.gif) |
Figure 4:
|
| Open with DEXTER | |
In this section, we first present the new stellar mass estimate and then we discuss the physical parameters of this disk, with respect to the limitation of the data, and compare them to the properties of disk encountered around other single CTTs such as DM Tau (Guilloteau & Dutrey 1998) or GM Aur (Dutrey et al. 1998).
The estimate for the mass of BP Tau that we determine,
![]() (Table 3), at the 140 pc fiducial
distance, is consistent with our earlier estimate,
(Table 3), at the 140 pc fiducial
distance, is consistent with our earlier estimate,
![]() (SDG). However, these error bars do not
include the coupling with other parameters. The coupling between q and
(SDG). However, these error bars do not
include the coupling with other parameters. The coupling between q and
![]() will result in lower values for M* for
smaller q, and higher values for larger q. For q=-0.1, the
derived mass becomes
will result in lower values for M* for
smaller q, and higher values for larger q. For q=-0.1, the
derived mass becomes
![]() .
.
Figure 5 shows these two extreme values of BP Tau's distance-independent
parameter L/M*2 plotted on a modified H-R diagram in the same format as in Fig. 3 of SDG. We use estimates of BP Tau's luminosity,
![]() ,
and spectral type, K7, from
Gullbring et al. (1998), as before. The L/M2 value lies between D'Antona &
Mazzitelli's (1997) tracks for 0.5 and 0.6
,
and spectral type, K7, from
Gullbring et al. (1998), as before. The L/M2 value lies between D'Antona &
Mazzitelli's (1997) tracks for 0.5 and 0.6
![]() stars, on the 0.8
stars, on the 0.8
![]() track of
Baraffe et al. (1998), and similarly for the tracks calculated by Palla & Stahler (1999)
and Siess et al. (2000). Our mass uncertainty rather affects the distance and the age
determination, since the dynamical mass obtained by our technique scales linearly with
distance (Table 3). Using M* = 0.8 from the evolutionary tracks, the distance derived
from the dynamical mass is
track of
Baraffe et al. (1998), and similarly for the tracks calculated by Palla & Stahler (1999)
and Siess et al. (2000). Our mass uncertainty rather affects the distance and the age
determination, since the dynamical mass obtained by our technique scales linearly with
distance (Table 3). Using M* = 0.8 from the evolutionary tracks, the distance derived
from the dynamical mass is ![]() pc for q=0.3, but becomes larger for smaller
values of q. This is a hint of, but not a strong argument for, a distance somewhat closer
than 140 pc (e.g. Favata et al. 1998, and see also Bertout et al.
1999).
pc for q=0.3, but becomes larger for smaller
values of q. This is a hint of, but not a strong argument for, a distance somewhat closer
than 140 pc (e.g. Favata et al. 1998, and see also Bertout et al.
1999).
It is worth stressing that all the other sources in the SDG sample possess optically thick CO disks that are much larger and brighter, so their outer radius, temperature law (q), inclination and hence stellar masses are quite reliably determined.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ms3001f5.eps}
\end{figure}](/articles/aa/full/2003/18/aa3001/Timg136.gif) |
Figure 5:
The location of BP Tau in the (L/M2 vs.
|
| Open with DEXTER | |
The BP Tau disk differs from all the other disks imaged in
![]() so far in two main
aspects: 1) both CO and dust emissions are very compact, and 2) the data itself, as we
argue in Sect. 2.3, shows that the CO is optically thin. Because of the latter point, the
radial profiles of density and temperature are coupled and the analysis is complicated by
the small angular size of the disk.
so far in two main
aspects: 1) both CO and dust emissions are very compact, and 2) the data itself, as we
argue in Sect. 2.3, shows that the CO is optically thin. Because of the latter point, the
radial profiles of density and temperature are coupled and the analysis is complicated by
the small angular size of the disk.
For the first calculation, we take the flux densities given in Tables 2 and 4. We assume the
![]() abundance found in TMC1
abundance found in TMC1
![]() )
and a
standard dust absorption coefficient with a gas-to-dust ratio of 100 (Beckwith et al. 1990,
see also Table 3). The kinetic temperature is derived from the CO model: we use
)
and a
standard dust absorption coefficient with a gas-to-dust ratio of 100 (Beckwith et al. 1990,
see also Table 3). The kinetic temperature is derived from the CO model: we use
![]() K as a mean value throughout the disk. A lower limit on the depletion
factor
K as a mean value throughout the disk. A lower limit on the depletion
factor
![]() is to a first order given by the ratio of the H2 mass estimates
derived from the thermal dust emission and the
is to a first order given by the ratio of the H2 mass estimates
derived from the thermal dust emission and the
![]()
![]() line.
line.
The mass derived from
![]()
![]() ,
,
![]() is gi- ven by:
is gi- ven by:
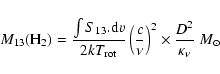 |
(1) |
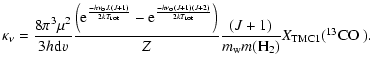 |
(2) |
Alternatively, we can also obtain this result using the physical disk model derived from
the
![]() interferometric data. The 30-m
interferometric data. The 30-m
![]() line flux from the disk is less than 0.12 Jy
line flux from the disk is less than 0.12 Jy
![]() (at
(at ![]() ). The best disk model derived from the
). The best disk model derived from the
![]() data predicts a flux
of 0.025 Jy
data predicts a flux
of 0.025 Jy
![]() in
in
![]()
![]() .
Hence, the
.
Hence, the
![]()
![]() data constrains the CO depletion f(
data constrains the CO depletion f(
![]() )
to be higher than f(
)
to be higher than f(
![]() )
/(0.12/0.025) = 40 (f(
)
/(0.12/0.025) = 40 (f(
![]() )
is given in Table 4).
)
is given in Table 4).
Using the same method for DM Tau,
![]() is found around 10 by Dartois et al. (2003). Moreover, contrary to BP Tau, the
is found around 10 by Dartois et al. (2003). Moreover, contrary to BP Tau, the
![]()
![]() emission in the DM Tau disk is
strongly optically thick.
emission in the DM Tau disk is
strongly optically thick.
In the modelling, the total disk mass, the CO depletion factor and therefore n100 the
density at 100 AU are derived from the fit of the continuum data (Sect. 3 and Table 4). First of all, the continuum fit at 3.4 and 1.3 mm reveals that the dust
spectral index ![]() has a value of
has a value of
![]() ,
somewhat smaller than the average
found for other T Tauri disks (
,
somewhat smaller than the average
found for other T Tauri disks (
![]() ,
Dutrey et al. 1996). The disk mass
is relatively low (
,
Dutrey et al. 1996). The disk mass
is relatively low (![]()
![]() ). This low value is a result of a lower
density, rather than of the small size of the disk. Surface density laws have been
estimated in some disks from the optically thin dust emission by Dutrey et al. (1996),
whose results suggest that the dust distribution follows shallow surface density laws with
). This low value is a result of a lower
density, rather than of the small size of the disk. Surface density laws have been
estimated in some disks from the optically thin dust emission by Dutrey et al. (1996),
whose results suggest that the dust distribution follows shallow surface density laws with
![]() and typical values for
and typical values for
![]() around
around
![]() cm-2.
Compared to these disks (most of them also possess large CO disks),
cm-2.
Compared to these disks (most of them also possess large CO disks),
![]() in BP Tau is significantly lower, by a factor 40, but the surface density exponent is similar (
in BP Tau is significantly lower, by a factor 40, but the surface density exponent is similar (
![]() ).
).
Taking q=0.3 as the most probable value, the
temperature at 100 AU is
T100 = 52 K. However, the rather large uncertainty on qallows T100 to vary from 35 (for q=0.5) to >100 K (for q<0) (see
Fig. 4). It is possible in special cases to have q<0 around the disk
mid-plane (e.g. Fig. 3 from D'Alessio et al. 1999). However, since the CO J=2-1 emission is
optically thin, it samples the whole disk, and measures a (vertically) averaged temperature
gradient, for which q is unlikely to be negative. Marginally lower temperatures can be
obtained by allowing the depletion
![]() to be
to be ![]() 150 (see
Fig. 4). This is somewhat hot for a K7 star: the expected blackbody temperature
at 100 AU would be only 26-38 K, depending on the assumed disk flaring. The same analysis
performed on the CO disks of the K 7 star GM Aur (Dutrey et al. 1998) or the M 1 star
DM Tau
(Guilloteau & Dutrey 1998) provide
150 (see
Fig. 4). This is somewhat hot for a K7 star: the expected blackbody temperature
at 100 AU would be only 26-38 K, depending on the assumed disk flaring. The same analysis
performed on the CO disks of the K 7 star GM Aur (Dutrey et al. 1998) or the M 1 star
DM Tau
(Guilloteau & Dutrey 1998) provide
![]() K,
as expected for flared passive disks heated by the central stars. In typical disks, because
of the opacity of the CO line, T100 is representative of a region located at about 2-4
scale heights above the disk mid-plane (Dartois et al. 2003), and the temperature in the
disk plane is lower (
K,
as expected for flared passive disks heated by the central stars. In typical disks, because
of the opacity of the CO line, T100 is representative of a region located at about 2-4
scale heights above the disk mid-plane (Dartois et al. 2003), and the temperature in the
disk plane is lower (![]() 13 K from Dartois et al. 2003, see also d'Alessio et al. 1999). In BP Tau where the CO emission is partly optically thin, T100 is closer to an
average value throughout the disk vertical structure. The BP Tau disk thus appears hotter
than the others.
13 K from Dartois et al. 2003, see also d'Alessio et al. 1999). In BP Tau where the CO emission is partly optically thin, T100 is closer to an
average value throughout the disk vertical structure. The BP Tau disk thus appears hotter
than the others.
Neither the viscous heating, which may only be efficient within the 10-20 central AU, nor
the differences in stellar luminosities between BP Tau (
![]() )
and GM Aur (
)
and GM Aur (
![]() ,
SDG) are enough to explain such a value for T100. It is more likely due to a
combination of several effects linked to the low angular resolution which complicates the
CO analysis and does not allow us to provide accurate estimates of q (see Sect. 3).
However, it also might be partly related to the lower disk mass of BP Tau, and to active
grain growth. If the dust opacity in the visible and near IR is much smaller in BP Tau than
either in GM Aur and DM Tau, because of the lower disk mass and perhaps also because of
different grain properties, it is possible that the "superheated'' layer (Chiang &
Goldreich 1997) occupies a significant fraction of the disk for BP Tau. In the extreme
limit where
,
SDG) are enough to explain such a value for T100. It is more likely due to a
combination of several effects linked to the low angular resolution which complicates the
CO analysis and does not allow us to provide accurate estimates of q (see Sect. 3).
However, it also might be partly related to the lower disk mass of BP Tau, and to active
grain growth. If the dust opacity in the visible and near IR is much smaller in BP Tau than
either in GM Aur and DM Tau, because of the lower disk mass and perhaps also because of
different grain properties, it is possible that the "superheated'' layer (Chiang &
Goldreich 1997) occupies a significant fraction of the disk for BP Tau. In the extreme
limit where
![]() ,
and with
,
and with
![]() ,
the whole disk could be
heated above the blackbody temperature.
,
the whole disk could be
heated above the blackbody temperature.
To do so, only a tiny fraction of small grains should still be in the disk. Small grains of
![]()
![]() m have
m have
![]() cm2 g-1 (for dust only,
Chiang & Goldreich 1997). Assuming
cm2 g-1 (for dust only,
Chiang & Goldreich 1997). Assuming
![]() ,
an opacity
,
an opacity
![]() at the disk
plane is reached for
at the disk
plane is reached for
![]() g cm-2 (of small grains), which
corresponds to a mass of small grains around
g cm-2 (of small grains), which
corresponds to a mass of small grains around
![]() .
Since the total dust mass
derived from mm continuum emission is
.
Since the total dust mass
derived from mm continuum emission is ![]()
![]() ,
the fraction of small
grains should not exceed
,
the fraction of small
grains should not exceed
![]() .
.
Unfortunately, imaging such an optically thin disk requires a very high sensitivity and is probably out of the possibilities of current adaptive optics systems on large telescopes. Detailed modelling of the BP Tau SED in the Visible and in the NIR may confirm or not our hypothesis.
Our analysis shows that the CO disk of BP Tau differs from the large CO and dust disks previously studied by mm interferometry. This is somewhat surprising because BP Tau presents in the optical and infrared all the characteristics of a CTTs, including a relatively strong accretion rate. At mm wavelengths, the BP Tau disk can be considered as atypical for the main following reasons:
Concerning point 3, we assume a gas-to-dust ratio of 100, as usually made in these kinds of studies. With a lower gas-to-dust ratio, the CO depletion should be accordingly less important with respect to H2. H2 itself could be depleted with respect to the dust but we cannot determine this without a direct detection of H2. The dust absorption coefficient remains also another possible source of uncertainty. Nevertheless, the CO depletion factor we have derived is significantly higher than in other TTauri disks. The low CO abundance may actually be a consequence of higher photodissociation resulting from the low H2 surface density. It cannot be due to condensation of CO on dust grains, since the mean temperature is higher than 50 K, well above the CO freezing temperature (17 K).
All these points argue in favor of a disk which has started to clear a significant fraction
of its primary gas and dust. This statement is reinforced by the relatively high
temperature of the disk, which might be explained by lower opacities of the dust in the
visible and in the near infrared. It is interesting to note that the only other known disk
with similar outer disk properties (small outer radius and small mm flux) has been
discovered around V 836 Tau, an object presenting all the characteristics of being in the
stage of inner disk dissipation from the optical data (Duvert et al. 2000). The BP Tau disk is however different because it still has a very active inner disk. This suggests
that inner and outer disks may not begin to dissipate simultaneously. Finally, the CO content of BP Tau cannot result from evaporation of proto-comets. Large active comets such
as Hale-Bopp contain about 1036 evaporated CO molecules (Biver et al. 1999). Since the
BP Tau disk mass is
![]() and the CO abundance
and the CO abundance
![]() ,
the disk
contains about
,
the disk
contains about
![]() CO molecules. Thus a few times 1011 large comets like Hale
Bopp would be required. Therefore the CO gas must be the remnant of the primordial nebula.
CO molecules. Thus a few times 1011 large comets like Hale
Bopp would be required. Therefore the CO gas must be the remnant of the primordial nebula.
Using the standard method we used to study Class II protoplanetary disks, we have analyzed
the
![]()
![]() and continuum observations at 3.4 and 1.3 mm of BP Tau. We find that:
and continuum observations at 3.4 and 1.3 mm of BP Tau. We find that:
Only ALMA has the potential to enable systematic surveys of such objects around stars
having a continuum flux at 1.3 mm of order
![]() mJy or less.
mJy or less.
Acknowledgements
We acknowledge all the Plateau de Bure IRAM staff for their help during the observations. We thank Claude Bertout for useful discussion on the distance measurement with Hipparcos, and Jacques Crovisier for discussion on the CO in comets. The work of M.S. was supported in part by NSF Grant 98-19694.