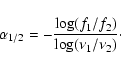 |
(2) |
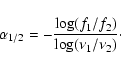 |
(2) |
To compare these indices with those from the literature, shifts
due to the use of different reference energies have to be taken into
account. It can be shown that these shifts are small as long as the
spectral shape within each band can be approximated by a single power
law and the spectrum is not curved.
Because the radio spectra are
flat (
![]() ), the flux does not change when different reference frequencies
are chosen in the radio domain. But by increasing the radio reference
frequency, the
), the flux does not change when different reference frequencies
are chosen in the radio domain. But by increasing the radio reference
frequency, the
![]() and
and
![]() indices steepen.
For example, if the reference
frequency is changed from 1.4 to 5 GHz the radio-X-ray index changes
by 6%:
indices steepen.
For example, if the reference
frequency is changed from 1.4 to 5 GHz the radio-X-ray index changes
by 6%:
![]() .
If our spectral indices are compared with those
using a larger X-ray reference energy, similar values for
.
If our spectral indices are compared with those
using a larger X-ray reference energy, similar values for
![]() and
and
![]() are expected. Because of
are expected. Because of
![]() ,
the
expected flux at a higher energy is lower and the flux ratios
increase. At the same time however, the frequency interval increases by about
the same factor, if we assume
,
the
expected flux at a higher energy is lower and the flux ratios
increase. At the same time however, the frequency interval increases by about
the same factor, if we assume
![]() ,
which is a good
approximation for the mean X-ray spectral energy index of BL Lac
objects
The same reasoning applies for the optical region, where
,
which is a good
approximation for the mean X-ray spectral energy index of BL Lac
objects
The same reasoning applies for the optical region, where
![]() ,
and larger changes of the relevant indices are not
expected.
,
and larger changes of the relevant indices are not
expected.
![]() overall spectral
indices:
overall spectral
indices:
![]() ,
,
![]()
![]() ,
,
![]() ,
if compared to
Wolter et al. (1998), Laurent-Muehleisen et al. (1999), and Beckmann et al. (2002).
,
if compared to
Wolter et al. (1998), Laurent-Muehleisen et al. (1999), and Beckmann et al. (2002).
The region
in the
![]() plane, which is covered by the HRX-BL Lac
sample, is shown in Fig. 3.
The
center of the area covered by this sample is similar to that of the
EMSS BL Lacs (see Padovani & Giommi 1995) though a larger range in
plane, which is covered by the HRX-BL Lac
sample, is shown in Fig. 3.
The
center of the area covered by this sample is similar to that of the
EMSS BL Lacs (see Padovani & Giommi 1995) though a larger range in
![]() and
and
![]() is covered.
is covered.
In order to get a more physical description of the spectral energy
distribution of the BL Lac objects, we used a simple model to fit the
synchrotron branch of the BL Lac. This has the advantage of describing
the SED with one parameter (the peak frequency) instead of a set of
three parameters (
![]() ,
,
![]() ,
and
,
and
![]() ). It has been shown
by several authors that the synchrotron branch of the BL Lac SED is
well approximated by a parabolic fit in the
). It has been shown
by several authors that the synchrotron branch of the BL Lac SED is
well approximated by a parabolic fit in the
![]() plane
(cf. Landau et al. 1986; Comastri et al. 1995; Sambruna et al. 1996; Fossati et al. 1998). In this way the peak position (
plane
(cf. Landau et al. 1986; Comastri et al. 1995; Sambruna et al. 1996; Fossati et al. 1998). In this way the peak position (
![]() ), the
total luminosity and the total flux of the synchrotron
emission can be derived. We chose the parameterization using
fluxes
), the
total luminosity and the total flux of the synchrotron
emission can be derived. We chose the parameterization using
fluxes
![]() .
Using luminosities instead of fluxes would change the absolute
constant c only, leaving the position of the peak frequency unaffected.
.
Using luminosities instead of fluxes would change the absolute
constant c only, leaving the position of the peak frequency unaffected.
A set of physical parameters which are correlated to the peak frequency are the luminosities in the different wavelength regions. To compute luminosities for all objects, the unknown redshifts were set to z = 0.3 which is the mean value for the HRX-BL Lac sample. While the luminosities LR in the radio, LK in the near infrared, and LB in the optical region are decreasing with increasing peak frequency, the situation at X-ray energies is the other way round (as reported also by e.g. Mei et al. 2002; Beckmann 1999a).
The details about the correlation analysis are listed in Table 5, including the confidence level of the correlations.
| region | rxy Pearson | confidence level | linear regressiona |
| coefficient | of correlation | ||
| radio
|
-0.23 | >97% |
|
| near IR (K-band) | -0.28 |
|
|
| optical (B-band) | -0.37 | >99.9% |
|
| X-ray
|
+0.51 | >99.9% |
|
| total (radio - X-ray) | -0.12 |
|
|
a Luminosities in
b The lower confidence level results from the lower number of objects (52) with known K-band magnitudes. The other correlations are using the 104 BL Lacs of the extended sample. |
The total luminosity
![]() within the synchrotron branch has been
derived by integrating the spectral energy distribution between the
radio and the X-ray band. This is a reasonable approximation as
long as the peak frequency is below 1 keV (
within the synchrotron branch has been
derived by integrating the spectral energy distribution between the
radio and the X-ray band. This is a reasonable approximation as
long as the peak frequency is below 1 keV (
![]() ), but
systematically underestimates
), but
systematically underestimates
![]() if the peak frequency is
shifted beyond
if the peak frequency is
shifted beyond
![]() .
The relation of peak frequency with the
total luminosities does not show a clear correlation.
.
The relation of peak frequency with the
total luminosities does not show a clear correlation.
Copyright ESO 2003